

Up: A 2.4-12 m spectrophotometric study quiescence
Subsections
3 Results and discussion
![\begin{figure}
\par\includegraphics[width=7cm,clip]{figCyg_spectr_draine.ps}\hspace*{2mm}
\includegraphics[width=7cm,clip]{figCyg_spectr_lutz.ps}
\end{figure}](/articles/aa/full/2002/48/aa2763/Timg27.gif) |
Figure 2:
Dereddened spectrum of Cygnus X-3 using either Draine (1989) law (left) or
Lutz et al. (1996) law (right). The asterisks (*) in
the lower panel represent the Ogley et al. (2001) ISOCAM results, after dereddening
by Draine (1989) (left) and Lutz (right). |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{draine.eps}\hspace*{2mm}
\includegraphics[width=9cm,clip]{figfitcontCygX3Lutz.ps}
\end{figure}](/articles/aa/full/2002/48/aa2763/Timg28.gif) |
Figure 3:
Best fitting of the two dereddened spectra of Cygnus X-3 shown in Fig. 2. |
The dereddening of the Cygnus X-3 spectrum is made using
either Lutz et al. (1996) or Draine (1989) laws, and using an
absorption value of AV= 20 mag (van Kerkwijk et al. 1996); the two
dereddened spectra are shown in Fig. 2. They have clearly
different shapes, but since the molecular composition of the
absorbing material on the line of sight to Cygnus X-3 is
unknown, we cannot choose between these two laws.
The spectral fitting of the dereddened spectra is shown in
Fig. 3 and the results are given in Table 2. With the
Lutz et al. (1996) law the best fit is obtained with a unique power law
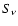
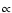
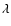
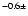 0.30.4 with a
reduced
0.30.4 with a
reduced 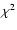 = 4.3 in the 2.4-12
= 4.3 in the 2.4-12 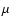 m range, in good
agreement with the Ogley et al (2001) result. With the
Draine (1989) law the best fit is obtained with the sum of two
components: a power law with slope
m range, in good
agreement with the Ogley et al (2001) result. With the
Draine (1989) law the best fit is obtained with the sum of two
components: a power law with slope 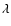
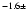 0.2 and a black body at T=250 K with a radius of 5000
0.2 and a black body at T=250 K with a radius of 5000 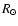 at a
distance of 10 kpc, (reduced
at a
distance of 10 kpc, (reduced 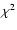 = 4.2 between 2.4 and
12
= 4.2 between 2.4 and
12 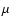 m), a hint of the presence of circumstellar dust. The
power law part of the continuum spectrum
(
m), a hint of the presence of circumstellar dust. The
power law part of the continuum spectrum
(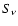
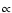
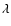
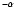 )
can be explained by
free-free emission of an expanding wind in the intermediate case
between optically thick (
)
can be explained by
free-free emission of an expanding wind in the intermediate case
between optically thick (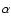 = 2) and optically thin
(
= 2) and optically thin
(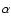
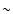 0) regimes (Wright & Barlow 1975).
0) regimes (Wright & Barlow 1975).
Using the ISO archive data we have analysed the SWS
spectra of four Wolf-Rayet stars: WR 147 (WN8+B0.5), WR 136
(WN6b), WR 134 (WN6) and WR 78 (WN7) whose main
characteristics are given in Table 3. We compare them to the
Cygnus X-3 spectrum, after smoothing the SWS spectra to the
resolution of the ISOPHOT-S instrument (using an IDL routine
of B. Schulz dowloaded from the Home Page of the ISO Data
Centre at Vilspa). The observed WR spectra are shown in Fig.
4 on top of the observed Cygnus X-3 spectrum; the
identification of the emission lines is from Morris et al. (2000).
a Dereddening with Draine (1989) law.
b Dereddening with Lutz et al. (1996) law; fit between 2.4-12 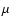 m. m.
c Fit between 2.4-6.5 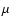 m. m.
d Fit between 2.4-12 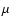 m. m.
e Fit between 2.4-8 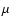 m. m.
|
The dereddened spectra of the Wolf-Rayet stars, using
either the Draine (1989) law or the Lutz et al. (1996) law with the AV shown in Table 3, have been fitted with power law slopes
given in Table 2. Wolf-Rayet stars emit free-free continuum
radiation from their extended ionized stellar wind envelopes and
the different slopes reflect different conditions in the wind
(Williams et al. 1997). It is noticeable that the mean continuum flux
density of Cygnus X-3 is the same (within a factor 1.5 at
4.7 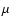 m as seen in Table 2) as that of the four WR stars when
their flux density is rescaled to a Cygnus X-3 distance of
10 kpc.
m as seen in Table 2) as that of the four WR stars when
their flux density is rescaled to a Cygnus X-3 distance of
10 kpc.
Table 3:
The four Wolf-Rayet stars observed with ISO/SWS.
|
Star |
Type |
Binarity |
Distance |
AVa |
Reference |
TDTNUM |
|
WR 78 |
WN7ha WNL |
No |
2.0 kpc |
1.48-1.87 |
Crowther et al. (1995a) |
45800705 |
| WR 134 |
WN6 |
possible |
 2.1 kpc 2.1 kpc |
1.22-1.99 |
Morel et al. (1999) |
17601108 |
| WR 136 |
WN6b(h) WNE-sb |
possible |
1.8 kpc |
1.35-2.25 |
Stevens & Howarth (1999) |
38102211 |
| WR 147 |
WN8(h) WNL |
B0.5V at 0.554'' |
630 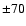 pc pc |
11.2 |
Morris et al. (1999, 2000) |
33800415 |
a From van der Hucht (2001) except for WR 147.
b From Crowther et al. (1995b).
|
![\begin{figure}
\par\includegraphics[width=13cm,clip]{figCygWRspectra_obs.ps}\end{figure}](/articles/aa/full/2002/48/aa2763/Timg37.gif) |
Figure 4:
Observed spectra of Cygnus X-3 and four Wolf-Rayet stars (not dereddened). An
arbitrary vertical offset has been added to the WR spectra for clarity. The
identification of the emission lines is from Morris et al. (2000). |
The comparison between the Cygnus X-3 spectrum and
that of the Wolf-Rayet WR 147 at 10 kpc is shown in Fig. 5
after dereddening with the Draine (1989) law (left) and with
the Lutz et al. (1996) law (right). The WR 147 spectrum appears
as the closest WR one to the Cygnus X-3 spectrum, with almost
the same mean flux density at 10 kpc and the same power law
slope (whithin the statistical errors).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{figCygX3Draine-WR147Draine...
...m}
\includegraphics[width=8.4cm,clip]{figCygX3Lutz-WR147Lutz-lin.ps}\end{figure}](/articles/aa/full/2002/48/aa2763/Timg38.gif) |
Figure 5:
Comparison between the spectral energy distribution of Cygnus X-3 and
the one of WR 147 when rescaled at 10 kpc: both dereddened with
Draine (1989) law (left) and the Lutz et al. (1996) law (right). |
We note that WR 147 is known as a colliding-wind binary that has been
spatially resolved (Williams et al. 1997; Skinner et al. 1999), with a separation on the sky large
enough for the wind-wind collision
zone between the stars to be resolved at near-infrared and radio (Williams et al. 1997),
and X-ray energies (Pittard et al. 2002). The spectral energy distribution of
WR 147 in the 0.5 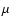 m to 2 mm wavelength range
(including all components) shown by Williams et al. (1997) is dominated by the free-free
emission from the stellar wind of the WN8 star; in the 2 to 10
m to 2 mm wavelength range
(including all components) shown by Williams et al. (1997) is dominated by the free-free
emission from the stellar wind of the WN8 star; in the 2 to 10 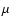 m
range these authors find
m
range these authors find 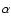 = 1.0, in good agreement with our
ISOPHOT-S measurement (when dereddened with the Lutz et al. 1996 law); and in
the mid-infrared to radio range they find
= 1.0, in good agreement with our
ISOPHOT-S measurement (when dereddened with the Lutz et al. 1996 law); and in
the mid-infrared to radio range they find 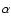 = 0.66.
= 0.66.
The measured 4.3 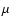 m line flux above the continuum in the
Cygnus X-3 spectrum is 58
m line flux above the continuum in the
Cygnus X-3 spectrum is 58 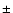 11 mJy (dereddening with the Draine 1989 law), and 126
11 mJy (dereddening with the Draine 1989 law), and 126 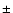 25 mJy (dereddening with the
Lutz et al. 1996 law), using respectively
25 mJy (dereddening with the
Lutz et al. 1996 law), using respectively 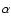 = 1.6 and
= 1.6 and
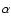 = 0.6, the best fitted continuum slopes as given in
Table 3, both detections being at more than 4.3
= 0.6, the best fitted continuum slopes as given in
Table 3, both detections being at more than 4.3 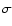 .
This
line is interpreted as the HeI (3p-3s) line at 4.295
.
This
line is interpreted as the HeI (3p-3s) line at 4.295 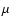 m, a
prominent line in the WR 147 (WN8+B0.5) spectrum as seen in
Morris et al. (2000) and in Fig. 4. Again WR 147 appears as the closest
WR to Cygnus X-3 as being the only WR in our sample with a HeI
emission line at 4.3
m, a
prominent line in the WR 147 (WN8+B0.5) spectrum as seen in
Morris et al. (2000) and in Fig. 4. Again WR 147 appears as the closest
WR to Cygnus X-3 as being the only WR in our sample with a HeI
emission line at 4.3 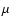 m, the only line clearly seen in our
Cygnus X-3 data. The other expected He lines at 2.62, 3.73, 4.05,
7.46 and 10.5
m, the only line clearly seen in our
Cygnus X-3 data. The other expected He lines at 2.62, 3.73, 4.05,
7.46 and 10.5 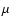 m are not detected, probably due to the
faintness of the object, at the limits of the instrument's
sensitivity. We note (Fig. 4) that the second highest peak in the
SS-part of the Cyg X-3 spectrum is at 3.73
m are not detected, probably due to the
faintness of the object, at the limits of the instrument's
sensitivity. We note (Fig. 4) that the second highest peak in the
SS-part of the Cyg X-3 spectrum is at 3.73 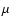 m, and there are
also local maxima at 4.05 and 10.5
m, and there are
also local maxima at 4.05 and 10.5 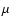 m. These expected lines
are all blended with H lines and the absence of H observed by
van Kerkwijk et al. (1996) in the I and K band spectra of Cygnus X-3 could
explain the weakness or absence of these lines in our data.
m. These expected lines
are all blended with H lines and the absence of H observed by
van Kerkwijk et al. (1996) in the I and K band spectra of Cygnus X-3 could
explain the weakness or absence of these lines in our data.
We note that the Br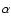 +HeI-II line at 4.05
+HeI-II line at 4.05 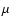 m is not
detected in Cygnus X-3 in quiescence, but is present in the four
Wolf-Rayet stars. Strong HeI and HeII lines have been previously
observed in the K-range in Cygnus X-3 during quiescence
(van Kerkwijk et al. 1992; 1996, Fender et al. 1999). These lines have been interpreted
(van Kerkwijk et al. 1996; Cherepashchuk & Moffat 1994), as emission from the wind of a massive companion
star to the compact object, and Fender et al. (1999) suggest that the best
candidate is probably an early WN Wolf-Rayet star. We note that the
close match we have found between the mid-infrared luminosity and the
spectral energy distribution, the HeI emission line in Cygnus X-3 in
quiescence, and that of the WR 147, is consistent with a
Wolf-Rayet like companion of WN8 type to the compact object in
Cygnus X-3, a later type than suggested by earlier works
(van Kerkwijk et al. 1996; Fender et al. 1999; Hanson et al. 2000).
m is not
detected in Cygnus X-3 in quiescence, but is present in the four
Wolf-Rayet stars. Strong HeI and HeII lines have been previously
observed in the K-range in Cygnus X-3 during quiescence
(van Kerkwijk et al. 1992; 1996, Fender et al. 1999). These lines have been interpreted
(van Kerkwijk et al. 1996; Cherepashchuk & Moffat 1994), as emission from the wind of a massive companion
star to the compact object, and Fender et al. (1999) suggest that the best
candidate is probably an early WN Wolf-Rayet star. We note that the
close match we have found between the mid-infrared luminosity and the
spectral energy distribution, the HeI emission line in Cygnus X-3 in
quiescence, and that of the WR 147, is consistent with a
Wolf-Rayet like companion of WN8 type to the compact object in
Cygnus X-3, a later type than suggested by earlier works
(van Kerkwijk et al. 1996; Fender et al. 1999; Hanson et al. 2000).
As Ogley et al. (2001), we evaluated the mass loss rate of this free-free emitting wind,
following the Wright & Barlow (1975) formula (8) giving the emitted flux density (in Jansky)
by a stellar wind assumed to be spherical, homogeneous and at a constant velocity:
where D is the distance to the source in kpc. It gives:
(where 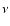 is in GHz).
With an assumed distance D=10 kpc, a Gaunt factor g=1, a flux density
deduced from the continuum fitting (Lutz et al. 1996 law, Fig. 3) of
is in GHz).
With an assumed distance D=10 kpc, a Gaunt factor g=1, a flux density
deduced from the continuum fitting (Lutz et al. 1996 law, Fig. 3) of 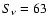 mJy at
6.75
mJy at
6.75 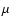 m (
m (
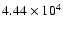 GHz),
and for a WN-type wind (where the mean atomic weight per nucleon
GHz),
and for a WN-type wind (where the mean atomic weight per nucleon 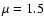 ,
the number of free electrons per nucleon
,
the number of free electrons per nucleon
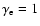 and the mean ionic charge
Z=1), and with a velocity of
and the mean ionic charge
Z=1), and with a velocity of
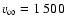 km s-1 (van Kerkwijk 1996),
one obtains
km s-1 (van Kerkwijk 1996),
one obtains
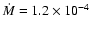
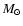 yr-1. This is in agreement with
the mass transfer rate estimated by van Kerkwijk et al. (1996) and (within a
factor of 2) by Ogley et al. (2001).
This result is in good agreement with the recent revised WN mass-loss rate estimates,
which have been lowered by a factor of 2 or 3 due to clumping in the wind (Morris et al. 1999).
Note that if we assume a flattened disc-like wind as reported by Fender et al. (1999),
who detected double peaked emission lines, the mass loss rate decreases but remains
within less than a factor of 2 of that obtained in the spherical case, in all but
extreme cases when the ratio of structural length scales exceeds about 10,
as shown by Schmid-Burgk (1982).
It is noticeable that Churchwell et al. (1992), considering the radio flux from the
southern, stellar wind component of WR 147, derived a mass-loss rate of
yr-1. This is in agreement with
the mass transfer rate estimated by van Kerkwijk et al. (1996) and (within a
factor of 2) by Ogley et al. (2001).
This result is in good agreement with the recent revised WN mass-loss rate estimates,
which have been lowered by a factor of 2 or 3 due to clumping in the wind (Morris et al. 1999).
Note that if we assume a flattened disc-like wind as reported by Fender et al. (1999),
who detected double peaked emission lines, the mass loss rate decreases but remains
within less than a factor of 2 of that obtained in the spherical case, in all but
extreme cases when the ratio of structural length scales exceeds about 10,
as shown by Schmid-Burgk (1982).
It is noticeable that Churchwell et al. (1992), considering the radio flux from the
southern, stellar wind component of WR 147, derived a mass-loss rate of
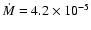
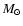 yr-1 and Williams et al. (1997) found a
non spherically symetric stellar wind with a mass-loss rate of
yr-1 and Williams et al. (1997) found a
non spherically symetric stellar wind with a mass-loss rate of
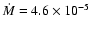
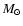 yr-1.
Since the length of this spectrophotometric measurement was comparable
to the 4.8 h modulation period seen in the K-band at the level of 5
yr-1.
Since the length of this spectrophotometric measurement was comparable
to the 4.8 h modulation period seen in the K-band at the level of 5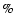 (Fender et al. 1995), we attempted to detect this modulation in our
data set. The points in Fig. 6 refer to the average for the
whole (2-12
(Fender et al. 1995), we attempted to detect this modulation in our
data set. The points in Fig. 6 refer to the average for the
whole (2-12 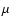 m) spectrum. Although, as shown in Fig. 6,
the measurement uncertainty of the orbitally
phase-resolved spectra was relatively high, the data clearly exclude
periodic variations of amplitude higher than 15
m) spectrum. Although, as shown in Fig. 6,
the measurement uncertainty of the orbitally
phase-resolved spectra was relatively high, the data clearly exclude
periodic variations of amplitude higher than 15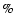 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{figCyg_lightcurve.ps}
\end{figure}](/articles/aa/full/2002/48/aa2763/Timg50.gif) |
Figure 6:
Flux density in the 2.4-12 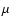 m range versus Cygnus X-3
orbital phase. m range versus Cygnus X-3
orbital phase. |
Figure 7 shows the mean flux density of Cygnus X-3 on
MJD 50180.3 from radio to hard X-rays. The quiescent state observed
in the mid-infrared range with ISO
was also seen during monitoring radio observations of Cygnus X-3 with the
Ryle telescope (Mullard Radio Observatory, Cambridge) shortly
before and after the ISO observations, the mean flux density at 15 GHz being
about 120 mJy (Pooley 1999), and with the Green Bank Interferometer (GBI)
monitoring program (McCollough et al. 1999) during a quiescent period
before the ISO observations,
the mean flux densities being 80 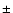 30 mJy at 2.25 GHz and
125
30 mJy at 2.25 GHz and
125 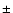 60 mJy at 8.3 GHz and the spectral index
60 mJy at 8.3 GHz and the spectral index 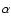 = 0.3
= 0.3 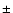 0.1 .
These flux densities are at least one order of
magnitude higher than that observed during the quench periods of very low
radio emission preceeding the major flares of Cygnus X-3 (McCollough et al. 1999). In fact, this quiescent
state was still present in 1996 May, June and July (Fender et al. 1999).
0.1 .
These flux densities are at least one order of
magnitude higher than that observed during the quench periods of very low
radio emission preceeding the major flares of Cygnus X-3 (McCollough et al. 1999). In fact, this quiescent
state was still present in 1996 May, June and July (Fender et al. 1999).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{figCygX3radioXnouv.ps}
\end{figure}](/articles/aa/full/2002/48/aa2763/Timg51.gif) |
Figure 7:
Quasi-simultaneous observations of Cygnus X-3 in the radio, infrared,
soft and hard X-rays on April 7, 1996, averaged over the orbital phase; the
ISOPHOT-S spectrum is dereddened with the Lutz et al. (1996) law and rebinned to the resolution
of 0.3 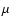 m;
note that the GBI was dormant after 1996 April 1 till November 1996, and
that the given flux densities (in dash lines) are mean values during the quiescent period
March 17 to April 1, 1996. m;
note that the GBI was dormant after 1996 April 1 till November 1996, and
that the given flux densities (in dash lines) are mean values during the quiescent period
March 17 to April 1, 1996. |
In the X-ray range, at the same epoch, the
 XTE/All Sky Monitor count
rate was
XTE/All Sky Monitor count
rate was  7.5 count s-1 corresponding to a
mean flux of
7.5 count s-1 corresponding to a
mean flux of  1 mJy from 2 to 12 keV (see XTE archive and Levine et al. 1996), and
the BATSE instrument on board the Compton Gamma Ray Observatory observed a mean photon flux
of 0.039 count s-1 corresponding to a flux density of 0.04 mJy in the
20-100 keV range. Thus the mid-infrared
continuum spectrum whose shape is explained by thermal free-free emission in an
expanding wind has a different origin than the non-thermal radio emission
and the hard X-ray emission which are closely coupled (Mioduszewski et al. 2001; Choudhury et al. 2002).
1 mJy from 2 to 12 keV (see XTE archive and Levine et al. 1996), and
the BATSE instrument on board the Compton Gamma Ray Observatory observed a mean photon flux
of 0.039 count s-1 corresponding to a flux density of 0.04 mJy in the
20-100 keV range. Thus the mid-infrared
continuum spectrum whose shape is explained by thermal free-free emission in an
expanding wind has a different origin than the non-thermal radio emission
and the hard X-ray emission which are closely coupled (Mioduszewski et al. 2001; Choudhury et al. 2002).


Up: A 2.4-12 m spectrophotometric study quiescence
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=7cm,clip]{figCyg_spectr_draine.ps}\hspace*{2mm}
\includegraphics[width=7cm,clip]{figCyg_spectr_lutz.ps}
\end{figure}](/articles/aa/full/2002/48/aa2763/Timg27.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{draine.eps}\hspace*{2mm}
\includegraphics[width=9cm,clip]{figfitcontCygX3Lutz.ps}
\end{figure}](/articles/aa/full/2002/48/aa2763/Timg28.gif)
![\begin{figure}
\par\includegraphics[width=13cm,clip]{figCygWRspectra_obs.ps}\end{figure}](/articles/aa/full/2002/48/aa2763/Timg37.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{figCygX3Draine-WR147Draine...
...m}
\includegraphics[width=8.4cm,clip]{figCygX3Lutz-WR147Lutz-lin.ps}\end{figure}](/articles/aa/full/2002/48/aa2763/Timg38.gif)
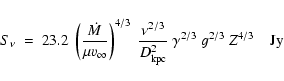
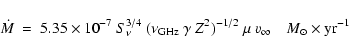
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{figCyg_lightcurve.ps}
\end{figure}](/articles/aa/full/2002/48/aa2763/Timg50.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{figCygX3radioXnouv.ps}
\end{figure}](/articles/aa/full/2002/48/aa2763/Timg51.gif)