A&A 396, 715-722 (2002)
DOI: 10.1051/0004-6361:20021388

The FERRUM Project: Experimental oscillator strengths of the UV 8 multiplet and other UV transitions from the y6P levels of Fe II

J. C. Pickering1 - M. P. Donnelly2 - H. Nilsson3 - A. Hibbert2 - S. Johansson3


1 - Physics Department, Blackett Laboratory, Imperial College, London SW7 2BZ, UK
2 - Department of Mathematics, Queen's University of Belfast, Northern Ireland
3 - Atomic Astrophysics, Lund Observatory, Lund University, PO Box 43, SE-22100 Lund, Sweden

Received 13 May 2002 / Accepted 20 September 2002

Abstract
We report on experimental branching fractions (BFs) for 19 transitions from the three 3d5(6S)4s4p(3P) y6P levels in Fe II, measured in Fourier transform spectra of a Penning discharge lamp and a hollow cathode lamp. The transition wavelengths span the interval between 1600 and 2850 Å. Absolute oscillator strengths (f-values) have been derived by combining the BFs with experimental radiative lifetimes recently reported in the literature. Theoretical f-values have been calculated using configuration interaction wavefunctions. The new experimental and theoretical f-values are compared with data available in the literature and in databases. The strongest lines measured belong to the UV 8 multiplet of Fe II, which has one ground state transition appearing as a prominent feature at 1608 Å in interstellar spectra. The line is accompanied by a satellite at 1611 Å due to a level mixing, which is discussed in the paper.

Key words: atomic data - line: identification - techniques: spectroscopic - stars: abundances - ISM: abundances


1 Introduction

Recent years have seen a dramatic increase in the need for accurate and complete atomic data especially in the VUV since the launch of the Hubble Space Telescope (HST) and its High Resolution Spectrograph (GHRS), replaced by the Space Telescope Imaging spectrograph (STIS) in 1999. The effect of the improvements in atomic data for the iron group elements can clearly be seen in the recent analysis of the spectrum of the chemically peculiar star $\chi $ Lupi (Leckrone et al. 1999), but there are still much atomic data that require new or improved measurements.

The UV spectrum of astrophysical plasmas at around 10 000 K is often dominated by Fe II lines, which can serve as a sensitive probe of the plasma conditions. Oscillator strengths (f-values) of weaker lines are needed for determinations of stellar abundances and those of the stronger lines for dilute plasmas. Transitions having large f-values but originating from higher energy levels may appear as weak absorption lines in stellar spectra and may be of great use in abundance analyses. The work we report in this paper is part of the collaborative FERRUM Project (Johansson 2001; Johansson et al. 2002 and references therein), in which f-values for transitions in the iron group elements are being measured. The aim of the FERRUM Project is to measure f-values for transitions in the ultraviolet and optical wavelength regions involving energy levels with an extended span in excitation energy.

In this paper we report on new measurements of branching fractions (BFs) for transitions from the three 3d5(6S)4s4p(3P) y6P fine structure levels in Fe II. The transitions fall in the UV to VUV spectral range between 1600 and 2850 Å (62 500-35 000 cm-1). The BFs are measured by high resolution Fourier transform spectrometry and combined with experimental radiative lifetimes reported by Li et al. (2000) to get absolute oscillator strengths for the lines. We have also calculated these f-values using configuration interaction wavefunctions. We compare our new measurements and calculations with previous work.

The first laboratory measurements of f-values in the UV8 multiplet (a6D-y6P) of Fe II were reported by Bergeson et al. (1996), who measured the $\lambda $1608 line using absorption spectroscopy. Mullman et al. (1997) applied the same method and measured f-values of six lines in the same multiplet, including the $\lambda $1608 line. In his extensive work on arc spectra of Fe II Moity (1983) published f-values of three lines with y6P as the upper term. These lines do not belong to the UV 8 multiplet, but to multiplets no. 176 and 190. The earliest measurement of the f-value of the $\lambda $1608 line was made by Shull et al. (1983) quoting an uncertainty of 30% in a curve-of-growth analysis of interstellar data from the Copernicus and International Ultraviolet Explorer (IUE) satellites. Cardelli & Savage (1995) discussed the reliability of a number of transition probabilities of Fe II lines between 1140 and 2600 Å and determined the f-value of the $\lambda $1608 line using HST/GHRS spectra of $\mu $ Col. They point out the importance of data for UV and VUV transitions of Fe II spanning a wide range of f-values. A set of accurate f-values allows the iron abundances in interstellar clouds to be studied with a large dynamic range in column density. Ekberg & Feldman (1993) presented transition probabilities in the 2000-2800 Å region measured in high resolution spectra of the solar chromosphere including two lines with y6P as upper term.

There have been a variety of theoretical calculations made for transitions from the three y6P levels by Nussbaumer et al. (1981), Fawcett (1988), Kurucz (2000), Nahar (1995), Raassen & Uylings (1998), and Donnelly & Hibbert (1999).

2 Intensity measurements

The iron spectra analysed in this work have been recorded with the VUV Fourier transform (FT) spectrometer at Imperial College, London, UK, and the UV FT spectrometer at Lund Observatory, Lund, Sweden (Thorne et al. 1987). Two different lamps were used as light sources: a Penning discharge (PD) lamp (Heise et al. 1994) and a hollow cathode (HC) lamp.

The spectra recorded with the FT-spectrometer at Imperial College were produced with a PD lamp run with a discharge current of 1.55 A and with a mixture of neon and argon as the carrier gas at a pressure of $1.7\times 10^{-3}$ mbar. The entrance window and beamsplitter of this instrument are made of MgF2 giving a detectable signal down to 1350 Å or 74 000 cm-1 (Thorne 1996). The optical path in this system was evacuated in order to reduce the O2 absorption at short wavelengths. Three spectral regions were recorded, 24 000-47 000 cm-1, 31 596-61 000 cm-1 and 51 000-66 000 cm-1. The spectra recorded with the Lund instrument were produced by a HC lamp in the spectral region 25 276-50 553 cm-1. The HC was run with 1.3 mbar of neon as the carrier gas and a discharge current of 1.2 A. The recorded interferograms were transformed with a computer code, GREMLIN, developed by J. W. Brault (Brault & Adams 1989). A Voigt profile was fitted to the lines and the integrated area under the profile was used as the line intensity. In order to obtain relative intensities, the lines were corrected for the instrument response. A deuterium lamp with a MgF2 window calibrated for spectral radiance by the Physikalisch-Technische Bundesanstalt (PTB), Berlin, Germany to within 8% (two standard deviations (2$\sigma$)) in the range 1660-3580 Å, and to within 12% in the range 1130-1660 Å, was used to determine the instrument response. The light source and the deuterium calibration lamp were placed at similar distances from the FT spectrometer entrance aperture. A mirror was used to switch between the lamps and a lens formed an enlarged image of both sources sufficiently close to the entrance aperture to ensure that they both used the full beamsplitter area. Any potential modulation drifts were allowed for by ensuring that calibration spectra were recorded immediately before and after each set of Fe interferogram coadds. The calibration spectra were compared to check that there had been no change in instrument response during the course of that particular interferogram acquisition. A more detailed description of how the calibration data from PTB was used to determine the instrument response curves is given in Pickering et al. (2001).

The intensities of the strong lines were checked for self absorption, but no indication of this effect was found. Since not all lines could be recorded in one spectrum, several different spectra had to be combined. The intensity scale was transferred from one spectrum to the other by measuring intensity ratios of lines appearing in both spectra in the overlapping regions.

3 Branching fractions and oscillator strengths

The BF of a line is defined as the transition probability ( $A_{\rm ul}$) of the line divided by the sum of the transition probabilities of all lines from the upper level "u''. Since the relative intensity of a line ( $I_{\rm ul}$) is proportional to $A_{\rm ul}$, the BF can be written as

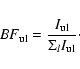\begin{displaymath}BF_{\rm ul}=\frac{I_{\rm ul}}{\Sigma_{l} I_{\rm ul}}\cdot \end{displaymath} (1)

Thus, a correct BF requires that the intensities of all lines from the upper level are measured. However, due to the large number of lines in complex spectra this is in most cases not possible. The weakest lines are not observed and some lines fall outside the recorded wavelength interval. The total intensity of such lines is estimated from theoretical predictions and collected in a residual BF. Transitions with $BF < 0.2\%$ could not be detected in the recorded iron spectra, and we used the calculations by Raassen & Uylings (1998) to estimate the residual. As can be seen in Table 4 the residual is small, about 1%, for all three y6P levels.

The BFs are converted to absolute transition probabilities $A_{\rm ul}$ by including the radiative lifetime ( $\tau_{\rm u}$) of the upper level according to

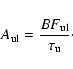\begin{displaymath}A_{\rm ul} = \frac{BF_{\rm ul}}{\tau_{\rm u}}\cdot \end{displaymath} (2)

The lifetimes have recently been measured by Li et al. (2000) using the laser induced fluorescence technique. The f-value can be derived from $A_{\rm ul}$ through

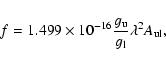\begin{displaymath}f=1.499 \times 10^{-16}\frac{g_{\rm u}}{g_{\rm l}}\lambda^{2}A_{\rm ul}, \end{displaymath} (3)

where $g_{\rm u}$ and $g_{\rm l}$ are the statistical weights for the upper and lower level, respectively, $\lambda $ is the wavelength in Å, and $A_{\rm ul}$ is in s-1.

The uncertainties of the f-values given in Table 4 are determined according to a recipe suggested by Sikström et al. (2002), and they include the uncertainty of the intensity measurements, the uncertainty arising when combining different spectral regions, the uncertainty in the intensity calibration of the spectra and the uncertainty in the lifetime measurements.

4 Theoretical calculations of oscillator strengths and transition probabilities


 

 
Table 1: Optimisation processes for the radial functions.
Orbital Configurations included Symmetry
4p 3d54s4p y6P$^{\rm o}$
5p 3d64p, 3d65p z6P$^{\rm o}$
6p 3d5msnp; m,n=4,5,6 y6P$^{\rm o}$
5s 3d54s4p, 3d55s4p z6P$^{\rm o}$
6s 3d5msnp; m,n=4,5,6 y6P$^{\rm o}$
4d 3d64p, 3d54s4p, 3d44s4p4d y6P$^{\rm o}$
5d 3d64p, 3d54s4p, 3d54p4d, 3d54p5d z6P$^{\rm o}$
4f 3d64s, 3d54p4f a6D


The oscillator strengths and transition probabilities calculated for the present work were obtained using configuration interaction (CI) wave functions of the form:

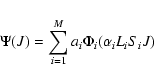\begin{displaymath}\Psi({J}) = \sum_{i=1}^{M} a_i \Phi_i(\alpha_iL_iS_iJ) \end{displaymath} (4)

generated by the code CIV3 (Hibbert 1975; Hibbert et al. 1991). For a specific choice of configuration state functions (CSFs) $\{\Phi_i\}$, where the angular momentum coupling scheme is defined by $\{\alpha_i\}$, the variationally optimal expansion coefficients $\{a_i\}$ are the eigenvector components of the diagonalized Hamiltonian whose typical element is Hij = $<\Phi_i\vert H\vert\Phi_j>$. The corresponding eigenvalue is an upper bound to the energy of the particular state. In particular, if the eigenvalues $\{E_i\}$ are ordered so that $E_1<E_2< \cdots$, then

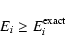\begin{displaymath}E_i \geq E_i^{\rm exact} \end{displaymath} (5)

is a consequence of the Hylleraas-Undheim theorem (Hylleraas & Undheim 1930).


 

 
Table 2: Optimised radial function parameters.
nl cjnl Ijnl $\xi_{jnl}$
5s 0.07552 1 19.02548
  -0.27401 2 9.35791
  0.57776 3 5.07754
  -1.03497 4 2.43824
  0.97510 5 1.29982
       
6s 0.06441 1 18.38583
  -0.16284 2 11.31165
  4.62987 3 2.03315
  -10.89075 4 2.13989
  7.93749 5 2.07416
  -1.98787 6 1.49966
       
4d 0.63694 3 5.15025
  -0.92313 4 1.90298
       
5d 0.44144 3 4.73722
  -0.77547 4 2.61070
  1.04299 5 1.28493
       
       
4p 5.70277 2 1.44819
  -1.88413 3 4.04161
  -3.85906 4 2.46303
       
5p 0.67165 2 2.83628
  -0.78204 3 4.21964
  5.72815 4 0.85910
  -6.48385 5 1.00256
       
6p 0.39729 2 14.25059
  -0.62942 3 6.78521
  8.20689 4 1.38066
  -18.08141 5 1.37593
  10.49901 6 1.42470
       
4f 1.00000 4 2.44380

Note: The radial functions of 1s, 2s, 2p, 3s, 3p, 3d, 4s are those given
in Table 2 of Clementi & Roetti (1974) for the ground state of Fe+.



 

 
Table 3: Configurations used.
a6D : 3d64s, 3d65s
  + 3d54s4d, 3d55s4d
  + 3d54p4f, 3d55p4f, 3d44s4p4f
  + 3d54p2, 3d54p5p, 3d54p6p
  + 3d44s4d2.
y6P$^{\rm o}$ : 3d64p, 3d65p, 3d54s4p, 3d54s5p, 3d55s4p, 3d55s5p
  + 3d54p4d, 3d55p4d, 3d44s4p4d, 3d54p5d, 3d55p5d
  + 3d54s4f, 3d54d4f
  + 3d54s6p, 3d55s6p, 3d54d6p
  + 3d44p4d2, 3d45p4d2, 3d34s4p4d2, 3d34s5p4d2, 3d35s4p4d2.



 

 
Table 4: Experimental BFs and transition probabilities from the 3d5(6S)4s4p(3P) y6P term in Fe II. Air wavelengths above 2000 Å.
Upper Lower $\lambda^1$ $\sigma$ BF Uncert A (s-1) Log gf
Level Level (Å) (cm-1) Exp. (% in gf) Exp. Exp. Theory2 Theory3
y6P3/2 b2P1/2 2852.864 35042.19 0.6 17 1.65E+06 -2.09 -3.36 -2.10
E=61974.93 cm-1 a6S5/2 2586.060 38657.30 2.2 37 5.75E+06 -1.64 -1.75 -2.11
$\tau=3.90 \pm 0.2$ ns b4P3/2 2489.110 40162.88 1.0 23 2.64E+06 -2.01 -2.91 -2.20
  a6D1/2 1639.401 60997.88 28.0 7 7.18E+07 -0.94 -0.93 -0.99
  a6D3/2 1636.331 61112.31 39.3 7 1.01E+08 -0.79 -0.78 -0.84
  a6D5/2 1631.129 61307.24 27.3 7 7.00E+07 -0.95 -0.95 -1.02
  Residual     1.4          
                   
y6P5/2 a6S5/2 2581.111 38731.41 2.9 10 7.61E+06 -1.34 -1.38 -1.80
E=62049.02 cm-1 a6D3/2 1634.349 61186.42 13.0 8 3.41E+07 -1.09 -1.14 -1.19
$\tau=3.80$ $\pm$ 0.2 ns a6D5/2 1629.159 61381.35 35.1 7 9.22E+07 -0.66 -0.66 -0.70
  a6D7/2 1621.685 61664.25 48.9 6 1.29E+08 -0.52 -0.51 -0.56
  Residual     0.2          
                   
y6P7/2 a6S5/2 2572.968 38853.99 2.9 8 7.89E+06 -1.20 -1.24 -1.53
E=62171.62 cm-1 b4F5/2 2548.157 39232.27 0.3 38 8.02E+05 -2.20 -2.49 -2.29
$\tau=3.65 \pm 0.2$ ns b4F7/2 2539.805 39361.27 2.1 12 5.64E+06 -1.36 -1.95 -1.64
  b4F9/2 2528.681 39534.42 0.8 34 2.27E+06 -1.76 -2.74 -2.33
  a4H7/2 2470.847 40459.72 0.2 41 5.35E+05 -2.41 -- -2.49
  b4P5/2 2418.168 41341.06 0.7 31 2.03E+06 -1.85 -2.15 -2.22
  a6D5/2 1625.912 61503.94 4.2 12 1.15E+07 -1.44 -1.55 -1.58
  a6D7/2 1618.468 61786.83 19.9 7 5.46E+07 -0.77 -0.76 -0.81
  a6D9/2 1608.451 62171.62 67.8 6 1.86E+08 -0.24 -0.21 -0.27
  Residual     1.0          

1Air wavelengths above 2000 Å.
2Calculations, this work.
3Calculations Raassen & Uylings (1998).


  \begin{figure} \par\includegraphics[angle=90,width=12cm,clip]{3733f1.eps} \end{figure} Figure 1: The GHRS spectrum of the star HD141637 in the vicinity of 1600 Å including the strong (narrow) interstellar Fe II line $\lambda $1608 (a6D9/2-y6P7/2), and the satellite line at 1611 Å (a6D9/2-y4F7/2), which appears due to level mixing (see text).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{3733f2.eps} \end{figure} Figure 2: An illustration of the mixing between the y6P7/2 and y4F7/2 levels in Fe II. Three of the resulting intercombination lines appear at 2539.8 Å, 2528.7 Å and 1611.2 Å. The spacing between the b4F levels is greatly exaggerated.
Open with DEXTER

The CSFs of all states are constructed from a common set of one-electron orbitals of the form

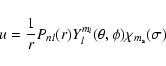\begin{displaymath}u = \frac{1}{r} P_{nl}(r) Y_l^{m_l}(\theta,\phi) \chi_{m_{\rm s}}(\sigma) \end{displaymath} (6)

whose angular momenta are coupled to give a total LiSi. This may vary from CSF to CSF but their resultant J is common to all CSFs in Eq. (4). The radial functions in Eq. (6) are expressed in analytic form as a linear combination of normalized Slater-type orbitals (STOs):

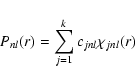\begin{displaymath}P_{nl}(r) = \sum_{j=1}^{k} c_{jnl}\chi_{jnl}(r) \end{displaymath} (7)

where the STOs take the form

\begin{displaymath}\chi_{jnl}(r) = \left[ \frac{(2\zeta_{jnl})^{2I_{jnl}+1}}{(2I_{jnl})!} \right]^{1/2} r^{I_{jnl}} \exp(-\zeta_{jnl}r). \end{displaymath} (8)

Equation (5) constitute a set of variational principles allowing the optimization of the radial function parameters on one or more of the energy eigenvalues of the Hamiltonian matrix. The integers $\{I_{jnl}\}$ are kept fixed but the exponents  $\{\zeta_{jnl}\}$ and the coefficients $\{c_{jnl}\}$ in Eq. (7) may be treated as variational parameters to be optimized subject to the orthonormality conditions:

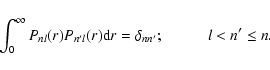\begin{displaymath}\int_{0}^{\infty} P_{nl}(r)P_{n^{\prime}l}(r) {\rm d}r = \delta_{nn^{\prime}} ; \hspace*{1.0cm} l < n^{\prime} \leq n. \end{displaymath} (9)

The optimization of the radial functions on, for example, the energy of just one state would lead to a serious imbalance in the accuracy to which the full set of states under consideration would be represented. Hence different orbitals are optimized on different eigenvalues, so that all the states are of a comparable level of accuracy and different optimal radial dependencies of the Pnl in different states may be accounted for. In the present work, the 1s, 2s, 2p, 3s, 3p, 3d, 4s functions were taken from the ground state Hartree-Fock functions given by Clementi & Roetti (1974): hence they are all optimized on the a 6D state, and we used the radial functions previously optimized in our calculations of the a 6D - y 6P$^{\rm o}$ transitions (Donnelly & Hibbert 1998). The additional orbitals consist of 5s, 6s, 4p, 5p, 6p, 4d, 5d, 4f. The method of optimization (involving only the non-relativistic Schrödinger Hamiltonian) is displayed in Table 1 and the radial function parameters are given in Table 2.


 

 
Table 5: Comparison between this work and previous work on log gf-values for transitions from 3d5(6S)4s4p(3P) y6P term in Fe II. All wavelengths are in vacuum.
$\lambda_{\rm vac}$ Transition Log gf1
(Å)   a b c d e f g h i j k l m
1608.451 a6D9/2-y6P7/2 -0.24 -0.21 -0.24 -0.24   -0.27 -0.129 -0.016 -0.37 -0.049 -0.21   -0.21
1618.468 a6D7/2-y6P7/2 -0.77 -0.76 -0.75     -0.81 -0.673 -0.55 -0.92 -0.60      
1621.685 a6D7/2-y6P5/2 -0.52 -0.51 -0.48     -0.56 -0.443 -0.31 -0.67 -0.34      
1625.912 a6D5/2-y6P7/2 -1.44 -1.55       -1.58 -1.451     -1.38      
1629.159 a6D5/2-y6P5/2 -0.66 -0.66 -0.77     -0.71 -0.581 -0.46 -0.82 -0.49      
1631.129 a6D5/2-y6P3/2 -0.95 -0.95 -0.97     -1.02 -0.889 -0.76 -0.90 -0.78      
1634.349 a6D3/2-y6P5/2 -1.09 -1.14       -1.19 -1.065            
1636.331 a6D3/2-y6P3/2 -0.79 -0.78 -0.89     -0.84 -0.713 -0.58 -0.95 -0.61      
1639.401 a6D1/2-y6P3/2 -0.94 -0.93 -1.01     -0.99 -0.860 -0.72 -1.11 -0.76      
2418.902 b4P5/2-y6P7/2 -1.85 -2.15       -2.22 -2.706            
2471.594 a4H7/2-y6P7/2 -2.41 --       -2.49 -3.255            
2489.861 b4P3/2-y6P3/2 -2.01 -2.91       -2.20 -2.484            
2529.441 b4F9/2-y6P7/2 -1.76 -2.74       -2.33 -3.980            
2540.568 b4F7/2-y6P7/2 -1.36 -1.95     -1.48 -1.64 -1.7202         <-1.35  
2548.922 b4F5/2-y6P7/2 -2.20 -2.49       -2.29 -2.996            
2573.738 a6S5/2-y6P7/2 -1.20 -1.24     -1.29 -1.53 -1.5302     -1.37   <-1.05  
2581.884 a6S5/2-y6P5/2 -1.34 -1.38     -1.46 -1.80 -1.7002     -1.49      
2586.834 a6S5/2-y6P3/2 -1.64 -1.75       -2.11 -2.472     -1.67      
2853.703 b2P1/2-y6P3/2 -2.09 -3.36       -2.10 -2.337            

1a) Exp: This work, b) Theory: This work, c) Exp: Mullman et al. (1997), d) Exp: Bergeson et al. (1996), e) Exp. Moity (1983), f) Theory: Raassen & Uylings (1998), g) Theory: Kurucz (2000), h) Theory: Nussbaumer et al. (1981), i) Theory: Facett (1988), j) Theory: Nahar (1994), k) Astrophysical: Shull et al. (1983), l) Astrophysical: Ekberg & Feldman (1992), m) Astrophysical: Cardelli & Savage (1995).
2From Fuhr et al. 1988.



The Hamiltonian used to determine the final wave functions consists of the non-relativistic Schrödinger Hamiltonian along with the following relativistic operators associated with the Breit-Pauli approximation: mass-correction, Darwin, spin-spin, spin-other-orbit and spin-orbit terms. However, the spin-spin-contact and the orbit-orbit terms, which do not contribute directly to fine-structure separations, are not included in the calculations.

When the LS calculation appears adequate, the relativistic effects of the Breit-Pauli Hamiltonian are added, and our LSJ calculation is completed. This allows oscillator strengths of individual lines ( $J \rightarrow J^{\prime}$) to be determined. In this calculation, intercombination lines (where $\Delta S \neq 0$) can be determined. They can arise through the mixing of different LS symmetries with a common J-value.

Even at this stage the calculated energies will not agree exactly with experiment. This is mainly due to the slow convergence of the summation (Eq. (4)). An extrapolation process known as fine-tuning (Brage & Hibbert 1989) significantly speeds convergence by making small adjustments to the diagonal elements of the Hamiltonian matrix hence bringing the calculated energies into agreement with experimental energy differences. The results in the following section are those obtained with this `fine-tuning' process.

This process has proved effective in improving the accuracy of calculated oscillator strengths for ab initio calculation which are already of a high degree of accuracy (Hibbert 1996).

5 Results

In Table 4 we present the results of our measurements and calculations of the observed lines decaying from the three fine structure levels of y6P in Fe II. For each transition we give the wavelength (in air above 2000 Å), wavenumber and LS notation for the lower energy level. The experimental BFs are tabulated together with transition probabilities, log gf-values (experimental and theoretical) and uncertainties. We also give the log gf-values by Raassen & Uylings (1998) as these are used for estimating the residual BF for lines that have not been observed.

In general, there is an extremely good agreement between experiment and theory for the sextet transitions, whereas deviations of up to one order of magnitude occur for spin-forbidden (quartet-sextet and even doublet-sextet) transitions, which appear because of level mixing. Since the level mixing is a result of similar energies for levels having the same parity and J-value the amount of mixing (and the log gf-values) is strongly sensitive to the accuracy of the calculated level energy. In the next section we show some examples of the effects of level mixing in astrophysical spectra.

In Table 5 we compare the log gf-values determined in this work with previous measurements and calculations. Note, that all wavelengths are in vacuum in Table 5, to facilitate the comparison with plots of satellite spectra. We give Ritz wavelengths derived from improved energy level values obtained in an ongoing term analysis of Fe II by one of the authors (S.J.). There is a good agreement between our log gf-values and the previous measurements by Bergeson et al. (1996) and Mullman et al. (1997) for the sextet lines, the largest deviation being 0.11 dex (25% in the f-value) for the $\lambda $1629 and $\lambda $1636 lines. It is especially satisfactory to see the perfect agreement in the log gf-value for the important $\lambda $1608 line not only between the two independent measurements but also with the two independent calculations by Raassen & Uylings (1998) and by Donnelly & Hibbert (this work).

6 Level mixing illustrated by stellar spectra

The main objective for this work was to measure the f-value for the interstellar $\lambda $1608 line of Fe II and obtain the branching ratio between this fast decay from y6P7/2 to the ground state a6D9/2 and the decay to the a6S5/2 level at 2573 Å. The two lines represent a 3d-4p and a 4s-4p transition, respectively, and would look at first glance to be reasonably strong LS transitions. However, the experimental branching ratio is 32 in favour of the 3d-4p transition, which illustrates the importance of a selection rule for the intermediate LS term arising in the coupling of the 4s4p and 4s2 electrons (Johansson 1978). The y6P term belongs to the 3d5(6S)4s4p(3P) subconfiguration, with the outer 4s and 4p electrons coupled to a 3P term, whereas the two 4s electrons in the 3d5(6S)4s2 subconfiguration, to which the a6S belongs, are coupled to a 1S term. Thus, the 4s-4p transition between a6S and y6P disobeys the LS selection rule for the outer LS coupling terms 1S and 3P, which explains its very low branching fraction. The opposite situation is found for the UV multiplet 191, where the x6P term of the 3d5(6S)4s4p(1P) subconfiguration preferentially decays to a6S, obeying the LS selection rule for the outer, intermediate LS terms in a 1S-1P transition.

  \begin{figure} \par\mbox{\includegraphics[width=7.5cm,clip]{fig3a.eps}\hspace*{1.5mm} \includegraphics[width=7.5cm,clip]{fig3b.eps} }\end{figure} Figure 3: The two b4F-y6P Fe II lines at $\lambda $$\lambda $2528, 2539 in the GHRS spectrum of $\chi $ Lupi. The solid curve represents the recorded spectrum. The dashed curve show the calculated spectra, the with experimental log gf-values from this work and the dotted curve with data from Kurucz (2000).
Open with DEXTER

The interstellar $\lambda $1608 line of Fe II multiplet UV8 appears in a GHRS spectrum of the star HD141637, shown in Fig. 1. Very close on the red side is a much weaker interstellar Fe II line, which is an appendage to the $\lambda $1608 line due to level mixing. The 1611 Å line corresponds to the LS-forbidden transition a6D9/2-y4F7/2, also originating from the ground state of Fe II. The upper levels of the two transitions, y6P7/2 and y4F7/2, are mixed because they are close in energy, have the same J-value and the same parity. The levels are mixed although they belong to different configurations, different spin and L states mainly as a result of the high level density in complex spectra like Fe II. A simple schematic energy level diagram in Fig. 2 illustrates the level mixing. The experimental log gf-value for the $\lambda $1611 line is -1.86 according to Pickering et al. (2001).

The level mixing of y6P7/2 with y4F7/2 opens a number of additional weak decay channels for each of the levels. The additional transitions from y6P7/2 (and a few from the y6P3/2 level) can be found in Table 4. Their branching fractions are typically of the order of a few percent. However, a few percent of a strong line might mean that we see a weak line in a stellar spectrum, which is suitable in abundance work. Since the line is the result of level mixing it might also mean that its log gf-value available in theoretical databases is less reliable. In Fig. 3 we have extracted two parts of the GHRS spectrum of the chemically peculiar star $\chi $ Lupi (Leckrone et al. 1999) containing two features, which are identified as two of the Fe II transitions studied in this work. The left panel shows a spectral interval containing a line at 2528.7 Å, which is the b4F9/2-y6P7/2 transition shown in Fig. 2 and given in Table 4. The dotted curve represents the calculated spectrum using atomic data from the Kurucz (2000) database which gives a calculated log gf- ${\rm value}=-3.980$ for $\lambda $2528.7. The dashed curve is obtained when the Kurucz value is replaced with the new experimental value of -1.76. As we see in Table 4, other theoretical values for this transition are also too small by up to one order of magnitude. The b4F7/2-y6P7/2 companion to the strong b4F7/2-y4F7/2 transition at 2547.4 Å appears at 2539.8 Å (see Fig. 2) and shows a large depth in the $\chi $ Lupi spectrum (right panel of Fig. 3). Using the log gf-value for $\lambda $2539.8 from Fuhr et al. (1988), which is a scaled experimental value from Moity (1983), we obtain the dotted curve, while the new experimental value is used in the dashed curve.

7 Conclusion

We present branching fraction measurements for 99% of the radiative decay from the three 3d5(6S)4s4p(3P) y6P levels in Fe II and provide accurate oscillator strengths for astrophysical applications. Branching fractions for 19 Fe II lines are measured using spectra recorded with the high resolution FT spectrometers at Imperial College, London, (in the UV-VUV region) and Lund Observatory, Lund University, (in the UV region) having a wide free spectral range, high resolution and linear response. The intensity measurements at Imperial College connect the fundamental 3d-4p and 4s-4p transitions in complex spectra, whereas complementary weak lines are measured with the Lund FT spectrometer to obtain as small a residual as possible. FT spectra of Fe II in the range 1520-4160 Å (24000-66000 cm-1) were produced with a PD lamp and a HC lamp. Absolute transition probabilities and log gf-values for the 19 lines are derived by combining the BFs with experimental radiative lifetimes recently reported by Li et al. (2000). The uncertainties in the f-values are less than 10% for strong lines. Our measurements are compared with the experimental work by Bergeson et al. (1996), Mullman et al. (1997) and Moity (1983), and with theoretical calculations by Nussbaumer et al. (1981), Fawcett (1988), Kurucz (2000), Nahar (1995), and Raassen & Uylings (1998). Our f-value (0.058) of the astrophysically important line at 1608 Å coincides with the f-values measured by Bergeson et al. (1996) and Mullman et al. (1997) (f=0.058) using an independent method. The theoretical f-values of $\lambda $1608 calculated in this work (f=0.062) and by Raassen & Uylings (1998) (f=0.055) are also in good agreement with the measurements.

The mixing of the y6P levels with other levels of the same symmetry, e.g. y4F, generates faint spectral lines, showing strange LS combinations and having branching fractions smaller than 3%. However, as illustrated, the lines may show substantial line opacity in high resolution stellar spectra, and could well be used in abundance work. The level mixing also generates a satellite line at 1611 Å to the strong interstellar Fe II line at 1608 Å.

Acknowledgements
JCP thanks PPARC of the UK for their support of the IC program of measurements of spectra of astrophysical importance. JCP is supported by a Royal Society University Research Fellowship. JCP also thanks Anne Thorne for many helpful discussions. Sadly Richard Learner of our group at IC died recently; JCP is grateful for all his support and contributions to the group's research in atomic spectroscopy for astrophysics over the years. JCP thanks Geoff Cox for his invaluable assistance in the preparatory experimental work using the Penning discharge lamp. The FERRUM Project is supported through a grant (SJ) from the Swedish Natural Science Research Council. MPD and AH thank PPARC (UK) for support under Rolling Grant PPA/G/2000/00024.

References

 

Copyright ESO 2002