A&A 396, 449-461 (2002)
DOI: 10.1051/0004-6361:20021403

H$\alpha $ surface photometry of galaxies in the Virgo cluster

IV. The current star formation in nearby clusters of galaxies[*],[*]

G. Gavazzi 1 - A. Boselli 2 - P. Pedotti 1 - A. Gallazzi 1 - L. Carrasco 3,4


1 - Università degli Studi di Milano-Bicocca, Piazza delle scienze 3, 20126 Milano, Italy
2 - Laboratoire d'Astrophysique de Marseille, Traverse du Siphon, 13376 Marseille Cedex 12, France
3 - Instituto Nacional de Astrofísica, Optica y Electrónica, Apartado Postal 51. C.P. 72000 Puebla, Pue., México
4 - Observatorio Astronómico Nacional, UNAM, Apartado Postal 877, C.P. 22860, Ensenada B.C., México

Received 31 July 2002 / Accepted 20 September 2002

Abstract
H$\alpha $+[NII] imaging observations of 369 late-type (spiral) galaxies in the Virgo cluster and in the Coma/A1367 supercluster are analyzed, covering 3 rich nearby clusters (A1367, Coma and Virgo) and nearly isolated galaxies in the Great-Wall. They constitute an optically selected sample (mp<16.0) observed with $\sim$$60 \%$ completeness. These observations provide us with the current (T<107 yrs) star formation properties of galaxies that we study as a function of the clustercentric projected distances ($\Theta$). The expected decrease of the star formation rate (SFR), as traced by the H$\alpha $ EW, with decreasing $\Theta$ is found only when galaxies brighter than $M_p \sim -19.5$ are considered. Fainter objects show no or reverse trends. We also include in our analysis Near Infrared data, providing information on the old (T>109 yrs) stars. Put together, the young and the old stellar indicators give the ratio of currently formed stars over the stars formed in the past, or "birthrate'' parameter b. For the considered galaxies we also determine the "global gas content'' combining HI with CO observations. We define the "gas deficiency'' parameter as the logarithmic difference between the gas content of isolated galaxies of a given Hubble type and the measured gas content. For the isolated objects we find that b decreases with increasing NIR luminosity. In other words less massive galaxies are currently forming stars at a higher rate than their giant counterparts which experienced most of their star formation activity at earlier cosmological epochs. The gas-deficient objects, primarily members of the Virgo cluster, have a birthrate significantly lower than the isolated objects with normal gas content and of similar NIR luminosity. This indicates that the current star formation is regulated by the gaseous content of spirals. Whatever mechanism (most plausibly ram-pressure stripping) is responsible for the pattern of gas deficiency observed in spiral galaxies members of rich clusters, it also produces the observed quenching of the current star formation. A significant fraction of gas "healthy'' (i.e. with a gas deficiency parameter less than 0.4) and currently star forming galaxies is unexpectedly found projected near the center of the Virgo cluster. Their average Tully-Fisher distance is found approximately one magnitude further away ( $\mu_{\rm o}=$ 31.77) than the distance of their gas-deficient counterparts ( $\mu_{\rm o}=$ 30.85), suggesting that the gas healthy objects belong to a cloud projected onto the cluster center, but in fact lying a few Mpc behind Virgo, thus unaffected by the dense IGM of the cluster.

Key words: galaxies: photometry - galaxies: clusters: individual: Virgo


1 Introduction

A significant trend of the global star formation rate (SFR) of galaxies with the projected clustercentric distance from rich clusters of galaxies is well documented in the local universe ( 0.05<z<0.1). The mean SFR, as traced by the equivalent width of the H$\alpha $ line (Kennicutt 1989), is found to decrease with decreasing distance from rich clusters (Lewis et al. 2002). This pattern is dominated by the "morphology segregation'' effect (Dressler 1980), i.e. there are more elliptical and spheroidal galaxies with little or no current star formation than the star forming galaxies in the center of rich clusters. What physical mechanism (nature vs. nurture) is responsible for the morphological transformation taking place in the densest environments is however not yet fully understood. To shed light on the various possibilities, i.e. galaxy harassment (Moore et al. 1996, 1998), tidal stirring (Mayer et al. 2001) or ram pressure stripping (Gunn & Gott 1972), it is crucial to establish observationally if, beside the morphology segregation, galaxies of a given morphological type, namely the spirals, are affected by a systematic SFR decrease toward the center of nearby clusters.

If on the one hand Kennicutt (1983) found that spirals in the Virgo cluster have their mean SFR as much as a factor of two lower than isolated galaxies, Gavazzi et al. (1998) did not confirm this evidence in the Coma and A1367 clusters. Moreover Iglesias-Paramo et al. (2002) found that the shape of the H$\alpha $ luminosity function of these two clusters does not differ significantly from the one of isolated galaxies. The result of Kennicutt (1983) was based on only a dozen giant galaxies with H$\alpha $ measurements from aperture photometry, thus requiring a confirmation on a larger sample with modern imaging data.

With the aim of solving this riddle we undertook an H$\alpha $ imaging survey of two optically complete samples of galaxies. The first is composed of nearly isolated objects selected from the CGCG (Zwicky et al. 1961-68) in the bridge between Coma and A1367, which we observed down to the limit of 15.7 mag. This constitutes our reference sample of non-cluster objects. The cluster sample is focused on A1367, the Coma and the Virgo clusters. We took H$\alpha $ imaging observations of these regions (Gavazzi et al. 1998; Gavazzi et al. 2002a, Paper I of this series; Boselli & Gavazzi 2002, Paper II; Boselli et al. 2002b, Paper III). Our own observations were complemented with data taken from the literature (Kennicutt & Kent 1983; Romanishin 1990; Gavazzi et al. 1991; Young et al. 1996; Koopmann et al. 2001).

Furthermore we performed a NIR imaging survey of the same regions (Gavazzi et al. 2000b and references therein), providing information on the old stars.

In the present paper we combine H$\alpha $ with NIR measurements to study the young and the old components of the stellar population integrated over the whole galaxy and we analyze the properties of the stars as a function of the clustercentric projected distance, of the luminosity and of the global gas content. We postpone to a forthcoming paper the morphological aspects of the analysis related to the spatial distribution of the young/old stars. The present paper is organized as follows: in Sect. 2 we briefly present the new H$\alpha $ imaging observations of 13 galaxies. The sample used in the present investigation is illustrated in Sect. 3. After defining the "birth-rate'' parameter (Sect. 4.1) and the "gas-deficiency'' parameter (Sect. 4.2), we analyze in Sect. 5.1 the clustercentric dependence of the current star formation rate. In Sects. 5.2 and 5.3 we study the current star formation properties of galaxies in 3 local clusters as a function of their global luminosity and gaseous properties. The conclusions are briefly discussed in Sect. 6 and summarized in Sect. 7.

2 New observations

Narrow band imaging in the H$\alpha $ emission line ($\lambda$ = 6562.8 Å) of 13 galaxies was obtained in March 20, 2002, using the 2.1 m telescope at San Pedro Martir Observatory (SPM) (Baja California, Mexico).

The target galaxies are listed in Table 3 as follows:

We used a Site 1024 $\times$ 1024 pixels CCD detector with pixel size of 0.31 arcsec. Each galaxy was observed through a narrow band interferometric filter ($\sim$90 Å width) centered at $\lambda$ 6603, for the galaxies at the redshift of Virgo ( $350<V<3000~{\rm km~s}^{-1}$), and at $\lambda$ 6723 Å, for galaxies in the Coma supercluster. These observations provided us with the ON-band images and required 15-20 min integration time. The OFF-band images were obtained through the r-Gunn filter and were exposed one fifth of the ON-band ones. The observations were obtained with the seeing ranging from 1.2 to 3 arcsec, but in photometric conditions. They were flux calibrated using the standard stars Feige 34 and Hz44 from the catalogue of Massey et al. (1988), observed every 2 hours. Repeated measurements gave <0.05 mag differences, which we assume as the typical uncertainty ($1 \sigma$) of the photometric results given in this work.

The reduction of the CCD frames follows a procedure identical to the one described in previous papers of this series (e.g. Gavazzi et al. 2002), based on the IRAF STSDAS[*] reduction packages, and it will be briefly summarized here. To remove the detector response each image was bias subtracted and divided by the median of several flat field exposures obtained on empty regions of the twilight sky. Cosmic rays were removed either using the task COSMICRAY in IRAF or manually by direct inspection of the frames. The sky background was determined in each frame in concentric object-free regions around the galaxies and then subtracted from the flat-fielded images. The typical uncertainty on the mean background is estimated 10% of the rms in the individual pixels. This represents the dominant source of error in low S/N regions.

H$\alpha $ fluxes and equivalent widths are estimated subtracting the contribution of the continuum from the ON-band measurements. As the continuum was estimated using the broad band r filter, which in fact includes the H$\alpha $ and [NII] lines, the corrected fluxes and equivalent widths are computed according to Eqs. (1) and (2) of Paper III, and their uncertainties are given by:

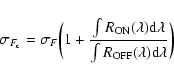\begin{displaymath}% {\sigma_{F_{\rm c}} = \sigma_{F}\bigg(1+{\frac{\int R_{{\rm... ...d}\lambda}{\int R_{{\rm OFF}}(\lambda){\rm d}\lambda}}\bigg) } \end{displaymath} (1)


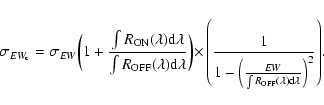\begin{displaymath}% {\sigma_{EW_{\rm c}} = \sigma_{EW} \bigg(1+{\frac{\int R_{{... ...{\int R_{{\rm OFF}}(\lambda){\rm d}\lambda}\right)^2}\right)}. \end{displaymath} (2)

Galaxies with substantial $\rm H\alpha +[NII]$ structure are given in Fig. 14. The contours of the OFF frames are superposed to the NET (ON-OFF) frames (grey-scale).

3 The sample


  \begin{figure} \par\includegraphics[width=6cm,clip]{ms2973f1.ps}\end{figure} Figure 1: Sky distribution of the 312 spiral galaxies brighter than $m_p \leq 16.0$ in the VCC. The filled symbols represent 235 galaxies with available H$\alpha $ data, the empty ones to unobserved galaxies. Circles are drawn at 2, 4, 6 deg projected radial distance from M 87 (cross).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{ms2973f2.ps}\end{figure} Figure 2: Sky distribution of the 256 spiral galaxies brighter than $m_p \leq 15.7$ in the CGCG in the Coma supercluster region (top). Wedge diagram (bottom). The filled symbols represent 158 galaxies with available H$\alpha $ data, the empty ones to unobserved galaxies.
Open with DEXTER

Including the new observations presented in this paper, this work comprises H$\alpha $ and NIR (H band) imaging observations of 369 late-type galaxies belonging to the Virgo cluster and to the Coma supercluster region.

The Virgo cluster galaxies were selected from the Virgo Cluster Catalogue (VCC) of Binggeli et al. (1985), with $m_p \leq 16.0$, Hubble type later than S0a (as given in the VCC) and classified as cluster members, possible members or belonging to the W, W', M clouds or to the southern extension (Binggeli et al. 1985, 1993; see also Gavazzi et al. 1999a) matching V<3000 $\rm km ~s^{-1}$ (see Fig. 1).

The late-type (> S0a) galaxies in the Coma supercluster region ( $\rm 18^o \le \delta \le 32^o$; $\rm 11.5^h \le \alpha \le 13.5^h$) were selected from the CGCG catalogue ( $m_p \leq ~15.7$) (Zwicky et al. 1961-68) and include members to the Coma Supercluster according to Gavazzi et al. (1999b) (see Fig. 2). Table 1 gives the details of the sample completeness in the two studied regions. The Coma supercluster members are divided in cluster (A1367+A1656) members, members to groups and pairs (see Gavazzi et al. 1999b) and strictly isolated supercluster objects (with projected separations >300 kpc). The H$\alpha $ observations were taken either from the present series of papers (Papers I, II, III, IV, primarily devoted to the Virgo cluster), from Gavazzi et al. (1991, 1998) (containing mostly observations of the Coma supercluster region) or from Kennicutt & Kent (1983), Kennicutt et al. (1984), Romanishin (1990), Koopmann et al. (2001) (see detailed references in Table 4).

The NIR observations were taken from the series of papers "Near-infrared H surface photometry of galaxies'' (Gavazzi et al. 1996a,b, 2000a; Boselli et al. 1997; Boselli et al. 2000 and from Gavazzi et al. 2001). Total asymptotic H band magnitudes were obtained by Gavazzi et al. (2000b) and by Gavazzi et al. (2001).

As listed in Table 1 the combined NIR+ H$\alpha $ observations cover more than 60% of the targets in all regions (except Coma supercluster groups+pairs), thus our data can be considered as representative of the late-type galaxies in the studied regions.


 

 
Table 1: The sample completeness.
region $m_p \leq 16.0$ with NIR with NIR & H$_\alpha$ Compl.
Virgo 323 271 205 63%
Coma S. (Clusters) 72 72 54 75%
Coma S. (Grps+Prs) 67 67 27 40%
Coma S. (Isolated) 119 83 83 69%
Tot. 568 480 356 63%


The analyzed galaxies are listed in Table 4 as follows:

4 Tools

4.1 The birthrate parameter

$\rm H_\alpha $ and NIR observations provide us with information on stellar populations with different time scales: $\sim$107 yrs the former and $\sim$1010 yrs the latter. The two quantities combined give the ratio of the current SFR to the average past SFR or the birthrate parameter b, as defined by Kennicutt et al. (1994).

Following Boselli et al. (2001), we use the Near Infrared luminosity $L_{\rm H}$ as a tracer of the global mass of old stars, assuming that disk galaxies have a constant $M_{{\rm Tot}}/L_{\rm H}=4.6$ within their optical radius (Gavazzi et al. 1996c). Thus we write the adimensional parameter b as:

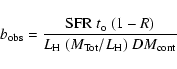\begin{displaymath}% b_{{\rm obs}} = \frac{{\rm SFR}~t_{\rm o}~(1-R)}{L_{\rm H} ~(M_{{\rm Tot}}/L_{\rm H})~DM_{{\rm cont}}} \end{displaymath} (3)

where SFR is derived from the $\rm H_\alpha $ luminosity with:

\begin{displaymath}% {\rm SFR} \left[M_\odot {\rm yr}^{-1}\right] = K_{{\rm H\alpha}} L_{{\rm H\alpha}} \left[{\rm erg~s}^{-1}\right]. \end{displaymath} (4)

Obviously the $\rm H_\alpha $ luminosity is deblended from the observed [NII] contribution and corrected for internal extinction as in Boselli et al. (2001). For consistency with Boselli et al. (2001) we adopt $K_{{\rm H\alpha}}= 1/1.16 \times 10^{41}$ for an IMF of slope -2.5 in the mass range 0.1-80 $M_\odot$.

$DM_{{\rm cont}}$ is the dark matter contribution at the optical radius, i.e. within the $25~{\rm mag~ arcsec}^{-2}$ B band isophote, that we assume $DM_{{\rm cont}}=$ 0.5, as in Kennicutt et al. (1994).

R=0.3 (Kennicutt et al. 1994) is the fraction of gas that stars re-injected through stellar winds into the interstellar medium during their lifetime, that we assume $t_{\rm o}$ $\sim$ 12 Gyrs.

If we assume that galaxies evolved as "closed'' systems following an exponential Star Formation History (SFH), with a characteristic decay time $\tau$ since their epoch of formation ($t_{\rm o}$), their birthrate parameter can be computed analytically (see Boselli et al. 2001) as:

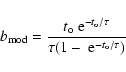\begin{displaymath}% b_{{\rm mod}} = \frac{t_{\rm o} ~{\rm e}^{-t_{\rm o}/\tau}}{\tau (1-~{\rm e}^{-t_{\rm o}/\tau})} \end{displaymath} (5)

$b_{{\rm mod}}$ can be written as a function of $L_{\rm H}$ using the relation between $\tau$ and $L_{\rm H}$ found by Boselli et al. (2001):

\begin{displaymath}% {\rm log} \tau = -0.4 \left({\rm Log} L_{\rm H} - 12 \right) [{\rm Gyr}] \end{displaymath} (6)

where

\begin{displaymath}% {\rm Log} L_{\rm H} = 11.36 -0.4 H + 2 {\rm log} ({\rm Dist}) [L_{{\rm H}_\odot}]. \end{displaymath} (7)

The dependence of $b_{{\rm mod}}$ on $L_{\rm H}$ is given as a dotted line in Figs. 8-10.

Although b and $\rm H_\alpha $ EW have distinct dimensions, they are strongly correlated quantities. In fact they are operationally obtained in a similar way: b is computed by normalizing the  $\rm H_\alpha $ line intensity to the NIR continuum intensity, while the equivalent width is divided by the continuum intensity underlying the $\rm H_\alpha $ line. This is shown in Fig. 3 which can be directly compared with Fig. 4 of Kennicutt et al. (1994).

  \begin{figure} \par\includegraphics[width=7cm,clip]{ms2973f3.ps}\end{figure} Figure 3: The relation between the birthrate parameter and the $\rm H_\alpha $ emission line equivalent width.
Open with DEXTER

4.2 The global gas deficiency parameter

For galaxies in our sample we estimate the "global gas content'' $M_{{\rm gas}}=M_{{\rm HI}}+M_{{\rm H2}}+M_{{\rm He}}$.

$M_{{\rm HI}}$ is available for most (95%) targets by direct 21 cm observations (see Scodeggio & Gavazzi 1993; Hoffman et al. 1996, and references therein). The mass of molecular hydrogen can be estimated from the measurement of the CO (1-0) line emission, assuming a conversion factor (X) between this quantity and the $\rm H_{2}$ surface density. X is known to vary in the range 1020 to 1021 [mol cm-2 (K km s-1)-1] from galaxy to galaxy, according to their metallicity and UV radiation field. We adopt the empirical calibration as a function of the H band luminosity:

\begin{displaymath}% {\rm log} X = 24.23 - 0.38\times{\rm log} L_{\rm H} \end{displaymath} (8)

found by Boselli et al. (2002a). The CO (1-0) line emission is unfortunately available for 52% of the considered sample (see Boselli et al. 2002a and references therein), and it is assumed 15% of the HI content for the remaining objects (as concluded by Boselli et al. 2002a).

The contribution of He, not directly observable, is estimated as 30% of $M_{{\rm HI}}+M_{{\rm H2}}$ (see Boselli et al. 2002a).

We define the "gas deficiency'' parameter $Def_{{\rm gas}}= {\rm Log} M_{{\rm gas~ref.}} - {\rm Log} M_{{\rm gas~obs.}}$ as the logarithmic difference between $M_{{\rm gas}}$ of a reference sample of isolated galaxies and $M_{{\rm gas}}$ actually observed in individual objects (in full analogy with the definition of HI deficiency by Giovanelli & Haynes 1985). Using a procedure similar to the one adopted by Haynes and Giovanelli (1984) we find that the gas content of 72 isolated objects in the Coma Supercluster correlates with their linear optical diameter (D): ${\rm Log} M_{{\rm gas~ref}}=a+b {\rm Log}(D)$, where a and b are weak functions of the Hubble type, as listed in Table 2. $Def_{{\rm gas}}$ are listed in Col. 7 of Table 4. Histograms of the $Def_{{\rm gas}}$ parameter are given in Fig. 4 for the Coma isolated objects and for the Virgo galaxies. Isolated objects have $Def_{{\rm gas}}=0 \pm 0.18$, while Virgo galaxies have significantly positive $Def_{{\rm gas}}=0.53 \pm 0.35$.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{ms2973f4.ps}\end{figure} Figure 4: Histograms of the $Def_{{\rm gas}}$ parameter for the isolated galaxies in the Coma supercluster (dashed line) and for Virgo galaxies (continuous line).
Open with DEXTER

5 Results

The $\rm H_\alpha $ EW of galaxies is known to increase systematically along the Hubble sequence, from virtually zero for the early types (E-S0) to several hundred Å for the latest types (Kennicutt 1998). A weak trend is confirmed when data limited to the Virgo spiral galaxies included in this work are used, as shown in Fig. 5. However the scatter in each of the morphological type bins is as much as an order of magnitude, even though the scatter is somewhat reduced when gas deficient galaxies are excluded. The Hubble type alone does not account for the star formation properties of galaxies in this cluster. To shed light on other possible dependences we will analyze how the SFR varies as a function of the projected clustercentric distance (Sect. 5.1), of the luminosity (Sect. 5.2) and of the gaseous content of galaxies (Sect. 5.3).


  \begin{figure} \par\includegraphics[width=7cm,clip]{ms2973f5.ps}\end{figure} Figure 5: The distribution of $\rm H_\alpha $ EW of spiral galaxies in the Virgo cluster as a function of Hubble type. Filled dots represent galaxies with normal gas content ( $Def_{{\rm gas}}<0.4$), open symbols are gas deficient objects. To avoid superposition of points, galaxies in each type bin are separated by a small random quantity. Crosses represent averages (including only the non gas-deficient galaxies) in each morphological type bin.
Open with DEXTER

5.1 The clustercentric dependence of the SFR

Lewis et al. (2002) analyzed the dependence of the galaxy SFR on the projected distance from clusters in the 2dF survey. Their volume limited samples comprise galaxies of all morphological types with 0.05<z<0.1, brighter than Mb<-19. They showed with high statistical significance that the median SFR of galaxies decreases with decreasing projected distance from clusters.

It would be interesting to compare these intermediate distance clusters with the 3 local clusters analyzed in this work, however a direct comparison cannot be carried out because data of early-type galaxies are not in our possession. The dependence of the $\rm H_\alpha $ EW on the clustercentric distance in units of virial radii can be analyzed only for the late-types galaxies, bearing in mind that our completeness is 60%. We compute $R_{{\rm virial}}=0.002\sigma_r h^{-1}$ (Girardi et al. 1998) for the 3 clusters assuming $\sigma_r$ = 775, 840, 925  $\rm km ~s^{-1}$ for Virgo, A1367 and Coma respectively.

The combined Coma and A1367 clusters (with Mb<-19) are shown in Fig. 6 enbedded in the Coma supercluster that we trace out to large clustercentric radial distances. We find a significant inner decrease only of the 25th percentile of the $\rm H_\alpha $ EW distribution. Both the median and the 75th percentile instead increase inwards. We find it unlikely that the $\rm H_\alpha $ EW distribution is biased toward high values due to incompleteness, since for the Coma+A1367 clusters our survey covers 75% of the sample. These clusters are inhabited by strong $\rm H_\alpha $ emitters to which the attention has been drawn by several authors. These include the "blue galaxies in the Coma cluster'' of Bothun & Dressler (1986) and the blue galaxy sample observed with ISO by Contursi et al. (2001). Many (13) galaxies with $\rm H_\alpha $ EW in excess of 50 Å  are found both in the inner regions ( $R/R_{{\rm virial}}<0.5$) and at intermediate distances ( $0.5<R/R_{{\rm virial}}<1.5$) from the observed clusters. Noticeably these galaxies are near the faint limit of our survey ( -19.5<Mb<-19 mag).

For the Virgo cluster we separate the bright sample (Mp<-19), with a luminosity cutoff and $\rm H_\alpha $ completeness similar to the Coma supercluster (75%), from the total sample (Mp<-15) and we show the two radial dependences separately in Fig. 7. The bright sample shows an inner decrease of the SFR. For the total sample this pattern no longer holds true. The Virgo cluster contains 24 galaxies with $\rm H_\alpha $ EW in excess of 50 Å  (11 are BCDs), the majority (14/24 objects) being fainter than -17.1 mag.

Because of their low optical luminosity the strong $\rm H_\alpha $ emitters belonging to Virgo would have all escaped detection in the 2dF survey. We conclude that, beside morphology segregation, the three local clusters analyzed in this work do not show a clear radial trend of the SFR distribution. The presence of the radial trend depends purely on a luminosity cutoff, which varies cluster to cluster between -17 and -19 mag. While spiral galaxies brighter than this cutoff luminosity have lower than average SFR at the cluster centers, galaxies fainter than this limit have SFR independent from the clustercentric projected distances. This is consistent with the idea that infall of small galaxies is occurring onto rich clusters at the present cosmological epoch.


  \begin{figure} \par\includegraphics[width=10cm,clip]{ms2973f6.ps}\end{figure} Figure 6: The distribution of $\rm H_\alpha $ EW as a function of (projected) clustercentric radius from the Coma and A1367 clusters (Mb<-19). The top and bottom lines represent the 75th and the 25th percentile of the EW distribution, while the central line is the median of the distribution.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms2973f7a.ps} % \includegraphics[width=8.8cm,clip]{ms2973f7b.ps}\end{figure} Figure 7: The distribution of $\rm H_\alpha $ EW as a function of (projected) clustercentric radius from the Virgo cluster. The top and bottom lines represent the 75th and the 25th percentile of the EW distribution, while the central line is the median of the distribution. The top panel shows the Virgo galaxies brighter than Mp=-19, while the bottom panel includes all galaxies surveyed in $\rm H_\alpha $ (Mb<-15).
Open with DEXTER

5.2 The SFR in the Coma supercluster


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms2973f8.ps}\end{figure} Figure 8: The relation between the birthrate parameter and the NIR luminosity (mass) for the Coma supercluster galaxies. Galaxies in the Coma+A1367 clusters are represented with empty symbols, filled symbols are non-cluster galaxies. The dotted line represents the expected b as a function of $L_{\rm H}$ in the closed-box model of Eq. (5). The dashed line represents the observational bias affecting the Coma galaxies due to their selection in the B band.
Open with DEXTER

Since, as concluded in the previous section, the present star formation rate of galaxies near the center of the studied clusters is a luminosity sensitive parameter, it is compelling to proceed to a systematic investigation of the luminosity dependence of the star formation properties. To this aim it is adequate to analyze the luminosity dependence of the birthrate parameter b (see Sect. 4.1). The most appropriate luminosity indicator, which we will adopt hereafter, is the NIR (H band) luminosity. This parameter traces at best the dynamical mass (within the optical disk) of spiral galaxies, as concluded by Gavazzi et al. (1996c), who found ${\rm Log} M_{{\rm dyn}}= {\rm Log} L_{\rm H} + 0.66$.

The dependence of the b parameter on $L_{\rm H}$, given in Fig. 8, shows that the star formation history of spiral galaxies in the Coma supercluster region is in almost inverse proportionality with the system luminosity (mass). The most massive spirals ( ${\rm Log} L_{\rm H} \sim 11.5 L_{{\rm H}_\odot} \sim 12.3~M_\odot$) have their b parameter as much as 100 times lower than less luminous (giant) galaxies ( ${\rm Log} L_{\rm H} \sim 10 L_{{\rm H}_\odot} \sim 10.8~M_\odot$). This confirms previous claims that the current SFR, as derived from the  $\rm H_\alpha $ EW, anti-correlates with the system mass (Gavazzi et al. 1998). Furthermore Fig. 8 shows that there is not a significant difference between the SFH of galaxies in the rich Coma+A1367 clusters and of relatively isolated objects in the same supercluster, in agreement with Gavazzi et al. (1998).

Both results are however biased by selection effects. The Coma supercluster galaxies were selected optically in the blue (photographic) band ( $m_p \leq ~15.7$). The selected targets were observed "a posteriori'' in $\rm H_\alpha $ and in the NIR, therefore at any given $L_{\rm H}$ only galaxies bluer than a certain threshold are sampled. In other words the B selection biases against faint-red galaxies, according to the relation between B-H and the infrared luminosity represented by Eq. (9) (see Scodeggio et al. 2002). This, combined with the fact that b correlates with the B-H color (see Eq. (10)), introduces a selection effect in the b vs. $L_{\rm H}$ plane (see Eq. (11)). These empirically determined relations are:

 \begin{displaymath}% B_{{\rm lim}} - H = -12.7 - 5~{\rm log}({\rm dist}) + 2.5~{\rm log} L_{\rm H} \end{displaymath} (9)

where $B_{{\rm lim}}=-19.2$ corresponds to the limiting magnitude ( $m_p \leq ~15.7$) at the Coma distance that we assume 96 Mpc.

 \begin{displaymath}% {\rm log} b = 0.56 - 0.52 (B-H) \end{displaymath} (10)


 \begin{displaymath}% {\rm log} b = 7.16 + 2.6~{\rm log}({\rm dist}) - 1.3~{\rm log} L_{\rm H}. \end{displaymath} (11)

Equation (11) is represented in Fig. 8 with a dashed line. In conclusion, faint-low star forming galaxies at the distance of Coma below the diagonal line of Fig. 8 are severely undersampled.


  .

 
Table 2: The $M_{{\rm gas}}$ vs. diameter relation for isolated galaxies.
Type a b R2
Sa-Sb 7.62 1.55 0.75
Sbc-Sc 7.48 1.68 0.75
Scd-Irr 7.74 1.49 0.77



 

 
Table 3: The newly observed galaxies.
VCC/CGCG NGC/IC UGC ${\rm RA}~~(J2000)$ Dec $m_{{\rm pg}}$ Vel $T_{{\rm on}}$ $R_{{\rm ON}}$
(1) (2) (3) (4) (5) (6) (7) (8) (9)
343 3148 - 121921.68 075213.8 15.1 2479 20 0.79
841 - - 122547.40 145711.4 15.6 501 20 0.66
15031 4771 8020 125321.85 011613.5 13.3 1119 15 0.85
15049 4845 8078 125801.33 013430.3 12.9 1097 15 0.85
15055 4904 8121 130058.89 -000142.4 13.2 1174 15 0.85
41041 4116 7111 120736.33 024133.1 13.0 1309 15 0.85
43028 4688 7961 124746.67 042005.3 14.5 984 15 0.84
43034 4701 7975 124911.87 032324.5 13.1 727 15 0.79
43054 4765 8018 125314.52 042749.4 13.0 725 15 0.79
69036 4067 7048 120411.46 105114.8 13.2 2424 15 0.8
100015 4758 8014 125244.16 155050.9 14.1 1240 15 0.85
157075 - - 115940.06 263248.7 15.7 6694 15 0.77
160121 - 8161 130329.11 263300.8 15.5 6676 20 0.77


5.3 The SFR in the Virgo cluster


  \begin{figure} \par\includegraphics[width=8cm,clip]{ms2973f9.ps}\end{figure} Figure 9: The relation between the birthrate parameter and the NIR luminosity (mass) for the Virgo galaxies. Empty symbols represent galaxies with normal gas content ( $Def_{{\rm gas}}<0.4$) while deficient galaxies ( $Def_{{\rm gas}}>0.4$) are given with filled symbols.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{ms2973f10.eps}\end{figure} Figure 10: The relation between the birthrate parameter and the NIR luminosity (mass) for Virgo+Coma galaxies with normal gas content ( $Def_{{\rm gas}}<0.4$).
Open with DEXTER

The selection effect mentioned above affects the Virgo sample to a much lesser extent, because Virgo is 3.7 mag closer than Coma. When we consider the Virgo galaxies alone in Fig. 9 we include dwarf systems with $L_{\rm H}$ fainter by almost 2 orders of magnitudes with respect to Coma. The scatter of the b vs. $L_{\rm H}$ relation increases considerably because the large majority of faint Virgo objects have b lower than Coma. This is in agreement with Kennicutt (1983) who found evidence for significant $\rm H_\alpha $ deficiency in 12 Virgo galaxies with respect to isolated galaxies. Galaxies with b as low as the ones in Virgo might exist in the Coma+A1367 clusters as well, but are not observed because of the previously mentioned observational bias. Thus we conclude that, at any given mass, spirals belonging to the Virgo cluster have their present star formation activity significantly lower than isolated galaxies.

It remains to be explained why. The first thing to explore is whether their gaseous content is sufficient for fueling the star formation. Cluster spirals are in fact known to suffer from HI deficiency (Giovanelli & Haynes 1985; Solanes et al. 2001), a pattern that is interpreted in the framework of the ram pressure mechanism (Gunn & Gott 1972).

When galaxies are separated according to their gas deficiency parameter (see Fig. 9), we recognize that, at any given $L_{\rm H}$, galaxies with "normal'' gas content ( $Def_{{\rm gas}}<0.4$) (open symbols) have their b parameter significantly higher than gas "deficient'' objects.


  \begin{figure} \par\includegraphics[width=8cm,clip]{ms2973f11.eps}\end{figure} Figure 11: Histograms of the residual $b_{{\rm obs}}-b_{{\rm mod}}$ for the Coma galaxies (dashed line), for Virgo (continuous line) and for the Virgo galaxies with normal HI content ( $Def_{{\rm gas}}<0.4$) (dashed histogram).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms2973f12.ps}\end{figure} Figure 12: The relation between $b_{{\rm obs}}-b_{{\rm mod}}$ and the $Def_{{\rm gas}}$ parameter. Empty circles are Coma supercluster galaxies, empty squares are "normal'' Virgo clouds (N, W, S), filled circles are "deficient'' Virgo clouds (A, B, E).
Open with DEXTER

Figure 10 is restricted to the non deficient galaxies of both the Virgo and Coma regions. In this and in the previous figures the dotted curve represents $b_{{\rm mod}}$ i.e. the b vs. $L_{\rm H}$ relation expected from the closed-box scenario, in the assumption that $\tau$ is inversely proportional to $L_{\rm H}$ according to Eq. (6). Galaxies in Fig. 10 are found in relatively good agreement with $b_{{\rm mod}}$, in other words their residuals $b_{{\rm obs}}-b_{{\rm mod}}$ are small. This is evidenced in the histograms of Fig. 11 where the distribution of the residuals $b_{{\rm resid}}= b_{{\rm obs}} - b_{{\rm mod}}$ is given separately for the Coma galaxies, for the Virgo galaxies and for the subsample of the Virgo galaxies with normal gas content ( $Def_{{\rm gas}}<0.4$). Large negative residuals, implying a factor of 3 lower SFR, are associated with significantly gas deficient galaxies. It is concluded that, at any given luminosity, the principal parameter regulating the current star formation activity in cluster spirals is the availability of gas at their interior. This is further evidenced in Fig. 12, where $b_{{\rm resid}}$ is plotted against the gas deficiency parameter, showing a significant linear anti-correlation: $b_{{\rm resid}}=0.04$- $0.68 \times Def_{{\rm gas}}$.


  \begin{figure} \par\includegraphics[width=6.3cm,clip]{ms2973f13.ps}\end{figure} Figure 13: The distribution of the "quenched" (empty symbols) and "healthy" (filled symbols) galaxies in the Virgo cluster. Positions of M87 and M49 are shown by crosses.
Open with DEXTER

6 Discussion and conclusions

We have shown that a large fraction of late-type galaxies in the Virgo cluster have their current star formation rate significantly quenched with respect to isolated objects. These systems coincide with the Virgo gas deficient galaxies. Since the "gas'' deficiency parameter is dominated by the HI phase (H2 contributes only to 15% of the HI), it is concluded that, to the first order, the star formation properties of galaxies in the Virgo cluster are determined by the pattern of HI deficiency. As earlier recognized by Kennicutt (1998), this is a somewhat surprising result, because the typical scales of HI and of star formation are very different in disk galaxies. HI reservoirs extend some 2 $\times$ the scale where the star formation takes place (Cayatte et al. 1994). We will re-examine this issue in more details in our forthcoming paper dedicated to the morphology of the star formation regions in galaxies, where a comparison between the scale-length of $\rm H_\alpha $, $\rm HI$ and $\rm H_{2}$ will be carried on specifically. Limiting ourself to the global quantities, they indicate that infall of HI gas occurs in the disks on time scales similar to the star formation time. If the gas replenishment fails, because the HI reservoir is reduced by some ablation mechanism (e.g. ram pressure), the star formation adjusts itself to significantly lower rates.


  \begin{figure} \par\includegraphics[width=14cm,clip]{ms2973f14a.eps}\end{figure} Figure 14: Newly observed galaxies with substantial $\rm H\alpha +[NII]$ structure. The NET (ON-OFF) frames are given with grey-scale, with superposed contours of the OFF frames. J2000 celestial coordinates are given.
Open with DEXTER


 \begin{figure} \par\includegraphics[width=14.4cm,clip]{ms2973f14b.eps} \end{figure} Figure 14: Continued.
Open with DEXTER


 \begin{figure} \par\includegraphics[width=14cm,clip]{ms2973f14c.eps} \end{figure} Figure 14: Continued.
Open with DEXTER

Galaxies with $b_{{\rm resid}}< -0.7 $ and $Def_{{\rm gas}}>0.4$ ("quenched'') are plotted in Fig. 13 with empty symbols, together with their "healthy'' counterparts (filled symbols). Beside a marginal clustering of deficient objects around M 87 (cluster A) and M 49 (cluster B) the two populations appear mixed in position. There is for example a considerable fraction of "healthy'' objects projected onto the center of cluster A. However Virgo is known to be a complex dynamical entity, composed by the main cluster (A) a secondary cluster (B), several Mpc behind A, and a number of clouds at approximately the distance of A, but with significantly discrepant velocities, suggesting infall (see Gavazzi et al. 1999a).

By considering galaxies with projected angular separation <3.7 deg from M 87 we isolate 68 bona fide members of cluster A. We divide them into 48 "quenched'' and 20 "healthy''. For a considerable fraction (22/48 and 13/20 respectively) their distance is available from Gavazzi et al. (1999a) based on the H band Tully-Fisher relation (Tully & Fisher 1977) (distances of few galaxies whose H magnitudes were not yet available to Gavazzi et al. 1999a were recomputed by us). To our surprise we find that, while the average distance modulus of the deficient objects ( $\mu_{\rm o}=$ 30.85) is in perfect agreement with the distance modulus of cluster A as a whole ( $\mu_{\rm o}=$ 30.82) (Gavazzi et al. 1999a), the distance modulus of the non-deficient galaxies projected onto A is $\mu_{\rm o}=$ 31.77 on average, thus almost one mag more distant. It is thus concluded that "healthy'' spirals projected onto the Virgo center belong in fact to a background cloud with a distance comparable with that of cluster B. This cloud has not yet entered the dense environment of cluster A.

7 Summary

Acknowledgements
This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.

References

 

Online Material


   
Table 4: Parameters of the analyzed galaxies.
Virgo
Gal Agg Type $\Theta$ H Dist. $Def_{{\rm gas}}$ ${\rm H_\alpha+[NII]} EW$ ${\rm Log} F({\rm H_\alpha})$ ref.
      deg mag Mpc   $\rm\AA$ $\rm erg~cm^{-2}~s^{-1}$  
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
VCC0001 VM BCD 5.63 12.75 32 - 12 -13.46 11
VCC0010 VM BCD 5.35 12.76 32 0.34 31 -12.98 6
VCC0017 VM Im 5.43 14.12 32 0.26 105 -12.78 9
VCC0025 VM Sc 6.10 9.96 32 -0.15 58 -11.50 11
VCC0047 VM Sa 4.62 10.70 32 0.79 16 -12.84 11
VCC0058 VM Sb 4.48 10.51 32 0.15 15 -12.31 11
VCC0066 VN Sc 4.68 9.01 17 -0.06 23 -11.45 1
VCC0067 VM Sc 4.66 11.27 32 0.36 27 -12.49 7
VCC0073 VW Sb 6.92 9.47 32 0.42 11 -12.19 11
VCC0081 VN Sc 4.85 12.78 17 -0.19 21 -13.06 11
VCC0083 VN Im 4.69 12.98 17 0.81 8 -13.73 6
VCC0087 VN Sm 5.17 13.66 17 0.39 20 -12.89 7
VCC0089 VM Sc 4.28 9.31 32 0.00 20 -11.73 1
VCC0092 VN Sb 4.84 7.06 17 0.30 9 -11.33 7
VCC0097 VM Sc 4.20 9.60 32 0.13 14 -12.13 11
VCC0120 VW Scd 7.70 10.42 32 0.18 54 -11.87 11
VCC0131 VN Sc 4.17 10.76 17 0.24 23 -12.48 11
VCC0144 VW BCD 7.66 12.95 32 0.07 144 -12.19 12
VCC0145 VN Sc 3.84 9.61 17 0.22 7 -11.84 7
VCC0152 VN Scd 4.69 9.77 17 0.39 9 -12.59 7
VCC0157 VN Sc 3.99 8.35 17 0.42 20 -11.43 1
VCC0159 VW Im 5.54 13.23 32 0.57 19 -13.16 7
VCC0162 VN Sd 4.06 11.48 17 0.48 30 -12.83 11
VCC0167 VN Sb 3.72 6.69 17 0.66 3 -11.32 7
VCC0199 VW Sa 6.05 8.86 32 0.84 10 -12.04 11
VCC0213 VN BCD 3.60 11.52 17 0.66 24 -12.62 12
VCC0221 VW Sc 9.35 11.23 32 0.54 53 -11.87 11
VCC0222 VW Sa 6.19 8.73 32 0.91 2 -12.55 7
VCC0226 VN Sc 4.42 8.89 17 -0.34 6 -12.23 1
VCC0234 VW Sa 6.59 9.23 32 1.40 14 -12.11 7
VCC0267 VB Sbc 6.55 10.92 23 0.16 11 -12.63 7
VCC0307 VN Sc 3.55 7.20 17 0.04 29 -10.76 7
VCC0318 VW Scd 4.57 12.97 32 0.04 51 -12.46 11
VCC0324 VS BCD 9.01 11.83 17 0.70 57 -12.27 12
VCC0328 VN Im 2.88 14.66 17 0.73 20 -13.62 9
VCC0341 VB Sa 6.90 8.70 23 0.94 2 -12.66 7
VCC0343 VA Sd 5.33 13.17 23 0.97 15 -13.37 T.W.
VCC0382 VW Sc 7.55 9.31 32 -0.27 31 -11.58 7
VCC0393 VB Sc 5.39 10.58 23 0.48 25 -12.14 11
VCC0410 VN BCD 2.57 16.37 17 0.61 77 -13.25 6
VCC0446 VB BCD 6.52 13.40 23 1.11 17 -13.43 7
VCC0459 VA BCD 5.74 12.72 17 0.27 47 -12.61 12
VCC0460 VA Sa 6.42 7.60 17 1.02 2 -11.65 1
VCC0465 VN Sc 2.49 9.86 17 0.27 57 -11.43 11
VCC0483 VA Sc 3.16 8.49 17 0.17 31 -11.41 7
VCC0491 VN Scd 2.41 10.99 17 0.02 74 -11.67 4
VCC0492 VB Sa 7.36 9.68 23 1.46 6 -12.54 11
VCC0497 VA Sc 3.13 8.11 17 0.46 15 -11.66 7
VCC0508 VS Sc 8.22 7.09 17 -0.02 34 -10.58 1
VCC0513 VS BCD 10.28 12.33 17 1.24 47 -12.67 12
VCC0524 VB Sbc 3.98 9.54 23 1.49 5 -12.32 7


 
Table 4: Continued.
Virgo
Gal Agg Type $\Theta$ H Dist. $Def_{{\rm gas}}$ ${\rm H_\alpha+[NII]} EW$ ${\rm Log} F({\rm H_\alpha})$ ref.
      deg mag Mpc   $\rm\AA$ $\rm erg~cm^{-2}~s^{-1}$  
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
VCC0530 VA Im 4.01 15.02 17 1.26 3 -14.06 9
VCC0534 VB Sa 5.66 9.95 23 1.56 8 -12.54 11
VCC0559 VA Sab 3.74 8.99 17 1.04 2 -12.66 7
VCC0562 VA BCD 2.02 15.75 17 0.85 84 -12.82 6
VCC0576 VB Sbc 3.65 9.61 23 0.16 14 -12.29 11
VCC0596 VA Sc 3.93 6.69 17 0.47 18 -10.81 7
VCC0613 VS Sa 7.39 8.67 17 0.54 6 -12.20 11
VCC0620 VA Sm 1.99 13.02 17 0.83 27 -13.64 7
VCC0630 VA Sd 2.11 9.77 17 1.20 7 -12.57 7
VCC0641 VB BCD 6.82 13.87 23 0.55 19 -13.51 7
VCC0655 VA BCD 5.44 10.66 17 0.68 6 -12.73 12
VCC0656 VB Sb 5.72 9.34 23 0.40 9 -12.06 7
VCC0664 VA Sc 1.73 12.24 17 0.70 101 -11.92 7
VCC0667 VB Sc 5.49 10.76 23 0.75 9 -12.77 11
VCC0688 VB Sc 4.90 11.00 23 0.63 9 -12.82 11
VCC0692 VA Sc 1.67 10.44 17 0.78 16 -12.27 13
VCC0697 VB Sc 5.60 11.05 23 0.80 14 -12.61 7
VCC0699 VB Pec 6.02 10.93 23 0.27 42 -12.22 11
VCC0713 VB Sc 4.18 9.81 23 1.44 8 -12.52 11
VCC0768 VA Sc 4.83 12.30 17 0.41 43 -12.63 11
VCC0785 VS Sa 7.59 8.41 17 0.28 8 -11.99 11
VCC0787 VB Scd 6.79 11.08 23 0.48 31 -12.31 12
VCC0792 VB Sab 2.73 8.55 23 0.86 10 -12.44 7
VCC0793 VA Im 1.50 15.29 17 0.59 2 -14.36 12
VCC0801 VA ? 4.28 9.63 17 -0.28 69 -11.52 7
VCC0802 VA BCD 1.71 14.64 17 0.77 36 -13.49 12
VCC0827 VB Sc 5.33 9.85 23 0.18 26 -12.05 11
VCC0836 VA Sab 1.26 8.21 17 0.73 15 -11.47 7
VCC0841 VA BCD 2.84 13.65 17 0.99 29 -13.08 T.W.
VCC0848 VB BCD 6.70 13.35 23 0.13 26 -13.00 12
VCC0849 VB Sbc 2.29 10.74 23 0.40 23 -12.10 4
VCC0851 VB Sc 4.99 10.71 23 0.38 20 -12.35 11
VCC0857 VA Sb 5.94 8.23 17 0.66 12 -11.77 7
VCC0865 VA Sc 3.48 10.33 17 0.51 34 -11.92 7
VCC0873 VA Sc 1.36 8.58 17 0.26 16 -11.76 12
VCC0874 VA Sc 3.96 9.63 17 0.42 3 -12.73 7
VCC0905 VB Sc 3.68 11.07 23 0.47 39 -12.44 7
VCC0912 VA Sbc 1.07 9.91 17 0.74 8 -12.36 7
VCC0921 VS Sbc 8.49 10.44 17 0.61 38 -11.83 11
VCC0938 VS Sc 4.58 10.20 17 0.52 20 -12.04 4
VCC0939 VB Sc 3.65 10.53 23 0.37 24 -12.17 4
VCC0950 VA Sm 1.28 12.98 17 0.23 23 -13.40 11
VCC0957 VS Sc 9.94 9.77 17 0.08 40 -11.55 1
VCC0958 VA Sa 2.82 8.03 17 0.22 7 -12.50 7
VCC0971 VB Sd 6.57 11.46 23 0.17 29 -12.47 11
VCC0975 VB Scd 5.21 11.06 23 0.39 26 -12.44 4
VCC0979 VB Sa 3.10 8.95 23 1.20 9 -12.02 7
VCC0980 VA Scd 3.61 12.45 17 0.88 40 -12.60 11
VCC0984 VA Sa 0.94 9.26 17 1.95 1 -12.97 7
VCC0995 VA Sc 1.75 13.03 17 -0.13 31 -12.79 7
VCC1002 VB Sc 6.19 9.65 23 0.53 9 -11.91 7
VCC1011 VS Sdm 4.82 12.30 17 0.78 13 -13.22 11
VCC1043 VA Sb 0.97 7.27 17 0.75 6 -11.57 13



 
Table 4: Continued.
Virgo
Gal Agg Type $\Theta$ H Dist. $Def_{{\rm gas}}$ ${\rm H_\alpha+[NII]} EW$ ${\rm Log} F({\rm H_\alpha})$ ref.
      deg mag Mpc   $\rm\AA$ $\rm erg~cm^{-2}~s^{-1}$  
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
VCC1110 VA Sab 4.73 7.13 17 0.93 2 -12.10 13
VCC1118 VB Sc 3.18 10.02 23 0.67 17 -12.14 11
VCC1126 VA Sc 2.66 9.39 17 1.48 11 -12.35 11
VCC1145 VS Sb 8.83 7.96 17 0.55 11 -11.53 7
VCC1179 VB BCD 2.43 13.25 23 1.25 20 -13.17 6
VCC1189 VS Sc 5.63 11.42 17 0.43 20 -12.47 7
VCC1190 VB Sa 3.66 8.27 23 2.07 3 -12.29 7
VCC1193 VS Sc 4.71 11.35 17 0.18 31 -12.38 11
VCC1200 VA Im 1.63 12.58 17 1.46 16 -13.56 7
VCC1205 VS Sc 4.58 10.23 17 0.05 11 -12.30 7
VCC1290 VS Sb 8.14 9.78 17 0.07 30 -11.89 11
VCC1313 VA BCD 0.35 15.60 17 0.38 291 -12.79 12
VCC1330 VS Sa 4.31 9.22 17 1.04 4 -12.48 11
VCC1356 VA BCD 0.91 13.10 17 0.43 43 -13.00 11
VCC1374 VA BCD 2.48 12.41 17 0.59 49 -12.48 6
VCC1375 VS Sc 8.45 11.17 17 0.09 28 -11.49 7
VCC1379 VA Sc 4.46 9.95 17 0.30 36 -11.72 11
VCC1393 VA Sc 2.74 10.87 17 0.43 38 -12.10 11
VCC1401 VA Sbc 2.05 6.60 17 0.41 6 -11.28 7
VCC1410 VA Sm 4.31 12.11 17 0.75 35 -12.66 11
VCC1411 VA Pec 0.65 13.83 17 0.53 2 -14.32 11
VCC1412 VA Sa 1.25 8.22 17 1.60 2 -12.32 7
VCC1419 VA S.. 1.08 10.39 17 1.77 5 -13.02 7
VCC1426 VA Im 0.63 13.13 17 1.24 6 -13.88 11
VCC1437 VS BCD 3.25 12.21 17 0.43 13 -13.19 12
VCC1450 VA Sc 1.72 10.85 17 0.65 69 -11.69 7
VCC1486 VA S.. 1.19 12.05 17 0.93 11 -13.14 7
VCC1508 VS Sc 3.79 9.73 17 -0.09 40 -11.58 11
VCC1516 VS Sbc 3.29 9.93 17 0.51 10 -12.19 13
VCC1532 VA Sc 3.06 10.68 17 1.00 17 -12.35 11
VCC1540 VS Sb 9.77 7.27 17 -0.18 20 -11.15 7
VCC1552 VA Sa 1.08 9.07 17 1.66 2 -12.78 7
VCC1554 VS Sm 5.99 9.79 17 -0.13 75 -11.35 13
VCC1555 VS Sc 4.28 7.64 17 0.23 17 -11.06 7
VCC1557 VS Scd 10.10 11.74 17 0.64 23 -12.69 11
VCC1562 VS Sc 10.24 7.78 17 0.18 20 -11.17 7
VCC1569 VA Scd 1.43 13.51 17 1.28 13 -13.42 7
VCC1575 VS Sm 5.32 11.27 17 0.35 13 -12.68 7
VCC1581 VS Sm 6.17 12.69 17 0.30 6 -13.41 11
VCC1585 VA Im 2.99 13.54 17 0.23 21 -13.04 9
VCC1588 VA Scd 3.31 9.43 17 0.74 3 -12.51 7
VCC1615 VA Sb 2.38 7.28 17 0.59 3 -11.78 1
VCC1624 VS Sc 9.43 10.35 17 0.80 11 -12.62 11
VCC1654 VA Im 2.79 14.22 17 0.48 20 -13.52 11
VCC1673 VA Sc 1.80 8.22 17 0.27 15 -11.80 7
VCC1675 VS Pec 4.56 12.56 17 1.40 4 -13.80 11
VCC1676 VA Sc 1.82 7.70 17 0.34 19 -11.54 7
VCC1678 VS Sd 5.94 12.52 17 0.18 51 -12.52 7
VCC1686 VA Sm 1.68 11.25 17 0.90 44 -12.12 11
VCC1690 VA Sab 1.65 7.02 17 0.80 2 -11.82 7
VCC1696 VA Sc 2.35 8.59 17 0.55 12 -11.86 4
VCC1699 VS Sm 5.68 12.47 17 0.36 24 -12.80 11
VCC1725 VS BCD 4.19 12.13 17 0.87 48 -12.56 12



 
Table 4: Continued.
Virgo
Gal Agg Type $\Theta$ H Dist. $Def_{{\rm gas}}$ ${\rm H_\alpha+[NII]} EW$ ${\rm Log} F({\rm H_\alpha})$ ref.
      deg mag Mpc   $\rm\AA$ $\rm erg~cm^{-2}~s^{-1}$  
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
VCC1726 VS Sdm 5.55 12.96 17 0.34 34 -12.75 7
VCC1727 VA Sab 1.78 6.77 17 0.45 4 -11.22 1
VCC1730 VS Sc 7.23 9.02 17 0.72 4 -12.42 7
VCC1757 VA Sa 1.96 10.81 17 1.57 7 -12.78 11
VCC1758 VS Sc 4.87 11.97 17 0.59 17 -12.87 11
VCC1760 VS Sa 8.29 8.74 17 1.03 5 -12.26 7
VCC1789 VS Im 7.74 12.95 17 0.91 16 -13.20 11
VCC1791 VS BCD 4.90 12.17 17 0.23 72 -12.37 11
VCC1811 VE Sc 3.64 9.92 17 0.28 11 -12.23 1
VCC1868 VE Scd 2.59 9.74 17 1.02 3 -13.13 7
VCC1918 VS Im 7.23 14.49 17 0.56 15 -13.85 11
VCC1923 VS Sbc 8.91 9.98 17 0.47 36 -11.73 11
VCC1929 VE Scd 3.48 10.78 17 0.57 12 -12.71 7
VCC1931 VE Im 3.02 13.04 17 0.45 36 -13.28 7
VCC1932 VE Sc 3.45 9.52 17 0.38 16 -12.13 7
VCC1943 VE Sb 3.06 8.90 17 0.31 24 -11.74 7
VCC1952 VE Im 5.62 14.60 17 0.29 32 -13.57 9
VCC1955 VE BCD 3.02 11.16 17 1.18 9 -13.05 12
VCC1972 VE Sc 3.21 8.38 17 0.12 16 -11.51 4
VCC1987 VE Sc 3.28 7.90 17 -0.18 30 -11.14 4
VCC1992 VE Im 3.27 14.10 17 0.23 24 -13.16 9
VCC2023 VE Sc 3.70 11.62 17 0.12 27 -12.36 11
VCC2033 VE BCD 5.42 13.06 17 1.06 13 -13.27 12
VCC2034 VE Im 4.36 13.23 17 0.72 2 -14.40 12
VCC2037 VE BCD 4.37 12.55 17 1.24 15 -13.42 7
VCC2058 VE Sc 4.34 8.37 17 0.72 13 -11.58 1
VCC2066 VE ? 4.49 9.28 17 0.89 6 -12.43 7
VCC2070 VE Sa 5.82 7.68 17 0.21 6 -11.78 4
Z013046 VZ Sa 12.53 8.93 17 0.36 17 -11.90 10
Z014062 VZ Scd 12.01 10.47 17 0.11 15 -12.52 4
Z014063 VZ Sc 12.29 7.61 17 0.41 32 -11.04 7
Z014110 VZ Sc 12.81 9.23 17 -0.21 34 -11.43 1
Z015031 VZ Sc 12.44 9.2 17 0.52 16 -12.11 T.W.
Z015049 VZ Sb 12.74 8.13 17 1.24 11 -11.89 T.W.
Z015055 VZ Sc 14.5 9.46 17 0.33 28 -11.89 T.W.
Z041041 VZ Scd 11.28 9.88 17 0.00 40 -11.77 T.W.
Z043028 VZ Sc 9.08 10.74 17 0.21 60 -11.82 T.W.
Z043034 VZ Sc 10.08 10.07 17 -0.05 51 -11.77 T.W.
Z043041 VZ Sc 8.51 9.62 17 -0.21 66 -11.29 4
Z043054 VZ Scd 9.67 10.97 17 0.00 71 -11.90 T.W.
Z043071 VZ Sc 10.18 9.25 17 -0.54 43 -11.37 1
Z043093 VZ Sc 12.34 8.87 17 0.07 40 -11.25 1
Z069036 VZ Sb 6.7 10.38 17 0.33 19 -12.32 T.W.
Z071060 VZ Sd 5.16 9.87 17 0.12 44 -11.92 7
Z098044 VZ Sa 4.87 8.78 17 1.20 7 -11.91 13
Z099098 VZ Sc 10.22 11.69 17 -0.43 18 -12.02 1
Z100004 VZ Sc 5.07 8.25 17 -0.11 20 -11.27 1
Z100015 VZ Scd 6.34 10.13 17 0.44 37 -12.06 T.W.
Coma/A1367 supercluster
Z097005 Iso Sc 2.74 12.41 81 -0.18 39 -12.66 11
Z097026 Prs Pec 1.77 11.65 83 -0.38 83 -12.18 11
Z097027 Prs Sc 1.77 11.84 88 0.37 22 -12.69 11



 
Table 4: Continued.
Coma/A1367 supercluster
Gal Agg Type $\Theta$ H Dist. $Def_{{\rm gas}}$ ${\rm H_\alpha+[NII]} EW$ ${\rm Log} F({\rm H_\alpha})$ ref.
      deg mag Mpc   $\rm\AA$ $\rm erg~cm^{-2}~s^{-1}$  
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
Z097062 A1367 Pec 0.53 12.94 91 0.34 37 -13.13 11
Z097063 A1367 Pec 0.55 13.56 91 0.18 22 -13.42 11
Z097064 A1367 S.. 0.58 12.41 91 0.20 1 -14.77 11
Z097068 A1367 Sbc 0.55 11.26 91 -0.25 41 -12.30 1
Z097072 A1367 Sa 0.44 11.36 91 0.32 5 -13.23 2
Z097073 A1367 Pec 0.37 13.19 91 0.00 111 -12.60 11
Z097076 A1367 Sb 0.36 11.39 91 1.39 1 -14.08 11
Z097079 A1367 Pec 0.33 13.15 91 0.10 129 -12.61 11
Z097087 A1367 Pec 0.20 11.01 91 0.14 77 -12.07 5
Z097091 A1367 Sa 0.27 11.07 91 -0.05 23 -12.66 14
Z097092 A1367 Sbc 0.38 12.57 91 0.04 28 -13.10 1
Z097093 A1367 Pec 0.09 12.90 91 0.47 9 -13.47 5
Z097102 A1367 Sa 0.40 11.40 91 0.44 2 -13.66 5
Z097114 A1367 Pec 0.11 13.19 91 - 36 -13.19 14
Z097120 A1367 Sa 0.10 10.55 91 0.45 4 -12.93 2
Z097122 A1367 Pec 0.38 11.74 91 0.43 46 -12.53 2
Z097129N A1367 Sb 0.22 9.77 91 -0.37 14 -12.23 5
Z097129S A1367 Sbc 0.22 11.91 91 - 17 -13.08 5
Z097138 A1367 Pec 0.38 13.92 91 -0.13 64 -12.77 5
Z097149 A1367 S.. 0.93 11.68 91 0.23 13 -13.26 3
Z097168 Iso S.. 1.81 12.41 80 0.42 78 -13.00 8
Z098002 Iso Sb 2.32 13.13 82 0.12 34 -12.76 8
Z098013 Iso Sc 3.49 11.73 92 -0.10 35 -12.58 5
Z098016 Iso Sc 4.12 12.12 86 0.17 31 -12.70 5
Z098023 Prs Sb 4.53 11.58 92 - 11 -13.00 5
Z098041 Grp Sc 4.66 11.86 97 0.70 66 -12.18 3
Z098046 Grp Sa 4.75 10.66 97 0.21 8 -12.76 3
Z098058 Iso Sbc 5.50 10.70 96 0.00 11 -12.70 5
Z098081 Prs Sa 6.52 11.57 96 - 14 -12.86 5
Z098085 Prs Sc 6.64 12.05 94 -0.04 29 -12.50 3
Z098116 Iso Sc 7.33 11.87 83 -0.25 39 -12.34 5
Z100005 Iso Pec 9.85 10.66 88 0.32 19 -12.54 3
Z100012 Iso Pec 10.10 12.47 86 -0.04 39 -12.89 5
Z101033 Iso Sc 9.80 12.29 89 0.14 16 -13.34 11
Z101049 Iso Sbc 10.09 11.49 95 -0.23 10 -12.88 11
Z101054 Iso Sab 12.05 10.75 88 -0.04 11 -12.61 5
Z127005 Iso Sbc 3.04 12.22 91 0.05 26 -12.82 5
Z127018 Iso Sb 3.06 12.33 92 - 16 -12.89 3
Z127025S Prs Sbc 2.74 11.20 94 -0.02 22 -12.39 2
Z127025N Prs Sc 2.76 11.73 95 - 21 -12.70 3
Z127026 Iso Sbc 6.01 11.30 91 -0.16 15 -12.70 11
Z127033 Iso Sc 5.02 11.46 84 0.06 10 -12.96 5
Z127035 Iso Sa 4.13 11.21 91 0.29 10 -12.93 5
Z127037 Iso Pec 5.19 12.90 82 -0.00 47 -12.77 5
Z127038 Iso Sc 2.91 10.54 92 -0.18 16 -12.27 2
Z127039 Iso Sbc 3.20 12.16 92 - 48 -12.54 3
Z127049 A1367 Pec 0.87 11.93 91 0.29 57 -12.84 8
Z127050 Grp Sbc 1.26 11.38 93 0.00 16 -12.53 2
Z127052 A1367 Sa 0.71 9.79 91 0.27 4 -12.70 5
Z127053 Iso Sbc 4.18 11.33 85 -0.10 17 -12.74 5
Z127054 Grp Sb 1.02 10.62 93 0.10 4 -12.81 5
Z127055 Iso Pec 1.55 12.06 89 - 41 -12.74 8
Z127061 Iso Sc 5.24 12.99 79 -0.12 29 -12.70 11



 
Table 4: Continued.
Coma/A1367 supercluster
Gal Agg Type $\Theta$ H Dist. $Def_{{\rm gas}}$ ${\rm H_\alpha+[NII]} EW$ ${\rm Log} F({\rm H_\alpha})$ ref.
      deg mag Mpc   $\rm\AA$ $\rm erg~cm^{-2}~s^{-1}$  
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
Z127071 Grp Pec 2.02 12.83 93 0.22 52 -12.71 3
Z127082 Grp Sc 2.20 11.39 93 0.11 22 -12.59 2
Z127095 Grp Sc 2.29 10.55 93 0.03 15 -12.36 2
Z127100 Grp Sb 2.37 11.05 93 0.06 10 -12.87 2
Z128003 Iso Pec 5.05 11.61 86 -0.07 41 -12.48 3
Z128015 Prs Sb 5.01 11.96 91 - 21 -12.78 5
Z128016 Iso S.. 5.32 12.07 88 -0.13 35 -12.69 3
Z128021 Iso Sbc 7.19 10.95 94 0.03 16 -12.68 5
Z128023 Grp Sa 5.08 10.70 97 -0.16 17 -12.43 3
Z128049 Iso Sc 8.58 11.31 86 0.41 20 -12.85 3
Z128063 Prs Sa 7.56 11.07 90 0.19 4 -13.28 3
Z128072 Iso Pec 9.20 12.26 91 - 37 -12.81 5
Z128073 Iso Sb 9.52 11.29 92 -0.02 16 -12.63 5
Z128080 Iso Sb 9.34 11.76 98 -0.13 24 -12.67 3
Z128087 Iso Sc 8.02 11.55 89 0.20 14 -12.83 5
Z128089 Iso Sa 9.15 10.76 91 0.40 9 -12.78 5
Z129004 Iso S.. 8.82 12.04 91 - 34 -12.77 5
Z129020 Iso Sb 7.99 10.94 87 0.15 10 -12.81 5
Z129021 Iso S.. 7.60 11.83 89 -0.96 24 -12.72 3
Z129022 Iso Sab 5.96 10.63 93 -0.10 8 -12.63 3
Z130003 Iso Sb 6.17 11.01 95 - 19 -12.60 5
Z130005 Iso Sbc 5.77 12.24 94 0.22 40 -12.69 11
Z130006 Iso Sbc 2.35 11.45 87 -0.04 32 -12.59 5
Z130008 Iso Sc 2.89 11.89 97 -0.41 49 -12.37 2
Z130014 Iso Sbc 4.07 11.36 94 0.05 20 -12.64 3
Z130021 Iso Sa 4.31 11.57 95 0.16 28 -12.54 5
Z130025 Iso Sa 7.10 11.18 93 0.17 1 -14.26 11
Z130026 Prs Sc 8.34 11.59 91 0.02 18 -12.67 11
Z130029 Prs Sc 8.40 11.35 90 - 54 -12.31 11
Z131008 Iso Sbc 9.48 11.16 79 -0.03 27 -12.67 11
Z131009 Iso Sc 7.40 12.39 100 0.05 27 -12.74 5
Z157012 Iso Sbc 9.08 12.40 91 -0.18 30 -12.65 3
Z157032 Iso Sa 9.78 9.79 91 0.78 1 -13.75 5
Z157035 Iso Sb 10.57 10.34 83 -0.18 19 -12.09 3
Z157044 Iso Pec 7.14 12.86 88 - 40 -13.00 5
Z157062 Iso Pec 11.64 14.53 92 0.12 77 -12.87 11
Z157064 Iso Sb 9.71 11.72 85 -0.02 11 -12.79 5
Z157075 Iso Sc 7.58 12.97 89 0.18 29 -13.14 T.W.
Z158009 Prs Sb 12.24 10.77 100 0.11 17 -12.41 3
Z158010 Prs Sbc 12.23 12.07 105 0.19 22 -12.89 3
Z158036 Iso Sb 8.89 10.24 87 -0.17 11 -12.51 5
Z158038 Iso Sab 11.23 11.66 90 0.23 23 -12.68 3
Z158054 Iso Pec 9.86 12.01 102 -0.02 72 -12.35 3
Z158081 Iso Pec 9.15 11.85 90 0.02 24 -12.80 3
Z158105 Iso Sbc 7.93 11.50 91 -0.12 17 -12.71 5
Z159008 Iso Sb 6.71 10.98 98 0.03 24 -12.44 5
Z159031 Prs Sa 5.09 11.55 100 -0.02 9 -12.99 3
Z159033 Iso Sa 4.98 10.85 102 0.65 2 -13.50 5
Z159037 Iso Sab 4.86 11.50 97 -0.13 44 -12.42 11
Z159040 Iso Sa 5.14 12.20 93 -0.19 26 -12.69 3
Z159059 Iso Sab 3.73 12.15 100 -0.26 61 -12.34 5
Z159061 Iso Sbc 4.77 11.18 93 0.29 4 -13.26 5
Z159071 Iso Sc 3.43 12.78 92 - 32 -12.84 11



 
Table 4: Continued.
Coma/A1367 supercluster
Gal Agg Type $\Theta$ H Dist. $Def_{{\rm gas}}$ ${\rm H_\alpha+[NII]} EW$ ${\rm Log} F({\rm H_\alpha})$ ref.
      deg mag Mpc   $\rm\AA$ $\rm erg~cm^{-2}~s^{-1}$  
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
Z159072S Prs Pec 4.06 10.84 88 0.01 12 -12.77 11
Z159072N Prs Pec 4.07 10.85 88 0.09 4 -13.30 11
Z159076 Iso Sbc 3.27 11.08 90 0.30 15 -12.61 2
Z159090 Prs Sc 2.05 12.25 111 -0.47 22 -12.83 2
Z159091 Iso S.. 2.17 11.74 86 -0.19 6 -13.34 3
Z159095 Iso Sbc 3.60 11.23 91 -0.20 4 -13.32 5
Z159096 Iso Sc 3.82 12.10 82 0.08 22 -12.76 5
Z159097 Iso Pec 1.98 12.22 86 - 18 -13.15 5
Z159101 Coma Pec 1.67 13.50 96 0.14 64 -12.78 5
Z159102 Coma Sab 1.60 10.60 96 -0.22 31 -12.28 5
Z160001 Coma Sb 1.66 12.34 96 0.10 15 -13.17 11
Z160005 Iso Sb 2.07 10.47 84 0.01 3 -13.35 5
Z160009 Coma S.. 1.25 11.44 96 - 6 -13.46 11
Z160020 Coma Pec 0.90 13.36 96 0.08 33 -12.84 5
Z160025 Coma Sa 1.25 10.35 96 1.03 2 -13.29 5
Z160026 Coma Sc 1.03 12.53 96 0.20 35 -12.87 5
Z160032 Coma Sb 1.64 11.69 96 0.52 10 -13.05 5
Z160055 Coma Sab 0.48 10.91 96 0.39 31 -12.34 14
Z160058 Coma Sbc 0.82 11.87 96 0.22 22 -12.82 2
Z160064 Coma Pec 0.77 12.79 96 0.32 67 -12.94 5
Z160067 Coma Pec 0.85 13.16 96 -0.21 78 -12.67 5
Z160073 Coma Pec 0.38 12.50 96 0.43 23 -12.98 5
Z160076 Coma Sc 0.65 13.64 96 -0.23 47 -12.83 5
Z160086 Coma Pec 0.37 13.18 96 0.76 41 -13.04 5
Z160088 Coma Sb 1.05 11.12 96 0.20 16 -12.65 5
Z160095 Coma Sb 0.35 9.50 96 0.72 4 -12.66 5
Z160096N Coma Pec 1.37 11.36 96 0.02 39 -12.51 3
Z160098 Coma Pec 0.77 12.04 96 0.17 22 -12.95 5
Z160102 Coma Sab 1.14 11.13 96 0.13 6 -12.63 2
Z160106 Coma Pec 0.59 10.84 96 0.33 20 -12.98 2
Z160108 Coma Pec 0.56 12.90 96 0.45 37 -13.00 11
Z160121 Coma Sb 1.64 11.21 96 0.05 21 -12.93 T.W.
Z160127 Coma Sc 1.21 13.29 96 -0.01 67 -12.53 5
Z160128 Coma Pec 1.29 13.67 96 - 87 -12.65 5
Z160137 Coma Sa 1.77 10.57 96 0.00 11 -12.51 2
Z160139 Coma Pec 1.71 13.26 96 -0.04 51 -12.58 5
Z160141 Coma Pec 1.61 12.51 96 0.39 30 -13.08 11
Z160148 Iso Sa 1.99 10.73 80 0.11 7 -12.83 2
Z160151 Iso Pec 2.48 12.57 83 0.40 28 -12.87 3
Z160152 Iso Sb 2.36 10.85 75 0.02 17 -12.32 2
Z160156 Prs Sa 2.91 10.98 97 0.23 10 -12.81 3
Z160168 Iso Sc 4.19 10.87 100 -0.34 15 -12.50 5
Z160182 Iso Sab 3.97 11.13 93 0.11 12 -12.72 3
Z160192 Iso Sb 4.27 10.49 88 -0.12 2 -13.20 5
Z160213 Coma Pec 0.24 13.07 96 -0.08 57 -12.87 7
Z160252 Coma Pec 0.18 12.37 96 0.10 37 -12.88 14
Z160257 Coma Sa 0.27 10.55 96 0.69 6 -12.93 2
Z160260 Coma Sa 0.30 10.29 96 0.50 11 -12.61 14
Z161040 Iso Sc 5.42 12.73 97 0.09 21 -13.18 11
Z161052 Iso Pec 6.15 12.55 94 -0.57 44 -12.67 11
Z161054 Iso Sa 6.62 12.84 90 - 43 -12.73 11
Z161063 Iso Sbc 6.83 12.62 95 -0.05 22 -12.89 5
Z161069 Iso Sb 7.22 11.15 95 -0.30 24 -12.46 7



 
Table 4: Continued.
Coma/A1367 supercluster
Gal Agg Type $\Theta$ H Dist. $Def_{{\rm gas}}$ ${\rm H_\alpha+[NII]} EW$ ${\rm Log} F({\rm H_\alpha})$ ref.
      deg mag Mpc   $\rm\AA$ $\rm erg~cm^{-2}~s^{-1}$  
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
Z161071 Iso Pec 7.40 13.22 64 -0.16 48 -12.55 3
Z161073 Iso Sb 7.55 10.31 97 -0.21 4 -12.83 3

References: (1) Kennicutt & Kent (1983); (2) Kennicutt et al. (1984); (3) Gavazzi et al. (1991); (4) Romanishin (1990); (5) Gavazzi et al. (1998); (6) Almoznino & Brosch (1998); (7) Boselli & Gavazzi (2002); (8) Moss et al. (1998); (9) Heller et al. (1999); (10) Usui et al. (1998); (11) Gavazzi et al. (2002a); (12) Boselli et al. (2002b); (13) Koopmann et al. (2001); (14) Iglesias et al. (2002); (T.W.) This work.

Copyright ESO 2002