![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{aa2895f1.ps}\end{figure}](/articles/aa/full/2002/47/aa2895/Timg17.gif) |
Figure 1:
Example of Gaussian fit for the blended lines H |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{aa2895f1.ps}\end{figure}](/articles/aa/full/2002/47/aa2895/Timg17.gif) |
Figure 1:
Example of Gaussian fit for the blended lines H |
The prominent spectral features of SFGs and AGNs include some
commonly found strong emission lines, such as [O II]3727, H![]() 4861,
[O III]4959,5007, H
4861,
[O III]4959,5007, H![]() 6563, [N II]6583, [S II]6716, 6731, and some less
common emission lines, such as H
6563, [N II]6583, [S II]6716, 6731, and some less
common emission lines, such as H![]() 4340, [O III]4363, He I5876, and
[O I]6300.
4340, [O III]4363, He I5876, and
[O I]6300.
The rest-frame equivalent widths, EWs, and integrated fluxes, F,
of the emission lines were measured by direct numerical integration,
using the SPLOT program in IRAF. The continuum levels and
integration limits for the lines were set interactively, with repeat
measurements made in difficult case. For single emission lines
such as H![]() 4861, [O III]5007, direct integral methods were used. This
method allows the measurement of lines with asymmetric shapes (i.e.
with deviations from Gaussian profiles). For blended lines such
as H
4861, [O III]5007, direct integral methods were used. This
method allows the measurement of lines with asymmetric shapes (i.e.
with deviations from Gaussian profiles). For blended lines such
as H![]() ,
[N II]6548,6583, and the [S II]6716, 6731 doublet, we used the
Gaussian deblending program of SPLOT. In Fig. 1, as an example,
we show the three narrow Gaussian components to fit of H
,
[N II]6548,6583, and the [S II]6716, 6731 doublet, we used the
Gaussian deblending program of SPLOT. In Fig. 1, as an example,
we show the three narrow Gaussian components to fit of H![]() ,
[N II]6548,6583 of III Zw 43. Note that in these blended cases, the
lines are only partly blended. The interactive method allows us to
control by eye the level of the continuum, taking into account
defects that may be present around the line measured. It does not
have the objectivity of automatic measurements, but it does allow
us to obtain reliable, accurate measurements.
,
[N II]6548,6583 of III Zw 43. Note that in these blended cases, the
lines are only partly blended. The interactive method allows us to
control by eye the level of the continuum, taking into account
defects that may be present around the line measured. It does not
have the objectivity of automatic measurements, but it does allow
us to obtain reliable, accurate measurements.
The equivalent widths of various emission lines are listed
in Table 1, for all SFGs and active galactic nuclei.
The objects are ordered by increasing right ascension at the epoch
2000 (
![]() ).
Column 1 lists the galaxy name (same as Table 1 of Paper I).
Columns 2-9 list the equivalent widths of the commonly found
emission lines.
Columns 10-13 list the equivalent widths of less commonly found
emission lines.
The second line for each entry lists an estimate of the error (see in
Sect. 3.2).
We use the convention that positive equivalent widths denote emission
to conserve space and improve readability. A dash in the table indicates
either that the corresponding segment of the spectrum is lacking or that
the spectrum was too noisy in the region to give a reliable value of
equivalent widths.
We have chosen an equivalent width of 1.0 Å as the lower limit for
true detection. The observed emission line fluxes (the Galactic
foreground reddening were corrected, see Kong & Cheng 2002) are listed
in Table 2.
).
Column 1 lists the galaxy name (same as Table 1 of Paper I).
Columns 2-9 list the equivalent widths of the commonly found
emission lines.
Columns 10-13 list the equivalent widths of less commonly found
emission lines.
The second line for each entry lists an estimate of the error (see in
Sect. 3.2).
We use the convention that positive equivalent widths denote emission
to conserve space and improve readability. A dash in the table indicates
either that the corresponding segment of the spectrum is lacking or that
the spectrum was too noisy in the region to give a reliable value of
equivalent widths.
We have chosen an equivalent width of 1.0 Å as the lower limit for
true detection. The observed emission line fluxes (the Galactic
foreground reddening were corrected, see Kong & Cheng 2002) are listed
in Table 2.
For measurements of emission lines and absorption lines where the
slope and curvature of the continuum are well defined, the main
sources of random errors in the flux and equivalent width
measurements are the uncertainty of the overall height of the
continuum level, the individual intensity points within the
interval of integration, the signal-to-noise ratio of the continuum,
and the uncertainty in the choice of the best-fitting profile
parameter. To estimate ![]() standard deviations of emission
lines, we followed the method outlined in Tresse et al. (1999), based
on the formulae of propagation of errors and Poisson statistics.
The derivation of error formulae can also be found in Longhetti et al. (1998).
standard deviations of emission
lines, we followed the method outlined in Tresse et al. (1999), based
on the formulae of propagation of errors and Poisson statistics.
The derivation of error formulae can also be found in Longhetti et al. (1998).
The error
![]() in the flux F of an emission line can be
expressed as (Tresse et al. 1999):
in the flux F of an emission line can be
expressed as (Tresse et al. 1999):
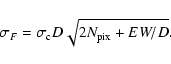 |
(1) |
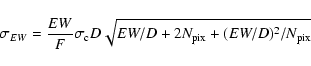 |
(2) |
In Fig. 2, we plot a logarithm of the detection level
of equivalent widths, log (
![]() ), versus log EW for
4 commonly found emission lines, [O II]3727, H
), versus log EW for
4 commonly found emission lines, [O II]3727, H![]() ,
[O III]5007, and H
,
[O III]5007, and H![]() with equivalent widths above 1.5 Å.
The result shows our equivalent widths limit is at a
with equivalent widths above 1.5 Å.
The result shows our equivalent widths limit is at a ![]() confidence level for those commonly found emission lines, and the
typical uncertainty in these measurements is less than 10%. For
those less common lines, such as H
confidence level for those commonly found emission lines, and the
typical uncertainty in these measurements is less than 10%. For
those less common lines, such as H![]() 4340, [O I]6300, the measurements
typically have confidence levels
4340, [O I]6300, the measurements
typically have confidence levels ![]() 2
2![]() ,
and the typical
uncertainty in these measurements is about 20%.
,
and the typical
uncertainty in these measurements is about 20%.
Fluxes of emission lines will be used to determine the internal
reddening of emission line regions, the star formation rate, and
the element abundance of galaxies. It is known that the
measurements are an underestimate of the real flux of the spectral
lines, because of the underlying absorption component. To correct
the underlying stellar absorption, some authors (such as
Popescu & Hopp 2000) adopt a constant equivalent width (1.5-2 Å)
for all the hydrogen absorption lines.
Because the real value of the absorption equivalent width is
uncertain and dependent on the age of star formation burst and star
formation history (Izotov et al. 1994; González Delgado et al. 1999), the other usual
correction
for the contamination by stellar absorption lines assumes absorption
equivalent widths, and iterates until the color excesses derived from
H![]() /H
/H![]() ,
H
,
H![]() /H
/H![]() ,
and H
,
and H![]() /H
/H![]() ratios converge to the same value
(Izotov et al. 1994).
ratios converge to the same value
(Izotov et al. 1994).
To derive the absorption equivalent width for hydrogen lines, we have applied an empirical population synthesis method, which uses observed properties of star clusters as a base (Cid Fernandes et al. 2001), to our BCG spectra. This empirical population synthesis method can give the synthetic stellar population spectrum, so we can measure these underlying stellar absorption features for hydrogen lines. A full description of this application and equivalent widths of underlying stellar absorption lines will be presented in a forthcoming paper.
Emission line fluxes of H![]() ,
H
,
H![]() ,
and H
,
and H![]() are corrected for this
underlying absorption effect as follows:
are corrected for this
underlying absorption effect as follows:
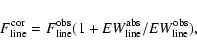 |
(3) |
The extinction of interstellar dust in SFGs
modifies the spectra of these objects. It is necessary to correct
all observed line fluxes for this internal reddening. The most
widely method used to correct the emission line spectra for the
presence of dust is based on the relative strengths of low order
Balmer lines. In order to have an internally
consistent sample, we applied this method to each of our objects,
using only the ratio of the two strongest Balmer lines, H![]() /H
/H![]() .
.
We used the effective absorption curve
![]() ,
which was introduced by
Charlot & Fall (2000). The color excesses
arising from attenuation by dust in a galaxy,
,
which was introduced by
Charlot & Fall (2000). The color excesses
arising from attenuation by dust in a galaxy,
![]() ,
can be written:
,
can be written:
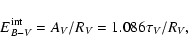 |
(4) |
![\begin{displaymath}\tau_V =
-\frac{{\rm ln}[F(\hbox{H$\alpha$ })/F(\hbox{H$\bet...
...m H\alpha}/5500)^{-0.7} - (\lambda_{\rm
H\beta}/5500)^{-0.7}]}
\end{displaymath}](/articles/aa/full/2002/47/aa2895/img36.gif) |
(5) |
The value of the color excess was then applied to the observed
spectrum, and the final, intrinsic line fluxes relative to H![]() for
each galaxy can be expressed as:
for
each galaxy can be expressed as:
![\begin{displaymath}\frac{I(\lambda)}{I(\rm H\beta)} =\frac{F(\lambda)}{F(\rm H\b...
...[(\lambda/5500)^{-0.7} - (\lambda_{\rm
H\beta}/5500)^{-0.7}]},
\end{displaymath}](/articles/aa/full/2002/47/aa2895/img44.gif) |
(6) |
Seven galaxies in our BCG sample - III Zw 43 (0211+038), II Zw 40 (0553+033), Mrk 5 (0635+756), I Zw 18 (0930+554), Haro 4 (1102+294), Haro 29 (1223+487), I Zw 123 (1535+554) - have been observed previously by Izotov, Thuan & Lipovetsky (1997, ITL97), Izotov & Thuan (1998, IT98), and Guseva et al. (2000, GIT00), with the Ritchey-Chretien spectrograph at the Kitt Peak National Observatory (KPNO) 4 m telescope, and with the GoldCam spectrograph at the 2.1 m KPNO telescope. These high signal-to-noise ratio spectrophotometric observations allow us to test the quality of our data. We perform a detailed comparison of these previous works in this subsection.
In III Zw 43, GIT00 did not detect [O III]4363 line, the [S II]6731
line intensity ratio is about 10% higher, and the other emission
line ratios are in good agreement with ours.
For II Zw 40 in GIT00, Haro 29 in ITL97, our data are
in fairly good agreement with these works. In Mrk 5, our [O I]6300
and [S II]6717 line intensities are about 25% higher, and [O II]
is ![]() 13% lower than that in IT98. In I Zw 18, our H
13% lower than that in IT98. In I Zw 18, our H![]() ,
[O III]4363, [S II] line intensities are stronger, but He I5876 is
weaker. In Haro 4, some less strong lines are not good agreement
with IT98.
Finally for I Zw 123, the agreement is not good as the other
galaxies, our
,
[O III]4363, [S II] line intensities are stronger, but He I5876 is
weaker. In Haro 4, some less strong lines are not good agreement
with IT98.
Finally for I Zw 123, the agreement is not good as the other
galaxies, our
![]() data have large differences with
ITL97, but the
data have large differences with
ITL97, but the
![]() are in good agreement with ITL97.
are in good agreement with ITL97.
We now display this comparison in a more visible form in Fig. 3.
The horizontal axis represent different spectral
lines, the vertical axis shows the differences between our line
intensities (
![]() )
and the values of GIT00,
IT98 and ITL97 (
)
and the values of GIT00,
IT98 and ITL97 (
![]() ). We found, our line
intensity ratios are in good agreement with these previous works for
most spectral lines of most galaxies, the difference between our
sample and these works is less than 10% for those strong emission
lines, and less than 15% for those less strong lines, such as
H
). We found, our line
intensity ratios are in good agreement with these previous works for
most spectral lines of most galaxies, the difference between our
sample and these works is less than 10% for those strong emission
lines, and less than 15% for those less strong lines, such as
H![]() 4340, [O III]4363, [O I]6300 of most galaxies.
4340, [O III]4363, [O I]6300 of most galaxies.
The observed fluxes of H![]() in our data are larger than those in
previous works, the explanation could be: 1) the data in these
previous works were not corrected for the Galactic extinction; 2)
Our slit width is larger than that of previous works; 3) the position
angle of slit is different between ours and those previous works.
We will discuss the slit effect and derive an aperture correction
for each galaxy in a future paper.
in our data are larger than those in
previous works, the explanation could be: 1) the data in these
previous works were not corrected for the Galactic extinction; 2)
Our slit width is larger than that of previous works; 3) the position
angle of slit is different between ours and those previous works.
We will discuss the slit effect and derive an aperture correction
for each galaxy in a future paper.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{aa2895f3.ps}\end{figure}](/articles/aa/full/2002/47/aa2895/Timg50.gif) |
Figure 3:
Difference between our line intensity ratios
|
Copyright ESO 2002