A&A 396, 693-703 (2002)
DOI: 10.1051/0004-6361:20021367

Stability analysis of relativistic jets from collapsars and its implications on the short-term variability of gamma-ray bursts

M.-A. Aloy1 - J.-M. Ibáñez2 - J.-A. Miralles3 - V. Urpin2,4


1 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, Postfach 1523, Garching, 85748, Germany
2 - Departamento de Astronomía y Astrofísica, Universidad de Valencia, 46100 Burjassot, Spain
3 - Departament de Física Aplicada, Universitat d'Alacant, Ap. Correus 99, 03080 Alacant, Spain
4 - A.F. Ioffe Institute of Physics and Technology, 194021 St. Petersburg, Russia

Received 2 July 2002 / Accepted 30 August 2002

Abstract
We consider the transverse structure and stability properties of relativistic jets formed in the course of the collapse of a massive progenitor. Our numerical simulations show the presence of a strong shear in the bulk velocity of such jets. This shear can be responsible for a very rapid shear-driven instability that arises for any velocity profile. This conclusion has been confirmed both by numerical simulations and theoretical analysis. The instability leads to rapid fluctuations of the main hydrodynamical parameters (density, pressure, Lorentz factor, etc.). However, the perturbations of the density are effectively decoupled from those of the pressure because the beam of the jet is radiation-dominated. The characteristic growth time of instability is much shorter than the life time of the jet and, therefore, may lead to a complete turbulent beam. In the course of the non-linear evolution, these fluctuations may yield to internal shocks which can be randomly distributed in the jet. In the case that internal shocks in a ultrarelativistic outflow are responsible for the observed phenomenology of gamma-ray bursts, the proposed instability can well account for the short-term variability of gamma-ray light curves down to milliseconds.

Key words: magnetohydradynamics (MHD) - gamma rays: bursts - gamma ray: theory - ISM: jets and outflows - galaxies: jets


1 Introduction

Catastrophic stellar events like massive stellar core collapse (see, e.g., van Putten 2001; Mészáros 2001 and references therein) or merging of a binary neutron star (Paszynski 1996; Eichler et al. 1989; Mochkovitch et al. 1993) have been proposed to explain the energetics of gamma-ray bursts (GRB). Nowadays, an increasing amount of observational evidence stresses the association, at least, of some GRB events with massive progenitors (Bulik et al. 1999; Bloom et al. 1999; Hanlon et al. 2000; Reeves et al. 2002). One of the most attractive scenarios is the collapsar model (Woosley 1993; MacFadyen & Woosley 1999) which can produce the required energy of a GRB even at cosmological distances. This model involves the collapse of the central core of a massive, evolved star to a newly-formed black hole (BH). The progenitor star can be, for instance, a rotating Wolf-Rayet star (1993). Hydrodynamic simulations of collapsars have been performed for a 35 $M_{\odot}$ main-sequence star whose 14 $M_{\odot}$helium core collapses to form 2-4 $M_{\odot}$ black hole. Provided that the core has a sufficient amount of angular momentum, a massive geometrically thick accretion disc of several tenths of a solar mass can be formed around the BH. The BH accretes matter from the disc at rates of the order of solar masses per second. The burst is generated by a local energy deposition due to the annihilation of $\nu-\bar{\nu}$ coming from the accretion disk or/and due to the release of the BH spin energy by means of magnetic fields. In either case, the energy is preferentially released along the rotation axis, close to the central engine and gives rise to a relativistically expanding bubble of radiation and pairs. The duration of the burst is given by the hydrodynamic time scale for the core of the star and its Helium envelope to collapse or by the viscous evolution time for the accretion disc, whichever is greater. In order to produce a long-duration GRB with a complex pulse structure, accretion is argued to proceed over a period of time comparable to the prompt phase of a GRB. The energy released due to accretion is sufficient to drive a collimated, baryon-dilute fireball that penetrates the outer layers of the star forming a relativistic jet (Aloy et al. 2000).

Recent observations indicate that the rapid temporal decay of several GRB afterglows is consistent with the evolution of a highly relativistic jet after it slows down and spreads laterally rather than with a spherical blast wave (Sari, Piran & Halpern 1999; Halpern et al. 1999; Kulkarni et al. 1999; Rhoads 1999). Therefore, formation of relativistic jets of baryon-clean material with bulk Lorentz factors $\sim$ 102- 103 represents a mayor problem in the collapsar model of GRB. Detailed simulations of formation and propagation of a relativistic jet in collapsars have been performed by Aloy et al. (2000). Assuming an enhanced efficiency of energy deposition in polar regions (with a constant or varying deposition rate), the authors obtained an ultrarelativistic jet along the rotation axis, which is highly focused (with the half-opening angle $\sim$ $ 6{-}10^{\circ}$) and is capable of penetrating the star. The simulations were performed with the multidimensional relativistic hydrodynamic code GENESIS (Aloy et al. 1999) using a two-dimensional spherical grid. A relativistic jet in this model forms within a fraction of a second and exhibits the main morphological elements of "standard'' jets: a terminal bow shock, a narrow cocoon, a contact discontinuity, and a hot spot. The maximum Lorentz factor is as large as $\sim$25-30 at break-out, and can be even greater after the break-out ($\approx$44 at the end of simulations). This Lorentz factor is only a bit smaller than the critical value $\sim$ 102-103 that one requires for the fireball model (Cavallo & Rees 1978; Piran 1999).

According to current views, the GRB is made either as the jet encounters a sufficient amount of mass in circumstellar matter or by internal shocks in the jet (Rees & Mészáros 1992, 1994; Daigne & Mockkovitch 1998, 2000). Therefore, the properties of jets from collapsars are of crucial importance for understanding the mechanism of GRBs. For example, the non-uniformity across the jet can influence the structure of internal shocks and, hence, the gamma-ray emission from these shocks. A transverse gradient can also drastically change the temporal decay rate of afterglows, making the decay flatter or steeper depending on the transverse structure (Mészáros et al. 1998). Gamma-ray light curves also show a great diversity of time dependences ranging from a smooth rise and quasi-exponential decay, through light curves with several peaks, to variable light curves with many peaks, and substructure sometimes down to milliseconds. Hydrodynamic instabilities arising in the jet can be responsible for the fine time structure of GRBs in a row with a temporal variability caused by accretion onto the BH and the circumstellar interaction. This complex time dependence can provide clues for the understanding of the geometry and physics of the emitting regions. Apart from this, instabilities and their associated fluctuating hydrodynamic motions can lead to the generation of magnetic fields in a highly conductive e- e+ plasma. In the presence of turbulent magnetic fields, the electrons can produce a synchrotron radiation spectrum (Mészáros & Rees 1993; Rees & Mészáros 1994) similar to that observed (Band et al. 1993). The inverse Compton scattering of these synchrotron photons can extend the spectrum even into the GeV range (Mészáros et al. 1994).

In the present paper, we consider the stability properties of jets which are formed and propagate in collapsars. Large-scale hydrodynamic instabilities can be the reason for the observed morphological complexity of "standard'' jets, and this has motivated many analytical (see, e.g., Birkinshaw 1984, 1991, 1997; Hardee & Norman 1988; Zhao et al. 1992; Hanasz & Sol 1996) and numerical (Hardee et al. 1992; Hardee et al. 1998; Bodo et al. 1998; Micono et al. 2000; Agudo et al. 2001) studies of the stability properties of jets. Usually, the jet is considered as a beam of gas with one bulk velocity and constant density surrounded by a very narrow shear layer separating it from the external medium. One possible mechanism of destabilizing such jets is often attributed to the well-known Kelvin-Helmholtz instability which, in its classical formulation, is the instability of a tangential discontinuity between two flows, generally having different density (see, e.g., Landau & Lifshitz 1978; Chandrasekhar 1981). However, jets in collapsars show a complex structure with the presence of strong transverse shear and substantial density stratification (Aloy et al. 2000). Obviously, the stability properties of such sheared, stratified jets may well be different from those of jets with constant bulk velocity and density.

The outline of this paper is as follows. In Sect. 2, we represent the results of numerical calculations and discuss the transverse structure of a jet originating in a collapsar. In Sect. 3, we represent the linear stability analysis of a sheared, stratified jet by making use of a WKB-approximation. Finally, in Sect. 4, we discuss the possible role of the instability in the evolution of jets.

   
2 Numerical simulations of jets from collapsars

The simulations performed are the same as in Aloy et al. (2000). Here we reproduce the technical details for completeness. The computational mesh is a two-dimensional spherical grid (with coordinates $r, \theta$). In the r-direction the computational grid has 200 zones spaced logarithmically between the inner boundary and the surface of the helium star at $R = 2.98 \times 10^{10}~$cm. Equatorial symmetry is assumed and the working angular resolution is $0.5^{\circ}$ close to the polar region ( $0^{\circ} \le \theta \le 30^{\circ}$) and decreases logarithmically between $30^{\circ} \le \theta \le 90^{\circ}$.

A central Schwarzschild BH of mass $3.762~M_{\odot}$ provides the gravitational field that couples the system. Self-gravity of the star is neglected, i.e., we consider only the gravitational potential of the BH. Our equation of state (EoS) includes the contributions of non-relativistic nucleons treated as a mixture of Boltzmann gases, radiation, and an approximate correction due to e+e--pairs as described in Witti et al. (1994). Complete ionization is assumed, and the effects due to degeneracy are neglected. We advect nine non-reacting nuclear species which are present in the initial model: C12, O16, Ne20, Mg24, Si28, Ni56, He4, neutrons and protons.


  \begin{figure} \par\includegraphics[width=10cm,clip]{2002_2863F1.eps}\end{figure} Figure 1: Snapshot of the logarithm of the rest-mass density after an evolution time of 5.24 s. The color scale indicates the value of the logarithm of the rest-mass density (in CGS units). The solid arc marks the limit of the exponentially decaying atmosphere while the dashed one marks the surface of the collapsing star. The numbers around the box represent distances in units of 1010 cm.
Open with DEXTER

In a consistent collapsar model a jet will be launched by any process which gives rise to a local deposition of energy and/or momentum, as e.g., $\nu \bar\nu$-annihilation, or magneto-hydrodynamic processes. We reproduce such a process by depositing energy at a prescribed rate homogeneously within a $30^{\circ}$ cone around the rotation axis. In the radial direction the deposition region extends from 200 km to 600 km. We have investigated a constant energy deposition rate $\dot E = 10^{50}~$erg s-1, of $\dot E = 10^{51}~$erg s-1, and a varying deposition rate with a mean value of 1050 erg s-1. The constant rates bracket the expected deposition rates of collapsar models, while the varying rate mimics, e.g., time-dependent mass accretion rates resulting in time-dependent $\nu \bar\nu$-annihilation (MacFadyen & Woosley 1999).

We have endowed the star with a Gaussian atmosphere, which at $R_{\rm a} = 1.8~ R$ passes over into an external uniform medium with a density 10-5 g cm-3 and a pressure 10-8 p(R). The computational domain is extended to $R_{\rm t} = 2.54 ~R$ with 70 additional zones. At the end of the simulation, a relativistic jet has broken out from the surface of the star and propagates through the added atmosphere.

We will focus in the following on the model C50 of Aloy et al. (2000). The logarithm of the rest-mass density and the Lorentz factor after an evolution time of 5.240 s are displayed in Figs. 1 and 2.

  \begin{figure} \par\includegraphics[width=10cm,clip]{2002_2863F2.eps}\end{figure} Figure 2: Snapshot of the Lorentz factor after an evolution time of 5.24 s. The color scale indicates the value of the Lorentz factor at every point of our computational domain. The solid arc marks the limit of the exponentially decaying atmosphere while the dashed one marks the surface of the collapsing star. The number around the box represent distances in units of 1010 cm. Note that the horizontal scale has been enlarged by a factor of 3 in order to display more details of the stratified structure of the fluid in the jet.
Open with DEXTER

Note that we have enlarged the horizontal scale in Fig. 2 in order to improve the readability of the transverse structure of the jet.

In Fig. 3,

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{aa2863f3.eps}\end{figure} Figure 3: Lorentz factor as a function of the radius for three different angles ( $\theta \approx 0^{\circ }, 5^{\circ }, 10^{\circ }$; see legends in the figure) after an evolution time of 5.24 s.
Open with DEXTER

we plot the radial dependence of a Lorentz factor, $\Gamma$, for a few selected polar angles. This dependence shows quite well that the jet is highly collimated. The Lorentz factor reaches maximum values at the axis where it can be as large as $\sim$20-30. However, $\Gamma$ drops very rapidly with increasing polar angle and, at $\theta = 10^{\circ}$, it becomes close to 1 in the main fraction of a collapsar volume ( $r \geq 10^{8}$ cm). Within the collapsar, on average, the Lorentz factor increases with r because of the decreasing density. The maximum in $\Gamma$ is caused by a very strong rarefaction wave behind the recollimation shock. Note that the Lorentz factor shows a well developed small-scale structure in the region with $r \geq 10^{8}$ cm. The characteristic length scale of variations increases from $\sim$107 cm at r=108 cm to $\sim$109 cm at r=1010 cm. These fluctuations may indicate the presence of a very rapid hydrodynamic instability in the jet.

Figure 4 shows the radial dependence of the rest-mass density for a few selected polar angles. The density shows an even stronger dependence on $\theta $ than does the Lorentz factor. For instance, the density contrast between the axis (where the density is extremely low, $\sim$ 10-3 - 10-4 g/cm3) and $\theta = 10^{\circ}$ is 4-6 orders of magnitude. This is in large contrast to the relatively small average change of the density with r which does not exceed one order of magnitude when r varies from $2 \times 10^{8}$ cm to R. The main reason for this change is the fact that the radial grid stretches logarithmically and, therefore, as r grows, there is a loss of numerical resolution that may suppress small-scale structures. Like the Lorentz factor, the density shows a very remarkable small-scale structure approximately with the same length scale as $\Gamma$. However, fluctuations of the density are larger (up to a factor of 102-103). The reason for this behavior of the density is that the beam is radiation dominated according to our EoS (see Sect. 2) because the average temperature of the beam is $\approx$ $ 5\times10^8~$K. In this radiation-dominated flow, the relative variation of the density, resulting from variations of temperature and of pressure, can be written as

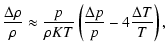$\displaystyle \frac{\Delta \rho}{\rho} \approx \frac{p}{\rho K T} \left( \frac{\Delta p}{p} - 4 \frac{\Delta T}{T}\right),$     (1)

where T, p and K are the temperature, the pressure and the Boltzmann constant, respectively. As the relative variations of the pressure and of the temperature are similar, it turns out that
$\displaystyle \frac{\Delta \rho}{\rho} \sim \frac{p}{\rho K T} \frac{\Delta p}{p}\cdot$     (2)

Therefore, $p / (\rho K T) >> 1$, we conclude that the relative variations of the density must be much larger than the relative variations of pressure or of temperature in a radiation-dominated beam.


  \begin{figure} \par\includegraphics[width=10cm,clip]{aa2863f4.eps}\end{figure} Figure 4: Rest-mass density as a function of the radius for three different angles ( $\theta \approx 0^{\circ }, 5^{\circ }, 10^{\circ }$; see legends in the figure) after an evolution time of 5.24 s.
Open with DEXTER

In Fig. 5,

  \begin{figure} \par\includegraphics[width=10cm,clip]{2002_2863F5.eps}\end{figure} Figure 5: Plots of four physical quantities as a function of the polar angle, $\theta $, at four different distances ( $10^8, 10^9, 3\times 10^9$ and 1010 cm; see legends in the figure). The upper left panel corresponds to the radial velocity (in units of c); the lower left panel to the rest-mass density and, the upper and lower right panels correspond to the sound speed (in units of c) and to the Lorentz factor, respectively. The evolution time is 5.24 s.
Open with DEXTER

we show transverse dependences of the radial velocity, sound speed, density and Lorentz factor at different distances. All quantities are collimated in a cone with a half-opening angle of about 6-10$^{\circ}$ with a better collimation for the Lorentz factor and a worse one for the density. Only close to the black hole ( $r \sim 10^{8}$ cm) is the collimation of the represented quantities (except the Lorentz factor) worse, $\sim$ $ 20^{\circ}$. Note also that all quantities except the Lorentz factor exhibit almost a self-similar behavior at r > 108 cm. The velocity profiles show the presence of a strong shear which is crucial for the dynamics of jets and their stability properties. The sound speed is close to the maximum possible value, $c/ \sqrt{3}$, in a significant fraction of the jet volume, i.e., the jet plasma is relativistic in the sense of both the bulk velocity and the thermal content. The mean temperature is $\sim$ $ 5 \times 10^{8}$ K, and the pressure is dominated by radiation. That is why the sound speed is relativistic despite the temperature being non-relativistic for particles. Note the presence of a substantial transverse gradient of the sound speed that may play an important role in the formation of internal shocks. Jets in collapsars exhibit a highly inhomogeneous density in contrast to the standard jet models. The density becomes extremely low at the jet axis and it grows almost exponentially with the angle reaching larger values at the jet surface. This behavior is caused by a velocity profile decreasing with $\theta $ and, likely, is typical for all sheared jets.

3 The dispersion equation for perturbations

We model the jet from collapsars by an infinitely long plasma cone with a half-opening angle $\theta_{0}$. From simulations, the typical value of $\theta_{0}$ is somewhat around 6-10$^{\circ}$. Plasma inside the jet moves with a velocity ${\bf V} = V(r, \theta) {\bf e}_{r}$ with respect to the ambient medium; r, $\theta $, $\varphi$ are the spherical coordinates with ${\bf e}_{r}$, ${\bf e}_{\theta}$, ${\bf e}_{\varphi}$ being the corresponding unit vectors. As seen from the behavior of the velocity profile (Fig. 5), we can distinguish two different regions within the jet: the central core where the flow is ultrarelativistic, and the surrounding transition layer where the velocity decreases from relativistic to non-relativistic values. In the core region, the Lorentz factor is large, $\geq$3, and may even reach values as high as $\sim$25-30(see Fig. 3). It is convenient to distinguish between these two regions in our analysis because of the difficulty of describing both relativistic and non-relativistic flows within the framework of the same analytical formalism. Basically, the thickness of the transition layer is smaller than the radius of the core. Since our main interest is the processes in the core region we will model the effect of the transition layer in terms of the boundary conditions. Note that outside this transition layer there exists an extended region where the flow is non-relativistic but we neglect the influence of this region because of its low energy.

In relativistic hydrodynamics the continuity, momentum, and energy equations read (see, e.g., Weinberg 1972)

 \begin{displaymath}\Gamma \left( \frac{\partial \rho}{\partial t} + {\bf v} \cdo... ...ma}{\partial t} + \nabla \cdot ( \Gamma {\bf v} ) \right] = 0, \end{displaymath} (3)


 \begin{displaymath}\Gamma^{2} \left( \rho + \frac{p}{c^{2}} \right) \left[ \frac... ...bla p - \frac{{\bf v}}{c^{2}} \frac{\partial p}{\partial t} , \end{displaymath} (4)


 \begin{displaymath}\frac{\partial}{\partial t} (p n^{- \gamma}) + {\bf v} \cdot \nabla (p n^{- \gamma}) = 0, \end{displaymath} (5)

where $\Gamma = (1 - v^{2}/c^{2})^{-1/2}$ is the Lorentz factor, p and $\rho$ are the gas pressure and density, respectively; n is the number density in the fluid's rest frame; $\gamma$ is the adiabatic index.

Our analysis of stability is based on the linearized set of Eqs. (3)-(5). Small perturbations will be marked by the index 1; for unperturbed quantities subscripts will be omitted with the exception of vector components. We consider the instability which arises on a time scale much shorter than the characteristic evolution time scale of the jet. Therefore, we can adopt a quasi-steady approximation neglecting the time dependence of unperturbed quantities. In this approximation, the linearized continuity, momentum and energy equations are

 
$\displaystyle \Gamma \left( \dot{\rho_{1}} + {\bf v}_{1} \cdot \nabla \rho + {\... ...{1} + \frac{p_{1}}{c^{2}} \right) \frac{\partial}{\partial r} (r^{2} \Gamma V),$     (6)


 
$\displaystyle \Gamma^{2} \rho_{*} \left[ \dot{\bf v}_{1} + ({\bf v}_{1} \cdot \... ...} + \frac{p_{1}}{c^{2}} + \frac{2 \Gamma^{2} V \rho_{*}}{c^{2}} v_{1r} \right),$     (7)


 
$\displaystyle \dot{p_{1}} + {\bf V} \nabla p_{1} + \frac{\gamma p}{\Gamma} \lef... ...p_{1} \frac{\gamma}{r^{2} \Gamma} \frac{\partial}{\partial r} (r^{2} V \Gamma),$     (8)

where $\rho_{*}= \rho + p/c^{2}$. In Eqs. (6)-(8) we took into account that $\Gamma_{1}=\Gamma^{3} ({\bf V} \cdot {\bf v}_{1})/c^{2}$. Since a quasi-steady state approximation is adopted, we have for the unperturbed state $\Gamma^{2} \rho_{*} ({\bf V} \cdot \nabla ) {\bf V} = - \nabla p$, and hence only the radial component of $\nabla p$ is non-vanishing.

In a conical jet with a small opening angle, the characteristic radial length scale of unperturbed quantities is of the order of the spherical radius and is much greater than the transverse length scale. Therefore, we can treat the radial and $\theta $-dependences of the perturbations separately. If we consider perturbations with the radial wave vector, k, satisfying the condition

 \begin{displaymath}kr \gg 1, \end{displaymath} (9)

then the terms on the right hand sides of Eqs. (6)-(8), which contain only the radial derivative of unperturbed quantities, are smaller by a factor kr than the corresponding terms on the left hand sides containing the derivatives of perturbations. Therefore, all terms on the r.h.s. of Eqs. (6)-(8) can be neglected if inequality (9) is fulfilled. The assumption (9) corresponds to the so-called local approximation in a stability analysis. Under this assumption, we have from (6)-(8)
 
$\displaystyle \Gamma \left( \dot{\rho_{1}} + {\bf v}_{1} \cdot \nabla \rho + {\... ... \left(\dot{v}_{1r} + V \frac{\partial v_{1r}}{\partial r} \right) \right] = 0,$     (10)


 
$\displaystyle \Gamma^{2} \rho_{*} \left[ \dot{\bf v}_{1} + ({\bf v}_{1} \cdot \... ...la) {\bf v}_{1} \right] + \nabla p_{1} + \frac{{\bf V}}{c^{2}} \dot{p}_{1} = 0,$     (11)


 
$\displaystyle \dot{p_{1}} + {\bf V} \nabla p_{1} + \frac{\gamma p}{\Gamma} \lef... ...\left( \dot{v}_{1r} + V \frac{\partial v_{1r}}{\partial r} \right) \right] = 0.$     (12)

Since the unperturbed quantities depend neither on t nor on $\varphi$ , the dependence of all perturbations on t, r and $\varphi$ can be taken in the form $\exp(i \omega t - i k r - i m \varphi)$ if we adopt condition (9). In the present paper, we consider axisymmetric perturbations with m=0. Substituting this dependence into Eq. (12), we can express the perturbation of pressure in terms of ${\bf v}_{1}$,

 \begin{displaymath}p_{1} = \frac{i \gamma p}{\sigma \Gamma} \left[ \nabla \cdot ... ...v}_{1}) + i \sigma \frac{\Gamma^{3}}{c^{2}} V v_{1r} \right], \end{displaymath} (13)

where $\sigma = \omega - k V$. The quantity kV is an advective frequency and has a kinematic origin. The perturbations of the velocity can be expressed in terms of p1 from the momentum Eq. (11) which under our assumptions can be rewritten as

 \begin{displaymath}\rho_{*} \Gamma^{2} \left( i \sigma {\bf v}_{1} + {\bf e}_{r... ... \left( \frac{\omega {\bf V}}{c^{2}} - i \nabla \right) p_{1}. \end{displaymath} (14)

Substituting expressions for v1r and $v_{1 \theta}$ into Eq. (13) and taking into account that for a small opening angle $\sin \theta \approx \theta$, we obtain the equation containing p1 alone
 
$\displaystyle p_{1}'' + \left[ \frac{1}{x} + \frac{2 \Gamma^{2} V'}{\sigma} \le... ...{\rm s}^{2}} - \left( k - \frac{\omega V}{c^{2}} \right)^{2} \right] p_{1} = 0.$     (15)

Here $c_{\rm s} = \sqrt{\gamma p / \rho_{*}}$ is the sound speed, $x=r \theta$, and the prime denotes a transverse derivative; for example, $p_{1}' = {\rm d} p_{1}/ $dx where dx=rd$\theta $. Equation (15) represents the behavior of small perturbations for any velocity and density profiles within a conical jet with a small opening angle. In our approach, the radial dependence of unperturbed quantities enters in Eq. (15) parametrically.

For our purposes, it will be convenient to use another form of the Eq. (15). Making the substitution

 \begin{displaymath}p_{1} = \sqrt{\frac{\rho_{*}}{x}} \exp \left[ - \int \frac{\... ... \left( k - \frac{\omega V}{c^{2}} \right) {\rm d}x \right] f, \end{displaymath} (16)

Eq. (15) can be transformed into

 
f'' + q2(r) f = 0, (17)

where
 
$\displaystyle q^{2} = \frac{\Gamma^{2} \sigma^{2}}{c_{\rm s}^{2}} - Q^{2} + \fr... ...}{c} - \xi \right) \left( \frac{\rho' V'}{\rho_{*}} - \frac{(xV')'}{x} \right),$     (18)

$\xi = kc /\sigma \Gamma^{2}$, and Q2 is given by

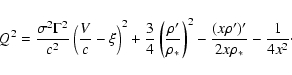\begin{displaymath}Q^{2} = \frac{\sigma^{2} \Gamma^{2}}{c^{2}} \left( \frac{V}{c... ...{2} - \frac{(x \rho')'}{2 x \rho_{*}} - \frac{1}{4 x^{2}}\cdot \end{displaymath} (19)

Since in the present paper we consider a stratified sheared jet the expression (17) for q2 differs from the corresponding equation derived by Urpin (2002) only due to the presence of terms containing derivatives of $\rho$.

In the core region where the temperature is high and the pressure is determined by radiation, the sound speed, $c_{\rm s}$, is of the order of $c/ \sqrt{3}$ and, hence, the acoustic frequency is comparable to that of the light, $\sim$kc. Since the turnover time scale, |V'|-1, characterizing the rate of hydrodynamical processes associated with shear is also very short, we can expect that typical frequencies in our model are sufficiently large. Therefore, we can try to obtain the solution of Eq. (17) in a high frequency limit when $\xi \ll 1$, or

 \begin{displaymath}\mid \sigma \mid \;\gg k c / \Gamma^{2}. \end{displaymath} (20)

We will see that this inequality is well fulfilled in our jet model. Restricting ourselves to the lowest terms in a small parameter $\xi$, we obtain from the expression (18)
 
$\displaystyle q^{2} \approx \frac{\eta \sigma^{2} \Gamma^{2}}{c_{\rm s}^{2}} + ... ...'}{\rho_{*}} \right)^{2} + \frac{(x \rho')'}{2 x \rho_{*}} + \frac{1}{4 x^{2}},$     (21)

where $\eta = 1 - c_{\rm s}^{2} V^{2}/c^{4}$. Since in the ultrarelativistic limit we have $c_{\rm s}^{2} \approx c^{2}/3 $ and $V \rightarrow c$, the factor $\eta$ varies in a narrow range from $\sim$1 to 2/3.

The behavior of q is determined by the $\theta $-dependence of the jet velocity and density. We consider the case closely related to the calculations represented in Sect. 2. These simulations indicate that the density profile within the jet core can be fitted with a sufficient accuracy by a simple exponential dependence,

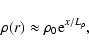\begin{displaymath}\rho(r) \approx \rho_{0} {\rm e}^{x/L_{\rho}}, \end{displaymath} (22)

where $\rho_{0}$ is the density at the jet axis, and $L_{\rho}$ is the characteristic length scale of stratification. Since the density contrast between the surface and axis is of the order of 3-5 orders of magnitude depending on the distance from the center of a collapsar, we can estimate $L_{\rho} \sim 0.1 x_{0}$.

The velocity profile can be modeled by the parabolic dependence,

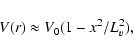\begin{displaymath}V(r) \approx V_{0} (1- x^{2}/L_{v}^{2}), \end{displaymath} (23)

where V0 is the velocity at the jet axis, and Lv is the length scale of the velocity distribution, $L_{v} \sim x_{0}$.

Since $\Gamma^{2}$ is large in the jet core, the contribution of the last four terms on the r.h.s. of Eq. (21) which are proportional to $\Gamma^{2}$ or $\Gamma^{0}$ is small compared to the second term ( $\propto \Gamma^{4}$) if we assume that $\Gamma^{2} \gg \max (L_{v}/L_{\rho}, L_{v}/ \sqrt{x L_{\rho}})$ in the main fraction of the core region where instability arises. After these simplifications, we obtain the following expression for q2 in the jet core

 \begin{displaymath}q^{2} \approx \Gamma^{2} \left( \frac{\eta \sigma^{2}}{c_{s}^{2}} + \frac{V'^{2} \Gamma^{2}}{c^{2}} \right)\cdot \end{displaymath} (24)

Consider the solution of Eq. (17) by making use of a WKB-approximation which is well justified in those regions of the jet where the condition |q x | > 1 is fulfilled. With the accuracy in linear terms in a small parameter |qx|-1, a WKB-solution of Eq. (17) can be written as

 \begin{displaymath}f(x) = \frac{1}{\sqrt{q(x)}} \left[ C_{1} {\rm e}^{i \int q {\rm d} x'} + C_{2} {\rm e}^{-i \int q {\rm d} x'} \right], \end{displaymath} (25)

(Landau & Lifshitz 1981) where C1 and C2 are constant that have to be chosen in such a way as to satisfy the boundary conditions. In some cases, the condition $\vert q x \vert \gg 1$holds everywhere within the jet, and the expression (25) applies at $x_{0} \geq x \geq 0$. However, since the dependence of qon x is rather complex, it is generally also possible that the condition of applicability can break at some point x = x* < x0where $q \approx 0$. By analogy with quantum mechanics this point can be called the turning point. We address this case as the most interesting one from the point of view of applications to jets from collapsars. Note that we have at x=x*

 \begin{displaymath}\sigma^{2} \approx - \frac{1}{\eta} \left( \frac{c_{s}}{c} \right)^{2} \Gamma^{2} V'^{2}. \end{displaymath} (26)

Since generally $\omega$ is complex,

 \begin{displaymath}\omega \equiv \Omega - i / \tau, \end{displaymath} (27)

where $\Omega$ is the frequency of an unstable mode and $\tau$ is its growth time, the condition (26) can be satisfied only if

 \begin{displaymath}1/ \tau \gg \vert \Omega - k V\vert \end{displaymath} (28)

at the turning point. We are interested in the most powerful instability (if it exists) with the growth time shorter than |kV|-1. For such instability the condition (28) should be fulfilled everywhere within the jet. If Eq. (28) holds then q2 is approximately real and q2 < 0 at $x_{*} > x \geq 0$ and q2 > 0 at x0 > x > x*.

It is convenient to represent a WKB-solution from both sides of the turning point in the form

 \begin{displaymath}f(x) = \frac{1}{\sqrt{q(x)}} \left[ C_{1}^{(r,l)} {\rm e}^{i ... ...2}^{(r,l)} {\rm e}^{-i \int_{x_{*}}^{x} q {\rm d} x'} \right], \end{displaymath} (29)

(Landau & Lifshitz 1981) where C1(r,l) and C2(r,l) are constant; indexes r and l refer to the right (x > x*) and left (x < x*) from x= x*, respectively. Note that generally $C_{1}^{(r)} \neq C_{1}^{(l)}$ and $C_{2}^{(r)} \neq C_{2}^{(l)}$.

To obtain the eigenvalues and eigenfunctions of Eq. (17) one needs the boundary conditions for perturbations. One of the boundary conditions is obvious: since p1 is a physical quantity it should be finite everywhere including the jet axis and, hence, f should vanish at x=0. If the turning point is not very close to 0, then usually it is sufficient to choose an exponentially decreasing solution at x < x*. It is known (see, e.g., Landau & Lifshitz 1981) that the solution (29) at x > x* matches an exponentially decreasing solution beyond the turning point (at x < x*) if $C_{1}^{(l)}= (C/2) \exp (i \pi / 4)$ and $C_{2}^{(l)}= (C/2) \exp (- i \pi / 4)$where C is constant. Hence, the solution at x>x* satisfying the true boundary condition at x=0 has the form

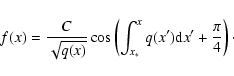\begin{displaymath}f(x) = \frac{C}{\sqrt{q(x)}} \cos \left( \int_{x_{*}}^{x} q(x') {\rm d} x' + \frac{\pi}{4} \right)\cdot \end{displaymath} (30)

The formulation of a true boundary condition at the outer boundary can face some problems but, fortunately, the properties of modes with a relatively small length scale in the $\theta $-direction are not sensitive to the particular choice of boundary conditions. We consider the case when the density in a surrounding medium is much larger than that in the jet. In this case (see, e.g., Glatzel 1988; Wu & Wang 1991), a much denser surrounding medium plays the role of a wall and the perturbations of the displacement in the $\theta $-direction vanish at the outer boundary, x= x0. As it follows from Eq. (14), $v_{1 \theta}$ vanishes if dp1/dx =0 at x=x0. Using the expression (16), we can rewrite this condition as

\begin{displaymath}f' + \left[ \frac{\Gamma'}{\Gamma} \left( 1 - \frac{c}{V} \xi... ... + \frac{\rho'}{2 \rho_{*}} - \frac{1}{2x_{0}} \right] f = 0. \end{displaymath} (31)

Since we consider the modes satisfying condition (20) and, in a WKB-approximation, the wavelength of perturbations is assumed to be much shorter than the characteristic length scales of any unperturbed quantity, the boundary condition at x=x0 can approximately be represented as

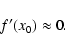\begin{displaymath}f'(x_{0}) \approx 0. \end{displaymath} (32)

With this boundary conditions, the dispersion equation reads

 \begin{displaymath}\int_{x_{*}}^{x_{0}} q(x) {\rm d}x = \pi \alpha, \end{displaymath} (33)

where $\alpha = n + 3/4$, n is integer. Substituting the expression (24) for q in (33), we have

 \begin{displaymath}\int_{x_{*}}^{x_{0}} \Gamma \left( \frac{\eta \sigma^{2}}{c_{... ...V'^{2} \Gamma^{2}}{c^{2}} \right)^{1/2} {\rm d}x = \pi \alpha. \end{displaymath} (34)

We can estimate the characteristic roots of Eq. (34) using the mean value theorem. We have

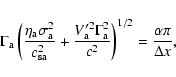\begin{displaymath}\Gamma_{\rm a} \left( \frac{\eta_{\rm a} \sigma^{2}_{\rm a}}{... ...rm a}^{2}}{c^{2}} \right)^{1/2} = \frac{\alpha \pi}{\Delta x}, \end{displaymath} (35)

where $\Delta x = x_{0}-x_{*}$ and the subscript a means the value of a quantity at $x=x_{\rm a}$, $x_{\rm a}$ is a mean point within the range from x* to x0. Since under the condition (28) we have $\sigma_{\rm a}^{2} \approx - 1/ \tau^{2}$, then the growth rate is given by

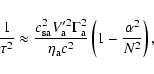\begin{displaymath}\frac{1}{\tau^{2}} \approx \frac{c_{\rm sa}^{2} V_{\rm a}'^{2... ...ta_{\rm a} c^{2}} \left( 1 - \frac{\alpha^{2}}{N^{2}} \right), \end{displaymath} (36)

where

\begin{displaymath}N^{2} = \frac{(\Delta x)^{2} V_{\rm a}'^{2}}{\pi^{2} c^{2}} \; \Gamma_{\rm a}^{4}. \end{displaymath} (37)

If n < N -3/4, then $\tau^{2}$ is positive and perturbations with such n are unstable. On the contrary, perturbations with very large n satisfying the condition n > N - 3/4 are stable. Note that $N \sim \Gamma_{\rm a}^{2}$. In the case $n \ll N$, we have

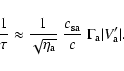\begin{displaymath}\frac{1}{\tau} \approx \frac{1}{\sqrt{\eta_{\rm a}}} \; \frac{c_{\rm sa}}{c} \; \Gamma_{\rm a} \vert V_{\rm a}'\vert. \end{displaymath} (38)

At $c_{\rm s} \sim c/\sqrt{3}$, we obtain a very simple estimate of the growth time

 \begin{displaymath}\frac{1}{\tau} \sim \Gamma_{\rm a} \vert V_{\rm a}'\vert. \end{displaymath} (39)

Jets with a relativistic sound speed turn out to be unstable for any velocity profile. The growth time is typically very short and depends on the shear being shorter for larger |V'|. Also, the instability arises faster for jets with a very high Lorentz factor. Note, however, that the origin of the factor $\Gamma_{a}$ in Eq. (39) is purely kinematic. The growth time of the instability in the comoving frame is of the order of |V'|, but since we consider the instability in the rest frame, the Lorentz transformation of the "comoving'' growth time yields the result (39).

The characteristic growth length, $L=V \tau$, can be estimated, for $c_{\rm s} \sim c/\sqrt{3}$, as

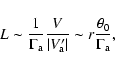\begin{displaymath}L \sim \frac{1}{\Gamma_{\rm a}} \frac{V}{\vert V'_{\rm a}\vert} \sim r \frac{\theta_{0}}{\Gamma_{\rm a}}, \end{displaymath} (40)

and is much shorter than the radius of a collapsar. Therefore, the instability can manifest itself even at the very early stage of the evolution of the jet.

4 Discussion

We have treated numerically and analytically the instability that can arise in jets from collapsars. The instability is caused by a combined action of shear, which is unavoidable in such jets, and an extremely high compressibility associated with a relativistic sound speed. It turns out that jets from collapsars are more unstable than, for example, standard extragalactic jets because of the relativistic compressibility. The fact of instability itself does not depend on a particular shape of the velocity profile: the instability can arise for any dependence $V(\theta)$. However, the growth time is shorter for flows with a stronger shear. Note that only non-homogeneous perturbations in the radial direction ($k \neq 0$) can be unstable.

Although it is commonly believed that three dimensional studies of the stability of relativistic jets will include additional instable modes (in many cases even more unstable that the axisymmetric ones), the recent work of Hardee & Rosen (1998), has pointed the fact that shear leads both to an enhancement of the axisymmetric modes and a suppression of the asymmetric modes. Hence, a fully three dimensional study would not yield to radically different results from the ones that we obtain here.

In the main fraction of the jet volume, the instability grows very rapidly. If we estimate the average Lorentz factor as $\sim$10 and the half-opening angle as $\sim$$ 5^{\circ}$ then the growth time (39) is of the order 0.01 r/c. This is much shorter than the life time of the jet even at $r \sim R$. Therefore, we can expect that shortly after jet formation the instability will generate well developed turbulent motions with substantial fluctuations of the Lorentz factor, density, pressure, etc. This conclusion is in good agreement with the results of numerical simulations (see Figs. 3 and 4). During the jet's propagation, fluctuations can become noticeable at a relatively early evolutionary stage and, hence, at a small distance from the formation region because the growth time is sufficiently short even in the inner region of the collapsar. Of course, the initial amplitude of fluctuations in the jet is quite uncertain. In our case, the initial fluctuations are triggered by numerical reasons, but it is quite likely that they mimic the irregularities of the process of accretion onto the central black hole. Usually the time $\tau_{0}$ required for an instability to amplify the amplitude of perturbations to a noticeable value is longer than the growth time, $\tau$, by some factor which is typically $\sim$(5-10), so $\tau_{0} \sim (5{-}10) \tau$. After this time, the fluctuations have grown by a factor $\sim$ 102-104 compared to their initial value which probably is sufficient to become significant. In the region where $\tau_{0}$ is shorter than the propagation time scale, which can be estimated as $\sim$r/c, fluctuations reach noticeable values. On the contrary, fluctuations seem to be insignificant in regions where $\tau_{0} > r/c$. We can define the radius where the instability starts to manifest itself as that where the condition $\tau_{0} \sim r/c$ is fulfilled. Substituting $\tau_{0}$, we obtain that

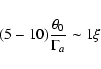\begin{displaymath}(5-10) \frac{\theta_{0}}{\Gamma_{a}} \sim 1 \xi \end{displaymath} (41)

at this radius. At small r ($\sim$ $ 8 \times 10^{8}~$cm well below jet break-out), the jet is less collimated ( $\theta_{0} \approx 10{-}12^{\circ}$) than on average (see Aloy et al. 2000). Therefore, the instability should manifest already in regions where $\Gamma \sim 1{-}2$. This conclusion is in qualitative agreement with what is shown in Fig. 3 where appreciable fluctuations appear in regions with a Lorentz factor between 1 and 2.

Note that the radial wave vector of unstable perturbations, k, should satisfy rather restrictive conditions. First, k has to be sufficiently large for the applicability of the local approximation (see Eq. (9)). On the other hand, condition (28) which is necessary for the existence of the turning point, implies that

 \begin{displaymath}\Gamma_{\rm a} \frac{\vert V'_{\rm a}\vert}{V} \sim \frac{\Gamma_{\rm a}}{x_{0}} \gg k. \end{displaymath} (42)

If the inequality (42) holds then the condition (20) used in our calculations is certainly fulfilled and the parameter $\xi$ is small. Combining Eqs. (9) and (42) and taking into account that $x_{0}= r \theta_{0}$, we obtain that

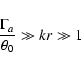\begin{displaymath}\frac{\Gamma_{a}}{\theta_{0}} \gg kr \gg 1 \end{displaymath} (43)

for unstable perturbations. Estimating $\Gamma \sim 10$ and $\theta_{0} \sim 5{-}6^{\circ}$ in the main fraction of the jet volume, we have $100 \gg kr \gg 1$. Numerical simulations (see Fig. 3) indicate that the characteristic length scale of fluctuations depends on r and varies within the range from 0.1rto 0.5r in good agreement with the prediction of the theory. Note that fluctuations with a shorter length scale cannot be resolved with the computational grid used in the simulations.

All this allows one to speculate that the calculated fluctuations of parameters within the jet are physical (i.e., not simply numerical artifacts) and reflect the presence of a very strong shear-driven instability. We can expect that inhomogeneities caused by this instability will produce shocks in the course of their non-linear evolution when faster fluctuations try to overtake slower ones or when fluctuations moving in the positive and negative radial directions collide. If this is the case then internal shocks might be more or less randomly distributed and oriented within the jet forming filamentary structures. It is often supposed that shocks in a ultrarelativistic wind or jet are responsible for GRBs themselves whereas the impact against the ambient matter of this wind produces an external shock which likely produces the observed afterglows (Rees & Mészáros 1992, 1994). Shocks can convert a portion of kinetic energy into a non-thermal gamma/X-ray transient emission which is usually ascribed to particle acceleration by shocks. Typically, the efficiency of this conversion is not high, $\sim$1-2%, but it can be much greater ($\sim$20-40%) for the interaction of fluctuations with very different Lorentz factors (Kobayashi et al. 1997; Kobayashi & Sari 2001). Since in our model the calculated fluctuations move with substantially different Lorentz factors we can expect a highly efficient transformation of their kinetic energy into radiation. The proposed instability can also accounts for the rapid variability of the gamma-ray light curves, which lasting from tens to hundreds of seconds, exhibit variability sometimes down to milliseconds (Fishman & Meegan 1995). Likely, the most rapid temporal variability associated with the shear-driven instability has a time scale of the order of the growth time (39). At the surface of a collapsar, for example, this time scale is as short as $\sim$10-3 s. Since the jet is highly inhomogeneous and the Lorentz factor varies strongly during the jet's propagation, a slower variability could also be represented in the gamma-ray light curves.

Another remarkable inference from the considered model is that the turbulent motions caused by the instability may also be important for the electron-proton energy exchange and, particularly, for the generation of the magnetic field in jets from collapsars.

Acknowledgements
This research was supported in part by the Russian Foundation of Basic Research and Deutsche Forschungsgemeinschaft (grant 00-02-04011). V.U. thanks Ministerio de Educación, Cultura y Deporte of Spain for the financial support under the grant SAB1999-0222. M.A.A. acknowledges the EU-Commission for a fellowship (MCFI-2000-00504). M.A.A. thanks E. Müller and P.E. Hardee for their enlightening discussions.

References

 

Copyright ESO 2002