A&A 396, 745-751 (2002)
DOI: 10.1051/0004-6361:20021441
A method to detect p-mode oscillations in solar-like star signals
C. Régulo1,2
-
T. Roca Cortés1,2
1 - Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
2 -
Dpto. de Astrofísica, Universidad de La Laguna, La Laguna, 38206, Tenerife, Spain
Received 24 April 2002 / Accepted 18 September 2002
Abstract
A good example of finding a signal buried in noise, a common problem in Astrophysics,
is the search for stellar oscillations in the acoustic power spectrum of solar-like stars.
In this work it is shown that it is possible to find this type of signal
in the power spectrum of stellar oscillations if the peaks
are "almost'' equally spaced in frequency, as the asymptotic theory for acoustic modes predicts.
This signature of the power spectra of the p-mode oscillations in solar-like stars is
used to design a method that allows the identification of the signal even when
this signal is completely buried in noise,
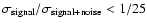 .
.
Key words: methods: data analysis - stars: oscillations
The success of helioseismology in probing the interior of the Sun with ever increasing
precision fostered the use of seismic techniques to study the interior of other stars. An
important part of the future of stellar seismology is related to the study of global
p-mode oscillations in solar-like stars. Several attempts at and even claims of the
detection of solar-like oscillations has been made in the past (Belmonte et al.
1990; Brown et al. 1991; Pottash et al.
1992; Edmonds & Cram 1995; Kjeldsen et al. 1995) which
have not been fully confirmed yet. More recently, using up to date techniques and new
observables, Kjeldsen et al. (1999), Martic et al. (1999), Schou &
Buzasi (2000), Bedding et al. (2001) and Bouchy & Carrier (2001) have improved the detection possibilities and we are nearer to an indisputable
detection. The current space missions COROT (Michel 1998), MONS (Christensen-Dalsgaard, 1998a) and MOST (Matthews 1998) open an extremely
interesting future in this field.
However, even from space and having in mind what is observed on the Sun, the signal to
noise ratio for solar-like star oscillations will be very small (Christensen-Dalsgaard & Frandsen 1983; Samadi & Houdek 2000). Indeed we are trying to
detect variations in intensity with respect to the background of one part per million or
less. Given this scenario, as was pointed out by Christensen-Dalsgaard (1998b),
one of the most important problems in the detection of stellar oscillations is related
to data analysis and the process of deciding whether a peak in a crowded spectrum is
due to a mode, as opposed to just noise.
In this paper we show a method that allows the detection of p-mode oscillation from
the power spectrum of solar-like star signals with a very small S/N in the power
spectrum of a month of simulated data.
The method suggested in Roca Cortés & Régulo (2001) is based on taking
advantage of the "almost'' equal frequency spacing that is present in the power spectrum
of the solar-like stellar acoustic oscillation signal. This behaviour produces a signature
clearly recognizable in the power spectrum of the power spectrum of the stars
luminosity or velocity, which allows the recovery of the original signal and the
measurement of the frequency modes in cases with very low S/N.
The next section describes the basis of the method with a numerically simulated
example. In Sect. 3 the method is applied to realistic examples while in Sect. 4 the analysis of
a time series of observed earth-based stellar data is shown.
The starting point for the analysis is the power spectrum of the noisy acoustic signal of
either luminosity or velocity or any other observable of a star whose acoustic frequencies
we are trying to measure.
The idea of the method is to work with the power spectrum of the power spectrum. The
frequency range in the power spectrum where the signal is supposed to be buried is selected
and its power spectrum is again obtained. Of course the new signal is again a series of
peaks equally spaced also buried in noise, but with the advantage that now the signal
spans all the transform domain with the first peak being at zero frequency. To find the
frequency spacing amongst the peaks in such conditions is much easier.
When the correct spacing is found, we go back to find the recovered spectrum of the signal
in the following way. In the complex power spectrum of the power spectrum of the signal,
all the equally spaced peaks are selected and the inverse Fourier Transform applied. The
result will be the recovered power spectrum of the stellar oscillation without noise.
The method can be summarized in the following way. Given an observed signal m(t):
m(t) = s(t) + r(t)
with s(t) being the signal and r(t) being the noise.
Then the FFT is found:
The hypothesis made is that p-modes present equally spaced frequency peaks showing a signature:
where ni, nj are integers such that
ni < nj,
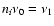 and
and
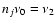 with
with 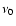 been the frequency spacing. Obviously
been the frequency spacing. Obviously 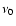 ,
,
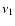 and
and 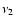 are unknown in general. However, they can be scaled from the known solar values (Kjeldsen & Bedding 1995) and even can be predicted from theory. Therefore, assuming
are unknown in general. However, they can be scaled from the known solar values (Kjeldsen & Bedding 1995) and even can be predicted from theory. Therefore, assuming 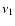 and
and 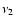 are known, a part of
are known, a part of 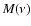 with
with
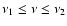 is selected and its Fourier Transform obtained, so:
is selected and its Fourier Transform obtained, so:
with:
The first term on the right hand side is,
Now, an iterative method is used to find out if there is signal only at
the bins spaced by
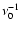 .
Using several values of
.
Using several values of 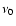 that cover a flexible range around the expected value, with a step of 1 bin, the power
at the bins with
that cover a flexible range around the expected value, with a step of 1 bin, the power
at the bins with
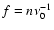 are statistically studied to search for the
best value that fits the best signature assumed above. The success in this
process obviously depends on the S/N ratio present in the data.
are statistically studied to search for the
best value that fits the best signature assumed above. The success in this
process obviously depends on the S/N ratio present in the data.
Once the spacing is found, the function
![$TF[M(\nu) \cdot H(\nu)]$](/articles/aa/full/2002/47/aa2618/img42.gif) is filtered by keeping only the bins that are a multiple of
is filtered by keeping only the bins that are a multiple of
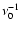 while setting all others to null. To this function the inverse Fourier
Transform is applied, that is:
while setting all others to null. To this function the inverse Fourier
Transform is applied, that is:
and when An=1, the result is exactly:
![\begin{displaymath}\sum_{n=- \infty}^{n= \infty} \delta[( \nu + \nu_{z}) - n \nu_{0}] ,
\end{displaymath}](/articles/aa/full/2002/47/aa2618/img44.gif)
however as
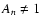 in general, some noise appears in the recovered signal whose level
depends on their values.
in general, some noise appears in the recovered signal whose level
depends on their values.
Let's give a practical example to illustrate how the method works. A signal of 182 days at
60 s sampling has been generated. The signal consists of 30 coherent sine waves, with the
same amplitudes (unity) and random phases, plus white noise (having zero average and a
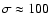 ); the frequency of the first sine wave is
2.1 mHz and the frequency spacing is 0.1267 mHz. Thus the S/N defined as
); the frequency of the first sine wave is
2.1 mHz and the frequency spacing is 0.1267 mHz. Thus the S/N defined as
 is equal to 0.039, although for any sine wave the
is equal to 0.039, although for any sine wave the
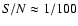 .
Notice that this S/N definition is made in time-space but this could be translated to frequency-space using Parseval's
theorem; however, it is much more difficult to calculate, especially when the signals are so small
that the real peaks interfere with the noise ones in either a constructive or destructive way, yielding a great variety of peak amplitudes (see Fig. 1). In Fig. 1 (top) a piece
of the power spectrum of the noisy signal is plotted and in Fig. 1 (second plot), the same
piece of the power spectrum of the signal is shown but without noise. With this level of
noise, to find the signal buried in it is almost impossible and even to try to find the
spacing among the peaks is very difficult; moreover, in a real case, we are not sure where
to look for it.
.
Notice that this S/N definition is made in time-space but this could be translated to frequency-space using Parseval's
theorem; however, it is much more difficult to calculate, especially when the signals are so small
that the real peaks interfere with the noise ones in either a constructive or destructive way, yielding a great variety of peak amplitudes (see Fig. 1). In Fig. 1 (top) a piece
of the power spectrum of the noisy signal is plotted and in Fig. 1 (second plot), the same
piece of the power spectrum of the signal is shown but without noise. With this level of
noise, to find the signal buried in it is almost impossible and even to try to find the
spacing among the peaks is very difficult; moreover, in a real case, we are not sure where
to look for it.
The analysis starts by selecting a sub-spectrum, say between
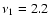 mHz and
mHz and
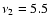 mHz, where we asume the signal is present; notice that is not precisely
so. First, the power spectrum of the sub-spectrum is done. From this power spectrum, the
frequency spacing of
mHz, where we asume the signal is present; notice that is not precisely
so. First, the power spectrum of the sub-spectrum is done. From this power spectrum, the
frequency spacing of
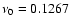 mHz is detected without problems
in this particular case. Moreover, this
is the only one detected, apart from its harmonics, by analysing the power at
the bins with exact multiples of
mHz is detected without problems
in this particular case. Moreover, this
is the only one detected, apart from its harmonics, by analysing the power at
the bins with exact multiples of
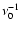 .
The original signal is then
recovered by selecting in the complex power spectrum of the sub-spectrum all bins spaced
0.1267-1 mHz-1 and doing the inverse Fourier Transform for this selected signal
as explained before.
.
The original signal is then
recovered by selecting in the complex power spectrum of the sub-spectrum all bins spaced
0.1267-1 mHz-1 and doing the inverse Fourier Transform for this selected signal
as explained before.
Looking at the recovered power spectrum, the peaks are clearly visible above the noise; however,
we can set some general criteria, such as: peaks are selected as signal if they have a power
greater than 50% of the highest peak and if their phases are close to 0.0. With these
criteria we try to avoid the selection of any peak resulting from noise, although some
signal peaks can be lost. As it can be see in Fig. 1 (third plot), the signal is recovered
in a perfect way. All signal peaks have been recovered with a precision in frequency
better than the spectral resolution (60 nHz), and no peak coming from noise
appears in the recovered signal.
Furthermore, if we assume that we have got a wrong spacing, say
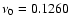 mHz, and
it is used to recover the original signal, the result is plotted in Fig. 1 (bottom). The
level of noise is now as low as in the case where the signal is well recovered, because
the same percentage of bins has been set to zero, but no signal appears above the noise.
Only when the real peaks of signal are selected among the noise do the phases have the
correct relation to reconstruct the signal; otherwise, a noise spectrum is recovered.
mHz, and
it is used to recover the original signal, the result is plotted in Fig. 1 (bottom). The
level of noise is now as low as in the case where the signal is well recovered, because
the same percentage of bins has been set to zero, but no signal appears above the noise.
Only when the real peaks of signal are selected among the noise do the phases have the
correct relation to reconstruct the signal; otherwise, a noise spectrum is recovered.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,height=3.52cm,clip]{MS2...
...ludegraphics[angle=90,width=8.8cm,height=3.52cm,clip]{MS2618f1d.ps}
\end{figure}](/articles/aa/full/2002/47/aa2618/Timg52.gif) |
Figure 1:
From top to bottom, first plot: a piece of the power spectrum of a 182 day generated signal, composed of 30 equidistant frequencies, that simulate the signal, plus white noise. Second plot: the same piece of the power spectrum of the simulated signal without noise. Third plot: the same piece of the power spectrum of the recovered signal after the method explained in the text has been applied. Fourth plot: the same piece of the power spectrum of the recovered signal when a wrong spacing is used. |
| Open with DEXTER |
Another fact to be taken into account is that when only one spacing is present in the data,
the signal is better recovered if the length of the sub-spectrum chosen is a multiple of
the spacing, because in that case, the signal we are working with is truly a periodic
signal in the FFT sense. It is important to note that the method is also able to recover
more than one spacing provided the spacings are present in the data, as was already shown in Roca
Cortés & Régulo (2001).
A problem will arise if the frequency spacing 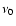 is not exactly constant because this will break our main assumption. Therefore, two related parameters appear in the method: the S/N level and the
departure of the frequency spacing
is not exactly constant because this will break our main assumption. Therefore, two related parameters appear in the method: the S/N level and the
departure of the frequency spacing 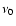 from constant.
from constant.
In order to get a quantitative measure of the relative importance of such parameters, the method
has been applied to 15 time series similar to the one already used, changing
both the S/N level and the uniformity in the frequency spacing. The spacing simulated is now a linear departure from uniform
in the following sense:
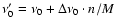 ,
where
,
where
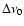 measures the departure from uniformity, n is the signal's peak number and M is the total number of signal
peaks. Time series with
measures the departure from uniformity, n is the signal's peak number and M is the total number of signal
peaks. Time series with
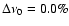
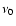 ,
0.25%
,
0.25% 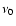 ,
0.50%
,
0.50% 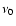 ,
1.0%
,
1.0% 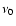 and 2.0%
and 2.0% 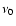 have been generated, each one with 3 different levels of noise, so that the
S/N = 0.077, 0.052 and 0.038. The departure from an exact frequency spacing in the new generated examples are plotted in Fig. 2 in an "echelle diagram''.
have been generated, each one with 3 different levels of noise, so that the
S/N = 0.077, 0.052 and 0.038. The departure from an exact frequency spacing in the new generated examples are plotted in Fig. 2 in an "echelle diagram''.
The method is applied to these new 15 series searching for uniform
frequency spacings in the same way as explained before. Results
are shown in Table 1, where the values found can be seen in each simulated
case. It is clear from theses results that the smaller the S/N level of our
observations, the smaller the departure from an uniform frequency spacing the method will be able to
accept.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,height=3.9cm,clip]{MS2618f2.ps}
\end{figure}](/articles/aa/full/2002/47/aa2618/Timg56.gif) |
Figure 2:
"Echelle diagram'' for the frequencies generated in Sect. 2. In this plot
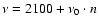 ,
where ,
where
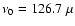 Hz and n is the signal's peak number. Hz and n is the signal's peak number.
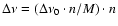 ,
being M the total number of peaks. The asterisks show the case with no departure from the regular pattern and correspond to ,
being M the total number of peaks. The asterisks show the case with no departure from the regular pattern and correspond to
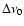 = 0.0%
= 0.0% 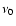 ,
the triangles correspond to ,
the triangles correspond to
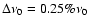 ,
squares for ,
squares for
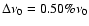 ,
X for ,
X for
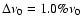 and diamonds for
and diamonds for
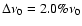 . . |
| Open with DEXTER |
To see the performance of the method in more realistic cases than the example presented in
the section above, two examples have been developed following the characteristics and
conditions that are expected for solar-like stellar oscillations.
One month of data has now been used in the examples because this is an expected period to
be obtained from current space missions and it is a reasonable maximum period
to be achieved from a network of two or three medium size ground based telescopes.
For each example the data has been simulated with and without gaps, to simulate observation
from ground-based observatories and from space.
In this first example data with 60 s sampling has been simulated in the following way: the
signal consists of 20 sine waves representing 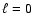 p-modes starting at 1.7450 mHz and
with a frequency spacing of 0.1252 mHz; added to this signal, 40 sine waves in couples,
separated by 800 nHz (simulating a frequency splitting of 400 nHz), represent
p-modes starting at 1.7450 mHz and
with a frequency spacing of 0.1252 mHz; added to this signal, 40 sine waves in couples,
separated by 800 nHz (simulating a frequency splitting of 400 nHz), represent 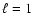 p-modes starting at 1.7926 mHz, with the same frequency spacing used for the
p-modes starting at 1.7926 mHz, with the same frequency spacing used for the 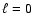 case;
further, added to this signal, another 60 sine waves in triplets, separated by 810 nHz
(simulating a splitting of 810 nHz between even m modes) represent
case;
further, added to this signal, another 60 sine waves in triplets, separated by 810 nHz
(simulating a splitting of 810 nHz between even m modes) represent 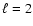 p-modes,
starting at 1.7300 mHz and with the same frequency spacing. Thus the signal simulates the
observed characteristics of the solar signal for
p-modes,
starting at 1.7300 mHz and with the same frequency spacing. Thus the signal simulates the
observed characteristics of the solar signal for 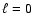 ,
,
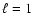 and
and 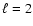 p-modes.
The amplitudes of the sine waves are all equal to unity but their phases are set at random;
to this signal, white noise is added with a
p-modes.
The amplitudes of the sine waves are all equal to unity but their phases are set at random;
to this signal, white noise is added with a
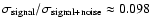 .
In the Fig. 3 (top) a slice of the power spectrum of the signal plus noise is
shown while in the central plot the power spectrum of the signal only is plotted.
.
In the Fig. 3 (top) a slice of the power spectrum of the signal plus noise is
shown while in the central plot the power spectrum of the signal only is plotted.
In the process of analysing such simulated time series, we assume that the signal could be
around 3.0 mHz and the search is done between 2.0 mHz and 4.0 mHz. Notice that in this
range, only 16 peaks of each 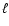 value are present. The first step is to calculate the
power spectrum of the sub-spectrum selected and look for any frequency spacing present. The
ability to find the frequency spacing depends on the signal to noise ratio. In
the present case the spacing of 0.1252 mHz is found without difficulty. With this spacing we
went back to recover the spectrum of the signal as it is explained in the previous section.
The recovered signal is shown in Fig. 3 (bottom).
value are present. The first step is to calculate the
power spectrum of the sub-spectrum selected and look for any frequency spacing present. The
ability to find the frequency spacing depends on the signal to noise ratio. In
the present case the spacing of 0.1252 mHz is found without difficulty. With this spacing we
went back to recover the spectrum of the signal as it is explained in the previous section.
The recovered signal is shown in Fig. 3 (bottom).
In the recovered spectrum the peaks are accepted as signal peaks if they follow the
criteria given in the previous section: their power must be 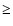 50% of the highest
peak and their phases
50% of the highest
peak and their phases 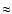 0.0. Following these criteria 15
0.0. Following these criteria 15 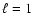 and 15
and 15 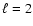 p-modes have been recovered.
p-modes have been recovered.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,height=3.9cm,clip]{MS26...
...cludegraphics[angle=90,width=8.8cm,height=3.9cm,clip]{MS2618f3c.ps}
\end{figure}](/articles/aa/full/2002/47/aa2618/Timg63.gif) |
Figure 3:
Top plot: a piece of the power spectrum of a month simulated signal; the signal is composed of 120 sine waves representing some 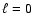 , ,
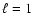 and
and 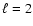 p-modes
plus white noise. Middle plot: the same piece of the power spectrum of the simulated signal
but without noise. Bottom plot: the same piece of the recovered power spectrum from the top
spectrum using the method described in the text.
p-modes
plus white noise. Middle plot: the same piece of the power spectrum of the simulated signal
but without noise. Bottom plot: the same piece of the recovered power spectrum from the top
spectrum using the method described in the text. |
| Open with DEXTER |
The 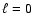 p-modes are not recovered at the level the others are; as it can be seen in Fig. 3 (bottom), they appear
in the recovered signal but with an amplitude so small that are not selected as signal
peaks because of the criteria used. However it is interesting to notice that in Fig. 3 (middle plot) where the simulated signal is shown without noise, the
p-modes are not recovered at the level the others are; as it can be seen in Fig. 3 (bottom), they appear
in the recovered signal but with an amplitude so small that are not selected as signal
peaks because of the criteria used. However it is interesting to notice that in Fig. 3 (middle plot) where the simulated signal is shown without noise, the 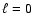 p-modes appear smaller than the
p-modes appear smaller than the 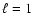 and
and 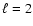 p-modes, although they were originally generated with the same amplitude. This is probably a result of the fact that the
p-modes, although they were originally generated with the same amplitude. This is probably a result of the fact that the 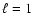 and
and 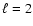 p-modes have structure (more than one peak) and some kind of constructive interference enhances the amplitude of these modes. No noise peak is selected as signal.
From the 15
p-modes have structure (more than one peak) and some kind of constructive interference enhances the amplitude of these modes. No noise peak is selected as signal.
From the 15 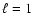 p-modes recovered, 11 are recovered as doublets with the exact
simulated frequencies; in the case of the 4 singlets only one of the two m components
is obtained. As far as the 15
p-modes recovered, 11 are recovered as doublets with the exact
simulated frequencies; in the case of the 4 singlets only one of the two m components
is obtained. As far as the 15 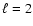 p-modes is concerned, 13 have been recovered as
singlets and 2 as doublets. For 6 of them, the recovered peak is the central one m=0,
for the rest, only one of the m components is recovered.
p-modes is concerned, 13 have been recovered as
singlets and 2 as doublets. For 6 of them, the recovered peak is the central one m=0,
for the rest, only one of the m components is recovered.
Although only one month of data has been generated and with a signal completely buried in
noise, the obtained results are quite good. Most of the signal peaks have been recovered,
even with their splitting, without any noise peaks among them. Changing the length and position
of the selected spectrum does not improve the results much, although using the
"known'' inputs, more signal is recovered.
Finally, using the same signal, gaps have been introduced to simulate observation from
Earth. Introducing gaps
decreases the signal to noise ratio. With the use of 25% of zeros every 24 hours
in a random way, slightly worse results are obtained; however, the signal spacing
0.1252 mHz still is obtained from the power spectrum of the power spectrum between 2.0 mHz and
4.0 mHz. Again, 15 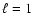 p-modes are recovered, 10 perfect doblets and 5 singlets, but
only 8
p-modes are recovered, 10 perfect doblets and 5 singlets, but
only 8 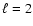 p-modes are obtained, all of them as singlets; in all cases, the recovered
peak is the m=0, given a perfect frequency for the mode.
p-modes are obtained, all of them as singlets; in all cases, the recovered
peak is the m=0, given a perfect frequency for the mode.
This is a more realistic case where one month of actually observed data from the GOLF
experiment onboard SOHO (Gabriel et al. 1995) has been used. To this real signal,
white noise has been added to simulate stellar conditions. In this example
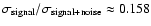 ,
which is the lowest signal that can be recovered
under these conditions. The problem now is that the frequencies in the power spectrum of this
signal are not exactly equally spaced and as already stated, the method proposed is based
on this hypothesis. See Fig. 4 for an echelle diagram of the frequencies used in the already simulated example
(Sect. 3.1) and the observed GOLF ones where the difference in the uniformity
of the spacings is very clear.
In this realistic case, the amplitudes are higher for the
,
which is the lowest signal that can be recovered
under these conditions. The problem now is that the frequencies in the power spectrum of this
signal are not exactly equally spaced and as already stated, the method proposed is based
on this hypothesis. See Fig. 4 for an echelle diagram of the frequencies used in the already simulated example
(Sect. 3.1) and the observed GOLF ones where the difference in the uniformity
of the spacings is very clear.
In this realistic case, the amplitudes are higher for the
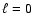 and
and 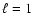 p-modes, keeping the average amplitude ratio observed in the
Sun. Moreover, the amplitudes are maximum around 3.2 mHz, falling rapidly on both sides;
see Fig. 5 (middle) where the true power spectrum of the observed GOLF data is shown.
p-modes, keeping the average amplitude ratio observed in the
Sun. Moreover, the amplitudes are maximum around 3.2 mHz, falling rapidly on both sides;
see Fig. 5 (middle) where the true power spectrum of the observed GOLF data is shown.
Therefore, in the analysis of this spectrum, in trying to minimize the problem instead of
using the power spectrum of the signal directly, an average of 2 spectra of half length
is used. The idea is to use a coarser frequency bin in order to move our spectrum signal
nearer to one with an equal spacing interval in the power spectrum. The price we pay,
of course, is worse resolution in frequency, which is now of 770 nHz. See Fig. 5 (top).
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,height=3.9cm,clip]{MS2618f4.ps}
\end{figure}](/articles/aa/full/2002/47/aa2618/Timg69.gif) |
Figure 4:
Echelle diagram for the frequencies of the examples in Sect. 3.1 (squares) and Sect. 3.2 (asterisks) where the deviation of the observed modes from an equally spaced pattern is clearly visible. In this plot, 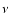 =
=
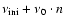 ;
for the squares ;
for the squares
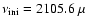 Hz, Hz,
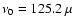 Hz and for the asterisks Hz and for the asterisks
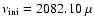 Hz, Hz,
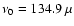 Hz, and n is the signal's peak number; Hz, and n is the signal's peak number;
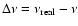 , ,
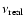 being the value of each frequency in the power spectrum.
being the value of each frequency in the power spectrum. |
| Open with DEXTER |
The average power spectrum of the 2 sub-series is analysed between 2.6 mHz and 3.7 mHz.
In this frequency range 8 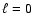 ,
8
,
8 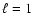 and 8
and 8 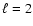 p-modes are present.
From the power spectrum of this selected sub-spectrum, a spacing of 0.1349 mHz is obtained.
With this spacing, the recovered spectrum is calculated and following the same criteria as
in previous examples, all the 8
p-modes are present.
From the power spectrum of this selected sub-spectrum, a spacing of 0.1349 mHz is obtained.
With this spacing, the recovered spectrum is calculated and following the same criteria as
in previous examples, all the 8 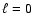 and the 8
and the 8 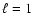 p-modes have been recovered,
but not the
p-modes have been recovered,
but not the 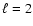 p-modes because of their lower amplitudes. See Fig. 5 (bottom).
p-modes because of their lower amplitudes. See Fig. 5 (bottom).
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,height=3.9cm,clip]{MS26...
...cludegraphics[angle=90,width=8.8cm,height=3.9cm,clip]{MS2618f5c.ps}
\end{figure}](/articles/aa/full/2002/47/aa2618/Timg70.gif) |
Figure 5:
Top plot: a piece of the mean power spectrum of one month of GOLF data cut into two pieces plus white noise. Middle plot: the same piece of the power spectrum of the GOLF data but without the added noise. Bottom plot: the same piece of the recovered power spectrum from the top spectrum using the method described in the text. |
| Open with DEXTER |
From the 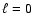 p-modes recovered, only one has a difference in frequency, with the real
one, bigger than the spectral resolution. From the
p-modes recovered, only one has a difference in frequency, with the real
one, bigger than the spectral resolution. From the 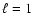 p-modes, all recovered as
singlets because of the spectral resolution, 4 of them have differences respect to the frequencies
of real peaks of around 1000 nHz, slightly above the spectral resolution.
p-modes, all recovered as
singlets because of the spectral resolution, 4 of them have differences respect to the frequencies
of real peaks of around 1000 nHz, slightly above the spectral resolution.
When gaps are added to the signal, produced as in the previous example every 24 hours in a
random way, the decrease in the signal to noise ratio prevents us from finding the spacing if
the percentage of zeros are between 12% and 25%. With 12% zeros, the 0.1349 mHz spacing is again found but when the spectrum is recovered with this spacing, only the
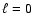 p-modes are found. However, they are all recovered and with a precision better
than the spectral resolution and, very importantly, no peaks from noise are selected as signal.
p-modes are found. However, they are all recovered and with a precision better
than the spectral resolution and, very importantly, no peaks from noise are selected as signal.
These results are very interesting because the example reproduces the expected stellar
data conditions with frequencies not exactly equally spaced and with a poor signal to
noise ratio. Even in these conditions a significant percentage of frequencies has been
well recovered and, more importantly, no peaks from noise have been selected.
In order to verify the performance of the method with even more real data, we have used
observations from 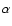 Cen A kindly provided by Hans Kjeldsen and Tim Bedding
(Kjeldsen et al. 1999). The data were collected over six nights in April 1995
from two sites (Siding Spring Observatory in Australia and the Europen Southern
Observatory at La Silla in Chile) with an overall duty cycle of 75%. They measured
Balmer line equivalent widths to look for solar-like oscillations and granulation.
Cen A kindly provided by Hans Kjeldsen and Tim Bedding
(Kjeldsen et al. 1999). The data were collected over six nights in April 1995
from two sites (Siding Spring Observatory in Australia and the Europen Southern
Observatory at La Silla in Chile) with an overall duty cycle of 75%. They measured
Balmer line equivalent widths to look for solar-like oscillations and granulation.
We started using the power spectrum of the data (produced by Kjeldsen et al.
1999). Although the true resolution of the data is only 2000 nHz, the data
has been padded with zeros to yield a spectral resolution of 100 nHz.
From the power spectrum of this power spectrum we tried to find the acoustic mode
signature in the frequency range between 1.6 and 2.8 mHz, where the signal is expected to
have its maximum amplitude according to the mass and effective temperature of the star
(Kjeldsen & Bedding 1995).
Applying the method described in this frequency range, only two possible frequency spacings
are barely found, one at 0.1057 mHz and a second one at 0.1394 mHz. Although the first one
approximately agrees with the expected value predicted by the stellar models (Morel et al.
2000), no clear signals are recovered from it when the inverse Fourier Transform
was applied, so the recovered power spectrum looks like the one shown in
Fig. 1 (bottom). Thus, if any signal is present in the data, it is too weak
compared to noise to be clearly detected using our method.
Trying to see whether the spacing found could be produced by a combination of noise and
the observing window function, a pure noise signal was simulated using the window function
and the weights of the real signal, and its power spectrum was obtained with a frequency
sampling of 500 nHz in a weighted iterative sine wave fitting procedure. However, in the
analysis of this power spectrum using our method, no frequency spacing was found.
To search for the limits of detection of the method in this particular case, a known
signal was injected into the observed data. The injected signal has the following
characteristics: 12 coherent sine waves, with the first one at 1.6 mHz
and having a frequency spacing of 0.1020 mHz. The window function and the weight values of
the observed series were used to produce this simulated signal. The amplitude of each sine
wave was left free to determine a minimum value for the detection method
to recover the injected signal. The result found is that it must have an amplitude
of at least 6 ppm (parts per million).
It is interesting to compare these results with the ones obtained by Bouchy & Carrier
(2001). Using the CORALIE spectrograph on the 1.2 m Swiss telescope
at the ESO observatory during 5 nights of observation, the authors claim a clear detection
of p-mode oscillations in 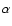 Cen A. The mean spacing found is 0.1057 mHz and the mean amplitude of the modes is about 0.3 m s-1. Such velocity amplitude can be
translated into intensity variations (ppm) given the effective temperature of the star (Kjeldsen & Bedding 1995). Therefore, assuming
Cen A. The mean spacing found is 0.1057 mHz and the mean amplitude of the modes is about 0.3 m s-1. Such velocity amplitude can be
translated into intensity variations (ppm) given the effective temperature of the star (Kjeldsen & Bedding 1995). Therefore, assuming
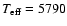 K
for
K
for 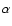 Cen A (Morel et al. 2000) the
Cen A (Morel et al. 2000) the 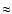 0.3 m s-1 velocity
amplitude obtained by Bouchy and Carrier corresponds to
0.3 m s-1 velocity
amplitude obtained by Bouchy and Carrier corresponds to 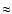 5 ppm. Although the data we have analysed, obtained by observing the equivalent widths of some Balmer lines, are slightly more sensitive than intensity variation, the 5 ppm could be somewhat higher and thus be close to the required signal level we would need to detect the oscillation.
5 ppm. Although the data we have analysed, obtained by observing the equivalent widths of some Balmer lines, are slightly more sensitive than intensity variation, the 5 ppm could be somewhat higher and thus be close to the required signal level we would need to detect the oscillation.
A method to detect the frequencies of several periodic functions of a signal buried in
noise has been developed. The signal must have only one specific characteristic: the
periodic functions that make up the signal must have frequencies "almost'' equally spaced.
Some previous knowledge about the signal is important to apply the method.
First, it is necessary to have an idea about the frequency range where the signal appears
and, second, it is important to know the order of magnitude of the frequency spacing.
These conditions are met in the stellar oscillations topic for which the method has been
developed.
The method works better when the frequencies are equally spaced. In this case, the method
is able to recover almost completely the power spectrum of the signal even with a
 .
Even if the frequencies depart from this exact
signature, the method still works well, although some precision is lost in the
recovered frequencies because of the necessity of increasing the frequency bin. Obviously,
the S/N ratio and the `departure' from an even or regular frequency spacing are parameters
that play a key role in the success of the method.
.
Even if the frequencies depart from this exact
signature, the method still works well, although some precision is lost in the
recovered frequencies because of the necessity of increasing the frequency bin. Obviously,
the S/N ratio and the `departure' from an even or regular frequency spacing are parameters
that play a key role in the success of the method.
Two realistic simulated series of data and one real observed series have been used to
analyse the performance of the method.
It is interesting to note that in the first example analysed, where all the 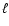 p-modes were generated with the same amplitude, the
p-modes were generated with the same amplitude, the 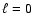 p-modes were not
recovered whereas almost all the
p-modes were not
recovered whereas almost all the 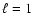 and
and 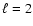 p-modes were obtained. It is clear
that having some structure, such as more than one peak, helps the process of recovering
the signal. However, in the second example the
p-modes were obtained. It is clear
that having some structure, such as more than one peak, helps the process of recovering
the signal. However, in the second example the 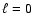 p-modes are well recovered, and
they are the only recovered peaks when gaps are introduced, due to their higher amplitude,
whereas the
p-modes are well recovered, and
they are the only recovered peaks when gaps are introduced, due to their higher amplitude,
whereas the 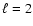 p-modes are not recovered, given their structure, because of their low
amplitude.
p-modes are not recovered, given their structure, because of their low
amplitude.
In both examples all frequencies of peaks are recovered with a precision of one frequency
bin, and in some cases even their splitting is well recovered. Even just the possibility
of obtaining the spacing is interesting enough, because it is capable of giving an
important restriction to the physical properties of the stars (Guenther 1998)
allowing one to restrict the models and to distinguish among different equally possible models.
The proposed procedure is also robust enough (it does not confuse real from noise peaks) to be
used to analyse stellar oscillation signals, as has been proved from the 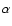 Cen A
data analysis. However, the present data seem to be at the limit of the signal to noise
ratio to allow clear identification of the individual p-mode frequency oscillations.
Cen A
data analysis. However, the present data seem to be at the limit of the signal to noise
ratio to allow clear identification of the individual p-mode frequency oscillations.
This method could be also useful to look for g-modes in solar data series,
especially in the asymptotic regime where the modes present regular signatures (now in
period rather than frequency), even though the signal to noise is predicted to be very low
(Kumar 1997). Such a possibility is being explored and is under development
at the moment.
Acknowledgements
The authors acknowledge M. Collados for many enlightening
discussions, H. Kjeldsen and T. Bedding for the use of their 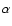 Cen A data and
R. García Bustinduy for the calibration of the GOLF data used. We would like also to
thank all our colleages: scientists, engineers and technicians involved with the GOLF project.
Cen A data and
R. García Bustinduy for the calibration of the GOLF data used. We would like also to
thank all our colleages: scientists, engineers and technicians involved with the GOLF project.
- Bedding, T. R., Butler, R. P., Kjeldsen, H., et al. 2001,
ApJ, 549, L105
In the text
NASA ADS
- Belmonte, J. A., Jones, A. R., Pallé, P. L., & Roca Cortés, T. 1990,
Ap&SS, 169, 77
In the text
NASA ADS
- Bouchy, F., & Carrier, F. 2001,
A&A, 374, L5
In the text
NASA ADS
- Brown, T. M., Gilliland, R. L., Noyes, R. W., & Ramsey, L. W. 1991,
ApJ, 368, 599
In the text
NASA ADS
- Christensen-Dalsgaard, J., & Frandsen, S. 1983,
Sol. Phys., 82, 469
In the text
NASA ADS
- Christensen-Dalsgaard, J. 1998a,
Proceedings of the First MONS Workshop, Aarhus, Denmark,
ed. H. Kjeldsen, & T.R. Bedding, Aarhus Universitet, 17
In the text
- Christensen-Dalsgaard, J. 1998b,
Proceedings of the SOHO 6/GONG 98 Workshop, Structure and Dynamics of the Interior of the Sun and Sun-like Stars, Boston, USA
ESA SP-418, 17
In the text
- Edmonds, P. D., & Cram, L. E. 1995,
MNRAS, 276, 1295
In the text
NASA ADS
- Gabriel, A. H., Grec, G., Charra, J., et al. 1995
Sol. Phys., 162, 61
In the text
NASA ADS
- Guenther, D. B. 1998,
Proceedings of the SOHO 6/GONG 98 Workshop, Structure and Dynamics of the Interior of the Sun and Sun-like Stars, Boston, USA
ESA SP-418, 375
In the text
- Kjeldsen, H., Bedding, T. R., Viskum, M., & Frandsen, S. 1995,
AJ, 109, 1313
In the text
NASA ADS
- Kjeldsen, H., & Bedding, T. R. 1995,
A&A, 293, 87
In the text
NASA ADS
- Kjeldsen, H., Bedding, T. R., Frandsen, S., & Dall, T. H. 1999,
MNRAS, 303, 579
In the text
NASA ADS
- Kumar, P. 1997,
Sounding Solar and Stellar Interiors, Nice, France, ed. J. Provost, & F.X. Schmider, IAU Symp. 181, 287
In the text
- Martic, M., Schmitt, J., Lebrun, J. C., et al. 1999,
A&A, 351, 993
In the text
NASA ADS
- Matthews, J. M. 1998,
Proceedings of the SOHO 6/GONG 98 Workshop, Structure and Dynamics of the Interior of the Sun and Sun-like Stars, Boston, USA
ESA SP-418, 395
In the text
- Michel, E. 1998,
Proceedings of the SOHO 6/GONG 98 Workshop, Structure and Dynamics of the Interior of the Sun and Sun-like Stars, Boston, USA
ESA SP-418, 399
In the text
- Morel, P., Provost, J., Lebreton, Y., Théveniu, F., & Berthomieu, G. 2000,
A&A, 363, 675
In the text
NASA ADS
- Pottash, E., Butcher, H. R., & van Hooesel, F. H. J. 1992,
A&A, 264, 138
In the text
NASA ADS
- Roca Cortés, T., & Régulo, C. 2001,
Proceedings of the SOHO 10/GONG 2000 Workshop, Helio- and Asteroseismology at the Dawn of the Millennium, Sta. Cruz de Tenerife, Spain,
ESA SP-464, 447
In the text
- Samadi, R., & Houdek, G. 2000
Proceedings of the Third MONS Workshop, Aarhus, Denmark,
ed. T.C. Teixeira, & T.R. Bedding, Aarhus Universitet, 27
In the text
- Schou, J., & Buzasi, D. L. 2000,
A&AS, 197, 4604
In the text
Copyright ESO 2002
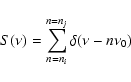
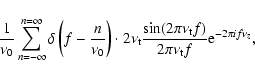
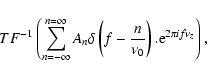
![\begin{displaymath}\sum_{n=- \infty}^{n= \infty} \delta[( \nu + \nu_{z}) - n \nu_{0}] ,
\end{displaymath}](/articles/aa/full/2002/47/aa2618/img44.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,height=3.52cm,clip]{MS2...
...ludegraphics[angle=90,width=8.8cm,height=3.52cm,clip]{MS2618f1d.ps}
\end{figure}](/articles/aa/full/2002/47/aa2618/Timg52.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,height=3.9cm,clip]{MS26...
...cludegraphics[angle=90,width=8.8cm,height=3.9cm,clip]{MS2618f3c.ps}
\end{figure}](/articles/aa/full/2002/47/aa2618/Timg63.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,height=3.9cm,clip]{MS26...
...cludegraphics[angle=90,width=8.8cm,height=3.9cm,clip]{MS2618f5c.ps}
\end{figure}](/articles/aa/full/2002/47/aa2618/Timg70.gif)