1 - Departament de Física Aplicada, Universitat Politècnica de Catalunya, c/Jordi Girona s/n, Módul B-4, Campus Nord, 08034 Barcelona, Spain
2 - Institute for Space Studies of Catalonia, c/Gran Capitá 2-4, Edif. Nexus 104, 08034 Barcelona, Spain

Abstract
The evolution of a star of initial mass 9 $M_{\odot}$ , and metallicity Z = 0.02 in a Close Binary System (CBS) is followed in the presence of different mass companions in order to study their influence on the final evolutionary stages and, in particular, on the structure and composition of the remnant components. In order to do that, we study two extreme cases. In the first one the mass of the secondary is 8 $M_{\odot}$ , whereas in the second one the mass was assumed to be 1 $M_{\odot}$ . For the first of those cases we have also explored the possible outcomes of both conservative and non-conservative mass-loss episodes. During the first mass transfer episode, several differences arise between the models. The system with the more extreme mass ratio (q=0.1) is not able to survive the first Roche lobe overflow (RLOF) as a binary, but instead, spiral-in of the secondary onto the envelope of the primary star is most likely. The system formed by two stars of comparable mass undergoes two mass transfer episodes in which the primary is the donor. We have performed two sets of calculations corresponding to this case in order to account for conservative and non-conservative mass transfer during the first mass loss episode. One of our main results is that for the non-conservative case the secondary becomes a Super-AGB star in a binary system. Such a star undergoes a final dredge-up episode, similar to that of a single star of comparable mass. The primary components do not undergo a Super-AGB phase, but instead a carbon-oxygen white dwarf is formed in both cases (conservative and non-conservative), before reversal mass transfer occurs. However, given the extreme mass ratios at this stage between the components of the binary system, especially for the conservative case, the possibility of merger episodes remains likely. We also discuss the presumable final outcomes of the system and possible observational counterparts.

Key words: stars: evolution - stars: binaries: general - stars: AGB and post-AGB - stars: white dwarfs

This is the second of a series of papers in which we intend to explore extensively the evolution of intermediate mass close binary systems (IMCBS). IMCBS are defined as those systems in which the primary component develops a partially degenerate carbon-oxygen core, after burning central helium in non-degenerate conditions. In particular, we focus on the evolution of heavy-weight intermediate mass stars, which have primary masses between $\sim$ $8~M_\odot$ and $11~M_\odot$ . These stars are thought to ultimately develop ONe cores (Ritossa et al. 1996), and populate the brightest portion of the Asymptotic Giant Branch. In this paper we follow the evolution of both components of the binary system from their main sequence phase until late evolutionary stages, paying special attention to the carbon burning phase, and to the final objects we can encounter afterwards.

Even though the evolution of isolated intermediate mass stars has recently been analyzed - see, for instance, Ritossa et al. (1999), and references therein - the evolution of this kind of star in binary systems has been very little studied. Probably one of the reasons for the absence of this kind of model in the literature is that the conversion of a CO core into an ONe core involves following the evolution of an unstable nuclear burning flame as it propagates first towards the center of the star and then outwards. The calculation is a very delicate and time-consuming task since the propagation of the flame front is not steady, but is interrupted by a series of rather violent shell flashes (García-Berro et al. 1997). The flashes are violent because the nuclear reaction rates are very temperature sensitive and the material is partially degenerate. Moreover, because of the near discontinuity in the physical variables at the flame front, following the inward motion of the flame requires very good spatial resolution and short time-steps. Furthermore, the evolution of stars within this range of masses in binary systems is even more complicated, since the presence of a close companion can dramatically alter the evolution of the primary star and its final outcome. As a result the only recent calculation in which a heavy-weight intermediate mass star is followed from its main sequence phase until carbon is exhausted in the core is that of Gil-Pons & García-Berro (2001), who followed the evolution of a $10~M_\odot$ star with solar metallicity in a binary system. Moreover, most of the developments in the field of binaries frequently disregarded the study of AGB stars, arguing that this phase is prematurely quenched in binary systems, due to significant mass loss in the evolution previous to the AGB phase. Important exceptions are the works of Jorissen (1999) and Smith et al. (1996) who proposed the existence of AGB stars in binary systems and, more recently, Van Eck et al. (2001), who found observational evidence of three AGB stars in binary systems.

In our previous paper (Gil-Pons & García-Berro 2001), we proposed a scenario in which a $10~M_\odot$ star could evolve to become a Super-AGB star and, ultimately, an ONe white dwarf, in spite of the fact that all the hydrogen-rich envelope and most of the helium layer had been lost in previous phases of the evolution. In this paper we consider again such an scenario but we relax some of the simplifying assumptions that were made there. In particular, we compute the evolution of a $9~ M_{\odot}$ primary (the initially most massive star) of the binary system, and we explore the effect of the mass of its companion. In doing so, we study two extreme cases; in the first one the initial mass ratio (q₀) is close to one (scenario 1), whereas in our second calculation this ratio is less than 0.2 (scenario 2). In fact, q₀=0.2 is a theoretical limit under which spiral-in of the less massive star onto the most massive and finally, the merger of components, cannot be avoided - see, e.g., Vanbeveren et al. (1998a).

Han et al. (2000) did a comprehensive study of the evolution of IMCBS in order to determine the influence of the initial mass ratio and orbital period on the final parameters of close binary systems whose primary initial mass is in the range $1~M_{\odot}$ to $8~M_\odot$ . Although they only consider the conservative case, a significant variation in the primary remnant masses is observed. In this paper we focus on more massive primaries - which have been little studied - and we extend our previous calculations in order to consider the evolution of the secondary. Furthermore, since there are still many uncertainties in relation to whether mass transfer is conservative or not, we have computed two evolutionary sequences for the first of our scenarios, and we have considered the two extreme cases that may occur during the first mass loss episode:

The paper is organized as follows. In Sect. 2, we present in detail our evolutionary scenarios. Section 3 is devoted to the study of the evolution of the first of the above mentioned scenarios in which a massive companion is assumed, whereas in Sect. 4 we explain in detail the evolution in the case of a low-mass secondary. The phase of reversal mass transfer in the first of our scenarios is fully explained in Sect. 5. Finally in Sect. 6 we discuss and summarize our major findings.

2 The scenarios

A general overview of the evolutionary scenarios mentioned in Sect. 1 can be found in Fig. 1, for the cases 1.a and 1.b, and in Fig. 2 for case 2.

2.1 Cases 1.a and 1.b: $\mathsfsl{9~ M_{\odot}}$ + $\mathsfsl{8~ M_{\odot}}$

The cases 1.a and 1.b (see Fig. 1) undergo two mass loss episodes. In both cases, the primary remnant has lost most of its hydrogen-rich envelope after the first one, but for the case 1.a, this mass is $\sim$ $1.8~M_{\odot}$ , slightly higher than the mass of the case 1.b remnant ( $\sim$ $1.6~M_{\odot}$ ). Depending on whether the mass transfer process is conservative or not the final mass of the secondary changes accordingly, with the corresponding values 8.7 and $15.4~M_{\odot}$ for the $B_{\rm c}$ and $B_{\rm r}$ cases, respectively. The final orbital periods also change after this phase, to 200 and 120 days for the conservative and non-conservative case respectively. Furthermore, using the prescription of Iben & Tutukov (1985) for non-conservative mass loss, we assume that that the angular momentum losses during the common envelope phase are as high as 70-80%. Orbital shrinkage is a direct consequence of this kind of mass loss, and therefore one can expect that the orbit of the binary system will be wider for the case of conservative mass transfer. We will come back to this point in Sect. 3.2. Despite these differences, the next mass transfer episode for both cases takes place during the helium-shell burning phase. At the end of the second mass transfer episode, the remnant of the primary consists of a carbon-oxygen core of about $\sim$ $1~M_{\odot}$ surrounded by a helium envelope of about $\sim$ $0.6~M_\odot$ . We would like to emphasize that considering convective overshooting might have led to somewhat more massive remnants for the primary. However, as we intend to keep consistent with our previous paper, and because no significant differences are expected, we have adopted the standard Schwarzschild criterion with no overshoot.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{fig01.eps}\end{figure}$	Figure 1: General overview of the evolution of the binary system and outline of the possible final outcomes, for the cases 1.a and 1.b, see text for details. CHeB stands for central He-burning, SHeB for shell He-burning, SAGB for Super-AGB and the rest of the acronyms have their usual meaning.
Open with DEXTER

At the end of the second mass transfer processes, the masses of the companions are 9.3 and $16.0~M_{\odot}$ and the orbital periods are 1000 and 700 days for cases 1.a and 1.b, respectively. After a very short phase in which carbon is partially burnt off-center in the core of the primary, the bulk of the carbon burning phase is ultimately avoided, and the remnant of the primary star is a CO white dwarf. At some point during the white dwarf cooling phase, the secondary becomes a red giant and reversal mass transfer ensues. The final outcome depends on the mass ratio of the binary system. Given that at this point the mass ratio is $q\leq 0.2$ , spiral-in of the white dwarf onto the secondary and, consequently, a merger of the two stars cannot be discarded. If, otherwise, the system is able to survive in spite of the extreme mass ratio, one can expect several different outcomes, which will be discussed in detail in Sect. 5.

2.2 Case 2: $\mathsfsl{9~ M_{\odot}}$ + $\mathsfsl{1~M_{\odot}}$

Figure 2 shows schematically the main evolutionary stages of our third evolutionary scenario. For this case there is only one episode of mass transfer, occuring when the primary reaches red giant dimensions. The most likely outcome is spiral-in of the secondary onto the primary and, ultimately, the merging of both components. This happens as a consequence of their initial mass ratio ( $q_0 \leq 0.2$ ). We simulate the process as a thermohaline mixing - see, for instance, Vanbeveren et al. (1998b). That is, we assume that all the material belonging to the secondary mixes instantaneously and homogeneously with the hydrogen-rich envelope of the primary. The final result of this process is a $10~M_\odot$ star. However, this star will have the core of a $9~ M_{\odot}$ star. A consequence of the merger is that the composition of the envelope is slightly changed, showing a slight overabuncances of C and O and an underabundance of N. After the merger, the product continues its evolution as a single star, very much in the way described by García-Berro & Iben (1994).

$\begin{figure} \par\includegraphics[width=6cm,clip]{fig02.eps}\end{figure}$	Figure 2: General overview of the evolution of the binary system, for the case 2 - see text for details.
Open with DEXTER

3 Evolution of the 9 $\mathsf{{\vec M}_{\odot}}$ and 8 $\mathsf{{\vec M}_{\odot}}$ system until reversal mass transfer

3.1 Evolution in the Hertzsprung-Russell diagram

In Fig. 3 the evolutionary tracks in the Hertzsprung-Russell diagram of the primary components of the CBS for both the case 1.a - left panel - and for the case 1.b - right panel - are shown. The mass loss episodes are represented as dotted lines. The primary starts losing mass just after the hydrogen core burning phase for case 1.a, whereas for the case 1.b the primary begins its RLOF when already climbing the red giant branch (RGB). Once this process is completed for both stars, they make their way to the left of the Hertzsprung-Russell diagram and become blue stragglers, since they are almost completely deprived of their hydrogen-rich envelopes. During this phase the bulk of core He-burning occurs, and once helium is depleted in the inner core, the primaries evolve towards decreasing effective temperatures.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{fig03.eps}\end{figure}$	Figure 3: Evolutionary tracks of the primary components of cases 1.a and 1.b in the Hertzsprung-Russell diagram. Mass transfer episodes are shown as dotted lines.
Open with DEXTER

The second mass loss episode for both cases starts when helium burns in a shell. At this point the luminosity increases at almost constant effective temperature for both cases. The mass loss processes in both cases continue while the primaries climb the giant branch and finish when the evolutionary paths of these stars are well advanced on the horizontal track for case 1.a, and just at the beginning of the horizontal track for case 1.b. Finally, once the primary components of the CBS are deprived of most of their envelope they become white dwarfs and follow the corresponding cooling tracks. On the contrary, the two secondary components (Fig. 4) look very different from each other. In particular, the narrow loop feature that appears in both cases before the top of the main sequence is reached are a consequence of the very high accretion rates at which mass transfer proceeds during the first RLOF. The second phase of accretion is less apparent, as it takes place at much smaller accretion rates. Once both episodes of mass transfer are over, the secondary for case 1.b evolves rather regularly, following the path on the Hertzsprung-Russell diagram of an isolated $\sim$ $9.3~M_{\odot}$ , which is very similar to that of a $9~ M_{\odot}$ star studied by García-Berro et al. (1997).

The evolution of the secondary for the case 1.a requires a more careful explanation. It starts its evolution as a normal $8~M_\odot$ single star. However, RLOF from its companion drives a mass transfer process during its early core hydrogen burning phase that allows it to almost double its mass (up to $15.4~M_{\odot}$ ) in a relatively brief interval of time. This translates into an important increase in the luminosity (see the left panel of Fig. 4) and a slight increase in the effective temperature. Accordingly, the surface radius of the secondary increases considerably (from $\sim$ $5~R_\odot$ to about $\sim$ $8~R_\odot$ ) but not enough to overflow its own Roche lobe. This effect has been already noted by Vanbeveren et al. (1998a) as being a direct consequence of the fact that the thermodynamic structure of the secondary is not able to adapt to the rapidly accreted matter.

The second mass transfer episode also happens during the core hydrogen burning phase of the secondary. During this episode the amount of accreted mass is relatively modest ( $\simeq$ $1~M_{\odot}$ ), and the accretion rates are much lower. The phase of core hydrogen burning for the secondary finishes shortly after this second accretion process. The subsequent evolution in the Hertzsprung-Russell diagram is similar to that of a high mass single star.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{fig04.eps}\end{figure}$	Figure 4: Evolutionary tracks of the secondary components of cases 1.a and 1.b in the Hertzsprung-Russell. Mass transfer episodes are shown as dotted lines.
Open with DEXTER

3.2 The mass loss episodes

As already mentioned, mass transfer in case 1.a begins shortly after the primary burns hydrogen in a shell. The presence of a radiative envelope surrounding the mass donor allows for moderate mass transfer rates. In fact, one can easily distinguish two phases in the mass loss episode - see the bottom panel of Fig. 5. The first phase corresponds to the beginning of mass transfer, proceeds at thermal time scales and the typical mass loss rates are $\dot M \approx 10^{-4}~M_{\odot}~{\rm yr}^{-1}$ . This phase lasts for about 10⁴ yr, and the bulk of the hydrogen-rich envelope is lost during it. The second phase takes place at much lower mass loss rates ( $\dot M \approx 10^{-6}$ - $10^{-5}~M_{\odot}~{\rm yr}^{-1}$ ), but it is considerably longer, lasting for, approximately, $4 \times 10^4$ yr. The upper panel of Fig. 5 shows how the surface abundances change as the mass transfer proceeds. The begining and the end of the mass transfer episode are clearly marked by the thin vertical lines. As it can be seen in this panel, at the end of the first mass loss episode the only CNO ash in the remaining envelope is ¹⁴N.

For case 1.b the primary starts losing mass while it is climbing the red giant branch. Consequently, the presence of a deep convective envelope during this evolutionary stage induces mass loss to proceed on fast time scales, during a common envelope phase, as was the case studied in Gil-Pons & García-Berro (2001). Since the first RLOF takes place on very fast time scales, and since the surface radius of the primary is well over the value of its Roche lobe radius during most of the time, we let the mass transfer proceed in such a way that the Roche lobe radius (Eggleton 1983) is proportional to the surface radius. As we intend to study very non-conservative mass transfer episodes, we assume that the Eddington accretion limit is valid, and we do not allow for super-Eddington accretion rates, as was done in the calculations of Podsialdowski et al. (2001) and Portegies-Zwart et al. (2000). That is, we consider that all the matter lost by the primary at a rate higher than the Eddington limit is lost by the system. During most of the first RLOF episode, mass loss proceeds at rates larger than $10^{-3}~M_\odot~{\rm yr}^{-1}$ and we obtain that only about $10 \%$ of the mass lost by the primary is actually accreted by the secondary.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{fig05.eps}\end{figure}$	Figure 5: Upper panel: evolution of the surface abundances of the primary for the case of a $B_{\rm r}$ mass transfer episode. Lower panel: evolution of the mass and the mass loss rate of the primary during the first RLOF episode.
Open with DEXTER

As for the conservative case, for this one we can also distinguish a fast and a slow phase in the mass transfer episode - see the bottom panel of Fig. 6. However, in this case the fast phase yields much larger mass loss rates ( $\dot M \approx 10^{-3}~M_{\odot}~{\rm yr}^{-1}$ ). The whole RLOF episode lasts for about $3 \times 10^4$ yr. Again, in the top panel of Fig. 6 the evolution of the surface abundances as the mass transfer episode proceeds is shown. It is easy to see that the final composition at the surface is very similar in both case 1.a and in case 1.b. Our final hydrogen abundance at the end of the first mass loss episode turns out to be $\simeq$ 0.3 in both cases, in very good agreement with the results of the calculations of de Loore & Vanbeveren et al. (1995). The second mass loss episode proceeds at much lower transfer rates, and thus the secondary is able to accrete all the matter that is lost by its companion, with little modification of its thermodynamical magnitudes (see the right panels of Figs. 3 and 4). This process starts after the development of a convective envelope surrounding the primary as a consequence of helium shell burning and it lasts until carbon is partially burnt in the helium-exhausted region.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{fig06.eps}\end{figure}$	Figure 6: Upper panel: evolution of the surface abundances of the primary for the case of a $B_{\rm c}$ mass transfer episode. Lower panel: evolution of the mass and the mass loss rate of the primary during the first RLOF episode.
Open with DEXTER

3.3 The structure and composition of the cores of the primary

Figure 7 shows the abundance profile of the primary for our case 1.a, and in Fig. 8 we show those abundance profiles for the case 1.b. The differences of composition for the central regions are negligible, the most abundant nuclei being oxygen ( $X_{\rm O}$ = 0.62), and carbon ( $X_{\rm C}$ = 0.37) in both cases. Minor differences in the shapes of the chemical profiles of the two cores appear as a consequence of the peculiarities of their evolution, specially in those phases in which mass loss or convection play an important role. The main difference is the size of the core, that happens to be smaller for the case 1.b ( $M_{\rm CO} = 0.78~M_{\odot}$ ), when compared to that of the case 1.a ( $M_{\rm CO} = 0.93~M_{\odot}$ ). This is a direct consequence of the fact that, because the orbit is wider for case 1.a, the corresponding CO core has more time to grow before a new RLOF occurs. The similarity between the primary cores before reversal mass transfer for the two cases supports one of the main hypotheses in Gil-Pons & García-Berro (2001) at this stage of the evolution, namely that the core of the primary is only slightly affected by the initial mass of the secondary.

3.4 The structure and composition of the secondary of Case 1.a

The secondary for case 1.a undergoes two accretion episodes while still burning hydrogen in its core. Computationally, we have treated accretion in the usual way, the so-called standard accretion model. That is, we have assumed that the infalling matter has the same specific entropy as the surface layers of the mass-gaining component - see, for instance, Pols (1994). As noted by Vanbeveren et al. (1998a), using this approximation has two important consequences. The first one is the sudden increase in the luminosity of the mass-gaining component which has been already commented on Sect. 3.1. The second one is the increase of the convective core as accretion occurs. This effect is clearly illustrated in the top panel of Fig. 9. The times at which the two accretion episodes begin are clearly marked by the thin vertical lines. The total mass of the star is also shown as a thick solid line. Since the second episode occurs at a much more modest pace, this effect is not as evident as it was for the first one. On the other hand, the change in the surface composition of the secondary is more evident in this case, as the accreted material onto its hydrogen-rich envelope is almost pure helium. The change in the composition has the effect of driving the evolution in the Hertzsprung-Russell diagram to higher luminosities than those corresponding to a star of the same mass and a non-polluted envelope.

After these two accretion episodes, the secondary evolves as a single $16~M_{\odot}$ star. When the secondary reaches red giant dimensions, superwinds start playing an important role. We have used the prescription of Jura (1987) in order to take into account the mass-loss rates due to stellar winds (see also Vanbeveren et al. 1998b). For our case the mass-loss rate turns out to be $\dot{M}_2 \sim 2\times 10^{-5}~M_\odot~{\rm yr}^{-1}$ . The effect of mass loss from the secondary is clearly seen for long enough times in the top panel of Fig. 9. However, it should be taken into account that several uncertainties surround this evolutionary phase, which can significantly affect the evolution of the binary system beyond this point. The main source of these uncertainties is the fact that the radius of the secondary gets very close to that of its Roche lobe. Therefore, it is difficult to ascertain whether or not reversal mass transfer occurs. Furthermore, there is the possibility of enhancement of the wind mass-loss rates due to the presence of a close companion or, even, partial capture of the wind by the primary remnant, as happens in symbiotic systems (Iben & Tutukov 1996). Moreover, when carbon is ignited at the center of the secondary, this star has not yet abandoned the red giant branch, and both the helium and the hydrogen burning shells remain active. We have not followed in detail the carbon burning phase because of these uncertainties. However, at this point of the evolution the resultant core is made of CO, with an oxygen abundance of $X_{\rm O} = 0.73$ and a carbon abundance of $X_{\rm C} = 0.23$ . The size of this helium-exhausted core is $4.5~M_{\odot}$ and it is surrounded by a helium envelope. However, since the uncertainties in the wind mass-loss rates are significant, we intentionally refrain from giving a precise value of its mass.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{fig09.eps}\end{figure}$	Figure 9: Convective regions for the evolution previous to carbon burning, for the secondaries of both our case 1.a (top panel) and 1.b (bottom panel).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{fig010.eps}\end{figure}$	Figure 10: Evolution of the main physical parameters of the secondary during carbon burning for case 1.b.
Open with DEXTER

3.5 The structure and composition of the secondary of Case 1.b. The evolution in the Super-AGB phase

The evolution of the secondary component for case 1.b (non-conservative) mass transfer presents some differences with respect to that of the case 1.a. These differences are not important, as far as the two accretion processes are concerned: in fact, both of them occur during the core hydrogen-burning phase of the mass gainer, and are accompanied by the same effects of overluminosity and extra growth of the helium core (see the top panel of Fig. 9). Note however that the first mass transfer episode starts earlier for case 1.a than for the case 1.b, as can be seen in Fig. 9. The differences become more remarkable once the accretion process is finished. The main reason for these differences is, of course, that the final masses of the secondaries are very unlike: $16~M_{\odot}$ for the case 1.a, and $9.3~M_{\odot}$ for the case 1.b, after the two accretion episodes. The new $9.3~M_{\odot}$ component evolves as an intermediate mass star, very much in the same way as the isolated $9~ M_{\odot}$ star studied by García-Berro et al. (1997). In spite of the important angular momentum loss that the system undergoes during the first mass transfer process, the final orbital separation after the second episode is such that the secondary component does not fill its Roche lobe until it reaches the Super-AGB phase. In fact, this star is able to undergo a dredge-up episode and a series of thermonuclear flashes caused by carbon burning in a degenerate core (see the top and bottom panels of Fig. 10).

Opposite to what happens to the $9~ M_{\odot}$ model studied by García-Berro et al. (1997), this dredge-up episode is not a consequence of energy release during the first carbon burning flash. Instead, it is the gravothermal energy release during the core contraction phase which follows the exhaustion of central helium that is responsible for the expansion and cooling of the outer envelope. Figures 10 and 11 help to explain this phenomenon by showing the evolution of the most important model parameters during this dredge-up episode. In particular the upper panel of Fig. 10 shows the evolution of carbon and helium luminosity, $L_{\rm C}$ and $L_{\rm He}$ , respectively. In this panel the flashes due to carbon ignition in a degenerate medium are apparent for times longer than $1.072 \times 10^{15}~{\rm s}$ . As usual, these thermonuclear flashes are accompanied by the formation of associated convective regions in the inner core (see the bottom panel of Fig. 10), and by expansion and cooling of the upper layers, leading to the temporary extinction of the helium burning shell. Note, however, that the dredge-up episode is not a consequence of the carbon flashes, since these flashes occur well after the fast penetration of the convective envelope, which occurs at $t \simeq 1.071\times 10^{15}~{\rm s}$ . Instead, in the lower panel of Fig. 10 it can be seen that the time at which the fast inner penetration of the base of the convective envelope is taking place is practically coincident with the time at which the surface radius increases at an almost constant surface luminosity, owing to an increase of the core density. In order to reinforce this argument, in Fig. 11 we show several relevant physical quantities for three selected models at three different times: before the fast advance inwards of the convective envelope (model a), during the advance (model b), and after it (model c). The location of these models is clearly shown in Fig. 10 and their corresponding times are labeled in Fig. 11. The upper panel of Fig. 11 shows the terms involved in the equation of energy conservation for model a. The minimum in the solid line corresponds to the gravitational energy release that, as can be seen, is transformed into work of expansion (dashed line), rather than into internal energy (dotted line). Note as well that this is done very close to the inner edge of the contracting envelope. The work of expansion induces a considerable increase in the surface radius of the star (central panel of Fig. 10). Ultimately, the cooling of the external layers has, as a main consequence, the increase in the envelope opacity - see the middle panel of Fig. 11. Consequently the radiative gradient increases and, at a certain point, allows the convective envelope to move inwards.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{fig011.eps}\end{figure}$	Figure 11: Energy variation rates for model a - upper panel - and opacity and temperature gradient profiles for models a, b and c - middle and bottom panels, respectively.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{fig012.eps}\end{figure}$	Figure 12: Abundance profiles of the secondary component at the end of the calculation for case 1.b.
Open with DEXTER

Finally, Fig. 12 shows the ONe core of the secondary component for the case 1.b. The size of this core is of about $0.94~M_{\odot}$ , and the main isotopes are oxygen ( $X_{\rm O} \simeq 0.60$ ), and neon ( $X_{\rm Ne} \simeq 0.25$ ). As can be seen in this figure, the neon-rich core is surrounded by a CO rich layer of irregular profile, as well as by a helium rich envelope, in agreement with the results of Gil-Pons & García-Berro (2001).

3.6 The reversal mass transfer

At the end of the carbon burning phase the surface radius has increased considerably, reaching values close to the Roche lobe radius ( $\sim$ $150~R_\odot$ ). At this evolutionary stage the situation is similar to that found in Gil-Pons & García-Berro (2001). Thus, it is difficult to determine the mass-loss rates, as there is the combined effect of RLOF and the typical superwinds of the AGB phase.

Perhaps the main uncertainty in this phase of the evolution is the fact that stellar winds from such a massive secondary might be enhanced - see, for instance, Iben & Tutukov (1996) - by the presence of a companion. Another uncertainty has to do with the efficiency of the secondary component in capturing the stellar wind. In order to provide an estimate of this efficiency, we proceed as in Iben & Tutukov (1996) and we assume that the remnant of the primary is able to accrete all the wind flowing into a disk that has the Bondi-Hoyle radius

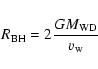$\begin{displaymath}% R_{\rm BH}=2\frac{GM_{\rm WD}}{v_{\rm w}} \end{displaymath}$

(1)

where $M_{\rm WD}$ is the mass of the remnant of the primary, and $v_{\rm w}$ is the velocity of the wind flowing from the secondary, that we have taken to be about 25 km s^-1, which is a typical value for red giants (Iben & Tutukov 1996). Note, however, that this value can vary significantly for different red giant stars. Under this assumption the accretion rate is:

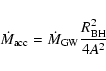$\begin{displaymath}% \dot{M}_{\rm acc}=\dot{M}_{\rm GW}\frac{{R_{\rm BH}^2}}{4A^2} \end{displaymath}$

(2)

where $\dot{M}_{\rm GW}$ is given by the expression of Jura (1987), and A is the orbital separation. We get that the accretion rates are between $\sim$ $1\%$ and $\sim$ $5\%$ of the wind mass loss rates. Therefore, $\dot{M}_{\rm acc} \sim 10^{-7}$ - $10^{-6}~M_{\odot}~{\rm yr}^{-1}$ . Analyzing this mass transfer process is certainly a very delicate task, as the extreme initial mass ratio between components is such that the possibility that the system would undergo a merger episode is non negligible. Hence, hydrodynamical simulations should be carried out in order to account for it in a realistic way - see, for instance, Hjellming & Taam (1991), Iben & Livio (1993), Lai et al. (1993) and, more recently, Taam & Sandquist (2000), and Ivanova & Podsiadlowski (2001). These calculations are beyond the scope of this paper, but, still, we will make some reasonable estimates of the possible final outcomes in Sect. 5.

4 Evolution of the $\mathsf{9~ {\vec M}_{\odot}}$ + $\mathsf{1~ {\vec M}_{\odot}}$ system

The system composed of a $9~ M_{\odot}$ and a $1~M_{\odot}$ star evolves in the following way: because the more massive star evolves much faster than its companion, it undergoes RLOF while the secondary component is still burning hydrogen in its core. The main characteristic that determines the evolution of the system is, in this case, the initial mass ratio between components, q = 0.1. This value is smaller than the critical mass ratio and, thus, no matter whether or not the initial period is such that the primary component is able to develop a deep convective envelope, the system is forced to undergo a merger episode (Vanbeveren et al. 1998a). This merger occurs at time $t = 7.3643 \times 10^{14}~{\rm s}$ , and in order to follow it we use the thermohaline mixing approximation. Once the merger has ended, the resulting single $10~M_\odot$ star behaves very much like the $10~M_\odot$ star studied by García-Berro & Iben (1994).

5 Discussion and conclusions

We have followed the evolution of a 9 $M_{\odot}$ star with solar metallicity in close binary systems with different initial orbital parameters. Our main goal has been to analyze the influence of the mass of the secondary component on the final possible outcomes of the close binary systems. In particular, we have computed a binary evolutionary scenario that allows the formation of Super-AGB stars in close binary systems. Our analysis encompassed all the relevant evolutionary phases, starting from the main sequence of both components, following the helium burning phase, and, if necessary the carbon burning phase. In summary, we have studied the following three cases:

For the last of these three cases the first mass transfer episode leads to the merger of components, due to the initial mass ratio between components: $q \la 0.2$ . The resulting $10~M_\odot$ single star behaves very much like the normal 10 $M_{\odot}$ star studied by García-Berro and Iben (1994), once the merger episode is over.

Cases 1.a and 1.b are more complicated. These two binary systems undergo two mass transfer episodes. This kind of evolution leads to very similar primary remnants: both of them are massive CO white dwarfs, $M_{\rm WD} \sim 0.98~M_{\odot}$ . However, the two systems are very different in orbital period and masses of the secondaries. For case 1.a the system is composed of a primary remnant and a $16~M_{\odot}$ main sequence star, with a hydrogen-rich envelope highly polluted by the CNO products from the primary remnant, dredged-up by convection and expelled in its second RLOF, and also by the products of its own helium burning shell. The secondary for case 1.b is a $9.3~M_{\odot}$ star. In many aspects the evolution of this star resembles very much that of the $9~ M_{\odot}$ single star previously studied by García-Berro et al. (1999), the only difference being that the second dredge-up is not caused by carbon burning, but, instead, by the gravothermal energy release at the end of core helium burning and before carbon is ignited off-center in the degenerate core.

Another important difference between case 1.a and case 1.b is the evolutionary stage of the secondary at the time at which reversal mass transfer occurs. For the case 1.a, it occurs when the secondary component climbs the red giant branch, whereas for case 1.b it only fills its Roche lobe when it reaches the Super-AGB phase. However, the uncertainties related to stellar winds, both in mass-loss rates and in the efficiency of mass accretion, do not allow us to determine the exact orbital parameters at the begining of reversal mass transfer and, ultimately, whether merger episodes could occur. In fact, if mass loss from the secondary (as a red giant or as a Super-AGB star) allows a significant decrease in its mass with low enough mass transfer rates, the steep change in the density profile of the mass losing star at the border of its core could brake the spiral-in of the primary. The system would then be able to survive as a binary, and the following possibilities may arise:

On the formation of Super-AGB stars in intermediate mass close binary systems

1 Introduction