A&A 396, 731-744 (2002)
DOI: 10.1051/0004-6361:20021406

Multiple field of view layer-oriented adaptive optics

Nearly whole sky coverage on 8 m class telescopes and beyond

R. Ragazzoni1,2 - E. Diolaiti3 - J. Farinato1 - E. Fedrigo4 - E. Marchetti4 - M. Tordi5 - D. Kirkman6


1 - INAF-Astrophysical Observatory of Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
2 - Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany as W. Paul awardee by the Alexander Von Humboldt Society
3 - Department of Astronomy, University of Padova, vicolo dell'Osservatorio 2, 35122 Padova, Italy
4 - European Southern Observatory, Karl-Schwarzschild Strasse 2, 85748, Germany
5 - INAF-Astronomical Observatory of Padova, vicolo dell'Osservatorio 5, 35122 Padova, Italy
6 - Center for Astrophysics and Space Science, UCSD, MS0424, La Jolla, CA 92093-0424, USA

Received 28 August 2001 / Accepted 16 September 2002

Abstract
In layer-oriented adaptive optics, multiconjugation is performed in a much more efficient way than conventional wavefront sensing. This improved efficiency is impressive for high altitude layers and moderate for ground ones. On the other hand, high altitude layers can be covered with only a limited field of view (where one can search for natural guide stars) while for ground layers the usable field of view is limited essentially by practical reasons. We introduce the further concept of multiple field of view layer-oriented adaptive optics where a combination of sampling and covered field leads easily to sky coverages for 8 m class telescopes that nearly approach the whole sky with the usage solely of natural guide stars. The extension of the concept to much larger apertures is also discussed.

Key words: telescopes - instrumentation: adaptive optics - techniques: high angular resolution


1 Introduction

Multi Conjugate Adaptive Optics (MCAO) has been introduced by Beckers (1989) as a way to overcome Field of View (FoV) limitations, typical of classical Adaptive Optics (AO, Beckers 1993). In MCAO more than one Deformable Mirror (DM) is conjugated to a specific height in the turbulent atmosphere in a way that, to a certain extent, one can cancel out the atmospheric turbulence in a three-dimensional way, although with a strong discretization along the range direction. While MCAO essentially refers to the way DMs introduces correction in the optical path, a key role is played in the way these DMs are driven by the WaveFront Sensor (WFS) unit(s). In this framework Tallon & Foy (1990) introduced the concept of tomography in order to disentangle numerically, and in an open-loop fashion, the turbulence at some altitudes, from the independent measurements on a certain number of reference stars by classical WFSs, like Shack-Hartmann (S-H) or curvature ones. Later this concept was rewritten in a more robust modal form, named modal tomography (Ragazzoni et al. 1999) that soon was proven on the sky (Ragazzoni et al. 2000) although in a very crude and preliminary form. In the meantime a completely different approach, named Layer-oriented (LO), has been introduced (Ragazzoni 1999a; Ragazzoni et al. 2000) where several reference stars are simultaneously sensed by a single WFS with one or more detectors that can be optically conjugated to a specific altitude. To increase the sky coverage using only Natural Guide Stars (NGS) on 8 m class telescopes, we introduce here an extension of the LO concept, called Multiple Field of View Layer-oriented Adaptive Optics. We show that this new approach allows for relevant sky coverage, of the order of one fifth of the sky at the Galactic Poles and approaching full coverage on the Galactic equator and at moderate Galactic latitudes. This new technique allows us to compete with LGS-based sky coverages even using a number of conservative assumptions. It must be pointed out that in the following we do not make any global optimizations but we adopt reasonable a priori choices on the parameters. Other important assumptions are that we limit the number of reference stars to 20, which is modest compared to similar figures for Multiple Object Spectrographs using similar technology (Fabricant et al. 1994; Watson et al. 2000; Gillingham et al. 2000), we implement the noise propagation coefficients of Shack-Hartmann rather than the pyramid ones and we assume quantum efficiencies and Read-Out-Noise in some cases even worse than what is really achieved on classical AO systems. Of course these features will play some role in the overall efficiency (Sect. 7), in a way that the final sky coverage will turn out to be even larger than devised here.

The structure of the article is the following:

-
in Sect. 2 we present a review of the LO approach;
-
in Sects. 3 and 4 the new concept is described;
-
a detailed calculation of the sky coverage achieved is performed in Sect. 5;
-
a possible opto-mechanical layout is presented in Sect. 6;
-
we discuss finally in Sect. 7 improvements resulting from the optimization of the system, together with possible extensions of the concept.

   
2 The layer-oriented concept

The major difference between the LO concept and the global reconstructor MCAO approach, described for instance in Ellerbroek (1994), is the different method of combining the wavefront information provided by the reference stars (Fig. 1). In the global reconstructor method, the wavefront sensing is performed in a star-oriented mode and the reference signals are combined by means of a global reconstruction matrix, to compute the commands for the DMs. In a LO system, a three-dimensional copy of the atmosphere is formed in the image space, by optically combining the light from the reference stars. Here several detectors are placed, conjugated to different atmospheric layers; each detector drives a DM conjugated to the same layer, forming an independent AO loop focussed onto a specific atmospheric slab. While a numerical implementation of LO is possible, collecting the wavefront measurements in a star-oriented fashion and combining them in a LO scheme, we limit here the discussion to the optical implementation. We also take the opportunity to clarify a misconception about LO, perhaps induced by its name: one might think that this approach would essentially correct only the layers where the DMs and the related detectors are conjugated. Of course this is not true (Diolaiti et al. 2001) and, moreover, provided that a proper choice of the reference stars is made, the volume of atmosphere can be corrected, with a degree of correction confined to the smaller frequencies as much as the considered layer is distant from the conjugated DM. According to Kolmogorov power distribution of the atmospheric turbulence, however, most of the turbulence itself can be compensated for a significant portion of height, the exact value depending upon the corrected FoV.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig1r.eps} \end{figure} Figure 1: Global reconstructor MCAO approach vs. layer-oriented.
Open with DEXTER

In the optical LO approach, whenever the loop closure is obtained, each detector essentially sees its conjugated atmosphere slab through the coaddition of several, even singularly faint, reference stars. On the other hand in global reconstructor MCAO the coaddition is still possible in a numerical fashion, but the sensitivity to fixed noise introduced by the WFSs, like read-out-noise in detectors or calibration errors, is unfavourable. One of the differences is the splitting of the light between the ground and the high altitude channels (in the case of two DMs), but this effect is taken into account in all the computations made in the following sections.

The complexity of the LO WFS essentially scales with the number of DMs and related detectors rather than with the number of sensed references. This allows, in principle, to sense simultaneously a huge number of stars, even faint and otherwise useless.

The advantages described so far are essentially of a technical nature and, although they are of great relevance, especially when scaling up to large telescope diameters, it has been evident to us from the beginning that the LO approach can achieve very efficient performance. Since each independent loop corrects a specific volume of atmosphere, it may be tuned to the statistical properties of that volume, namely the Fried parameter r0 and Greenwood frequency $f_{\rm G}$. In this way, for instance, the detector conjugated to the high altitude layer could be used in a sampling mode embracing a local r0 that can be significantly larger than the ground one and, the wind speed on the ground being significantly lower than the high altitude one, integration times for the ground layer conjugated detector can be significantly longer. This tuning of the system translates into an optimization of the photon density per subaperture on the detectors, thus improving the Signal to Noise Ratio (SNR).

LO MCAO has been studied with regards to stability and it has been found essentially equivalent to the global reconstructor MCAO approach in a set of interesting conditions (Diolaiti et al. 2001). Moreover it is easy to see that it is nearly equivalent to the optimum achievable correction, at least in a linear sense (Ragazzoni & Ghedina 2000).

An additional interesting feature is that it allows the natural use of the pyramid wavefront sensor (Ragazzoni 1996). Actually the LO approach fits well with any pupil-plane WFS but the advantage of using the pyramid is represented by the limiting magnitude gain over the Shack-Hartmann WFS (SHS), as pointed out by Ragazzoni & Farinato (1999) and by Esposito & Riccardi (2001).

All the mentioned above concepts lead to the speculation that, provided all these conditions (tuning of spatial and temporal sampling to a restricted volume of atmosphere, large number of references and additional gain introduced by the closed loop operations on a pyramid WFS) are successfully met and combined positively, good sky coverages could be obtained with the usage of NGSs alone, solving istantaneously (as a plus, in case this would be necessary) the tip-tilt indetermination problem (Pilkington 1987; Rigaut & Gendron 1992) and of course all the technical issues of reliability and efficiency related to the massive use of a significant number of artificial reference beacons. This approach is completely different from a previous conjecture (Ragazzoni 1999b) that assumed the global reconstructor MCAO had to be adopted, leading to very large FoVs. This raised doubts (Rigaut et al. 2000) on its practical implementation possible only on Extremely Large Telescopes (ELTs, Gilmozzi et al. 1998; Nelson 2000).

   
3 Where is the gain in the layer-oriented approach?

In LO AO the concept of limiting magnitude, common in conventional AO and to a certain extent applicable also to global reconstructor MCAO, is lost in favour of the concept of equivalent photon density at a given layer. Such a photon density is obtained by the concurrent fluxes of several stars. It is clear that the achievable correction depends upon the light coming from different references, in a way that these, while sensing the atmospheric turbulence, co-add to produce a SNR higher than the one achievable by simple AO. In LO AO this coadding is obtained optically: the signal from the reference stars are superimposed with single re-imaging optics and the read-out is performed only once on the overall signal. As it has been shown by Ragazzoni et al. (2000), the total signal delivered by the multi-pyramid WFS is the weighted average of the signals provided by the single stars, with weights proportional to the corresponding intensity. This property makes the estimated wavefront more sensitive to bright stars than to faint ones. However faint stars are more frequent than bright ones in any NGS asterism (Marchetti et al. 2002) and a group of faint sources is substantially equivalent in LO to a single bright star, thanks to the optical co-addding of the light.

The aim of LO is not to find out the maximum correctable FoV for a given performance; on the contrary it starts from a given FoV, where the reference stars are spread, and allows one to obtain a compensation (a partial one whenever the FoV is large) as good as possible in the whole FoV. With respect to this, it has been shown (Diolaiti et al. 2001) that the correction provided by LO is optimal, in the framework of linear systems theory, when the FoV is discretized according to the directions of the guide stars.

In principle, enlarging the technical FoV where the guide stars are selected allows us to increase the probability of finding suitable reference sources for wavefront sensing and this translates into a higher photon density and SNR. A major limitation in this respect is the existence of an upper limit $\theta_\gamma$ on the FoV that can be adopted to increase the photon density on a given altitude layer, as we show in the following. Let us define $\gamma$ as the average number of photons per square meter per second and per unit solid angle falling on a surface exposed to a given FoV of angular aperture $\theta $. Of course $\gamma$ has just a statistical significance and depends on the galactic latitude and longitude (l,b) where the cone beam of aperture $\theta $ is centered. Moreover it may depend on how the starlight is pre-treated: without any selection of stars, $\gamma$coincides with the equivalent sky brightness (Roach & Megill 1960, 1961) and, for practical reasons, the selection may be limited only to a certain number of stars $N_{\rm S}$. Nevertheless, we suppose that the figure $\gamma(N_{\rm s}, l, b)$ can be retrieved in some way.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig2.eps} \end{figure} Figure 2: A telescope of diameter D, collecting light from a given FoV $\theta $, will experience a certain equivalent density of photons per unit area dS that is different depending on the considered distance from the entrance pupil, reaching its maximum at the ground. It is shown in the text, although it may be evident from the drawing itself, that the photon density grows with $\theta ^2$ for the ground layer, while it approaches a certain limit for a given distance h.
Open with DEXTER

Assuming we use a telescope with a circular aperture of diameter D embracing a FoV of full angular size $\theta $, a layer at altitude h (see Fig. 2) will experience an average density of photons given by

 \begin{displaymath} \sigma = \frac{\pi \gamma \theta^2 S_0}{4S} \end{displaymath} (1)

where S is the area of the meta-pupil, representing the circular region including all the star footprints projected onto the considered layer, and S0is the area of the telescope pupil, given by

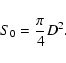\begin{displaymath}S_0 = \frac{\pi}{4}D^2. \end{displaymath} (2)

Recalling that the diameter of the meta-pupil at the given altitude h is larger than the pupil diameter D by the amount $h\theta$, one can write

\begin{displaymath}S=S_0\left[1+ 2 \frac{h\theta}{D} + \left( \frac{h\theta}{D}\right)^2 \right] \end{displaymath} (3)

where the terms related to the linear obstruction ratio $\varepsilon$ have been omitted for simplicity. One can now define a characteristic angle

\begin{displaymath}\theta_\gamma = \frac{D}{h} \end{displaymath} (4)

such that Eq. (1) can be written as

 \begin{displaymath}\sigma = \frac{\pi \gamma\theta^2_\gamma}{4} \times \frac{\le... ...+ 2\theta/\theta_\gamma+ \left(\theta/\theta_\gamma \right)^2} \end{displaymath} (5)

and, in the special case of very large FoV with respect to the angle $\theta_\gamma$,

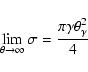\begin{displaymath}\lim_{\theta \rightarrow \infty} \sigma = \frac{\pi\gamma \theta_\gamma^2}{4} \end{displaymath} (6)

showing that, incrementing the FoV, the photon density does not steadily increase but tends to the one given by the $\theta_\gamma$ angle. This result can be understood considering that, when the FoV is increased more than a certain angle, the footprints generated by the angular directions at the edge of such a FoV no longer overlap and a further FoV enlargement increases the amount of collected starlight, but also the area over which the photons are spread, with no net density improvement.

The treatment followed above is a very rough one and it is easy to see that it fails to predict the exact behaviour of $\sigma(\theta)$ just around $\theta \approx \theta_\gamma$. In fact it is assumed that the additional starlight collected by enlarging the FoV is uniformly spread over the whole surface S. It is clear that this is not true and, for instance, in a footprint centered on the optical axis, there will be strictly no improvement of photon density whenever the FoV is larger than $\theta_\gamma$ (a consideration that gives to $\theta_\gamma$ a significance even larger than what expected from Eq. (5)). It is also clear that a more accurate analysis has to include a number of details and the inherent discretization of the problem leads us to the convinction that only a detailed numerical simulation, that is beyond the limits of this paper, can give some more significance to the $\sigma(\theta)$ behaviour.

The angle $\theta_\gamma$ is not the only limitation. First of all it has to be recalled that increasing the FoV has to be paid in terms of efficiency of the atmospheric correction in the portion of atmosphere far away from the locations where the DMs are conjugated. But there are also practical limitations to the arbitrary increase of the FoV. Once the technology for the DMs has been chosen, one is faced with the problem of designing the optical system to conceive a certain FoV with the proper altitude reimaging onto such DMs. This imposes practical limits on the maximum achievable FoV. This limit, on the other hand, is inherently existing also in the optical design of the telescopes. While we do not exploit here the comparison with the FoV required by LGSs, we just note that a practical limit much smaller than, for instance, $1^{\circ}$ has to be practically accomplished (the exact figure depending upon the type of telescope, the adopted DM technology and a number of other factors). Therefore $\theta_\gamma$ may be unrelevant with respect to more practical limitations. Trivially, this is the case for the ground layer where h=0 and $\theta_\gamma = \infty$. Even a h=1 km layer (a figure exceeding all the reasonable assumptions for ground layer conjugation) on a D=8 m class telescope gives $\theta_\gamma \approx 0.5^\circ$, by far larger than the maximum FoV imposed by practical limits. On the same telescope, however, considering a layer at h=10 km, we obtain $\theta_\gamma \approx 2^{\prime} 45^{\prime\prime}$, hence increasing the FoV in a LO approach more than this angle will give only marginal or no gain. We just note here that for a much larger telescope, $\theta_\gamma$ can easily become unimportant with respect to other factors and the LO approach should exhibit a steady improvement in photon density in the whole range of reasonable FoVs. The main conclusion of this discussion is that the limiting angle $\theta_\gamma$ may be important, with respect to practical limitations to the FoV, when considering high altitude layers on 8 m-class telescopes.

The optimization of the FoV for wavefront sensing is not the only degree of freedom to improve the photon density and the SNR. As already mentioned in Sect. 2, the system efficiency can be improved by tuning each loop to the spatial and temporal properties of the corresponding atmosphere slab. Roughly speaking, an increase of the local r0 translates into a photon collection gain that scales with the third power of such an increase. In fact the spatial sampling area scales quadratically with r0, while the integration times scales linearly, leading to the cubic power scaling law. An increase of the local r0 with respect to the overall one by a factor $2 \ldots 3$(for a more detailed discussion on this point see Sect. 5.1 and Fig. 6) leads to an increase in limiting magnitude in the remarkable range $2.2 \ldots 3.6$, even though we recall that this result has been obtained assuming a flat wind speed distribution. A less favourable distribution will lead to a scaling law with a power in the range $2 \ldots 3$. It is important to note that the gain that can be achieved by tuning the spatial and temporal sampling of the loops is relatively small on the ground layer, but it can be large for the high altitude portion of the atmosphere.

We conclude this discussion with a couple of key statements, which are the basis of the Multiple FoV Adaptive Optics concept that we are going to describe in the following section:

1.
the significative gain for the correction of the layers close to the ground can be achieved essentially by the adoption of a large FoV where enough photons can be collected efficiently from different directions in the sky;
2.
on the opposite side, the gain in the high altitude layers is limited by an angle comparable to $\theta_\gamma$ and must resides only in the spatio-temporal gain offered by the LO approach.
It is already evident from these considerations that the driver in terms of sky coverage will not depend upon the ground layer correction (where one can technically expand the covered FoV within reasonable limits) but on the high altitude layers, where the atmosphere sets the maximum achievable correction. Although we are going to confirm this result in the following sections, we leave to further investigation the task to identify possible strategies to relax such a limitation.

   
4 The multiple FoV concept

The most straightforward approach, though not the only one, to take into consideration the key points mentioned in the previous section is simply to use different covered FoVs for the different conjugated detectors. Moreover, once the ratio between the various FoVs is quite large, one should also consider the possibility to use nested anular fields: in fact, sharing the light from the innermost FoV will lead only to a limited improvement for the larger FoV, while it can substantially degradate the innermost one. In its simplest form, the Multiple-FoV layer-oriented MCAO concept can be conceived as follows:

Following the discussion of the previous section, we adopt for the smaller FoV, associated with the high altitude layer, a reasonable figure of $2^{\prime }$, representative of a 8 m-class telescope. Concerning the ground layer, instead, we consider a  $6^{\prime }$FoV and, according to the previous remark, we limit this FoV to an anular region with inner and outer radius of $1^{\prime}$ and $3^{\prime}$respectively. This figure is chosen here as a reasonable one, without attempting any optimization.

The basic layout of such a system is illustrated in Fig. 3. Two DMs are considered: the first is conjugated to the ground, or very close to it, while the second is conjugated to a certain altitude. The correction applied by the first DM is driven by a set of reference stars embracing a FoV of $6^{\prime }$ in this example, while the second DM is driven by a different set of reference stars embracing a smaller FoV of  $2^{\prime }$ in the drawing. Layers not exactly conjugated to any DM will be corrected only at spatial frequencies lower than the ones defined by the footprints of the selected FoVs, like in any MCAO system. In this way the correction performed by the DM with larger FoV degradates more rapidly with the distance of the layer from the altitude where the DM itself is conjugated.

There are a number of comments possible on the described concept. Provided a suitable setup is adopted, a full correction, in a MCAO sense, can be achieved only within the small  $2^{\prime }$ portion of the FoV, which may be identified with the science FoV of interest. The anular region associated to the larger  $6^{\prime }$FoV can be corrected only for ground turbulence. Although both compensations work in a closed loop fashion, in fact, the ground turbulence correction is perturbed by the uncorrected contribution of the high altitude layers. Strictly speaking the introduced compensation should correct (at least in the high SNR regime) the ground turbulence and should apparently replace it with superimposed replicas of the high altitude layers, one replica for each star in the  $6^{\prime }$ anular FoV, introducing some very low spatial frequency residual. Although the physical origin of these residuals is in the high altitude layers, these will appear optically, inside the MCAO system, as coming from the ground. One can say, in other words, that the effect of the LO closed loop associated to the large FoV and conjugated to the ground is to replace the ground layer with an hampered version of the high altitude turbulence. The consequence of the last consideration is that the system should really consider a number of three independent loops, the third concerning the correction of the ground residual mentioned above.

A more detailed description of the conceived system is shown in Fig. 4. The same layout, seen from the data flow point of view, is shown in Fig. 5. From the wavefront sensing point of view, the system can be seen as a combination of two LO units. The first WFS is associated to the central $2^{\prime }$ FoV and has two detectors, one conjugated to the ground, the other to the high altitude layer. The second LO WFS is associated to the  $6^{\prime }$ anular FoV and includes only one detector, focused onto the ground portion of the turbulence. The system includes two DMs. The one conjugated to the high altitude layer is driven by the corresponding detector in the  $2^{\prime }$ WFS. The DM conjugated to the ground, instead, is driven by the detector of the  $6^{\prime }$ WFS and by the remaining detector of the  $2^{\prime }$WFS conjugated to the ground. The former measures the ground turbulence collecting the information provided by a large number of stars over the  $6^{\prime }$ FoV, whereas the latter measures the residual due to the high altitude turbulence optically transferred onto the ground. From the opto-mechanical point of view, two different zones have to be considered on the focal plane: a central one, collecting the light from both the ground and the high altitude portion of the atmosphere in a  $2^{\prime }$ FoV, and a larger anular zone associated to the ground with a  $6^{\prime }$ FoV. A more detailed discussion on this point is presented in Sect. 6.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig3.eps} \end{figure} Figure 3: Multiple-FoV system layout: conjugated planes and associated FoVs.
Open with DEXTER

We just comment here on the fact that the third detector (the one measuring the high-altitude turbulence residual optically transferred onto the ground) may probably be avoided, also eliminating a beam-splitter in the 2$^{\prime }$channel, which actually results in a loss of light on the detector conjugated to the high altitude layer. The corresponding signal might be computed with signal-processing dedicated techniques, applied to the measurements of the remaining two detectors. Although this point deserves attention, we leave it to further investigation and we consider in this paper the solution with three detectors.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig4.eps} \end{figure} Figure 4: A simplified optical setup of the multiple-FoV concept, showing the basic loop structure.
Open with DEXTER

The spatial and temporal sampling of the three detectors has to be tuned according to the properties of the corresponding portion of atmosphere at the wavefront sensing wavelength. The detector conjugated to the ground layer, looking at the larger anular FoV, has spatial and temporal sampling typical of the lowest part of the atmosphere. The other detector conjugated to the ground layer, looking at the inner  $2^{\prime }$ FoV, has spatial and temporal sampling typical of the higher part of the atmosphere, suitably adjusted in order to take into account the smoothing effect corresponding to the superposition of different shifted replicas of the turbulence, one for each reference star in the anular FoV. Finally the detector conjugated to the high altitude layer, looking at the inner  $2^{\prime }$ FoV, has a spatial and temporal sampling typical of the higher part of the atmosphere.

Even though a complete analysis of the loop stability of such a system is beyond the scope of this paper, we just note that the ground layer loop, associated to the  $6^{\prime }$ FoV, is likely to be very robust, due to the high number of reference stars, translating into a high SNR, and to the fact that the star fooprints overlap perfectly on the telescope pupil, hence the photon density is uniform. Furthermore the major contribution to the overall turbulence is usually concentrated in the ground layer and the effect associated to the high altitude turbulence should be negligible, or at least not sufficiently strong to perturb the stability of the ground loop (furthermore these will drop to nearly zero once the whole set of loops is closed).

   
5 Sky coverage calculation

The correction achievable by the MCAO system is limited by several factors, among which we mention the number of DMs and the size of the associated FoVs, the temporal bandwidth and the brightness of the reference stars. Once these parameters are fixed, the maximum achievable Strehl Ratio (SR) can be computed for a given atmospheric model. In practice this value of SR will be achieved only in the limiting case of arbitrarily large SNR, otherwise the measurement noise imposes a limitation on the accuracy of the correction. The sky coverage may then be defined as the fraction of sky where the number and brightness of reference stars ensure a SR at least as large as 50% the ideal value, achievable in the noise-free case.

  \begin{figure} \par\includegraphics[width=8.7cm,clip]{fig5.eps} \end{figure} Figure 5: The equivalent information flow for the multiple-FoV layer-oriented MCAO.
Open with DEXTER

   
5.1 Models of the atmosphere

We consider in this section two different models of the atmosphere:

The profiles are defined by a set of normalized weights Wi corresponding to the sampled altitudes Hi. The weights represent the relative strength of the respective layers and they are scaled in order to fulfill the normalization condition:

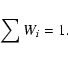\begin{displaymath}\sum W_i = 1. \end{displaymath} (7)

For each turbulence profile, we have computed the characteristic Fried parameter r0 of the lower and upper portion of the atmosphere, divided in two slabs by an ideal interface placed at a certain altitude H, which is depending on the conjugation range of the DMs. This interface separates the influence regions of the two DMs (see Sect. 5.2). The values of $r_{0,{\rm bottom}}$and $r_{0,{\rm top}}$ for different profiles have been computed according to the relations

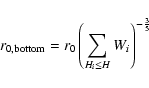\begin{displaymath}r_{\rm0,bottom} = r_0\left(\sum_{H_i\le H}W_i\right)^{-\frac{3}{5}} \end{displaymath} (8)

and

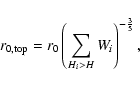\begin{displaymath}r_{\rm0,top} = r_0\left(\sum_{H_i > H}W_i\right)^{-\frac{3}{5}}, \end{displaymath} (9)

where an overall Fried parameter r0=30 cm has been assumed. The graphs in Fig. 6 show the resulting $r_{0,{\rm bottom}}$ and  $r_{0,{\rm top}}$ plotted as a function of the interface altitude H. Choosing for instance the interface altitude at 4 km, from Fig. 6 it can be easily seen that in the case of Paranal atmosphere there is a difference of a factor 2 between the r0 value of the lower and the upper part of the atmosphere. This difference increases to a factor 3 in the case of the Cerro Pachon atmospheric model. The proper choice of the DM conjugation range and thus of the interface altitude H should be found by the means of a minimisation of the residual turbulence power shown in Fig. 7 (bottom) which is left to further investigation. It should be noticed that if the separation is very close to the ground, r0,top approaches r0, since there is no turbulence left in the bottom region; otherwise, as the separation of the two regions approaches the maximum altitude, $r_{\rm0,bottom}$ reaches the value of the overall r0.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig6a.eps}\par\includegraphics[width=8.8cm,clip]{fig6b.eps} \end{figure} Figure 6: The equivalent r0 of the two regions of atmosphere separated at altitude H: the calculation is made using the power distribution of the atmospheric profiles of Cerro Paranal (top) and Cerro Pachon (bottom), scaled to an overall r0= 30 cm.
Open with DEXTER

   
5.2 The maximum achievable Strehl

The adopted configuration, with two DMs (ground and high altitude layer) and associated FoVs of  $6^{\prime }$ and  $2^{\prime }$respectively, imposes a limitation on the maximum achievable SR. In an ideal noise-free case under the hypothesis of perfect knowledge of the turbulence, the conjugated layers are perfectly corrected. The non-conjugated layers, instead, are corrected by a given DM up to a spatial frequency $f_{\rm c} \propto 1/\left(\theta \Delta h\right)$, where $\theta $ is the FoV associated to the considered DM and $\Delta h$ is the distance of the layer from the conjugation plane. This relation describes a hyperbole in a plane $\left(f,h\right)$. The curves corresponding to the two DMs intersect at a certain altitude H (see Sect. 5.1) representing a kind of interface: below this altitude the correction is essentially due to the DM conjugated to the ground, above the interface the major effect is due to the other DM. Using this approximation, it is easy to compute the residual CN2 profile (Fig. 7), which is plotted vs. the altitude h and the spatial frequency f. In other words the turbulence at the conjugated altitudes is completely removed while at different altitudes the compensation is only partial, up to a spatial frequency inversely proportional to the distance from the conjugation altitude; this is the consequence of the smoothing effect introduced by the finite FoV associated to the DMs and related detectors. The DM conjugated to the ground adopts a larger FoV and hence the degradation of the correction is faster than for the other DM, characterized by a smaller FoV. The bottom graph in Fig. 7 shows the integral along h of the residual turbulence, exhibiting a spectrum where the low spatial spatial frequencies have been removed.

Using the approximations mentioned before, we have computed the structure function of the residual phase (Roddier 1999) and, finally, the corrected Point Spread Function (PSF) (Fig. 8). The comparison of this PSF to the ideal diffraction-limited case gives an estimate of the maximum achievable SRwith the adopted configuration. Of course the result depends on the exact conjugation range of the DMs, even though for our considerations we may adopt ${SR} \approx 0.2$ as a representative value of the best achievable correction.

   
5.3 Noise propagation

We now proceed to estimate the photon budget for the multiple-FoV system, following the modal analysis of Rigaut & Gendron (1992) of a single-reference AO system. The wavefront is expressed as linear combination of Zernike polynomials (Noll 1976) and the AO correction is applied only to the low order terms. The variance of the residual phase in a given angular direction $\alpha$ is

 
$\displaystyle \sigma_{\rm res}^2$ = $\displaystyle \sum_{j=J_{\rm max}}^\infty <a_j^2> + \sum_{j=2}^{J_{\rm max}}<b_j^2>$  
    $\displaystyle +\sum_{j=2}^{J_{\rm max}}<\left(a_j(0)-a_j(\alpha)\right)^2>$ (10)


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig7.eps} \end{figure} Figure 7: Top: the average CN2 profile of Cerro Paranal compensated by a Multiple-FoV layer-oriented system with two DMs conjugated at 800 m and $\approx $8.5 km and FoV of  $6^{\prime }$ and  $2^{\prime }$respectively. Bottom: residual turbulence power spectrum after DMs correction. No optimization of the DMs altitude based on the minimization of the residual power has been performed.
Open with DEXTER


where $J_{\rm max}$ is the highest corrected Zernike mode. The first term in Eq. (10) is the turbulent residual error, associated to the high order modes, the second represents the noise propagated in the wavefront reconstruction and the third one gives the contribution of anisoplanatism, since the residual phase is considered here in the angular direction $\alpha$ displaced from the reference star ($\alpha=0$). These terms can be re-arranged according to the expression

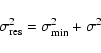\begin{displaymath}\sigma_{\rm res}^2 = \sigma_{\rm min}^2 + \sigma^2 \end{displaymath} (11)

where $\sigma_{\rm min}^2$ is the combined effect of the high orders and of the anisoplanatism and represents a kind of lower limit to the phase variance, attainable in a noise-free case, whereas $\sigma^2$ is the variance associated to the measurement noise, propagating in the wavefront reconstruction. According to the approximation

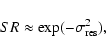\begin{displaymath}{SR} \approx {\rm exp}({-\sigma_{\rm res}^2}), \end{displaymath} (12)

the SR can therefore be expressed as the product of two factors: the first is the achievable SR in a noise-free case, the second is the SRreduction due to the noise. For our photon budget evaluation, we are interested in the noise term and therefore we can simplify the expression of the residual phase variance $\sigma_{\rm res}^2$considering only the $\sigma^2$ term. For a Shack-Hartmann WFS (Rousset 1987) the phase variance due to the measurement noise is

 \begin{displaymath}\sigma^2 = \left(\frac{\lambda_{\rm WFS}}{\lambda}\right)^2 \frac{2\pi}{{NR}^2}\sum_{j=2}^{J_{\rm max}}p_j \end{displaymath} (13)

where $\lambda_{\rm WFS}$ ($0.7~\mu$m here) is the wavefront sensing wavelength, $\lambda$ ($0.8~\mu$m here) is the imaging wavelength, SNR is the signal to noise ratio and pj are the noise propagation coefficients for the jth Zernike mode. These coefficients are given by the relation (Rigaut & Gendron 1992)

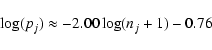\begin{displaymath}{\rm log}(p_j) \approx -2.00 \log(n_j+1) - 0.76 \end{displaymath} (14)

which holds for the jth Zernike polynomial of radial degree nj, except the last two given by

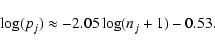\begin{displaymath}{\rm log}(p_j) \approx -2.05 \log (n_j+1) - 0.53. \end{displaymath} (15)

The sum of Eq. (13) is extended up to the $J_{\rm max}$ Zernike polynomial; in our calculation we fix $J_{\rm max}$ in order to fill the radial degree $N_{\rm max}=D/r_0$, where D is the diameter of the pupil or the meta-pupil and r0 is the Fried parameter characteristic of the layer we want to correct. Hence we have three different values of $N_{\rm max}$and, considering the contribution of the three loops completely uncorrelated, the basic relation for the photon budget becomes

 \begin{displaymath}\sigma^2 = \sigma_{\rm GL6}^2 + \sigma_{\rm GL2}^2 + \sigma_{\rm HL}^2 \end{displaymath} (16)

where GL6, GL2 and HL represent respectively the  $6^{\prime }$ FoV detector conjugated to the ground, the  $2^{\prime }$ FoV detector conjugated to the ground and the  $2^{\prime }$ FoV detector conjugated to the high altitude layer. The phase variance contributions of the three loops are
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig8.eps} \end{figure} Figure 8: The PSF computed using the residual turbulence profile shown in Fig. 7 is here plotted and compared to the theoretical diffraction-limited PSF and to an uncompensated one.
Open with DEXTER


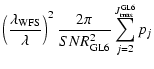$\displaystyle \sigma_{\rm GL6}^2$ = $\displaystyle \left(\frac{\lambda_{\rm WFS}}{\lambda}\right)^2 \frac{2\pi}{{SNR^2_{\rm GL6}}}\sum_{j=2}^{J_{\rm max}^{\rm GL6}}p_j$  
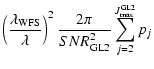$\displaystyle \sigma_{\rm GL2}^2$ = $\displaystyle \left(\frac{\lambda_{\rm WFS}}{\lambda}\right)^2 \frac{2\pi}{{SNR^2_{\rm GL2}}}\sum_{j=2}^{J_{\rm max}^{\rm GL2}}p_j$ (17)
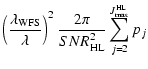$\displaystyle \sigma_{\rm HL}^2$ = $\displaystyle \left(\frac{\lambda_{\rm WFS}}{\lambda}\right)^2 \frac{2\pi}{{SNR^2_{\rm HL}}}\sum_{j=2}^{J_{\rm max}^{\rm HL}}p_j$  

where, called RON the detector Read Out Noise, the SNR is defined by:

 \begin{displaymath}{SNR} =\frac{N}{\sqrt{N + 4 {RON}^2}} \end{displaymath} (18)

and N is the total number of collected photons arriving respectively in the GL6, GL2 and HL areas. The spatial and temporal sampling of the detectors conjugated to the ground (GL6) and high altitude layers (HL) has been adjusted in order to match the statistical properties (Fried parameter r0and coherence time $\tau _0$) of the corresponding portions of the atmosphere. In particular r0 has been computed as in Sect. 5.1, fixing the conjugation altitude of the DMs to $\approx $0 km and $\approx $8.5 km respectively. The third detector (GL2) measures a smoothed version of the high altitude turbulence, according to the superposition of the shifted footprints of the reference stars in the  $6^{\prime }$ anular FoV. Given the low probability of superposition, the corresponding copies of the high altitude turbulence can be considered uncorrelated and the equivalent Fried parameter is

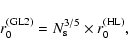\begin{displaymath}r_0^{\left(\rm GL2\right)} = N_{\rm s}^{3/5} \times r_0^{\left(\rm HL\right)}, \end{displaymath} (19)

where $N_{\rm s}$ is the number of stars in the anular FoV. We have deliberately limited the number of stars to the reasonable figure $N_{\rm s}=20$. Furthermore, since the equivalent r0 of the two atmosphere portions is quite sensitive to the specific turbulence profile, as shown in Sect. 5.1, we have considered four different cases, characterized by various combinations of the basic parameters of the lower and upper atmosphere. A complete summary is reported in Table 1, along with the corresponding number of Zernike polynomials considered in each case.

According to Eq. (16) and assuming the same contribution to the overall variance from the three loops, we have evaluated the SNR on each detector needed to give an overall SR=0.5, corresponding to 50% of the maximum achievable SR in the absence of noise (Sect. 5.2). The SNR has been computed including both photon noise and detector Read-Out-Noise (RON). We have considered two cases with different RON (0.5 and 2.5 e-). The photon losses have been accounted for an overall QE=0.1. This figure includes optical losses on the whole optical train and, at a careful analysis, appears to be a conservative choice. For example, in the case of a MCAO demonstrator made by ESO in which one WFS channel is LO based, the final throughput is 0.21 (Marchetti et al. 2002). The computed values of SNR have been transformed into equivalent photon density on each detector considering a wavefront sensing wavelength $\lambda_{\rm WFS}=0.7~\mu$m (R band) and a bandwidth $\Delta \lambda=0.5~\mu$m. The results are reported in Table 2, expressed in terms of equivalent magnitudes, assuming a zero point ${ZP}=6.11 \times 10^{11}~{\rm photons} ~ {\rm s}^{-1} ~{\rm m}^{-2}~ \mu{\rm m}^{-1}$.

5.4 Sky coverage

According to the results obtained in the previous section, the sky coverage is likely to be limited by the photon density on the $6^{\prime }$ FoV detector conjugated to the ground (GL6) and on the one conjugated to the high altitude layer (HL). The obtained figures have to be compared with the actual photon density realized by integrating the brightness of the natural reference stars within the corresponding FoVs. This computation has been accomplished considering the Bahcall & Soneira (1981) model of the star distribution in the Galaxy. The plots in Fig. 9 show the normalized probability to have a given integrated magnitude over each of the two FoVs of interest, as a function of the magnitude itself and for different values of the Galactic coordinates. It should be noticed that only the 20 brightest stars have been considered in each FoV to compute the equivalent integrated brightness.

 

 
Table 1: Parameters of the atmospheric regions used to evaluate the photon budget; r0, $\tau _0$ and v represent the Fried parameter, the turbulence coherence time and the wind speed; $J_{\rm max}$ and $N_{\rm max}$ represent the number of Zernike polynomials and the maximum radial order. The values for the GL2 WFS are obtained considering the turbulence introduced in closed-loop by the GL6 WFS.
    Case 1 Case 2 Case 3 Case 4
  r0 0.33 m 0.33 m 0.33 m 0.33 m
  v 10 m s-1 10 m s-1 10 m s-1 10 s-1
GL6 $\tau _0$ 33 ms 33 ms 33 ms 33 ms
  $J_{\rm max}^{\rm GL6}$ 324 324 324 324
  $N_{\rm max}^{\rm GL6}$ 24 24 24 24
  r0 0.60 m 0.60 m 0.90 m 0.90 m
  v 20 m s-1 30 m s-1 20 m s-1 30 m s-1
HL $\tau _0$ 30 ms 20 ms 45 ms 3 0ms
  $J_{\rm max}^{\rm HL}$ 104 104 54 54
  $N_{\rm max}^{\rm HL}$ 13 13 9 9
  r0 3.62 m 3.62 m 5.43 m 5.43 m
  v 20 m s-1 30 m s-1 20 m s-1 30 m s-1
GL2 $\tau _0$ 180 ms 120 ms 270 ms 180 ms
  $J_{\rm max}^{\rm GL2}$ 9 9 5 5
  $N_{\rm max}^{\rm GL2}$ 3 3 2 2



 

 
Table 2: Photon density (expressed in term of R magnitudes) on each detector giving a 50% Strehl ratio reduction due to noise effects. Cases 1, 2, 3, 4 correspond to different combinations of atmospheric parameters, described in Table 1.
RON Case 1 Case 2
  GL2 GL6 HL GL2 GL6 HL
0.5 22.7 15.0 16.3 22.2 15.0 15.9
2.5 21.3 13.8 15.1 20.9 13.8 14.6
RON Case 3 Case 4
  GL2 GL6 HL GL2 GL6 HL
0.5 24.2 15.0 17.7 23.8 15.0 17.3
2.5 22.8 13.8 16.5 22.4 13.8 16.0


Since the probabilities related to the two FoV are uncorrelated, the overall one is the product of the two. The resulting sky coverage, for different Galactic latitudes and atmospheric conditions corresponding to the cases 2 and 4 described in Table 1, is reported in Table 3. In regions close to the Galactic Plane it ranges from 1/2 to almost the full sky for average atmospheric conditions depending on the RON. At the Galactic Pole, where the natural star density is much lower, it ranges from 1/6 to 1/3 of the sky. It should be stressed here that this result has been obtained without any optimization of the system and, first of all, considering the noise propagation coefficients of the Shack-Hartmann WFS, hence neglecting the limiting magnitude gain achievable in closed-loop with the pyramid WFS.

   
6 An optomechanical design

We consider in the following a possible optomechanical layout like the one devised in Fig. 10. We assume that the MCAO optical relay has been suitably designed in order to conjugate the DMs with the proper altitude and with a suitable sampling of the inter-actuator spacing for the chosen DM technology. Here we just focus on the portion of optical design that strictly refers to the layer-oriented approach. First we show that diffraction-limited imaging performance over a  $6^{\prime }$ FoV can be easily achieved on the telescope focal plane with a simple field flattener. Then we show a possible design of the objectives which re-image the pupils for layer-oriented wavefront sensing. An additional 1:1 optical relay is shown in Fig. 10, placed between the pick up mirror of the central field and the reflective pyramids support. This element is not considered here, because its specifications can be easily retrieved from several literature or commercial designs.

6.1 Field flattener

The field curvature of the telescope has been corrected with a simple doublet placed near the focal plane. The field flattener, described in Table 4, is composed of two spherical lenses and ensures diffraction-limited imaging perfomance (Strehl ratio higher than 0.8) over a  $6^{\prime }$ FoV and a wavelength range from 0.6 to 1.0 $\mu$m. The focal ratio of the optical system including the telescope and the corrector is approximately F/15.

6.2 Optical relays

The pupil images are focused onto the detectors by means of two objectives (Figs. 11 and 12), whose optical specifications are reported in Table 5.

The objective of the  $6^{\prime }$ FoV channel conjugated to the ground is composed of five single lenses, whereas the other one includes one singlet and three doublets. All the surfaces are spherical. The focal ratio is F/2.5 in both cases and using a commercial fiber taper with shrinking ratio 5:1 it can be scaled to F/0.5. The optical specifications of the two relays are reported in Tables 6 and 7. The imaging performance has been optimized by ray-tracing in the wavelength range, from 0.6 to 1.0 $\mu$m. The resulting optical quality is such that 80% of the total energy is included in a region smaller than 1/10 of the equivalent r0 size (see Table 8): in this way the spatial resolution of the relays is much better than the sub-aperture size for the LO wavefront sensing.

   
7 Further developments

The sky coverage evaluation presented in Sect. 5 has been performed adopting the noise propagation coefficients of the Shack-Hartmann WFS and without any optimization of the main parameters of the system. For these reasons we consider the derived estimate a very conservative one. Furthermore we have neglected a number of items that should be taken into account in a practical implementation of the concept, in order to improve the achievable performance, in terms of Strehl ratio and relative sky coverage.

7.1 Using the pyramid WFS

The pyramid WFS (PS) has been conceived by Ragazzoni (1996) as an alternative approach to wavefront sensing in astronomical AO. Over the past few years, the properties of the PS have been extensively studied, both from the theoretical point of view and by laboratory experiments (Riccardi 1998). The PS has been implemented on AdOpt@TNG, the AO module of the Italian Telescopio Nazionale Galileo (Ragazzoni et al. 2000).

A notable feature of the PS is the easily adjustable gain and sensitivity, translating into a considerable gain in the limiting magnitude of the reference source over the Shack-Hartmann WFS (SHS). This result has been pointed out in closed loop operation (Ragazzoni & Farinato 1999) and then has been extended to the partial correction regime (Esposito & Riccardi 2001). The basic reason of this gain is that, in closed loop, the size of the spot on the pyramid pin is essentially equal to the diffraction limit of the telescope. A $\lambda/D$ tilt aberration, for instance, produces a spot displacement comparable to the spot size and therefore a large signal. In a SHS, instead, the spot size is always limited by the diffraction on the lenslet aperture and the same wavefront aberration considered before generates a much smaller signal, requiring much more photons for a reliable detection. For the same reason, it is clear that the PS gain is larger and larger as the telescope diameter increases.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig_anello.eps}\includegraphics[width=8.8cm,clip]{fig_centro.eps} \end{figure} Figure 9: Top: normalized probability to find a given surface brightness (integrated R magnitude) over the  $6^{\prime }$ anular FoV, plotted as a function of the magnitude itself. Bottom: same as before, for the inner  $2^{\prime }$ FoV. Only the 20 brightest stars have been considered in each case to compute the integrated R magnitude (l and b are the galactic co-ordinates, longitude and latitude respectively).
Open with DEXTER


 

 
Table 3: The first two columns of the upper and lower block are the probability to have the required integrated magnitude on the two FoVs separately. The third column is the combined probability, i.e. the actual sky coverage. The upper block refers to a read-out-noise ${RON} = 2.5~\rm e^-$, the lower one to a read-out-noise ${RON} = 0.5~\rm e^-$. Each probability is actually a range of values, corresponding to two limiting cases of atmosphere, a bad one (case 2) and a good one (case 4). It should be stressed that "bad'' and "good'' refer to the turbulence distribution between the lower and the upper portion of the atmosphere and not to the total turbulence strength.
Gal. Lat. LO with SHS noise coefficients and ${RON} = 2.5~\rm e^-$
  GL6 HL Total
$b=20^{\circ}$ 1.00 $\dots$ 1.00 0.46 $\dots$ 0.96 0.46 $\dots$ 0.96
$b=50^{\circ}$ 0.83 $\dots$ 0.83 0.19 $\dots$ 0.51 0.16 $\dots$ 0.42
$b=90^{\circ}$ 0.61 $\dots$ 0.61 0.13 $\dots$ 0.34 0.08 $\dots$ 0.21
Gal. Lat. LO with SHS noise coefficients and ${RON} = 0.5~\rm e^-$
  GL6 HL Total
$b=20^{\circ}$ 1.00 $\dots$ 1.00 0.86 $\dots$ 0.99 0.86 $\dots$ 0.99
$b=50^{\circ}$ 0.99 $\dots$ 0.99 0.38 $\dots$ 0.72 0.38 $\dots$ 0.72
$b=90^{\circ}$ 0.89 $\dots$ 0.89 0.27 $\dots$ 0.53 0.24 $\dots$ 0.47



 

 
Table 4: Field flattener optical specifications. All lengths are in mm. Curvature radii are positive if the center of curvature is to the right from the surface vertex. Each thickness value represents the distance from a given surface to the following one.
Radius Thickness Glass Diameter
-626.845 20 BK7 222
-244.685 10 FK51 222
-2458.999 50 air 222



 

 
Table 5: Optical requirements of the two re-imaging objectives.
  Clear Aperture FoV F/ Focal length
$6^{\prime }$ channel 230 mm 11.4$^{\circ}$ 2.5 575 mm
$2^{\prime }$ channel 80 mm 20.0$^{\circ}$ 2.5 200 mm



  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig10.eps} \end{figure} Figure 10: An overall sketch of a possible opto-mechanical configuration. The inner  $2^{\prime }$ FoV is folded by a mirror close to the telescope focal plane and sent, through a 1:1 optical relay, to a magnetic positioner of reflective pyramids, that are to be accomodated by a robotic arm to sense the 20 brightest stars. These pyramids reflects the splitted light into an objective and, through a folding mirror, the light is fed to two CCDs conjugated to the ground and high altitude layer respectively. The 20 brightest stars in the $6^{\prime }$ anular FoV are sensed by a set of refractive pyramids set up in the focal plane by a polar robotic positioner and fed, through a dedicated objective, to a CCD conjugated to the ground layer. Fiber tapers are part of the optical design, allowing to a reasonable size of the re-imaged pupils onto the CCDs, allowing the use of commercially available ones.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig11.eps} \end{figure} Figure 11: The  $6^{\prime }$ channel conjugated to the ground adopts refractive pyramids. This translates into a considerable amount of unwanted background light that is re-imaged onto a central pupil. The vertex angle of the pyramids, hence, has to be large enough in order to have the four reference pupils suitably separated on the detector plane and avoid any contamination from the background light. This translates into a more demanding performances of this objective in terms of covered field.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig12.eps} \end{figure} Figure 12: The objective of the  $2^{\prime }$ channel has to re-image the full meta-pupil embracing the science FoV at the highest altitude where the second DM can be conjugated, assumed to be 15 km here.
Open with DEXTER

The limiting magnitude gain of the PS can now be considered in the present sky coverage evaluation, leading to the figures reported in the lower of Table 9. One can see a substantial increase in the overall sky coverage, although its order of magnitude is not changed. We stress that these figures are obtained assuming no gain in the large FoV anulus (where only a moderate correction is expected and no high-Strhel is achieved) and a partial gain in the central FoV, accordingly to the results published by Esposito & Riccardi (2001).

7.2 A strategy for the reference stars

We have limited our considerations to 20 stars in each FoV, a reasonable number indeed. The 20 brightest stars have been considered, even though this might not always be the optimal choice. The homogeneity of the stars distribution, in fact, is an important factor, in order to have not only the largest amount of photons but also a sufficiently uniform distribution of the light on the high altitude layers. A very uneven brightness distribution among the reference stars might lead to a non-uniform correction, and, in some limiting cases, to instability of the layer-oriented loop. This is a direct consequence of the optical weighting of the reference signals, inherent to layer-oriented, which weights more the brighter stars. It is therefore clear that the choice of the stars must be accomplished in a way to optimize the field homogeneity in the layer conjugated to the higher DM, and this might be done even in spite of the total flux. We just mention here that a new method has been recently proposed (Ragazzoni et al. 2001) to accomplish the PS modulation with no moving part, using a light diffusing plate in an intermediate pupil plane. If a different plate is selected for each star, with a scattering coefficient proportional to the intensity of the star itself, then it is possible to avoid the above mentioned troubles related to the signal weighting.


 

 
Table 6: Specifications of optical relay for the 6$^{\prime }$ channel. Conventions and units are as in Table 4.
Radius Thickness Glass Diameter
325.97 55.00 FCD1 240
-353.41 7.33 air 240
-340.05 13.57 LAFN7 240
1957.91 20.17 air 240
527.08 33.73 BAF51 240
-2009.60 407.73 air 240
-135.72 7.33 K7 130
-473.06 0.37 air 130
203.49 27.00 TAF4 130
252.12 42.14 air 130



 

 
Table 7: Specifications of optical relay for the  $2^{\prime }$ channel. Conventions and units are as in Table 4.
Radius Thickness Glass Diameter
120.61 21.00 SK2 84
299.54 4.20 air 84
71.19 27.00 SK4 84
-86.77 5.70 LF5 84
49.21 44.85 air 84
-41.94 6.00 F4 70
-286.66 15.90 LAF2 90
-60.79 13.36 air 90
261.15 7.00 LF5 100
74.08 28.00 BK7 100
-143.23 103.10 air 100



 

 
Table 8: Polychromatic performance of optical relays, compared with the equivalent r0 size on the relay image plane. The physical r0 values, corresponding to the lower and upper portions of the atmosphere, are 30 and 60 cm respectively. The optical performance is represented by the size of the square including 80% of the total energy of the spot produced by the relay for a source at a given field angle; the figure reported here is averaged over different field angles. Units are mm.
  r0 80% EE
$6^{\prime }$ channel 1.438 0.078
$2^{\prime }$ channel 1.000 0.096



 

 
Table 9: Same as Table 3 considering the pyramid WFS gain.
Gal. Lat. LO with PS magnitude gain and ${RON} = 2.5~\rm e^-$
  GL6 HL Total
$b=20^{\circ}$ 1.00 $\dots$ 1.00 0.67 $\dots$ 0.99 0.67 $\dots$ 0.99
$b=50^{\circ}$ 0.83 $\dots$ 0.83 0.28 $\dots$ 0.63 0.23 $\dots$ 0.52
$b=90^{\circ}$ 0.61 $\dots$ 0.61 0.20 $\dots$ 0.45 0.12 $\dots$ 0.27
Gal. Lat. LO with PS magnitude gain and ${RON} = 0.5~\rm e^-$
  GL6 HL Total
$b=20^{\circ}$ 1.00 $\dots$ 1.00 0.97 $\dots$ 1.00 0.97 $\dots$ 1.00
$b=50^{\circ}$ 0.99 $\dots$ 0.99 0.54 $\dots$ 0.79 0.54 $\dots$ 0.79
$b=90^{\circ}$ 0.89 $\dots$ 0.89 0.37 $\dots$ 0.62 0.33 $\dots$ 0.55


7.3 Overall optimization

The overall optimization of the system will also be somehow important to improve the final performance. Considering the number of parameters to optimize, the final gain might not be small, even if probably not comparable to the gain introduced by the PS. We identify in this section some items that have to be taken into account for the fine tuning of the system, with a brief description of the related problems.

7.4 Scaling to more than two DMs

In case there is a strong requirement in term of SR, without FoV reductions, or in case the properties of the atmospheric turbulence at the telescope site are such that there is a strong contribution from turbulence located far away from the layers where the DMs are conjugated, the introduction of further DMs is required. There is an almost natural way to generalize the multiple FoV layer-oriented concept, considering different FoVs for each specific DM. The simplest case of three DMs is shown in Fig. 13. Concerning the number of required detectors, we just mention here that it might not be necessary to use a specific detector for the intermediate DM added in this example, being possible to reconstruct the correction using the signal collected from the WFS conjugated to the ground layer (Farinato et al. 2001).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{fig13.eps} \end{figure} Figure 13: Generalizing the multiple-FoV concepts to more than two DMs, one can conceive different FoVs for each specific DM. Because of the different smoothing of the layers distant from the conjugated planes, the covered volumes, along the range direction, are likely to be roughly inversely proportional to the different FoVs: a smaller range for the larger FoV on the lowest DM, and progressively larger volumes for smaller FoVs at the higher DMs.
Open with DEXTER

7.5 Scaling to ELTs

The multiple FoV concept can be scaled to ELTs. Apparently the major problem is represented by the size of the optics in the WFS. Scaling the components presented here for a 8 m class telescope results in exceedingly large lenses. However it is possible to modify the optical design (Marchetti & Ragazzoni 2001), in order to keep the size of the lenses to a reasonable level; this can be accomplished with a longer, though straightforward, optical train.

Recently, however, novel optical solutions (Ragazzoni et al. 2001) have been introduced in order to keep optics, and especially pupil size on the detector, nearly arbitrarily low. We do not speculate here on these possibilities, just because a further bunch of degree of freedom can be introduced, making an overall optimization a mandatory approach for such giant telescopes.

Another interesting consideration refers to the pupil shape of ELTs that is expected to be significantly more complex than 8 m class telescopes because of large mechanical structures on the incoming beams (like big wires to keep in shape the mechanical truss holding the various optical elements) and the related choice of reference stars is to be carefully tuned in order to avoid that the related shadows (whose conjugation is expected to be a variable and complicated one, because of the large overall size of the ELTs structure) will produce too poor a SNR on some pupil regions.

8 Conclusion

The layer-oriented approach is a very efficient implementation of the MCAO concept. Among the strong points of such a scheme, we recall the possibility to tune the spatial and temporal sampling of each independent AO loop, the optical co-addition of the light from the reference sources and the limiting magnitude gain of the pyramid WFS in closed loop operation. These concepts, positively combined, lead to the speculation that a layer-oriented system would allow for significant sky coverage using NGS only.

In this paper we have presented a new idea, mostly based on the layer-oriented approach, which leads to a very relevant sky coverage, close to the whole sky on the Galactic Plane and as high as one fifth of the sky at the Galactic Pole, using NGS. The new concept adopts different FoVs for the different portions of the corrected atmospheric volume, in order to maximize the photon density on the relevant scale of interest for wavefront sensing. A larger FoV is used for the ground turbulence, where the photon density might not always be sufficiently high and, on the other hand, the spatial and temporal sampling gain is moderate; a narrower FoV is adopted instead for the high altitude layers, where the tuning of the spatial and temporal sampling ensures an impressive gain. Of course full correction, in a MCAO sense, is possible only within the latter FoV, which can be identified with the science field of interest.

We have described a very simple implementation of the new concept, and, without any optimization, we have derived the above-mentioned relevant results described in Table 3. In our evaluation we made some simplifications: for instance, we assumed that the integrated light of the stars is uniformly spread over the whole FoV; this approximation is quite strong for an 8 m class telescope, where the overlap at 10 km of altitude for a 2$^{\prime }$ FoV is $\approx $$40\%$, but it is very close to the reality in the case of ELTs, where the overlap of the pupils is very high (94% for a 100 m telescope with 2$^{\prime }$ FoV at 10 km). Furthermore, we did not consider a number of key points, like the optimization of the main parameters of the system and moreover the properties of the pyramid wavefront sensor, which will lead to a further substantial improvement, in terms of achievable correction and sky coverage, as shown in Table 9. Due to its inherent simplicity, the new concept can be easily modified, either increasing the number of DMs or scaling to much larger telescopes.

Acknowledgements
Thanks are due to Piero Salinari and to Wolfgang Gaessler for the useful comments on the subject discussed in this paper. Many thanks also to the anonymous referee who significantly contributed to improve the manuscript quality.

References

 

Copyright ESO 2002