A&A 396, 683-692 (2002)
DOI: 10.1051/0004-6361:20021431
Prolonged millimeter-wave radio emission from a solar flare
near the limb
S. Pohjolainen1,2 - J. Hildebrandt3
- M. Karlický4 - A. Magun5 - I. M. Chertok6
1 - Tuorla Observatory, Väisälä Institute for Space
Physics and Astronomy, 21500 Piikkiö, Finland
2 - Observatoire de Paris, DASOP, 92195 Meudon, France
3 - Astrophysical Institute Potsdam, 14482 Potsdam,
Germany
4 - Astronomical Institute Ondrejov, 25165 Ondrejov,
Czech Republic
5 - Institute of Applied Physics, 3012 Bern, Switzerland
6 - IZMIRAN, Russian Academy of Sciences, Troitsk,
Moscow Region, 142190 Russia
Received 3 November 2000 / Accepted 26 September 2002
Abstract
We present a multi-wavelength analysis of a gradual radio flare
on June 27, 1993 which showed emission at millimeter waves long after
the soft X-ray flux had peaked. The radio flare located at S12 E75
was associated with a GOES class M3.6 flare that lasted for more than
one hour and hard X-ray emission during the rising phase of the
soft X-ray/radio emission. The maximum radio flux
density at 35 GHz was 60 sfu, but the calculated thermal
bremsstrahlung flux from the GOES soft X-rays was less than half of
that. The possible explanations for this prolonged millimeter wave
emission could be accelerated high-energy electrons gyrating along the
field-lines (nonthermal gyrosynchrotron emission) or thermal
bremsstrahlung from evaporating chromospheric warm and dense plasma
(cool enough to go undetected by GOES), or a mixture of these. Our
model calculations show that even an inhomogeneous source containing
both kinds of particles would not be able to produce such a spectral
shape. A second source with extremely high electron densities
(>1016 m-3), large source dimensions (>1015 m2),
and very low temperatures (<106 K) must be assumed to explain the
observed radio spectra.
Key words: Sun: chromosphere - Sun: corona - Sun: flares - Sun: radio radiation - X-rays: general
In many radio flares observed at millimeter and centimeter wavelengths
a gradual thermal component starts to dominate after the impulsive phase,
in agreement with the evolution in soft X-rays
(Kundu et al. 1994; Pohjolainen et al. 1996).
Also, radio flares that peak long after the soft X-ray flux maximum
have been observed (Kundu et al. 1994; Pohjolainen et al.
1997).
The statistical study by Pohjolainen et al. (1996) that analysed
all the Metsähovi solar radio bursts from 1989-1992 showed
that in 15 out of the analysed 34 gradual-type bursts
(i.e., radio emission that shows a gradual rise and fall burst
with a duration longer than 10 min) the flux curves could be
explained solely by thermal bremsstrahlung.
Also, in 23 of the events the time of the calculated thermal
bremsstrahlung maximum coincided with the observed burst maximum,
even if the flux densities did not completely agree.
Table 1:
Millimeter-wave rich gradual solar radio flares.
| Date |
Start time |
Radio flare location |
37/34 GHz flux |
GOES class |
| July 7, 1992 |
11:32 UT |
S10 E80 |
35 sfu |
M4.1 |
| June 27, 1993 |
11:14 UT |
S12 E75 |
38 sfu |
M3.6 |
| July 9, 2000 |
04:15 UT |
N18 E72 |
115 sfu |
C3(?) |
A comparison between five Metsähovi 37-GHz gradual radio events and the
corresponding CGRO BATSE hard X-ray events (Pohjolainen et al. 1997)
showed again how two events agreed perfectly with a thermal bremsstrahlung
explanation but three did not (neither in flux density nor in temporal
evolution).
These three were also associated with hard X-ray emission
that was very impulsive in the beginning of the event but then decayed
gradually.
One of these events (February 15, 1992) was a small (3 sfu)
rise-and-fall event (duration <10 min), and therefore does not fully
fit into the category of gradual radio flares that normally have much
larger fluxes and longer duration,
but the other two are listed in Table 1
(July 7, 1992, and June 27, 1993).
To see how common millimeter-wave rich gradual flares really are,
the Nobeyama Radioheliograph Web Archive (17 and 34 GHz observations)
was searched. From their 1993-2000 solar radio data only one gradual
event was found that showed more intense emission at
millimeter waves than at centimeter waves (July 9, 2000). This event
happened during Yohkoh night time (as did the five Metsähovi events
described earlier) and also by this time CGRO had stopped observing.
The main characteristics of the three millimeter-wave rich events
(two Metsähovi, one Nobeyama) are summarised in Table 1.
We present here a multi-wavelength analysis of the June 27, 1993 event.
It was selected on the basis that it has the largest number of data
available of the three. The beginning of the flare was imaged by Yohkoh,
although the main gradual radio phase happened during Yohkoh night time.
We discuss the interpretation of the radio spectrum, and compare the
millimeter wavelength observations with other wavelength data.
We also suggest possible explanations for the long-lasting, high
millimeter-wave flux, although in the absence of simultaneous imaging
and hard X-ray observations for the complete duration of the flare,
this remains somewhat speculative.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{pohjo1.eps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg4.gif) |
Figure 1:
Hard X-ray and radio data from June 27, 1993
at 11:15-12:00 UT. BATSE count rates in the 33-107 keV energy
range (top), Nancay Radioheliograph East-West scans over the solar
disk at 435 and 236 MHz (middle), and Bern full disk flux at 8.4
and 19.6 GHz (bottom). The times of the strongest type II emissions
are depicted in the plot at the top. The 2-D source positions of
the 1-D temporal features 1, 2, 3, and 4 (at 435 MHz), and of A
and B (at 236 MHz) are given in Fig. 3.
Arrows mark the times of the spectral plots in Fig. 7.
The error bar in the 19.6 GHz plot marks the maximum error in flux
density at that frequency around 12 UT. The error is less at earlier
times and at lower frequencies. |
The June 27, 1993 flare that occurred between 11:00 and 12:00 UT was
observed with several radio instruments at millimeter and centimeter
(i.e. microwave) wavelengths (Bern and Metsähovi) and at
decimeter/meter wavelengths (Ondrejov, IZMIRAN, and Nancay), see
Fig. 1.
We used the full disk flux density observations from Bern at 8.4, 11.8, 19.6,
and 35.0 GHz, with 0.1 s time resolution.
Active region tracking with 0.05 s time resolution was obtained from
Metsähovi at 37 GHz. The 2.4 arcmin beam of the telescope was
pointed to the active region (S12 E75) and the flux density from that area
was recorded.
Full disk flux density observations at 3 GHz from Ondrejov (0.01 s time
resolution) and from IZMIRAN (0.04 s time resolution)
were used to construct radio spectra during the flare.
IZMIRAN dynamic spectra at 45-180 MHz (recorded on film in 1993)
were used for detecting spectral drifts during or after the flare.
Nancay radioheliograph East-West and North-South solar disk scans at
five selected frequencies in the 164-435 MHz frequency range were
analysed to determine the burst source locations.
The Nancay radioheliograph has a 0.5 s time resolution at each frequency.
The radio fluxes reported in the Solar Geophysical Data Reports were
checked for comparison.
CGRO BATSE observed enhanced hard X-ray count rates in the two lowest
energy channels of the instrument (DISCLA rate every 1.024 s),
between 25 and 100 keV.
BATSE solar viewing times are indicated in Fig. 1.
GOES satellites provided the soft X-ray fluxes in 3 s time resolution,
and Yohkoh SXT the soft X-ray images (image cadence depends on the
observing mode).
Yohkoh HXT hard X-ray counts (0.5 s time resolution) were observed
mainly in the 14-53 keV energy range.
Yohkoh observations were interrupted very early in the event
due to satellite night time, see Fig. 2.
![\begin{figure}
\par\includegraphics[width=9.5cm,clip]{pohjo2.eps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg5.gif) |
Figure 2:
From top to bottom:
IZMIRAN dynamic spectra at 45-180 MHz at 11:33-11:38 UT
on June 27, 1993. Arrows mark the strongest fragmented type II
radio emission features in the plot. The times of the strongest type
II features are also marked in Fig. 1.
GOES soft X-rays on June 27, 1993 during 11:00-13:00 UT,
where the shaded areas represents Yohkoh satellite night time.
Metsähovi 37 GHz flux from the active region area
(2.4 arcmin beam area) during 11:15-12:15 UT.
The "calc. brem.'' curve shows the calculated amount of thermal
bremsstrahlung at the same frequency, and "temp'' the calculated
plasma temperature (from GOES soft X-ray flux, assuming isothermal
plasma density). Arrows mark the times of the spectral plots in
Fig. 7. |
Figure 2 shows the Metsähovi single frequency observations
at 37 GHz (8 mm) during 11:15-12:15 UT. The flux density was recorded
from a beam area with a diameter of 2.4 arcmin which was pointed to
the active region. The figure shows a gradual rise and fall event
with a flux maximum around 11:33 UT. The calculated amount of thermal
radio bremsstrahlung ("calc. brem.'' in Fig. 2) at 37 GHz
is seen to be significantly less than what was observed. The calculation
(see Thomas et al. 1985; Pohjolainen et al. 1996)
assumes an isothermal plasma density model which does not necessarily
reflect the true conditions on the Sun, but gives an approximation.
The GOES observations are reliable within 5% for plasma temperatures
in the range of 5-30 MK, but the temperature is known to be a monotonic
function of the flux ratio down to a 1 MK temperature - i.e., we can
still determine if the temperature and emissivity of the plasma are
increasing or decreasing (Bornmann 1990).
The bottom panel in Fig. 1 presents the Bern full disk flux
density observations at 8.4 and 19.6 GHz, corrected for atmospheric
transmission and integrated over 60 s.
At microwaves (8.4 GHz),
two distinct flux maxima are visible around 11:19 and 11:23 UT
(times marked by the first two arrows in Fig. 1).
The frequency in between microwaves and millimeter waves (19.6 GHz) shows
the first maxima, but then the flux rises gradually
and does not peak until 11:33 UT (third arrow in Fig. 1).
The 19 GHz flux maximum occurred some 8 min after the GOES soft X-ray
flux maximum (at 11:25 UT), and a few minutes after the H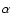 flare
maximum (at 11:29 UT). The radio emission at 3 GHz (Ondrejov and Izmiran)
showed good correlation with the hard X-rays up to the time when BATSE
entered night time at 11:33 UT, and by 13:50 UT the radio
flux had fallen to the pre-flare level.
flare
maximum (at 11:29 UT). The radio emission at 3 GHz (Ondrejov and Izmiran)
showed good correlation with the hard X-rays up to the time when BATSE
entered night time at 11:33 UT, and by 13:50 UT the radio
flux had fallen to the pre-flare level.
The observed radio spectra at 11:19 UT (first hard X-ray and microwave
burst), 11:23 UT (second hard X-ray and microwave burst), 11:33 UT
(19/35/37 GHz flux maximum), and 12:00 UT (decline phase of the flare)
are plotted in Fig. 7 (symbols). The first spectrum at
11:19 UT shows a typical radio burst spectrum with a turn-over
frequency around 5 GHz. The second spectrum at 11:23 UT shows how
the radio flux at higher frequencies has started to rise.
After 11:23 UT the 35 GHz radio flux exceeds the lower
frequency fluxes, and the radio spectrum at 11:33 UT has a rising slope
towards the high frequencies. Due to the small number of data points it is
difficult to determine the spectral peak frequency, but it could be
higher than 37 GHz. In the declining phase at 12:00 UT the radio spectrum
is still dominated by high-frequency radiation.
The Bern 35 GHz flux was somewhat higher than the Metsähovi 37 GHz
flux (Bern flux maximum 60 sfu, Metsähovi 40 sfu). Both Bern and
Metsähovi fluxes are calculated relative to the quiet Sun level,
but the Bern high frequency observations are sometimes affected by
slow drifts in the atmospheric absorption.
This drift is attributed to a slow decrease in the atmospheric
transmission. The 8.4 and 19.6 GHz burst flux profiles presented in
Fig. 1 were corrected for this effect.
However, at 35 GHz where the drift in flux is much larger it becomes
very difficult to do reliable flux corrections after 11:33 UT.
For the 19.6 GHz flux an error of less than 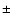 25% at 12 UT can be
given. For 35 GHz the lower limit of the peak flux is 60 sfu.
For the Metsähovi 37 GHz observations the flux error due to instrumental
effects is less than 0.1 sfu. The recording was done on a clear, dry,
and sunny day near noon time (highest elevation), which gives the best
possible observing conditions. Full disk solar maps were recorded before
and after the 2 hour tracking period for calibration purposes, and they
did not show any significant variation in atmospheric transmission.
The optical depth is different at different antenna (target) elevations
(see, e.g., Pohjolainen & Urpo 1997 for Metsähovi observations)
and in this case the flux error due to the atmosphere should be less
than 1 sfu.
On the other hand, the Bern 35 GHz and Metsähovi 37 GHz flux curves
also showed slightly different time evolution. An alternative explanation
for the difference in the Metsähovi 37 GHz and the Bern 35 GHz flux is
that Metsähovi may have recorded only part of the flux, within the 2.4 arcmin beam centered over the active region, while Bern could have recorded
the full flux (i.e., from a larger emitting area). If interpreted this way,
the Metsähovi 40 sfu at 37 GHz would give the lower flux limit.
25% at 12 UT can be
given. For 35 GHz the lower limit of the peak flux is 60 sfu.
For the Metsähovi 37 GHz observations the flux error due to instrumental
effects is less than 0.1 sfu. The recording was done on a clear, dry,
and sunny day near noon time (highest elevation), which gives the best
possible observing conditions. Full disk solar maps were recorded before
and after the 2 hour tracking period for calibration purposes, and they
did not show any significant variation in atmospheric transmission.
The optical depth is different at different antenna (target) elevations
(see, e.g., Pohjolainen & Urpo 1997 for Metsähovi observations)
and in this case the flux error due to the atmosphere should be less
than 1 sfu.
On the other hand, the Bern 35 GHz and Metsähovi 37 GHz flux curves
also showed slightly different time evolution. An alternative explanation
for the difference in the Metsähovi 37 GHz and the Bern 35 GHz flux is
that Metsähovi may have recorded only part of the flux, within the 2.4 arcmin beam centered over the active region, while Bern could have recorded
the full flux (i.e., from a larger emitting area). If interpreted this way,
the Metsähovi 40 sfu at 37 GHz would give the lower flux limit.
![\begin{figure}
\par\includegraphics[angle=270,width=18cm,clip]{pohjo3.eps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg8.gif) |
Figure 3:
Left: Yohkoh SXT soft X-ray image at 12:40 UT (post-flare),
with radio source locations 1, 2, 3a, 3b, and 4 at 435 MHz.
Right: radio source locations A and B at 236 MHz over the Yohkoh
image. The source locations correspond to the burst features seen
in the spectra, presented in Fig. 1. |
Decimetric emission at 435 MHz shows bursts starting around 11:19, 11:23,
11:26, and 11:32 UT. The first two (labelled "1'' and "2'' in
Fig. 1) coinside with the microwave flux density peaks at
8.4 GHz and with the two hard X-ray count rate peaks.
The third burst (labelled "3a'' and "3b'' in Fig. 1) does not
seem to have any counterpart at other observed wavelengths, but the
fourth (labelled "4'' in Fig. 1) starts around the time of
the millimeter wave flux maximum at 11:33 UT.
The four above-mentioned bursts at 435 MHz occured at different
locations on the disk, seen in the Nancay radioheliograph images
in Fig. 3:
the first (source "1'') was located near the limb but the next ones
(sources "2'' and "3a'') were closer to the soft X-ray flare site
(labelled "F1'' in Fig. 4) in the beginning
of the flare.
Sources "3b'' and "4'' were again located near the limb. From the soft
X-ray images it looks as if the decimetric bursts followed some of
the loop structures.
At metric wavelengths (164 and 236 MHz) two bursts were observed at
separate locations on the disk, starting around 11:37 UT.
Figure 1 shows the time and the 1-D spatial evolution of
these bursts at 236 MHz (sources "A'' and "B'' in the East-West scans).
Figure 3 shows their source positions on the solar disk.
The 236 MHz flux source "A'', in the rising phase around 11:37 UT, was
very near the location where the soft X-ray flare started and most of
the hard X-ray emission was coming from before Yohkoh night time set in
(location labelled "F1'' in Fig. 4).
The fainter 'B' source was located over the limb (labelled "B''
Fig. 3). Source "B'' was visible until around 12 UT,
and after that also the flux of source "A'' started to decrease.
At 164 MHz a similar source to "B'' was observed, at a larger distance
from the limb.
At longer metric wavelengths, the dynamic spectra at 45-180 MHz shows
fragmented type II radio emission between 11:33 and 11:38 UT
(IZMIRAN dynamic spectra in Fig. 2). Distinct frequency-drifting
radio type II emission was observed around 11:34 UT just below 90 MHz
and around 11:36 UT at lower frequencies, indicating plasma emission at
the local plasma frequency after a passing disturbance. These fragmented
emission sources were too faint to be resolved in the Nancay 164 MHz scans.
The GOES soft X-rays show a class M3.6 flare during 11:11-12:15 UT
(Fig. 2). The GOES maximum was around
11:25 UT. In hard X-rays, a flare event was observed during
11:16-11:33 UT by CGRO BATSE (observations interrupted by satellite
night time at that point), see Fig. 1. Impulsive burst peaks
superposed on the gradual component were observed from 11:17 UT until
11:25 UT, with two count rate peaks around 11:19 and 11:23 UT.
After this more impulsive phase the hard X-ray counts diminished gradually
to the pre-flare level, except in the 33-56 keV energy range (BATSE DISCLA)
which continued to show some counts above the backgound level, with some
hints of a rising count rate just before satellite night time set in.
A short hard X-ray burst was observed near the time when the satellite
started observing again, at 11:55 UT, in the late phase of the radio flare.
The Yohkoh hard X-ray images, Fig. 4, show an extended source
with a diameter of about 1 arcmin near the time of the first flux peak
at 11:19 UT.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pohjo4a.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{pohjo4b.ps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg9.gif) |
Figure 4:
Left: Yohkoh HXT 14-23 keV hard X-ray sources at
11:18:28 UT (contours) over the Yohkoh SXT soft X-ray image at
11:11:07 UT.
"F1'' points to the location where the soft X-ray flare started
and most of the hard X-ray emission was coming from before
Yohkoh night time set in.
The white circle represents the Metsähovi 2.4 arcmin radio beam, pointed to the active region and recording
the total flux density from that area.
Right: Yohkoh HXT 14-23 keV hard X-ray sources at
11:18:40 UT (contours) over the Yohkoh SXT soft X-ray image at
11:18:35 UT.
The hard X-ray sources observed in the 14-53 keV energy range
were located in the sigmoid-shaped flaring region.
In later images the hard X-ray source was elongated into
a loop-like structure with a diameter around 1 arcmin. |
A super-hot thermal component can be ruled out because of the spectral
distribution in X-rays during the flare. Also the millimeter and microwave
fluxes are too high for a super-hot component. This leaves basically two
mechanisms that can create a high mm-wave flux without creating soft X-ray
emission detectable by GOES: a) thermal bremmstrahlung from warm
- or even cool (<1 MK) -
and dense plasma and b) gyrosynchrotron emission by high-energy electrons.
We will now look more closely into these two emission mechanisms.
a)
Contribution of Coulomb bremsstrahlung from evaporating chromospheric
warm (T < 5 MK) and dense plasma (undetected by GOES), filling up
the microwave source and overcoming gyrosychrotron emission at high
frequencies have been shown to be possible (Chertok et al. 1995;
Urpo et al. 1986). The examples in Chertok et al.
(1995) required large bursts with microwave fluxes larger
than 100 sfu, and sufficiently intense soft X-ray emission correlated
with the mm-wave bursts.
Separate flaring sites at different plasma temperatures cannot be ruled
out as we do not have spatial information from the high mm-wave flux period.
On the other hand, suppression and absorption effects would be needed
to explain the low cm-wave flux in comparison with the high mm-wave flux,
as the radio bremsstrahlung spectrum should basically be flat. This would
be difficult to achieve, as loops are less dense in the high corona. The
difference in flux between the full disk and the 2.4 arcmin beam radio
observations also suggest that the emission source was extended.
b)
For gyrosynchrotron emission an increasing magnetic field strength and
a decreasing electron power law index can move the spectral peak towards
the higher frequencies, while changes in the source electron density and
temperature alter the flux density, but do not significantly change the
general spectral shape. Although gyrosynchrotron emissivity is a strong
function of magnetic field strength (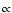 B3), the emissivity also
depends on the angle
B3), the emissivity also
depends on the angle 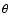 between the line of sight and the magnetic
field (
between the line of sight and the magnetic
field (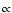
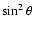 ), see e.g. Dulk (1985). An
increase in B can significantly lower the number of radio-emitting
electrons required, but it also increases the spectral peak frequency -
which is consistent with our observations. Loop footpoints would therefore
be bright at millimeter waves (stronger magnetic fields), and a favourable
viewing angle near the limb would further enhance the emissivity.
), see e.g. Dulk (1985). An
increase in B can significantly lower the number of radio-emitting
electrons required, but it also increases the spectral peak frequency -
which is consistent with our observations. Loop footpoints would therefore
be bright at millimeter waves (stronger magnetic fields), and a favourable
viewing angle near the limb would further enhance the emissivity.
In impulsive solar flares, the cm-wave emission is claimed to be
produced by electrons in the range 100 keV-1 MeV and the mm-wave
emission by electrons with energies of 0.5 MeV and above (Kundu et al. 1994). In the case where we have prolonged but weak
acceleration of electrons up to 1 MeV - these electrons will be
trapped in flare loops for the time proportional to
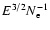 (Aschwanden et al. 1997) - the energy of the
electrons is collisionally decreasing as
(Aschwanden et al. 1997) - the energy of the
electrons is collisionally decreasing as
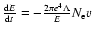 ,
where E is the energy of the
electron, e is the electron charge,
,
where E is the energy of the
electron, e is the electron charge, 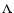 is the Coulomb
logarithm,
is the Coulomb
logarithm, 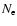 the electron density of the surrounding plasma,
and v is the electron speed (Emslie 1978). From these
formulas we see that keV electrons can be accumulated for a long time
only in a low-density corona where their collisional losses are low.
Trapping times for keV electrons are in the range of several tens of
seconds. For mm-wave emitting electrons the corresponding upper limit
for trapping times can be several tens of minutes (Aschwanden et al.
1997). Prolonged acceleration will be needed to explain
both the decimetric-metric emission as well as the high mm-wave flux.
However, the small amount of hard
X-rays after the impulsive phase and during the millimeter flux rise
poses a problem. It has been shown previously (Raulin et al.
1999) that a small number of MeV electrons trapped in a
loop can produce mm-wave emission with a hard X-ray flux not likely to
be detected by BATSE. The precipitation flux of the keV and MeV
electrons would be low during trapping - as long as electrons are
trapped they can produce cm- and mm-wave emission, but if they radiate
hard X-rays they are lost from the system (Hudson & Ryan
1995).
the electron density of the surrounding plasma,
and v is the electron speed (Emslie 1978). From these
formulas we see that keV electrons can be accumulated for a long time
only in a low-density corona where their collisional losses are low.
Trapping times for keV electrons are in the range of several tens of
seconds. For mm-wave emitting electrons the corresponding upper limit
for trapping times can be several tens of minutes (Aschwanden et al.
1997). Prolonged acceleration will be needed to explain
both the decimetric-metric emission as well as the high mm-wave flux.
However, the small amount of hard
X-rays after the impulsive phase and during the millimeter flux rise
poses a problem. It has been shown previously (Raulin et al.
1999) that a small number of MeV electrons trapped in a
loop can produce mm-wave emission with a hard X-ray flux not likely to
be detected by BATSE. The precipitation flux of the keV and MeV
electrons would be low during trapping - as long as electrons are
trapped they can produce cm- and mm-wave emission, but if they radiate
hard X-rays they are lost from the system (Hudson & Ryan
1995).
The model used for the calculations in order to fit the observed
spectra is geometrically rather simple and will be only briefly
described here. A more detailed description can be found in
Hildebrandt et al. (1998). It calculates the escaping
intensity for each wanted frequency solving the equation of radiative
transfer along the line of sight. In the case of a homogeneous source
this is similar to the procedures of, e.g., Benka & Holman
(1992) or Ramaty (1969). For inhomogeneous
sources we use a multi-layer model, i.e., the distributions for all
parameters necessary to calculate the coefficients must be given along
the ray trajectory. As relevant emission processes we consider
gyrosynchrotron radiation (GSR) from nonthermal power-law (PL)
electrons and gyroresonance absorption (GRA) as well as
Coulomb-bremsstrahlung (CBS) from the thermal background plasma.
Special attention was focussed on the computation of the GSR emission
and absorption coefficients (full code, no approximation formulae).
Polarization effects are also included but not considered here.
Assuming a "single'' PL distribution function for the nonthermal
particles, the following parameters are finally needed for the
calculation:
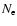 |
- |
number density of the thermal (background) plasma |
| B |
- |
magnetic field strength |
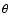 |
- |
angle between the magnetic field vector and the line of sight |
| L |
- |
thickness of the emission volume (in the line-of-sight direction) |
| T |
- |
temperature of the (background) plasma |
| N |
- |
number density of the nonthermal electrons |
| E2 |
- |
high-energy boundary of the PL distribution |
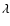 |
- |
PL index. |
(The low-energy boundary E1 is already determined by the
temperature and the ratio of number densities
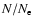 using the
normalization condition for the distribution functions; cf.
Hildebrandt et al. 1998 for more details.)
using the
normalization condition for the distribution functions; cf.
Hildebrandt et al. 1998 for more details.)
To compare the calculated intensity values with real observed spectra
we have to convert them into flux density units by assuming an effective
emission area
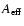 .
So we have finally 9 free parameters which gives us enough space to
play with them. On the other hand, every
additional information is highly welcome and must be used in order to
restrict the number of free parameters. It should be also mentioned
here that a constant
.
So we have finally 9 free parameters which gives us enough space to
play with them. On the other hand, every
additional information is highly welcome and must be used in order to
restrict the number of free parameters. It should be also mentioned
here that a constant
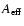 is mearly a rough assumption which
gives us only an upper limit for the resulting flux. But a (more
realistic) numerical integration over the relevant area assuming
three-dimensional inhomogeneity would take too much time and efforts,
in particular, if many test calculations are necessary.
is mearly a rough assumption which
gives us only an upper limit for the resulting flux. But a (more
realistic) numerical integration over the relevant area assuming
three-dimensional inhomogeneity would take too much time and efforts,
in particular, if many test calculations are necessary.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pohjo5.ps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg22.gif) |
Figure 5:
Height profiles of the parameters in the compact nonthermal
source (CNTS) used for the model calculations in order to interpret the
observed spectrum at 11:33 UT.
The hatched range marks the loop with thickness L = 8000 km located at
z = 22 000 km where temperature and density of the background plasma
are enhanced. Only inside the loop nonthermal (power-law) electrons are
assumed (top four panels). All parameters show a smooth behaviour,
i.e., the most extreme (energetic) values occur around the center
decreasing in direction to the loop boundary (no "jumps''). |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pohjo6.ps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg23.gif) |
Figure 6:
Same as Fig. 5, but for the extended thermal source
(EXTS) with (evaporated) cooler and more dense plasma inside the
hatched region with thickness
L = 20 000 km centered at
z = 25 000 km. |
All attemps to fit the four considered spectra assuming a single
homogeneous source failed except for the first one. Only at 11:19 UT
the spectrum has a more or less "typical'' gyrosynchroton shape, i.e.
it decreases towards higher frequencies after its spectral maximum at
about 2-5 GHz (see Fig. 7 top left). For example,
assuming B=200 G,
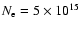 m-3,
T =
107 K,
m-3,
T =
107 K,
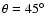 ,
,
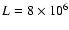 m,
m,
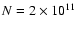 m-3 (
m-3 (
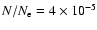 ),
),
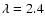 ,
and E2=15 MeV, one obtains - at least for
,
and E2=15 MeV, one obtains - at least for 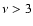 GHz -
a spectrum which would satisfactorily fit the observed one. However,
the assumed values for the energetic particles (
GHz -
a spectrum which would satisfactorily fit the observed one. However,
the assumed values for the energetic particles (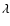 and E2)
are already rather extreme and not necessarily typical for solar flare
conditions. Considering the next spectra, it becomes clear that their
shapes cannot be explained assuming homogenous and GSR dominated
sources. The spectrum at 11:23 UT has a nearly constant flux in the
range 10-30 GHz and the observed spectrum at 11:30 UT shows even a
clear increase up to 37 GHz! The (theoretically possible) case that
the peak of the GSR spectrum is shifted towards such high frequencies
due to strong B inside the source must also turned down because this
would require magnetic fields of about 5000 G (
and E2)
are already rather extreme and not necessarily typical for solar flare
conditions. Considering the next spectra, it becomes clear that their
shapes cannot be explained assuming homogenous and GSR dominated
sources. The spectrum at 11:23 UT has a nearly constant flux in the
range 10-30 GHz and the observed spectrum at 11:30 UT shows even a
clear increase up to 37 GHz! The (theoretically possible) case that
the peak of the GSR spectrum is shifted towards such high frequencies
due to strong B inside the source must also turned down because this
would require magnetic fields of about 5000 G (
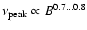 )! Increasing fluxes in this frequency range
can only be caused by CBS from a very dense and not too hot
(<106 K) plasma. However, the coexistence of such `evaporated'
plasma together with high-energy electrons in the framework of one
inhomogeneous source (i.e. along one trajectory) brings a new serious
problem: Either the low-frequency (GSR) part of the spectrum is
totally suppressed by the thermal (CBS) part or the nonthermal source
must be located so high in the corona that the magnetic field can
hardly be strong enough (the thermal source must have a certain
extension to produce fluxes of more than 30 sfu). Therefore, the
only solution is to assume two neighboring sources (both located
inside the antenna beam size of 2.4 arcmin) which are responsible
together for the observed flux spectra. This does not contradict to
spatially resolved observations at other wavelengths, for instance, to
soft X-ray images (cf., e.g., Fig. 4).
)! Increasing fluxes in this frequency range
can only be caused by CBS from a very dense and not too hot
(<106 K) plasma. However, the coexistence of such `evaporated'
plasma together with high-energy electrons in the framework of one
inhomogeneous source (i.e. along one trajectory) brings a new serious
problem: Either the low-frequency (GSR) part of the spectrum is
totally suppressed by the thermal (CBS) part or the nonthermal source
must be located so high in the corona that the magnetic field can
hardly be strong enough (the thermal source must have a certain
extension to produce fluxes of more than 30 sfu). Therefore, the
only solution is to assume two neighboring sources (both located
inside the antenna beam size of 2.4 arcmin) which are responsible
together for the observed flux spectra. This does not contradict to
spatially resolved observations at other wavelengths, for instance, to
soft X-ray images (cf., e.g., Fig. 4).
The two sources finally used for the spectral fits are based on
typical parameter profiles of the atmosphere above a sunspot,
i.e., with
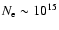 m-3 and
m-3 and
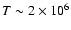 K at low coronal heights.
The characteristic deviations from these values are defined to be
concentrated on a certain region at about 25 000 km height,
where
K at low coronal heights.
The characteristic deviations from these values are defined to be
concentrated on a certain region at about 25 000 km height,
where 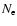 is enhanced (for both sources).
In the case of the "compact nonthermal source'' (CNTS), this region has
a vertical extension of 8000 km which corresponds to typical loop
diameters. Also the magnetic field values are such as they will be
found in loop structures near sunspots (
is enhanced (for both sources).
In the case of the "compact nonthermal source'' (CNTS), this region has
a vertical extension of 8000 km which corresponds to typical loop
diameters. Also the magnetic field values are such as they will be
found in loop structures near sunspots (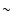 250 G). T is also
enhanced there (
250 G). T is also
enhanced there (
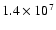 K at the maximum) and nonthermal
particles are defined to be present only inside this region. By
contrast, the so-called "extended thermal source'' (EXTS) is mainly
characterized by larger extensions (
K at the maximum) and nonthermal
particles are defined to be present only inside this region. By
contrast, the so-called "extended thermal source'' (EXTS) is mainly
characterized by larger extensions (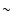 20 000 km in vertical
direction) and a diminished temperature (down to
20 000 km in vertical
direction) and a diminished temperature (down to
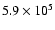 K),
which is, together with the enhanced electron density
(
K),
which is, together with the enhanced electron density
(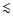
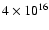 m-3), necessary to produce the measured
fluxes at
m-3), necessary to produce the measured
fluxes at 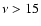 GHz. Such sources are possibly a result of
chromospheric evaporation processes.
GHz. Such sources are possibly a result of
chromospheric evaporation processes.
The basic characteristics (parameter profiles) are shown in
Figs. 5 (CNTS) and 6 (EXTS). At the four considered
times the curves are very similar and we show therefore only the most
extreme case at 11:33 UT. The quantitative differences can be found
in Table 2, where the extreme numbers (or ranges) are given
for all four cases including the relevant effective areas. It should
be mentioned that for our calculations nearly smoothed distributions
(144 layers with variable thickness) were used, therefore, the
"effective'' (averaged) parameter values in the hatched regions may be
more moderate than the given extrema suggest. Although our
multi-layer model is rather time-consuming, the resultant spectra
seem to justify such a procedure. They are smoother (especially in the
low-frequency range) and many of the spectral features (harmonic
structures) that occurred when simpler (and less realistic) models were
used are suppressed now.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{pohjo7.ps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg40.gif) |
Figure 7:
Observed radio spectra at 11:19 UT, 11:23 UT, 11:33 UT,
and 12:00 UT (symbols) and the relevant fits by our model
calculations (lines). The solar fluxes are from different stations as
given in the legend (top left). The Ondrejov, Bern, and Metsähovi
radio fluxes are calculated relative to the quiet Sun level. The
top-right legend explains the calculated fluxes: thin black lines
show the contributions of the two different sources (CNTS - compact
nonthermal source, EXTS - extended thermal source; see
Table 2 and Figs. 5, 6). Thick gray
lines refer to the resultant spectra. All flux values are corrected
to the quiet Sun level. Further explanations are given in the text. |
All calculated flux values in Fig. 7 are corrected to the
quiet Sun, i.e., the flux coming from the quiet Sun was subtracted.
The thin dashed and dashed-dotted curves represent the contributions
from the two sources. It can clearly be seen that even at 11:33 and
12:00 UT the thermal source alone would not be able to produce the
observed fluxes, i.e., at each time we need a second source. We do
not claim that our parameter sets for CNTS are the only possible
choices to fit the observed spectra. One can, of course, find
parameter configurations for CNTS which are slightly different from
ours and would also give a sufficient fit of the spectra. But we
tried to avoid extreme numbers and use well-balanced values for our fits.
Nevertheless, some parameters (in particular for EXTS)
are rather difficult to explain, but their development shows at least a
physically reasonable tendency:
Whereas the number of PL electrons is slightly decaying after 11:19 UT,
the density of the evaporated plasma reaches its maximum at 11:33 UT
before it also starts to decrease.
At the start of the analysed flare impulsive emission was observed
in hard X-rays, cm-waves, and meter-decimeter waves. After this impulsive
phase the hard X-ray counts dropped gradually, the flux at cm-waves started
to decrease, and the mm-wave flux continued to rise. The metric emission
locations traced a large post-flare soft X-ray arcade for about 20 min,
indicating trapped electrons. During the metric emission the mm-wave flux
stayed high but started to decrease gradually. In comparison,
the cm-wave flux had already gone down significantly - in agreement with
the calculated thermal bremsstrahlung flux from the cooling flare plasma.
The type II emission at 50-100 MHz, observed soon after the mm-wave flux
peak, indicates a disturbance travelling in the solar atmosphere. Whether
it was a shock wave, a plasmoid or a CME cannot be verified without
simultaneous imaging observations.
The observed decimetric bursts originated from widely separated locations,
over complex loop systems near and over the limb, suggesting that some
of the decimetric flaring activity might have been limb-occulted.
The decimetric-metric emission can only originate in the high corona
(at least 70 000-100 000 km above the photosphere) where the magnetic
field strengths and electron densities are low, and where the precipitating
keV electrons can generate only negligible hard X-rays.
Radio emission at centimeter and millimeter waves is generally
thought to originate at low heights, either from dense loops (thermal
bremsstrahlung) or near the loop footpoints (gyrosynchrotron emission
from places with strong magnetic fields).
The difference between the observed mm-wave flux of the full-disk
observations and the 2.4 arcmin collecting area observations may suggest
that some of the mm-wave flux originated from an area larger than
the 2.4 arcmin diameter area around the active region.
Our model calculations for the radio source show that two separate
sources are needed to produce the observed flat spectra:
one source with high-energy electrons and a second source with
extremely high electron densities
(>1016 m-3), large source dimensions (>1015 m2),
and very low temperatures (<106 K).
What this cool material consists of is unkown.
Filaments are cool and dense but then they are also much more
common than our type of mm-wave rich events.
The active role of cool (104 K) plasma during a flare, and without
any observed presence of a prominence, has recently been reported by
Kliem et al. (2002).
We do not claim that our interpretation is the only imaginable one, but
it is one possibility to explain these flat spectra in the context of
direct emission processes.
We propose multi-frequency and good spatial resolution radio imaging
observations together with high-sensitivity observations in the MeV
range to better determine what role exactly the cool, high-density
plasma could play in the evolution of the gradual radio flares.
Acknowledgements
The authors wish to thank N. Vilmer, H. Hudson, and E. Valtaoja
for helpful comments on the manuscript and the anonymous referee for
improving the clarity of the paper.
Yohkoh is a Japanese solar mission, with several internationally
operated instruments.
The archive of solar flare hard X-ray data from the BATSE
experiment on the Compton Gamma Ray Observatory (CGRO) is part of the
Solar Data Analysis Center (SDAC) at Goddard Space Flight Center.
We thank the radio group at DASOP, Observatoire de Paris, France
for the use of Nancay Radioheliograph data, and Metsähovi Radio
Observatory, Helsinki Univ. of Technology, Finland, for the use of
their radio data. S.P. was supported in Meudon by the Academy of
Finland Contract No. 42576. J.H. was supported by DFG grant No. STA 351/6.
-
Aschwanden, M. J., Bynum, R. M., Kosugi, T., Hudson, H., & Schwartz, R. A. 1997,
ApJ, 487, 936
In the text
NASA ADS
-
Benka, S. G., & Holman, G. D. 1992, ApJ, 381, 854
In the text
-
Bornmann, P. L. 1990, ApJ, 356, 733
In the text
NASA ADS
-
Chertok, I. M., Fomichev, V. V., Gorgutsa, R. V., et al. 1995, Sol. Phys., 160, 181
In the text
NASA ADS
-
Dulk, G. A. 1985, ARA&A, 23, 169
In the text
NASA ADS
-
Emslie, A. G. 1978, ApJ, 224, 241
In the text
NASA ADS
-
Hildebrandt, J., Krüger, A., Chertok, I. M., Fomichev, V. V.,
& Gorgutsa, R. V. 1998, Sol. Phys., 181, 337
In the text
NASA ADS
-
Hudson, H., & Ryan J. 1995, ARA&A, 33, 239
In the text
NASA ADS
-
Kliem, B., Dammasch, I. E., Curdt, W., & Wilhelm, K. 2002, ApJ, 568, 61
In the text
-
Kundu, M. R., White, M., Gopalswamy, N., & Lim, J. 1994, ApJS, 90, 599
In the text
NASA ADS
-
Pohjolainen, S., & Urpo, S. 1997, Proc. of the 5th SOHO Workshop,
ESA-SP 404, 619
In the text
-
Pohjolainen, S., Valtaoja, E., & Urpo, S. 1996, A&A, 314, 947
In the text
NASA ADS
-
Pohjolainen, S., Valtaoja, E., & Urpo S. 1997, Adv. Space Res., 20, 12, 2337
In the text
NASA ADS
-
Ramaty, R. 1969, ApJ, 158, 753
In the text
NASA ADS
-
Raulin, J.-P., White, S. M., Kundu, M. R., Silva, A. V. R., & Shibasaki, K. 1999,
ApJ, 522, 547
In the text
NASA ADS
-
Thomas, R. J., Starr, R., & Crannell, C. J. 1985, Sol. Phys., 95, 323
In the text
NASA ADS
-
Urpo, S., Krüger, A., & Hildebrandt, J. 1986, A&A, 163, 340
In the text
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{pohjo1.eps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg4.gif)
![\begin{figure}
\par\includegraphics[width=9.5cm,clip]{pohjo2.eps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg5.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=18cm,clip]{pohjo3.eps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg8.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pohjo4a.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{pohjo4b.ps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg9.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pohjo5.ps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg22.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pohjo6.ps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{pohjo7.ps}
\end{figure}](/articles/aa/full/2002/47/aa10430/Timg40.gif)