A&A 396, 1-19 (2002)
DOI: 10.1051/0004-6361:20021341
Analysis of two-point statistics of cosmic shear
I. Estimators and covariances
P. Schneider
1,2 -
L. van Waerbeke3,4 -
M. Kilbinger1
-
Y. Mellier3,5
1 - Institut f. Astrophysik u. Extr. Forschung, Universität Bonn,
Auf dem Hügel 71, 53121 Bonn, Germany
2 -
Max-Planck-Institut f. Astrophysik, Postfach 1317,
85741 Garching, Germany
3 -
Institute d'Astrophysique de Paris, 98bis boulevard
Arago, 75014 Paris, France
4 -
Canadian Institute for Theoretical Astrophysics, 60 St
Georges Str., Toronto, M5S 3H8 Ontario, Canada
5 -
Observatoire de Paris, DEMIRM/LERMA, 61 avenue de
l'Observatoire, 75014 Paris, France
Received 13 June 2002 / Accepted 12 September 2002
Abstract
Recently, cosmic shear, the weak lensing effect by the
inhomogeneous matter distribution in the Universe, has not only
been detected by several groups, but the observational results have
been used to derive constraints on cosmological parameters. For
this purpose, several cosmic shear statistics have been
employed. As shown recently, all second-order statistical measures can
be expressed in terms of the two-point correlation functions of the
shear, which thus represents the basic quantity; also, from a
practical point-of-view, the two-point correlation functions are
easiest to obtain from observational data which typically have
complicated geometry. We derive in this paper expressions for the
covariance matrix of the cosmic shear two-point correlation
functions which are readily applied to any survey
geometry. Furthermore, we consider the more special case of a
simple survey geometry which allows us to obtain approximations for
the covariance matrix in terms of integrals which are readily
evaluated numerically. These results are then used to study the
covariance of the aperture mass dispersion which has been employed
earlier in quantitative cosmic shear analyses. We show that the
aperture mass dispersion, measured at two different angular scales,
quickly decorrelates with the ratio of the scales. Inverting the
relation between the shear two-point correlation functions and the
power spectrum of the underlying projected matter distribution, we
construct estimators for the power spectrum and for the band
powers, and show that they yields accurate approximations; in
particular, the correlation between band powers at different wave
numbers is quite weak. The covariance matrix of the shear
correlation function is then used to investigate the expected
accuracy of cosmological parameter estimates from cosmic shear
surveys. Depending on the use of prior information, e.g. from CMB
measurements, cosmic shear can yield very accurate determinations
of several cosmological parameters, in particular the normalization
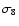 of the power spectrum of the matter distribution, the
matter density parameter
of the power spectrum of the matter distribution, the
matter density parameter
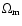 ,
and the shape parameter
,
and the shape parameter
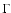 .
.
Key words: dark matter - gravitational lensing - large-scale
structure of the Universe
Cosmic shear, the distortion of the images of distant galaxies by the
tidal gravitational field of intervening matter inhomogeneities,
offers a direct way of probing the statistical properties of the
large-scale (dark) matter distribution in the Universe, without making
any assumption on the relation between dark and luminous matter (e.g.,
Blandford et al. 1991; Miralda-Escude 1991; Kaiser 1992, 1998; Jain &
Seljak 1997; Bernardeau et al. 1997; Schneider et al. 1998, hereafter
SvWJK; van Waerbeke et al. 1999; Bartelmann & Schneider 1999; Jain et al. 2000; White & Hu 2000; see Mellier 1999 and Bartelmann &
Schneider 2001 for recent reviews). The first detections of cosmic
shear on wide-field imaging data (Bacon et al. 2000, 2002; Kaiser et al. 2000; van Waerbeke et al. 2000, 2001, 2002; Wittman et al. 2000;
Maoli et al. 2001; Rhodes et al. 2001; Hämmerle et al. 2002;
Hoekstra et al. 2002; Refregier et al. 2002) has demonstrated the
feasibility of this new window of observational cosmology, and yielded
already the first constraints on cosmological parameters, most
noticibly the normalization 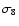 of the dark matter power
spectrum, but also on the matter density parameter
of the dark matter power
spectrum, but also on the matter density parameter
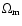 (van Waerbeke et al. 2002; Hoekstra et al. 2002).
(van Waerbeke et al. 2002; Hoekstra et al. 2002).
Most analytical work on cosmic shear has been done on second-order
statistical measures of the distortion field, such as the shear
correlation functions, the shear variance in an apertures, or the
aperture mass (see Sect. 2 for a definition of these
quantitities). Although higher-order statistical measures, such as the
skewness of the shear (Bernardeau et al. 1997), are likely to yield
additional, if not even superior constraints on cosmological
parameters, their theoretical predictions are more uncertain at
present. Recently, an estimator for the skewness of the shear was
developed (Bernardeau et al. 2002a), and applied to wide-field survey
data (Bernardeau et al. 2002b), yielding a significant detection.
In this paper we consider second-order statistical measures only. All
of them can be derived in terms of the correlation functions, as shown
in, e.g., Crittenden et al. (2002, hereafter C02) and Schneider et
al. (2002, hereafter SvWM), and since the measurement of the
correlation functions is easier in practice than the other
second-order statistics (e.g., gaps in the data are easily dealt
with), we consider the correlation functions as the fundamental
observables from a cosmic shear survey. In order to use them for
determining cosmological parameters, it is important to know a
practical and unbiased estimator for them, and to determine the
covariance of this estimator. Two effects enter this covariance: a
random part, which is due to the intrinsic ellipticity of the galaxies
from which the shear is measured, together with measurement noise, and
sampling (or cosmic) variance. The first of these effects is expected
to dominate on small angular scales, whereas the second determines the
covariance for large separations. The covariance will depend not only
on the total survey area, but also on the survey geometry. As has been
pointed out by Kaiser (1998), in order to decrease the sampling
variance on large scales, it may be favourable to choose a survey
geometry that samples those scales sparsely. In order to design an
optimized survey geometry, the covariance as a function of survey
geometry needs to be calculated.
Here, we calculate the covariance matrices for the shear correlation
functions binned in angular separation. In Sect. 2, we introduce
our notation and briefly summarize the second-order cosmic shear
measures and their interrelations. Unbiased estimators of the two
basic correlation functions are derived in Sect. 3, togther with
the corresponding unbiased estimators of the aperture mass and the
shear dispersion. The covariance matrices of these correlation
function estimators are then derived in Sect. 4, expressed in terms
of a set of galaxy positions. From these expressions, the covariances
can be determined for an arbitrary survey geometry. In a forthcoming
paper (Kilbinger et al., in preparation), we shall use the results of
Sect. 4 to design an optimized geometry for a planned cosmic shear
survey.
For the case of a filled survey geometry, the ensemble average of
these covariances can be further analyzed; using a few
approximations, we express in Sect. 5 the covariances for this case
in terms of integrals. The corresponding expressions have been
evaluated, for a particular cosmological model, and are illustrated in
a set of figures. In Sect. 6 we derive the covariance for the
aperture mass dispersion, which can be expressed simply in terms of the
covariances of the correlation functions. The variance of the aperture
mass dispersion, as well as the covariance, is then explicitly
calculated for a survey with filled geometry, showing that indeed the
aperture mass at two angular scales decorrelates quickly as the scale
ratio decreases away from unity.
We then turn in Sect. 7 to a simple estimator of the power spectrum
of the projected cosmic density field, which can be expresed in terms
of the correlation functions. Since the correlation functions will be
known only over a finite range in angular separation, the simple
estimator we derive is biased. We show that, provided the angular
range on which the correlation functions can be measured is as large
as can be expected with the next generation of cosmic shear surveys,
this bias is indeed very small over a large range of wave
numbers. We derive the covariance of the power spectrum estimator and
calculate it explicitly for the filled survey geometry case; the
resulting error bars on the estimated power spectrum are quite a bit
smaller than one might have expected, given the simplicity of the
approach. In Sect. 8 we consider the accuracy with which the
parameters of the cosmological model can be constrained, given a
survey area. In fact, by fitting the correlation function directly to
model predictions, even the currently available cosmic shear surveys
can yield fairly accurate constraints on cosmological parameter.
Finally, we summarize our results in Sect. 9.
In this paper we shall assume that the observable shear is due to the
tidal gravitational field of the cosmological matter distribution
only; in this case, the two shear components are not mutually
independent. This is due to the fact that the gravitational field is a
gradient field. In the language of some recent papers (e.g., C02; Pen
et al. 2002; SvWM), we thus assume that the shear field is a pure
E-mode field. B-modes (or the "curl component'') can in principle be
generated if the intrinsic orientation of the galaxies from which the
shear is measured are correlated, e.g. due to tidal interactions of
dark matter halos in which these galaxies are formed (Croft & Metzler
2000; Pen et al. 2000; Heavens et al. 2001; Catelan et al. 2001;
Mackey et al. 2002; Brown et al. 2002). Also, the clustering of source
galaxies in redshift space generates a B-mode contribution which,
however, turns out to be fairly small (SvWM). This restriction to
E-modes only affects the interrelations between various two-point
statistics. Inclusion of B-modes would not change the results of
Sects. 3 through 5, and much of Sects. 6 and 7 will also be left
unaffected in the presence of a B-mode contribution; we shall indicate
this in due course.
We follow here the notation of Bartelmann & Schneider (2001). The
power spectrum of the projected density field is denoted by
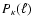 ,
where
,
where 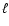 is the Fourier variable on the sky.
is the Fourier variable on the sky.
The shear correlation functions are defined by considering pairs of
positions
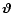 and
and
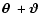 ,
and defining the
tangential and cross-component of the shear
,
and defining the
tangential and cross-component of the shear
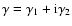 at position
at position
 for this pair as
for this pair as
 |
(1) |
where  is the polar angle of the separation vector
is the polar angle of the separation vector
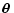 .
Then we define the two shear correlation functions (e.g.,
Kaiser 1992)
.
Then we define the two shear correlation functions (e.g.,
Kaiser 1992)
 |
(2) |
where the Bessel function J0 (J4) corresponds to the
"+'' ("-'') correlation function. The shear dispersion in a circle of
radius 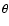 is defined by considering circular
apertures and ensemble-averaging over the square of the complex shear;
its relation to the power spectrum reads (e.g., Kaiser 1992)
is defined by considering circular
apertures and ensemble-averaging over the square of the complex shear;
its relation to the power spectrum reads (e.g., Kaiser 1992)
 |
(3) |
Furthermore, the aperture mass
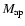 in an aperture of radius
in an aperture of radius
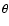 is defined as a weighted average over the tangential shear
component (see, e.g. Schneider 1996; SvWJK), and its dispersion is
related to the power spectrum by
is defined as a weighted average over the tangential shear
component (see, e.g. Schneider 1996; SvWJK), and its dispersion is
related to the power spectrum by
 |
(4) |
where the same weight function in the definition of
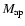 as in
SvWM was assumed.
as in
SvWM was assumed.
All these second-order statistics are thus linearly filtered versions of
the power spectrum 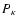 ,
where the filter functions are quite
different between the various statistics. For the correlation
function
,
where the filter functions are quite
different between the various statistics. For the correlation
function 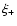 ,
the filter function
,
the filter function 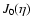 is very broad,
about constant for
is very broad,
about constant for 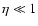 ,
and oscillating for large
,
and oscillating for large 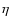 ,
with
an amplitude decreasing as
,
with
an amplitude decreasing as
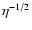 .
The filter function
.
The filter function
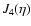 for
for  has the same slow decrease, but behaves as
has the same slow decrease, but behaves as
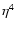 for small
for small 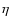 ,
and is therefore more localized than the one
for
,
and is therefore more localized than the one
for 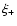 .
The filter function for the shear dispersion,
.
The filter function for the shear dispersion,
![$[2 {J}_1(\eta)/\eta]^2$](/articles/aa/full/2002/46/aah3767/img84.gif) ,
is a low-pass filter, i.e. constant for
,
is a low-pass filter, i.e. constant for 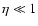 ,
and
then decreasing in amplitude as
,
and
then decreasing in amplitude as 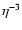 for large
for large 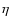 .
Finally,
the filter function for the aperture mass dispersion is
.
Finally,
the filter function for the aperture mass dispersion is
![$[24 {J}_4(\eta)/\eta^2]^2$](/articles/aa/full/2002/46/aah3767/img86.gif) and thus behaves like
and thus behaves like 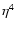 for small
for small 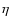 ,
and decreases oscillatory as
,
and decreases oscillatory as 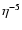 for
for
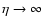 .
Hence,
.
Hence,
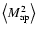 yields the most local estimate of the underlying
power spectrum of the projected mass. On the other hand, because it is
so localized, it contains less power in its filter, so that the value
of
yields the most local estimate of the underlying
power spectrum of the projected mass. On the other hand, because it is
so localized, it contains less power in its filter, so that the value
of
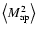 is smaller than that of
is smaller than that of
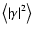 on the same filter scale
on the same filter scale 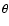 .
.
The various second-order statistics of the shear are related to each
other; in particular, they can all be expressed in terms of the
two-point correlation functions, as was shown in C02, Pen et al. (2002) and SvWM. We briefly summarize the results here.
Making use of the orthogonality of Bessel functions,
the power spectrum can be expressed in terms of the correlation
functions
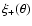 and
and
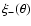 ,
by multiplying Eq. (2) by
,
by multiplying Eq. (2) by
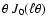 and
and
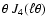 ,
respectively, and then integrating over
,
respectively, and then integrating over
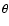 ,
to obtain
,
to obtain
 |
(5) |
These equations express the power spectrum directly in terms of
the observable correlation function; however, in order to evaluate
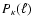 from them, one would need to know the correlation
functions for all angles. In Sect. 7 below, we shall investigate
how well the power spectrum can be determined from knowing the
correlation function over a limited range of separations.
from them, one would need to know the correlation
functions for all angles. In Sect. 7 below, we shall investigate
how well the power spectrum can be determined from knowing the
correlation function over a limited range of separations.
The two Eqs. (2) and (5) allow us to express
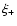 in terms of
in terms of  ,
and reversely (see SvWM for a derivation),
,
and reversely (see SvWM for a derivation),
 |
(6) |
Hence one can obtain
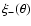 from the correlation function
from the correlation function
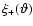 in the interval
in the interval
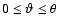 ,
and so this
relation can be directly applied to observational data, with a minor
extrapolation to small separations. The reverse
relation, expressing
,
and so this
relation can be directly applied to observational data, with a minor
extrapolation to small separations. The reverse
relation, expressing 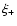 in terms of
in terms of  ,
is less useful in
practice, owing to the infinite range of integration.
,
is less useful in
practice, owing to the infinite range of integration.
Next we express the shear dispersion (3) in terms of the
correlation function, by inserting (5) into
(3); this yields (van Waerbeke 2000; SvWM)
 |
(7) |
where
| S+(x) |
= |
 |
|
| S-(x) |
= |
 |
(8) |
and H(x) is the Heaviside step function. The first form for
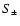 is obtained directly from inserting (5) into
(3), after some renaming of variables, and the details of
evaluating the integrals over the triple product of Bessel functions
are given in SvWM. The same is true for Eqs. (10)
below. We see that the function S+(x) vanishes for x>2, so that
the shear dispersion can be expressed as a finite-range integral over
the correlation function
is obtained directly from inserting (5) into
(3), after some renaming of variables, and the details of
evaluating the integrals over the triple product of Bessel functions
are given in SvWM. The same is true for Eqs. (10)
below. We see that the function S+(x) vanishes for x>2, so that
the shear dispersion can be expressed as a finite-range integral over
the correlation function 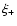 ;
this is not the case for S-.
;
this is not the case for S-.
Similarly, one can express the aperture mass dispersion in terms of
the correlation functions, by inserting (5) into
(4):
 |
(9) |
where
Both of these functions vanish for x>2, so that
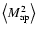 can be expressed by a finite integral over either
can be expressed by a finite integral over either 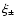 .
The functions
.
The functions 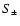 and
and 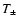 are plotted in SvWM.
are plotted in SvWM.
The fact that we can express the shear dispersion and the aperture
mass dispersion directly in terms of the correlation function over a
finite interval is expected, given that the
estimators of both statistics include products of ellipticities of
pairs of objects separated by no more than the diameter of the
aperture. However, what could not have been guessed a priori is that
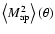 can be expressed by a finite integral
over
can be expressed by a finite integral
over 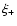 and
and  separately.
The determination of these statistics in terms of the
correlation function is in practice easier than laying down apertures,
owing to the holes and gaps in a data set; in addition, a comparison
of the directly determined shear and aperture mass dispersion with
those obtained from the correlation functions yields a useful
check on the integrity of the data.
separately.
The determination of these statistics in terms of the
correlation function is in practice easier than laying down apertures,
owing to the holes and gaps in a data set; in addition, a comparison
of the directly determined shear and aperture mass dispersion with
those obtained from the correlation functions yields a useful
check on the integrity of the data.
We shall now consider practical estimators of the correlation
functions and the other second-order statistics. The observable
ellipticity
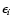 of a galaxy image at angular position
of a galaxy image at angular position
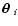 is related to the intrinsic ellipticity
is related to the intrinsic ellipticity
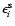 and the shear
and the shear
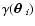 by
by
 |
(11) |
where it has been assumed that
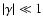 for this weak
lensing relation to be valid. In addition to an ellipticity, each
galaxy may carry a weight factor wi which reflects the precision
with which its ellipticity can be determined - noisy objects can then
be downweighted by assigning small values of wi to them (Hoekstra
et al. 2000; Erben et al. 2001; Bacon et al. 2001; Pen et al. 2002). We shall assume that the correlation function is to be
estimated in bins of angular width
for this weak
lensing relation to be valid. In addition to an ellipticity, each
galaxy may carry a weight factor wi which reflects the precision
with which its ellipticity can be determined - noisy objects can then
be downweighted by assigning small values of wi to them (Hoekstra
et al. 2000; Erben et al. 2001; Bacon et al. 2001; Pen et al. 2002). We shall assume that the correlation function is to be
estimated in bins of angular width
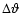 ,
and define the
function
,
and define the
function
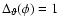 for
for
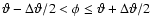 ,
and zero otherwise; hence,
,
and zero otherwise; hence,
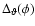 defines the bin at angle
defines the bin at angle
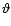 .
An estimator for
the correlation function
.
An estimator for
the correlation function
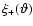 is then
is then
 |
(12) |
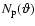 is the effective "number of pairs'' in the bin
considered (in fact, if all weights are unity,
is the effective "number of pairs'' in the bin
considered (in fact, if all weights are unity, 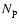 is twice
the number of pairs), and the tangential and cross components of the
ellipticity are defined in analogy to the corresponding shear
components in (1). The expectation value of this estimator
is obtained by averaging over the source ellipticities, assumed to be
randomly oriented, and an ensemble average of the shear field. Since
is twice
the number of pairs), and the tangential and cross components of the
ellipticity are defined in analogy to the corresponding shear
components in (1). The expectation value of this estimator
is obtained by averaging over the source ellipticities, assumed to be
randomly oriented, and an ensemble average of the shear field. Since
 |
(13) |
where
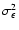 is the dispersion of the intrinsic galaxy
ellipticity, we see immediately that
is the dispersion of the intrinsic galaxy
ellipticity, we see immediately that
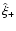 is an unbiased
estimator of
is an unbiased
estimator of 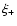 ,
,
 |
(14) |
since the product
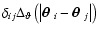 vanishes for
all pairs i,j. Analogously, an unbiased estimator for
vanishes for
all pairs i,j. Analogously, an unbiased estimator for  is
is
 |
(15) |
Next we obtain an unbiased estimator for the aperture mass
dispersion. For that we assume that the centers of the bins on
which the correlation function is calculated are described by
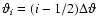 ,
and that the aperture radius
,
and that the aperture radius 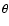 is an
integer multiple of the bin width,
is an
integer multiple of the bin width,
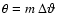 .
Then, the
integrals in (9) are replaced by sums over the bins,
yielding an estimator for
.
Then, the
integrals in (9) are replaced by sums over the bins,
yielding an estimator for
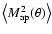 ,
,
 |
(16) |
where K+ describes the relative contributions of the two
expressions (9). For example, in the presence of B-modes,
one needs to use K+=1/2 (SvWM). Similarily, an unbiased estimator
for the shear dispersion is
 |
(17) |
again, in the presence of B-modes, K+=1/2 shall be chosen (however,
the infinite support of S- requires the knowledge of the
correlation function  for all separations). Both of
the above are unbiased estimators,
for all separations). Both of
the above are unbiased estimators,
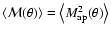 ,
,
 .
.
Next we calculate the covariance of the various estimators, starting
with the correlation functions. Hence, we define
 |
(18) |
Consider first the "++''-covariance function, for which one needs to
evaluate
 |
(19) |
where we defined
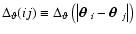 and
used the fact that
and
used the fact that
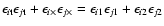 .
Next, the four-point correlation function of the ellipticities needs
to be evaluated. For that, we use (11) and expand the
resulting expression. Only terms of even power in
.
Next, the four-point correlation function of the ellipticities needs
to be evaluated. For that, we use (11) and expand the
resulting expression. Only terms of even power in
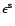 and
and
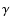 survive the averaging over the source ellipticities and the
ensemble average. Then,
survive the averaging over the source ellipticities and the
ensemble average. Then,
 |
|
|
(20) |
valid for 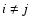 and
and 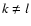 ,
as needed in (19); here,
Greek letters are
,
as needed in (19); here,
Greek letters are
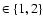 .
To evaluate the four-point function of
the shear, we shall assume that the shear field is Gaussian, so that
the four-point function can be written as a sum over products of
two-point functions. We shall later comment on the effect this
assuption has on the determination of the covariances. The four-point
function of the intrinsic ellipticity also factorizes, since at most
two of the indices i,j,k,l are equal. Therefore,
.
To evaluate the four-point function of
the shear, we shall assume that the shear field is Gaussian, so that
the four-point function can be written as a sum over products of
two-point functions. We shall later comment on the effect this
assuption has on the determination of the covariances. The four-point
function of the intrinsic ellipticity also factorizes, since at most
two of the indices i,j,k,l are equal. Therefore,
The correlation functions of the shear components can be expressed as
(Kaiser 1992)
 |
(22) |
where we have written
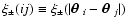 ,
and
,
and
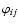 is the polar angle of the difference vector
is the polar angle of the difference vector
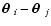 .
From these relations, one obtains for the
covariance matrix
.
From these relations, one obtains for the
covariance matrix
where the function
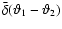 is zero if the two
separation bins are different, and is 1 if they are the same. The
first term in (23) therefore contributes only to the
diagonal terms in the covariance matrix. In the absence of shear
correlations, the covariance matrix would be diagonal; correlation
populates the off-diagonal elements of the covariance tensor.
is zero if the two
separation bins are different, and is 1 if they are the same. The
first term in (23) therefore contributes only to the
diagonal terms in the covariance matrix. In the absence of shear
correlations, the covariance matrix would be diagonal; correlation
populates the off-diagonal elements of the covariance tensor.
To calculate the covariance matrix for the  correlation
function, we first write
correlation
function, we first write
inserting this into the definition of the covariance matrix and
performing the same step as for the "++'' covariance, one finds
Finally, the mixed covariance matrix can be calculated in the same
manner, yielding
Given a model for the shear correlation, the covariances
(23)-(25) can be calculated using the actual galaxy
positions and their weight factors; in principle, this procedure is
straightforward to apply to a given data set. Alternatively, given the
geometry of a data field, then by randomly distributing galaxy
positions the expected covariance of the shear correlation can be
determined; this procedure can be used to design and optimize cosmic
shear surveys (Kilbinger et al., in preparation). These calculations
are, however, time-consuming, given the sum over three and four galaxy
positions. It is therefore of interest to consider a relatively simple
situation where fairly explicit expressions for the covariance
matrices can be obtained. In particular, we shall calculate the
ensemble average of the covariance matrices. We consider here a
survey geometry which consists of a single data field of solid angle
A and galaxy number density n, so that N=nA is the total number
of galaxies in the survey. The survey geometry is assumed to be
"simple'', i.e. consisting of a simply connected region, say, a
quadratic field. We shall assume that all weight factors are unity,
wi=1. Furthermore, we shall consider separations
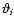 which are
small compared to the "diameter'' of the survey field,
which are
small compared to the "diameter'' of the survey field,
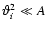 ;
in this case, we can neglect "boundary effects'' which otherwise would
complicate the analysis tremendously. With these assumptions, the
number of pairs in the bin characterized by
;
in this case, we can neglect "boundary effects'' which otherwise would
complicate the analysis tremendously. With these assumptions, the
number of pairs in the bin characterized by
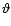 is then
is then
 |
(26) |
The ensemble average over galaxy positions is carried out by the
averaging operator
i.e. the galaxies are assumed to be randomly placed on the field.
The average of the first term in (23) and (24) is
simple and reads
 |
(27) |
As expected, this term depends explicitly on the bin size chosen,
since
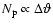 .
In practical units,
.
In practical units,
As we shall see, the other terms
are independent of the choice of the bins. To evaluate the other
terms, one notes that the expectation value of all terms involving a
sum over three galaxy positions can be written in terms of
 |
(28) |
or linear combinations thereof. Applying the averaging operator, we
note that there are
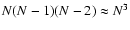 permutations of galaxies,
so that
permutations of galaxies,
so that
where in the second step we have written
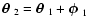 ,
,
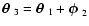 ,
so that
,
so that
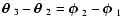 ,
,
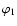 and
and
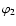 denote the polar angles of
denote the polar angles of
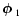 ,
,
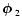 ,
respectively. After this substitution, the integral becomes
independent of
,
respectively. After this substitution, the integral becomes
independent of
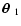 ,
which can be integrated to yield a
factor A. Assuming that the bin width
,
which can be integrated to yield a
factor A. Assuming that the bin width
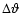 is small, one can
evaluate the
is small, one can
evaluate the 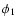 and
and 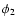 integrals, to obtain
integrals, to obtain
 |
(29) |
Similarily, the expectation value of all terms involving a
sum over four galaxy positions can be written in terms of
where in the second step we defined
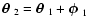 ,
,
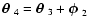 ;
then, the arguments of the
functions
;
then, the arguments of the
functions 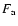 and
and 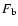 become
become
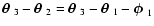 and
and
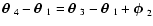 ,
i.e. they
depend only on the difference
,
i.e. they
depend only on the difference
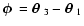 ,
so
that the integral over
,
so
that the integral over
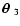 can be carried out, yielding a
factor A. Performing the
can be carried out, yielding a
factor A. Performing the 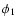 and
and 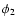 integration, assuming
small bin width, one obtains
integration, assuming
small bin width, one obtains
 |
(30) |
where the vectors
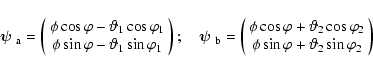 |
(31) |
have been defined for later convenience.
Next we shall evaluate the second term of (23) which is of
the form (28), with
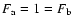 ,
,
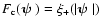 ;
inserting these expressions into
(29), the expectation value of the second term in
(23) becomes
;
inserting these expressions into
(29), the expectation value of the second term in
(23) becomes
 |
(32) |
The expectation value of the third term in (23) can be
calculated by splitting it up into three parts: in the first,
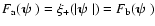 ,
and the other two are
obtained by expanding the cosine-term, so that for one of them,
,
and the other two are
obtained by expanding the cosine-term, so that for one of them,
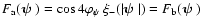 ,
and for
the other, cos is replaced by sin; here,
,
and for
the other, cos is replaced by sin; here,
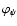 is the polar angle
of
is the polar angle
of
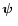 .
Note that all three terms have
.
Note that all three terms have
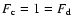 .
The final result then reads
.
The final result then reads
 |
(33) |
where D and q++ have been defined in (27) and
(32), respectively,
| r+0 |
= |
 |
|
| r+1 |
= |
 |
(34) |
and
 ,
,
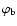 are the polar angles of
are the polar angles of
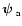 ,
,
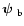 ,
respectively,
,
respectively,
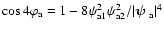 ,
,
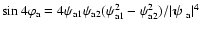 ,
and the analogous expressions for
,
and the analogous expressions for
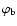 .
Note that the
.
Note that the  -integration present in (30)
has dropped out as the integrand depends only on
-integration present in (30)
has dropped out as the integrand depends only on
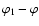 ,
and
,
and
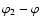 ;
hence, the
;
hence, the  -integration can be carried out and one
can use
-integration can be carried out and one
can use 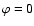 in (31).
in (31).
Several issues are worth mentioning: (1) only the first term
containing the "delta function'' depends on the bin width
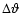 ;
thus, the bin width only affects the autovariance. (2) All terms are
proportional to A-1; hence, the relative contribution of the
terms is independent of the survey area, at least for separations well
below the "diameter'' of the survey area for which the foregoing
procedure of the ensemble averaging is valid. (3) The terms denoted by
"r'' are independent of the intrinsic ellipticity dispersion and of
the number density of galaxies. Hence, these terms describe the cosmic
variance and thus provide a limit on the accuracy of the determination
of the correlation function for a given survey geometry, independent
of the observing conditions which determine n.
;
thus, the bin width only affects the autovariance. (2) All terms are
proportional to A-1; hence, the relative contribution of the
terms is independent of the survey area, at least for separations well
below the "diameter'' of the survey area for which the foregoing
procedure of the ensemble averaging is valid. (3) The terms denoted by
"r'' are independent of the intrinsic ellipticity dispersion and of
the number density of galaxies. Hence, these terms describe the cosmic
variance and thus provide a limit on the accuracy of the determination
of the correlation function for a given survey geometry, independent
of the observing conditions which determine n.
The expectation values of the other covariance matrices are calculated
in a similar manner. Consider the "-'' covariance (24)
next; the first term agrees with that of (23). For the
second term, we can apply (29), after expanding the cosine;
then
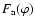 and
and
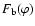 are either
are either
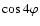 or
or
 ,
and
,
and
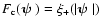 .
Similarily, (30)
can be applied to the third term of (24), after expanding
the cosine; using (30) term by term, and combining the
results afterwards, one obtains
.
Similarily, (30)
can be applied to the third term of (24), after expanding
the cosine; using (30) term by term, and combining the
results afterwards, one obtains
 |
(35) |
where
Finally, the expectation value of (25), the mixed
covariance, is calculated in a similar manner, yielding
 |
(37) |
with
| q+- |
= |
 |
|
| r+- |
= |
![$\displaystyle {1\over \pi A}\int_0^\infty{\rm d}\phi~\phi
\int_0^{2\pi}{\rm d}\...
...ditalics \hbox{$\bf\psi$ }}_{\rm b}\vert)\;
\cos[4(\varphi_2-\varphi_{\rm b})].$](/articles/aa/full/2002/46/aah3767/img231.gif) |
(38) |
Hence, as already seen from (25), the cross-covariance
matrix has no pure noise term from the intrinsic galaxy ellipticity
dispersion as the other two covariance matrices.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{3767f1.eps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg232.gif) |
Figure 1:
The correlation functions. In the left panel, we have
plotted the covariance matrices
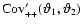 (thick solid curves) and
(thick solid curves) and
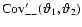 ,
i.e. the
covariance matrices with the shot-noise term removed. For ,
i.e. the
covariance matrices with the shot-noise term removed. For
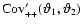 ,
the contours are linearly spaced, with
the lowest value at 10-9 (outer-most contour) and highest
value ,
the contours are linearly spaced, with
the lowest value at 10-9 (outer-most contour) and highest
value
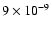 for small
for small
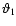 , ,
 .
For .
For
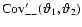 ,
contours are logarithmically spaced,
with consecutive contours differing by a factor 1.5. The
solid contours display positive values of ,
contours are logarithmically spaced,
with consecutive contours differing by a factor 1.5. The
solid contours display positive values of
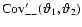 ,
starting from 10-14, with the
maximum value of ,
starting from 10-14, with the
maximum value of
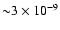 in the upper right corner,
and dotted contours show negative values of
in the upper right corner,
and dotted contours show negative values of
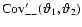 ,
starting at -10-15. In the right
panel, ,
starting at -10-15. In the right
panel,
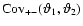 is shown, again with
logarithmically spaced contours differing by a factor of 1.5. Solid
contours are for positive values of
is shown, again with
logarithmically spaced contours differing by a factor of 1.5. Solid
contours are for positive values of
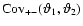 ,
starting at 10-14, negative values are shown by dotted contours,
starting at -10-13. ,
starting at 10-14, negative values are shown by dotted contours,
starting at -10-13. |
| Open with DEXTER |
We have obtained numerical estimates for the ensemble-averaged
covariance matrices derived above (see Fig. 1). In the
numerical estimates given in this paper (except for Sect. 8.2), we
have used a standard set of parameters. The cosmological parameters
are those of a by-now standard  -dominated universe,
-dominated universe,
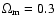 ,
,
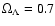 .
The power spectrum of the
density fluctuations is described by its primordial slope of n=1, a
shape parameter
.
The power spectrum of the
density fluctuations is described by its primordial slope of n=1, a
shape parameter
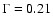 ,
and a normalization of
,
and a normalization of
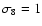 .
We
used the fit formula of Bardeen et al. (1986) for the linear power
spectrum, and the prescription of Hamilton et al. (1991) in the form
given in Peacock & Dodds (1996) to describe the non-linear evolution
of the power spectrum
.
We
used the fit formula of Bardeen et al. (1986) for the linear power
spectrum, and the prescription of Hamilton et al. (1991) in the form
given in Peacock & Dodds (1996) to describe the non-linear evolution
of the power spectrum![[*]](/icons/foot_motif.gif) . Furthermore, we fix the survey
properties to be described by a fiducial area of
. Furthermore, we fix the survey
properties to be described by a fiducial area of
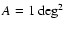 ,
a
number density
,
a
number density
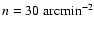 of source galaxies, and an
intrinsic ellipticity dispersion of
of source galaxies, and an
intrinsic ellipticity dispersion of
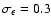 .
The source
galaxies were assumed to have a redshift distribution
.
The source
galaxies were assumed to have a redshift distribution
![$p(z)\propto
z^2~\exp[-(z/z_0)^{1.5}]$](/articles/aa/full/2002/46/aah3767/img237.gif) ,
so that the mean redshift is
,
so that the mean redshift is
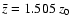 .
For the examples shown in Sects. 5 through 7, we take
z0=1. Note that all covariances simply scale with A-1, so that
the results displayed here are easily translated to other survey
sizes. This scaling is also implicitly implied when considering scales
of order a degree or more - all the numerical estimates are for the
ensemble averaged covariances, and their validity as given here
depends on the assumption
.
For the examples shown in Sects. 5 through 7, we take
z0=1. Note that all covariances simply scale with A-1, so that
the results displayed here are easily translated to other survey
sizes. This scaling is also implicitly implied when considering scales
of order a degree or more - all the numerical estimates are for the
ensemble averaged covariances, and their validity as given here
depends on the assumption
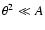 .
.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{3767f2.eps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg245.gif) |
Figure 2:
Left panel: the square root of the variances
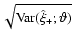 and
and
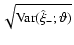 shown as dotted and long-dashed curves, together with the
correlation functions
shown as dotted and long-dashed curves, together with the
correlation functions
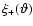 and
and
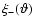 as solid and
short-dashed curves, respectively. The model parameters are as
described in the text; in particular, a fiducial value of the
survey area of
as solid and
short-dashed curves, respectively. The model parameters are as
described in the text; in particular, a fiducial value of the
survey area of
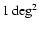 has been taken. For the diagonal part
of the covariance matrix, we have assumed a relative bin size of
has been taken. For the diagonal part
of the covariance matrix, we have assumed a relative bin size of
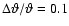 .
For small .
For small
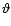 ,
the variance behaves as ,
the variance behaves as
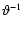 ,
as it is dominated by the noise from the intrinsic
ellipticity of the source galaxies, i.e. the term D (27), whereas for larger values of ,
as it is dominated by the noise from the intrinsic
ellipticity of the source galaxies, i.e. the term D (27), whereas for larger values of
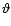 ,
the main
contribution comes from cosmic variance. Right panel: the
correlation coefficient ,
the main
contribution comes from cosmic variance. Right panel: the
correlation coefficient
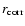 ,
as defined in
(39), as a function of ,
as defined in
(39), as a function of
 ,
for various values of ,
for various values of
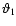 .
Solid curves show .
Solid curves show
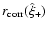 ,
dashed
curves show ,
dashed
curves show
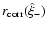 .
The value of .
The value of
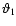 corresponding to each curve can be read off from the point where a
curve attains the value
corresponding to each curve can be read off from the point where a
curve attains the value
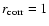 . .
|
| Open with DEXTER |
Figure 2 displays in the left panel the square root of the
(auto)variance of
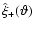 and
and
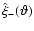 ,
with
,
with
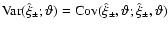 .
To
calculate the value of D (27) which enters the diagonal
part of the covariance matrix, we have assumed a bin width of
.
To
calculate the value of D (27) which enters the diagonal
part of the covariance matrix, we have assumed a bin width of
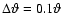 .
The square
root of the variance - or noise per bin - for
.
The square
root of the variance - or noise per bin - for 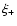 is smaller
than
is smaller
than 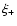 for
for
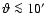 ,
and larger for larger angles (for
the assumed value of
,
and larger for larger angles (for
the assumed value of
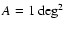 ), whereas the noise for
), whereas the noise for
 is smaller than
is smaller than  in an interval of
in an interval of
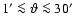 .
The determination of
.
The determination of  on small angular scales
is much more difficult than for
on small angular scales
is much more difficult than for 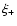 ,
owing to the smallness of
,
owing to the smallness of
 for small
for small
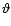 .
Note that the noise scales like A-1/2,
so that from a survey of
.
Note that the noise scales like A-1/2,
so that from a survey of
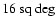 ,
like the DESCART survey
(see van Waerbeke et al. 2001) one should be able to obtain reliable
measurements of
,
like the DESCART survey
(see van Waerbeke et al. 2001) one should be able to obtain reliable
measurements of 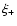 for
for
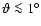 ,
and of
,
and of  for
for
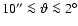 in bins of relative width of
0.1. Of course, the covariance of the shear will not only depend on
the survey area, but also on its geometry; one might therefore design
survey geometries which yield the desired noise behaviour as a function
of angular scale (see, e.g., Kaiser 1998).
in bins of relative width of
0.1. Of course, the covariance of the shear will not only depend on
the survey area, but also on its geometry; one might therefore design
survey geometries which yield the desired noise behaviour as a function
of angular scale (see, e.g., Kaiser 1998).
In order to show how strongly the correlation estimators at two
angular scales are correlated, we define the correlation coefficient
 |
(39) |
which is unity for
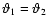 .
Here, the prime indicates that the
first term in the covariances [the one proportional to
.
Here, the prime indicates that the
first term in the covariances [the one proportional to
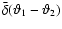 ]
has been subtracted off, in order to show
the correlation induced by cosmic shear. The correlation coefficient
is plotted in the right panel of Fig. 2. The
]
has been subtracted off, in order to show
the correlation induced by cosmic shear. The correlation coefficient
is plotted in the right panel of Fig. 2. The  correlation function decorrelates quickly: once the ratio between the
angular scales is larger than
correlation function decorrelates quickly: once the ratio between the
angular scales is larger than 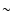 2, the correlation coefficient
(39) has decreased to less than 10%. In contrast to
this, the correlation function
2, the correlation coefficient
(39) has decreased to less than 10%. In contrast to
this, the correlation function 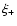 is correlated over much larger
angular scales. This was expected, given that the filter function
which relates the correlation function to the power spectrum is much
broader for
is correlated over much larger
angular scales. This was expected, given that the filter function
which relates the correlation function to the power spectrum is much
broader for 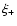 than for
than for  .
.
Due to the particular interest in the aperture mass dispersion, we
shall consider here the covariance matrix of the estimator
(16),
 |
(40) |
Munshi & Coles (2000) have calculated the statistical properties of
the aperture mass, using the hierarchical ansatz. We shall consider
here the covariance in terms of the covariance of the two-point
correlation function. Inserting (16) into this expression,
the covariance matrix of
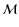 becomes
becomes
where we used the abbreviated notation
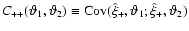 etc. The values of the
aperture radius are taken to be
etc. The values of the
aperture radius are taken to be
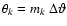 for k=1,2,
and
for k=1,2,
and
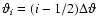 ,
as before. Hence, the covariance of the
aperture mass dispersion can be obtained directly in terms of the
covariances of the shear correlation functions. We can also obtain the
ensemble-averaged covariance matrix; for this purpose, we separate the
"delta-function'' term in C++ and C- from the rest and thus
write
,
as before. Hence, the covariance of the
aperture mass dispersion can be obtained directly in terms of the
covariances of the shear correlation functions. We can also obtain the
ensemble-averaged covariance matrix; for this purpose, we separate the
"delta-function'' term in C++ and C- from the rest and thus
write
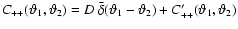 ,
similarily for
C-. Then the ensemble-average of (41) becomes
,
similarily for
C-. Then the ensemble-average of (41) becomes
As expected, the covariance matrix of
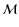 does not depend on the
binning of the correlation function. For the calculation of
does not depend on the
binning of the correlation function. For the calculation of
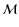 for
observational data, it is therefore best to choose very small bin
widths, in order to minimize discretization errors.
for
observational data, it is therefore best to choose very small bin
widths, in order to minimize discretization errors.
The first term in (42) yields the covariance in the absence
of cosmic shear correlations, i.e. the covariance of the estimator
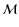 due to the intrinsic ellipticity of the source galaxies. This
term can be written as
due to the intrinsic ellipticity of the source galaxies. This
term can be written as
where
| f(R) |
= |
 |
|
| |
= |
 |
(43) |
where the explicit relation has been obtained by making use of the
original definitions of 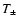 .
The function
f(R) is maximized at R=1, where its value is
.
The function
f(R) is maximized at R=1, where its value is
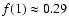 ,
and it decreases quickly for appreciable ratios of the aperture
radii. The dependence on K+ is simple, and obviously this noise
term is minimized for K+=1/2, i.e. when both correlation functions
enter the estimate
,
and it decreases quickly for appreciable ratios of the aperture
radii. The dependence on K+ is simple, and obviously this noise
term is minimized for K+=1/2, i.e. when both correlation functions
enter the estimate
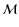 with equal weight. The
variance of the estimator
with equal weight. The
variance of the estimator
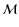 in the absence of shear correlations
can be compared with the corresponding expression obtained in SvWJK,
obtained from their Eqs. (5.12) and (5.16), yielding
in the absence of shear correlations
can be compared with the corresponding expression obtained in SvWJK,
obtained from their Eqs. (5.12) and (5.16), yielding
where G=1.2 is a numerical coefficient (calculated from the filter
function in the definition of
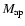 ), and
), and 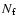 is the
number of independent apertures that can be placed on the data field,
taken to be
is the
number of independent apertures that can be placed on the data field,
taken to be
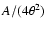 .
Together with
.
Together with
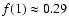 ,
one
clearly sees that the variance of the estimator
,
one
clearly sees that the variance of the estimator
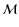 is substantially
smaller than that used in SvWJK which was based on placing
non-overlapping apertures
on the data field. The main reason for this difference is that in the
latter method, only one component of the source ellipticities is used;
furthermore, apertures separated by less than their diameter are
statistically nearly independent. Hence, the determination of
is substantially
smaller than that used in SvWJK which was based on placing
non-overlapping apertures
on the data field. The main reason for this difference is that in the
latter method, only one component of the source ellipticities is used;
furthermore, apertures separated by less than their diameter are
statistically nearly independent. Hence, the determination of
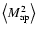 through the shear correlation function is not
only more practical in the presence of gaps in the data field, but
also far more efficient than the alternative method.
through the shear correlation function is not
only more practical in the presence of gaps in the data field, but
also far more efficient than the alternative method.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{3767f3.eps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg278.gif) |
Figure 3:
Left panel: the square-root of the autovariance of
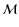 as a function of angular scale. The long-dashed and
dash-dotted curves show the minimum variance, i.e. in the absence
of a shear correlation; this variance is due solely to the
intrinsic ellipticity of source galaxies. Curves are shown for
K+=0, 1/2, 1, where the minimum variance is the same for K+=0 and 1. The solid, dashed and dotted curves show the variance
in the presence of a cosmic shear; also here, the cases K+=0 and
K-=1 are nearly the same, and the variance is smallest for
K+=1/2. For comparison,
as a function of angular scale. The long-dashed and
dash-dotted curves show the minimum variance, i.e. in the absence
of a shear correlation; this variance is due solely to the
intrinsic ellipticity of source galaxies. Curves are shown for
K+=0, 1/2, 1, where the minimum variance is the same for K+=0 and 1. The solid, dashed and dotted curves show the variance
in the presence of a cosmic shear; also here, the cases K+=0 and
K-=1 are nearly the same, and the variance is smallest for
K+=1/2. For comparison,
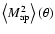 is plotted
as thick solid curve. As for the other figures shown before, our
standard set of parameters
is plotted
as thick solid curve. As for the other figures shown before, our
standard set of parameters
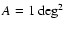 , ,
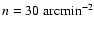 and
and
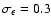 has been used; the variance
scales as A-1. Right panel: the correlation coefficient
has been used; the variance
scales as A-1. Right panel: the correlation coefficient
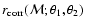 of the covariance of the
estimator
of the covariance of the
estimator
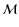 is plotted as a function of
is plotted as a function of 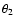 ,
for various
values of ,
for various
values of 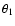 ;
the values of ;
the values of 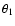 can be localized as
those points where the correlation function attains the value
unity. The solid curves are for K+=0, i.e. when only the
correlation function
can be localized as
those points where the correlation function attains the value
unity. The solid curves are for K+=0, i.e. when only the
correlation function  is used in the estimate of
is used in the estimate of
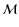 ,
the
dotted curves are for K+=1/2, and the dashed curves for
K+=1. The width of all three families of curves is very similar
and (in logarithmic terms) basically independent of ,
the
dotted curves are for K+=1/2, and the dashed curves for
K+=1. The width of all three families of curves is very similar
and (in logarithmic terms) basically independent of 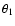 .
The
K+=0 curves do not develop a tail of anticorrelation, as is the
case for K+=1 (and therefore also for K+=1/2). Hence, whereas
K+=1/2 yields the smallest variance of the estimator .
The
K+=0 curves do not develop a tail of anticorrelation, as is the
case for K+=1 (and therefore also for K+=1/2). Hence, whereas
K+=1/2 yields the smallest variance of the estimator
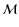 ,
it
leads to a small but long-range correlation between different
angular scales. ,
it
leads to a small but long-range correlation between different
angular scales.
|
| Open with DEXTER |
We have plotted in Fig. 3 the square root of the variance
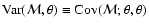 of
of
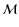 ,
both
for the case of no correlations, and for our standard model for the
cosmic shear. For small angular scales, the variance is completely
dominated by the intrinsic source ellipticities, whereas the cosmic
variance is the important noise error for larger angular scales. For
the parameters used here, the transition between these two regimes
occurs at a few arcminutes. It must be noted that the shape of the
variance curves are independent of the survey area A. The results
shown in Fig. 3 can be seen as an a posteriori
justification of using the Gaussian assumption for the calculation of
the shear four-point function in Sect. 4. In Fig. 4 of van
Waerbeke et al. (2002), the influence of the non-linear density
evolution on the kurtosis of
,
both
for the case of no correlations, and for our standard model for the
cosmic shear. For small angular scales, the variance is completely
dominated by the intrinsic source ellipticities, whereas the cosmic
variance is the important noise error for larger angular scales. For
the parameters used here, the transition between these two regimes
occurs at a few arcminutes. It must be noted that the shape of the
variance curves are independent of the survey area A. The results
shown in Fig. 3 can be seen as an a posteriori
justification of using the Gaussian assumption for the calculation of
the shear four-point function in Sect. 4. In Fig. 4 of van
Waerbeke et al. (2002), the influence of the non-linear density
evolution on the kurtosis of
 was studied, using
ray-tracing simulations through numerically generated cosmological
matter distributions. The non-Gaussian effects start to become
non-negligible for angular scales below
was studied, using
ray-tracing simulations through numerically generated cosmological
matter distributions. The non-Gaussian effects start to become
non-negligible for angular scales below 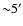 .
As can be seen in
Fig. 3, this is about the scale where the transition occurs
between the variance being dominated by the intrinsic ellipticity
distribution and the cosmic variance. Hence, we can expect that a more
advanced treatment of the shear four-point function would yield a
slightly larger variance in this transition region around
.
As can be seen in
Fig. 3, this is about the scale where the transition occurs
between the variance being dominated by the intrinsic ellipticity
distribution and the cosmic variance. Hence, we can expect that a more
advanced treatment of the shear four-point function would yield a
slightly larger variance in this transition region around 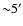 :
for significantly smaller scales, it is dominated by the intrinsic
ellipticity noise, and for larger scales, the shear four-point
function is basically Gaussian.
:
for significantly smaller scales, it is dominated by the intrinsic
ellipticity noise, and for larger scales, the shear four-point
function is basically Gaussian.
The variances of
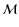 for the cases K+=0 and K+=1 are basically
identical, and larger by a factor
for the cases K+=0 and K+=1 are basically
identical, and larger by a factor
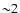 than the variance of the
estimator for K+=1/2. Hence, to minimize the variance of the
estimator
than the variance of the
estimator for K+=1/2. Hence, to minimize the variance of the
estimator
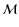 ,
K+=1/2 should be chosen. With this choice, the
results are unchanged even in the presence of a B-mode contribution
(see SvWM). As was already mentioned by C02, using cosmic shear
estimators which use
,
K+=1/2 should be chosen. With this choice, the
results are unchanged even in the presence of a B-mode contribution
(see SvWM). As was already mentioned by C02, using cosmic shear
estimators which use 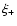 and
and  with equal weight reduces the
resulting noise by a factor 2-1/2. One notes that the variance
for large
with equal weight reduces the
resulting noise by a factor 2-1/2. One notes that the variance
for large 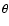 rises, but very slowly. We can compare the
behavior of the variance of
rises, but very slowly. We can compare the
behavior of the variance of
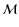 with that derived in SvWJK for a
more direct estimator for the aperture mass dispersion; using Eqs. (5.12) and (5.16) of that paper, one finds in the limit of large
angles (and, to make the estimate comparable to the one obtained here,
zero kurtosis) that
with that derived in SvWJK for a
more direct estimator for the aperture mass dispersion; using Eqs. (5.12) and (5.16) of that paper, one finds in the limit of large
angles (and, to make the estimate comparable to the one obtained here,
zero kurtosis) that
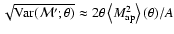 ,
where
,
where
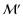 is the estimator
used in SvWJK. The functional behavior with
is the estimator
used in SvWJK. The functional behavior with 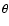 is similar to
that seen in Fig. 3, but the amplitude is lower by a factor
of about 2 for K+=0, 1, and about 3 for K+=1/2; this again shows
the superiority of the estimator considered here in comparison to
laying down independent apertures on the data field.
is similar to
that seen in Fig. 3, but the amplitude is lower by a factor
of about 2 for K+=0, 1, and about 3 for K+=1/2; this again shows
the superiority of the estimator considered here in comparison to
laying down independent apertures on the data field.
To investigate the correlation of the estimator
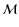 between different
angular scales, we define the correlation coefficient
between different
angular scales, we define the correlation coefficient
 |
(44) |
which has the property that
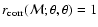 .
The
dependence of this correlation on the ratio of the angular scales then
provides information on the correlated error of the determination of
the aperture mass dispersion on different angular scales. In the right
panel of Fig. 3 we have plotted this correlation
coefficient as a function of
.
The
dependence of this correlation on the ratio of the angular scales then
provides information on the correlated error of the determination of
the aperture mass dispersion on different angular scales. In the right
panel of Fig. 3 we have plotted this correlation
coefficient as a function of 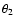 ,
for various values of
,
for various values of
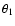 .
The logarithmic representation clearly shows that this
correlation coefficient depends mainly on the ratio
.
The logarithmic representation clearly shows that this
correlation coefficient depends mainly on the ratio
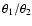 .
The correlation drops off quickly, so that
estimates of
.
The correlation drops off quickly, so that
estimates of
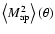 for two angles with ratio
for two angles with ratio
 or
or
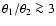 are
practically uncorrelated. This was to be expected given that
are
practically uncorrelated. This was to be expected given that
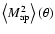 is obtained from the power spectrum
is obtained from the power spectrum
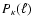 through a very well localized filter function. Hence,
the estimator
through a very well localized filter function. Hence,
the estimator
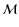 decorrelates much faster than those of the shear
correlation functions. Also seen in Fig. 3 is the fact that
in the case of K+=1/2 and K+=1, the correlation coefficient
attains long negative, but low-amplitude tails, whereas they are
basically absent if K+=0. This is due to the much faster
decorrelation of
decorrelates much faster than those of the shear
correlation functions. Also seen in Fig. 3 is the fact that
in the case of K+=1/2 and K+=1, the correlation coefficient
attains long negative, but low-amplitude tails, whereas they are
basically absent if K+=0. This is due to the much faster
decorrelation of  with scale ratio than that of
with scale ratio than that of 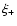 .
.
The relations (5) may be used to define an estimator for the
power spectrum
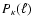 as
as
 |
(45) |
where
![$K_+\in[0,1]$](/articles/aa/full/2002/46/aah3767/img290.gif) again describes the relative contribution from the
again describes the relative contribution from the
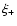 correlation. Here,
correlation. Here,
 and
and
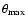 describe the range over which the correlation function has been
measured. If this range extends from zero to infinity, the estimator
(45) would be unbiased (and would yield the E-mode power
spectrum for K+=1/2 even in the presence of B-modes); for real
datasets, where this range is finite, (45) is a biased
estimator. Note that in the absence of B-modes, Eq. (45) remains valid even if the factor K+ is chosen to
be a function of
describe the range over which the correlation function has been
measured. If this range extends from zero to infinity, the estimator
(45) would be unbiased (and would yield the E-mode power
spectrum for K+=1/2 even in the presence of B-modes); for real
datasets, where this range is finite, (45) is a biased
estimator. Note that in the absence of B-modes, Eq. (45) remains valid even if the factor K+ is chosen to
be a function of 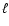 .
The expectation value can be obtained by
inserting the relation (2) between the correlation functions
and the true power spectrum into (45) to yield
.
The expectation value can be obtained by
inserting the relation (2) between the correlation functions
and the true power spectrum into (45) to yield
 |
(46) |
with
 |
(47) |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{3767f4.eps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg295.gif) |
Figure 4:
The thick solid line displays the dimensionless projected
power spectrum
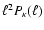 ,
whereas the other two
curves show the "observed'' power spectrum, as defined in
(46). The dotted curve is for K+=0, i.e. only ,
whereas the other two
curves show the "observed'' power spectrum, as defined in
(46). The dotted curve is for K+=0, i.e. only  enters the determination of the observed power spectrum in this
case; the dashed curve is for K+=1. In this plot is was assumed
that the correlation functions are known between
enters the determination of the observed power spectrum in this
case; the dashed curve is for K+=1. In this plot is was assumed
that the correlation functions are known between
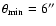 and
and
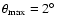 . .
|
| Open with DEXTER |
We have plotted the "observed'' power spectrum as
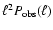 in Fig. 4, for K+=0 and K+=1, assuming
that
in Fig. 4, for K+=0 and K+=1, assuming
that
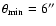 and
and
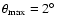 .
A
comparison with the underlying power spectrum (shown as heavy solid
curve) shows that
.
A
comparison with the underlying power spectrum (shown as heavy solid
curve) shows that
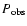 traces the true power spectrum over a
wide range of
traces the true power spectrum over a
wide range of 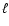 -values, though in an oscillatory way. If
-values, though in an oscillatory way. If
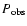 is determined solely from
is determined solely from  (i.e. K+=0), it
substantially underestimates the power for
(i.e. K+=0), it
substantially underestimates the power for
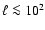 (that
is, approximately for
(that
is, approximately for
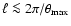 ), but
traces the true power spectrum out to the largest values of
), but
traces the true power spectrum out to the largest values of 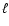 plotted. Conversely, the observed power determined from
plotted. Conversely, the observed power determined from 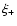 yields
good estimates of the true power for small values of
yields
good estimates of the true power for small values of 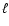 ,
but
deviates from it strongly for
,
but
deviates from it strongly for
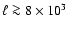 ,
that is for
values of
,
that is for
values of 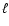 much less than
much less than
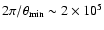 .
The different behavior of the two estimates again is due to the
different filter function through which correlation function and power
spectrum are related. Figure 4 suggests that the best
estimate for the power spectrum is obtained by choosing K+=1 for
small values of
.
The different behavior of the two estimates again is due to the
different filter function through which correlation function and power
spectrum are related. Figure 4 suggests that the best
estimate for the power spectrum is obtained by choosing K+=1 for
small values of 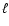 ,
and K+=0 for large
,
and K+=0 for large 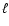 .
.
The covariance matrix of 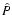 reads, for K+=1,
reads, for K+=1,
 |
(48) |
the generalization for other values of K+ is obvious and shall not
be reproduced here.
To estimate the power spectrum from cosmic shear data, it is useful to
define the power in a band with upper and lower 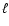 -values
-values
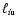 and
and
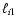 as
as
![\begin{displaymath}\P_i:={1\over \Delta_i}
\int_{\ell_{i{\rm l}}}^{\ell_{i{\rm u...
...ell_{i{\rm u}}\theta)-g_-(\ell_{i{\rm
l}}\theta)\Bigr]\bigg\},
\end{displaymath}](/articles/aa/full/2002/46/aah3767/img306.gif) |
(49) |
where
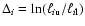 is the
logarithmic width of the band, and
is the
logarithmic width of the band, and
 |
(50) |
One expects that the band power traces
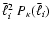 ,
where
,
where
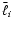 is the geometric mean of
is the geometric mean of
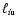 and
and
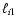 ,
i.e. the center of the bin.
The covariance of the band power of two bins i and j is
,
i.e. the center of the bin.
The covariance of the band power of two bins i and j is
where
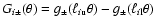 .
In (51), we have already split off the
"delta-function'' part of the correlation covariance matrices, which
yields the first term. It should be noted that the foregoing
expressions remain valid if K+ is varied as a function of
.
In (51), we have already split off the
"delta-function'' part of the correlation covariance matrices, which
yields the first term. It should be noted that the foregoing
expressions remain valid if K+ is varied as a function of
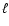 .
From Fig. 3 it is clear that in order to get the
least bias, one wants to choose
.
From Fig. 3 it is clear that in order to get the
least bias, one wants to choose  for small
for small 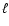 ,
and
,
and
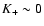 for large
for large 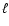 ;
for the intermediate region, setting
K+=1/2 should yield the smallest error on the power spectrum. We
have therefore constructed a function
;
for the intermediate region, setting
K+=1/2 should yield the smallest error on the power spectrum. We
have therefore constructed a function 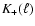 which has these
desired properties.
which has these
desired properties.
![\begin{figure}
\par\includegraphics[width=10.5cm,clip]{csnfig5.tps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg321.gif) |
Figure 5:
The large panel shows the estimates of the band power,
shown as horizontal bars whose length indicates the bins used. The
error bar on each bin shows the square root of the autovariance of
the band power, and the solid curve is the underlying power
spectrum,
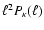 .
For this figure, we have assumed
that the correlation functions are measured for .
For this figure, we have assumed
that the correlation functions are measured for
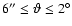 ,
from a survey of ,
from a survey of
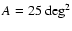 .
The inset figure shows
the correlation coefficient between the 13 different bins, where
the triangles indicate the center .
The inset figure shows
the correlation coefficient between the 13 different bins, where
the triangles indicate the center 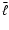 of each bin. One sees
that the bands are very little correlated, except for the three
bins with smallest
of each bin. One sees
that the bands are very little correlated, except for the three
bins with smallest 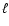 ;
in fact, the first three band power
estimates are fully correlated. This explains why the band-power
estimator yields reasonable results even for ;
in fact, the first three band power
estimates are fully correlated. This explains why the band-power
estimator yields reasonable results even for
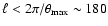 - this is just a coincidence.
- this is just a coincidence.
|
| Open with DEXTER |
In Fig. 5 we have plotted the band power for our reference
model parameters, in 13 bins of width
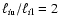 ,
between
,
between  and
and
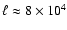 .
The band
power is shown as crosses, and vertical error bars show the range of
the bins. For comparison, the solid curve shows
.
The band
power is shown as crosses, and vertical error bars show the range of
the bins. For comparison, the solid curve shows
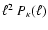 ;
as expected, with this new choice of
;
as expected, with this new choice of
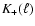 ,
the band power traces the underlying power spectrum over
a very wide range of wavenumbers. Only in the bins with the smallest
and largest value of
,
the band power traces the underlying power spectrum over
a very wide range of wavenumbers. Only in the bins with the smallest
and largest value of 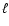 is there a significant bias; over the
range
is there a significant bias; over the
range
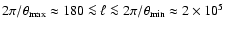 ,
the band power estimator
is practically unbiased. Next we calculated the error bars on the
band power, by taking the square root of the diagonal part of
(51). For this calculation, we have assumed to have a
total area of
,
the band power estimator
is practically unbiased. Next we calculated the error bars on the
band power, by taking the square root of the diagonal part of
(51). For this calculation, we have assumed to have a
total area of
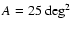 ,
for which the condition
,
for which the condition
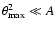 for the validity of the treatment of the ensemble average
in Sect. 5 is approximately satisfied. The square root of this
autovariance is plotted as errorbars on the band power in
Fig. 5; as can be seen from this figure, the
signal-to-noise ratio is larger than unity in all bins shown, and in
fact very large for intermediate values of
for the validity of the treatment of the ensemble average
in Sect. 5 is approximately satisfied. The square root of this
autovariance is plotted as errorbars on the band power in
Fig. 5; as can be seen from this figure, the
signal-to-noise ratio is larger than unity in all bins shown, and in
fact very large for intermediate values of 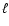 .
Hence, the power
spectrum
.
Hence, the power
spectrum
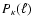 can be measured over a broad range of
can be measured over a broad range of 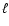 for the parameters chosen here.
for the parameters chosen here.
Of course, in order to interpret the error bars correctly, it is
important to see the degree of correlated noise between different
bands. The correlation matrix for the bins (defined in full analogy to
(44)) was calculated and its values are plotted in the
inset of Fig. 5. One sees that errors of the bins for
intermediate and high values of 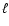 are essentially uncorrelated
(the correlation coefficient for neighboring bins is
are essentially uncorrelated
(the correlation coefficient for neighboring bins is  10%
for
10%
for
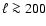 ); however, for
); however, for
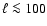 the bins
become strongly correlated. In fact, the agreement of the band powers
with the underlying power spectrum is forticious for
the bins
become strongly correlated. In fact, the agreement of the band powers
with the underlying power spectrum is forticious for
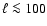 :
the three band powers at lowest
:
the three band powers at lowest 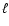 are nearly fully
correlated, so that these three points contain practically the same
information of the underlying power spectrum.
are nearly fully
correlated, so that these three points contain practically the same
information of the underlying power spectrum.
The method presented here for the determination of the power spectrum
has the virtue of its simplicity. Other methods for determining the
power spectrum from shear data have been investigated, e.g. by Kaiser
(1998), Seljak (1998) and Hu & White (2001). Our approach has the
property that it makes use only of the shear correlation functions,
not on the spatial distribution of the shear. Since the shear
correlation function contains all two-point statistical information of
the shear field, no information loss occurs. Comparing the results of
Fig. 5 with those of Hu & White (2001) it seems that both
methods yield very similar error bars of the power spectrum, and that
in the respective 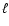 -range of applicability, the decorrelation
between neighboring bins is equally quick. Since our method does not
require the "pixelization'' of shear data, it can estimate the power
spectrum to larger values of
-range of applicability, the decorrelation
between neighboring bins is equally quick. Since our method does not
require the "pixelization'' of shear data, it can estimate the power
spectrum to larger values of 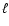 .
.
One of the central goals of cosmic shear research is the determination
of cosmological parameters. Since the power spectrum 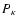 ,
and
thus the shear correlation functions, depend on the cosmological
model, precise measurements of cosmic shear can be used to tie down
the range of allowable model parameters (e.g., Jain & Seljak 1997;
Bernardeau et al. 1997). The largest cosmic shear survey today
already yielded significant model constraints (van Waerbeke et al. 2001, 2002; Hoekstra et al. 2002). We shall briefly discuss the
expected confidence regions in parameter space, using the previously
calculated covariance matrix of the shear correlation functions.
For that, we consider a figure-of-merit function
,
and
thus the shear correlation functions, depend on the cosmological
model, precise measurements of cosmic shear can be used to tie down
the range of allowable model parameters (e.g., Jain & Seljak 1997;
Bernardeau et al. 1997). The largest cosmic shear survey today
already yielded significant model constraints (van Waerbeke et al. 2001, 2002; Hoekstra et al. 2002). We shall briefly discuss the
expected confidence regions in parameter space, using the previously
calculated covariance matrix of the shear correlation functions.
For that, we consider a figure-of-merit function
 |
(52) |
where the index  indicates the correlation function of the
input model, p is a set of model parameters, and the summation indices
label the angular bins of the correlation function. We shall consider
three different kinds of the function (52): in the first,
named
indicates the correlation function of the
input model, p is a set of model parameters, and the summation indices
label the angular bins of the correlation function. We shall consider
three different kinds of the function (52): in the first,
named 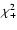 hereafter, the correlation functions in
(52) are the
hereafter, the correlation functions in
(52) are the 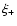 correlations, and the covariance
matrix corresponds to (23). The second kind is denoted by
correlations, and the covariance
matrix corresponds to (23). The second kind is denoted by
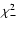 and uses the
and uses the  correlation function. The third kind,
correlation function. The third kind,
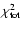 ,
is obtained by constructing a vector
,
is obtained by constructing a vector
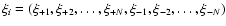 ,
when there are N angular
bins in which
,
when there are N angular
bins in which 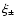 has been measured. Correspondingly, the
covariance matrix in (52) is the
has been measured. Correspondingly, the
covariance matrix in (52) is the
 -block matrix with C++ and C- in the upper left
and lower right quadrant, respectively, and C+- in the other two.
-block matrix with C++ and C- in the upper left
and lower right quadrant, respectively, and C+- in the other two.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{3767f6.eps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg337.gif) |
Figure 6:
1-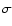 ,
2- ,
2-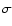 and 3-
and 3-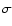 confidence
contours in the
confidence
contours in the
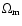 - -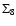 -plane, where -plane, where 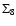 is a scaled version of the power spectrum normalization parameter
is a scaled version of the power spectrum normalization parameter 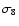 ,
as indicated. Dotted, dashed and solid contours
correspond to ,
as indicated. Dotted, dashed and solid contours
correspond to 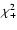 , ,
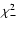 and
and
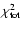 .
In the
left panel, the shape parameter of the power spectrum .
In the
left panel, the shape parameter of the power spectrum
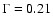 ,
whereas in the right panel, ,
whereas in the right panel,
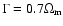 .
The reference model is the one used before, i.e. .
The reference model is the one used before, i.e.
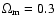 , ,
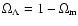 , ,
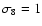 .
The
contours are obtained by assuming a survey area of .
The
contours are obtained by assuming a survey area of
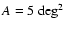 ,
and that the correlation functions were measured in the
range ,
and that the correlation functions were measured in the
range
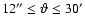 . .
|
| Open with DEXTER |
We first have calculated  for a two-parameter set of
cosmological models, by varying
for a two-parameter set of
cosmological models, by varying
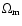 and
and 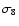 ;
these
two parameters were considered before in van Waerbeke et al. (2001). We kept the other cosmological parameters fixed, except that
flat Universes are considered, i.e.
;
these
two parameters were considered before in van Waerbeke et al. (2001). We kept the other cosmological parameters fixed, except that
flat Universes are considered, i.e.
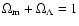 .
From the confidence contours plotted in van
Waerbeke et al., it is anticipated that the
.
From the confidence contours plotted in van
Waerbeke et al., it is anticipated that the 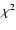 -function,
considered as a function of
-function,
considered as a function of
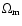 and
and 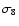 ,
will have
a long and curved valley close to its minimum. This was verified
here. It is therefore useful to consider the combination
,
will have
a long and curved valley close to its minimum. This was verified
here. It is therefore useful to consider the combination
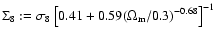 as parameter
when plotting contours of
as parameter
when plotting contours of 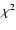 (the numerical values occurring in
this definition have been obtained by a fit through the valley line in
the
(the numerical values occurring in
this definition have been obtained by a fit through the valley line in
the
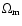 -
-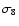 plane).
plane).
In Fig. 6 we have plotted contours of constant 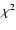 in
the
in
the
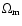 -
-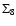 plane, corresponding to 1-
plane, corresponding to 1-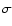 ,
2-
,
2-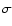 and 3-
and 3-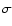 confidence regions. In the left panel, we
kept the shape parameter of the power spectrum fixed,
confidence regions. In the left panel, we
kept the shape parameter of the power spectrum fixed,
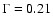 ,
whereas in the right panel we used
,
whereas in the right panel we used
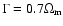 ,
adequate for a (dimensionless) Hubble constant of h=0.7. Shown are
the confidence regions for all three functions
,
adequate for a (dimensionless) Hubble constant of h=0.7. Shown are
the confidence regions for all three functions 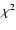 ,
as
indicated. The first point to note is that, for a given value of
,
as
indicated. The first point to note is that, for a given value of
 ,
,
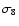 is very well
constrained, to within a few percent. This implies that the
normalization of the power spectrum is very well determined from
cosmic shear observations. Secondly, the 1-
is very well
constrained, to within a few percent. This implies that the
normalization of the power spectrum is very well determined from
cosmic shear observations. Secondly, the 1-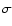 uncertainty on
uncertainty on
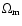 is about 0.1 for an assumed survey size of
is about 0.1 for an assumed survey size of
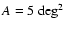 ;
indeed, the left panel of Fig. 6 can be compared
directly with similar figures in van Waerbeke et al., and the
constraints on
;
indeed, the left panel of Fig. 6 can be compared
directly with similar figures in van Waerbeke et al., and the
constraints on
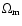 are quite similar. Third, if the shape
parameter changes with
are quite similar. Third, if the shape
parameter changes with
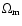 ,
the confidence regions are
narrower than when setting
,
the confidence regions are
narrower than when setting
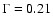 as constant, which implies
that the shear correlation functions are sensitive measures for
as constant, which implies
that the shear correlation functions are sensitive measures for
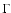 .
.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{csnfig7.ps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg344.gif) |
Figure 7:
1-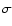 ,
2- ,
2-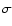 and 3-
and 3-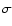 confidence contours for the maximum
likelihood analysis on the four parameters
confidence contours for the maximum
likelihood analysis on the four parameters
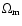 , ,
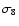 , ,
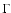 and the source redshift parameter
and the source redshift parameter 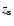 (see text). The six possible pairs of parameters are displayed. On
each figure, the two hidden parameters are marginalized such that
(see text). The six possible pairs of parameters are displayed. On
each figure, the two hidden parameters are marginalized such that
![$\Omega _{\rm m}\in [0.2,0.4]$](/articles/aa/full/2002/46/aah3767/img56.gif) , ,
![$\sigma _8\in [0.8,1.1]$](/articles/aa/full/2002/46/aah3767/img57.gif) , ,
![$\Gamma \in [0.1,0.3]$](/articles/aa/full/2002/46/aah3767/img58.gif) and
and
![$z_{\rm s}\in [0.4,0.5]$](/articles/aa/full/2002/46/aah3767/img59.gif) ,
and the cosmological
constant is fixed to ,
and the cosmological
constant is fixed to
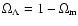 .
The reference
model is .
The reference
model is
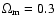 , ,
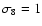 , ,
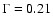 and
and
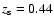 .
The survey area is .
The survey area is
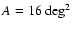 ,
the
galaxy ellipticity rms is 0.3, and the correlation functions
are measured in the range ,
the
galaxy ellipticity rms is 0.3, and the correlation functions
are measured in the range
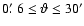 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=10cm,clip]{csnfig8.ps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg345.gif) |
Figure 8:
Same as
Fig. 7 with strong priors: in each figure, the
two hidden parameters as assumed to be known perfectly. These plots
show the degeneracy directions among all the possible pairs of
parameters obtained from
 , ,
 , ,
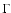 and
and
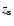 .
Note that the wiggles at the edge of the contours are not
real features of the probability constraints. Their are inherent to
the sampling limitation of the 4-dimensional cube of models given
the memory limit of our machines. Also note that the upper left
panel is the analogue of Fig. 6, but without the scaling
employed there. .
Note that the wiggles at the edge of the contours are not
real features of the probability constraints. Their are inherent to
the sampling limitation of the 4-dimensional cube of models given
the memory limit of our machines. Also note that the upper left
panel is the analogue of Fig. 6, but without the scaling
employed there. |
| Open with DEXTER |
In the prospect of measuring the cosmological parameters, we must also
allow for our lack of knowledge of some parameters which might have a
significant effect on our observable, but which are poorly
constrained. In particular, it is important to explore the possible
directions of degeneracies and to identify which combination of
parameters offers the most promising measurements. As shown in Jain &
Seljak (1997), the shear second-order statistics depend primarily on four
parameters:
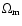 ,
,
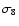 ,
,
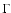 and
and 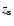 ,
the source redshift parameter. We now model the source redshift
distribution with
,
the source redshift parameter. We now model the source redshift
distribution with
![\begin{displaymath}p(z)={\beta\over z_{\rm s} \ \Gamma\left({1+\alpha\over \beta...
...alpha \exp\left[-\left({z\over z_{\rm
s}}\right)^\beta\right],
\end{displaymath}](/articles/aa/full/2002/46/aah3767/img346.gif) |
(53) |
where we choose 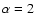 and
and 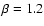 ,
and take
,
and take 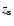 as
the free parameter; note that the mean redshift of the sources is
as
the free parameter; note that the mean redshift of the sources is
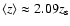 .
This choice is motivated from observational
considerations (see van Waerbeke et al. 2002). We therefore
constructed the 4-dimensional figure-of-merit function
(52), where now
.
This choice is motivated from observational
considerations (see van Waerbeke et al. 2002). We therefore
constructed the 4-dimensional figure-of-merit function
(52), where now
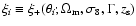 .
The fiducial model is chosen to be
.
The fiducial model is chosen to be
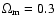 ,
,
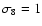 ,
,
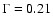 and
and
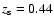 .
It is assumed that the shear correlation function is
measured in the range
.
It is assumed that the shear correlation function is
measured in the range
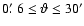 ,
comparable with the
most recent cosmic shear measurements. We also fix the survey area to
,
comparable with the
most recent cosmic shear measurements. We also fix the survey area to
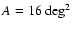 and the galaxy intrinsic ellipticity rms to
0.3. Figure 7 shows the confidence regions,
assuming weak priors on pairs of hidden parameters. From the four
parameters to be determined, we can construct 6 pairs of parameters,
and for each pair, the other two parameters are marginalized, in such
a way that
and the galaxy intrinsic ellipticity rms to
0.3. Figure 7 shows the confidence regions,
assuming weak priors on pairs of hidden parameters. From the four
parameters to be determined, we can construct 6 pairs of parameters,
and for each pair, the other two parameters are marginalized, in such
a way that
![$\Omega _{\rm m}\in [0.2,0.4]$](/articles/aa/full/2002/46/aah3767/img56.gif) ,
,
![$\sigma _8\in [0.8,1.1]$](/articles/aa/full/2002/46/aah3767/img57.gif) ,
,
![$\Gamma \in [0.1,0.3]$](/articles/aa/full/2002/46/aah3767/img58.gif) and
and
![$z_{\rm s}\in [0.4,0.5]$](/articles/aa/full/2002/46/aah3767/img59.gif) .
The
marginalization intervals are chosen to be consistent with realistic
constraints coming from other experiments, especially from the Cosmic
Microwave Background (e.g., Sievers et al. 2002), the 2dF (Lahav et al. 2002) and the SLOAN (Szalay et al. 2001) results, and photometric
redshifts. Note that we always fix the cosmological constant to
.
The
marginalization intervals are chosen to be consistent with realistic
constraints coming from other experiments, especially from the Cosmic
Microwave Background (e.g., Sievers et al. 2002), the 2dF (Lahav et al. 2002) and the SLOAN (Szalay et al. 2001) results, and photometric
redshifts. Note that we always fix the cosmological constant to
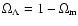 ,
that is we assume the (correct)
flat geometry. The strongest constraints are found for the
,
that is we assume the (correct)
flat geometry. The strongest constraints are found for the
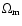 -
-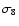 ,
,
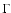 -
-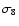 and
and
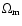 -
-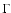 pairs, suggesting that once the redshift distribution of
the sources is known we can obtain stringent constraints on the
cosmological parameters from cosmic shear. The degeneracy directions
can be better studied with a strong prior likelihood analysis as shown
in Fig. 8. On this plot, we assume that the two
hidden parameters of each constrained pair are known and fixed at
their true value. Again we see that the best constraints come from
pairs of parameters which exclude the redshift information. It is
remarkable that the degeneracy among these parameters can be broken
quite efficiently, given that the cosmic shear signal has so few
"spectral features'', compared to the cosmic microwave background for
instance. In fact, the degeneracy can be broken when using linear and
non-linear scales simultaneously (as discussed in Jain & Seljak
1997). One would obtain an even better degeneracy breaking by going
further into the linear regime (up to 1 or 2 degrees). Also, it is
interesting to note that the parameters which are least affected
by the marginalization (compare Figs. 7 and 8) is the
pairs, suggesting that once the redshift distribution of
the sources is known we can obtain stringent constraints on the
cosmological parameters from cosmic shear. The degeneracy directions
can be better studied with a strong prior likelihood analysis as shown
in Fig. 8. On this plot, we assume that the two
hidden parameters of each constrained pair are known and fixed at
their true value. Again we see that the best constraints come from
pairs of parameters which exclude the redshift information. It is
remarkable that the degeneracy among these parameters can be broken
quite efficiently, given that the cosmic shear signal has so few
"spectral features'', compared to the cosmic microwave background for
instance. In fact, the degeneracy can be broken when using linear and
non-linear scales simultaneously (as discussed in Jain & Seljak
1997). One would obtain an even better degeneracy breaking by going
further into the linear regime (up to 1 or 2 degrees). Also, it is
interesting to note that the parameters which are least affected
by the marginalization (compare Figs. 7 and 8) is the
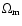 -
-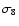 pair, which
is most directly comparable to cluster normalization constraints
(see a discussion on the comparison between cluster normalization and
cosmic shear constraints in van Waerbeke et al. 2002).
pair, which
is most directly comparable to cluster normalization constraints
(see a discussion on the comparison between cluster normalization and
cosmic shear constraints in van Waerbeke et al. 2002).
In this paper we have obtained general expressions for the covariance
of an estimator for the shear correlation function as it is determined
from cosmic shear data. Using the approximation that the four-point
function of the shear separates in products of two-point functions, the
covariance can be expressed directly in terms of the correlation
functions, as given in (23)-(25) and can, for a
given data set, be calculated directly. The covariance of the
correlation functions depends on the number of pairs that enter their
estimate, which in turn depends on the solid angle covered by the
survey and the survey geometry (see also Kaiser 1998); in addition, it
depends on the intrinsic galaxy ellipticities and the number density
of galaxies.
Next, considering a survey geometry of a single compact region of
solid angle A, we have calculated the ensemble average of the
covariances, using approximations which a valid for separations
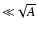 .
The ensemble average of the covariances can then be
reduced to integrals which are readily evaluated numerically. The
estimate for the correlation function
.
The ensemble average of the covariances can then be
reduced to integrals which are readily evaluated numerically. The
estimate for the correlation function
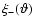 decorrelates
quickly, i.e. estimates of
decorrelates
quickly, i.e. estimates of  for two angular scales which differ
by more than a factor
for two angular scales which differ
by more than a factor 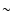 2 are essentially decorrelated. On the
other hand, the estimates of
2 are essentially decorrelated. On the
other hand, the estimates of 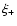 are correlated over much larger
angular scales. The cross-correlation between
are correlated over much larger
angular scales. The cross-correlation between
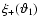 and
and
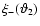 is significant for
is significant for
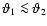 ,
which is due
to the properties of the different filters with which these
correlation functions are related to the power spectrum
,
which is due
to the properties of the different filters with which these
correlation functions are related to the power spectrum
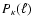 .
.
Using these ensemble-averaged covariances for the correlation
functions, we have obtained the covariances for other second-order
measures of the cosmic shear, primarily the aperture mass dispersion
and the power spectrum. Of particular interest is the reconstruction
of the power spectrum
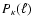 from the correlation functions;
we have constructed a simple estimator for
from the correlation functions;
we have constructed a simple estimator for  and the band
powers of it in terms of the
and the band
powers of it in terms of the 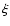 's and found that the band power can
be obtained with surprisingly large accuracy from even a
moderately-sized cosmic shear survey. Finally, we have investigated
the confidence regions for the most relevant cosmological parameters
(
's and found that the band power can
be obtained with surprisingly large accuracy from even a
moderately-sized cosmic shear survey. Finally, we have investigated
the confidence regions for the most relevant cosmological parameters
(
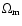 ,
,
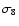 ,
,
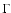 and
and 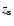 )
with a maximum
likelihood approach. We studied our ability to constrain
simultaneously these parameters from a measurement of the shear
correlation function, as well as the effect of some level of lack of
knowledge using the marginalization technique.
)
with a maximum
likelihood approach. We studied our ability to constrain
simultaneously these parameters from a measurement of the shear
correlation function, as well as the effect of some level of lack of
knowledge using the marginalization technique.
In a future paper, we shall investigate strategies for conducting
cosmic shear surveys by optimizing the survey geometry.
Acknowledgements
We thank the referee Dipak Munshi for his constructive comments on the
manuscript. This work was supported by the TMR Network
"Gravitational Lensing: New Constraints on Cosmology and the
Distribution of Dark Matter'' of the EC under contract
No. ERBFMRX-CT97-0172, by the German Ministry for Science and
Education (BMBF) through the DLR under the project 50 OR 0106, and by
the Deutsche Forschungsgemeinschaft under the project SCHN 342/3-1.
-
Bacon, D. J., Refregier, A. R., & Ellis, R. S. 2000, MNRAS, 318, 625
In the text
NASA ADS
-
Bacon, D. J., Massey, R., Refregier, A. R., & Ellis, R. S. 2002,
MNRAS, submitted [astro-ph/0203134]
In the text
-
Bardeen, J. M., Bond, J. R., Kaiser, N., & Szalay, A. S. 1986, ApJ,
304, 15
In the text
NASA ADS
-
Bartelmann, M., & Schneider, P. 1999, A&A, 345, 17
In the text
NASA ADS
-
Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291
In the text
NASA ADS
-
Benitez, N., Sanz, J. L., & Martinez-Gonzalez, E. 2001, MNRAS, 320, 241
NASA ADS
-
Bernardeau, F., van Waerbeke, L., & Mellier, Y. 1997, A&A, 322, 1
In the text
NASA ADS
-
Bernardeau, F., van Waerbeke, L., & Mellier, Y. 2002a [astro-ph/0201029]
In the text
-
Bernardeau, F., Mellier, Y., & van Waerbeke, L. 2002b, A&A, 389, L28
In the text
NASA ADS
-
Blandford, R. D., Saust, A. B., Brainerd, T. G., & Villumsen,
J. V. 1991, MNRAS, 251, 600
In the text
NASA ADS
-
Brown, M., Taylor, A., Hambly, N., & Dye, S. 2002, MNRAS, 333, 501
In the text
NASA ADS
-
Catelan, P., Kamionkowski, M., & Blandford, R. D. 2001, MNRAS, 320, L7
In the text
NASA ADS
-
Crittenden, R. G., Natarajan, P., Pen, U.-L., & Theuns, T. 2002,
ApJ, 568, 20 (C02)
In the text
NASA ADS
-
Croft, R. A. C., & Metzler, C. A. 2001, ApJ, 545, 561
NASA ADS
-
Dolag, K., & Bartelmann, M. 1997, MNRAS, 291, 446
NASA ADS
-
Erben, T., Van Waerbeke, L., Bertin, E., Mellier, Y., & Schneider, P.
2001, A&A, 366, 717
In the text
NASA ADS
-
Hämmerle, H., Miralles, J.-M., Schneider, P., et al. 2002, A&A, 385, 743
NASA ADS
-
Hamilton, A. J. S., Matthews, A., Kumar, P., & Lu, E. 1991, ApJ, 374, L1
In the text
NASA ADS
-
Heavens, A. F., Refregier, A., & Heymans, C. E. C. 2000, MNRAS, 319,
649
NASA ADS
-
Hoekstra, H., Franx, M., & Kuijken, K. 2000, ApJ, 532, 88
In the text
NASA ADS
-
Hoekstra, H., Yee, H., & Gladders, M., ApJ, in press [astro-ph/0204295]
In the text
-
Hu, W., & White, M. 2001, ApJ, 554, 67
In the text
NASA ADS
-
Jain, B., & Seljak, U. 1997, ApJ, 484, 560
In the text
NASA ADS
-
Jain, B., Seljak, U., & White, S. D. M. 2000, ApJ, 530, 547
In the text
NASA ADS
-
Kaiser, N. 1992, ApJ, 388, 272
In the text
NASA ADS
-
Kaiser, N. 1998, ApJ, 498, 26
In the text
NASA ADS
-
Kaiser, N., Wilson, G., & Luppino, G. 2000 [astro-ph/0003338]
In the text
-
Lahav, O., Bridle, S. L., Percival, W. J., et al. 2002, MNRAS, 333, 961
In the text
NASA ADS
-
Mackey, J., White, M., & Kamionkowski, M. 2002, MNRAS, 332, 788
In the text
NASA ADS
-
Maoli, R., van Waerbee, L., Mellier, Y., et al. 2001, A&A, 368, 766
In the text
NASA ADS
-
Mellier, Y. 1999, ARA&A, 37, 127
In the text
NASA ADS
-
Menard, B., & Bartelmann, M. 2002, A&A, 386, 784
NASA ADS
-
Miralda-Escudé, J. 1991, ApJ, 380, 1
In the text
NASA ADS
-
Munshi, D., & Coles, P. 2000 [astro-ph/0003481]
In the text
-
Munshi, D., & Jain, B. 2001, MNRAS, 322, 107
NASA ADS
-
Peacock, J. A., & Dodds, S. J. 1996, MNRAS, 280, L19
In the text
NASA ADS
-
Pen, U.-L., Jounghun, L., & Seljak, U. 2000, ApJ, 543, 107
In the text
-
Pen, U.-L., van Waerbeke, L., & Mellier, Y. 2002, ApJ, 567, 31
In the text
NASA ADS
-
Refregier, A., Rhodes, J., & Groth, E. J. 2002, ApJ, 572, 131
In the text
-
Rhodes, J., Refregier, A., & Groth, E. J. 2001, ApJ, 552, L85
In the text
NASA ADS
-
Schneider, P. 1996, MNRAS, 283, 837
In the text
NASA ADS
-
Schneider, P., van Waerbeke, L., Jain, B., & Kruse, G. 1998, MNRAS, 296,
873 (SvWJK)
In the text
NASA ADS
-
Schneider, P., van Waerbeke, L., & Mellier, Y. 2002, A&A, 389, 729
(SvWM)
In the text
NASA ADS
-
Seljak, U. 1998, ApJ, 506, 64
In the text
NASA ADS
-
Sievers, J. L., Bond, J. R., Cartwright, J. K., et al. 2002, ApJ, submitted [astro-ph/0205387]
In the text
-
Smith, R. E., Peacock, J. A., Jenkins, A., et al. 2002 [astro-ph/0207664]
-
Szalay, A. S., Jain, B., Matsubara, T., et al. 2001, ApJ, submitted [astro-ph/0107419]
In the text
-
van Waerbeke, L. 2000, MNRAS, 313, 524
In the text
NASA ADS
-
van Waerbeke, L., Bernardeau, F., & Mellier, Y. 1999, A&A, 243, 15
In the text
-
van Waerbeke, L., Mellier, Y., Erben, T., et al. 2000, A&A, 358, 30
In the text
NASA ADS
-
van Waerbeke, L., Mellier, Y., Radovich, M., et al. 2001, A&A, 374, 757
In the text
NASA ADS
-
van Waerbeke, L., Mellier, Y., Pello, R., et al. 2002 [astro-ph/0202503]
In the text
-
White, M., & Hu, W. 2000, ApJ, 537, 1
In the text
NASA ADS
-
Wittman, D. M., Tyson, J. A., Kirkman, D., Dell'Antonio, I., &
Bernstein, G. 2000, Nature, 405, 143
In the text
NASA ADS
Copyright ESO 2002










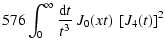
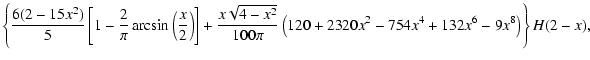










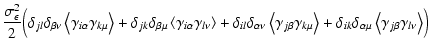
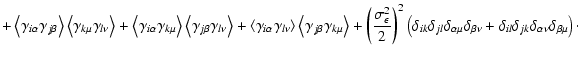

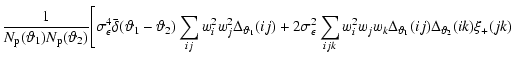
![$\displaystyle +\sum_{ijkl}w_iw_jw_kw_l
\Delta_{{\vartheta}_1}(ij) \Delta_{{\var...
...varphi_{il}-\varphi_{jk} \right) \right\rbrack
\xi_-(il)\xi_-(jk)\Bigr)\Biggr],$](/articles/aa/full/2002/46/aah3767/img154.gif)
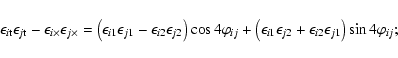
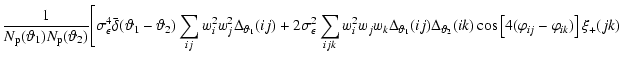
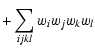
![$\displaystyle \Delta_{{\vartheta}_1}(ij) \Delta_{{\vartheta}_2}(kl)
\Bigl(\cos\...
...hi_{ij}-\varphi_{kl} \right) \right\rbrack
\xi_+(il)\xi_+(jk)\Bigr)\Biggr]\cdot$](/articles/aa/full/2002/46/aah3767/img160.gif)
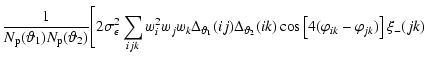
![$\displaystyle +2\sum_{ijkl}w_iw_jw_kw_l
\Delta_{{\vartheta}_1}(ij) \Delta_{{\va...
...brack 4(\varphi_{il}-\varphi_{kl}) \right\rbrack
\xi_-(il)\xi_+(jk)\Biggr]\cdot$](/articles/aa/full/2002/46/aah3767/img163.gif)

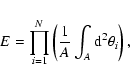

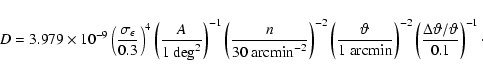

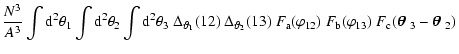
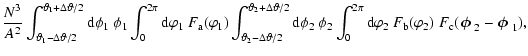

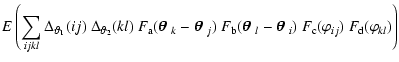
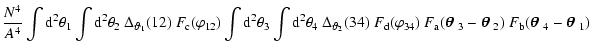
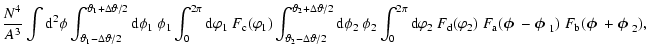

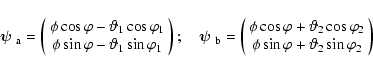





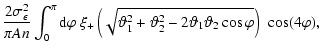
![$\displaystyle {1\over (2\pi) A}\int_0^\infty{\rm d}\phi~\phi
\int_0^{2\pi}{\rm ...
...}_{\rm b}\vert)\;
\cos[4(\varphi_1+\varphi_2-\varphi_{\rm a}-\varphi_{\rm b})],$](/articles/aa/full/2002/46/aah3767/img227.gif)
![$\displaystyle {1\over (2\pi) A}\int_0^\infty{\rm d}\phi~\phi
\int_0^{2\pi}{\rm ...
...1=\bolditalics \hbox{$\bf\psi$ }}_{\rm b}\vert)\;
\cos[4(\varphi_1-\varphi_2)].$](/articles/aa/full/2002/46/aah3767/img228.gif)


![$\displaystyle {1\over \pi A}\int_0^\infty{\rm d}\phi~\phi
\int_0^{2\pi}{\rm d}\...
...ditalics \hbox{$\bf\psi$ }}_{\rm b}\vert)\;
\cos[4(\varphi_2-\varphi_{\rm b})].$](/articles/aa/full/2002/46/aah3767/img231.gif)
![\begin{figure}
\par\includegraphics[width=11cm,clip]{3767f1.eps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg232.gif)
![\begin{figure}
\par\includegraphics[width=10cm,clip]{3767f2.eps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg245.gif)


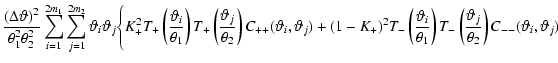
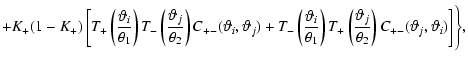
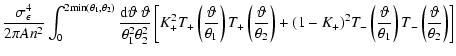
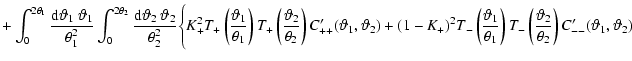
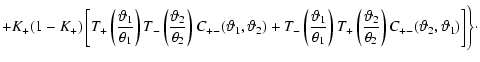
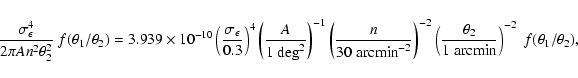


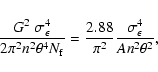
![\begin{figure}
\par\includegraphics[width=10cm,clip]{3767f3.eps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg278.gif)




![\begin{figure}
\par\includegraphics[width=9cm,clip]{3767f4.eps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg295.gif)

![\begin{displaymath}\P_i:={1\over \Delta_i}
\int_{\ell_{i{\rm l}}}^{\ell_{i{\rm u...
...ell_{i{\rm u}}\theta)-g_-(\ell_{i{\rm
l}}\theta)\Bigr]\bigg\},
\end{displaymath}](/articles/aa/full/2002/46/aah3767/img306.gif)

![$\displaystyle {2\pi\sigma_{\epsilon}^4\over \Delta_i~\Delta_j~A~n^2}
\int_{\the...
...K_+^2~G_{i+}(\theta)G_{j+}(\theta)
+(1-K_+)^2G_{i-}(\theta)G_{j-}(\theta)\Bigr]$](/articles/aa/full/2002/46/aah3767/img312.gif)
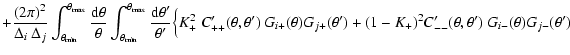
![\begin{figure}
\par\includegraphics[width=10.5cm,clip]{csnfig5.tps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg321.gif)

![\begin{figure}
\par\includegraphics[width=10cm,clip]{3767f6.eps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg337.gif)
![\begin{figure}
\par\includegraphics[width=10cm,clip]{csnfig7.ps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg344.gif)
![\begin{figure}
\par\includegraphics[width=10cm,clip]{csnfig8.ps} \end{figure}](/articles/aa/full/2002/46/aah3767/Timg345.gif)
![\begin{displaymath}p(z)={\beta\over z_{\rm s} \ \Gamma\left({1+\alpha\over \beta...
...alpha \exp\left[-\left({z\over z_{\rm
s}}\right)^\beta\right],
\end{displaymath}](/articles/aa/full/2002/46/aah3767/img346.gif)