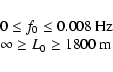A&A 396, 353-360 (2002)
DOI: 10.1051/0004-6361:20021422
Non-Kolmogorov features of differential image motion restored
from the Multichannel Astrometric Photometer data
P. F. Lazorenko
Main Astronomical Observatory,
National Academy of Sciencies of Ukraine,
Zabolotnogo 27, 03680 Kyiv-127, Ukraine
Received 14 March 2002 / Accepted 10 September 2002
Abstract
In this paper we present a new restoration of atmospheric turbulent
parameters
using published data on image motion observations with the
Multichannel Astrometric Photometer. These data have been
previously analyzed by Han (1989) whose
estimate of the power of the phase structure function
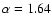 was close to the 5/3 value expected for the Kolmogorov
atmospheric turbulence.
Investigating the temporal image motion spectrum, we show, however,
that the
experimental data do not follow predictions of the Kolmogorov
model. The best fitting of the observed spectrum is achieved with
was close to the 5/3 value expected for the Kolmogorov
atmospheric turbulence.
Investigating the temporal image motion spectrum, we show, however,
that the
experimental data do not follow predictions of the Kolmogorov
model. The best fitting of the observed spectrum is achieved with
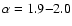 ,
which is
typical of non-classic phase distortions.
The outer scale of turbulence
was found to be 1800 m or longer. Expressions for
the non-Kolmogorov temporal spectrum of differential image motion
allowing for a finite outer scale length are given.
,
which is
typical of non-classic phase distortions.
The outer scale of turbulence
was found to be 1800 m or longer. Expressions for
the non-Kolmogorov temporal spectrum of differential image motion
allowing for a finite outer scale length are given.
Key words: atmospheric effects - turbulence -
methods: data analysis -
astrometry
Atmospheric turbulence is a factor that strongly deteriorates
image quality observed through the atmosphere, and
causes image motion, which affects the position of stars.
Atmospheric effects have been intensely studied for some decades.
The basic assumption used in most
theoretical considerations (e.g. Fried 1965; Tatarsky 1961)
was that atmospheric turbulence
follows the Kolmogorov theory of a fully developed 3D
turbulence. Predictions made on this basis, in particular for
image motion, usually
give correct results and fit experimental data well (Lindegren
1980; Martin 1987; Sarazin & Roddier 1990).
Some studies, however, testify that turbulence sometimes may
display
significant deviations from its classical behavior. Thus,
meteorological studies of the temperature and wind spatial
spectra measured in the turbulent atmospheric layers often
indicate strong deviations from the classic behaviour
(Vinnichenko et al. 1976; Hogstrom et al. 1998).
A short bibliography
of meteorological, theoretical and astronomical data testifying
that the non-Kolmogorov turbulence actually occurs was given
by Lazorenko (2002, hereinafter Paper I). Concerning distortions
of the turbulent light phase, these data suggest
that both the power
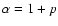 of a phase structure function
and a slope of -3-p in Eq. (3) for the spatial power
spectral
density (PSD) of phase fluctuations should be considered as the
quantities that vary from a sample to sample. The value of
parameter p which is equal to 2/3 in case of the
Kolmogorov turbulence depends on physical conditions in the
given atmospheric layer,
and may vary
in a wide range from -1/3 to 1. Moreover, it is a function of
spatial scale. Thus, while on scales of 1-300 m, p varies
normally from 1/3 to 2/3, with a mean value of about 0.5, at
longer 200-1000 m scales the PSD often shows saturation
described by von Karman statistics. Here p decreases, sometimes
to negative values.
of a phase structure function
and a slope of -3-p in Eq. (3) for the spatial power
spectral
density (PSD) of phase fluctuations should be considered as the
quantities that vary from a sample to sample. The value of
parameter p which is equal to 2/3 in case of the
Kolmogorov turbulence depends on physical conditions in the
given atmospheric layer,
and may vary
in a wide range from -1/3 to 1. Moreover, it is a function of
spatial scale. Thus, while on scales of 1-300 m, p varies
normally from 1/3 to 2/3, with a mean value of about 0.5, at
longer 200-1000 m scales the PSD often shows saturation
described by von Karman statistics. Here p decreases, sometimes
to negative values.
In analytical expressions derived for
the variance 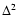 of differential image motion,
Lindegren (1980) used a variable term
of differential image motion,
Lindegren (1980) used a variable term
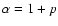 representing the power of a phase structure function. His numerical
estimates originally were given in dual form: with
representing the power of a phase structure function. His numerical
estimates originally were given in dual form: with
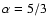 for the Kolmogorov type of
turbulence and
for the Kolmogorov type of
turbulence and
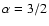 consistent with the model of
the absolute image motion spectrum suggested by Hog (1967).
Lindegren did not specify which of the above estimates is to be used.
In many subsequent studies, however, the variance of differential
image motion was calculated only with
consistent with the model of
the absolute image motion spectrum suggested by Hog (1967).
Lindegren did not specify which of the above estimates is to be used.
In many subsequent studies, however, the variance of differential
image motion was calculated only with
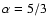 ,
or p=2/3.
Besides being theoretically substantiated, the correctness
of the p=2/3 value experimentally was confirmed later by
Han (1989),
whose analysis of observational data supported
Kolmogorov distortions of a turbulent wave-front.
In his study, Han derived differential image motion characteristics
from the Multichannel Astrometric
Photometer (MAP) observational data, and obtained an estimate p=0.64, very close to the Kolmogorov 2/3 value. Hence this
result was often referred to as a direct experimental proof of the
applicability of a classic theory of turbulence to astronomical
measurements.
,
or p=2/3.
Besides being theoretically substantiated, the correctness
of the p=2/3 value experimentally was confirmed later by
Han (1989),
whose analysis of observational data supported
Kolmogorov distortions of a turbulent wave-front.
In his study, Han derived differential image motion characteristics
from the Multichannel Astrometric
Photometer (MAP) observational data, and obtained an estimate p=0.64, very close to the Kolmogorov 2/3 value. Hence this
result was often referred to as a direct experimental proof of the
applicability of a classic theory of turbulence to astronomical
measurements.
In this paper we present a new interpretation of the MAP
image motion statistics that is described in Sect. 2.
Our analysis is based on rigorous expressions for the differential
image motion spectrum derived in Sect. 3 and is
valid for a variable
value of p. In Sect. 4 we use
these expressions for a simulation of the MAP data, and
restore parameters of turbulence.
Here, we show that the experimental
data do not follow predictions of the conventional theory, and
establish the
best estimate 0.9-1.0 for p. In Sects. 5 and 6 we verify
the reliability of the model by applying it to simulation of the
observed
dependences of the variance 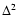 on the star separation
and exposure. In Sect. 7 we consider effects which should be
present in the temporal power spectrum of differential image motion
in the case of a finite outer scale of turbulence, and establish its
feasible values.
on the star separation
and exposure. In Sect. 7 we consider effects which should be
present in the temporal power spectrum of differential image motion
in the case of a finite outer scale of turbulence, and establish its
feasible values.
In this investigation, we refer to observational data given
by Han (1989) and presented largely in the form of graphs.
Below we give
some necessary information important for an understanding of our
analysis.
Observations were carried out with the Multichannel
Astrometric Photometer (MAP). The
telescope (Gatewood 1987) is a refractor (D=0.78 m) used for
determination of parallaxes and proper motions. The
principal metric element of the MAP is a Ronchi ruling
consisted of a set of transparent lines and opaque
spaces of equal width. The ruling, moving across a
focal plane, produces modulation of light from stars.
The scanning of star images is performed in two directions.
First, the ruling moves along the x-axis (right
ascention),
then images are scanned perpendicularly, along the y-axis
(declinations). The total duration of each scan is
about 10 min.
On a temporal scale, one period of the ruling
corresponds to the
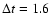 s interval, and some
effective time of image exposure T1 which depends on
the image size.
Thus, in the event of a dot element image,
s interval, and some
effective time of image exposure T1 which depends on
the image size.
Thus, in the event of a dot element image,
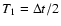 ,
increasing to
,
increasing to
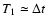 for a blurred image.
With image
sizes normally equal to a half of the ruling period, T1
is in the range between these two extremes.
In further calculations we assumed that approximately
for a blurred image.
With image
sizes normally equal to a half of the ruling period, T1
is in the range between these two extremes.
In further calculations we assumed that approximately
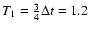 s.
The discreteness of measured data allows averaging of star
positions over some m sequential periods. In that way the
effective exposure is incresed to
s.
The discreteness of measured data allows averaging of star
positions over some m sequential periods. In that way the
effective exposure is incresed to
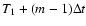 or
or
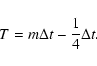 |
(1) |
In the original paper, the variance of differential image motion 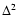 was found as the average
of
was found as the average
of
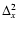 and
and
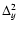 variances representing image
motion along the x and y axes.
variances representing image
motion along the x and y axes.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2465f1.eps}\end{figure}](/articles/aa/full/2002/46/aa2465/Timg30.gif) |
Figure 1:
Dependence of the variance 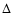 on star separation
on star separation
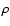 at T=10 s. Observed data (Han 1989) (squares)
with a linear approximation (1); curvilinear function (2)
calculated with p=0.94, and the asymptotic power law (3)
expected at long
at T=10 s. Observed data (Han 1989) (squares)
with a linear approximation (1); curvilinear function (2)
calculated with p=0.94, and the asymptotic power law (3)
expected at long
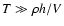 ;
lower (4) and upper (5) boundaries
for measured points at positional angles of star
pairs ;
lower (4) and upper (5) boundaries
for measured points at positional angles of star
pairs
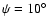 and
and
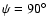 correspondingly.
correspondingly. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2465f2.eps}\end{figure}](/articles/aa/full/2002/46/aa2465/Timg32.gif) |
Figure 2:
Temporal image motion PSD versus frequency f at T=1.2 s
and 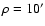 .
Observed spectrum G(f) (broken line); best simulated .
Observed spectrum G(f) (broken line); best simulated
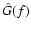 with p=0.94 (solid), p=2/3 (dashed) and
with allowance for an outer scale L0=1800 m, see Sect. 7
(open circles).
with p=0.94 (solid), p=2/3 (dashed) and
with allowance for an outer scale L0=1800 m, see Sect. 7
(open circles). |
| Open with DEXTER |
The observed dependence of measured 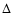 values
versus a separation
values
versus a separation 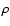 between the two stars is
reproduced in Fig. 1 for the integration time T=10 s.
In log-log coordinates the measured points are fitted
by a straight line 1 with a slope of
0.32 obtained by Han and is near the expected p/2=1/3
value for the
Kolmogorov turbulence (Lindegren 1980). One may notice, however,
that due to insufficient statistics and, especially, the narrow range
of
between the two stars is
reproduced in Fig. 1 for the integration time T=10 s.
In log-log coordinates the measured points are fitted
by a straight line 1 with a slope of
0.32 obtained by Han and is near the expected p/2=1/3
value for the
Kolmogorov turbulence (Lindegren 1980). One may notice, however,
that due to insufficient statistics and, especially, the narrow range
of 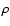 variation, the fitting is not quite reliable: the measured points
can be approximated equally well by lines with different slopes.
Moreover, a linear (in logarithmic plot) approximation
of the function
variation, the fitting is not quite reliable: the measured points
can be approximated equally well by lines with different slopes.
Moreover, a linear (in logarithmic plot) approximation
of the function
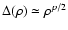 is valid only at the asymptotic condition
is valid only at the asymptotic condition
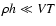 (here
h and V stand for the height and wind velocity of the
turbulent layer) which is not evident and, as we testify
below, is incorrect.
In the non-asymptotic case, the function
(here
h and V stand for the height and wind velocity of the
turbulent layer) which is not evident and, as we testify
below, is incorrect.
In the non-asymptotic case, the function
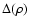 is expanded into a power series
of
is expanded into a power series
of 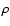 as
as
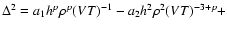 ...where a1, a2 are some
constants dependent on p and the intensity of turbulence
(Eq. (24) of Paper I).
Because the second
...where a1, a2 are some
constants dependent on p and the intensity of turbulence
(Eq. (24) of Paper I).
Because the second 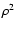 term of the expansion is negative,
the slope of the function
term of the expansion is negative,
the slope of the function
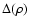 decreases with
decreases with
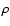 .
For that reason, the data in Fig. 1 only set a restriction
p > 0.64.
.
For that reason, the data in Fig. 1 only set a restriction
p > 0.64.
The key information is contained in the measured temporal
PSD of differential image motion
G(f) which is reproduced in Fig. 2 (broken
line) with a high spectral resolution up to
the Nyquist frequency
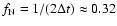 Hz.
The PSD was derived
with the shortest sample rate
Hz.
The PSD was derived
with the shortest sample rate
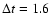 s and
effective integration time T=1.2 s;
these data are an average
over all observations and correspond to the mean stellar
separation 10'.
Owing to a rather complicated shape, this plot is very
informative, and when used in the fitting
procedure allows one to recover original parameters of the
turbulent wave-front distortions.
s and
effective integration time T=1.2 s;
these data are an average
over all observations and correspond to the mean stellar
separation 10'.
Owing to a rather complicated shape, this plot is very
informative, and when used in the fitting
procedure allows one to recover original parameters of the
turbulent wave-front distortions.
To find the model spectrum g(f) related to the measured
function G(f), we start with a common expression for the 2D
spatial power spectrum
F (u, v) of differential image motion derived
in Paper I. This expression has a form
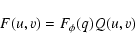 |
(2) |
of the product of two functions: first is the 2D spatial PSD
of a turbulent phase
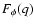 entering the telescope pupil
and which is generated by some
atmospheric layer at a height h, and the second is a
filter function Q(u,v) that accounts for observational
(non-atmospheric) details alone:
exposure, telescope aperture, the structure and size of stellar
configurations measured etc. Here u, v are spatial frequences,
and
entering the telescope pupil
and which is generated by some
atmospheric layer at a height h, and the second is a
filter function Q(u,v) that accounts for observational
(non-atmospheric) details alone:
exposure, telescope aperture, the structure and size of stellar
configurations measured etc. Here u, v are spatial frequences,
and
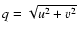 is a circular frequency measured in
units of m-1. The function
is a circular frequency measured in
units of m-1. The function
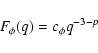 |
(3) |
describes 2D fluctuations of phase, 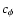 is a normalizig
factor, and p is the parameter to be established in this study.
A model with an outer scale will be discussed later in Sect. 7.
is a normalizig
factor, and p is the parameter to be established in this study.
A model with an outer scale will be discussed later in Sect. 7.
Expression (2) describes filtration of atmospherically
induced wave front distortions, which accur in the process of
observations, and is valid, generally, for any phase-related
quantity.
In our case, a measured quantity is the angular
separation 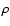 between the two stars, and its fluctuation
between the two stars, and its fluctuation
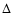 .
As shown in Paper I, in this case the function Q (u, v)is expressed as a product of four elemental filter functions
Q1...Q4 originating from the following effects and procedures
that are peculiar to differential astrometric techniques:
.
As shown in Paper I, in this case the function Q (u, v)is expressed as a product of four elemental filter functions
Q1...Q4 originating from the following effects and procedures
that are peculiar to differential astrometric techniques:
1) Displacement of star images caused by the gradient of
the wave-front in the direction of measurements that
forms some angle 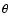 with the u-axis. If the latter
is directed along the wind vector, then
with the u-axis. If the latter
is directed along the wind vector, then
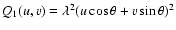 ;
;
2) Averaging due to a finite exposure:
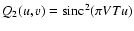 ;
;
3) Averaging over the telescope aperture:
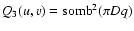 ;
;
4) Formation of a difference in the two points of a phase
screen at which it is crossed by light beams passing from the
stars. The relative position of the points is defined by the star
separation 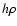 and the positional angle
and the positional angle  measured
with reference to the wind. Then
measured
with reference to the wind. Then
![$Q_4(u,v)=2\{1-\cos~[2\pi \rho h(u\cos\psi+
v~{\rm sin}~\psi)] \}$](/articles/aa/full/2002/46/aa2465/img49.gif) .
In the above expressions
.
In the above expressions 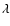 is wavelength,
is wavelength,
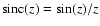 ,
,
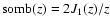 ,
and J1 is the Bessel function
of the order 1.
,
and J1 is the Bessel function
of the order 1.
With these expressions, Eq. (2) is rewritten as
![\begin{displaymath}
\begin{array}{ll}
F(u,v)= & \lambda^2 c_{\phi}q^2 {\rm sinc}...
... cos}~\psi+
v~{\rm sin}~\psi)] \} F_{\phi}(q). \\
\end{array}\end{displaymath}](/articles/aa/full/2002/46/aa2465/img53.gif) |
(4) |
Since the measured variances and spectra given by Han
are averaged over the two perpendicular
axes, the
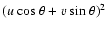 term in
the function Q1 accounting for a direction
term in
the function Q1 accounting for a direction 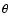 of image motion
measurements, was substituted here with its mean q2/2.
of image motion
measurements, was substituted here with its mean q2/2.
Transformation of spatial PSD F(u,v) into
temporal spectrum g(f) is performed (Martin 1987; Conan et al.
1995)
by integration of F (u, v) over spatial frequency v (across
a wind), with a
subsequent application of the Taylor transformation u=f/V:
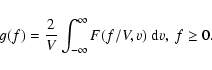 |
(5) |
Calculation of the integral (5)
for small apertures
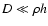 when
when
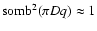 ,
and using
equality (Gradstein & Ryzhik 1971)
,
and using
equality (Gradstein & Ryzhik 1971)
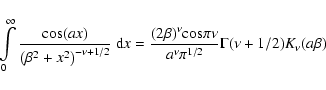 |
(6) |
where 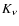 is the modified Bessel function of the order
is the modified Bessel function of the order 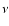 ,
yields
,
yields
![\begin{displaymath}
\begin{array}{ll}
\displaystyle g(f) = & 2c{\rm sinc}^2 (\pi...
...si)
{\rm cos} (2bf{\rm cos}~\psi)\right]\cdot \\
\end{array}\end{displaymath}](/articles/aa/full/2002/46/aa2465/img61.gif) |
(7) |
Here
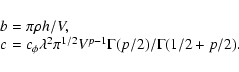 |
(8) |
In the high frequency (large
separations 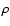 )
domain
)
domain 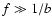 ,
the Bessel
function is exponentially damping with f, so that
(7) simplifies to
,
the Bessel
function is exponentially damping with f, so that
(7) simplifies to
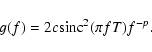 |
(9) |
Equation (9) evidently represents a doubled temporal PSD of the
absolute image motion for integration time T.
The structure of Eq. (9) allows one to identify the
c-term defined by Eq. (8) with a factor normalizing
the absolute image motion spectrum.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2465fa.eps}\end{figure}](/articles/aa/full/2002/46/aa2465/Timg66.gif) |
Figure 3:
The temporal PSD
of differential image motion (7) at c=1/2 and
T=0 (the function
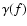 ), in units of bp versus
a non-dimensional frequency
bf. The function is plotted at p=0.5, ), in units of bp versus
a non-dimensional frequency
bf. The function is plotted at p=0.5,
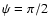 (long dash),
(long dash),
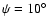 (dash) and
(dash) and
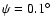 (short dash). The function
(short dash). The function
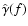 (averaged over
(averaged over  )
is
shown by a thick line. )
is
shown by a thick line. |
| Open with DEXTER |
Comparison of Eqs. (7) and (9) shows that
intrinsic features of the differential image motion spectrum are
brought about by the factor marked in (7) by
square brackets. To study its properties, we denote it
(with the adjacent term f-p) as
a new function
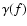 .
Rewriting Eq. (7) as
.
Rewriting Eq. (7) as
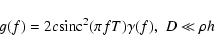 |
(10) |
we notice that
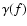 is equal to the PSD g (f) at T=0
with a numerical calibration c=1/2.
The shape of the function
is equal to the PSD g (f) at T=0
with a numerical calibration c=1/2.
The shape of the function
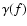 depends on the positional angle
depends on the positional angle  .
In Fig. 3,
.
In Fig. 3,
 is
plotted for orientation of star pairs almost along the wind
(
is
plotted for orientation of star pairs almost along the wind
(
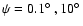 ),
across it (
),
across it (
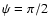 ), and when
), and when
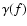 is averaged over
is averaged over
 in the range 0-2
in the range 0-2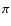 .
Each type of PSD shape in Fig. 3 corresponds to some peculiar
condition that we specify below.
Thus, occurance of the first three (non-averaged over
.
Each type of PSD shape in Fig. 3 corresponds to some peculiar
condition that we specify below.
Thus, occurance of the first three (non-averaged over  )
PSDs
is limited to the
particular case of the single-layer turbulence, and
observations of a single star pair. In other cases, the PSD
)
PSDs
is limited to the
particular case of the single-layer turbulence, and
observations of a single star pair. In other cases, the PSD
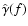 averaged over
averaged over  is
detectable. The averaging over
is
detectable. The averaging over  refers to
observations of a few randomly (with respect to
refers to
observations of a few randomly (with respect to  )
oriented star pairs, with a
single- or multi-layer turbulence (which is a case studied by Han).
In a multilayer turbulent atmosphere, detection of
)
oriented star pairs, with a
single- or multi-layer turbulence (which is a case studied by Han).
In a multilayer turbulent atmosphere, detection of
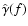 - like PSDs is common, even
for observations of a single arbitrary oriented star pair;
an averaging effect is produced here by the changes of wind direction
with height.
- like PSDs is common, even
for observations of a single arbitrary oriented star pair;
an averaging effect is produced here by the changes of wind direction
with height.
At high frequencies, the function
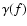 oscillates
around its mean
oscillates
around its mean
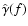 with an asymptote
with an asymptote
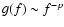 .
The amplitude of
oscillations is higher at small
.
The amplitude of
oscillations is higher at small  ,
and rapidly decreases with
an increase in
,
and rapidly decreases with
an increase in  .
A deep modulation in PSDs, like that plotted for
.
A deep modulation in PSDs, like that plotted for
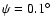 ,
of course, cannot be registered in observations, because both the
layered structure of the atmosphere and a certain dispersion of the
wind direction produce the effect of averaging which suppresses
small
,
of course, cannot be registered in observations, because both the
layered structure of the atmosphere and a certain dispersion of the
wind direction produce the effect of averaging which suppresses
small  components. With the effective
components. With the effective
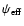 about
about
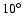 ,
modulations become moderately weak (Fig. 3).
,
modulations become moderately weak (Fig. 3).
In the 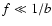 frequency domain, expansion of
the function (7) into powers of f yields
frequency domain, expansion of
the function (7) into powers of f yields
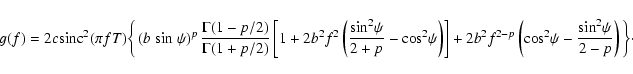 |
(11) |
The amplitude of 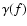 at f=0 is proportional to
at f=0 is proportional to
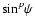 .
For stars oriented exactly along the wind,
the PSD increases proportionally to f2-p, which is in
agreement with theoretical results by Martin (1987) and
Conan et al. (1995) drawn at p=2/3. At orthogonal position of
stars, the PSD is slowly decreasing with f, and up to
.
For stars oriented exactly along the wind,
the PSD increases proportionally to f2-p, which is in
agreement with theoretical results by Martin (1987) and
Conan et al. (1995) drawn at p=2/3. At orthogonal position of
stars, the PSD is slowly decreasing with f, and up to
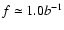 is approximately a white noise spectrum.
is approximately a white noise spectrum.
Averaging of Eq. (11) over  results in
results in
![\begin{displaymath}
\hat{ \gamma} (f)=b^p\left[ \gamma_0+\frac{1-p}{2-p}(bf)^{2-p}-
\frac{2\gamma_0}{(1+p)^2}(bf)^2\right]
\end{displaymath}](/articles/aa/full/2002/46/aa2465/img77.gif) |
(12) |
where
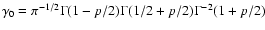 .
At low frequencies, the
.
At low frequencies, the
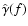 function (thick line in Fig. 3) approximately is a flat white noise
spectrum with a small maximum at
function (thick line in Fig. 3) approximately is a flat white noise
spectrum with a small maximum at
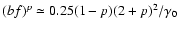 ,
or
,
or
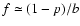 .
At f=0 there is a shallow spectral gap, which is better displayed
in Fig. 5 on non-logarithmic axes where the upper curve is
the same
.
At f=0 there is a shallow spectral gap, which is better displayed
in Fig. 5 on non-logarithmic axes where the upper curve is
the same
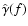 function as that shown
by a thick line in Fig. 3.
The magnitude of the peak is only
function as that shown
by a thick line in Fig. 3.
The magnitude of the peak is only
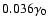 at p=1/3, yet
smaller,
at p=1/3, yet
smaller,
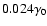 at p=2/3, and vanishes at p=1.
at p=2/3, and vanishes at p=1.
Note that g (f) not can be directly compared to the function
G (f) due to the different nature of the data they are formed
upon. Really,
while g (f) refers to some continuous measured
quantity and therefore is defined for any 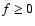 ,
G(f) is calculated on the basis of the data sampled with a rate
,
G(f) is calculated on the basis of the data sampled with a rate
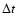 .
That limits the function G(f) frequency domain
by the bandwidth 0-
.
That limits the function G(f) frequency domain
by the bandwidth 0-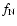 .
Correct comparison of the two spectra requires
taking into account the well-known
aliasing effect
(e.g. Vinnichenko et al. 1976), due to which the frequency
component of g(f) at
.
Correct comparison of the two spectra requires
taking into account the well-known
aliasing effect
(e.g. Vinnichenko et al. 1976), due to which the frequency
component of g(f) at
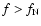 is imaged in a discrete
spectrum as a low-frequency harmonic. Conversion of g(f)into the observed PSD
is imaged in a discrete
spectrum as a low-frequency harmonic. Conversion of g(f)into the observed PSD
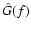 is found by summing
is found by summing
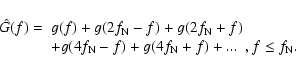 |
(13) |
Performing the integration of Eqs. (7) or (13)
over f yields the variance of differential image motion
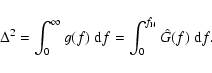 |
(14) |
Now, proceeding to a quantitative consideration, we use
Eqs. (7) and (13) in order
to fit the observed spectrum G(f) with the model function
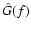 .
Only a single-layer turbulence was considered,
which, nevertheless, yielded a good result.
Expressions for
.
Only a single-layer turbulence was considered,
which, nevertheless, yielded a good result.
Expressions for
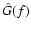 depend on
depend on  ,
,
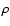 and
three parameters
c, h/V and p related to the turbulent layer.
In view of a rather
small
and
three parameters
c, h/V and p related to the turbulent layer.
In view of a rather
small 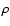 spread in values, for simulation purposes
we used its mean
spread in values, for simulation purposes
we used its mean 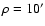 .
Also,
due to a random orientation of star pairs, the function
.
Also,
due to a random orientation of star pairs, the function
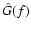 was averaged over a positional angle
was averaged over a positional angle  which
thus dropped out of consideration.
When finding parameters c, h/V and p, we required
best representation of the observed PSD shape (minimum
squared deviation) in all frequency ranges. The
integral
which
thus dropped out of consideration.
When finding parameters c, h/V and p, we required
best representation of the observed PSD shape (minimum
squared deviation) in all frequency ranges. The
integral
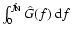 was claimed to be
equal to the observed variance of differential image motion,
whose value, 0.0093 arcsec2, was found both numerically by
integration of the
PSD shown
in Fig. 2 of this paper, and directly from Fig. 2
given by Han (1989)
as
was claimed to be
equal to the observed variance of differential image motion,
whose value, 0.0093 arcsec2, was found both numerically by
integration of the
PSD shown
in Fig. 2 of this paper, and directly from Fig. 2
given by Han (1989)
as 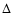 taken at the exposure T1=1.2 s.
taken at the exposure T1=1.2 s.
Using a fixed p=2/3, the best fit is achieved with
c=0.003105 arcsec2 Hz-1/3 and
h/V=1700 s. The relevant function
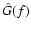 (Fig. 2, dashed line) fits observations relatively well, but
some deviations, such as a positive offset at high frequencies
mounting to 40% of G(f), may be seen.
(Fig. 2, dashed line) fits observations relatively well, but
some deviations, such as a positive offset at high frequencies
mounting to 40% of G(f), may be seen.
Better results are achieved when p is considered as a free
parameter of simulation. It was found that
to within random fluctuations of measurements a good, practically
equal quality of fitting is obtained with any p in the
limits of 0.9-1.0. Fluctuations in the PSD do not allow us to
determine
the p value more accurately, therefore in future calculations
we assume p=0.94.
Thus, the best parameters fitting the measured G(f)
and representing the atmospheric turbulence are
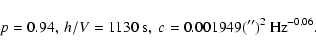 |
(15) |
Parameters h and V not can be
determined separately.
Assuming V=15 m s-1, we estimate
h=17 km which places the turbulence in the stratosphere.
Note that such a
distinctive feature of the function G(f) shape as
a steep slope over a wide spectral region 0.05-0.25 Hz
not can be simulated with p=2/3, even considering
the atmosphere with 2-3 turbulent layers.
Of course, this does not
mean a null turbulence at low altitudes because its contribution
in PSD is attenuated due to the dependence
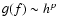 stated
by Eq. (11).
stated
by Eq. (11).
It is interesting to note that in spite of a large difference in pvalues (2/3 and 0.94), the PSDs plotted in Fig. 2 do not differ
much in their form. This is a consequence of a relatively
narrow range of the frequency f variations as a result of which
observed non-Kolmogorov PSDs
may be sometimes misidentified as classic PSDs. To avoid
confusion, a careful interpretation of the data is required.
In the previous section we used the observed temporal PSD in order
to determine parameters of the turbulent layer. Now,
using atmospheric parameters (15) and Eqs. (7)
and (14), we
calculate 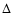 as a function of the star separation
as a function of the star separation 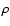 .
The calculated function (curve 2, Fig. 1) allows us
to verify how well the model
acconts for a change of the parameter
.
The calculated function (curve 2, Fig. 1) allows us
to verify how well the model
acconts for a change of the parameter 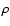 which until now
was assumed to be a fixed quantity.
One can see that both this curve and the line 1 originally
plotted by Han fit observations almost equally well.
This fact supports correctness of the present simulation
in which the information given in Fig. 1 was not used at all.
Besides, while parameters (15) were found from the
data obtained with a short 1.2 s exposure, Fig. 1 refers to
much longer T=10 s.
which until now
was assumed to be a fixed quantity.
One can see that both this curve and the line 1 originally
plotted by Han fit observations almost equally well.
This fact supports correctness of the present simulation
in which the information given in Fig. 1 was not used at all.
Besides, while parameters (15) were found from the
data obtained with a short 1.2 s exposure, Fig. 1 refers to
much longer T=10 s.
Note that curve 2 is not a straight line, as in the asymptotic
case. Its slope depends on
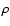 ,
is about 0.43 at
,
is about 0.43 at 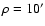 ,
and decreases
to the "conventional''
1/3 value at
,
and decreases
to the "conventional''
1/3 value at 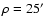 .
Deviation from the asymptotic power
law
.
Deviation from the asymptotic power
law
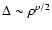 (line 3 with a slope of p/2=0.47)
is due to a violation of the asymptotic
condition
(line 3 with a slope of p/2=0.47)
is due to a violation of the asymptotic
condition
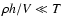 at wide
at wide 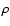 ,
thus a linear
approximation of the observed data in Fig. 1 seems to be invalid.
,
thus a linear
approximation of the observed data in Fig. 1 seems to be invalid.
The individual scatter of points in Fig. 1 is
caused partially by random errors which, according Han (1989), are
small. Therefore we may suppose that the scatter is due primarily
to different orientations  of star pairs, and check this
assumption by computations. Unfortunately,
no data on
of star pairs, and check this
assumption by computations. Unfortunately,
no data on  are given by Han. Therefore the
effect in
are given by Han. Therefore the
effect in 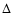 caused by the dispersion of
caused by the dispersion of  we estimated only tentatively, with the assumption that
we estimated only tentatively, with the assumption that  angles
changed in the range from their possible minimum value
angles
changed in the range from their possible minimum value
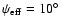 (Sect. 3)
to 90
(Sect. 3)
to 90
 .
The functions corresponding to these extreme
angles (the curves 4 and 5) have been calculated with the integration
of Eq. (7) over
.
The functions corresponding to these extreme
angles (the curves 4 and 5) have been calculated with the integration
of Eq. (7) over  .
An offset of curves 4 and 5 from the
mean line 2 is large at small
.
An offset of curves 4 and 5 from the
mean line 2 is large at small
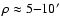 (about 20-30%
of
(about 20-30%
of 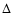 ),
and almost vanishes at
),
and almost vanishes at
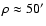 .
We can see that most of
experimental points are in the predicted limits;
thus, the observed
scatter of
.
We can see that most of
experimental points are in the predicted limits;
thus, the observed
scatter of 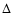 values is really
caused largely by different orientations of star pairs.
values is really
caused largely by different orientations of star pairs.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2465f3.eps}\end{figure}](/articles/aa/full/2002/46/aa2465/Timg99.gif) |
Figure 4:
The variance 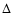 versus integration
time T at
versus integration
time T at 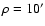 .
Observed dependence (broken line); the simulated
functions: with atmospheric parameters (14) - long dashed,
with p=2/3 - short dashed,
with the model (17)
and outer scale L0=1800 m - open circles.
Straight line
is the asymptotic dependence at .
Observed dependence (broken line); the simulated
functions: with atmospheric parameters (14) - long dashed,
with p=2/3 - short dashed,
with the model (17)
and outer scale L0=1800 m - open circles.
Straight line
is the asymptotic dependence at
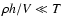 . . |
| Open with DEXTER |
The use of parameters (15) allows us also to adequately
predict the
dependence of  on the exposure T. This is demonstrated by
Fig. 4, where our numerical results (long dashed line)
found by integration (14) of the PSD (7)
are compared to the observed data (broken curve). Performing
calculations, we adopted the mean separation
on the exposure T. This is demonstrated by
Fig. 4, where our numerical results (long dashed line)
found by integration (14) of the PSD (7)
are compared to the observed data (broken curve). Performing
calculations, we adopted the mean separation 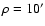 between
stars. As noted above, the change of effective integration time
T was achieved by averaging measurements over some msequential periods of the MAP rulling. In the original study,
however, a small difference
between the
between
stars. As noted above, the change of effective integration time
T was achieved by averaging measurements over some msequential periods of the MAP rulling. In the original study,
however, a small difference
between the  value and T expressed by Eq. (1)
was not taken into account.
Therefore Han's experimental points (his Fig. 2)
were transferred into Fig. 4 with corrections
(1). The difference
between
value and T expressed by Eq. (1)
was not taken into account.
Therefore Han's experimental points (his Fig. 2)
were transferred into Fig. 4 with corrections
(1). The difference
between 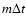 and T is small and essential
only at
and T is small and essential
only at 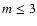 .
Within statistical fluctuations, the calculated
curve fits observations well enough. Here, as well as
in Fig. 1, the measured behaviour is correctly predicted over a wide
range of the argument variation,
and under a strong nonlinearity of the function examined
(the asymptotic dependence
.
Within statistical fluctuations, the calculated
curve fits observations well enough. Here, as well as
in Fig. 1, the measured behaviour is correctly predicted over a wide
range of the argument variation,
and under a strong nonlinearity of the function examined
(the asymptotic dependence
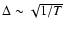 is shown in
Fig. 4 by a straight
line). This is an extra confirmation of the validity of a model
based on a different data source,
a temporal spectrum of differential image motion.
is shown in
Fig. 4 by a straight
line). This is an extra confirmation of the validity of a model
based on a different data source,
a temporal spectrum of differential image motion.
It is interesting to note that equally good fitting is
achieved with p=2/3 and
corresponding parameters c and h/V (short dash). Both
curves calculated with p=2/3 and p=0.94 are practically
identical over a given range of the argument change and they diverge
at T much smaller than used in observations.
Figure 2 shows that the measured temporal spectrum at low 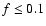 Hz
frequencies is approximately a flat white noise spectrum.
One can notice however that slight positive fluctuations
are present here at f<0.01 Hz, turning
into a shallow spectral gap at
Hz
frequencies is approximately a flat white noise spectrum.
One can notice however that slight positive fluctuations
are present here at f<0.01 Hz, turning
into a shallow spectral gap at
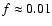 -0.02 Hz. Most likely,
both features are caused by random noise in the data.
Nevertheless, we will try to consider now whether some details of
this low-frequency
microstructure of the observed spectrum can be explained by
assuming a finite outer scale
of turbulence L0 which, as is known, may affect this frequency
band.
Introduction of L0 in the model will allow us to determine its
probable value, or at least establish a lower limit of L0.
Note that frequencies 0.01-0.02 Hz at V=15 m s-1 correspond to
scales of 750-1500 m, which are comparable to some known estimates
of L0 covering a range from 5 m (Coulman et al. 1988) to
100-1000 m (Vinnichenko et al. 1976).
-0.02 Hz. Most likely,
both features are caused by random noise in the data.
Nevertheless, we will try to consider now whether some details of
this low-frequency
microstructure of the observed spectrum can be explained by
assuming a finite outer scale
of turbulence L0 which, as is known, may affect this frequency
band.
Introduction of L0 in the model will allow us to determine its
probable value, or at least establish a lower limit of L0.
Note that frequencies 0.01-0.02 Hz at V=15 m s-1 correspond to
scales of 750-1500 m, which are comparable to some known estimates
of L0 covering a range from 5 m (Coulman et al. 1988) to
100-1000 m (Vinnichenko et al. 1976).
Saturation of turbulence at large scales is described by
a von Karman model of 3-D refractivity spectrum
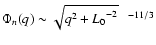 (e.g. Goodman 1985).
This spectral
model can be considered formally as a modification of the
corresponding Kolmogorov expression
(e.g. Goodman 1985).
This spectral
model can be considered formally as a modification of the
corresponding Kolmogorov expression
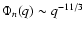 ,
which is performed by substitution of
q on a new spatial frequency
,
which is performed by substitution of
q on a new spatial frequency
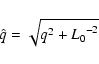 |
(16) |
restricted below with L0-1. A 2D power spectrum of a phase
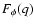 in the von Karman model therefore differs from
the Kolmogorov one
in the von Karman model therefore differs from
the Kolmogorov one
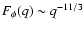 also with use
of the frequency
also with use
of the frequency 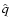 .
In further calculations thus we
adopted a model
.
In further calculations thus we
adopted a model
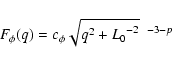 |
(17) |
which corresponds to the von Karman spectrum except for use of a
variable power, and inherits a structure of Eq. (3).
At
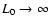 ,
Eqs. (3) and (17)
are equivalent.
,
Eqs. (3) and (17)
are equivalent.
Convertion to temporal frequencies
is performed as described in Sect.3 and involves
integration (5) of expression (4), where
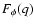 is given by (17), with respect
to the frequency v. To obtain the result, let us represent
a term
is given by (17), with respect
to the frequency v. To obtain the result, let us represent
a term
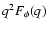 in Eq. (4) as
in Eq. (4) as
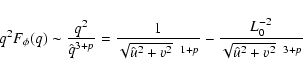 |
(18) |
where
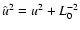 .
Comparison of the first term in
Eq. (18) with an expression
.
Comparison of the first term in
Eq. (18) with an expression
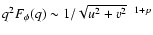 valid for the model
(3) shows that the only difference is in the use of
frequencies
valid for the model
(3) shows that the only difference is in the use of
frequencies
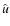 and u. Therefore we may utilize the results of integration
over v previously derived in Sect. 3, replacing only u by
and u. Therefore we may utilize the results of integration
over v previously derived in Sect. 3, replacing only u by
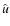 .
The following Taylor transformation u=f/V then leads
to the expression having the structure of Eq. (7) where
f is substituted (except terms
.
The following Taylor transformation u=f/V then leads
to the expression having the structure of Eq. (7) where
f is substituted (except terms
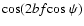 and
and
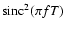 )
for a modified frequency
)
for a modified frequency
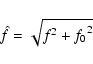 |
(19) |
where f0=V/L0 is a measure of L0 in a temporal scale.
Processing of a second term in Eq. (18) is accomplished
in the same way but by replacing p by p+2.
Finally, we derive a temporal PSD of differential image motion
with allowance for L0:
| g(f) |
= |
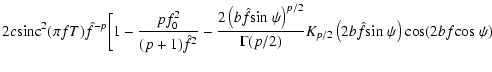 |
|
| |
|
![$\displaystyle +\frac{ 4\left(b\hat{f}{\rm sin}~\psi\right)^{p/2+1}}{(p+1)\Gamma...
...} \left(2b\hat{f}{\rm sin}~\psi\right) {\rm cos} (2bf{\rm cos}~\psi)\bigg]\cdot$](/articles/aa/full/2002/46/aa2465/img121.gif) |
(20) |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{2465fm.eps}\end{figure}](/articles/aa/full/2002/46/aa2465/Timg122.gif) |
Figure 5:
The temporal spectrum
of differential image motion based on the model (17)
at p=0.5, c=1/2 and T=0 versus a non-dimensional
frequency bf. The functions are plotted in descending order
for outer scales
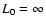 (upper thick line), 5bV, 2bV, bV and
0.2bV (lower curve); numerical
averaging with respect to the wind-dependent angle
(upper thick line), 5bV, 2bV, bV and
0.2bV (lower curve); numerical
averaging with respect to the wind-dependent angle  was applied.
was applied. |
| Open with DEXTER |
Figure 5 shows the function (20) behavior for several outer
scale lengths from 5bV to 0.2bV (corresponding to f0 from
0.2b-1 to 5b-1). As in Fig. 3, calculations were executed
with parameters p=0.5, c=1/2, T=0, and numerically averaged
with
respect to the position angle  .
The upper curve corresponds
to the case of infinite scale analyzed in Sect. 3 and is shown in Fig. 3
with a thick line. The lower curve plotted at very short L0<bV
is of a form typical of the (doubled) absolute image motion PSD,
which is valid at large separations
.
The upper curve corresponds
to the case of infinite scale analyzed in Sect. 3 and is shown in Fig. 3
with a thick line. The lower curve plotted at very short L0<bV
is of a form typical of the (doubled) absolute image motion PSD,
which is valid at large separations
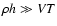
![\begin{displaymath}
g(f) = 2c{\rm sinc}^2 (\pi fT) {\sqrt{f^2+f_0^2}}^{~~-p} \left[1-
\frac{p}{p+1}\frac{f_0^2}{f^2+f_0^2} \right]\cdot
\end{displaymath}](/articles/aa/full/2002/46/aa2465/img124.gif) |
(21) |
A shape of the function g(f) varies depending upon a relative
magnitude of L0 and a linear size
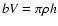 of a line
connecting the two stars in projection on the turbulent layer.
For long
of a line
connecting the two stars in projection on the turbulent layer.
For long
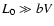 ,
the effect is weak (Fig. 5) resulting mainly in
a decrease of spectral height at low frequencies
,
the effect is weak (Fig. 5) resulting mainly in
a decrease of spectral height at low frequencies
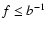 ;
at
;
at
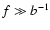 there is practically no noticable effect.
there is practically no noticable effect.
In the case of L0<bV or
f0>b-1 the effect is evidently strong
(lower curve),
but also in the low frequency range. Here, at
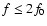 ,
the PSD is reduced to a height of about
,
the PSD is reduced to a height of about
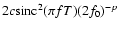 ;
at f>2f0 the asymptotic
law (9) remains valid.
;
at f>2f0 the asymptotic
law (9) remains valid.
Note that the shape of the function g(f) in cases of either long or
short L0 is similar in that they both have flat white noise
and (9) asymptotes; the difference is that a knee frequency
separating these loci occurs
at physically different frequencies
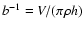 and
f0=V/L0 (dependent or not dependent on angular separation
between the stars
and
f0=V/L0 (dependent or not dependent on angular separation
between the stars 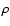 ).
).
The model (17) discussed in the above subsection was
applied to the fitting of the observed power spectrum G(f) so
as to extract probable values of L0 and f0 parameters.
A solution was found at
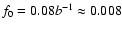 Hz and
parameters (15). The model PSD matches the PSD obtained
previously (thick line in Fig. 2) except at low frequencies where
a new function is shown by open circles. The quality of fitting
rapidly deteriorates with the increase of f0, therefore a value
0.008 Hz can be considered rather as the upper limit of f0. As seen
from Fig. 2, both models (3) corresponding to f0=0 and
(17) yield
equally good fitting, and no one can be favoured due to noise
in the experimental data. Thus, for this particular stratospheric
layer detected at
Hz and
parameters (15). The model PSD matches the PSD obtained
previously (thick line in Fig. 2) except at low frequencies where
a new function is shown by open circles. The quality of fitting
rapidly deteriorates with the increase of f0, therefore a value
0.008 Hz can be considered rather as the upper limit of f0. As seen
from Fig. 2, both models (3) corresponding to f0=0 and
(17) yield
equally good fitting, and no one can be favoured due to noise
in the experimental data. Thus, for this particular stratospheric
layer detected at
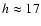 km, we fix limits
km, we fix limits
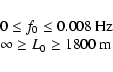 |
(22) |
where tranformation to spatial scales L0=V/f0 was
performed assuming V=15 m s-1.
In Fig. 4, by open circles we show a bias
in the dependence of the variance 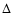 on integration time T caused by the presence of outer scale
(22); a new corrected dependence is in a slightly better
agreement with experimental data.
on integration time T caused by the presence of outer scale
(22); a new corrected dependence is in a slightly better
agreement with experimental data.
The sample estimate p=0.9-1.0 derived in this study and
corresponding to the particular stratospheric layer is larger
than the typical 1/3-2/3 values found from observations with infrared
interferometers (Bester et al. 1992; Busher et al. 1995).
Large p values were detected, for example, by Belen'kii et al.
(1997) who
observed Polaris image motion with a telescope bolted in
place so as to minimize uncontrolled telescope movements. For the
tilt power spectra they
found approximately a -1 slope in the low frequency range, which
corresponds to p=1.
The rather close estimates p=0.97 and
0.01 <f0 < 0.025 Hz
(
1500<L0< 600 m at V=15 m s-1) had been derived
earlier by the author (Lazorenko 1992), who analyzed results of
photographic and visual studies of the absolute image motion
obtained
for site testing programs in the former USSR. It should be
noted, however, that absolute image
motion data refer rather to the low altitude turbulence which is
usually stronger and is not attenuated by the factor hp present
in expression (11) for differential measurements.
Our aim was to derive analytical expressions for a temporal
image motion spectrum, and apply them to the MAP experimental data.
A restoration of atmospheric turbulent parameters from
the differential image motion spectrum appears to be succesful
due to the
presence in the measured spectrum of both the white noise locus and
the exponentially decreasing region (corresponding to the absolute
image motion). The spectral data had not been used in the original
study (Han 1989), the
results obtained were based on the fit of the
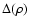 function
alone.
This limitation, combined with a significant scatter of measured
points in Fig. 1 (probably caused by a dispersion of
function
alone.
This limitation, combined with a significant scatter of measured
points in Fig. 1 (probably caused by a dispersion of  angles),
non-linearity of the function
angles),
non-linearity of the function
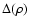 ,
and a narrow range of
,
and a narrow range of
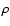 change, resulted in a biased estimate of p.
change, resulted in a biased estimate of p.
Concerning the measurements in wide fields
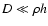 ,
we notice that the shape of functions
,
we notice that the shape of functions
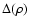 ,
,
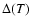 and G(f)is not critically sensitive to the actual value of p. This is
demonstrated by Figs. 1, 2 and 4 where the observed data was
well fitted with different p. We conclude that:
and G(f)is not critically sensitive to the actual value of p. This is
demonstrated by Figs. 1, 2 and 4 where the observed data was
well fitted with different p. We conclude that:
1) Sufficiently good predictions of 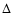 to be used in
practical applications can be derived in a conventional
Kolmogorov model, with no loss of accuracy even at large
deviations of p from 2/3. Thus, the empirical dependence
to be used in
practical applications can be derived in a conventional
Kolmogorov model, with no loss of accuracy even at large
deviations of p from 2/3. Thus, the empirical dependence
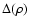 derived in Paper I is still valid for moderate
derived in Paper I is still valid for moderate
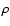 ;
;
2) In image motion studies, the non-classic distortions
of phase are detected with difficulty and are easily
confused with the classic distortions.
Acknowledgements
The author thanks the anonymous referee for useful
comments concerning outer scale effects in the image
motion data.
- Belen'kii, M. S., Karis, S. J., Brown, J. M.,
& Fugate, R. Q. 1997, SPIE Proc., 3126, 113
In the text
- Bester, M., Danchi, W. C., Degiacomi, C. G., et al.
1992, ApJ, 392, 357
In the text
NASA ADS
- Buscher, D. F., Armstrong, J. T., Hummel, C. A.,
et al. 1995, Appl. Opt., 34, 1081
NASA ADS
- Conan, J., Rousset, G., & Madec, P. 1995, JOSA A, 12,
1559
In the text
- Fried, D. L. 1965, JOSA, 55, 1427
In the text
- Gatewood, G. D. 1987, AJ, 94, 213
In the text
NASA ADS
- Goodman, J. W. 1985, Statistical optics
(Wiley-Interscience publication, New York)
In the text
- Gradstein, I. S., & Ryzhik, I. M. 1971,
The tables of integrals, sums, series and products
(Nauka, Moscow)
In the text
- Han, I. 1989, AJ, 97, 607
In the text
NASA ADS
- Hog, E. 1968, Z. Astrophys., 69, 313
NASA ADS
- Hogstrom, U., Smedman, A., & Bergstrom, H. 1998,
J. Atmos. Sci., 56, 959
In the text
- Lazorenko, P. F. 1992, Kin. Phys. Celest. Bodies,
3, 78
In the text
- Lazorenko, P. F. 2002, A&A, 382, 1125
In the text
NASA ADS
- Lindegren, L. 1980, A&A, 89, 41
In the text
NASA ADS
- Martin, H. M. 1987, PASP, 99, 1360
In the text
NASA ADS
- Sarazin, M., & Roddier, F. 1990, A&A, 227, 294
In the text
NASA ADS
- Tatarsky, V. I. 1961, Wave propagation in a
turbulent medium (Dover, New York)
In the text
- Vinnichenko, N. K., Pinus, N. Z., Shmeter, S. M.,
& Shur, G. N. 1976, The turbulence in a free atmosphere (Hydrometeoizdat, Leningrad)
In the text
Copyright ESO 2002
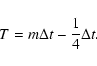
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2465f1.eps}\end{figure}](/articles/aa/full/2002/46/aa2465/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2465f2.eps}\end{figure}](/articles/aa/full/2002/46/aa2465/Timg32.gif)
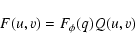
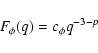
![\begin{displaymath}
\begin{array}{ll}
F(u,v)= & \lambda^2 c_{\phi}q^2 {\rm sinc}...
... cos}~\psi+
v~{\rm sin}~\psi)] \} F_{\phi}(q). \\
\end{array}\end{displaymath}](/articles/aa/full/2002/46/aa2465/img53.gif)
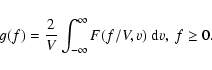
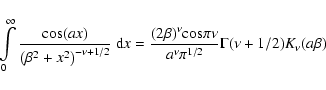
![\begin{displaymath}
\begin{array}{ll}
\displaystyle g(f) = & 2c{\rm sinc}^2 (\pi...
...si)
{\rm cos} (2bf{\rm cos}~\psi)\right]\cdot \\
\end{array}\end{displaymath}](/articles/aa/full/2002/46/aa2465/img61.gif)
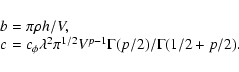
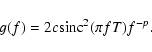
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2465fa.eps}\end{figure}](/articles/aa/full/2002/46/aa2465/Timg66.gif)
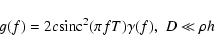
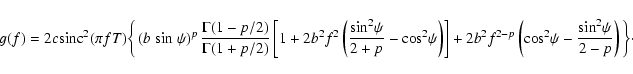
![\begin{displaymath}
\hat{ \gamma} (f)=b^p\left[ \gamma_0+\frac{1-p}{2-p}(bf)^{2-p}-
\frac{2\gamma_0}{(1+p)^2}(bf)^2\right]
\end{displaymath}](/articles/aa/full/2002/46/aa2465/img77.gif)
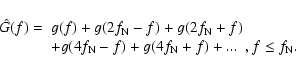
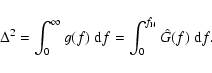
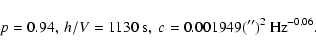
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2465f3.eps}\end{figure}](/articles/aa/full/2002/46/aa2465/Timg99.gif)
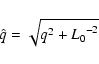
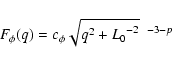
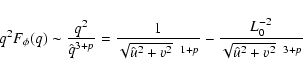
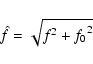
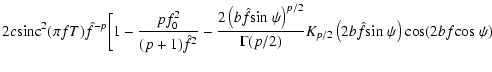
![$\displaystyle +\frac{ 4\left(b\hat{f}{\rm sin}~\psi\right)^{p/2+1}}{(p+1)\Gamma...
...} \left(2b\hat{f}{\rm sin}~\psi\right) {\rm cos} (2bf{\rm cos}~\psi)\bigg]\cdot$](/articles/aa/full/2002/46/aa2465/img121.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{2465fm.eps}\end{figure}](/articles/aa/full/2002/46/aa2465/Timg122.gif)
![\begin{displaymath}
g(f) = 2c{\rm sinc}^2 (\pi fT) {\sqrt{f^2+f_0^2}}^{~~-p} \left[1-
\frac{p}{p+1}\frac{f_0^2}{f^2+f_0^2} \right]\cdot
\end{displaymath}](/articles/aa/full/2002/46/aa2465/img124.gif)