A&A 396, 255-267 (2002)
DOI: 10.1051/0004-6361:20021361
Temporal variability in the Doppler-shift
of solar transition
region lines
J. G. Doyle1 - M. S. Madjarska1 - I. Roussev1,2
- L. Teriaca3 - J. Giannikakis4
1 - Armagh Observatory, College Hill, Armagh, BT61 9DG, N. Ireland
2 -
Center for Space Environment Modeling, 1414 Space Research Building, The University
of Michigan, Ann Arbor, MI 48109-2143, USA
3 -
Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze,
Italy
4 -
Sect. of Astrophysics, Astronomy and Mechanics, Dept. of Physics,
Univ. of Athens, Athens 15783, Greece
Received 19 December 2001 / Accepted 19 September 2002
Abstract
High cadence datasets taken in C III 977 Å, O
VI 1032 Å and Ne VIII 720 Å were analysed
in an effort to establish the extent of the variability in the Doppler-shift of
typical mid-transition region lines. The shortest time-scale variability seems
to occur in the network boundary regions where the line-shift can vary by
7-8 km
 in less than 1 min. The internetwork region also shows
variability although this tends to be longer lived,
in less than 1 min. The internetwork region also shows
variability although this tends to be longer lived,  2-3 min. The average
line-shift in C III is a red-shift which ranges from
2-3 min. The average
line-shift in C III is a red-shift which ranges from  2 km
2 km
 to
to
 20 km
20 km
 with an average value for all regions selected being around
10 km
with an average value for all regions selected being around
10 km
 in very good agreement with that derived by others. The red-shift
values indicate a clear difference between network and internetwork regions,
with the largest red-shift being present at the network boundary. For O VI,
this gives an average red-shift ranging from 5 to 10 km
in very good agreement with that derived by others. The red-shift
values indicate a clear difference between network and internetwork regions,
with the largest red-shift being present at the network boundary. For O VI,
this gives an average red-shift ranging from 5 to 10 km
 .
For Ne VIII, there
is a 13 km
.
For Ne VIII, there
is a 13 km
 difference between internetwork and bright network plasma with the bright
network being more red-shifted. This could imply that the bright network regions are
dominated by spicule down-flow.
difference between internetwork and bright network plasma with the bright
network being more red-shifted. This could imply that the bright network regions are
dominated by spicule down-flow.
In the second part we present results from 2-dimensional (2D) dissipative
magnetohydrodynamic (MHD) simulations of the response of the
solar transition region to micro-scale energy depositions. A variety
of temperatures at which the energy deposition takes place as well as the amount
of energy deposited are examined. This work is a continuation of previous
related simulations where small-scale energy depositions were modelled in 1D
hydrodynamics. The observable consequences of such transient events are then computed
for three transition region lines, namely C IV 1548 Å,
O VI 1032 Å, and Ne VIII 770 Å, under the consideration of
non-equilibrium ionization.
Key words: Sun: atmosphere - Sun: transition region - Sun: activity
1 Introduction
It is now well established that spectral lines formed at around 100 000 K in the
solar transition region exhibit a net red-shift. If this observed red-shift can be
attributed to plasma down-flow, it should be very important from the point of the
transition region dynamics and may have implications for the energy balance in the outer
solar atmosphere. Models attempting to explain the net mass flows in magnetic loops
include those where the flows are driven by asymmetries (such as heating or pressure
imbalances) between the two legs of the loop (Mariska & Boris 1983; Mariska 1988;
Spadaro et al. 1991) or by radiatively-cooling condensations (Reale et al. 1997).
Another model suggests that the observed red-shift could be due to the return of
spicular material (Pneuman & Kopp 1978). This model has recently been
re-evaluated by Wilhelm (2000).
Hansteen (1993) showed that red-shifted transition region lines are predicted
for downward propagating acoustic waves, and blue-shifted lines are predicted when the
perturbations propagate towards the corona (Hansteen & Wikstøl 1994). A followup study
by Hansteen et al. (1977) give additional simulation results using nonlinear Alfven waves
which give larger line-shifts. In general, impulsive energy release
(nano/micro-flaring), at the top of magnetic loops can generate
downward traveling MHD waves, perhaps steepening into shocks and leading to
both red- and blue-shifts, depending on the line formation temperature. Recently,
Chae et al. (1997) showed that the enthalpy flux due to down-flow determines
the overall energy balance in the transition region at temperatures below 105 K.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{2215f1.ps}\end{figure}](/articles/aa/full/2002/46/aa2215/Timg9.gif) |
Figure 1:
Line radiance variations ( erg cm-2 s-1 sr-1) and
Doppler shift ( km s-1) of the C III 977 Å. An integration
along the slit (left panel) was performed over
4 pixels (as labeled). The left panel image represents the intensity along the
slit. The data have a cadence of  18 s. 18 s. |
| Open with DEXTER |
In a recent observational paper, we looked at the behaviour of spectral
lines from the chromosphere to the corona (Teriaca et al. 1999a). It was found
that the Doppler velocities ranged from  0 km
0 km
 at
at  20 000 K to
a red-shift of 10 km
20 000 K to
a red-shift of 10 km
 at
at
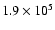 K for the "quiet Sun'',
and to
K for the "quiet Sun'',
and to  15 km
15 km
 at 105 K for an active region. At higher
temperature an opposite behaviour was observed. In the "quiet'' Sun a blue-shift of
at 105 K for an active region. At higher
temperature an opposite behaviour was observed. In the "quiet'' Sun a blue-shift of  -2 km
-2 km
 was derived at the Ne VIII formation
temperature (
was derived at the Ne VIII formation
temperature (
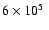 K), while in the active region, a blue-shifted
value around -8 km
K), while in the active region, a blue-shifted
value around -8 km
 was observed for the same spectral line.
was observed for the same spectral line.
![\begin{figure}
\par\includegraphics[width=14.5cm,height=4.5cm,clip]{MS2215_fig2a...
...par\includegraphics[width=14.5cm,height=3.4cm,clip]{MS2215_fig2d.ps}\end{figure}](/articles/aa/full/2002/46/aa2215/Timg12.gif) |
Figure 2:
Line radiance variations ( erg cm-2 s-1 sr-1) and
Doppler shift ( km s-1) of the O VI 1032 Å. In all cases, an
integration along the slit (see top panel) was performed over 5 pixels. |
| Open with DEXTER |
The above observational work was, however, time-averaged and did not cover
the important area of time variability. Doyle et al. (1998) found periods
approaching  5 min to be present in lines due to O III, O IV
and O V. In one dataset a period approaching 10 min was present for
5 min to be present in lines due to O III, O IV
and O V. In one dataset a period approaching 10 min was present for
 40 min. The size of these emitting features was limited to a few arcsec. In
all datasets examined, there was excess power below 4 mHz everywhere along the
slit, although the observed periods did not always come from the most intense
regions. Banerjee et al. (2001) in an analysis of network data detected
intensity as well as velocity oscillations for very small regions of the
network boundary, for a wide range of temperature lines starting from the low
chromosphere, N I, to the transition region, O VI. The periods
were often intermittent, occurring only during part of the full time sequence.
Wikstøl et al. (2000) showed that in the internetwork there was a phase
shift relation between the intensity of the continuum around 1043 Å and the O VI line shifts that could indicate the presence of
upward propagating waves. In the network, the existence of an opposite phase
relation between C II and O VI line shifts, indicated that waves may
propagate downwards in these regions.
It was also noted that C II and O VI line
profiles reveal, on statistical average, more red-shifted emission in the
network than in the internetwork lanes. A similar result was also found by
Hansteen et al. (2000). Recently, a detailed analysis of transition region line
profiles performed by Peter (2000, 2001) brought further support to the
hypothesis that different mechanisms may dominate the transition region
dynamics in the network and internetwork regions. Thus, any attempt to study
the temporal and spatial behaviour of spectral lines originating from
transition region temperatures should also distinguish between the network and
internetwork regions.
40 min. The size of these emitting features was limited to a few arcsec. In
all datasets examined, there was excess power below 4 mHz everywhere along the
slit, although the observed periods did not always come from the most intense
regions. Banerjee et al. (2001) in an analysis of network data detected
intensity as well as velocity oscillations for very small regions of the
network boundary, for a wide range of temperature lines starting from the low
chromosphere, N I, to the transition region, O VI. The periods
were often intermittent, occurring only during part of the full time sequence.
Wikstøl et al. (2000) showed that in the internetwork there was a phase
shift relation between the intensity of the continuum around 1043 Å and the O VI line shifts that could indicate the presence of
upward propagating waves. In the network, the existence of an opposite phase
relation between C II and O VI line shifts, indicated that waves may
propagate downwards in these regions.
It was also noted that C II and O VI line
profiles reveal, on statistical average, more red-shifted emission in the
network than in the internetwork lanes. A similar result was also found by
Hansteen et al. (2000). Recently, a detailed analysis of transition region line
profiles performed by Peter (2000, 2001) brought further support to the
hypothesis that different mechanisms may dominate the transition region
dynamics in the network and internetwork regions. Thus, any attempt to study
the temporal and spatial behaviour of spectral lines originating from
transition region temperatures should also distinguish between the network and
internetwork regions.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{2215f3.ps}\end{figure}](/articles/aa/full/2002/46/aa2215/Timg13.gif) |
Figure 3:
Line radiance variations ( erg cm-2 s-1 sr-1) and
Doppler shift ( km s-1) of the Ne VIII 770 Å. An integration
along the slit (left panel) was performed over
4 pixels (as labeled). The left panel image represents the intensity along the
slit. The data have a cadence of  14 s. 14 s. |
| Open with DEXTER |
Teriaca & Doyle (2001) presented a comparison of observations versus numerical simulations of
the response of the solar atmosphere to an energy perturbation of
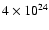 ergs representing an energy release during magnetic reconnection in a 1D
semi-circular flux tube. The temporal evolution of the thermodynamic state of
the loop were converted into C III 977, C IV 1548, O V 630,
O VI 1032, Ne VII 465 and Ne VIII 770 line profiles
via non-equilibrium calculation of ion populations.
Performing an integration over the entire period of simulation, red-shifts of 8.5, 6.1 and 1.7 km
ergs representing an energy release during magnetic reconnection in a 1D
semi-circular flux tube. The temporal evolution of the thermodynamic state of
the loop were converted into C III 977, C IV 1548, O V 630,
O VI 1032, Ne VII 465 and Ne VIII 770 line profiles
via non-equilibrium calculation of ion populations.
Performing an integration over the entire period of simulation, red-shifts of 8.5, 6.1 and 1.7 km
 ,
were found for C III, C IV, and
O V while blue-shifts of -1.8, -3.9 and -10.7 km
,
were found for C III, C IV, and
O V while blue-shifts of -1.8, -3.9 and -10.7 km
 were derived
for O VI, Ne VII and Ne VIII respectively, in good agreement
with observations.
were derived
for O VI, Ne VII and Ne VIII respectively, in good agreement
with observations.
The objective of the present paper is two-fold, in the first part we present further
evidence via selected high cadence observational sequences that the Doppler-shift is
highly time dependent, down to a few seconds for lines formed over a large fraction of the
transition region. For this we choose "quiet'' Sun datasets taken in
C III  977 Å, O VI
977 Å, O VI  1032 Å and
Ne VIII
1032 Å and
Ne VIII  770 Å obtained by the SUMER
instrument on-board the SoHO satellite. The region observed included cells,
network areas, and the boundaries between them.
770 Å obtained by the SUMER
instrument on-board the SoHO satellite. The region observed included cells,
network areas, and the boundaries between them.
In the second part we examine the observable consequences, in terms of
line profiles, of small-scale energy depositions of different magnitudes taking
place at different heights in a 2D "quiet'' Sun transition region environment and
whether such a model can explain both the variability and the direction of the
observed line-shift. To this end, the equilibrium initial state is perturbed by an
ad hoc heating term in the
energy equation. The underlying motivation to choose small-scale energy depositions
instead of driving magnetic reconnection (like in the reconnection studies of
Roussev et al. 2001a,b) was to use the energy that goes to heat the plasma as an
input parameter, instead of an output parameter (i.e. a reconnection model). The
idea is to study the value of Doppler shift as a function of the energy
input. For this, we choose three different values for the total amount of energy
release, E0, i.e.,
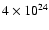 ergs,
ergs,
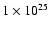 ergs, and
ergs, and
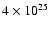 ergs, respectively. These values could, in principle, represent a
nano-flare event as a result of an ongoing magnetic reconnection. Each of these
energy depositions is then considered to occur at four different plasma
temperatures, i.e.,
ergs, respectively. These values could, in principle, represent a
nano-flare event as a result of an ongoing magnetic reconnection. Each of these
energy depositions is then considered to occur at four different plasma
temperatures, i.e.,
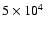 K,
K,
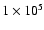 K,
K,
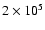 K, and
K, and
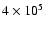 K,
respectively.
K,
respectively.
Roussev et al. (2001a,b) recently presented a numerical study relevant to explosive events,
where 2D MHD calculations were converted into line profiles representative of
transition region lines. The calculations of ion populations allow for
departures from equilibrium ionization, which proved to be important since
these dynamic events involve time scales smaller than the ionization and
recombination times. We adopt this procedure in these simulations.
SUMER is a normal incidence spectrograph operating over the wavelength range
 500 to 1610 Å (details can be obtained from
Wilhelm et al. 1995; Lemaire et al. 1997). The datasets selected were obtained
on March 21, 1997 (C III 977 Å), April 30, 1996 (O VI 1032 Å)
and May 1, 1997 (Ne VIII 770 Å) on the "quiet'' Sun in a sit-and-stare
mode with no compensation of solar rotation applied (although many other high
cadence datasets exist, only a few of these have a corresponding full
spectrum which is required for absolute wavelength calibration).
For the C III line, slit 8 (
500 to 1610 Å (details can be obtained from
Wilhelm et al. 1995; Lemaire et al. 1997). The datasets selected were obtained
on March 21, 1997 (C III 977 Å), April 30, 1996 (O VI 1032 Å)
and May 1, 1997 (Ne VIII 770 Å) on the "quiet'' Sun in a sit-and-stare
mode with no compensation of solar rotation applied (although many other high
cadence datasets exist, only a few of these have a corresponding full
spectrum which is required for absolute wavelength calibration).
For the C III line, slit 8 (
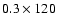 arcsec2)
was used with detector B with an integration time of 2.5 s from
18:23:40 to 18:39:09 UT. However, the electronics readout time leads to
an effective observing cadence of
arcsec2)
was used with detector B with an integration time of 2.5 s from
18:23:40 to 18:39:09 UT. However, the electronics readout time leads to
an effective observing cadence of  6 s.
The short integration time combined with the narrow slit ensured that the
count-rate for this strong line remained below the non-linear limit of
10 cts s-1 pixel-1.
Since the slit is only 0.3 arcsec wide, in 15 min it covers, due to the
absence of solar rotation compensation, approximately a 3 arcsec region on the
Sun.
The O VI line was registered on detector A using slit 4 (
6 s.
The short integration time combined with the narrow slit ensured that the
count-rate for this strong line remained below the non-linear limit of
10 cts s-1 pixel-1.
Since the slit is only 0.3 arcsec wide, in 15 min it covers, due to the
absence of solar rotation compensation, approximately a 3 arcsec region on the
Sun.
The O VI line was registered on detector A using slit 4 (
 arcsec2) with an exposure time of 6 s from 22:29:01 to 22:55:20 UT.
The Ne VIII line was taken using slit 2 (
arcsec2) with an exposure time of 6 s from 22:29:01 to 22:55:20 UT.
The Ne VIII line was taken using slit 2 (
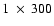 arcsec2) on detector B
exposing for 7 s from 20:49 to 22:48 UT.
arcsec2) on detector B
exposing for 7 s from 20:49 to 22:48 UT.
The reduction of SUMER raw images followed several stages,
i.e., local gain correction, flat-field subtraction, a correction for
geometrical distortion and radiometric calibration (providing the conversion
from counts px-1 s-1 to Watt m-2 sr-1 Å-1).
The signal to noise level is determined by the photon statistics.
The position of the SUMER slit during the C III and Ne VIII observations was set on
heliographic coordinates X = 0
 ,
Y = 0
,
Y = 0
 .
As can be seen from
Figs. 1-3 (see text below), the slit covered several network and internetwork
structures in each dataset. In order to increase the
S:N (signal-to-noise) level, in the C III case we binned over three consecutive spectra
(leading to a time resolution of
.
As can be seen from
Figs. 1-3 (see text below), the slit covered several network and internetwork
structures in each dataset. In order to increase the
S:N (signal-to-noise) level, in the C III case we binned over three consecutive spectra
(leading to a time resolution of  18 s) and over 4 spatial pixels (giving a spatial
resolution of 4 arcsec along the slit). Different locations along the slit were
analysed, representative of a variety of different features. The O VI
dataset consists of 1024 images centered on heliographic coordinates
X = 199
18 s) and over 4 spatial pixels (giving a spatial
resolution of 4 arcsec along the slit). Different locations along the slit were
analysed, representative of a variety of different features. The O VI
dataset consists of 1024 images centered on heliographic coordinates
X = 199
 ,
Y= 102
,
Y= 102
 .
An integration along the slit over five
pixels was performed in order to improve the signal-to-noise ratio. The
evolution of 20 regions along the slit was studied. For the Ne VIII dataset,
we binned over two spectra (obtaining a temporal resolution of 14 s) and 4 spatial pixels.
For all datasets, there was no rotational
compensation applied and therefore it is important to note that after 390 s the slit is no longer pointing at the same region.
.
An integration along the slit over five
pixels was performed in order to improve the signal-to-noise ratio. The
evolution of 20 regions along the slit was studied. For the Ne VIII dataset,
we binned over two spectra (obtaining a temporal resolution of 14 s) and 4 spatial pixels.
For all datasets, there was no rotational
compensation applied and therefore it is important to note that after 390 s the slit is no longer pointing at the same region.
Since we are interested in absolute line shifts, an absolute wavelength
calibration is vital. On SUMER there is no on-board calibration source, so the
wavelength calibration is usually done using chromospheric lines of neutral
atoms. A full spectrum image with an exposure time of 300 s
was taken just before the temporal series in C III allowing us to perform
the wavelength calibration. For the O VI dataset, one half detector image
with an exposure time of 150 s is available. The dispersion relation
was calculated using O I reference lines (for details see Teriaca et al.
1999a). The situation for the Ne VIII line was not optimum since the data
were registered in first order on detector B and therefore with the lack of
chromospheric lines, an "absolute'' calibration is not possible.
Moreover, since the data were taken at disk center, the other used method of
an off-limb average zero Doppler shift can not be applied (see Sect. 3.3).
3 Discussion on the observational results
The regions sampled (see Fig. 1) include: (a) the network region, (b) an
internetwork region, (c) a network region, (d) a network boundary, (e) a
network region and (f) the boundary of a bright network. All of the sampled
6 regions showed short time-scale variability in the absolute line-shift.
The shortest time-scale variability seems to occur in the network
boundary regions where the line-shift can vary by 7-8 km
 in less than 1 min. The internetwork region also shows variability although this tends to be
smaller. The average line-shift in all regions is for a red-shift, ranging from 8 km
in less than 1 min. The internetwork region also shows variability although this tends to be
smaller. The average line-shift in all regions is for a red-shift, ranging from 8 km
 in (a), 2 km
in (a), 2 km
 in (b), 7 km
in (b), 7 km
 in (c), 12 km
in (c), 12 km
 in (d),
20 km
in (d),
20 km
 in (e) and 13 km
in (e) and 13 km
 in (f). These figures indicate a clear
difference between network and internetwork regions, with the largest red-shift
being present at the network boundary. Only in the internetwork, did the
C III line show some evidence for a blue-shift. Hansteen et al. (2000)
reported that the internetwork showed on average a 4 km s-1 red-shift.
There is no evidence for high frequency oscillations in either the intensity or
the velocity in the C III data and since the dataset is only
in (f). These figures indicate a clear
difference between network and internetwork regions, with the largest red-shift
being present at the network boundary. Only in the internetwork, did the
C III line show some evidence for a blue-shift. Hansteen et al. (2000)
reported that the internetwork showed on average a 4 km s-1 red-shift.
There is no evidence for high frequency oscillations in either the intensity or
the velocity in the C III data and since the dataset is only  15 min
long, oscillations as detected by Doyle et al. (1998) were not observable. The
data, however, is highly variable, which could be perhaps interpreted as a series
of small energy releases, as distinct from explosive events which are ruled out
due to the lack of non-Gaussian line profiles.
15 min
long, oscillations as detected by Doyle et al. (1998) were not observable. The
data, however, is highly variable, which could be perhaps interpreted as a series
of small energy releases, as distinct from explosive events which are ruled out
due to the lack of non-Gaussian line profiles.
The regions sampled in the O VI datasets include (a) a weak network region,
(b) a strong network region and (c) an internetwork region (see Fig. 2). The average
velocities in each of these indicate a net red-shift of (a) 4.8 km
 ,
(b)
10 km
,
(b)
10 km
 and (c) 6.5 km
and (c) 6.5 km
 .
As in the C III dataset, there are
locations which show quite fast changes, e.g. in region (c) we see a sharp
decrease in the line-shift from 10 km
.
As in the C III dataset, there are
locations which show quite fast changes, e.g. in region (c) we see a sharp
decrease in the line-shift from 10 km
 to -5 km
to -5 km
 and finally back to
10 km
and finally back to
10 km
 in less than 60 s. The strong network locations show a gradual
change in the line-shift occurring over an interval of
in less than 60 s. The strong network locations show a gradual
change in the line-shift occurring over an interval of  200-300 s. Note
that the time of peak red-shift does not necessary correspond to the time of
peak intensity. Furthermore, at various times/locations in the strong network
region, the line-shift approaches zero although, as seen from the values quoted
above, the largest time-averaged net red-shift corresponds to the strong network
feature. Note that the spatial region covered by the slit in the E-W direction
is
200-300 s. Note
that the time of peak red-shift does not necessary correspond to the time of
peak intensity. Furthermore, at various times/locations in the strong network
region, the line-shift approaches zero although, as seen from the values quoted
above, the largest time-averaged net red-shift corresponds to the strong network
feature. Note that the spatial region covered by the slit in the E-W direction
is  4 arcsec compared to the slit width of 1 arcsec.
4 arcsec compared to the slit width of 1 arcsec.
The regions sampled (see Fig. 3) include: (a) a network region, (b) an internetwork region
and (c) a bright network boundary. In order to interpret our results we had
to rely on measurements of Doppler shifts given in the literature. Brekke
et al. (1997) and Chae et al. (1998) found a red-shift of 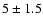 km
km
 .
These studies,
however, adopted the vacuum wavelength of of 770.409 Å for Ne VIII.
Dammasch et al. (1999) deduced the solar wavelength for this line for different regions
on the Sun and derived a rest wavelength of
.
These studies,
however, adopted the vacuum wavelength of of 770.409 Å for Ne VIII.
Dammasch et al. (1999) deduced the solar wavelength for this line for different regions
on the Sun and derived a rest wavelength of
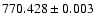 .
Their rest wavelength
determination was based on the assumption of no average Doppler shift above the solar
limb and a comparison with laboratory wavelengths of cool chromospheric
lines. They obtained an outflow
from a coronal hole with a velocity of 9 km
.
Their rest wavelength
determination was based on the assumption of no average Doppler shift above the solar
limb and a comparison with laboratory wavelengths of cool chromospheric
lines. They obtained an outflow
from a coronal hole with a velocity of 9 km
 ,
while for the "quiet'' Sun the average
velocity gave a blue-shift of
,
while for the "quiet'' Sun the average
velocity gave a blue-shift of 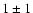 km
km
 .
Teriaca et al. (1999a) and Peter & Judge
(1999) found similar results of
.
Teriaca et al. (1999a) and Peter & Judge
(1999) found similar results of
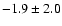 km
km
 ,
using the chromospheric lines
method and
,
using the chromospheric lines
method and
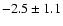 km
km
 applying the off-limb zero Doppler shift assumption,
respectively.
applying the off-limb zero Doppler shift assumption,
respectively.
The Doppler shifts of Ne VIII given in this work represent a relative value
applying a spectral pixel size of 44.73 mÅ (W. Curdt, private communication).
The relative wavelength is obtained from a single Gaussian fit of an average line
profile over the whole time series. Despite the fact that the routine for
geometric corrections was applied, we sampled regions which are close
enough along the slit to avoid introducing errors due to geometric
distortions.
As can be clearly seen from Fig. 3, there is a large difference between the
velocities in the three regions. In the network we have an average
velocity of -8 km
 ,
while the internetwork gives -3 km
,
while the internetwork gives -3 km
 and the bright
network +5 km
and the bright
network +5 km
 .
Within each of these regions, the
variation can be as large as
.
Within each of these regions, the
variation can be as large as 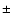 8 km
8 km
 .
.
As in the C III and O VI datasets, such short time-scale variability could
be interpreted as small energy releases. In the following sections, we enquire whether
such small-scale energy depositions can produce observable Doppler shift in our lines.
4 Physical model
4.1 Initial configuration
We consider the same 2D physical model approximating the solar transition region
as that presented in Roussev et al. (2001a). Refer to this earlier study for a
detailed description of the governing MHD equations, normalization units, etc.
We allow for a shallow temperature gradient along the field lines, and thus the
initial configuration is more like a "cool loop'' (see Mariska 1992). For the sake
of simplicity, the effects of gravity are neglected, and therefore the 2D
atmosphere presented below is not stratified. In terms of normalized physical
variables, the initial state is:
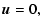 |
|
|
(1) |
and
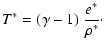 |
|
|
(5) |
Here e is the thermal energy, 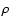 the mass density,
the mass density, 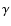 the
adiabatic index,
the
adiabatic index, 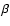 is the ratio of the gas pressure to the magnetic
pressure,
is the ratio of the gas pressure to the magnetic
pressure, 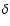 is a model parameter used to control the width of the current
concentration,
is a model parameter used to control the width of the current
concentration, 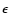 is the steepness of the transition region and
is the steepness of the transition region and 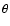 is a free parameter (one over the polytropic index) which defines the density
profile across the current concentration (i.e., in the x-direction). Also,
the parameter
is a free parameter (one over the polytropic index) which defines the density
profile across the current concentration (i.e., in the x-direction). Also,
the parameter
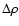 defines the density (and also temperature) jump
across the transition region,
defines the density (and also temperature) jump
across the transition region,
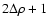 .
Values of all these
parameters used in the present modelling are given in Roussev et al. (2001a).
.
Values of all these
parameters used in the present modelling are given in Roussev et al. (2001a).
We further assume an energy balance for the initial state, which is used to
derive the 2D spatial distribution of the volumetric heating sources,
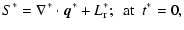 |
|
|
(6) |
where 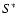 ,
,
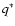 and
and 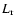 are the volumetric heating rate,
field-aligned conductive flux, and radiative losses, respectively. This way,
apart from referring to a static equilibrium state in the initial background
plasma, we also ensure there are no heating or cooling sources
throughout the computational domain at time zero.
are the volumetric heating rate,
field-aligned conductive flux, and radiative losses, respectively. This way,
apart from referring to a static equilibrium state in the initial background
plasma, we also ensure there are no heating or cooling sources
throughout the computational domain at time zero.
![\begin{figure}
\par\mbox{\includegraphics[width=8.7cm,clip]{MS2215_fig4a.ps}\hsp...
...\hspace*{2mm}
\includegraphics[width=8.7cm,clip]{MS2215_fig4d.ps} }
\end{figure}](/articles/aa/full/2002/46/aa2215/Timg44.gif) |
Figure 4:
The initial state for temperature (top left), mass density (top right), current density and
magnetic field topology (bottom left) and thermal energy (bottom right). |
| Open with DEXTER |
In Fig. 4 we show the physical variables for the initial state, i.e. the mass density,
temperature, thermal energy, current density and magnetic field topology.
4.2 Model of small-scale energy depositions
In the present study, the localized energy release is placed at the current
concentration and is assigned for a finite time. The explicit form of this
additional heating term is chosen as
![$\displaystyle E_{\rm dep} = E_0 ~ \alpha ~ F(t^\ast)
\exp\left\{ - \left[{{x^\ast}^2 + \left(y^\ast - y_0^\ast \right)^2 \over {\sigma}}
\right] \right\},$](/articles/aa/full/2002/46/aa2215/img45.gif) |
|
|
(7) |
where
![$\displaystyle F(t^\ast) =
\left\{\begin{array}{ll}
t^\ast / t_{\rm rise}^\ast; ...
...t^\ast - t^\ast_{\rm rise})}]; & t^\ast_{\rm rise} < t^\ast.
\end{array}\right.$](/articles/aa/full/2002/46/aa2215/img46.gif) |
|
|
(8) |
Here E0 is the total amount of energy release and
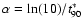 (where
(where
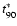 represents the time during
which 90% of the total energy deposition is released). Equation (8)
describes a linear increase in the additional heating rate up to
represents the time during
which 90% of the total energy deposition is released). Equation (8)
describes a linear increase in the additional heating rate up to
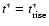 ,
followed by an exponential decay in time.
The distribution of the energy release in space is chosen as a symmetric double
Gaussian centered at
,
followed by an exponential decay in time.
The distribution of the energy release in space is chosen as a symmetric double
Gaussian centered at
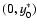 .
The free parameter
.
The free parameter 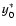 is used to move the position of energy deposition
along the current concentration so that this takes place at different initial
plasma temperatures. The parameters controlling the shape of the temporal and
spatial distribution of the energy release are
is used to move the position of energy deposition
along the current concentration so that this takes place at different initial
plasma temperatures. The parameters controlling the shape of the temporal and
spatial distribution of the energy release are 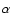 and
and 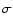 .
As to the
latter,
.
As to the
latter,
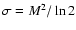 ,
where M is the full width at half maximum
(see Sarro et al. 1999). The parameter
,
where M is the full width at half maximum
(see Sarro et al. 1999). The parameter 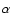 is such that 90% of the total
energy released is deposited in the first
is such that 90% of the total
energy released is deposited in the first
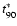 s of the simulation,
if there were no initial linear increase in the additional heating term up to
s of the simulation,
if there were no initial linear increase in the additional heating term up to
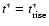 ,
i.e., if
,
i.e., if
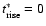 .
By introducing
.
By introducing
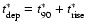 ,
the amount of energy which
is released after
,
the amount of energy which
is released after
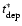 is
is
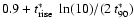 times the total amount of energy deposition, E0.
times the total amount of energy deposition, E0.
4.3 Numerical setup
All numerical experiments are performed using a 2D compressible MHD code based
on staggered meshes (see Roussev et al. 2001a). A stretching of the numerical
grid is applied in order to better resolve the region around the current
concentration where the most important dynamics of the experiments is expected
to take place. The numerical setup is the same as that presented in Roussev et al.
(2001a). In brief, the 2D grid on which the eleven experiments are carried out
is of size
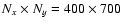 .
The numerical domain is chosen to
be of size
.
The numerical domain is chosen to
be of size
![$[2 ~ x_{\rm max}^\ast, 2 ~ y_{\rm max}^\ast] = [6, 8]$](/articles/aa/full/2002/46/aa2215/img60.gif) .
The
stretching of the grid is applied in the x-direction only (across the current
channel), and is such that 50% of the grid points are located within
.
The
stretching of the grid is applied in the x-direction only (across the current
channel), and is such that 50% of the grid points are located within
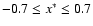 .
The parameter set used in the present modelling is as follows:
.
The parameter set used in the present modelling is as follows:
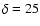 ,
,
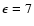 ,
,
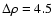 ,
,
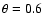 ,
,
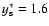 ,
,
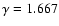 ,
,
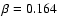 ,
M = 0.05,
,
M = 0.05,
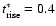 and
and
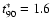 .
.
5 Discussion on the numerical results
In the following section we discuss the results obtained from our numerical
modelling. The general dynamics shared by all of the experiments is analysed
in Sect. 5.1. The observable consequences, in terms of line profiles,
are presented in Sect. 5.2. A summary of the results and final
conclusions are given in Sect. 6.
5.1 General dynamics
In all of the experiments, the energy depositions occur on one and the same
dynamic time-scale. The linear increase of the ad hoc heating term
is assigned at t = 0 and operates until
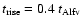 ,
corresponding to 6.5 s. The characteristic time of
"exponential decay'' of the driver term, t90, is chosen as
,
corresponding to 6.5 s. The characteristic time of
"exponential decay'' of the driver term, t90, is chosen as
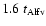 ,
equivalent to 26.5 s.
,
equivalent to 26.5 s.
All energy depositions take place in the current channel along the symmetry
axis
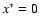 of the physical model. Energy release of the same amount
(for example experiments A1-4) is initiated at four different locations along
of the physical model. Energy release of the same amount
(for example experiments A1-4) is initiated at four different locations along
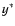 ,
i.e.,
,
i.e., 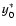 ,
characterized by the following values of
,
characterized by the following values of 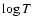 in the initial background plasma: 4.7, 5.0, 5.3, and 5.6.
in the initial background plasma: 4.7, 5.0, 5.3, and 5.6.
With the onset of energy release, both the kinetic gas pressure and temperature
start rising, thus creating an excess of pressure at the site of the explosion.
As the pressure gradient grows in time, the plasma heated at the site of energy
release expands dynamically into the yet non-affected surrounding plasma.
Furthermore, the onset of this small-scale transient event also initiates a fast
MHD wave that propagates away from the site of the explosion.
Since the plasma beta parameter outside the current "sheet'' is less than unity
(i.e.,
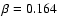 ), the increased plasma pressure at the site of the explosion
can be balanced only by a small perturbation of the Lorentz force in the
direction perpendicular to the current concentration. The plasma expansion
therefore occurs mainly along the magnetic field lines, and thus the heated
plasma spreads preferably along the current concentration. This does not imply
that similar results may be obtained if the localized energy release were to occur in a
simple magnetic loop without the current concentration since the plasma beta parameter
goes to infinity as one approaches the field reversal line,
), the increased plasma pressure at the site of the explosion
can be balanced only by a small perturbation of the Lorentz force in the
direction perpendicular to the current concentration. The plasma expansion
therefore occurs mainly along the magnetic field lines, and thus the heated
plasma spreads preferably along the current concentration. This does not imply
that similar results may be obtained if the localized energy release were to occur in a
simple magnetic loop without the current concentration since the plasma beta parameter
goes to infinity as one approaches the field reversal line, 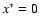 .
This means that
exactly in the mid-plane of the current sheet the increased kinetic gas pressure cannot
be balanced by the very small Lorentz force, unlike the situation where
there is a unipolar region. As one moves outward from the mid-plane of the
current sheet, the plasma beta decreases and the magnetic pressure becomes
more and more dominant. Right outside the current structure, the plasma
beta parameter approaches its value at large distances, i.e. 0.164. This
means that if the kinetic gas pressure increases by say 100%, this would be balanced
by a 16.4 percent increase in the magnetic pressure.
.
This means that
exactly in the mid-plane of the current sheet the increased kinetic gas pressure cannot
be balanced by the very small Lorentz force, unlike the situation where
there is a unipolar region. As one moves outward from the mid-plane of the
current sheet, the plasma beta decreases and the magnetic pressure becomes
more and more dominant. Right outside the current structure, the plasma
beta parameter approaches its value at large distances, i.e. 0.164. This
means that if the kinetic gas pressure increases by say 100%, this would be balanced
by a 16.4 percent increase in the magnetic pressure.
In addition, the
effect of field-aligned thermal conduction is to expand the enhanced temperature
region along the magnetic field lines even further than just a pure expansion
(nearly adiabatic) of hot plasma. As an increasing amount of energy is
deposited in the system, the peak temperature at the site of the explosion
continues rising as a function of time. This occurs because of a combination of
several factors. In the first place, the time-dependent increase in temperature
initiates the expansion of heated plasma, which locally leads to a decrease in
mass density. As the mass density decreases, the radiative losses (
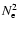 dependence) decrease too, while the temperature increase goes even further
before a balance can be reached. Secondly, since the background heating,
dependence) decrease too, while the temperature increase goes even further
before a balance can be reached. Secondly, since the background heating,
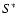 ,
is maintained at the same level, while the mass density decreases in
time, the same amount of energy input will support a higher steady-state of the
plasma temperature. This is therefore a run-away process which is slowed down
by the combined effect of plasma expansion, field-aligned heat conduction, and
exponential decrease of the energy input with time.
,
is maintained at the same level, while the mass density decreases in
time, the same amount of energy input will support a higher steady-state of the
plasma temperature. This is therefore a run-away process which is slowed down
by the combined effect of plasma expansion, field-aligned heat conduction, and
exponential decrease of the energy input with time.
As the region of enhanced temperature expands, the plasma surrounding the current
concentration is pushed away. Since an increasing amount of energy is deposited
into the system, the hot plasma blown out from the site of the explosion is
dynamically accelerated and bow shocks are subsequently formed at the locations
where the unperturbed plasma is being hit. The initial physical conditions are
such that the sound speed takes maximum values along the symmetry axis,
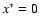 ,
while the Alfvén velocity is zero here. Comparing the flow velocity with
the local sound speed and Alfvén velocity in the vicinity of the current
channel around
,
while the Alfvén velocity is zero here. Comparing the flow velocity with
the local sound speed and Alfvén velocity in the vicinity of the current
channel around
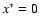 ,
it appears that this velocity is both supersonic and
super-Alfvénic in all of the experiments. One would therefore expect to
observe maximum outflow velocities away from the symmetry axis at the locations
where the flow becomes sub-Alfvénic rather than along this axis (although the
largest pressure gradient is reached here). This is what causes two sets of
outflow velocity peaks to appear on each side of the density depletion region. It
is found that the peak velocity first increases in time and then starts to decline
after reaching some maximum value of
,
it appears that this velocity is both supersonic and
super-Alfvénic in all of the experiments. One would therefore expect to
observe maximum outflow velocities away from the symmetry axis at the locations
where the flow becomes sub-Alfvénic rather than along this axis (although the
largest pressure gradient is reached here). This is what causes two sets of
outflow velocity peaks to appear on each side of the density depletion region. It
is found that the peak velocity first increases in time and then starts to decline
after reaching some maximum value of
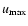 .
The peak flow velocity is found
to depend on the amount of energy released, nearly as
.
The peak flow velocity is found
to depend on the amount of energy released, nearly as  E01/2.
Furthermore, the highest velocities of bulk motions are found to be located at
the edges of the enhanced temperature region, clearly indicating the direction of
plasma expansion.
E01/2.
Furthermore, the highest velocities of bulk motions are found to be located at
the edges of the enhanced temperature region, clearly indicating the direction of
plasma expansion.
As time progresses, there are two density features that are dynamically created
and evolve in the opposite 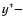 direction. They propagate along
direction. They propagate along 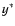 due to the fact that the magnetic field outside the current concentration acts
nearly like rigid walls (low plasma "beta''), and because of the radial
expansion of the temperature front moving along the current concentration.
due to the fact that the magnetic field outside the current concentration acts
nearly like rigid walls (low plasma "beta''), and because of the radial
expansion of the temperature front moving along the current concentration.
The higher the amount of energy deposition, the denser the outflow feature
becomes, as well as the higher the temperature increase at the site of the
explosion. Also, the more energy that is deposited into the system, the higher
the value of the maximum flow velocity,
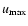 .
.
The basic difference of the same amount of energy deposition taking place at
different initial temperatures is basically on the dynamic time-scale on which
the plasma responds to such energy release.
In the first place, because
of the higher value of the sound speed at increased plasma temperature, the
expansion of heated plasma will occur faster, and thus involve a shorter dynamic
time-scale. Secondly, the importance of thermal conduction and radiative losses
will also vary, with an effect of a slight predominance of the heat conduction
over the radiative losses, as being more non-linear with respect to changes in
the physical conditions. The higher the initial temperature at the site of
explosion, the faster the thermal conduction,
as well as it's importance over the radiative losses.
In the next section, it will be shown that all this influence the observational
consequences of such micro-scale transient events in various resonance transition
region lines formed at different plasma temperatures.
5.2 Line synthesis
As pointed out by Joselyn et al. (1979a,b) and more recently by
Sarro et al. (1999) and Roussev et al. (2001b), the ionization
balance (EI) is a valid approximation only when bulk motions and gradients in the
physical parameters of the emitting plasma involve dynamic time-scales that are long
compared to the ionization and recombination times. In circumstances where
this does not hold true, time-dependent ion populations need to be calculated
in order to describe the emitting properties of the plasma more accurately.
In the case of non-equilibrium ionization (non-EI), the full time-dependent ion
populations are given via
![$\displaystyle \frac{\partial N_i}{\partial t} + u_y \cdot \frac{\partial N_i}{\...
...i-1,i} + N_{i+1} \alpha_{\rm r}^{i+1,i} N_{i+1} \alpha_{\rm d}^{i+1,i} \right],$](/articles/aa/full/2002/46/aa2215/img79.gif) |
|
|
(9) |
where
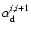 is the collisional-dielectronic recombination coefficient
from level i to i+1,
is the collisional-dielectronic recombination coefficient
from level i to i+1,
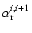 is the radiative recombination coefficient
from level i to i+1, Si,i+1 is the collisional-dielectronic ionization
coefficient from level i to i+1, and Ni is the number density of ion i.
is the radiative recombination coefficient
from level i to i+1, Si,i+1 is the collisional-dielectronic ionization
coefficient from level i to i+1, and Ni is the number density of ion i.
From the numerical perspective, solving Eq. (9) is a rather stiff problem, and there
is currently little progress made in computing time-dependent ion populations in 2D.
In the 1D case, we use a code as presented by Sarro et al. (1999)
to solve Eq. (9).
Since the experiments discussed in the previous section were done in 2D, we reduced
the MHD results to that which can be viewed along a line-of-sight by a spectrograph.
This was done by considering as a line-of-sight the symmetry axis
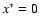 ,
and
averaging the 2D MHD solution over 19 grid points in the
,
and
averaging the 2D MHD solution over 19 grid points in the 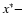 direction (in
symmetrical manner with respect to
direction (in
symmetrical manner with respect to
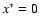 ). This way we obtained a 1D MHD
solution along the line-of-sight (only
). This way we obtained a 1D MHD
solution along the line-of-sight (only 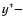 dependence), that represents a
region 1 arcsec wide in the
dependence), that represents a
region 1 arcsec wide in the 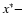 direction, as scaled on the Sun. The 1D code
uses as input, the values of
direction, as scaled on the Sun. The 1D code
uses as input, the values of 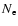 ,
T, and uy provided by the simulated 1D MHD
solutions.
,
T, and uy provided by the simulated 1D MHD
solutions.
Once the ion populations of a given element are computed using this 1D code,
the emissivity of a given emission line per unit interval of wavelength in
an optically thin, collisionally excited resonance line can be obtained
from
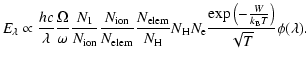 |
|
|
(10) |
Here h is the Planck constant, c is the speed of light, 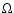 is the Maxwellian
averaged collisional strength,
is the Maxwellian
averaged collisional strength, 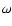 is the statistical weight of the lower level,
is the statistical weight of the lower level,
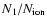 is the ratio of ions responsible for the emission in the ground
state relative to the total number of ions per unit volume,
is the ratio of ions responsible for the emission in the ground
state relative to the total number of ions per unit volume,
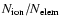 is the relative population of the ion,
is the relative population of the ion,
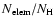 is the
element abundance,
is the
element abundance, 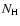 is the proton density,
is the proton density, 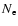 is the electron
density, W is the energydifference between the upper and lower levels,
is the electron
density, W is the energydifference between the upper and lower levels, 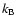 is
the Boltzmann constant, T is the temperature, and
is
the Boltzmann constant, T is the temperature, and
![$\displaystyle \phi(\lambda)=\frac{\exp{-\left[\frac{(\lambda-\lambda_0-\lambda_{\rm s})}
{\Delta \lambda_0}\right]^2}}{\Delta \lambda_0 \sqrt{\pi}}$](/articles/aa/full/2002/46/aa2215/img92.gif) |
|
|
(11) |
is the line profile. In the above definition of
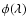 ,
,
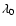 is the
rest wavelength of the resonance line and
is the
rest wavelength of the resonance line and
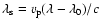 is the Doppler-shift corresponding to the velocity of the plasma projected on the
line-of-sight,
is the Doppler-shift corresponding to the velocity of the plasma projected on the
line-of-sight, 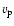 .
The Doppler width of the line,
.
The Doppler width of the line,
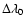 ,
is assumed
to be due to thermal motions only, and is given by
,
is assumed
to be due to thermal motions only, and is given by
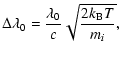 |
|
|
(12) |
where mi is the mass of the ion emitting in the resonance line of
interest.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2215_fig5a.ps}\par\inclu...
...215_fig5b.ps}\par\includegraphics[width=8.8cm,clip]{MS2215_fig5c.ps}\end{figure}](/articles/aa/full/2002/46/aa2215/Timg99.gif) |
Figure 5:
Sample line profiles for C IV 1548 Å (upper panel),
O VI 1032 Å (middle panel) and Ne VIII 770 Å, respectively,
for the case of an energy deposition of
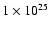 ergs at
ergs at
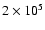 K.
The simulations for this case end at t = 192 s and on this figure we plot 6
line profiles with a time-difference of 35 s each. K.
The simulations for this case end at t = 192 s and on this figure we plot 6
line profiles with a time-difference of 35 s each. |
| Open with DEXTER |
By knowing the distribution of emissivities along the line-of-sight, the total
intensity can be computed as
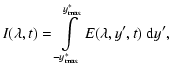 |
|
|
(13) |
where
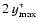 is the total length of the emitting source projected
on the line-of-sight. We use the above to perform line synthesis of the
resonance lines of C IV 1548 Å, O VI 1032 Å, and Ne VIII 770 Å, as discussed below.
is the total length of the emitting source projected
on the line-of-sight. We use the above to perform line synthesis of the
resonance lines of C IV 1548 Å, O VI 1032 Å, and Ne VIII 770 Å, as discussed below.
In Fig. 5 we show sample line profiles for
C IV 1548 Å, O VI 1032 Å and Ne VIII 770 Å for the
case of an energy deposition of
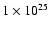 ergs at
ergs at
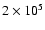 K. The
simulations end at 192 s and on this figure we plot 6 line
profiles with a time-difference of 35 s each. Thus, the last line profile will
correspond to t=175 s. The time evolution may be more clearly seen in Fig. 6,
where we show the line-shift as a function of time for two different energy
depositions, namely
K. The
simulations end at 192 s and on this figure we plot 6 line
profiles with a time-difference of 35 s each. Thus, the last line profile will
correspond to t=175 s. The time evolution may be more clearly seen in Fig. 6,
where we show the line-shift as a function of time for two different energy
depositions, namely
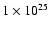 erg and
erg and
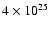 erg at all four
locations. Each line is discussed in detail below.
erg at all four
locations. Each line is discussed in detail below.
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=8cm,clip]{MS2215_fig6a...
...{2mm}
\includegraphics[angle=-90,width=8cm,clip]{MS2215_fig6d.ps} }
\end{figure}](/articles/aa/full/2002/46/aa2215/Timg102.gif) |
Figure 6:
Line shift, in km
 ,
for an energy deposition of ,
for an energy deposition of
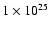 ergs
at ergs
at
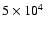 K and K and
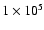 K (top left panel), an energy deposition of K (top left panel), an energy deposition of
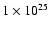 ergs at ergs at
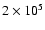 K and K and
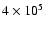 K (top right panel), an
energy deposition of K (top right panel), an
energy deposition of
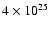 ergs at ergs at
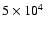 K and K and
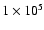 K
(bottom left panel), and an energy deposition of K
(bottom left panel), and an energy deposition of
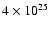 ergs at ergs at
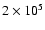 K and K and
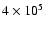 K (bottom right panel) for C IV 1548 Å,
O VI 1032 Å and Ne VIII 770 Å. K (bottom right panel) for C IV 1548 Å,
O VI 1032 Å and Ne VIII 770 Å. |
| Open with DEXTER |
5.2.1 The C IV line
In all experiments with index "2'', i.e., A2-B2-C2 (see Table 1), the energy
depositions take place at a temperature of the initial background plasma
that is rather close to the temperature of formation of the C IV
1548 Å resonant line. In all other experiments, the energy release
happens at higher temperature, i.e.,
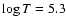 and 5.6, or in the case
of index "1'' experiments at a lower temperature.
and 5.6, or in the case
of index "1'' experiments at a lower temperature.
The behavior of the C IV line in all experiments where the energy
deposition take place at the same initial temperature is rather similar.
The main difference is in the maximum value of red-shift reached
in each individual experiment.
In the A1 and B1 experiments, we initially see blue-shifted plasma up until
 120 s, there-ward it is zero. The "C1'' experiment initially shows
two jets, blue and red with the blue being dominant for the first
20 s. Thereafter, the red-shift is dominant, decreasing from a maximum
value of
120 s, there-ward it is zero. The "C1'' experiment initially shows
two jets, blue and red with the blue being dominant for the first
20 s. Thereafter, the red-shift is dominant, decreasing from a maximum
value of  17 km
17 km
 to zero after 80 s. Thus for higher
energy deposition, the line will always be mostly red-shifted.
In A2, B2, and C2 experiments, the time series show an increasing Doppler
shift of the line profile towards the red part of the spectra up to a certain
time (approx. 10 s), followed by a turn-over point, and then a gradual shift
back to some small amount of red-shift at the end of the time series. The
latter ends at times: 202 s (A2), 192 s (B2), and 118 s (C2), respectively.
By comparing these cases, the main conclusion is: the higher the amount of
energy deposition, the higher the peak value of red-shift. The latter is
derived to be 3.7 km
to zero after 80 s. Thus for higher
energy deposition, the line will always be mostly red-shifted.
In A2, B2, and C2 experiments, the time series show an increasing Doppler
shift of the line profile towards the red part of the spectra up to a certain
time (approx. 10 s), followed by a turn-over point, and then a gradual shift
back to some small amount of red-shift at the end of the time series. The
latter ends at times: 202 s (A2), 192 s (B2), and 118 s (C2), respectively.
By comparing these cases, the main conclusion is: the higher the amount of
energy deposition, the higher the peak value of red-shift. The latter is
derived to be 3.7 km
 (A2), 9.5 km
(A2), 9.5 km
 (B2), and 18.6 km
(B2), and 18.6 km
 (C2),
respectively. At the end of the time series for these three cases, there is
a non-zero red-shift of the order of 0.4 km
(C2),
respectively. At the end of the time series for these three cases, there is
a non-zero red-shift of the order of 0.4 km
 (A2), 0.7 km
(A2), 0.7 km
 (B2), and
1.2 km
(B2), and
1.2 km
 (C2), respectively.
(C2), respectively.
A similar behavior in the time series is also seen in the experiments where
the energy deposition takes place at
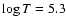 ,
i.e., experiments
A3, B3, and C3. The peak values of red-shift are reached at a slightly later
time than in the previous case, i.e., approx. 12 s. The main difference
is then found to occur in the value of this maximum red-shift, i.e., 5.2 km
,
i.e., experiments
A3, B3, and C3. The peak values of red-shift are reached at a slightly later
time than in the previous case, i.e., approx. 12 s. The main difference
is then found to occur in the value of this maximum red-shift, i.e., 5.2 km
 (A3), 9.6 km
(A3), 9.6 km
 (B3), and 18.0 km
(B3), and 18.0 km
 (C3), respectively. The time
series relevant
to these three particular experiments end at the same time as the corresponding
ones of the previous three, i.e., 202 s (A3), 192 s (B3), and 118 s (C3),
respectively. The overall red-shift reached at the end of the time
series, is of the order of 0.4 km
(C3), respectively. The time
series relevant
to these three particular experiments end at the same time as the corresponding
ones of the previous three, i.e., 202 s (A3), 192 s (B3), and 118 s (C3),
respectively. The overall red-shift reached at the end of the time
series, is of the order of 0.4 km
 (A3), 0.8 km
(A3), 0.8 km
 (B3), and 1.7 km
(B3), and 1.7 km
 (C3), respectively.
(C3), respectively.
In A4 and B4, the energy is released at
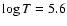 .
Comparing with the previous two sets of experiments, here we
again find a similar trend in the response of the C IV line to such
small-scale energy deposition. The maximum value of red-shift is reached at
an even later time than in the previous two cases, and corresponds to approx. 18 s.
The values of red-shift at this instant of time are, respectively, 4.5 km
.
Comparing with the previous two sets of experiments, here we
again find a similar trend in the response of the C IV line to such
small-scale energy deposition. The maximum value of red-shift is reached at
an even later time than in the previous two cases, and corresponds to approx. 18 s.
The values of red-shift at this instant of time are, respectively, 4.5 km
 (A4),
and 8.6 km
(A4),
and 8.6 km
 (B4). At the end of the time series there is again a net red-shift,
which is of the same value as in the previous two cases, i.e., 0.4 km
(B4). At the end of the time series there is again a net red-shift,
which is of the same value as in the previous two cases, i.e., 0.4 km
 (A4),
and 0.7 km
(A4),
and 0.7 km
 (B4), respectively.
(B4), respectively.
5.2.2 The O VI line
Unlike the C IV line, the response of the O VI 1032 Å line
is rather interesting. In the A1, B1, C1, A2 and B2 experiments, the
Doppler-shift is towards the blue part of the spectra. On the contrary, the
behavior of the former line is mostly in the opposite direction - towards
the red part of the spectra. In the A1 and B1 experiments, the maximum value of
blue-shift is reached at t=40 s, and the corresponding
values of blue-shift are, respectively, -1.2 km
 (A1), and -2.6 km
(A1), and -2.6 km
 (B1). In "C1'' it reaches a maximum blue-shift of -8.3 km
(B1). In "C1'' it reaches a maximum blue-shift of -8.3 km
 after 80 s.
after 80 s.
In the A2 and B2 experiments, the maximum value of blue-shift is reached at
t=22 s (A2), and t=12 s (B2), and the corresponding values of
blue-shift are, respectively, -1.7 km
 (A2), and -3.2 km
(A2), and -3.2 km
 (B2). In the
C2 experiment, we first observe a blue-shift in the time series of the
O VI line, alternated with a red-shift at approx t=6 s. The maximum
value of the red-shift is reached at t=12 s, and corresponds to
1.9 km
(B2). In the
C2 experiment, we first observe a blue-shift in the time series of the
O VI line, alternated with a red-shift at approx t=6 s. The maximum
value of the red-shift is reached at t=12 s, and corresponds to
1.9 km
 .
The red-shift is found to change back to blue-shift at
about t=34 s. In all three experiments A2-B2-C2, a net blue-shift of the
O VI line profile is found to be present at the end of the time series.
The corresponding values of this blue-shift are -1.2 km
.
The red-shift is found to change back to blue-shift at
about t=34 s. In all three experiments A2-B2-C2, a net blue-shift of the
O VI line profile is found to be present at the end of the time series.
The corresponding values of this blue-shift are -1.2 km
 (A2), -2.2 km
(A2), -2.2 km
 (B2), and -6.1 km
(B2), and -6.1 km
 (C2), respectively.
(C2), respectively.
In experiments A3, B3, and C3, where the energy depositions take place at
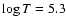 ,
the O VI line responds in a rather similar manner to
the previous case of
,
the O VI line responds in a rather similar manner to
the previous case of
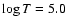 .
Note that this time the micro-scale
explosions occur at a temperature which is rather close to
the O VI line formation temperature. The value of blue-shift in
experiments A3 and B3 first increases, reaches some maximum value, decreases,
and then starts increasing again. The first peak value in the blue-shift is
reached at t=10 s for experiment A3, and t=4 s for experiment B3,
respectively. The corresponding values of blue-shift are -1.5 km
.
Note that this time the micro-scale
explosions occur at a temperature which is rather close to
the O VI line formation temperature. The value of blue-shift in
experiments A3 and B3 first increases, reaches some maximum value, decreases,
and then starts increasing again. The first peak value in the blue-shift is
reached at t=10 s for experiment A3, and t=4 s for experiment B3,
respectively. The corresponding values of blue-shift are -1.5 km
 (A3),
-1.2 km
(A3),
-1.2 km
 (B3), respectively. In experiment A3 this is the maximum value
of blue-shift reached throughout the time series, while in experiment B3, in
turn, the maximum value of blue-shift is observed at the end of the time series.
The net blue-shift reached at the end of experiments A3 and B3 is -1.3 km
(B3), respectively. In experiment A3 this is the maximum value
of blue-shift reached throughout the time series, while in experiment B3, in
turn, the maximum value of blue-shift is observed at the end of the time series.
The net blue-shift reached at the end of experiments A3 and B3 is -1.3 km
 and -2.9 km
and -2.9 km
 ,
respectively. Similar to the response of O VI in
experiment C2, in experiment C3 we again see the appearance of a Doppler-shifted
component towards the blue part of the spectra, though occurring at a smaller
relative intensity than in the former case, as well as lasting longer
(approx. 100 s). A red-shift is also seen in the time series that reaches
a maximum value of 2.3 km
,
respectively. Similar to the response of O VI in
experiment C2, in experiment C3 we again see the appearance of a Doppler-shifted
component towards the blue part of the spectra, though occurring at a smaller
relative intensity than in the former case, as well as lasting longer
(approx. 100 s). A red-shift is also seen in the time series that reaches
a maximum value of 2.3 km
 at t=12 s, subsequently changes into blue-shift
at later times. The maximum value of blue-shift is reached at the end of the
time series, and corresponds to -6.3 km
at t=12 s, subsequently changes into blue-shift
at later times. The maximum value of blue-shift is reached at the end of the
time series, and corresponds to -6.3 km
 .
.
In the case of an energy release taking place at
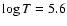 ,
i.e., experiments
A4 and B4, first we see red-shifts, which eventually change into blue-shifts at
later times. The maximum red-shift observed in experiment A4 is 0.3 km s-1,
reached at t=8 s. Similarly, in experiment B4 the corresponding value of
red-shift is 0.5 km
,
i.e., experiments
A4 and B4, first we see red-shifts, which eventually change into blue-shifts at
later times. The maximum red-shift observed in experiment A4 is 0.3 km s-1,
reached at t=8 s. Similarly, in experiment B4 the corresponding value of
red-shift is 0.5 km
 ,
and is reached at t=12 s. At t=16 s for A4, and
t=22 s for B4, respectively, the red-shift changes into a blue-shift. The
values of the latter at the end of the time series are -1.4 km s-1 (A4)
and -3.7 km s-1 (B4), respectively.
,
and is reached at t=12 s. At t=16 s for A4, and
t=22 s for B4, respectively, the red-shift changes into a blue-shift. The
values of the latter at the end of the time series are -1.4 km s-1 (A4)
and -3.7 km s-1 (B4), respectively.
5.2.3 The Ne VIII line
Similar to the O VI line, the response of the Ne VIII 770 Å line
to small-scale energy depositions is also quite interesting. In both experiments
A1 and B1, the Doppler-shifts of the Ne VIII resonant line are all towards
the blue part of the spectra. The maximum blue-shift is reached towards the end
of the experiment,  120 s corresponding to
120 s corresponding to  - 1.8 km
- 1.8 km
 (A1) and -4.5 km
(A1) and -4.5 km
 (B1). In both experiments A2 and B2, the Doppler-shift of
the Ne VIII resonant line are also towards the blue. The maximum value of
blue-shift in experiment A2 is reached at the end of the time series, while in
experiment B2 this happens at t=26 s, and the corresponding value of
blue-shift is -5.4 km
(B1). In both experiments A2 and B2, the Doppler-shift of
the Ne VIII resonant line are also towards the blue. The maximum value of
blue-shift in experiment A2 is reached at the end of the time series, while in
experiment B2 this happens at t=26 s, and the corresponding value of
blue-shift is -5.4 km
 .
At the end of the time series the
blue-shift is -1.8 km
.
At the end of the time series the
blue-shift is -1.8 km
 for A2, and -3.0 km
for A2, and -3.0 km
 for B2, respectively. In experiments C1 and C2, the response of the Ne VIII
line is even more complex than that of O VI. In this case,
the appearance of two Doppler-shifted components is seen - one in the blue,
and another one in the red part of the spectra which appears first, and lasts
longer than the blue-shifted component. In C1, the blue component reaches a
maximum value of relative intensity at t=12 s, and then starts gradually
disappearing. The red-shifted component is present until t=60 s, while thereafter
only the blue-shifted plasma remains. The maximum values of blue- and red-shift
at which these two components appear are -40 km
for B2, respectively. In experiments C1 and C2, the response of the Ne VIII
line is even more complex than that of O VI. In this case,
the appearance of two Doppler-shifted components is seen - one in the blue,
and another one in the red part of the spectra which appears first, and lasts
longer than the blue-shifted component. In C1, the blue component reaches a
maximum value of relative intensity at t=12 s, and then starts gradually
disappearing. The red-shifted component is present until t=60 s, while thereafter
only the blue-shifted plasma remains. The maximum values of blue- and red-shift
at which these two components appear are -40 km
 ,
and 25 km
,
and 25 km
 ,
respectively. The net blue-shift reached at the end of the time series
corresponds to -1.9 km s-1.
,
respectively. The net blue-shift reached at the end of the time series
corresponds to -1.9 km s-1.
In C2, the blue component reaches a maximum value of relative intensity after
t=12 s, and then starts gradually disappearing. The red-shifted component
becomes dominant in the spectra approx. 6 s later than the blue counterpart.
The maximum values of blue- and red-shift at which these two components appear
are -40 km
 ,
and 25 km
,
and 25 km
 ,
respectively. The two Doppler components
gradually diminish, and after approx. t=60 s there is only blue-shifted
emission. The net blue-shift reached at the end of the time series
is -4.5 km
,
respectively. The two Doppler components
gradually diminish, and after approx. t=60 s there is only blue-shifted
emission. The net blue-shift reached at the end of the time series
is -4.5 km
 .
.
In the case where the energy deposition takes place at
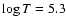 ,
i.e.,
experiments A3 and B3, the dynamic response of the Ne VIII line is rather
similar to that of the previous case. Note that in both cases the energy
deposition takes place at a temperature that is below the temperature of
formation of the Ne VIII line. The maximum value of blue-shift in experiment A3 is reached at the end of the time series, and corresponds to -1.8 km
,
i.e.,
experiments A3 and B3, the dynamic response of the Ne VIII line is rather
similar to that of the previous case. Note that in both cases the energy
deposition takes place at a temperature that is below the temperature of
formation of the Ne VIII line. The maximum value of blue-shift in experiment A3 is reached at the end of the time series, and corresponds to -1.8 km
 .
In
experiment B3, in turn, the peak value of blue-shift is obtained at t=14 s,
and corresponds to -8.7 km
.
In
experiment B3, in turn, the peak value of blue-shift is obtained at t=14 s,
and corresponds to -8.7 km
 .
The blue-shifted plasma at the end of the time
series is -2.8 km s-1. The two Doppler-shifted components found in the
spectra of the Ne VIII line relevant to experiment C2 are again present
in the spectra for the case of experiment C3. Just like before, the blue-shifted
component appears first and lasts longer, although the dominant relative
intensity comes from the red-counterpart. The two components also appear at
slightly higher absolute values of Doppler-shift than in the previous case
and these are, respectively, -50 km
.
The blue-shifted plasma at the end of the time
series is -2.8 km s-1. The two Doppler-shifted components found in the
spectra of the Ne VIII line relevant to experiment C2 are again present
in the spectra for the case of experiment C3. Just like before, the blue-shifted
component appears first and lasts longer, although the dominant relative
intensity comes from the red-counterpart. The two components also appear at
slightly higher absolute values of Doppler-shift than in the previous case
and these are, respectively, -50 km
 ,
and 30 km
,
and 30 km
 .
These components
disappear from the spectra at almost the same time as in the previous case,
i.e., at approx. t=60 s. There is again a blue-shifted line profile at the
end of the time series. The value of blue-shift is of the order of -10.6 km
.
These components
disappear from the spectra at almost the same time as in the previous case,
i.e., at approx. t=60 s. There is again a blue-shifted line profile at the
end of the time series. The value of blue-shift is of the order of -10.6 km
 .
.
In the last two experiments A4 and B4, the peak value of blue-shift is reached
at t=24 s for experiment A4, and t=32 s for experiment B4, respectively.
The corresponding values of blue-shift are -1.7 km
 (A4), and -5.9 km
(A4), and -5.9 km
 (B4), respectively. At the end of the time series, there is an overall blue-shift
in both cases that corresponds to a value of -1.8 km
(B4), respectively. At the end of the time series, there is an overall blue-shift
in both cases that corresponds to a value of -1.8 km
 for experiment A4, and
-3.1 km
for experiment A4, and
-3.1 km
 for experiment B4.
for experiment B4.
6 Conclusions and future work
In the present simulations, we use small-scale energy depositions to study
the effect on observable parameters such as line profiles, line-shifts and
intensities.
The main conclusion following the C IV simulations is that the
higher the temperature at which the energy deposition takes place, the later
the response of the line. In particular, the peak value of red-shift
is reached at a later time if the energy release occurs at a higher temperature
of the initial background plasma. For C IV, the maximum red-shift varies
between 4 and 19 km
 for a variety of energy depositions and temperatures
in the atmosphere. Towards the end of each simulation, the line-shift approaches
zero.
for a variety of energy depositions and temperatures
in the atmosphere. Towards the end of each simulation, the line-shift approaches
zero.
From the O VI results, one can conclude that, as the energy deposition
takes place at increasing initial plasma temperatures, there is a
turn-over point at which the blue-shift of the line profile changes into
red-shift at early times. Furthermore, the more energy is released, the
more complex the related changes in the spectra. In particular, at some high
value of energy deposition, more than one Doppler-shifted component start to be
present in the spectra. For O VI 1032 Å and for energy deposition below
the line formation temperature, we have a blue-shift ranging from -2 km
 to -8 km
to -8 km
 .
.
For Ne VIII, only blue-shifts are observed in the time series. This
is because in all these cases the initial temperature at the site of the
explosion is either below or close (experiments A4 and B4) to the temperature
of formation of the Ne VIII line. Just like in the case of the O VI
line, at some high value of the energy deposition, Doppler-shifted
components start to be present in the spectra. This time, however, two
components are seen instead of only one in the case of O VI.
The intensity variations resulting from these experiments are quite different
from an earlier study by Teriaca et al. (1999b) and Teriaca & Doyle (2001).
Here, we have a very different initial state, e.g., the above paper had a
coronal loop but here there is a magnetic field reversal region. Secondly, the
distribution of physical variables along the loop in the above work
is different than that in this model.
Thirdly, the previous modelling was a 1D hydrodynamic simulation, while
these are 2D MHD.
Comparing the C IV modelling results with the C III 977 Å
observations (the C III line is formed at 80 000 K compared with
C IV at 100 000 K), we see that there is good overall agreement. The
observed time-averaged C III line-shift varies between 2 and 20 km
 depending on the amount of magnetic activity, similar to the C IV line
simulations. The highly variable nature of the observed line-shift could be
re-produced via a series of energy releases (of the order of magnitude as given
in Table 1), occurring approximately every 20 to 60 s. with the most of these
being low energy events, probably less than
depending on the amount of magnetic activity, similar to the C IV line
simulations. The highly variable nature of the observed line-shift could be
re-produced via a series of energy releases (of the order of magnitude as given
in Table 1), occurring approximately every 20 to 60 s. with the most of these
being low energy events, probably less than
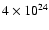 erg. On the other hand,
the agreement between the O VI simulations and observations is poor, with
the simulations indicating an average blue-shifted plasma of a few km
erg. On the other hand,
the agreement between the O VI simulations and observations is poor, with
the simulations indicating an average blue-shifted plasma of a few km
 while
the observations show a slightly red-shifted plasma. For Ne VIII, both the
internetwork and network observational data imply an up-flow, in agreement with the
models. However, the bright network observations show a down-flow. This could indicate
that the bright network is the region where
spicular down-flows are dominant and therefore the simple model presented here is
more applicable to the internetwork and "normal'' network regions.
while
the observations show a slightly red-shifted plasma. For Ne VIII, both the
internetwork and network observational data imply an up-flow, in agreement with the
models. However, the bright network observations show a down-flow. This could indicate
that the bright network is the region where
spicular down-flows are dominant and therefore the simple model presented here is
more applicable to the internetwork and "normal'' network regions.
Acknowledgements
Research at Armagh Observatory is grant-aided by the N. Ireland Dept. of Culture,
Arts and Leisure. We are very thankful to K. Galsgaard for useful
comments and suggestions made while the manuscript was prepared, to R. Erdélyi
for initial discussions and K. Curdt for discussions on the wavelength calibration.
This work was in part supported by PPARC
grants PPA/G/S/1999/00055, PPA/V/S/1999/00628 and PPA/V/S/1999/00668 while the
SUMER project is financially supported by DLR, CNES, NASA, and PRODEX.
- Banerjee, D., O'Shea, E., Doyle, J. G., & Goossens, M. 2001,
A&A, 371, 1137
In the text
NASA ADS
- Brekke, P., Hassler, D. M., & Wilhelm, K. 1997, Sol. Phy., 175, 349
In the text
- Chae, J., Yun, H. S., & Poland, A. I. 1997, ApJ, 480, 817
In the text
NASA ADS
- Chae, J., Yun, H. S., & Poland, A. I. 1998, ApJS, 114, 151
In the text
NASA ADS
- Dammasch, I. E., Wilhelm, K., Curdt, W., & Hassler, D. M. 1999, A&A, 346, 285
In the text
NASA ADS
- Doyle, J. G., van den Oord, G. H. J., O'Shea, E., & Banerjee, D.
1998, Sol. Phys., 181, 51
In the text
NASA ADS
- Hansteen, V. H. 1993, ApJ, 402, 741
In the text
NASA ADS
- Hansteen, V. H., & Wikstøl, O. 1994, A&A, 290, 995
In the text
NASA ADS
- Hansteen, V. H., Maltby, P., & Malagoli, A. 1977, ASP Conf. Ser.,
111, ed. R. D. Bentley, & J. T. Mariska, 116
In the text
- Hansteen, V. H., Betta, R., & Carlsson, M. 2000, A&A, 360, 742
In the text
NASA ADS
- Lemaire, P., Wilhelm, K., & Curdt, W., et al. 1997, Sol. Phys.,
170, 105
NASA ADS
- Joselyn, J. A., Munro, R. H., & Holzer, T. E. 1979a, Sol. Phys., 64, 57
NASA ADS
- Joselyn, J. A., Munro, R. H., & Holzer, T. E. 1979b, ApJS, 40, 793
NASA ADS
- Mariska, J. T., & Boris, J. P. 1983, ApJ, 267, 409
In the text
NASA ADS
- Mariska, J. T. 1988, ApJ, 334, 489
In the text
NASA ADS
- Mariska, J. T. 1992, The Solar Transition Region
(Cambridge University Press, Cambridge)
In the text
- Peter, H. 2000, A&A, 360, 761
In the text
NASA ADS
- Peter, H. 2001, A&A, 374, 1108
In the text
NASA ADS
- Peter, H., & Judge, P .G. 1999, ApJ, 522, 1148
In the text
NASA ADS
- Pneuman, G. W., & Kopp, R. A. 1978, Sol. Phys., 57, 49
In the text
NASA ADS
- Reale, F., Peres, G., & Serio, S. 1997, A&A, 318, 506
NASA ADS
- Roussev, I., Galsgaard, K., Erdélyi, R., & Doyle, J. G. 2001a,
A&A, 370, 298
In the text
NASA ADS
- Roussev, I., Doyle, J. G., & Galsgaard, K., & Erdélyi, R.
2001b, A&A, 380, 719
In the text
NASA ADS
- Sarro, L. M., Erdélyi, R., Doyle, J. G., & Perez, E. P. 1999,
A&A, 351, 721
In the text
NASA ADS
- Spadaro, D., Antiochos, S. K., & Mariska, J. T. 1991, Sol. Phys.,
382, 338
In the text
- Teriaca, L., Banerjee, D., & Doyle, J. G. 1999a, A&A, 349, 636
In the text
NASA ADS
- Teriaca, L., Doyle, J. G., Erdélyi, R., & Sarro, L. M. 1999b,
A&A, 352, L99
In the text
NASA ADS
- Teriaca, L., Doyle, J. G., Erdélyi, R., Sarro, L. M., & Banerjee,
D. 1999c, Proc. 9th European Meet. on Sol. Phys., ESA SP-448, 379
- Teriaca, L., & Doyle, J. G. 2001, Ap&S, 259, 307
In the text
- Wikstøl, Ø., Hansteen, V. H., Carlsson, M., & Judge, P. G.
2000, ApJ, 531, 1150
NASA ADS
- Wilhelm, K., Curdt, W., Marsch, E., et al. 1995, Sol. Phys., 162, 189
NASA ADS
- Wilhelm, K. 2000, A&A, 360, 351
In the text
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=12cm,clip]{2215f1.ps}\end{figure}](/articles/aa/full/2002/46/aa2215/Timg9.gif)
![\begin{figure}
\par\includegraphics[width=14.5cm,height=4.5cm,clip]{MS2215_fig2a...
...par\includegraphics[width=14.5cm,height=3.4cm,clip]{MS2215_fig2d.ps}\end{figure}](/articles/aa/full/2002/46/aa2215/Timg12.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{2215f3.ps}\end{figure}](/articles/aa/full/2002/46/aa2215/Timg13.gif)
![$\displaystyle \left[{(1 + \beta - b_y^2) \over \beta}
\right]^{\theta}
\left\{ ...
... -
\tanh \left[ \epsilon ~ (y^\ast + y_{\rm s}^\ast) \right]
\right\} \right\},$](/articles/aa/full/2002/46/aa2215/img30.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=8.7cm,clip]{MS2215_fig4a.ps}\hsp...
...\hspace*{2mm}
\includegraphics[width=8.7cm,clip]{MS2215_fig4d.ps} }
\end{figure}](/articles/aa/full/2002/46/aa2215/Timg44.gif)
![$\displaystyle E_{\rm dep} = E_0 ~ \alpha ~ F(t^\ast)
\exp\left\{ - \left[{{x^\ast}^2 + \left(y^\ast - y_0^\ast \right)^2 \over {\sigma}}
\right] \right\},$](/articles/aa/full/2002/46/aa2215/img45.gif)
![$\displaystyle F(t^\ast) =
\left\{\begin{array}{ll}
t^\ast / t_{\rm rise}^\ast; ...
...t^\ast - t^\ast_{\rm rise})}]; & t^\ast_{\rm rise} < t^\ast.
\end{array}\right.$](/articles/aa/full/2002/46/aa2215/img46.gif)
![$\displaystyle \frac{\partial N_i}{\partial t} + u_y \cdot \frac{\partial N_i}{\...
...i-1,i} + N_{i+1} \alpha_{\rm r}^{i+1,i} N_{i+1} \alpha_{\rm d}^{i+1,i} \right],$](/articles/aa/full/2002/46/aa2215/img79.gif)
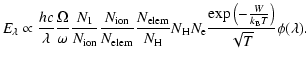
![$\displaystyle \phi(\lambda)=\frac{\exp{-\left[\frac{(\lambda-\lambda_0-\lambda_{\rm s})}
{\Delta \lambda_0}\right]^2}}{\Delta \lambda_0 \sqrt{\pi}}$](/articles/aa/full/2002/46/aa2215/img92.gif)
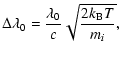
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2215_fig5a.ps}\par\inclu...
...215_fig5b.ps}\par\includegraphics[width=8.8cm,clip]{MS2215_fig5c.ps}\end{figure}](/articles/aa/full/2002/46/aa2215/Timg99.gif)
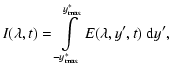
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=8cm,clip]{MS2215_fig6a...
...{2mm}
\includegraphics[angle=-90,width=8cm,clip]{MS2215_fig6d.ps} }
\end{figure}](/articles/aa/full/2002/46/aa2215/Timg102.gif)