2 Perturbation theory

Our aim is to investigate smaller effects like slow streaming large-scale poloidal fields. The first step is to solve the forward problem, i.e., to calculate theoretically the influence on the solar acoustic modes. We will follow the work of Lavely & Ritzwoller (1992). The starting point for these calculations is a reference model; we base our work on "Model S'' from Christensen-Dalsgaard et al. (1996). The reference model describes the Sun as a star in hydrostatic equilibrium. It is one-dimensional, i.e., all physical quantities depend on one variable, the distance r from the solar center. It follows that the solar model is spherically symmetric, non-rotating, non-magnetic, and static.

This reference model is subject to acoustic modes, which are characteristic spatial displacement patterns $\vec{\delta r}(r,\theta,\phi;\tau)$, that oscillate with fixed frequencies ($\theta$ and $\phi$ are the colatitude and the longitude; $\tau$ is the time). The equation of motion of such an oscillatory displacement $\vec{\delta r}=\vec{\xi}\exp\{-{\rm i}\omega \tau\}$ with amplitude $\vec{\xi}(r,\theta,\phi)$ and angular frequency $\omega$ is derived in Christensen-Dalsgaard (1998) and is given by

$$\rho_0\frac{\partial^2\vec{\delta r}}{\partial \tau^2} = -\om... ...ec{\delta r} = -\nabla p' + \rho_0 \vec{g}' + \rho'\vec{g}_0 ,$$ (1)

where p', $\rho'$, and $\vec{g}'$ are perturbations of the equilibrium quantities pressure p₀, density $\rho_0$ and gravitational acceleration $\vec{g}$.

Equation (1) has a spectrum of eigensolutions with eigenvalues $\omega^2_k$, where k=(n,l,m) stands for a triplet of indices, respectively, the radial order, the harmonic degree, and the azimuthal order. We will concentrate on the p-modes whose restoring force is the pressure gradient.

For a spherical symmetric solar model the solar p-modes are degenerate, i.e., each p-mode of a multiplet that consists of the 2l+1 eigenfunctions with identical n and l values has the same frequency $\omega_{nl}$ independent of m. In Fig. 1 we show the spectrum or $(l,~\nu)$ diagram of the p-modes with $l\le 150$ and $\nu=\omega/2\pi\le 5$  mHz that were calculated on the basis of "Model S'' (Christensen-Dalsgaard et al. 1996).

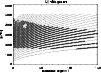Figure 1: $(l,~\nu)$ diagram for the used solar model. The marked modes are the ones used for the numerical experiment and correspond to the modes observed by GONG.

In this paper we investigate velocity fields $\vec{v}$ in the convection zone; they lift the degeneracy by an additional advection term in the equation of motion (1), (Christensen-Dalsgaard 1998; Lavely & Ritzwoller 1992)

$${-\omega^2\rho_0\vec{\xi} - 2 {\rm i}\omega \rho_0 {(\vec{v}\... ...\xi}}} = {{-\nabla {p'}} + \rho_0 \vec{g}' + \rho'\vec{g}_0}.$$ (2)

If the magnitude of the velocity $\vec{v}$ is small compared with the sound speed, first-order perturbation theory can be used to calculate corrections $\delta\omega^2$ of the eigenvalue $\omega^2$caused by the influences of velocity fields

$$\delta\omega^2=-2{\rm i}\omega \frac{\int \rho_0 \vec{\xi}_{k... ...d}^3r}{\int\rho_0 \vert\vec{\xi}_{k'}\vert^2~ {\rm d}^3r}\cdot$$ (3)

Here we treated the Hermitian operator

$$\mathcal{H}_1\equiv- 2 {\rm i} \omega \rho_0 (\vec{v}\cdot \nabla)$$ (4)

in Eq. (2) as perturbation of the Hermitian operation

$$\mathcal{H}_0\vec{\xi} \equiv -\nabla p' + \rho_0 \vec{g}' + \rho' \vec{g}_0\ = -\omega^2 \rho_0\vec{\xi}.$$ (5)

For our purposes $\vec{v}$ is decomposed into a toroidal and a poloidal field and the two components are expanded in spherical harmonics Y_s^t defined by

$$Y_s^t(\theta,\phi)= \frac{(-1)^{s+t}}{2^s s!} \left[\frac{(2s+1)(... ...al}{\partial(\cos\theta)}\right]^{s+t}(\sin\theta)^{2s} {\rm e}^{{\rm i}t \phi}$$ (6)

  with harmonic degree s and azimuthal order t. Hence

$$\vec{v}(\vec{r})=\sum_{s=0}^{\infty}\sum_{t=-s}^s \left[\vec{T}_s^t(r,\theta,\phi) + \vec{P}_s^t(r,\theta,\phi)\right] ,$$ (7)

where

$$\vec{T}_s^t(r,\theta,\phi)=-w_s^t(r)\vec{e}_r\times\nabla_h Y_s^t(\theta,\phi)$$ (8)

is the toroidal and

$$\vec{P}_s^t(r,\theta,\phi)=u_s^t(r)Y_s^t(\theta,\phi)\vec{e}_r + v_s^t(r) \nabla_h Y_s^t(\theta,\phi) ,$$ (9)

is the poloidal field component. The quantities w_s^t(r), u_s^t(r), and v_s^t(r) are the depth-dependent expansion coefficients, and $\nabla_h$ is the surface gradient operator (Lavely & Ritzwoller 1992). This allows us to study the influence of differential rotation and of convection cells on the mode frequencies.

2.1 Differential rotation

The differential rotation, which is a pure toroidal velocity field, can be expanded in zonal components of spherical harmonics Y_s⁰ according to Eqs. (7) and (8)

$$\vec{v}_{\rm rot}(\vec{r})=\sum_s -w_s^0(r) \vec{e}_r \times \nabla_h Y_s^0(\theta) .$$ (10)

The results of a degenerate perturbation calculation (n'=n, l'=l in Eq. (3)) are corrected frequencies that depend on the azimuthal order m

  

$$\omega_{nl}(m) \omega_{nl} + \sum_{s\ {\rm odd}}\int\limits_0^R K_{nls}(r) w_s^0... ...\rm d}r \left(\begin{array}{ccc} {s}&{l}&{l}\\ {0}&{m}&{-m}\end{array} \right)$$ = (11)

$$\omega_{nl}+ \sum_{s\ {\rm odd}} a_{s}(n,l) P_s^{(l)}(m) ,$$ = (12)

where K_nls(r) depends on the eigenfunction and the geometry of the velocity field component indexed with s. The last factor in Eq. (11) is a Wigner 3j symbol (Edmonds 1960), for which we also use the notation (l₁ l₂ l₃/m₁ m₂ m₃), with the l_i as the harmonic degrees and the m_i as the azimuthal orders. The sum in Eq. (11) is only carried out over odd sbecause K_nls(r) vanishes for even s (Lavely & Ritzwoller 1992). The frequency shift can also be expressed more generally in terms of any orthogonal functions P_s^(l)(m). This is given in Eq. (12), where we imply that symmetry properties of these functions lead to a mirroring of the rotation in the odd components. Hence, the inferred rotation rates are symmetric about the equator. The expansion coefficients a_s(n,l) are weighted averages of the component w_s⁰(r) of the rotation

$$a_s(n,l)=\int\limits_0^R K_{nls}(r) w_s^0(r) r^2~ {\rm d}r .$$ (13)

The weighting is governed by the kernels K_nls(r) that depend on the region a mode samples (moreover the kernels depend on the structure of the solar interior, so that the determination of the frequency shift and later on the inversion for the solar interior are only as good as the model used). Hence the differential rotation results in a lifting of the degeneracy of the p-mode frequencies. Figure 2 shows an example for three multiplets (we use the same sign convention as GONG where within a multiplet frequencies decrease with increasing m as adopted by Hathaway 1992).

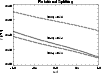Figure 2: Lifting of degeneracy by differential rotation (solar $\Omega (r,\theta )$, first obtained by inversion of GONG data) for several multiplets l=34, n=15; l=40, n=14; l=30, n=16.

2.2 Large-scale flows

In this section we study the effect of large-scale flows, located in the convection zone, on solar oscillations. By large-scale flows we mean flows that have only poloidal and non-zonal toroidal components. We refer to zonal toroidal components as differential rotation, for which we already did the calculations in the last section.

We focus only on the effect of the poloidal components on the solar oscillations, because the effect of the non-zonal toroidal flow components should be the smallest (Roth 2001). A poloidal flow field will result in a frequency shift of $\delta\omega=0$ in the case (n',l',m')=(n,l,m), because of three selection rules (Lavely & Ritzwoller 1992). The first two rules arise from properties of the Wigner 3j symbols which vanish except when the harmonic degrees l, l', and s satisfy a triangular condition (Edmonds 1960), i.e.

$$\vert l'-s\vert\le l ,\ \vert s-l\vert\le l',\ \vert l-l'\vert\le s ,$$ (14)

and the azimuthal orders satisfy the equation

 

t+m-m'=0 . (15)

The third rule comes from the radial integration in (3) and means that toroidal flows contribute to the frequency shift only if s+l+l' is odd, and poloidal flows only if s+l+l' is even. In the case of self-coupling, i.e. (n',l')=(n,l), poloidal flows have no influence on the frequencies. But for $(n',l')\not=(n,l)$ the calculations of quasi-degenerate perturbation theory result in non-zero frequency shifts. Because of the analogy to the coupling of angular momenta this is called coupling of p-modes. For the coupling of only two modes the shifted squares of the frequencies $\omega_{nl}^2$and $\omega_{n'l'}^2$ of the two p-modes involved are given by

 

$$\omega_{nl/n'l'}^2(m)=\frac{\omega_{nl}^2+\omega_{n'l'}^2}{2}\pm\... ...a_{nl}^2-\omega_{n'l'}^2\right)^2 + 4 \left\vert H_{nn'll'}^{mm'}\right\vert^2}$$ (16)

where

$$H_{nn'll'}^{mm'}=\int\limits_0^R K_{nn'll' s}(r) u_s^t(r) r^2... ...n{array}{ccc} {s}&{l}&{l'}\\ {t}&{m}&{-m'} \end{array}\right)$$ (17)

with K_{nn'll' s}(r) being a kernel that depends on the eigenfunctions of the modes involved in the coupling and the angular geometry of the flow field (for a derivation of K_{nn'll' s}(r) compare with Eq. (90) in Lavely & Ritzwoller 1992). This means that coupling ( $H_{nn'll'}^{mm'}\not=0$) causes the frequency of one partner to be shifted upwards and that of the other partner shifted downwards (Roth & Stix 1999). As t is not necessarily equal to zero, the shifts within a multiplet are, due to properties of the Wigner 3j symbols, not necessarily symmetric about the frequency of the mode with azimuthal order m=0, which may itself be shifted. Coupling of one mode with several other modes is also possible; in this case the shifted frequencies are determined from the eigenvalues of the supermatrix Zwith elements $Z_{nn'll'}^{mm'}=\omega_{nl}^2 \delta_{nn'}\delta_{ll'}\delta_{mm'} + H_{nn'll'}^{mm'}$ described in Lavely & Ritzwoller (1992). This shows that the supermatrix Z is the sum of two matrices, a diagonal matrix consisting of $(2l+1) \times (2l+1)$ block matrices with entries $\omega_{nl}^2$ and the coupling matrix consisting of $(2l+1) \times (2l'+1)$ block matrices with the elements H_nn',ll'^mm'. The azimuthal-order superscripts determine the position of the matrix element within the respective block matrix.

For the numerical determination of the shifted frequencies it is helpful to limit the number of possible coupling partners by the requirement $\vert\omega_{n'l'}-\omega_{nl}\vert\le \Omega_{\rm range}$ with given $\Omega_{\rm range}$. In principle, we have to include all possible coupling partners. But according to Eq. (16), the strength of the coupling decreases with increasing difference in frequency, as can be seen by an expansion of the square root. This is characteristic for perturbation theory of quasi-degenerate eigenstates; it is for this reason that only modes with frequencies in close vicinity need to be taken into account. For the highest amplitudes of the velocity fields used in our calculations the contributions become more and more negligible for frequency differences above $\Omega_{\rm range}^{\rm max}=30$  $\mu$Hz. We can thus limit the number of possible partners and speed up the numerical calculations by setting  $\Omega_{\rm range} = 2 ~ \Omega_{\rm range}^{\rm max}$ without loss of generality. Moreover the selection rules will further reduce the number of couplers.

Coupling of modes leads to additional, and in the case $t\not=0$ to asymmetric, shifts in a multiplet, cf. the examples in Figs. 3 and 4.

Figure 3: Asymmetric shifted frequencies within the multiplet l=34, n=15 due to coupling to modes from the multiplets l=40, n=14 and l=30, n=16, caused by a poloidal flow field s=8, t=8 with $u_{\rm char}=100$  m s-1. The arrows indicate which shifts are caused by which coupling partner.

Figure 4: The multiplet l=34, n=15 and its coupling partners affected by a zonal poloidal flow s=8, t=0, $u_{\rm char}=100$ m s-1. The resulting frequency shifts are symmetric to m=0.

At this point we add a few remarks about the symmetry of the Wigner 3j symbols and the resulting sensitivity to various flows. These remarks will become essential for the understanding of the results presented in Sect. 4. The differential rotation leads to splittings that are anti-symmetric with respect to m=0 (cf. Fig. 2); the Wigner 3j symbols that represent these splitting are the (s l l/0 m -m)-symbols. Due to the third selection rule the contribution to the frequency shift is non-zero only for odd s. Therefore the expansion of the rotational splitting was given by the odd a_s-coefficients. Conversely the meridional flows lead to splittings symmetric about m=0 (cf. Fig. 4); the corresponding Wigner 3j symbols are the (s l l'/0 m -m)-symbols. Due to the selection rules the contribution to the frequency shift is non-zero for even s+l+l'. Therefore the expansion of the meridional-flow-splitting in terms of functions that are symmetric and anti-symmetric with respect to m=0 will be given by the expansion coefficients corresponding to the even functions. Any other poloidal flow field with $t\not=0$ will result in a distribution of the frequency shifts with no symmetry with respect to m=0, due to the second selection rule (15); therefore these shifts cannot be assigned to only even or only odd functions in an expansion.

As result of the combined effect of differential rotation and poloidal velocity fields, the frequencies within a multiplet might be distributed as shown in the example of Fig. 5 for differential rotation plus a poloidal velocity field with s=t=8.

Figure 5: Poloidal velocity fields (here s=t=8) lead to a deviation (+-symbols) from the rotational splitting (dots). To emphasize the deviation an amplitude $u_{\rm char}=200$ m s-1 was chosen.

Details on the models for the differential rotation and the poloidal flows underlying Figs. 2-5 are given in Sect. 3.1.