Our high signal-to-noise spectra enabled us to measure the intensity of the [Ne III] $\lambda$ 3869 line, and to derive upper limits to the intensities of [S III] $\lambda$ 9069 and [Ar III] $\lambda$ 7135, which allow us to make some inferences on the abundances of Ne, S and Ar.

$\begin{figure} \par\includegraphics[width=17.2cm,clip]{h3796f7}\end{figure}$

Figure 7: This figure presents various physical parameters for the grid of models in Fig. 5. From left to right, the columns present [O III] $\lambda$ 5007/ HH $\beta$ , the temperature in the O⁺⁺ zone, the weighted fraction of oxygen in the form of O⁺⁺, and the ionization correction factors for Ne⁺⁺, S⁺⁺, and Ar⁺⁺⁺ with respect to O⁺⁺. These data are required to derive the abundances of Ne, S, and Ar in PNG 135.9+55.9.

To compute abundances, we must rely upon the electron temperature and ionization structure provided by our models. The relevant quantities are shown in Fig. 7 for the models from Fig. 5. The first column of panels on the left repeats the [O III] $\lambda$ 5007/HH $\beta$ ratio from Fig. 7 for reference. The second column of panels gives the value of $T({\rm O^{++}})$ defined as:

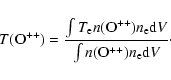$\begin{displaymath}% T({\rm O^{++}})= \frac{\int{T_{\rm e} n({\rm O^{++}}) n_{\rm e}{\rm d}V}}{\int {n({\rm O^{++}}) n_{\rm e}{\rm d}V}}\cdot \end{displaymath}$

(1)

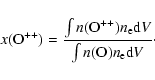$\begin{displaymath}% x({\rm O^{++}})= \frac{\int{ n({\rm O^{++}}) n_{\rm e}{\rm d}V}}{\int {n({\rm O}) n_{\rm e}{\rm d}V}}\cdot \end{displaymath}$

(2)

Using the same atomic data as in the photoionization code and taking as a characteristic temperature of the emission of the [Ne III] $\lambda$ 3869 and [O III] $\lambda$ 5007 lines a value of 30 000 K derived from our preferred models (Fig. 5), we find that Ne⁺⁺/O⁺⁺ $= 0.70\pm 0.4$ , where the uncertainty reflects the uncertainties of the [O III] $\lambda$ 5007 and [Ne III] $\lambda$ 3869 line intensities. We furthermore note that both O⁺⁺ and Ne⁺⁺ are minority ions (Fig. 7). Generally, one adopts Ne⁺⁺/O⁺⁺ = Ne/O. In our preferred models (those corresponding to $T_{\star }$ = 100 000 K), we find from Fig. 7 that the ionization correction factor is rather around 0.7, thus leading to ${\rm Ne}/{\rm O} = 0.5 \pm 0.3$ .

In a similar fashion, our observed limits on the intensities of the [Ar IV] $\lambda\lambda$ 4711, 4740 lines allow us to derive that Ar⁺⁺⁺/O⁺⁺ < 0.45. From our models (Fig. 7) we find that the ionization correction factor is 0.5, and therefore Ar/O < 0.23.

Given that the nebula is strongly density-bounded, the observed limits on the [N II] $\lambda$ 6584 and [S II] $\lambda$ 6716, $\lambda$ 6731 line intensities give only crude limits on abundance ratios involving these elements. With the ionization correction factors from our preferred model, we find N/H $<2.3\times 10^{-5}$ and S/H $<7\times 10^{-5}$ . Such limits are not very useful, except to infer that the N/H ratio is at most equal to that in the Orion nebula.

Our infrared spectra allow us to estimate upper limits to the intensities of [S III] $\lambda$ 9069 and [Ar III] $\lambda$ 7135, which are respectively $8\times 10^{-4}$ and $6\times 10^{-4}$ of the intensity of HH $\beta$ . These upper limits imply that ${\rm S}^{++}/{\rm O}^{++}< 0.031$ and ${\rm Ar}^{++}/{\rm O}^{++} < 0.012$ . In our preferred photoionization models, the ionization correction factor to derive Ar/O from ${\rm Ar}^{++}/{\rm O}^{++}$ is around 20, so that the upper limit on [Ar III] $\lambda$ 7135 implies Ar/O < 0.24 (in agreement with the upper limit derived from [Ar IV] $\lambda\lambda$ 4711, 4740). Regarding sulfur, we find that the ionization correction factor is around 3 for S/O from our models (Fig. 7), implying that ${\rm S}/{\rm O} < 0.094$ . It must be noted that the atomic data concerning the ionization structure of S and Ar are uncertain (see e.g. Ferland et al. 1998). Our models, were computed without including dielectronic recombination to low-lying levels for these ions. It is likely that the real ionization fractions of S⁺⁺and Ar⁺⁺⁺ are actually higher than predicted by the models, giving smaller ionization correction factors and more stringent limits.

**Table 6:** $\alpha$ -element abundance ratio comparison with other objects.
object	Ne/O	S/O	Ar/O
PNG 135.9+55.9 ^a	$0.5\pm 0.3$	<0.094	<0.23
Galactic disk PNe ^b	0.26	0.017	0.005
Galactic halo PNe ^c	0.13	0.016	0.0016
Orion nebula ^d	0.18	0.03	0.014
Sun ^e	0.18	0.03	0.004

^a This work.
^b Kingsburgh & Barlow (1994).
^c Howard et al. (1997). These authors also show that the abundance ratios are more dispersed in halo PNe than in disk PNe.
^d Esteban et al. (1998).
^e Grevesse & Sauval (1998).

It is interesting to compare the ratios of Ne/O, S/O and Ar/O we find for PNG 135.9+55.9 with those of other kinds of objects. Table 6 shows the values for a sample of PNe in the Galactic disk (Kingsburgh & Barlow 1994) and in the Galactic halo (Howard et al. 1997), for the Orion nebula (Esteban et al. 1998), and for the Sun (Grevesse & Sauval 1998). This table is of course subject to uncertainties. Even the solar abundances are quite uncertain for Ne, Ar and O (see Grevesse & Sauval 1998; the recent oxygen abundance determination from Allende Prieto et al. 2001 yields a value that is only 73% that obtained by Grevesse & Sauval 1998). One might then argue that the Ne/O ratio in PNG 135.9+55.9 is compatible with the solar value, but we note that it is about twice the value found in the Orion nebula and in disk planetary nebulae, where the systematic errors in the abundance derivations are likely to be similar. Supposing our Ne/O ratio is corect, it might indicate some conversion of O into Ne by $\alpha$ capture. A few similar cases are known among planetary nebulae (e.g., BB-1 has a ${\rm Ne}/{\rm O} = 0.77$ ; Howard et al. 1997). Another possibility is that the material from which the progenitor of PNG 135.9+55.9 formed had an anomalous Ne/O ratio. Abundance studies of metal-poor stars indicate that the very early galaxy was chemically-inhomogeneous, with individual sites of star formation being influenced by the explosions of nearby supernovae (e.g., Burris et al. 2000). The yields of O and Ne from individual supernovae are also a function of the stellar mass (Woosley & Weaver 1995; Thielemann et al. 1996), while observations of metal-poor halo stars indicate that the scatter in oxygen abundances is 0.3-0.5 dex at very low oxygen abundances (e.g., Israelian et al. 2001). As a result, it is probably not surprising that the progenitor of PNG 135.9+55.9 might not have formed out of material with the same Ne/O ratio that has characterized the more recent Galactic disk. Regardless, any conversion of O into Ne is at most modest. Even were all of the Ne formed by nuclear processing from oxygen, the initial oxygen abundance would have been only 0.18 dex larger than our preferred values. Thus, the extremely low oxygen abundance in PNG 135.9+55.9 is genuine and not due to nuclear and mixing processes in the progenitor star. The oxygen abundance in PNG 135.9+55.9 should consequently reflect the chemical composition of the medium out of which the star was made. The limits we obtain on S/O and Ar/O in our object are consistent with this view (although the limits are not very stringent).

The accuracy of the helium line intensities achieved in the present observations raised the hope of obtaining very accurate helium abundances. Taking the intensities determined from our CFHT observations and adopting a temperature of 30 000 K as inferred from our models and case B coefficients from Storey & Hummer (1995) we find that He⁺⁺/H⁺ $= (7.50 \pm 0.14)\times 10^{-2}$ . The upper limit to the intensity of He I $\lambda$ 5876 in the same spectra gives an upper limit to He⁺/H⁺ of $0.24\times 10^{-2}$ when using the emissivities from Benjamin et al. (1999) in the low density limit. A proper determination of the uncertainty in the derived helium abundance should, however, account for collisional excitation of the lines, a possible small amount of reddening, possible deviations from case B, possible underlying absorption, as well as temperature gradients inside the nebula. All of this can only be attempted once the H $\alpha$ /HH $\beta$ problem is solved. It is therefore premature to propose an accurate value for the helium abundance in PNG 135.9+55.9.

5 The abundances of the remaining elements