**Table 2:** Raw line intensities relative to H $\beta$ for the optical spectra^a.
ion	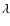$\lambda$	SPM1	SPM2	CFHT	SPM3^b	SPM4
[Ne V	3426			<9.6
[O II]	3727			<2.1
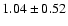[Ne III]	3869			$1.04\pm 0.52$
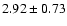H I	3889			$2.92\pm 0.73$
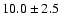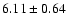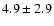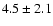H I	3970	$10.0\pm 2.5$		$6.11\pm 0.64$	$4.9\pm 2.9$	$4.5\pm 2.1$
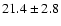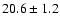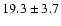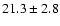H I	4101	$21.4\pm 2.8$		$20.6\pm 1.2$	$19.3\pm 3.7$	$21.3\pm 2.8$
C II	4267			<1.1		<3.0
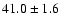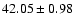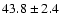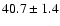H I	4340	$41.0\pm 1.6$		$42.05\pm 0.98$	$43.8\pm 2.4$	$40.7\pm 1.4$
[O III]	4363	<1.9		<0.88		<1.8
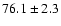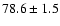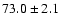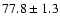He II	4686	$76.1\pm 2.3$		$78.6\pm 1.5$	$73.0\pm 2.1$	$77.8\pm 1.3$
[Ar IV]^c	4711	<2.0		<1.0		<1.4
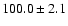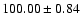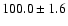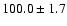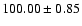H I	4861	$100.0\pm 2.1$	$100.00\pm 0.84$	$100.0\pm 1.6$	$100.0\pm 1.7$	$100.00\pm 0.85$
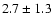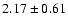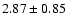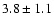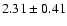[O III]	5007	$2.7\pm 1.3$	$2.17\pm 0.61$	$2.87\pm 0.85$	$3.8\pm 1.1$	$2.31\pm 0.41$
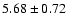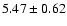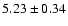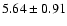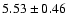He II	5412	$5.68\pm 0.72$	$5.47\pm 0.62$	$5.23\pm 0.34$	$5.64\pm 0.91$	$5.53\pm 0.46$
He I	5876	<0.47	<0.69	<0.28	<1.4	<0.62
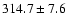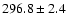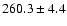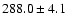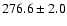H I	6563	$314.7\pm 7.6$	$296.8\pm 2.4$	$260.3\pm 4.4$	$288.0\pm 4.1$	$276.6\pm 2.0$
[N II]	6583	<3.2	<1.4	<0.45	<1.3	<0.74
[S II]	6716				<1.3	<0.74
[S II]	6731				<1.3	<0.74
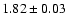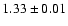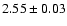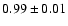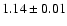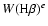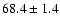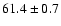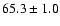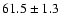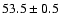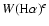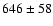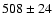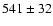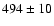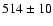$F({\rm H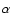\beta})^d$		$1.82\pm 0.03$	$1.33\pm 0.01$	$2.55\pm 0.03$	$0.99\pm 0.01$	$1.14\pm 0.01$
$W({\rm H\beta})^e$		$68.4\pm 1.4$	$61.4\pm 0.7$	$65.3\pm 1.0$	$61.5\pm 1.3$	$53.5\pm 0.5$
$W({\rm H\alpha})^e$		$646\pm 58$	$508\pm 24$	$541\pm 32$	$494\pm 10$	$514\pm 10$
H $\alpha$ range^f		304-318	256-350	258-267	265-324	241-321

^a When no uncertainty is given, the value represents a $2\sigma$ upper limit to the flux in the line.
^b These observations were obtained through clouds.
^c These upper limits also apply to [Ar IV] $\lambda$ 4740.
^d This is the total flux in emission measured at H $\beta$ in units of 10^-14 erg s^-1 cm^-2.
^e These are the equivalent widths in Å of H $\beta$ and H $\alpha$ in emission.
^f This is the total range spanned by the values of ${\rm H}\alpha/{\rm H}\beta$ among the individual spectra.

Table 1 presents a summary of our new spectroscopic observations of PNG 135.9+55.9. This table includes the dates of the observations, the instrumental configuration, and the flux and wavelength standards that were used. The only observing run that suffered from non-photometric conditions was that of 5 Mar. 2002, when significant cloud cover affected observations of both PNG 135.9+55.9 and the standard star.

The spectroscopy from the Observatorio Astronómico Nacional in San Pedro Mártir, Baja California, Mexico (SPM) was obtained using the Boller & Chivens spectrograph (B&C) and three different gratings during four observing runs. For the 2001 observations, a rather wide slit (3 $.\!\!^{\prime\prime}$ 8) was used to better measure the total fluxes, while, for the 2002 observations, a narrower slit was used to obtain higher spectral resolution and better sensitivity to fainter lines. The standard stars were observed with an even wider slit (9 $^{\prime\prime}$ ). In all cases, the slit was oriented east-west on the sky. Spectra of the illuminated dome wall were obtained to serve as flat field images. Bias images were obtained at the beginning and end of the night.

The spectroscopy at the Canada-France-Hawaii Telescope (CFHT) was obtained with the Multi-Object Spectrograph (MOS; Le Fèvre et al. 1994). Both the object and the standard star were observed through a 5 $^{\prime\prime}$ slit. However, the observations of PNG 135.9+55.9 were obtained the night before those of the standard star. Spectra of the internal halogen lamp were obtained to serve as flat field images.

The spectroscopy at the William Herschel Telescope (WHT) was obtained using the red arm of the ISIS spectrograph. The object was observed through a 1 $^{\prime\prime}$ slit, while the standard stars were observed with a 10 $^{\prime\prime}$ slit. For these observations, the slit was oriented at the parallactic angle. Spectra of the internal lamp were obtained to serve as flat field images while spectra of the sky were used to correct for the slit illumination.

All of the spectroscopy was reduced using the Image Reduction and Analysis Facility (IRAF) software package (specifically the specred package). In all cases, the overscan bias was subtracted from each image. For the SPM data, the overscan-subtracted bias images obtained during the night were combined and subtracted from all of the images. Next, the pixel-to-pixel variations were removed by division of the flat field image. For the WHT data, the slit illumination correction was then applied. The sky emission was subtracted during the extraction of the one dimensional spectra by defining sky regions on both sides of the object spectra and interpolating between them with a straight line. The wavelength calibration was performed using arc lamp spectra obtained at the time of the object observations. Finally, the spectra were calibrated in flux using the observations of the standard stars (Table 1) to determine the instrumental sensitivity function. The individual spectra were calibrated in both wavelength and flux before being summed together.

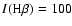Table 2 presents the raw line intensities relative to H $\beta$ measured in the optical spectral region for PNG 135.9+55.9, normalized such that $I({\rm H}\beta)=100$ . The line intensities presented in Table 2 are those for the summed spectra from each observing run. The line intensities were measured using the software described by McCall et al. (1985). 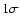The uncertainties quoted for each line intensity ( $1 \sigma$ ) include contributions from the fit to the line itself, from the fit to the reference line, and from the noise in the continuum for both the line and reference line. When only a limit is given, this corresponds to a 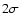$2\sigma$ upper limit to undetected lines.

**Table 3:** Raw line fluxes for the WHT spectra.
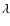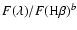ion	$\lambda$	flux^a	$F(\lambda)/F({\rm H}\beta)^b$
[Ar III]	7135	<0.45	<0.06
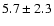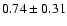H I	8750	$5.7\pm 2.3$	$0.74\pm 0.31$
[S III]	9069	<0.59	<0.08
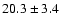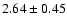H I	9229	$20.3\pm 3.4$	$2.64\pm 0.45$

^a The fluxes are given in units of $10^{-17}~{\rm erg}~{\rm s}^{-1}~{\rm cm}^{-2}$ . When no uncertainty is given, the value is a 2 $\sigma$ upper limit to the flux in the line.
^b These flux ratios are relative to $F({\rm H}\beta)$ measured for the CFHT spectrum on a scale where $I({\rm H}\beta)=100$ .

$\begin{figure} \par\includegraphics[angle=90,width=14.2cm,clip]{h3796f1}\end{figure}$

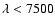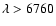Figure 1: We compare the spectra of PNG 135.9+55.9 and the standard star G191B2B on an arbitrary magnitude scale. For PNG 135.9+55.9, we plot the CFHT spectrum for $\lambda < 7500$ Å and the WHT spectrum for $\lambda > 6760$ Å, neither corrected for reddening. The WHT spectrum was normalized to the CFHT spectrum as described in the text. For G191B2B ( B-V = -0.32 mag), we plot the Oke (1990) fluxes. As noted by Tovmassian et al. (2001), PNG 135.9+55.9 has a remarkably blue continuum.

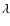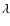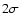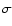Table 3 presents the raw fluxes and the intensity ratios relative to H $\beta$ for the WHT spectrum. The only line definitely detected is P9 $\lambda$ 9229; P12 $\lambda$ 8750 is detected at only the $2\sigma$ level. Again, when no uncertainty is given, the value represents a 2 $\sigma$ upper limit to the line intensity. These line intensities and limits were measured using IRAF's splot routine. The fluxes represent the fluxes measured directly in the summed WHT spectrum. The intensity ratios relative to H $\beta$ were computed adopting the H $\beta$ flux from the CFHT spectrum and correcting the WHT fluxes for the difference in the slit widths used. 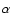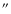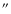Based upon the spatial profile of H $\alpha$ from the CFHT spectrum, a 5 $^{\prime\prime}$ slit intercepts 3.32 times more nebular emission than a 1 $^{\prime\prime}$ slit. The WHT fluxes were then multiplied by this factor when computing the relative intensities presented in Table 3. Comparing the continuum fluxes measured in the CFHT and WHT spectra in the 6760-7500 Å region, where the fringing in the CFHT spectrum is not too severe, the continuum flux in the WHT spectrum should be scaled upwards by a factor of 2.07 to match that in the CFHT spectrum. 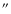This scale factor is in good agreement with the value of 1.95 expected based upon the 1 $^{\prime\prime}$ slit used for the WHT spectra and the 1 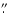$.\!\!^{\prime\prime}$ 22 seeing measured from the spatial profile of the continuum in the summed spectrum.

Generally, there is excellent agreement among the line intensities over the wavelength range H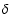 $\delta$ -He II 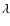$\lambda$ 5412. In the near-ultraviolet, the SPM spectrograph has very low efficiency and the upper limits we derive from those spectra are considerably less restrictive than the detections or limits from the CFHT spectrum. We give upper limits to the [S II] line intensities only for the last two SPM runs, since the CCD used for the first two SPM observing runs and that at CFHT suffered from fringing in the red.

**Table 4:** Log of the direct imaging observations.
Telescope	Date	CCD	Instrument	Filter^a	Exposure time^b

SPM 2.1 m	27-28 May 2001	SITe3^c	Mexman	H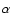 $\alpha$ (6565 Å, 11 Å)	3900 s (5)
				red cont. (6650 Å, 46 Å)	1500 s (3)
NOT 2.6 m	1-2 June 2001	CCD7^d	ALFOSC	y # 18(5470 Å, 220 Å)	2700 s (4)
				H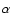 $\alpha$ # 21(6564 Å, 33 Å)	2700 s (4)

^a The central wavelength and the bandpass width for each filter are given in parentheses.
^b The number of images is given in parentheses.
^c This CCD has 24 $\mu$ m pixels in a $1024\times 1024$ format. Its gain and readnoise are 1.3 e $^- /{\rm pix}$ and 8 e^-, respectively. The plate scale is $0\hbox{$.\!\!^{\prime\prime}$ }312/{\rm pix}$ .
^d This CCD has 15 $\mu$ m pixels in a $2048\times 2048$ format. Its gain and readnoise are $\sim$ $1~{\rm e}^- /{\rm pix}$ and 6 e^-, respectively. The plate scale is $0\hbox{$.\!\!^{\prime\prime}$ }188/{\rm pix}$ .

The notable exception to the good agreement among the line intensities is H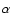 $\alpha$ . There is significant variation in the 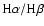${\rm H}\alpha/{\rm H}\beta$ ratio among the summed spectra for the different observing runs and between individual spectra for at least the SPM2 and SPM4 observing runs. In both the SPM2 and SPM4 data sets, the dispersion among the H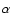 $\alpha$ fluxes for the individual spectra also significantly exceeds that for the H $\beta$ fluxes. 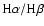In the last line of Table 2, we indicate the range of ${\rm H}\alpha/{\rm H}\beta$ values found among the individual spectra during each observing run. This variation is very puzzling, since we normally obtained all of the spectra consecutively on the same night (SPM2 is the exception). If this variation is real, it is occurring (irregularly) on a time scale of the order of an hour. Such behaviour is not at all expected in a nebular plasma (e.g., Aller 1987). 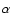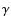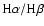In a typical SPM spectrum (of a half hour duration), at least 50 000, 15 000, and 2500 photons are detected at H $\alpha$ , H $\beta$ , and H $\gamma$ , respectively, so the variation we see in the ${\rm H}\alpha/{\rm H}\beta$ ratio would not appear to be due to poor photon statistics. Over this wavelength range, we do not see any variation exceeding more than a few percent in any of the standard star observations. We made no effort to orient the slit at the parallactic angle, but the wide slits used, particularly for the 2001 observing runs, should compensate for the effects of differential refraction. 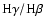Regardless, were differential refraction the culprit, we should see nearly equally large variations in ${\rm H}\gamma/{\rm H}\beta$ as we see in 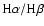${\rm H}\alpha/{\rm H}\beta$ (Filippenko 1982), but we see none. Three instrumental effects, however, affect the 2001 data from SPM. First, the object was acquired by blind offset, so the centering of the object in the slit was almost certainly not optimal. Second, the offset guider is known to flex relative to the instrument field of view, so the object centering was likely somewhat variable for the 2001 observations at SPM. Finally, the spectrograph was out of focus due the CCD being mis-aligned with the camera's focal plane. It is not clear, however, how any of these might introduce variations in the 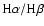${\rm H}\alpha/{\rm H}\beta$ ratio alone without affecting other line ratios. 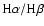None of these issues affect the CFHT data nor those from SPM in 2002, yet the ${\rm H}\alpha/{\rm H}\beta$ variations exist in these data sets as well. Tovmassian et al. (2001) found similar variations, from a variety of observing sites, though they attributed them to the poor observing conditions affecting their observations. 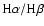Although unusual, it would appear that the variations in ${\rm H}\alpha/{\rm H}\beta$ are real.

In Fig. 1, we compare the spectra of PNG 135.9+55.9 and the standard star G191B2B (Oke 1990). For PNG 135.9+55.9, we plot the CFHT spectrum for 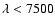$\lambda < 7500$ Å and the WHT spectrum for 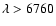$\lambda > 6760$ Å, without applying any reddening correction to either spectrum. The WHT spectrum was scaled upwards by a factor of 2.07, as described previously. As noted by Tovmassian et al. (2001), this planetary nebula has a remarkably blue continuum.

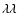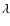Finally, these new data do not provide any direct diagnostic of the physical conditions in the nebular plasma. No density diagnostic has been detected to date, though [Ar IV] $\lambda\lambda$ 4711, 4740 might have been expected given the high degree of ionization. Similarly, the only temperature diagnostic available is the upper limit to the [O III] $\lambda$ 4363/5007 ratio and it provides no useful constraint unless the density is unusually high, 10⁶-10⁷ cm^-3, which is excluded given the nebular flux and size (see Sect. 4).

2.2 Reddening

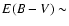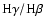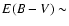From the Schlegel et al. (1998) reddening maps, the expected foreground reddening is $E(B-V)\sim$ 01-0.02 mag. The ${\rm H}\gamma/{\rm H}\beta$ and ${\rm H}\delta/{\rm H}\beta$ ratios imply $E(B-V)\sim$ 0.3-0.35 mag, based upon a temperature of 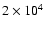$2\times 10^{4}$ K, a density of 10³-10⁴ cm^-3, the Storey & Hummer (1995) line emissivities, and the Fitzpatrick (1999) monochromatic reddening law parametrized with a ratio of total-to-selective extinction of 3.041 (McCall & Armour 2000). 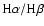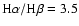On the other hand, the ${\rm H}\alpha/{\rm H}\beta$ ratio implies a reddening E(B-V) < 0.23 mag for the same physical conditions, reddening law, and line emissivities, even if we consider the largest line ratio we observe, ${\rm H}\alpha/{\rm H}\beta = 3.5$ . 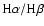For ${\rm H}\alpha/{\rm H}\beta$ ratios at the low end of the range observed, the reddening is zero or negative. 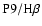The intensity of ${\rm P9}/{\rm H}\beta$ from the WHT spectrum implies E(B-V)=0.05 mag. 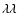We can also compute a reddening using He II $\lambda\lambda$ 4686, 5412. 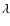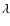Adopting the same physical conditions, reddening law, and line emissivities, we find negative reddenings, i.e., He II $\lambda$ 4686 is too bright relative to He II $\lambda$ 5412 by 12%. In any case, it appears that the reddening is at most modest, with E(B-V) < 0.3-0.35 mag. In the remainder of this paper, we shall assume that the reddening is zero. None of the conclusions would be affected had we adopted a modest reddening.

2 Spectroscopy

2.1 Observations

2.2 Reddening