A&A 395, 929-941 (2002)
DOI: 10.1051/0004-6361:20021315
M. G. Richer1,![]() -
G. Tovmassian1 -
G. Stasinska2 -
R. F. Jameson3,
-
G. Tovmassian1 -
G. Stasinska2 -
R. F. Jameson3,
![]() -
P. D. Dobbie3,
-
P. D. Dobbie3,![]() -
C. Veillet4,
-
C. Veillet4,![]() -
-
C. Gutierrez5,![]() -
F. Prada6,
-
F. Prada6,![]()
1 - Observatorio Astronómico Nacional, Instituto de
Astronomía, UNAM, PO Box 439027, San Diego,
CA 92143-9027, USA
2 -
LUTH, Observatoire de Meudon, 5 place Jules Janssen,
92195 Meudon Cedex, France
3 -
University of Leicester, University Road, Leicester
LE1 7RH, UK
4 -
Canada-France-Hawaii Telescope Corp., PO Box 1597,
Kamuela, HI 96743, USA
5 -
Instituto de Astrofísica de Canarias, C/Vía
Láctea s/n, 38200, La Laguna, Tenerife, Spain
6 -
Centro Astronómico Hispano Alemán, C/Jesús
Durbán Remón 2-2, 04004, Almería,
Spain
Received 26 June 2002 / Accepted 9 September 2002
Abstract
We present extensive new spectroscopy and imaging of PNG 135.9+55.9.
We use these data as constraints to photoionization models
to derive limits on the oxygen abundance.
We find that PNG 135.9+55.9 has an oxygen abundance less than 1/50 of
the solar value.
Our models favour a value of
![]() between 5.8 and 6.5 dex,
confirming that PNG 135.9+55.9 is the most
oxygen-poor planetary nebula known (Tovmassian et al. 2001). We
also derive
between 5.8 and 6.5 dex,
confirming that PNG 135.9+55.9 is the most
oxygen-poor planetary nebula known (Tovmassian et al. 2001). We
also derive
![]() ,
,
![]() ,
and
,
and
![]() .
Although the value of Ne/O is nominally high, it need not
imply that
the progenitor of PNG 135.9+55.9 converted any of its initial oxygen
abundance to neon.
The helium abundance appears to be very low,
.
Although the value of Ne/O is nominally high, it need not
imply that
the progenitor of PNG 135.9+55.9 converted any of its initial oxygen
abundance to neon.
The helium abundance appears to be very low,
![]() ,
but a precise determination will require a much
more detailed study. We find that
,
but a precise determination will require a much
more detailed study. We find that
![]() is lower than expected and
perhaps variable, a finding for which we have no clear explanation.
is lower than expected and
perhaps variable, a finding for which we have no clear explanation.
Key words: planetary nebulae: individual: PNG 135.9+55.9
Recently, SBS 1150+599A has been recognized as a planetary nebula in the
Galactic halo by Tovmassian et al. (2001) and
renamed PNG 135.9+55.9. The spectra then available for this object were
quite unusual for a planetary nebula, presenting only the Balmer
lines of hydrogen, He II
![]() 4686, 5411, and very
weak [O III]
4686, 5411, and very
weak [O III] ![]() 5007 (
5007 (![]()
![]() of HH
of HH![]() ). A photoionization model analysis
showed that such a spectrum implies a strongly density bounded and
extremely oxygen-poor nebula ionized by a very hot star. The
oxygen abundance was estimated to be less than 1/50 of the solar
value, and probably between 1/100 and 1/500 of solar assuming
canonical properties for the central star, making of PNG 135.9+55.9 by far
the most oxygen-poor planetary nebula known, with an oxygen
abundance similar to the lowest measured to date in stars
(Boesgaard et al. 1999; Howard et al.
1997).
). A photoionization model analysis
showed that such a spectrum implies a strongly density bounded and
extremely oxygen-poor nebula ionized by a very hot star. The
oxygen abundance was estimated to be less than 1/50 of the solar
value, and probably between 1/100 and 1/500 of solar assuming
canonical properties for the central star, making of PNG 135.9+55.9 by far
the most oxygen-poor planetary nebula known, with an oxygen
abundance similar to the lowest measured to date in stars
(Boesgaard et al. 1999; Howard et al.
1997).
In this paper, we report detailed follow-up observations, aimed at providing more stringent constraints on the nature of this exceptional object. Section 2 presents the new spectroscopic data, while Sect. 3 deals with narrow-band imaging. In Sect. 4, we present an updated photoionization model analysis, taking full advantage of the constraints provided by our new observational data. This leads to a limit on the oxygen abundance which is now independent of any assumption about the evolutionary status of the central star. In Sect. 5, we estimate the abundances of the other elements. Section 6 presents a brief concluding discussion.
| SPM1 | SPM2 | CFHT | WHT | SPM3a | SPM4 | |
| date | 22 Jan. 2001 | 23-24 Jan. 2001 | 3-4 Mar. 2001 | 11 May 2001 | 5 Mar. 2002 | 8 Apr. 2002 |
| CCD | Thomson | Thomson | EEV | Tektronix | SITe | SITe |
| format |
|
|
|
|
|
|
| pixel sizeb | ||||||
| gain (e-/ADU) | 0.5 | 0.5 | 1.8 | 1.4 | 1.3 | 1.3 |
| read noise (e-) | 4.8 | 4.8 | 3.1 | 4.6 | 8 | 8 |
| spectrograph | B&C | B&C | MOS | ISIS | B&C | B&C |
| gratingc | 300/4550 Å | 600/4550 Å | B400/5186 Å | R158R/6500 Å | 300/4550 Å | 400/5150 Å |
| slit width | 3
|
3
|
5
|
1
|
2
|
2
|
| spectral resolutiond | 12.7 Å | 5.6 Å | 23.0 Å | 7.8 Å | 8.1 Å | 5.8 Å |
| wavelength interval | 3700-6700 Å | 4745-7200 Å | 3400-8000 Å | 6820-9740 Å | 3600-7100 Å | 3660-6760 Å |
| arc lamp | HeAr | HeAr | HgNeAr | CuNe+CuAr | HeAr | HeAr |
| standard stars | HD 93521 | G191B2B | Feige 66 | Hz44 | BD+33 |
HD 93521 |
| BD+33 |
HD 93521 | BD+33 |
||||
| total exp. time | 4500 s | 7800 s | 7200 s | 3600 s | 5400 s | 12600 s |
| number of spectra | 3 | 4 | 4 | 3 | 3 | 7 |
a These observations were obtained through clouds.
b Both the physical pixel size and the angle subtended on the sky are given.
c The gratings are described by their ruling (lines/mm)
and effective blaze wavelength. For the grism used at CFHT, the
ruling and zero deviation wavelength are given. All of the
observations were obtained in first order.
d This is the spectral resolution measured at H![]() ,
defined as the FWHM of the H
,
defined as the FWHM of the H![]() line, except for the WHT spectrum, where this is the FWHM of P9
line, except for the WHT spectrum, where this is the FWHM of P9![]() 9229.
9229.
| ion | SPM1 | SPM2 | CFHT | SPM3b | SPM4 | |
| [Ne V | 3426 | <9.6 | ||||
| [O II] | 3727 | <2.1 | ||||
| [Ne III] | 3869 |
|
||||
| H I | 3889 |
|
||||
| H I | 3970 |
|
|
|
|
|
| H I | 4101 |
|
|
|
|
|
| C II | 4267 | <1.1 | <3.0 | |||
| H I | 4340 |
|
|
|
|
|
| [O III] | 4363 | <1.9 | <0.88 | <1.8 | ||
| He II | 4686 |
|
|
|
|
|
| [Ar IV]c | 4711 | <2.0 | <1.0 | <1.4 | ||
| H I | 4861 |
|
|
|
|
|
| [O III] | 5007 |
|
|
|
|
|
| He II | 5412 |
|
|
|
|
|
| He I | 5876 | <0.47 | <0.69 | <0.28 | <1.4 | <0.62 |
| H I | 6563 |
|
|
|
|
|
| [N II] | 6583 | <3.2 | <1.4 | <0.45 | <1.3 | <0.74 |
| [S II] | 6716 | <1.3 | <0.74 | |||
| [S II] | 6731 | <1.3 | <0.74 | |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
| H |
304-318 | 256-350 | 258-267 | 265-324 | 241-321 |
a When no uncertainty is given, the value
represents a ![]() upper limit to the flux in the line.
upper limit to the flux in the line.
b These observations were obtained through
clouds.
c These upper limits also apply to
[Ar IV]![]() 4740.
4740.
d This is the total flux in emission measured at
H![]() in units of 10-14 erg s-1 cm-2.
in units of 10-14 erg s-1 cm-2.
e These are the equivalent widths in Å of
H![]() and H
and H![]() in emission.
in emission.
f This is the total range spanned by the
values of
![]() among the
individual spectra.
among the
individual spectra.
Table 1 presents a summary of our new spectroscopic observations of PNG 135.9+55.9. This table includes the dates of the observations, the instrumental configuration, and the flux and wavelength standards that were used. The only observing run that suffered from non-photometric conditions was that of 5 Mar. 2002, when significant cloud cover affected observations of both PNG 135.9+55.9 and the standard star.
The spectroscopy from the Observatorio Astronómico Nacional in
San Pedro Mártir, Baja California, Mexico (SPM) was obtained
using the Boller & Chivens spectrograph (B&C) and three
different gratings during four observing runs. For the 2001
observations, a rather wide slit (3
![]() 8) was used to better
measure the total fluxes, while, for the 2002 observations, a
narrower slit was used to obtain higher spectral resolution and
better sensitivity to fainter lines. The standard stars were
observed with an even wider slit (9
8) was used to better
measure the total fluxes, while, for the 2002 observations, a
narrower slit was used to obtain higher spectral resolution and
better sensitivity to fainter lines. The standard stars were
observed with an even wider slit (9
![]() ). In all cases, the
slit was oriented east-west on the sky. Spectra of the
illuminated dome wall were obtained to serve as flat field images.
Bias images were obtained at the beginning and end of the night.
). In all cases, the
slit was oriented east-west on the sky. Spectra of the
illuminated dome wall were obtained to serve as flat field images.
Bias images were obtained at the beginning and end of the night.
The spectroscopy at the Canada-France-Hawaii Telescope (CFHT) was
obtained with the Multi-Object Spectrograph (MOS; Le Fèvre et al. 1994). Both the object and the standard star
were observed through a 5
![]() slit. However, the observations
of PNG 135.9+55.9 were obtained the night before those of the
standard star. Spectra of the internal halogen lamp were obtained
to serve as flat field images.
slit. However, the observations
of PNG 135.9+55.9 were obtained the night before those of the
standard star. Spectra of the internal halogen lamp were obtained
to serve as flat field images.
The spectroscopy at the William Herschel Telescope (WHT) was
obtained using the red arm of the ISIS spectrograph. The object
was observed through a 1
![]() slit, while the standard stars
were observed with a 10
slit, while the standard stars
were observed with a 10
![]() slit. For these observations, the
slit was oriented at the parallactic angle. Spectra of the
internal lamp were obtained to serve as flat field images while
spectra of the sky were used to correct for the slit illumination.
slit. For these observations, the
slit was oriented at the parallactic angle. Spectra of the
internal lamp were obtained to serve as flat field images while
spectra of the sky were used to correct for the slit illumination.
All of the spectroscopy was reduced using the Image Reduction and
Analysis Facility (IRAF)![]() software package
(specifically the specred package). In all cases, the overscan
bias was subtracted from each image. For the SPM data, the
overscan-subtracted bias images obtained during the night were
combined and subtracted from all of the images. Next, the
pixel-to-pixel variations were removed by division of the flat
field image. For the WHT data, the slit illumination correction
was then applied. The sky emission was subtracted during the
extraction of the one dimensional spectra by defining sky regions
on both sides of the object spectra and interpolating between them
with a straight line. The wavelength calibration was performed
using arc lamp spectra obtained at the time of the object
observations. Finally, the spectra were calibrated in flux using
the observations of the standard stars (Table 1) to
determine the instrumental sensitivity function. The individual
spectra were calibrated in both wavelength and flux before being
summed together.
software package
(specifically the specred package). In all cases, the overscan
bias was subtracted from each image. For the SPM data, the
overscan-subtracted bias images obtained during the night were
combined and subtracted from all of the images. Next, the
pixel-to-pixel variations were removed by division of the flat
field image. For the WHT data, the slit illumination correction
was then applied. The sky emission was subtracted during the
extraction of the one dimensional spectra by defining sky regions
on both sides of the object spectra and interpolating between them
with a straight line. The wavelength calibration was performed
using arc lamp spectra obtained at the time of the object
observations. Finally, the spectra were calibrated in flux using
the observations of the standard stars (Table 1) to
determine the instrumental sensitivity function. The individual
spectra were calibrated in both wavelength and flux before being
summed together.
Table 2 presents the raw line intensities relative to
H![]() measured in the optical spectral region for PNG 135.9+55.9, normalized such that
measured in the optical spectral region for PNG 135.9+55.9, normalized such that
![]() .
The
line intensities presented in Table 2 are those for
the summed spectra from each observing run. The line intensities
were measured using the software described by McCall et al.
(1985). The uncertainties quoted for each line
intensity (
.
The
line intensities presented in Table 2 are those for
the summed spectra from each observing run. The line intensities
were measured using the software described by McCall et al.
(1985). The uncertainties quoted for each line
intensity (![]() )
include contributions from the fit to the
line itself, from the fit to the reference line, and from the
noise in the continuum for both the line and reference line. When
only a limit is given, this corresponds to a
)
include contributions from the fit to the
line itself, from the fit to the reference line, and from the
noise in the continuum for both the line and reference line. When
only a limit is given, this corresponds to a ![]() upper
limit to undetected lines.
upper
limit to undetected lines.
| ion | fluxa |
|
|
| [Ar III] | 7135 | <0.45 | <0.06 |
| H I | 8750 |
|
|
| [S III] | 9069 | <0.59 | <0.08 |
| H I | 9229 |
|
|
a The fluxes are given in units of
![]() .
When
no uncertainty is given, the value is a 2
.
When
no uncertainty is given, the value is a 2![]() upper limit to
the flux in the line.
upper limit to
the flux in the line.
b These flux ratios are relative to
![]() measured for the CFHT spectrum on a scale where
measured for the CFHT spectrum on a scale where
![]() .
.
![\begin{figure}
\par\includegraphics[angle=90,width=14.2cm,clip]{h3796f1}\end{figure}](/articles/aa/full/2002/45/aah3796/Timg106.gif) |
Figure 1:
We compare the spectra of PNG 135.9+55.9 and the standard star
G191B2B on an arbitrary magnitude scale. For PNG 135.9+55.9, we plot the
CFHT spectrum for
|
| Open with DEXTER | |
Table 3 presents the raw fluxes and the intensity
ratios relative to H![]() for the WHT spectrum. The only line
definitely detected is P9
for the WHT spectrum. The only line
definitely detected is P9 ![]() 9229; P12
9229; P12 ![]() 8750 is
detected at only the
8750 is
detected at only the ![]() level. Again, when no uncertainty
is given, the value represents a 2
level. Again, when no uncertainty
is given, the value represents a 2![]() upper limit to the line
intensity. These line intensities and limits were measured using
IRAF's splot routine. The fluxes represent the fluxes measured
directly in the summed WHT spectrum. The intensity ratios relative
to H
upper limit to the line
intensity. These line intensities and limits were measured using
IRAF's splot routine. The fluxes represent the fluxes measured
directly in the summed WHT spectrum. The intensity ratios relative
to H![]() were computed adopting the H
were computed adopting the H![]() flux from the CFHT
spectrum and correcting the WHT fluxes for the difference in the
slit widths used. Based upon the spatial profile of H
flux from the CFHT
spectrum and correcting the WHT fluxes for the difference in the
slit widths used. Based upon the spatial profile of H![]() from the CFHT spectrum, a 5
from the CFHT spectrum, a 5
![]() slit intercepts 3.32 times
more nebular emission than a 1
slit intercepts 3.32 times
more nebular emission than a 1
![]() slit. The WHT fluxes were
then multiplied by this factor when computing the relative
intensities presented in Table 3. Comparing the
continuum fluxes measured in the CFHT and WHT spectra in the
6760-7500 Å region, where the fringing in the CFHT spectrum is
not too severe, the continuum flux in the WHT spectrum should be
scaled upwards by a factor of 2.07 to match that in the CFHT spectrum. This scale factor is in good agreement with the value
of 1.95 expected based upon the 1
slit. The WHT fluxes were
then multiplied by this factor when computing the relative
intensities presented in Table 3. Comparing the
continuum fluxes measured in the CFHT and WHT spectra in the
6760-7500 Å region, where the fringing in the CFHT spectrum is
not too severe, the continuum flux in the WHT spectrum should be
scaled upwards by a factor of 2.07 to match that in the CFHT spectrum. This scale factor is in good agreement with the value
of 1.95 expected based upon the 1
![]() slit used for the WHT spectra and the 1
slit used for the WHT spectra and the 1
![]() 22 seeing measured from the spatial profile
of the continuum in the summed spectrum.
22 seeing measured from the spatial profile
of the continuum in the summed spectrum.
Generally, there is excellent agreement among the line intensities
over the wavelength range H![]() -He II
-He II![]() 5412. In
the near-ultraviolet, the SPM spectrograph has very low efficiency
and the upper limits we derive from those spectra are considerably
less restrictive than the detections or limits from the CFHT spectrum. We give upper limits to the [S II] line
intensities only for the last two SPM runs, since the CCD used for
the first two SPM observing runs and that at CFHT suffered from
fringing in the red.
5412. In
the near-ultraviolet, the SPM spectrograph has very low efficiency
and the upper limits we derive from those spectra are considerably
less restrictive than the detections or limits from the CFHT spectrum. We give upper limits to the [S II] line
intensities only for the last two SPM runs, since the CCD used for
the first two SPM observing runs and that at CFHT suffered from
fringing in the red.
| Telescope | Date | CCD | Instrument | Filtera | Exposure timeb |
| SPM 2.1 m | 27-28 May 2001 | SITe3c | Mexman | H |
3900 s (5) |
| red cont. (6650 Å, 46 Å) | 1500 s (3) | ||||
| NOT 2.6 m | 1-2 June 2001 | CCD7d | ALFOSC | y # 18(5470 Å, 220 Å) | 2700 s (4) |
| H |
2700 s (4) |
a The central wavelength and the bandpass
width for each filter are given in parentheses.
b The number of images is given in parentheses.
c This CCD has 24 ![]() m pixels in a
m pixels in a
![]() format. Its gain and readnoise are 1.3 e
format. Its gain and readnoise are 1.3 e
![]() and 8 e-, respectively. The plate scale is
and 8 e-, respectively. The plate scale is
![]() .
.
d This CCD has 15 ![]() m pixels in a
m pixels in a
![]() format. Its gain and readnoise are
format. Its gain and readnoise are ![]()
![]() and 6 e-, respectively. The plate scale is
and 6 e-, respectively. The plate scale is
![]() .
.
The notable exception to the good agreement among the line
intensities is H![]() .
There is significant variation in the
.
There is significant variation in the
![]() ratio among the summed
spectra for the different observing runs and between individual
spectra for at least the SPM2 and SPM4 observing runs. In both
the SPM2 and SPM4 data sets, the dispersion among the H
ratio among the summed
spectra for the different observing runs and between individual
spectra for at least the SPM2 and SPM4 observing runs. In both
the SPM2 and SPM4 data sets, the dispersion among the H![]() fluxes for the individual spectra also significantly exceeds that
for the H
fluxes for the individual spectra also significantly exceeds that
for the H![]() fluxes. In the last line of Table 2,
we indicate the range of
fluxes. In the last line of Table 2,
we indicate the range of
![]() values found among the individual spectra during each observing
run. This variation is very puzzling, since we normally obtained
all of the spectra consecutively on the same night (SPM2 is the
exception). If this variation is real, it is occurring
(irregularly) on a time scale of the order of an hour. Such
behaviour is not at all expected in a nebular plasma (e.g., Aller
1987). In a typical SPM spectrum (of a half hour
duration), at least 50 000, 15 000, and 2500 photons are detected
at H
values found among the individual spectra during each observing
run. This variation is very puzzling, since we normally obtained
all of the spectra consecutively on the same night (SPM2 is the
exception). If this variation is real, it is occurring
(irregularly) on a time scale of the order of an hour. Such
behaviour is not at all expected in a nebular plasma (e.g., Aller
1987). In a typical SPM spectrum (of a half hour
duration), at least 50 000, 15 000, and 2500 photons are detected
at H![]() ,
H
,
H![]() ,
and H
,
and H![]() ,
respectively, so the
variation we see in the
,
respectively, so the
variation we see in the
![]() ratio
would not appear to be due to poor photon statistics. Over this
wavelength range, we do not see any variation exceeding more than
a few percent in any of the standard star observations. We made no
effort to orient the slit at the parallactic angle, but the wide
slits used, particularly for the 2001 observing runs, should
compensate for the effects of differential refraction. Regardless,
were differential refraction the culprit, we should see nearly
equally large variations in
ratio
would not appear to be due to poor photon statistics. Over this
wavelength range, we do not see any variation exceeding more than
a few percent in any of the standard star observations. We made no
effort to orient the slit at the parallactic angle, but the wide
slits used, particularly for the 2001 observing runs, should
compensate for the effects of differential refraction. Regardless,
were differential refraction the culprit, we should see nearly
equally large variations in
![]() as we see in
as we see in
![]() (Filippenko
1982), but we see none. Three instrumental
effects, however, affect the 2001 data from SPM. First, the object
was acquired by blind offset, so the centering of the object in
the slit was almost certainly not optimal. Second, the offset
guider is known to flex relative to the instrument field of view,
so the object centering was likely somewhat variable for the 2001
observations at SPM. Finally, the spectrograph was out of focus
due the CCD being mis-aligned with the camera's focal plane. It is
not clear, however, how any of these might introduce variations in
the
(Filippenko
1982), but we see none. Three instrumental
effects, however, affect the 2001 data from SPM. First, the object
was acquired by blind offset, so the centering of the object in
the slit was almost certainly not optimal. Second, the offset
guider is known to flex relative to the instrument field of view,
so the object centering was likely somewhat variable for the 2001
observations at SPM. Finally, the spectrograph was out of focus
due the CCD being mis-aligned with the camera's focal plane. It is
not clear, however, how any of these might introduce variations in
the
![]() ratio alone without
affecting other line ratios. None of these issues affect the CFHT
data nor those from SPM in 2002, yet the
ratio alone without
affecting other line ratios. None of these issues affect the CFHT
data nor those from SPM in 2002, yet the
![]() variations exist in these data sets as
well. Tovmassian et al. (2001) found similar
variations, from a variety of observing sites, though they
attributed them to the poor observing conditions affecting their
observations. Although unusual, it would appear that the
variations in
variations exist in these data sets as
well. Tovmassian et al. (2001) found similar
variations, from a variety of observing sites, though they
attributed them to the poor observing conditions affecting their
observations. Although unusual, it would appear that the
variations in
![]() are real.
are real.
In Fig. 1, we compare the spectra of PNG 135.9+55.9 and the
standard star G191B2B (Oke 1990). For PNG 135.9+55.9, we plot the
CFHT spectrum for
![]() Å and the WHT spectrum for
Å and the WHT spectrum for
![]() Å, without applying any reddening correction to
either spectrum. The WHT spectrum was scaled upwards by a factor
of 2.07, as described previously. As noted by Tovmassian et al.
(2001), this planetary nebula has a remarkably blue continuum.
Å, without applying any reddening correction to
either spectrum. The WHT spectrum was scaled upwards by a factor
of 2.07, as described previously. As noted by Tovmassian et al.
(2001), this planetary nebula has a remarkably blue continuum.
Finally, these new data do not provide any direct diagnostic of
the physical conditions in the nebular plasma. No density
diagnostic has been detected to date, though
[Ar IV]
![]() 4711, 4740 might have been expected
given the high degree of ionization. Similarly, the only
temperature diagnostic available is the upper limit to the
[O III]
4711, 4740 might have been expected
given the high degree of ionization. Similarly, the only
temperature diagnostic available is the upper limit to the
[O III]![]() 4363/5007 ratio and it provides no useful
constraint unless the density is unusually high,
106-107 cm-3, which is excluded given the nebular
flux and size (see Sect. 4).
4363/5007 ratio and it provides no useful
constraint unless the density is unusually high,
106-107 cm-3, which is excluded given the nebular
flux and size (see Sect. 4).
From the Schlegel et al. (1998) reddening maps,
the expected foreground reddening is
![]() 01-0.02 mag.
The
01-0.02 mag.
The
![]() and
and
![]() ratios imply
ratios imply
![]() 0.3-0.35 mag, based upon a temperature of
0.3-0.35 mag, based upon a temperature of
![]() K, a density of 103-104 cm-3, the Storey & Hummer (1995) line emissivities, and the Fitzpatrick
(1999) monochromatic reddening law parametrized
with a ratio of total-to-selective extinction of 3.041 (McCall &
Armour 2000). On the other hand, the
K, a density of 103-104 cm-3, the Storey & Hummer (1995) line emissivities, and the Fitzpatrick
(1999) monochromatic reddening law parametrized
with a ratio of total-to-selective extinction of 3.041 (McCall &
Armour 2000). On the other hand, the
![]() ratio implies a reddening
E(B-V) <
0.23 mag for the same physical conditions, reddening law, and
line emissivities, even if we consider the largest line ratio we
observe,
ratio implies a reddening
E(B-V) <
0.23 mag for the same physical conditions, reddening law, and
line emissivities, even if we consider the largest line ratio we
observe,
![]() .
For
.
For
![]() ratios at the low end of the range
observed, the reddening is zero or negative. The intensity of
ratios at the low end of the range
observed, the reddening is zero or negative. The intensity of
![]() from the WHT spectrum implies
E(B-V)=0.05 mag. We can also compute a reddening using
He II
from the WHT spectrum implies
E(B-V)=0.05 mag. We can also compute a reddening using
He II
![]() 4686, 5412. Adopting the same physical
conditions, reddening law, and line emissivities, we find negative
reddenings, i.e., He II
4686, 5412. Adopting the same physical
conditions, reddening law, and line emissivities, we find negative
reddenings, i.e., He II![]() 4686 is too bright relative
to He II
4686 is too bright relative
to He II![]() 5412 by 12%. In any case, it appears that
the reddening is at most modest, with
E(B-V) < 0.3-0.35 mag. In
the remainder of this paper, we shall assume that the reddening is
zero. None of the conclusions would be affected had we adopted a modest reddening.
5412 by 12%. In any case, it appears that
the reddening is at most modest, with
E(B-V) < 0.3-0.35 mag. In
the remainder of this paper, we shall assume that the reddening is
zero. None of the conclusions would be affected had we adopted a modest reddening.
We obtained direct images of PNG 135.9+55.9 in narrow-band filters from
two sites (Table 4). Images were obtained in the
emission line of H![]() and a nearby continuum bandpass with
the 2.1 m telescope in SPM. The Mexman filter wheel was used for
observations. The seeing was modest, with stellar images having
FWHM of 1
and a nearby continuum bandpass with
the 2.1 m telescope in SPM. The Mexman filter wheel was used for
observations. The seeing was modest, with stellar images having
FWHM of 1
![]() 5 or worse. Images were also obtained using ALFOSC
at the 2.6 m Nordic Optical telescope (NOT) on La Palma, Canary
Islands, Spain. A narrow filter centred at H
5 or worse. Images were also obtained using ALFOSC
at the 2.6 m Nordic Optical telescope (NOT) on La Palma, Canary
Islands, Spain. A narrow filter centred at H![]() was used, but
the continuum was measured using a Stromgren y filter. The NOT
images benefited from better seeing,
was used, but
the continuum was measured using a Stromgren y filter. The NOT
images benefited from better seeing, ![]()
![]() ,
on the
first night of this run. The spectrophotometric standard stars
HZ44 and Feige 67 were observed along with the object on the
second night for calibration purposes. During both imaging runs,
sequences of at least 3 images in each filter were obtained, with
one long exposure usually not exceeding 20 min and two shorter
ones. This tactic allowed us to keep cosmic ray rate within
reasonable limits in order to later combine the images for
improved statistics and to permit the removal of cosmic rays.
,
on the
first night of this run. The spectrophotometric standard stars
HZ44 and Feige 67 were observed along with the object on the
second night for calibration purposes. During both imaging runs,
sequences of at least 3 images in each filter were obtained, with
one long exposure usually not exceeding 20 min and two shorter
ones. This tactic allowed us to keep cosmic ray rate within
reasonable limits in order to later combine the images for
improved statistics and to permit the removal of cosmic rays.
The images were processed using IRAF. The steps included bias substraction, flat field correction, image combination, and apperture photometry. The STSDAS package within IRAF was used for the deconvolution of the images.
The primary uses of the H![]() images were to determine the
angular size of the nebula and to derive the density distribution
of the gas. Two selected NOT images from the first night, where
the seeing was better and the focus was good were combined to
produce the image presented in Fig. 2. The nebula
appears to be slightly elliptical in shape. No substructure is
evident in the main body of the nebula. Its size comfortably
exceeds the PSF of stellar objects, so the instrumental profile
should not affect its shape. Nonetheless, we conducted series of
deconvolution experiments on the nebular images using the
Lucy-Richardson method (Lucy 1974; Richardson
1972) that showed that the size and shape of the
nebula were unchanged after deconvolution. This is our strongest
evidence that the central star does not emit significantly in
H
images were to determine the
angular size of the nebula and to derive the density distribution
of the gas. Two selected NOT images from the first night, where
the seeing was better and the focus was good were combined to
produce the image presented in Fig. 2. The nebula
appears to be slightly elliptical in shape. No substructure is
evident in the main body of the nebula. Its size comfortably
exceeds the PSF of stellar objects, so the instrumental profile
should not affect its shape. Nonetheless, we conducted series of
deconvolution experiments on the nebular images using the
Lucy-Richardson method (Lucy 1974; Richardson
1972) that showed that the size and shape of the
nebula were unchanged after deconvolution. This is our strongest
evidence that the central star does not emit significantly in
H![]() .
For comparison the image of the central star obtained
in the Stromgren y filter is presented in the bottom panel of
Fig. 2 with the H
.
For comparison the image of the central star obtained
in the Stromgren y filter is presented in the bottom panel of
Fig. 2 with the H![]() contours of the nebula
superposed. We used the SPM observations, where the continuum
filter was much closer in wavelength to the line filter, to
substract the image of central stellar object from that of the
nebula. Figure 3 presents the spatial profiles of
the nebular emission in H
contours of the nebula
superposed. We used the SPM observations, where the continuum
filter was much closer in wavelength to the line filter, to
substract the image of central stellar object from that of the
nebula. Figure 3 presents the spatial profiles of
the nebular emission in H![]() from the NOT image without
subtracting the central star and from the SPM image after
substraction of central star. Except for a slight depression
around the peak, the shape of the nebula in both observations is
very similar.
from the NOT image without
subtracting the central star and from the SPM image after
substraction of central star. Except for a slight depression
around the peak, the shape of the nebula in both observations is
very similar.
![\begin{figure}
\par\includegraphics[width=8.8cm]{aah3796f2.eps}\end{figure}](/articles/aa/full/2002/45/aah3796/Timg122.gif) |
Figure 2:
The upper panel presents the image of PNG 135.9+55.9 in the light of H |
| Open with DEXTER | |
The NOT observations in the Stromgren y filter were used to
estimate the magnitude of the central star. We inferred
![]() mag, corresponding to a flux of F5556 =
mag, corresponding to a flux of F5556 =
![]() in a good agreement with the flux determined from
spectroscopy. This continuum measurement should be reliable since
there are almost no lines in the spectrum of this planetary
nebula, the contribution of He II
in a good agreement with the flux determined from
spectroscopy. This continuum measurement should be reliable since
there are almost no lines in the spectrum of this planetary
nebula, the contribution of He II
![]() Å being
negligible.
Å being
negligible.
The angular diameter of the planetary nebula is an important
parameter since, in combination with the H![]() flux, it allows
a determination of the electron density and the nebular mass. We
followed the recipe of Bedding & Zijlstra
(1994) to assure that our measurements
correspond to common standards. (For cautionary remarks, see van Hoof 2000.) There are a variety of definitions of
the diameter of a PN in the literature: the FWHM, the surface
brigthness contour at 10% of the maximum surface brightness, and
the outermost contour at which emission is found. Since
PNG 135.9+55.9 appears to have a slightly elliptical shape in
the H
flux, it allows
a determination of the electron density and the nebular mass. We
followed the recipe of Bedding & Zijlstra
(1994) to assure that our measurements
correspond to common standards. (For cautionary remarks, see van Hoof 2000.) There are a variety of definitions of
the diameter of a PN in the literature: the FWHM, the surface
brigthness contour at 10% of the maximum surface brightness, and
the outermost contour at which emission is found. Since
PNG 135.9+55.9 appears to have a slightly elliptical shape in
the H![]() images, we have measured the diameter of the nebula
along two axes. We find that the diameter of the nebula is
11
images, we have measured the diameter of the nebula
along two axes. We find that the diameter of the nebula is
11
![]() 4
4![]() 9
9
![]() 8 if we use the outermost contour,
6
8 if we use the outermost contour,
6
![]() 3
3![]() 5
5
![]() 2 if we use the 10% surface brightness
contour, and 3
2 if we use the 10% surface brightness
contour, and 3
![]() 5
5![]() 2
2
![]() 95 if we use the FWHM.
95 if we use the FWHM.
Figure 4 shows the density and flux distributions
adopted in our models. The symbols correspond to the observed H![]() emission profiles across the major and minor axes obtained from the
SPM images (shown in Fig. 3). The curve corresponds
to a spherical model with a density distribution described by
emission profiles across the major and minor axes obtained from the
SPM images (shown in Fig. 3). The curve corresponds
to a spherical model with a density distribution described by
![]() ,
where
,
where ![]() is the angular
distance to the center in seconds of arc. In this model, the
emissivity of H
is the angular
distance to the center in seconds of arc. In this model, the
emissivity of H![]() is taken to be simply proportional to n2and is computed for a uniform temperature. Such a simple
representation accounts very satisfactorily for the observed H
is taken to be simply proportional to n2and is computed for a uniform temperature. Such a simple
representation accounts very satisfactorily for the observed H![]() emission profile.
emission profile.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3796f3}\end{figure}](/articles/aa/full/2002/45/aah3796/Timg129.gif) |
Figure 3:
This figure presents the spatial profiles of the nebula
from the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3796f4}\end{figure}](/articles/aa/full/2002/45/aah3796/Timg130.gif) |
Figure 4:
The density distribution used for the model calculations is
presented in the lower panel. The predicted flux distribution
from our models is drawn with a solid line in the upper panel,
supposing that the emissivity is proportional to n2 and
computed at a constant temperature.
The open and filled squares denote the spatial distributions of
the nebular emission along the major and minor axes, respectively,
obtained from the SPM observations, as shown in Fig. 3.
The abscissa denotes relative angular size normalized to the
maximum, azimuthally-averaged radius of 5
|
| Open with DEXTER | |
In the analysis of the photoionization models that follows, we
adopt a nebular radius of 5
![]() 6, i.e., similar to the diameter
of the outermost contour.
6, i.e., similar to the diameter
of the outermost contour.
The observational data do not permit a direct estimate of the oxygen abundance, since nothing is known of the electron temperature or of the presence of oxygen ions more charged than O++. It is therefore necessary to rely upon photoionization models.
We have constructed sequences of photoionization models in which
the oxygen abundance varies over several orders of magnitude. The
models are constrained by the available observations, which
consist of the observed line intensities, the equivalent width of HH![]() ,
the total flux in HH
,
the total flux in HH![]() ,
the size of the nebula, and the radial distribution of H
,
the size of the nebula, and the radial distribution of H![]() shown in Fig. 3. As already
noted by Tovmassian et al. (2001), the shape
of the stellar continuum only implies that the star is hotter than
50 000 K. The models are computed with the photoionization code
PHOTO, using the atomic data listed in Stasinska & Leitherer
(1996). The central star is assumed to radiate as a blackbody of
temperature
shown in Fig. 3. As already
noted by Tovmassian et al. (2001), the shape
of the stellar continuum only implies that the star is hotter than
50 000 K. The models are computed with the photoionization code
PHOTO, using the atomic data listed in Stasinska & Leitherer
(1996). The central star is assumed to radiate as a blackbody of
temperature ![]() .
The hydrogen density at a radius r is taken
to be n =
.
The hydrogen density at a radius r is taken
to be n = ![]() exp
-(r/h)2, where
exp
-(r/h)2, where ![]() is a free parameter and
is a free parameter and
![]() ,
where d,
the distance to the nebula (in the same units as h and r), is
also a free parameter. The ionizing radiation field is treated in
the outward-only approximation. The computations start close to
the star and are stopped when the equivalent width in HH
,
where d,
the distance to the nebula (in the same units as h and r), is
also a free parameter. The ionizing radiation field is treated in
the outward-only approximation. The computations start close to
the star and are stopped when the equivalent width in HH![]() ,
W(HH
,
W(HH![]() ),
becomes equal to the observed value, taken to be 70 Å.
),
becomes equal to the observed value, taken to be 70 Å.
|
|
|
d | z |
|
|
|
|
[K] |
[erg s-1] | [erg cm-2 s-1] | [kpc] | [kpc] | [cm] | [ |
[cm-3] |
| 100 000 | 6 |
0.48 | 25.0 | 20.7 | 1.8 |
0.78 | 125 |
|
1 |
0.080 | 10.2 | 8.5 | 6.3 |
0.070 | 190 |
| 125 000 | 6 |
0.29 | 19.2 | 15.9 | 1.6 |
0.45 | 148 |
|
1 |
0.048 | 7.8 | 6.5 | 6.1 |
0.044 | 223 |
| 150 000 | 6 |
0.20 | 16.0 | 13.3 | 1.3 |
0.29 | 163 |
| 150 000 | 1 |
0.032 | 6.5 | 5.4 | 4.8 |
0.027 | 245 |
With such a representation of the nebula, it is easy to show that,
for each assumed stellar temperature ![]() and total luminosity
and total luminosity
![]() ,
the total observed flux in HH
,
the total observed flux in HH![]() implies a certain distance
to the planetary nebula. The observed angular size of the image
then fixes the outer radius of the nebula. By trial and error, we
determine the value of
implies a certain distance
to the planetary nebula. The observed angular size of the image
then fixes the outer radius of the nebula. By trial and error, we
determine the value of ![]() for which the radius
for which the radius
![]() corresponding to W(HH
corresponding to W(HH![]() ) = 70 Å is close to
) = 70 Å is close to
![]() .
Table 5 gives some global
properties of selected sequences of photoionization models. This
includes the distance, d, and the height above the Galactic
plane, z, implied by these models. Note that
.
Table 5 gives some global
properties of selected sequences of photoionization models. This
includes the distance, d, and the height above the Galactic
plane, z, implied by these models. Note that
![]() and the nebular mass,
and the nebular mass,
![]() ,
are decreasing functions
of the electron temperature. The values given in the table
correspond to the low metallicity end of the model sequences.
,
are decreasing functions
of the electron temperature. The values given in the table
correspond to the low metallicity end of the model sequences.
The chemical abundances in each sequence of models are
parametrized by O/H, with the abundances of the heavy elements
with respect to oxygen following the recipe of McGaugh (1991).
Note that the abundance ratios in PNG 135.9+55.9, as in any PN, may be
significantly different from those assumed in McGaugh's recipe,
especially for carbon and nitrogen. For helium, we assume an
abundance of 0.08 with respect to hydrogen in all models. This is
close to the value estimated from the observed HeII 4686/HH![]() ratio and using the upper limit for He I
ratio and using the upper limit for He I ![]() 5876
given by the CFHT spectrum (see Sect. 5). In any event, our
estimate of the chemical composition of PNG 135.9+55.9 is independent of
the relative abundances adopted in the model sequences since our
estimate uses the observed line intensities and relies on the
ionization and temperature structure of the nebula, which depend
essentially on hydrogen and helium in the domain of interest.
5876
given by the CFHT spectrum (see Sect. 5). In any event, our
estimate of the chemical composition of PNG 135.9+55.9 is independent of
the relative abundances adopted in the model sequences since our
estimate uses the observed line intensities and relies on the
ionization and temperature structure of the nebula, which depend
essentially on hydrogen and helium in the domain of interest.
Figure 5 presents the results of our models as a function of
![]() .
Each row of panels
corresponds to a different central star temperature:
.
Each row of panels
corresponds to a different central star temperature:
![]() =100 000 K,
=100 000 K, ![]() =125 000 K, and
=125 000 K, and ![]() =150 000 K, as indicated in the first panel. Each
column of panels displays a different line ratio. In each panel,
two series of models are represented with different symbols.
Circles correspond to models with central stars having a total
number of ionizing photons,
=150 000 K, as indicated in the first panel. Each
column of panels displays a different line ratio. In each panel,
two series of models are represented with different symbols.
Circles correspond to models with central stars having a total
number of ionizing photons,
![]() ,
equal to
,
equal to
![]() ,
while squares correspond
to models with a total number of ionizing photons of
,
while squares correspond
to models with a total number of ionizing photons of
![]() ,
values that roughly bracket
the luminosities of the central stars of planetary nebulae as
computed by post-AGB evolutionary models (Blöcker 1995). The
horizontal lines show the observed values: thick lines for
measured values or limits, thin lines indicating the uncertainties
in measured values, and upward- and downward-pointing arrows
denoting lower and upper limits, respectively. For the
observational data, we adopted the CFHT observations, since they
provide the most accurate measurements and the most stringent
limits. For the H
,
values that roughly bracket
the luminosities of the central stars of planetary nebulae as
computed by post-AGB evolutionary models (Blöcker 1995). The
horizontal lines show the observed values: thick lines for
measured values or limits, thin lines indicating the uncertainties
in measured values, and upward- and downward-pointing arrows
denoting lower and upper limits, respectively. For the
observational data, we adopted the CFHT observations, since they
provide the most accurate measurements and the most stringent
limits. For the H![]() /HH
/HH![]() ratio, however, we plot the value derived
from the SPM1 observations. As noted earlier, our observations
give inconsistent results for the H
ratio, however, we plot the value derived
from the SPM1 observations. As noted earlier, our observations
give inconsistent results for the H![]() /HH
/HH![]() ratio. Values of
H
ratio. Values of
H![]() /HH
/HH![]() around 3.1 are easily accounted for by our models, but
lower values are extremely difficult to explain. We will return to
this issue in Sect. 4.3.
around 3.1 are easily accounted for by our models, but
lower values are extremely difficult to explain. We will return to
this issue in Sect. 4.3.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{h3796f5}\end{figure}](/articles/aa/full/2002/45/aah3796/Timg144.gif) |
Figure 5:
This figure presents our grid of photoionization models. Each row
of panels corresponds to a particular central star temperature, indicated
in the first panel. Each column of panels plots a different line
intensity ratio. In each panel, two
sequences of models are included: circles denote models with ionizing
luminosities of
|
| Open with DEXTER | |
| |
Figure 6:
Here, we compare two models with |
| Open with DEXTER | |
The new observations allow us to eliminate the models with
![]()
![]() K, since these produce a [Ne V]/[Ne III] ratio much larger than is observed. Our models show that
K, since these produce a [Ne V]/[Ne III] ratio much larger than is observed. Our models show that ![]() should be around 100 000 K.
should be around 100 000 K. ![]() cannot be much lower than
this value since He I
cannot be much lower than
this value since He I ![]() 5876 would then be observed. Note that the
observed lower limit to [O III]/[O II] provides no useful constraint
upon the ionization structure (or central star temperature) of our
models.
5876 would then be observed. Note that the
observed lower limit to [O III]/[O II] provides no useful constraint
upon the ionization structure (or central star temperature) of our
models.
For the models with ![]() = 100 000 K shown in Fig. 5, the oxygen abundances compatible with the
observed [O III]/HH
= 100 000 K shown in Fig. 5, the oxygen abundances compatible with the
observed [O III]/HH![]() ratio are
ratio are
![]() dex. Allowing for a reasonable uncertainty in
dex. Allowing for a reasonable uncertainty in ![]() implies
implies
![]() dex. The upper limit to
[Ne V]/[Ne III] eliminates models excited by a star with a
temperature significantly above 100 000 K which would otherwise
permit
dex. The upper limit to
[Ne V]/[Ne III] eliminates models excited by a star with a
temperature significantly above 100 000 K which would otherwise
permit
![]() of the order of 7-8 dex.
of the order of 7-8 dex.
We have constructed other series of models to test the robustness
of these conclusions. For example, we have calculated models in
which the nebular radius, total nebular flux, and HH![]() equivalent
width were varied, but the conclusions remain unchanged.
equivalent
width were varied, but the conclusions remain unchanged.
We have also considered models in which the gas is distributed in
small clumps with the same global density law as above, but with
an overall filling factor of 0.1. Although the H![]() image is
smooth at our resolution, we cannot a priori exclude the presence
of small scale clumps or filaments. Clumpy models that fit the
observational constraints will result in a lower global
ionization level than smoothly-distributed models. For the
purposes of illustration, Fig. 6 compares the
smooth model of Fig. 5 with
image is
smooth at our resolution, we cannot a priori exclude the presence
of small scale clumps or filaments. Clumpy models that fit the
observational constraints will result in a lower global
ionization level than smoothly-distributed models. For the
purposes of illustration, Fig. 6 compares the
smooth model of Fig. 5 with ![]() = 150 000 K
and
= 150 000 K
and
![]()
![]() (circles) with a clumpy model whose filling factor is 0.1 (squares). Because the
ionization is lower in the clumpy model, the
(circles) with a clumpy model whose filling factor is 0.1 (squares). Because the
ionization is lower in the clumpy model, the
![]() ratio is lowered with respect to the
smooth model, while the [O III]
ratio is lowered with respect to the
smooth model, while the [O III] ![]() 5007/HH
5007/HH![]() ratio is raised. Consequently,
the oxygen abundance compatible with the observed [O III]
ratio is raised. Consequently,
the oxygen abundance compatible with the observed [O III] ![]() 5007/HH
5007/HH![]() ratio
is smaller than in the smooth case. Note that the model
presented here gives
ratio
is smaller than in the smooth case. Note that the model
presented here gives
![]() dex, but still violates the [Ne V]
dex, but still violates the [Ne V] ![]() 3426/[Ne III]
3426/[Ne III] ![]() 3869 and H
3869 and H![]() /HH
/HH![]() constraints. The total nebular mass of a model of given total HH
constraints. The total nebular mass of a model of given total HH![]() luminosity and given radius is roughly proportional to the square
of the filling factor. Therefore, clumpy models that satisfy the
observational constraints will have lower nebular masses than the
corresponding models listed in Table 5. Finally,
if the density in the clumps were extremely high, models with high
metallicities, even as high as solar, could account for the weak
intensities of the forbidden lines, because these lines would be
quenched by collisional de-excitation. For this to occur,
densities exceeding
luminosity and given radius is roughly proportional to the square
of the filling factor. Therefore, clumpy models that satisfy the
observational constraints will have lower nebular masses than the
corresponding models listed in Table 5. Finally,
if the density in the clumps were extremely high, models with high
metallicities, even as high as solar, could account for the weak
intensities of the forbidden lines, because these lines would be
quenched by collisional de-excitation. For this to occur,
densities exceeding
![]() are required for
both [O III]
are required for
both [O III] ![]() 5007 and [Ne III]
5007 and [Ne III] ![]() 3869. Given that the HH
3869. Given that the HH![]() flux and equivalent
width as well as the size of the nebula are known, such high
densities would imply that the filling factor would have to be of
the order of 10-8 or less, which is highly unrealistic.
flux and equivalent
width as well as the size of the nebula are known, such high
densities would imply that the filling factor would have to be of
the order of 10-8 or less, which is highly unrealistic.
Our computations were made assuming that the star radiates as a
blackbody. However, a more realistic stellar atmosphere would give
a different spectral energy distribution for the ionizing photons,
particularly at the largest energies. One expects that extended,
metal-poor atmospheres could have larger fluxes at energies above
100 eV. This would increase the [Ne V]/[Ne III] ratio and
consequently strenghten our conclusion that
![]() dex. On the other hand, absorption by metals
could depress the number of photons able to produce [Ne V] (Rauch
2002), in which case a star with
dex. On the other hand, absorption by metals
could depress the number of photons able to produce [Ne V] (Rauch
2002), in which case a star with ![]()
![]() K
could become acceptable. In this case, however, the excitation of
the nebula would be lower than that predicted by blackbody models
with
K
could become acceptable. In this case, however, the excitation of
the nebula would be lower than that predicted by blackbody models
with ![]() = 150 000 K and the line ratios would resemble
those produced by the blackbody model with
= 150 000 K and the line ratios would resemble
those produced by the blackbody model with ![]() =100 000 K,
again implying
=100 000 K,
again implying
![]() dex. In
any case, the amount of metals in the atmosphere is not expected
to be large, unless the atmosphere contains dredged-up carbon. A definitive answer to this problem can only come from a direct
measurement of lines from more highly charged ions.
dex. In
any case, the amount of metals in the atmosphere is not expected
to be large, unless the atmosphere contains dredged-up carbon. A definitive answer to this problem can only come from a direct
measurement of lines from more highly charged ions.
Note that the distance we obtain for our object (see Table 5) indicates that it is located in the Galactic halo, in agreement with its radial velocity (Tovmassian et al. 2001). Its derived nebular mass is compatible with the range of nebular masses derived for Magellanic Cloud PNe (Barlow 1987).
To conclude this section, we emphasize that our new observational
data allow us to confirm that PNG 135.9+55.9 is an extremely oxygen-poor
planetary nebula, with an oxygen abundance less than 1/50 of the
solar value. Our models favour a value of
![]() between 5.8 and 6.5 dex, compared with the solar
value of
between 5.8 and 6.5 dex, compared with the solar
value of
![]() dex
(Grevesse & Sauval 1998). Our modelling
experiments indicate that this conclusion is independent of
plausible changes in the properties assumed for the central star
or nebular envelope.
dex
(Grevesse & Sauval 1998). Our modelling
experiments indicate that this conclusion is independent of
plausible changes in the properties assumed for the central star
or nebular envelope.
Our preferred models with ![]() = 100 000 K and low
metallicities are compatible with the H
= 100 000 K and low
metallicities are compatible with the H![]() /HH
/HH![]() ratio derived from
the SPM1 data, as well as with the highest values found in
individual spectra from the other SPM observations (Table 2, Fig. 5). However, as discussed
earlier, we find apparently significant variations of the H
ratio derived from
the SPM1 data, as well as with the highest values found in
individual spectra from the other SPM observations (Table 2, Fig. 5). However, as discussed
earlier, we find apparently significant variations of the H![]() /HH
/HH![]() ratio between the different observing runs and even among
individual spectra obtained during individual runs. The majority
of the individual spectra indicate that H
ratio between the different observing runs and even among
individual spectra obtained during individual runs. The majority
of the individual spectra indicate that H![]() /HH
/HH![]() is below 3, as do
the observations reported by Tovmassian et al.
(2001).
is below 3, as do
the observations reported by Tovmassian et al.
(2001).
Because of collisional excitation of the hydrogen lines, H![]() /HH
/HH![]() cannot have the recombination value, but is expected to be larger.
Collisional excitation is unavoidable at electron temperatures
above
cannot have the recombination value, but is expected to be larger.
Collisional excitation is unavoidable at electron temperatures
above ![]() 15 000 K as soon as there is a small fraction of
residual neutral hydrogen. The amount by which H
15 000 K as soon as there is a small fraction of
residual neutral hydrogen. The amount by which H![]() /HH
/HH![]() exceeds
the recombination value (2.75 at 20 000 K, 2.70 at 30 000 K, using
the case B coefficients of Storey & Hummer 1995) depends upon
both the electron temperature, which is higher for higher values
of
exceeds
the recombination value (2.75 at 20 000 K, 2.70 at 30 000 K, using
the case B coefficients of Storey & Hummer 1995) depends upon
both the electron temperature, which is higher for higher values
of ![]() ,
and on the amount of neutral hydrogen. For example, the
models with
,
and on the amount of neutral hydrogen. For example, the
models with ![]() = 125 000 K predict a value of H
= 125 000 K predict a value of H![]() /HH
/HH![]() around 3.4 at low metallicities. With our observational
constraints, there is not much room for a drastic reduction of the
proportion of neutral hydrogen in our models. Indeed, for a given
around 3.4 at low metallicities. With our observational
constraints, there is not much room for a drastic reduction of the
proportion of neutral hydrogen in our models. Indeed, for a given
![]() and chemical composition, the proportion of H0 at each
point in the nebula is completely determined by (and roughly
proportional to)
and chemical composition, the proportion of H0 at each
point in the nebula is completely determined by (and roughly
proportional to)
![]() ,
where
,
where
![]() is the local electron density, LV is
the stellar luminosity in the V band and R is the distance of
this point to the star.
LV/R2 is a
distance-independent quantity that relates the stellar flux in the
V band to the angular distance of this point to the star;
is the local electron density, LV is
the stellar luminosity in the V band and R is the distance of
this point to the star.
LV/R2 is a
distance-independent quantity that relates the stellar flux in the
V band to the angular distance of this point to the star;
![]() is determined by the density distribution law
obtained from our H
is determined by the density distribution law
obtained from our H![]() images and the value of
images and the value of ![]() is
imposed by the observational constraints on W(HH
is
imposed by the observational constraints on W(HH![]() )
and the total
angular radius, as explained in Sect. 4.1. Our models of PNG 135.9+55.9 with
)
and the total
angular radius, as explained in Sect. 4.1. Our models of PNG 135.9+55.9 with ![]() = 100 000 K indicate that the H
= 100 000 K indicate that the H![]() /HH
/HH![]() ratio should
not be lower than 3 if the nebula is metal-poor. Values of
ratio should
not be lower than 3 if the nebula is metal-poor. Values of ![]() significantly below 100 000 K could be consistent with some of
the observed values of H
significantly below 100 000 K could be consistent with some of
the observed values of H![]() /HH
/HH![]() but they are excluded by the
failure to observe He I
but they are excluded by the
failure to observe He I ![]() 5876 in this object.
5876 in this object.
Does this mean that the object is not as oxygen-poor as inferred
above? There are several arguments against a higher abundance. In
our ![]() = 100 000 K models, H
= 100 000 K models, H![]() /HH
/HH![]() < 3 implies
< 3 implies
![]() dex, but this is clearly
incompatible with the observed value of [O III]
dex, but this is clearly
incompatible with the observed value of [O III] ![]() 5007/HH
5007/HH![]() ,
as seen in Fig. 5. At the other extreme, for our
,
as seen in Fig. 5. At the other extreme, for our ![]() =
150 000 K models, H
=
150 000 K models, H![]() /HH
/HH![]() < 3 implies
< 3 implies
![]() dex, which, though marginally compatible with the
observed [O III]
dex, which, though marginally compatible with the
observed [O III] ![]() 5007/HH
5007/HH![]() ,
predicts a value for the [Ne V]
,
predicts a value for the [Ne V] ![]() 3426/[Ne III]
3426/[Ne III] ![]() 3869 ratio
far larger than observed.
3869 ratio
far larger than observed.
Nor is it likely that any possible variability of the H![]() /HH
/HH![]() ratio affects our oxygen abundances. Supposing that this variation
is real and refers entirely to the nebular radiation, one would
then expect the [O III]
ratio affects our oxygen abundances. Supposing that this variation
is real and refers entirely to the nebular radiation, one would
then expect the [O III] ![]() 5007/HH
5007/HH![]() ratio to vary as a consequence of
variable ionization or temperature conditions, but this is not
seen. All of the line intensities apart from H
ratio to vary as a consequence of
variable ionization or temperature conditions, but this is not
seen. All of the line intensities apart from H![]() remain
remarkably constant, including the [O III]
remain
remarkably constant, including the [O III] ![]() 5007 line. Therefore, we
believe that the H
5007 line. Therefore, we
believe that the H![]() /HH
/HH![]() problem does not affect our conclusions
as regards the oxygen abundance in PNG 135.9+55.9.
problem does not affect our conclusions
as regards the oxygen abundance in PNG 135.9+55.9.
However, this H![]() /HH
/HH![]() problem is extremely puzzling. One does not
expect this ratio to vary in nebular conditions for an extended
object. One possibility could be that PNG 135.9+55.9 harbours a compact
disk. Such a suggestion has been made for other planetary nebulae
based upon either morphological, spectroscopic, or variability
arguments (He 2-25: Corradi 1995; IC 4997: Miranda & Torrelles
2000; Lee & Hyung 2000; and M 2-9: Livio & Soker 2001).
Accretion disks in close, interacting binary systems have the
particularity of both being variable (Warner 1995)
and having H
problem is extremely puzzling. One does not
expect this ratio to vary in nebular conditions for an extended
object. One possibility could be that PNG 135.9+55.9 harbours a compact
disk. Such a suggestion has been made for other planetary nebulae
based upon either morphological, spectroscopic, or variability
arguments (He 2-25: Corradi 1995; IC 4997: Miranda & Torrelles
2000; Lee & Hyung 2000; and M 2-9: Livio & Soker 2001).
Accretion disks in close, interacting binary systems have the
particularity of both being variable (Warner 1995)
and having H![]() /HH
/HH![]() ratios much smaller than 3, sometimes
attaining values below unity (e.g., Williams 1995). If PNG 135.9+55.9 contained such an accretion disk and if this disk contributed to
the emission of the hydrogen and helium lines in the central part
of the nebula, this could explain both the variability of the
H
ratios much smaller than 3, sometimes
attaining values below unity (e.g., Williams 1995). If PNG 135.9+55.9 contained such an accretion disk and if this disk contributed to
the emission of the hydrogen and helium lines in the central part
of the nebula, this could explain both the variability of the
H![]() /HH
/HH![]() ratio in PNG 135.9+55.9 and the values of 2.7 or lower observed in
some of our spectra. However, an accretion disk would be an
unresolved point source in our images, and our deconvolution
experiments found no significant contribution to the H
ratio in PNG 135.9+55.9 and the values of 2.7 or lower observed in
some of our spectra. However, an accretion disk would be an
unresolved point source in our images, and our deconvolution
experiments found no significant contribution to the H![]() emission from the central source. Likewise, the lack of
Dopper-broadened emission lines (Tovmassian et al. 2001) also argues against an accretion disk
as the origin of a significant fraction of the line emission
(Warner 1995).
emission from the central source. Likewise, the lack of
Dopper-broadened emission lines (Tovmassian et al. 2001) also argues against an accretion disk
as the origin of a significant fraction of the line emission
(Warner 1995).
Our high signal-to-noise spectra enabled us to measure the
intensity of the [Ne III] ![]() 3869 line, and to derive upper limits to the
intensities of [S III]
3869 line, and to derive upper limits to the
intensities of [S III] ![]() 9069 and [Ar III]
9069 and [Ar III] ![]() 7135, which allow us to make some
inferences on the abundances of Ne, S and Ar.
7135, which allow us to make some
inferences on the abundances of Ne, S and Ar.
![\begin{figure}
\par\includegraphics[width=17.2cm,clip]{h3796f7}\end{figure}](/articles/aa/full/2002/45/aah3796/Timg163.gif) |
Figure 7:
This figure presents various physical parameters for the grid of
models in Fig. 5. From left to right, the columns
present [O III] |
| Open with DEXTER | |
To compute abundances, we must rely upon the electron temperature
and ionization structure provided by our models. The relevant
quantities are shown in Fig. 7 for the models from
Fig. 5. The first column of panels on the left
repeats the [O III] ![]() 5007/HH
5007/HH![]() ratio from Fig. 7 for
reference. The second column of panels gives the value of
ratio from Fig. 7 for
reference. The second column of panels gives the value of
![]() defined as:
defined as:
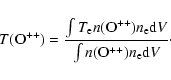 |
(1) |
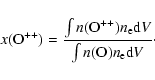 |
(2) |
Using the same atomic data as in the photoionization code and
taking as a characteristic temperature of the emission of the
[Ne III] ![]() 3869 and [O III]
3869 and [O III] ![]() 5007 lines a value of 30 000 K derived from our
preferred models (Fig. 5), we find that Ne++/O++
5007 lines a value of 30 000 K derived from our
preferred models (Fig. 5), we find that Ne++/O++
![]() ,
where the uncertainty reflects the uncertainties
of the [O III]
,
where the uncertainty reflects the uncertainties
of the [O III] ![]() 5007 and [Ne III]
5007 and [Ne III] ![]() 3869 line intensities. We furthermore note
that both O++ and Ne++ are minority ions (Fig. 7). Generally, one adopts Ne++/O++ = Ne/O. In our
preferred models (those corresponding to
3869 line intensities. We furthermore note
that both O++ and Ne++ are minority ions (Fig. 7). Generally, one adopts Ne++/O++ = Ne/O. In our
preferred models (those corresponding to ![]() = 100 000 K), we
find from Fig. 7 that the ionization correction
factor is rather around 0.7, thus leading to
= 100 000 K), we
find from Fig. 7 that the ionization correction
factor is rather around 0.7, thus leading to
![]() .
.
In a similar fashion, our observed limits on the intensities of
the [Ar IV]
![]() 4711, 4740 lines allow us to
derive that Ar+++/O++ < 0.45. From our models (Fig. 7) we find that the ionization correction factor is 0.5, and therefore Ar/O < 0.23.
4711, 4740 lines allow us to
derive that Ar+++/O++ < 0.45. From our models (Fig. 7) we find that the ionization correction factor is 0.5, and therefore Ar/O < 0.23.
Given that the nebula is strongly density-bounded, the observed
limits on the [N II] ![]() 6584 and [S II]
6584 and [S II] ![]() 6716,
6716, ![]() 6731 line intensities give only crude
limits on abundance ratios involving these elements. With the
ionization correction factors from our preferred model, we find
N/H
6731 line intensities give only crude
limits on abundance ratios involving these elements. With the
ionization correction factors from our preferred model, we find
N/H
![]() and S/H
and S/H
![]() .
Such limits
are not very useful, except to infer that the N/H ratio is at most
equal to that in the Orion nebula.
.
Such limits
are not very useful, except to infer that the N/H ratio is at most
equal to that in the Orion nebula.
Our infrared spectra allow us to estimate upper limits to the
intensities of [S III] ![]() 9069 and [Ar III]
9069 and [Ar III] ![]() 7135, which are respectively
7135, which are respectively
![]() and
and
![]() of the intensity of HH
of the intensity of HH![]() .
These
upper limits imply that
.
These
upper limits imply that
![]() and
and
![]() .
In our preferred
photoionization models, the ionization correction factor to derive
Ar/O from
.
In our preferred
photoionization models, the ionization correction factor to derive
Ar/O from
![]() is around 20, so that
the upper limit on [Ar III]
is around 20, so that
the upper limit on [Ar III] ![]() 7135 implies Ar/O < 0.24 (in agreement
with the upper limit derived from
[Ar IV]
7135 implies Ar/O < 0.24 (in agreement
with the upper limit derived from
[Ar IV]
![]() 4711, 4740). Regarding sulfur, we
find that the ionization correction factor is around 3 for S/O
from our models (Fig. 7), implying that
4711, 4740). Regarding sulfur, we
find that the ionization correction factor is around 3 for S/O
from our models (Fig. 7), implying that
![]() .
It must be noted that the atomic data
concerning the ionization structure of S and Ar are uncertain (see e.g. Ferland et al. 1998). Our models, were computed without
including dielectronic recombination to low-lying levels for these
ions. It is likely that the real ionization fractions of S++and Ar+++ are actually higher than predicted by the models,
giving smaller ionization correction factors and more stringent
limits.
.
It must be noted that the atomic data
concerning the ionization structure of S and Ar are uncertain (see e.g. Ferland et al. 1998). Our models, were computed without
including dielectronic recombination to low-lying levels for these
ions. It is likely that the real ionization fractions of S++and Ar+++ are actually higher than predicted by the models,
giving smaller ionization correction factors and more stringent
limits.
| object | Ne/O | S/O | Ar/O |
| PNG 135.9+55.9 a |
|
<0.094 | <0.23 |
| Galactic disk PNe b | 0.26 | 0.017 | 0.005 |
| Galactic halo PNe c | 0.13 | 0.016 | 0.0016 |
| Orion nebula d | 0.18 | 0.03 | 0.014 |
| Sun e | 0.18 | 0.03 | 0.004 |
a This work.
b Kingsburgh & Barlow (1994).
c Howard et al. (1997).
These authors also show that the abundance ratios are more
dispersed in halo PNe than in disk PNe.
d Esteban et al. (1998).
e Grevesse & Sauval (1998).
It is interesting to compare the ratios of Ne/O, S/O and Ar/O we
find for PNG 135.9+55.9 with those of other kinds of objects. Table 6 shows the values for a sample of PNe in the
Galactic disk (Kingsburgh & Barlow 1994) and in the Galactic
halo
(Howard et al. 1997), for the Orion nebula (Esteban et al. 1998),
and for the Sun (Grevesse & Sauval 1998). This table is of course
subject to uncertainties. Even the solar abundances are quite
uncertain for Ne, Ar and O (see Grevesse & Sauval
1998; the recent oxygen abundance
determination from Allende Prieto et al. 2001 yields a value that is only 73% that
obtained by Grevesse & Sauval 1998). One
might then argue that the Ne/O ratio in PNG 135.9+55.9 is compatible with
the solar value, but we note that it is about twice the value
found in the Orion nebula and in disk planetary nebulae, where the
systematic errors in the abundance derivations are likely to be
similar. Supposing our Ne/O ratio is corect, it might indicate
some conversion of O into Ne by ![]() capture. A few similar
cases are known among planetary nebulae (e.g., BB-1 has a
capture. A few similar
cases are known among planetary nebulae (e.g., BB-1 has a
![]() ;
Howard et al. 1997). Another
possibility is that the material from which the progenitor of
PNG 135.9+55.9 formed had an anomalous Ne/O ratio. Abundance studies of
metal-poor stars indicate that the very early galaxy was
chemically-inhomogeneous, with individual sites of star formation
being influenced by the explosions of nearby supernovae (e.g.,
Burris et al. 2000). The yields of O and Ne from
individual supernovae are also a function of the stellar mass
(Woosley & Weaver 1995; Thielemann et al.
1996), while observations of metal-poor halo
stars indicate that the scatter in oxygen abundances is
0.3-0.5 dex at very low oxygen abundances (e.g., Israelian et al.
2001). As a result, it is probably not
surprising that the progenitor of PNG 135.9+55.9 might not have formed out
of material with the same Ne/O ratio that has characterized the
more recent Galactic disk. Regardless, any conversion of O into
Ne is at most modest. Even were all of the Ne formed by
nuclear processing from oxygen, the initial oxygen abundance would
have been only 0.18 dex larger than our preferred values. Thus,
the extremely low oxygen abundance in PNG 135.9+55.9 is genuine and not due
to nuclear and mixing processes in the progenitor star. The oxygen
abundance in PNG 135.9+55.9 should consequently reflect the chemical
composition of the medium out of which the star was made. The
limits we obtain on S/O and Ar/O in our object are consistent with
this view (although the limits are not very stringent).
;
Howard et al. 1997). Another
possibility is that the material from which the progenitor of
PNG 135.9+55.9 formed had an anomalous Ne/O ratio. Abundance studies of
metal-poor stars indicate that the very early galaxy was
chemically-inhomogeneous, with individual sites of star formation
being influenced by the explosions of nearby supernovae (e.g.,
Burris et al. 2000). The yields of O and Ne from
individual supernovae are also a function of the stellar mass
(Woosley & Weaver 1995; Thielemann et al.
1996), while observations of metal-poor halo
stars indicate that the scatter in oxygen abundances is
0.3-0.5 dex at very low oxygen abundances (e.g., Israelian et al.
2001). As a result, it is probably not
surprising that the progenitor of PNG 135.9+55.9 might not have formed out
of material with the same Ne/O ratio that has characterized the
more recent Galactic disk. Regardless, any conversion of O into
Ne is at most modest. Even were all of the Ne formed by
nuclear processing from oxygen, the initial oxygen abundance would
have been only 0.18 dex larger than our preferred values. Thus,
the extremely low oxygen abundance in PNG 135.9+55.9 is genuine and not due
to nuclear and mixing processes in the progenitor star. The oxygen
abundance in PNG 135.9+55.9 should consequently reflect the chemical
composition of the medium out of which the star was made. The
limits we obtain on S/O and Ar/O in our object are consistent with
this view (although the limits are not very stringent).
The accuracy of the helium line intensities achieved in the
present observations raised the hope of obtaining very accurate
helium abundances. Taking the intensities determined from our CFHT observations and adopting a temperature of 30 000 K as inferred
from our models and case B coefficients from Storey & Hummer
(1995) we find that He++/H+
![]() .
The upper limit to the intensity of He I
.
The upper limit to the intensity of He I ![]() 5876 in
the same spectra gives an upper limit to He+/H+ of
5876 in
the same spectra gives an upper limit to He+/H+ of
![]() when using the emissivities from Benjamin et al. (1999)
in the low density limit. A proper determination of the
uncertainty in the derived helium abundance should, however,
account for collisional excitation of the lines, a possible small
amount of reddening, possible deviations from case B, possible
underlying absorption, as well as temperature gradients inside the
nebula. All of this can only be attempted once the H
when using the emissivities from Benjamin et al. (1999)
in the low density limit. A proper determination of the
uncertainty in the derived helium abundance should, however,
account for collisional excitation of the lines, a possible small
amount of reddening, possible deviations from case B, possible
underlying absorption, as well as temperature gradients inside the
nebula. All of this can only be attempted once the H![]() /HH
/HH![]() problem is solved. It is therefore premature to propose an
accurate value for the helium abundance in PNG 135.9+55.9.
problem is solved. It is therefore premature to propose an
accurate value for the helium abundance in PNG 135.9+55.9.
Using these data as constraints, we constructed a new set of
nebular models from which we derived the abundance of oxygen and
the Ne/O, S/O, and Ar/O abundance ratios. We confirm the
extremely low value of the oxygen abundance, which we find to be
less than 1/50 of the solar value: our models favour a value of
![]() between 5.8 and 6.5 dex. The
distance implied by these models places PNG 135.9+55.9 in the Milky Way
halo, in accordance with its radial velocity (Tovmassian et al.
2001). The models also imply nebular masses
in the range expected.
between 5.8 and 6.5 dex. The
distance implied by these models places PNG 135.9+55.9 in the Milky Way
halo, in accordance with its radial velocity (Tovmassian et al.
2001). The models also imply nebular masses
in the range expected.
For the ![]() -element ratios, we find
-element ratios, we find
![]() ,
,
![]() ,
and
,
and
![]() .
The Ne/O ratio may be somewhat higher than is commonly found
in planetary nebulae in the Milky Way disk (e.g., Henry
1989; Kingsburgh & Barlow
1994). One possibility is that the
progenitor of PNG 135.9+55.9 converted some of its O to Ne. It is also
possible that the anomalous Ne/O ratio is the result of discrete
chemical enrichment in the very early evolution of the galaxy
(e.g., Burris et al. 2000). Regardless, of the
cause, any conversion of O to Ne has been modest and does not
affect our conclusion that PNG 135.9+55.9 is the progeny of an
intrinsically very oxygen-poor star.
.
The Ne/O ratio may be somewhat higher than is commonly found
in planetary nebulae in the Milky Way disk (e.g., Henry
1989; Kingsburgh & Barlow
1994). One possibility is that the
progenitor of PNG 135.9+55.9 converted some of its O to Ne. It is also
possible that the anomalous Ne/O ratio is the result of discrete
chemical enrichment in the very early evolution of the galaxy
(e.g., Burris et al. 2000). Regardless, of the
cause, any conversion of O to Ne has been modest and does not
affect our conclusion that PNG 135.9+55.9 is the progeny of an
intrinsically very oxygen-poor star.
An unusual characteristic of PNG 135.9+55.9 is its low H
![]() ratio, for which we find no clear explanation. Despite
its low metallicity and the concomitant high electron temperature
that should result in collisionally excited Balmer lines of
H I, PNG 135.9+55.9 has an
ratio, for which we find no clear explanation. Despite
its low metallicity and the concomitant high electron temperature
that should result in collisionally excited Balmer lines of
H I, PNG 135.9+55.9 has an
![]() ratio
typically below 3. Furthermore,
ratio
typically below 3. Furthermore,
![]() appears to be variable between observing runs and even within a single night. One possible explanation for both the low
appears to be variable between observing runs and even within a single night. One possible explanation for both the low
![]() ratio and its variability is if PNG 135.9+55.9 contains an accretion disk, though the evidence is not convincing.
At any rate, this issue does not appear to affect our conclusions
regarding the chemical abundances.
ratio and its variability is if PNG 135.9+55.9 contains an accretion disk, though the evidence is not convincing.
At any rate, this issue does not appear to affect our conclusions
regarding the chemical abundances.
We also measure a low
![]() ratio of
ratio of ![]() 0.08.
This makes PNG 135.9+55.9 interesting as a probe of the pregalactic He abundance. However, the derivation of a very precise He abundance
will require the resolution of a number of outstanding issues,
including the
0.08.
This makes PNG 135.9+55.9 interesting as a probe of the pregalactic He abundance. However, the derivation of a very precise He abundance
will require the resolution of a number of outstanding issues,
including the
![]() problem, the
foreground reddening, and the internal temperature structure.
problem, the
foreground reddening, and the internal temperature structure.
Acknowledgements
MGR thanks Anabel Arrieta, Leonid Georgiev, Felipe Montalvo, and Salvador Monrroy for their able assistance with the observations at SPM. GT, GS, MGR, and CV are grateful for the receipt of Director's discretionary time at the CFHT. We are grateful to the WHT staff for the spectrum obtained through service time. GS acknoledges useful discussions with Y. Izotov, J. M. Huré and M. Mouchet. PDD is a PPARC-supported PDRA. MGR acknowledges financial support from DGAPA project IN100799 and CONACyT project 37214-E. GS acknowledges financial support from DGAPA project IN114601. GT and GS acknowledge financial support from CONACyT project 34521-E.