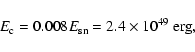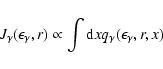A&A 395, 943-953 (2002)
DOI: 10.1051/0004-6361:20021219
Emission of SN 1006 produced by accelerated cosmic rays
E. G. Berezhko
1 -
L. T. Ksenofontov
1 -
H. J. Völk
2
1 - Institute of Cosmophysical Research and Aeronomy,
31 Lenin Av., 677891 Yakutsk, Russia
2 -
Max Planck Institut für Kernphysik,
Postfach 103980, 69029 Heidelberg, Germany
Received 8 April 2002 / Accepted 23 August 2002
Abstract
The nonlinear kinetic model of cosmic ray (CR)
acceleration in supernova remnants (SNRs) is used to describe the
properties of the remnant of SN 1006. It is shown, that the theory fits
the existing data in a satisfactory way within a set of parameters which
is consistent with the idea that SN 1006 is a typical source of Galactic
CR nucleons, although not necessarily of CR electrons. The adjusted
parameters are those that are not very well determined by present theory
or not directly amenable to astronomical observations. The calculated
expansion law and the radio-, X-ray and  -ray emissions produced by
the accelerated CRs in SN 1006 agree quite well with the observations. A
rather large interior magnetic field
-ray emissions produced by
the accelerated CRs in SN 1006 agree quite well with the observations. A
rather large interior magnetic field
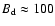
 G is
required to give a good fit for the radio and X-ray synchrotron emission.
In the predicted TeV
G is
required to give a good fit for the radio and X-ray synchrotron emission.
In the predicted TeV  -ray flux from SN 1006, the
-ray flux from SN 1006, the 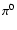 -decay
-decay
 -rays, generated by the nuclear CR component, dominate over the
inverse Compton (IC)
-rays, generated by the nuclear CR component, dominate over the
inverse Compton (IC)  -rays, generated by the CR electrons in the
cosmic microwave background. The predicted source morphology in high
energy
-rays, generated by the CR electrons in the
cosmic microwave background. The predicted source morphology in high
energy  -rays roughly corresponds to that of the synchrotron
emission. The predicted integral
-rays roughly corresponds to that of the synchrotron
emission. The predicted integral  -ray flux
-ray flux
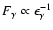 extends up to energies
extends up to energies  100 TeV if CR
diffusion is as strong as the Bohm limit. Only if the interior magnetic
field is much lower in the SNR,
100 TeV if CR
diffusion is as strong as the Bohm limit. Only if the interior magnetic
field is much lower in the SNR,
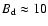
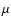 G, then the
observed
G, then the
observed  -ray emission can be due to the accelerated electron
component alone. In this case, not plausible physically in our view, the
lowest permissible value of the electron to proton ratio is rather high,
and the maximum individual energy and total energy content of accelerated
nucleons so small, that SN 1006 can not be considered as a typical source
of the nuclear Galactic CRs.
-ray emission can be due to the accelerated electron
component alone. In this case, not plausible physically in our view, the
lowest permissible value of the electron to proton ratio is rather high,
and the maximum individual energy and total energy content of accelerated
nucleons so small, that SN 1006 can not be considered as a typical source
of the nuclear Galactic CRs.
Key words: ISM: cosmic rays - acceleration of particles - stars: supernovae: individual: SN 1006 - radio continuum: ISM - X-rays:
ISM - gamma rays: theory
In the last years significant efforts have been made to obtain direct
observational evidence whether the Galactic cosmic rays (CRs) -
relativistic nucleons and electrons - are indeed generated in supernova
remnants (SNRs). The expected 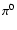 -decay
-decay  -ray emission,
produced in nearby SNRs by the accelerated protons in their collisions
with thermal gas nuclei, is marginally high enough to be detectable by the
present generation of imaging atmospheric Cherenkov telescopes (e.g. Drury
et al. 1994; Naito & Takahara 1994; Berezhko & Völk
1997). Positive results of such observations would constitute a
necessary condition for a dominant role of SNRs in the production of the
Galactic CRs and of their energy spectrum up to the knee energy
-ray emission,
produced in nearby SNRs by the accelerated protons in their collisions
with thermal gas nuclei, is marginally high enough to be detectable by the
present generation of imaging atmospheric Cherenkov telescopes (e.g. Drury
et al. 1994; Naito & Takahara 1994; Berezhko & Völk
1997). Positive results of such observations would constitute a
necessary condition for a dominant role of SNRs in the production of the
Galactic CRs and of their energy spectrum up to the knee energy 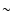 1015 eV.
1015 eV.
If SNRs accelerate nucleons at least to 100 TeV/n as it is required for
Galactic CRs (e.g Berezhko & Ksenofontov 1999), then in smooth
extension of the expected hadronically generated 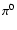 -decay
-decay
 -ray peak at 67.5 MeV (e.g. Stecker 1971; Dermer
1986) one expects the nucleonic
-ray peak at 67.5 MeV (e.g. Stecker 1971; Dermer
1986) one expects the nucleonic  -ray spectrum to have an
almost single power-law form to about 1 TeV, before turning over
above 10 TeV. At the same time the leptonic Inverse Compton (IC)
-ray spectrum to have an
almost single power-law form to about 1 TeV, before turning over
above 10 TeV. At the same time the leptonic Inverse Compton (IC)
 -ray spectrum may be quenched at a lower cut-off energy due to
electron synchrotron losses (as in our model). Then
-ray spectrum may be quenched at a lower cut-off energy due to
electron synchrotron losses (as in our model). Then  -ray
observations within the range from
10 MeV to 100 TeV would be useful in discriminating between the nucleonic
and leptonic components.
-ray
observations within the range from
10 MeV to 100 TeV would be useful in discriminating between the nucleonic
and leptonic components.
Recent observations of nonthermal X-rays and  -rays indicate that
at least CR electrons are accelerated in SNRs. SN 1006 is one of the SNRs
for which there is evidence that electrons reach energies of about 100 TeV
(Koyama et al. 1995; Tanimori et al. 1998, 2001).
It is also one of the three shell type SNRs in which TeV
-rays indicate that
at least CR electrons are accelerated in SNRs. SN 1006 is one of the SNRs
for which there is evidence that electrons reach energies of about 100 TeV
(Koyama et al. 1995; Tanimori et al. 1998, 2001).
It is also one of the three shell type SNRs in which TeV  -ray
emission has been detected up to now. However, the interpretation of these
data is not unique. Depending on the assumed values for the unknown
physical parameters of SN 1006 (mainly the value of the magnetic field,
the electron to proton ratio, and to some extent also the nucleon
injection rate), the observed high-energy
-ray
emission has been detected up to now. However, the interpretation of these
data is not unique. Depending on the assumed values for the unknown
physical parameters of SN 1006 (mainly the value of the magnetic field,
the electron to proton ratio, and to some extent also the nucleon
injection rate), the observed high-energy  -ray emission can be
predominantly either inverse Compton radiation due to CR electrons
scattering on the microwave background radiation (as predicted
by Mastichiadis 1996; Pohl 1996;
Mastichiadis & de Jager 1996; and Yoshida & Yanagita
1997 from the X-ray synchrotron emission, and through the
interpretation of the X-ray and
-ray emission can be
predominantly either inverse Compton radiation due to CR electrons
scattering on the microwave background radiation (as predicted
by Mastichiadis 1996; Pohl 1996;
Mastichiadis & de Jager 1996; and Yoshida & Yanagita
1997 from the X-ray synchrotron emission, and through the
interpretation of the X-ray and  -ray data by Aharonian
1999; Aharonian & Atoyan 1999; Berezhko et al.
1999), or
-ray data by Aharonian
1999; Aharonian & Atoyan 1999; Berezhko et al.
1999), or 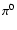 -decay emission due to hadronic
collisions of CRs with gas nuclei (Aharonian 1999; Aharonian &
Atoyan 1999; Berezhko et al. 1999; Berezhko
et al. 2001).
-decay emission due to hadronic
collisions of CRs with gas nuclei (Aharonian 1999; Aharonian &
Atoyan 1999; Berezhko et al. 1999; Berezhko
et al. 2001).
The thermal and nonthermal X-ray emission has recently been
rediscussed by Allen et al. (2001) who draw phenomenological
conclusions on the  -ray emission to be dominated by IC radiation as
well as on the production and the characteristics of the nonthermal
nucleonic particle component which they estimate to have a total
energy of 1050 ergs.
-ray emission to be dominated by IC radiation as
well as on the production and the characteristics of the nonthermal
nucleonic particle component which they estimate to have a total
energy of 1050 ergs.
In contrast, our starting point is the overall SNR dynamics and the
acceleration theory of the nonthermal component. Thus we accept the X-ray
results and the quantitative distinction between thermal X-ray emission
and the nonthermal synchrotron components, including the constraints on
the external density derived from them. We calculate the outer
shock size, speed and compression ratio as well as the nonthermal
quantities as solutions of the nonlinear, time-dependent kinetic equations
for electrons and protons as functions of space, time and particle
momentum, rather than phenomenologically assuming forms of the electron
and proton momentum distribution functions.
In this way we also obtain full morphological information. We determine
the unknown parameters like the upstream magnetic field strength and the
electron to proton ratio, and constrain the nucleon injection rate which
cannot yet be accuratetely calculated from known theory, by comparing with
the observations. For this purpose we use the selfconsistent kinetic model
of diffusive acceleration of CRs in SNRs (Berezhko et al. 1996;
Berezhko & Völk 1997) and investigate the  -ray emission
from SN 1006. A preliminary version of our results is given in Berezhko et
al. (2001).
-ray emission
from SN 1006. A preliminary version of our results is given in Berezhko et
al. (2001).
In contrast to a previous study (Berezhko et al. 1999) we restrict
ourselves to the so-called Bohm limit for CR diffusion near the shock,
assuming efficient and strong excitation of magnetohydrodynamic waves by
the accelerating particles themselves. This is consistent with the large
magnetic field strengths which we infer for this remnant.
Our considerations show that, together with a renormalization due to the
lack of spherical symmetry of the nucleon injection, the existing SNR data
are consistent with very efficient acceleration of CR nuclei at the SN
shock wave which converts a significant fraction of the initial SNR energy
content into CR energy as required for a typical source of the Galactic CR
nuclei. The relative amount of energetic electrons is rather small, and
may require additional sources to SNe type Ia like SN 1006. Therefore the
observed  -ray emission of SN 1006 can indeed be of hadronic
origin, and we consider this as the physically most plausible solution
from the point of view of acceleration theory.
-ray emission of SN 1006 can indeed be of hadronic
origin, and we consider this as the physically most plausible solution
from the point of view of acceleration theory.
Nevertheless, the existing observations do not strongly exclude a solution
in which nuclear CRs play no important role and all nonthermal emissions
are of leptonic origin. Therefore we analyze whether the existing data can
also be fitted by an essentially different set of parameters. We
demonstrate that there is an alternative possibility to fit the overall
data, albeit with somewhat lower quality.
It implies a (physically not plausible) much lower injection rate and
acceleration efficiency of protons, a rather large electron to proton
ratio, and a lower magnetic field value compared with the case of
efficient CR nucleon acceleration. If we would assume SN 1006 to be a
typical representative, in this second case we could not consider the SNRs
as the source population of the Galactic CRs due to the low proton
acceleration efficiency. To discriminate empirically between these rather
different scenarios from our results  -ray measurements above
10 TeV are required: in this very high energy range we expect a measurable
-ray measurements above
10 TeV are required: in this very high energy range we expect a measurable
 -ray flux only in the case of efficient nucleonic CR production.
We also confirm the earlier result (Aharonian 1999; Aharonian &
Atoyan 1999; Berezhko et al. 1999; Berezhko et al.
2001) that the IC
-ray flux only in the case of efficient nucleonic CR production.
We also confirm the earlier result (Aharonian 1999; Aharonian &
Atoyan 1999; Berezhko et al. 1999; Berezhko et al.
2001) that the IC  -ray emission should cover the SNR
almost uniformly, whereas the
-ray emission should cover the SNR
almost uniformly, whereas the 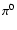 -decay emission should be peaked
behind the shock front and limited to two polar caps where the
interstellar magnetic field is parallel to the shock normal.
-decay emission should be peaked
behind the shock front and limited to two polar caps where the
interstellar magnetic field is parallel to the shock normal.
Since SN 1006 is a type Ia supernova (SN) we suggest that its evolution
takes place in a uniform interstellar medium (ISM), not modified by a wind
from the progenitor star. The general picture is then well-known.
A SN explosion ultimately ejects a shell of matter with total energy
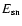 and mass
and mass
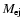 .
During an initial period the
shell material has a broad distribution in velocity v. The fastest part
of these ejecta is described by a power law
.
During an initial period the
shell material has a broad distribution in velocity v. The fastest part
of these ejecta is described by a power law
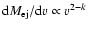 (e.g. Jones et al. 1981; Chevalier 1982).
The interaction of the ejecta with the ISM creates a strong shock there
which accelerates particles.
(e.g. Jones et al. 1981; Chevalier 1982).
The interaction of the ejecta with the ISM creates a strong shock there
which accelerates particles.
Our nonlinear model (Berezhko et al. 1996; Berezhko & Völk
1997) is based on a fully time-dependent solution of the CR
transport equation together with the gas dynamic equations in spherical
symmetry. It yields at any given phase of the SNR evolution the complete
spatial distribution of gas and accelerated CRs and their spectrum. This
makes it possible to calculate any kind of emission, and its morphology,
produced by the accelerated particles.
The CR diffusion coefficient is taken as the Bohm limit
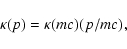 |
(1) |
where approximately
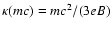 ,
e and m are the particle
charge and mass, p denotes the particle momentum, B is the magnetic
field strength, and c is the speed of light. With this diffusion
coefficient we assume that the production of scattering waves is so strong
that limitations due to wave refraction (Malkov et al. 1995) do
not come in to influence the solution.
,
e and m are the particle
charge and mass, p denotes the particle momentum, B is the magnetic
field strength, and c is the speed of light. With this diffusion
coefficient we assume that the production of scattering waves is so strong
that limitations due to wave refraction (Malkov et al. 1995) do
not come in to influence the solution.
The number of suprathermal protons injected into the acceleration process
is described by a dimensionless injection parameter 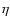 which is a
fixed fraction of the ISM particles entering the shock front. For
simplicity it is assumed that the injected particles have a velocity four
times higher than the postshock sound speed. Unfortunately there is no
complete selfconsistent theory of a collisionless shock transition which
can predict the value of the injection rate and its dependence on the
shock parameters. For the case of a purely parallel plane shock hybrid
simulations predict a quite high ion injection (e.g. Scholer et al.
1992; Bennet & Ellison 1995) which corresponds to the
value
which is a
fixed fraction of the ISM particles entering the shock front. For
simplicity it is assumed that the injected particles have a velocity four
times higher than the postshock sound speed. Unfortunately there is no
complete selfconsistent theory of a collisionless shock transition which
can predict the value of the injection rate and its dependence on the
shock parameters. For the case of a purely parallel plane shock hybrid
simulations predict a quite high ion injection (e.g. Scholer et al.
1992; Bennet & Ellison 1995) which corresponds to the
value
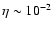 of our injection parameter. Such a high
injection is consistent with analytical models (Malkov & Völk
1995, 1996; Malkov 1998) and confirmed by
measurements near the Earth's bow shock (Trattner & Scholer 1994).
We note however that in our spherically symmetric model these results can
only be used with some important modification. In reality we must consider
the evolution of the large scale SN shock which expands into the ISM with
its magnetic field. In the case of SN 1006, at the current evolutionary
phase, the shock has a size of several parsecs. On such a scale the
unshocked interstellar magnetic field can be considered as uniform since
its random component is characterized by a much larger main scale of about
100 pc. Then our spherical shock is quasi-parallel in the polar regions
and quasi-perpendicular in the equatorial region. This magnetic field
essentially suppresses the leakage of suprathermal particles from the
downstream region back upstream when the shock is more and more oblique
(Ellison et al. 1995; Malkov & Völk 1995). Applied to
the spherical shock in the uniform external magnetic field it would mean
that only small regions near the poles, covering less than 10% of the
shock surface, allow a sufficiently high injection that ultimately leads
to the transformation of an essential part (more than a few percent) of
the shock energy into CR energy, whereas the main part of the shock is an
inefficient CR accelerator. If one takes into account the Alfvén wave
excitation due to CR streaming (which becomes efficient already at a very
low injection rate
of our injection parameter. Such a high
injection is consistent with analytical models (Malkov & Völk
1995, 1996; Malkov 1998) and confirmed by
measurements near the Earth's bow shock (Trattner & Scholer 1994).
We note however that in our spherically symmetric model these results can
only be used with some important modification. In reality we must consider
the evolution of the large scale SN shock which expands into the ISM with
its magnetic field. In the case of SN 1006, at the current evolutionary
phase, the shock has a size of several parsecs. On such a scale the
unshocked interstellar magnetic field can be considered as uniform since
its random component is characterized by a much larger main scale of about
100 pc. Then our spherical shock is quasi-parallel in the polar regions
and quasi-perpendicular in the equatorial region. This magnetic field
essentially suppresses the leakage of suprathermal particles from the
downstream region back upstream when the shock is more and more oblique
(Ellison et al. 1995; Malkov & Völk 1995). Applied to
the spherical shock in the uniform external magnetic field it would mean
that only small regions near the poles, covering less than 10% of the
shock surface, allow a sufficiently high injection that ultimately leads
to the transformation of an essential part (more than a few percent) of
the shock energy into CR energy, whereas the main part of the shock is an
inefficient CR accelerator. If one takes into account the Alfvén wave
excitation due to CR streaming (which becomes efficient already at a very
low injection rate
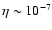 )
the local injection rate has to be
averaged over the fluctuating magnetic field directions and is lower than
for the purely parallel case by a factor of hundred. Therefore we adopt
here the value
)
the local injection rate has to be
averaged over the fluctuating magnetic field directions and is lower than
for the purely parallel case by a factor of hundred. Therefore we adopt
here the value
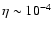 for the injection parameter (Völk et
al. 2002). The detailed choice
for the injection parameter (Völk et
al. 2002). The detailed choice
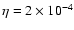 in the next
section is made in order to achieve a nonlinear shock modification that is
consistent with the observed radio spectral index.
in the next
section is made in order to achieve a nonlinear shock modification that is
consistent with the observed radio spectral index.
According to our above estimate a substantial part of the shock still
efficiently injects and accelerates CRs. This fraction is effectively
increased relative to the above percentage due to broadening of the
injection region by the strong wave field as well as by CR diffusion
perpendicular to the mean magnetic field. In addition, the overall
conservation equations ensure an approximately spherical character of the
overall dynamics. Therefore, we assume the spherically symmetric approach
for the nonlinear particle acceleration process to be approximately valid
in those shock regions where injection is efficient. To take the effective
injection fraction
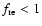 into account, we then need to
introduce a renormalization factor for the CR acceleration efficiency and
for all the effects which it produces in the SNR. A rough estimate
performed for the simple case of spherical shock expended in the uniform
outer magnetic field (Völk et al. 2002) gives
into account, we then need to
introduce a renormalization factor for the CR acceleration efficiency and
for all the effects which it produces in the SNR. A rough estimate
performed for the simple case of spherical shock expended in the uniform
outer magnetic field (Völk et al. 2002) gives
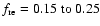 .
.
Note that such a picture is consistent with the observed structure of
SN 1006: the intense radio and X-ray emissions come from two bright rims
with radially oriented magnetic field (Reynolds & Gilmore 1993).
They may be the polar regions of a quasispherical shock in an outer
magnetic field. The  -ray observations may indicate a similar
asymmetry (Tanimori et al. 1998) which would be well explained by
a corresponding concentration of the accelerated nucleons towards the
polar regions.
-ray observations may indicate a similar
asymmetry (Tanimori et al. 1998) which would be well explained by
a corresponding concentration of the accelerated nucleons towards the
polar regions.
We assume that electrons are also injected into the acceleration process,
still at nonrelativistic energies below
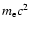 .
Since the
electron injection mechanism is not very well known (e.g. Malkov & Drury
2001) for simplicity we consider their acceleration starting from
the same momentum as that of protons. At relativistic energies (for
protons) these electrons have exactly the same dynamics as the protons.
Therefore, neglecting synchrotron losses,
their distribution function at any given time has the form
.
Since the
electron injection mechanism is not very well known (e.g. Malkov & Drury
2001) for simplicity we consider their acceleration starting from
the same momentum as that of protons. At relativistic energies (for
protons) these electrons have exactly the same dynamics as the protons.
Therefore, neglecting synchrotron losses,
their distribution function at any given time has the form
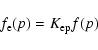 |
(2) |
with some factor
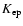 which is about 10-2 for the
average CRs in
the Galaxy. We take it here as a parameter.
which is about 10-2 for the
average CRs in
the Galaxy. We take it here as a parameter.
The electron distribution function
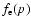 deviates only at sufficiently large momenta from
this relation
due to synchrotron losses,
which are taken into account by supplementing the ordinary diffusive
transport equation with a loss term:
deviates only at sufficiently large momenta from
this relation
due to synchrotron losses,
which are taken into account by supplementing the ordinary diffusive
transport equation with a loss term:
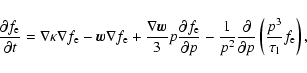 |
(3) |
where the first three terms in the right hand side of this equation
describe diffusion, convection due to the mass velocity 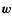 of
the gas
and adiabatic effects, respectively. The synchrotron loss time in the
third term is determined by the expression (e.g. Berezinskii et al.
1990)
of
the gas
and adiabatic effects, respectively. The synchrotron loss time in the
third term is determined by the expression (e.g. Berezinskii et al.
1990)
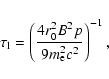 |
(4) |
where 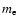 is the electron mass and
r0 the classical electron radius.
is the electron mass and
r0 the classical electron radius.
The solution of the dynamic equations at each instant of time yields the
CR spectrum and the spatial distributions of CRs and gas. This allows us
to calculate the expected flux
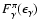 of
of  -rays from
-rays from 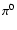 -decay due to hadronic (p-p)
collisions of CRs with the gas nuclei. Following the work of Dermer
(1986)
and its later improvement by Naito & Takahara
(1994) we use here the
isobar model at the protons kinetic energies
-decay due to hadronic (p-p)
collisions of CRs with the gas nuclei. Following the work of Dermer
(1986)
and its later improvement by Naito & Takahara
(1994) we use here the
isobar model at the protons kinetic energies
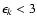 GeV
and the scaling model at
GeV
and the scaling model at
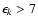 GeV with a linear connection between 3 and 7 GeV.
This model agrees very well with the simpler
approach, introduced by Drury et al. (1994) (see also Berezhko &
Völk 1997, 2000; Berezhko et al. 1999) at high
energies
GeV with a linear connection between 3 and 7 GeV.
This model agrees very well with the simpler
approach, introduced by Drury et al. (1994) (see also Berezhko &
Völk 1997, 2000; Berezhko et al. 1999) at high
energies
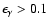 GeV, except in the cutoff region, where
the scaling model yields an essentially smoother turnover of the
GeV, except in the cutoff region, where
the scaling model yields an essentially smoother turnover of the
 -ray spectrum at somewhat lower energies.
-ray spectrum at somewhat lower energies.
The choice of
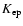 allows us to determine in addition the electron
distribution function and
to calculate the associated emission. The expected synchrotron
flux at distance dfrom the SNR is given by the expression (e.g. Berezinskii et al.
1990)
allows us to determine in addition the electron
distribution function and
to calculate the associated emission. The expected synchrotron
flux at distance dfrom the SNR is given by the expression (e.g. Berezinskii et al.
1990)
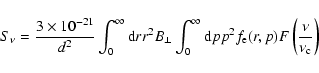 |
(5) |
in erg/(cm2 s), where
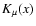 is the modified
Bessel function,
is the modified
Bessel function,
![$\nu_{\rm c}=3e B_{\perp} p^2 /[ 4\pi (m_{\rm e}c)^3]$](/articles/aa/full/2002/45/aah3593/img44.gif) and
and
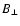 is the magnetic field component
perpendicular to the line of sight.
is the magnetic field component
perpendicular to the line of sight.
Since in the shock region where particle injection and acceleration is
efficient the upstream magnetic field is assumed to be almost completely
randomized due to intense Alfvén wave generation. For such a strongly
turbulent upstream field, consistent with Bohm diffusion, the postshock
field strength B2 is given by by
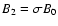 ,
where
,
where
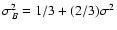 .
We shall approximately equate
.
We shall approximately equate
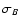 with the gas compression ratio
with the gas compression ratio 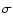 at the shock that
We suggest also that in such a young SNR like SN 1006 the downstream
magnetic field
at the shock that
We suggest also that in such a young SNR like SN 1006 the downstream
magnetic field 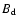 in a relatively thin region between the
shock and the ejecta is approximately uniform and we shall take
in a relatively thin region between the
shock and the ejecta is approximately uniform and we shall take
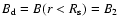 .
.
The relativistic electrons produce  -ray emission due to
IC scattering of background photons. It is not
difficult to show that due to the hard spectrum of
accelerated electrons only the 2.7 K cosmic microwave background (CMB) is
important in the case considered. The expected differential flux of IC
-ray emission due to
IC scattering of background photons. It is not
difficult to show that due to the hard spectrum of
accelerated electrons only the 2.7 K cosmic microwave background (CMB) is
important in the case considered. The expected differential flux of IC
 -rays as a function of their energy
-rays as a function of their energy
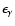 can be
represented in the form:
can be
represented in the form:
in photons/(cm2s erg),
where (Blumenthal & Gould 1970)
is the differential cross section for the up-scattering of a photon
with incident energy 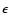 to energy
to energy
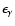 by
the elastic collision with an electron of energy
by
the elastic collision with an electron of energy
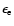 ,
,
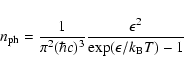 |
(8) |
is the blackbody spectrum of the CMB, 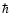 and
kB are Planck and Boltzmann constant respectively, T=2.7 K,
and
kB are Planck and Boltzmann constant respectively, T=2.7 K,
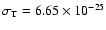 cm2 is the Thomson
cross-section,
cm2 is the Thomson
cross-section,
![$q=\epsilon_{\gamma}/[\Gamma (\epsilon_{\rm e}
-\epsilon_{\gamma})]$](/articles/aa/full/2002/45/aah3593/img63.gif) ,
,
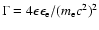 ,
and
,
and
 is the minimal momentum of electron, whose
energy
is the minimal momentum of electron, whose
energy
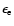 is determined by the condition q=1.
is determined by the condition q=1.
Energetic electrons produce also nonthermal bremstrahlung (NB) emission,
interacting with both ambient electrons and protons. We use standard
formulae for the cross section to calculate the NB  -ray flux
-ray flux
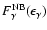 (e.g. Baring et al. 1999). As
it was already demonstrated by these last authors, in young SNRs the
primary energetic electron number density due to electrons directly
accelerated from the suprathermal postshock distribution by far exceeds
that of secondaries which were produced via the decay of charged pions
created in p-p collisions. Hence the contribution of secondaries to the
NB, IC, and synchrotron emission can be neglected.
(e.g. Baring et al. 1999). As
it was already demonstrated by these last authors, in young SNRs the
primary energetic electron number density due to electrons directly
accelerated from the suprathermal postshock distribution by far exceeds
that of secondaries which were produced via the decay of charged pions
created in p-p collisions. Hence the contribution of secondaries to the
NB, IC, and synchrotron emission can be neglected.
Since SN 1006 is a type Ia SN we use typical SN Ia parameters
in our calculations:
ejected mass
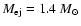 ,
k=7, and
a uniform ambient ISM.
,
k=7, and
a uniform ambient ISM.
The ISM density is the most relevant parameter, especially for the
 -ray production (e.g. Berezhko et al. 1999). Here we use
the most appropriate value of the ambient number density of ISM hydrogen
-ray production (e.g. Berezhko et al. 1999). Here we use
the most appropriate value of the ambient number density of ISM hydrogen
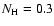 cm-3 as well as the distance d=1.8 kpc,
consistent with X-ray and optical imagery of SN 1006 (Winkler & Long
1997, see also Allen et al. 2001 and references therein).
cm-3 as well as the distance d=1.8 kpc,
consistent with X-ray and optical imagery of SN 1006 (Winkler & Long
1997, see also Allen et al. 2001 and references therein).
The value T0=104 K is used for the ISM temperature. Note that SNR
and CR dynamics are not sensitive to T0, because the shock
structure is mainly determined by the Alfvénic Mach number.
The other important parameter is the ISM magnetic field B0.
Unfortunately there is no direct way to determine its value from the
observations. Since it influences the synchrotron spectrum in an essential
way, we use an upstream magnetic field value B0=20 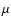 G. It is
required to provide the observed shape of the synchrotron spectrum in the
radio and the X-ray bands.
G. It is
required to provide the observed shape of the synchrotron spectrum in the
radio and the X-ray bands.
The gas dynamics problem is characterized by the following length,
time, and velocity scales:
which are the sweep-up radius, sweep-up time and mean ejecta speed
respectively. Here
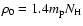 is the ISM
mass density;
is the ISM
mass density; 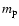 is the proton mass.
is the proton mass.
The
shock expansion law during the free expansion phase (t<t0) is then
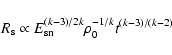 |
(9) |
(Chevalier 1982) which for k=7 gives
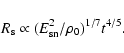 |
(10) |
In the adiabatic phase
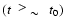 we have
we have
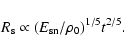 |
(11) |
The observed expansion law of SN 1006 (Moffett et al. 1993) is
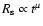 with
with
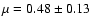 .
We conclude that within the
observational errors SN 1006
should already be in the adiabatic phase.
.
We conclude that within the
observational errors SN 1006
should already be in the adiabatic phase.
![\begin{figure}
\par\includegraphics[width=7.5cm]{SN1006_fig1.eps}\end{figure}](/articles/aa/full/2002/45/aah3593/Timg78.gif) |
Figure 1:
a) Shock radius 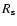 and shock speed
and shock speed
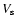 ;
b) total shock
( ;
b) total shock
(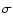 )
and subshock ( )
and subshock (
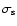 )
compression ratios; c) ejecta
( )
compression ratios; c) ejecta
(
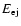 ),
CR
( ),
CR
(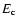 ), gas thermal ( ), gas thermal (
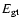 ), and gas kinetic
( ), and gas kinetic
(
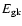 )
energies
as a function of time.
Scale values are R0=3.2 pc,
V0=14 675 km s-1,
t0=212 years. The dotted vertical line marks the current
epoch.
The observed size and speed of the shock
(Moffett et al. 1993), are shown as well. )
energies
as a function of time.
Scale values are R0=3.2 pc,
V0=14 675 km s-1,
t0=212 years. The dotted vertical line marks the current
epoch.
The observed size and speed of the shock
(Moffett et al. 1993), are shown as well. |
| Open with DEXTER |
The calculations together with the experimental data are shown in
Figs. 1-5. For the assumed SN distance and ISM density an
explosion energy
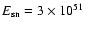 erg fits the observed SNR
size
erg fits the observed SNR
size  and its expansion rate
and its expansion rate 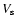 (Moffet et al.
1993). The shown uncertainties of
(Moffet et al.
1993). The shown uncertainties of 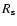 and
and
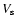 are calculated
as the uncertainties of the angular size and expansion rate times the
distance d=1.8 kpc.
are calculated
as the uncertainties of the angular size and expansion rate times the
distance d=1.8 kpc.
According to Fig. 1a SN 1006 is indeed already in the
adiabatic phase. The assumed injection rate
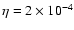 leads to a significant modification of the shock which at the current
epoch, t=995 yr, has a total compression ratio
leads to a significant modification of the shock which at the current
epoch, t=995 yr, has a total compression ratio
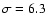 and a
subshock compression ratio
and a
subshock compression ratio
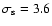 (Fig. 1b).
(Fig. 1b).
The different SNR energy components, the ejecta energy
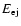 ,
the gas kinetic (
,
the gas kinetic (
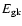 ), and thermal (
), and thermal (
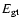 )
energies,
and the CR energy
)
energies,
and the CR energy 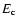 ,
are presented in Fig. 1c as
functions of time. The acceleration process is characterized by a high
efficiency in spherical symmetry: at the current time
t/t0=4.68 about
53% of the explosion energy has been already transferred to CRs, and the
CR energy content
,
are presented in Fig. 1c as
functions of time. The acceleration process is characterized by a high
efficiency in spherical symmetry: at the current time
t/t0=4.68 about
53% of the explosion energy has been already transferred to CRs, and the
CR energy content 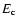 continues to increase to a maximum of
about 60% in the later Sedov phase (Fig. 1c), when particles start
to leave the source. As usually predicted by the model, the CR
acceleration efficiency is
significantly higher than required for the
average replenishment of the Galactic CRs by SNRs, corresponding to
continues to increase to a maximum of
about 60% in the later Sedov phase (Fig. 1c), when particles start
to leave the source. As usually predicted by the model, the CR
acceleration efficiency is
significantly higher than required for the
average replenishment of the Galactic CRs by SNRs, corresponding to
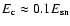 .
As discussed before, this
discrepancy can be attributed to the physical conditions at the shock
surface which influence the injection efficiency. The magnetic field
geometry is the most important factor: at the quasiperpendicular portion
of the shock ion injection (and subsequent acceleration) is presumably
depressed compared with the quasiparallel portion. Therefore the number of
nuclear CRs, calculated within the spherically-symmetrical approximation,
should be renormalized by this depression factor (see Völk et al.
2002 for details). Assuming SN 1006 to be an average Galactic CR
source, the renormalizing factor should be
.
As discussed before, this
discrepancy can be attributed to the physical conditions at the shock
surface which influence the injection efficiency. The magnetic field
geometry is the most important factor: at the quasiperpendicular portion
of the shock ion injection (and subsequent acceleration) is presumably
depressed compared with the quasiparallel portion. Therefore the number of
nuclear CRs, calculated within the spherically-symmetrical approximation,
should be renormalized by this depression factor (see Völk et al.
2002 for details). Assuming SN 1006 to be an average Galactic CR
source, the renormalizing factor should be
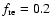 .
It means
that according to our calculation the actual energy of accelerated protons
in SN 1006 at the present epoch is
.
It means
that according to our calculation the actual energy of accelerated protons
in SN 1006 at the present epoch is
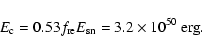 |
(12) |
Note that such a factor is consistent with observations which show that
efficient CR acceleration takes place at about 25% of the shock surface
(e.g. Allen et al. 2001).
![\begin{figure}
\par\includegraphics[width=7.5cm]{SN1006_fig2_new.eps}\end{figure}](/articles/aa/full/2002/45/aah3593/Timg85.gif) |
Figure 2:
The overall (= spatially integrated) CR spectrum as function of
momentum. Solid and dashed
lines correspond to protons and electrons, respectively. Thick and thin
lines correspond to efficient and inefficient proton acceleration,
respectively. |
| Open with DEXTER |
The volume-integrated (or overall) CR spectrum
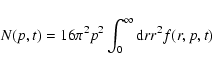 |
(13) |
has, for the case of protons, almost a pure power-law form
 over a wide momentum range from
over a wide momentum range from
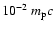 up to
the cutoff momentum
up to
the cutoff momentum
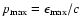 ,
where
,
where
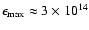 eV is the maximum CR energy
(Fig. 2). The limitation of this numerically determined value
eV is the maximum CR energy
(Fig. 2). The limitation of this numerically determined value
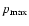 can be understood mainly in terms of the influence of
geometrical factors which are the finite size and speed of the shock, its
deceleration and the adiabatic cooling effect in the downstream region
(Berezhko 1996). Due to the shock modification the power-law index
slowly varies from
can be understood mainly in terms of the influence of
geometrical factors which are the finite size and speed of the shock, its
deceleration and the adiabatic cooling effect in the downstream region
(Berezhko 1996). Due to the shock modification the power-law index
slowly varies from
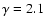 at
at
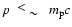 to
to
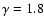 at
at
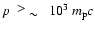 .
.
The shape of the overall electron spectrum
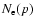 deviates from
that of the proton spectrum N(p) at high momenta
deviates from
that of the proton spectrum N(p) at high momenta
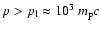 ,
due to the synchrotron losses in the downstream region
with magnetic field
,
due to the synchrotron losses in the downstream region
with magnetic field
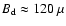 G which is assumed
uniform in this region (
G which is assumed
uniform in this region (
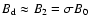 ). According
to expression (4) the synchrotron losses should become important
for electron momenta greater than
). According
to expression (4) the synchrotron losses should become important
for electron momenta greater than
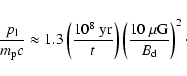 |
(14) |
Substituting the SN age t=103 yr into this expression, we have
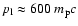 ,
in reasonable agreement with the
numerical results
(Fig. 2).
,
in reasonable agreement with the
numerical results
(Fig. 2).
In detail the momentum dependence of the spatially integrated electron
spectrum  from Eq. (13) is somewhat more complicated at high
energies. This can be understood as follows:
from Eq. (13) is somewhat more complicated at high
energies. This can be understood as follows:
The shock constantly produces the electron spectrum
 with
with
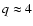 up to the maximum momentum
up to the maximum momentum
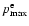 which is much larger than
which is much larger than 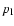 .
This
spectrum is not modified by synchrotron losses within the downstream
region of thickness
.
This
spectrum is not modified by synchrotron losses within the downstream
region of thickness
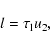 |
(15) |
where
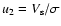 is the gas speed with respect to the
shock. At low momenta
is the gas speed with respect to the
shock. At low momenta
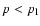 the loss time
the loss time
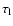 exceeds the age of the system. Formally this means that the size of the
lossfree region is greater than the thickness
exceeds the age of the system. Formally this means that the size of the
lossfree region is greater than the thickness
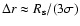 of the swept up shell. At large momenta
of the swept up shell. At large momenta
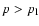 we have
we have
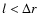 .
Within the downstream region
.
Within the downstream region
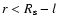 the electron spectrum therefore becomes essentially
modified (
the electron spectrum therefore becomes essentially
modified (
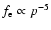 )
by the influence of the
synchrotron losses. At a given radius
)
by the influence of the
synchrotron losses. At a given radius
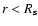 accelerated
electrons have an age of
accelerated
electrons have an age of
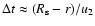 and
therefore, cf. Eq. (14), their spectrum has a break at
and
therefore, cf. Eq. (14), their spectrum has a break at
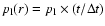 .
According to its
definition (13) the spatially integrated electron spectrum
.
According to its
definition (13) the spatially integrated electron spectrum
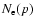 is a mixture of electron spectra with different
is a mixture of electron spectra with different
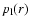 .
Qualitatively one would expect that within the momentum
range
.
Qualitatively one would expect that within the momentum
range
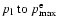 ,
the overall
electron spectrum is close to the form
,
the overall
electron spectrum is close to the form
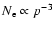 ,
somewhat
hardening towards
,
somewhat
hardening towards
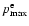 .
This is in agreement with
the calculation.
.
This is in agreement with
the calculation.
![\begin{figure}
\includegraphics[width=12cm]{SN1006_fig3_color.eps}
\end{figure}](/articles/aa/full/2002/45/aah3593/Timg122.gif) |
Figure 3:
Synchrotron emission flux as a function of frequency for the
same two cases as in Fig. 2. Solid and dashed lines correspond to efficient and inefficient proton acceleration,
respectively. The observed X-ray (in black color: Hamilton et al. 1986; in red color: Allen
et al. 1999) and radio emissions (in black color: Reynolds 1996) are shown. |
| Open with DEXTER |
The maximum electron momentum
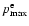 can be estimated
by equating the synchrotron loss time (4) and the acceleration
time
can be estimated
by equating the synchrotron loss time (4) and the acceleration
time
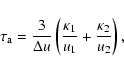 |
(16) |
where
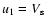 and
and
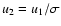 are the upstream and
downstream gas velocities relative to the shock front, and
are the upstream and
downstream gas velocities relative to the shock front, and
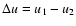 .
During the acceleration time
.
During the acceleration time
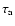 the electrons
spent the time
the electrons
spent the time
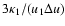 in the upstream magnetic field
B0, and
in the upstream magnetic field
B0, and
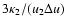 in the downstream magnetic field
in the downstream magnetic field
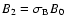 (in the case considered
(in the case considered
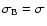 ). Therefore, in the general case the maximum
electron momentum
). Therefore, in the general case the maximum
electron momentum
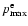 is a solution of the
equation
is a solution of the
equation
![\begin{displaymath}\tau_{\rm a}(p)^{-1}=\left[\tau_{\rm l}^{-1}(B_0,p)+
\tau_{\r...
...B_2,p)\sigma/\sigma_{\rm B}\right]
/(1+\sigma/\sigma_{\rm B}),
\end{displaymath}](/articles/aa/full/2002/45/aah3593/img133.gif) |
(17) |
which can be written in the form
The main part of the electrons with the highest energies
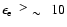 TeV is produced at the end of the free
expansion phase. At this stage
TeV is produced at the end of the free
expansion phase. At this stage
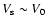 which leads to a
maximum electron momentum
which leads to a
maximum electron momentum
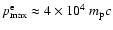 in agreement with the numerical results (Fig. 2).
in agreement with the numerical results (Fig. 2).
The parameters
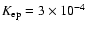 and
and
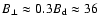
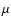 G provide good agreement between the
calculated and the measured synchrotron emission in the radio- and X-ray
ranges (Fig. 3). The steepening of the electron spectrum at high
energies due to synchrotron losses naturally yields a fit to the X-ray
data with their soft spectrum. Note that two kinds of X-ray data are
presented in Fig. 3. The Hamilton et al. (1986) data
represent the total (i.e. thermal plus nonthermal) X-ray emission in a
relatively wide frequency range, where the nonthermal synchrotron emission
contribution dominates at frequencies
G provide good agreement between the
calculated and the measured synchrotron emission in the radio- and X-ray
ranges (Fig. 3). The steepening of the electron spectrum at high
energies due to synchrotron losses naturally yields a fit to the X-ray
data with their soft spectrum. Note that two kinds of X-ray data are
presented in Fig. 3. The Hamilton et al. (1986) data
represent the total (i.e. thermal plus nonthermal) X-ray emission in a
relatively wide frequency range, where the nonthermal synchrotron emission
contribution dominates at frequencies
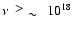 Hz. At these highest frequencies the Allen et al.
(1999) RXTE nonthermal data are also presented (in red color), lying
slightly below the Hamilton et al. data points. Clearly our nonthermal
model spectra must lie below the Hamilton et al. spectral points at
Hz. At these highest frequencies the Allen et al.
(1999) RXTE nonthermal data are also presented (in red color), lying
slightly below the Hamilton et al. data points. Clearly our nonthermal
model spectra must lie below the Hamilton et al. spectral points at
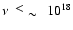 Hz. Such a smooth spectral behavior is achieved in a 20
Hz. Such a smooth spectral behavior is achieved in a 20  G
upstream field.
G
upstream field.
Since the total number of accelerated protons has to be reduced by the
factor
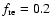 ,
the same number of accelerated electrons then
corresponds to a renormalized parameter
,
the same number of accelerated electrons then
corresponds to a renormalized parameter
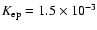 .
Then the total energy of accelerated electrons in SN 1006 is
.
Then the total energy of accelerated electrons in SN 1006 is
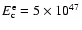 erg.
erg.
The ratio of accelerated electrons to protons thus comes out lower by a
factor of about 6 than the canonical ratio of 0.01, generally deduced from
observations of the Galactic CRs. This is an interesting consequence of
our model: if SN 1006 is typical for the nuclear Galactic CR source
population, then other sources like young Pulsars or Pulsar Nebulae must
also significantly contribute to the Galactic CR electron population (e.g.
Aharonian et al. 1995; Pohl & Esposito 1998). An additional
fraction might come from secondary interstellar electrons/positrons due to
the decay of charged pions that are produced in inelastic collisions of CR
nuclei with nuclei of the interstellar gas. Since the majority of Galactic
Supernovae is not of the type Ia to which SN 1006 belongs, but rather
occurs as a consequence of core collapse events, there is the alternative
possibility that core collapse Supernovae produce a higher electron to
proton ratio. Such an increase might have to do with the different
circumstellar magnetic field structure of massive stars, but this is
indeed only a possibility for which we have no proof at present.
The radio data are fitted by a power law spectrum
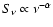 ,
whose index
,
whose index
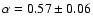 (Allen et al.
2001) is noticeably larger than 0.5, corresponding to the electron
spectrum
(Allen et al.
2001) is noticeably larger than 0.5, corresponding to the electron
spectrum
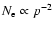 produced by an unmodified shock with
compression ratio
produced by an unmodified shock with
compression ratio 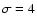 .
In our case the shock is essentially
modified by the backreaction of the accelerated protons (see
Fig. 1b): its compression ratio
.
In our case the shock is essentially
modified by the backreaction of the accelerated protons (see
Fig. 1b): its compression ratio
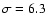 .
At the same time low
energy electrons with momenta
.
At the same time low
energy electrons with momenta
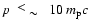 (
(
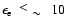 GeV), which produce synchrotron
emission at
GeV), which produce synchrotron
emission at
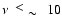 GHz, are accelerated at the subshock which has the compression ratio
GHz, are accelerated at the subshock which has the compression ratio
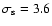 .
Therefore these electrons have a steeper spectrum
.
Therefore these electrons have a steeper spectrum
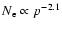 that leads to the expected radio spectrum
that leads to the expected radio spectrum
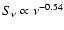 ,
fitting the experimental data very well (Fig. 3).
The fact that the observed value of the radio power law index
,
fitting the experimental data very well (Fig. 3).
The fact that the observed value of the radio power law index 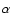 exceeds the value 0.5 can be considered as an indication that the shock is
essentially modified. A relatively high upstream magnetic field strength
B0=20
exceeds the value 0.5 can be considered as an indication that the shock is
essentially modified. A relatively high upstream magnetic field strength
B0=20 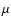 G, compared with typical ISM values B0=5
G, compared with typical ISM values B0=5 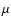 G, and a
corresponding downstream value
G, and a
corresponding downstream value
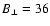
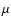 G are required to have
radio emitting electron energies in the steep part of their spectrum
G are required to have
radio emitting electron energies in the steep part of their spectrum
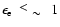 GeV on the one hand, and to give a
smooth rollover of the synchrotron spectrum
GeV on the one hand, and to give a
smooth rollover of the synchrotron spectrum
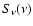 at frequencies
at frequencies
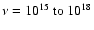 Hz on the other. According to model
calculations by Lucek & Bell (2000), the existing ISM field can
indeed be significantly amplified near a strong shock by CR streaming.
Hz on the other. According to model
calculations by Lucek & Bell (2000), the existing ISM field can
indeed be significantly amplified near a strong shock by CR streaming.
Such a strongly nonlinear behavior has three consequences in that (i) it
leads to the high magnetic field strength, required to understand the
measured nonthermal synchrotron spectrum, (ii) it is consistent with our
assumption of Bohm diffusion, and (iii) it suggests a value
 for the injection parameter that we use (see also Sect. 2).
for the injection parameter that we use (see also Sect. 2).
![\begin{figure}
\par\includegraphics[width=7.5cm]{SN1006_fig4_SED.eps}\end{figure}](/articles/aa/full/2002/45/aah3593/Timg160.gif) |
Figure 4:
IC (dashed lines),  -decay (solid lines) and NB (dash-dotted
lines) integral -decay (solid lines) and NB (dash-dotted
lines) integral
 -ray energy
fluxes as a function of -ray energy
fluxes as a function of  -ray energy for the same cases as in
Fig. 2.
High energy -ray energy for the same cases as in
Fig. 2.
High energy  -ray data (Tanimori et al. 1998), the
EGRET upper limit as given by Mastichiadis & de Jager (1996), and
the JANZOS upper
limit (Allen et al. 1995) are shown. -ray data (Tanimori et al. 1998), the
EGRET upper limit as given by Mastichiadis & de Jager (1996), and
the JANZOS upper
limit (Allen et al. 1995) are shown. |
| Open with DEXTER |
The calculated integral IC and 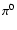 -decay
-decay  -ray energy fluxes
are presented in
Figs. 4 and 5 together with the available experimental data.
-ray energy fluxes
are presented in
Figs. 4 and 5 together with the available experimental data.
In Fig. 4 we present also the integral NB  -ray fluxes; they play no
important role for SN 1006. Note that the number of accelerated protons,
which produce
-ray fluxes; they play no
important role for SN 1006. Note that the number of accelerated protons,
which produce 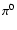 -decay
-decay  -rays, has been reduced by the factor
-rays, has been reduced by the factor
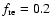 .
.
According to the calculation, the hadronic  -ray production exceeds
the electron contribution by a factor of about 7 at energies
-ray production exceeds
the electron contribution by a factor of about 7 at energies
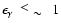 TeV, and dominates at
TeV, and dominates at
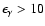 TeV (Fig. 4). The calculation is in good
agreement with the TeV-measurements reported by the CANGAROO collaboration
(Tanimori et al. 1998), and it does not contradict the EGRET
upper limit
TeV (Fig. 4). The calculation is in good
agreement with the TeV-measurements reported by the CANGAROO collaboration
(Tanimori et al. 1998), and it does not contradict the EGRET
upper limit
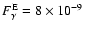 cm- 2 s-1 at
cm- 2 s-1 at
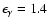 GeV (cf. Mastichiadis & de Jager 1996).
This is also confirmed by Fig. 5, where we compare our calculations
with the revised CANGAROO data (Tanimori et al. 2001) plus an
extended set of EGRET upper limits (Naito et al. 1999).
GeV (cf. Mastichiadis & de Jager 1996).
This is also confirmed by Fig. 5, where we compare our calculations
with the revised CANGAROO data (Tanimori et al. 2001) plus an
extended set of EGRET upper limits (Naito et al. 1999).
The differential 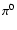 -decay
-decay  -ray flux
-ray flux
 has the expected peak at photon
energy
has the expected peak at photon
energy
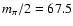 MeV (see also Naito & Takahara 1994).
This feature may be used for the identification of a hadronic contribution
to the observed
MeV (see also Naito & Takahara 1994).
This feature may be used for the identification of a hadronic contribution
to the observed  -ray flux at the particle energies <10 GeV
mainly producing it. However, two considerations weaken this possibility.
First
of all, for reasons of instrumental sensitivity, we expect only nearby
SNRs to be detectable in the foreseeable future. Such objects have
diameters approaching 1 degree, and SN 1006 is an example. The diffuse
Galactic
-ray flux at the particle energies <10 GeV
mainly producing it. However, two considerations weaken this possibility.
First
of all, for reasons of instrumental sensitivity, we expect only nearby
SNRs to be detectable in the foreseeable future. Such objects have
diameters approaching 1 degree, and SN 1006 is an example. The diffuse
Galactic  -ray background is large at these energies due to the
steep spectrum of the Galactic CRs that produce it, as pointed out by
Drury et al. (1994). Therefore, we expect SNRs to be best
observable at much higher
-ray background is large at these energies due to the
steep spectrum of the Galactic CRs that produce it, as pointed out by
Drury et al. (1994). Therefore, we expect SNRs to be best
observable at much higher  -ray energies
-ray energies
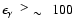 GeV, where the
hard source spectra typically dominate over the background emission.
Secondly, from a strictly empirical point of view, such a nuclear CR
component that produces the
GeV, where the
hard source spectra typically dominate over the background emission.
Secondly, from a strictly empirical point of view, such a nuclear CR
component that produces the 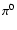 -decay bump need not extend far beyond
the GeV region. For the existence, in a SNR, of a nuclear CR component
approaching the energy region of the knee in the Galactic spectrum, the
detection of a 67.5 MeV
-decay bump need not extend far beyond
the GeV region. For the existence, in a SNR, of a nuclear CR component
approaching the energy region of the knee in the Galactic spectrum, the
detection of a 67.5 MeV  -ray feature is therefore neither a
necessary nor a sufficient condition.
-ray feature is therefore neither a
necessary nor a sufficient condition.
![\begin{figure}
\par\includegraphics[width=7.5cm]{SN1006_fig5_SED.epsi}\end{figure}](/articles/aa/full/2002/45/aah3593/Timg168.gif) |
Figure 5:
Differential 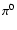 -decay ( solid lines) and IC (
dashed lines) -decay ( solid lines) and IC (
dashed lines)
 -ray energy fluxes as a function of -ray energy fluxes as a function of  -ray energy
for the same cases as in
Fig. 2. The recent differential
high energy -ray energy
for the same cases as in
Fig. 2. The recent differential
high energy  -ray energy flux data (Tanimori et al. 2001)
and
EGRET upper limits (Naito et al. 1999) are also shown. -ray energy flux data (Tanimori et al. 2001)
and
EGRET upper limits (Naito et al. 1999) are also shown. |
| Open with DEXTER |
On the other hand, due to the high magnetic field strength which we deduce
for this remnant, the  -ray spectra produced by the electronic and
hadronic CR components have rather similar shapes in the energy interval
0.1 GeV
-ray spectra produced by the electronic and
hadronic CR components have rather similar shapes in the energy interval
0.1 GeV
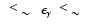 10 TeV due to electron synchrotron losses.
As a consequence the best observational possibility to discriminate
between leptonic and hadronic contributions at high energies
10 TeV due to electron synchrotron losses.
As a consequence the best observational possibility to discriminate
between leptonic and hadronic contributions at high energies 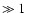 GeV is to measure the
GeV is to measure the  -ray spectrum at energies higher than
10 TeV, where we expect these two spectra to be essentially different.
Therefore the clear detection of a substantial flux at energies
-ray spectrum at energies higher than
10 TeV, where we expect these two spectra to be essentially different.
Therefore the clear detection of a substantial flux at energies
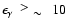 TeV would provide direct evidence for
its hadronic origin.
TeV would provide direct evidence for
its hadronic origin.
The set of parameters which was discussed until now is limited by the
existing measurements. There is almost no freedom for a substantial change
of any parameter value without a loss of agreement between theory and
experiment. For example, the proton injection rate which determines the
number of accelerated protons and the 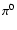 -decay
-decay  -ray emission,
was taken to produce the shock modification which in turn is required to
produce a steep electron spectrum
-ray emission,
was taken to produce the shock modification which in turn is required to
produce a steep electron spectrum
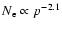 needed to
fit the observed radio emission of SN 1006. For this injection rate
needed to
fit the observed radio emission of SN 1006. For this injection rate
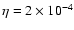 a relatively high upstream magnetic field is unavoidably required in order
to produce the observed synchrotron emission.
a relatively high upstream magnetic field is unavoidably required in order
to produce the observed synchrotron emission.
On the other hand one may dismiss the relevance of a deviation of the
observed radio spectrum from the form
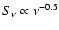 ,
and of
a likely thermal contribution to the soft X-ray flux around 1017 Hz,
and try to reproduce all the observed emissions by effects of electrons
alone (e.g. Pohl 1996; Mastichiadis & de Jager 1996;
Yoshida & Yanagita 1997; Aharonian & Atoyan 1999).
The number of injected and
accelerated protons and all the effects which they can produce in SN 1006
is suggested to be negligibly small in this extreme case. For example, the
proton contribution to the TeV
,
and of
a likely thermal contribution to the soft X-ray flux around 1017 Hz,
and try to reproduce all the observed emissions by effects of electrons
alone (e.g. Pohl 1996; Mastichiadis & de Jager 1996;
Yoshida & Yanagita 1997; Aharonian & Atoyan 1999).
The number of injected and
accelerated protons and all the effects which they can produce in SN 1006
is suggested to be negligibly small in this extreme case. For example, the
proton contribution to the TeV  -ray emission should be at least an
order of magnitude lower compared with the previous case. At such low
proton numbers the nonlinear shock modification due to their backreaction
is negligible, and shock acceleration takes place in the test particle
limit.
-ray emission should be at least an
order of magnitude lower compared with the previous case. At such low
proton numbers the nonlinear shock modification due to their backreaction
is negligible, and shock acceleration takes place in the test particle
limit.
In order to make clear how different the required set of relevant physical
parameters compared to the case of efficient CR nucleon acceleration is,
we performed a calculation which corresponds to inefficient CR
acceleration. We use a proton injection rate
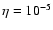 which yields
an upper limit for the proton acceleration efficiency that is consistent
with their low contribution to the
which yields
an upper limit for the proton acceleration efficiency that is consistent
with their low contribution to the  -ray production. This low CR
nucleon production efficiency also implies that the effect of magnetic
field amplification due to CR streaming is small. Therefore we have used a
typical upstream ISM magnetic field strength B0=4
-ray production. This low CR
nucleon production efficiency also implies that the effect of magnetic
field amplification due to CR streaming is small. Therefore we have used a
typical upstream ISM magnetic field strength B0=4 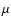 G. We note that
such a low value was even assumed to be required in the compressed downstream region -
G. We note that
such a low value was even assumed to be required in the compressed downstream region -
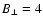
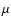 G - to fit the experimental data
(Tanimori et al. 2001). All other ISM and SN parameters are the
same as in the previous case of efficient CR acceleration. Since during
the early evolutionary phase the global SNR dynamics is rather insensitive
to the number of accelerated CRs, the observed SNR size and its expansion
rate are equally well reproduced in this case.
G - to fit the experimental data
(Tanimori et al. 2001). All other ISM and SN parameters are the
same as in the previous case of efficient CR acceleration. Since during
the early evolutionary phase the global SNR dynamics is rather insensitive
to the number of accelerated CRs, the observed SNR size and its expansion
rate are equally well reproduced in this case.
In this test particle regime the electron spectrum, produced by a strong
unmodified shock, can be analytically approximated by (Berezhko
1996)
![\begin{displaymath}N_{\rm e}\propto
p^{-\gamma}\exp[-\kappa(p)/\kappa(p_{\rm max}^{\rm e})],
\end{displaymath}](/articles/aa/full/2002/45/aah3593/img175.gif) |
(19) |
with
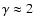 ,
where
,
where
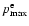 is the maximum
CR momentum, which is determined by geometrical factors. Any essential
deviation from
is the maximum
CR momentum, which is determined by geometrical factors. Any essential
deviation from
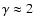 would be inconsistent with diffusive
shock acceleration which is believed to be the main process of energetic
particle production in SNRs. For a Bohm-type diffusion coefficient,
would be inconsistent with diffusive
shock acceleration which is believed to be the main process of energetic
particle production in SNRs. For a Bohm-type diffusion coefficient,
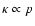 ,
the cutoff region of this spectrum has the same form
,
the cutoff region of this spectrum has the same form
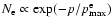 as it was
suggested by Mastichiadis & de Jager (1996) and by Tanimori et
al. (2001). At the same time, cf. Eq. (19), the spectrum
of the electrons accelerated at a strong unmodified shock is essentially
harder compared to what was used
as it was
suggested by Mastichiadis & de Jager (1996) and by Tanimori et
al. (2001). At the same time, cf. Eq. (19), the spectrum
of the electrons accelerated at a strong unmodified shock is essentially
harder compared to what was used
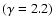 to fit the radio, X-ray
and
to fit the radio, X-ray
and  -ray data (Tanimori et al. 2001). It is clear that the
spectrum cf. Eq. (19), with
-ray data (Tanimori et al. 2001). It is clear that the
spectrum cf. Eq. (19), with 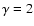 which has the same number
of GeV electrons to produce the same radio flux, has an order of magnitude
more electrons with
which has the same number
of GeV electrons to produce the same radio flux, has an order of magnitude
more electrons with
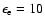 TeV compared with the case
TeV compared with the case
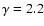 .
Therefore, to fit the radio, X-ray, and
.
Therefore, to fit the radio, X-ray, and  -ray data
with this harder electron spectrum, we need a large downstream magnetic
field
-ray data
with this harder electron spectrum, we need a large downstream magnetic
field
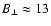
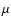 G. Since even for
G. Since even for
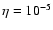 nucleon
acceleration can produce a strong Alfvénic wave field, the upper limit
for the downstream field strength
nucleon
acceleration can produce a strong Alfvénic wave field, the upper limit
for the downstream field strength 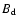 equals 16
equals 16 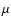 G. To
this extent
G. To
this extent
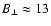
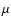 G can still be consistent with a
4
G can still be consistent with a
4 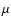 G ISM magnetic field as used by Tanimori et al. (2001),
although these authors used 4
G ISM magnetic field as used by Tanimori et al. (2001),
although these authors used 4 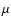 G also downstream.
G also downstream.
![\begin{figure}
\par\includegraphics[width=7.5cm]{SN1006_fig6.eps}\end{figure}](/articles/aa/full/2002/45/aah3593/Timg184.gif) |
Figure 6:
Observed total radio flux of SN 1006 (Reynolds 1996) as
a function of frequency with model spectra superimposed. Solid and dashed
curves correspond in this figure to the high and low proton
injection/acceleration
efficiency, respectively. |
| Open with DEXTER |
Since the energies
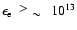 eV of electrons, whose synchrotron emission in the given magnetic
field corresponds to X-ray energies
eV of electrons, whose synchrotron emission in the given magnetic
field corresponds to X-ray energies
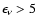 keV, should be in
the exponential cutoff region, the required value of the maximum CR
momentum is
keV, should be in
the exponential cutoff region, the required value of the maximum CR
momentum is
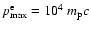 .
If we assume
the same momentum dependence
.
If we assume
the same momentum dependence
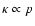 ,
this maximum CR momentum
is consistent with the diffusion coefficient
,
this maximum CR momentum
is consistent with the diffusion coefficient
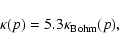 |
(20) |
which exceeds the Bohm limit by a factor 5.3 for an upstream field of 4 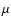 G.
G.
The results for this inefficient proton injection/acceleration case are
also presented in Figs. 2-7. One can see from Fig. 2
that, due to the lower magnetic field value, one needs about five times
more accelerated electrons compared with the previous case to fit the
radio and X-ray data (see Fig. 3).
In the inefficient case the  -ray production is dominated by the
electron contribution (Fig. 4). Since synchrotron losses are not
important, the predicted IC spectrum is essentially harder for
-ray production is dominated by the
electron contribution (Fig. 4). Since synchrotron losses are not
important, the predicted IC spectrum is essentially harder for
 -ray energies between about 109 and 1011 eV than in the
efficient proton acceleration model. The differential
-ray energies between about 109 and 1011 eV than in the
efficient proton acceleration model. The differential  -ray
CANGAROO spectrum appears in better agreement with the
-ray
CANGAROO spectrum appears in better agreement with the 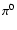 -decay
emission of the efficient model than with the inefficient model IC
prediction (Fig. 5).
-decay
emission of the efficient model than with the inefficient model IC
prediction (Fig. 5).
In Fig. 6 the calculated synchrotron fluxes are compared with the
experimental data in the radio range. One can see that the steeper
spectrum
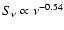 which corresponds to the efficient
CR acceleration case gives a better fit to the radio data than the
spectrum
which corresponds to the efficient
CR acceleration case gives a better fit to the radio data than the
spectrum
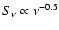 corresponding to the case of
inefficient proton injection, even though the experimental accuracy does
not very clearly distinguish between these to variants. Note that
corresponding to the case of
inefficient proton injection, even though the experimental accuracy does
not very clearly distinguish between these to variants. Note that
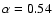 is the average value of the power-law index within the
frequency range shown in Fig. 6. In fact, due to the concave shape
of the electron spectrum, the index slightly decreases with increasing
frequency, with
is the average value of the power-law index within the
frequency range shown in Fig. 6. In fact, due to the concave shape
of the electron spectrum, the index slightly decreases with increasing
frequency, with
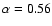 and
and
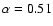 at the lowest and largest
frequency, respectively.
at the lowest and largest
frequency, respectively.
![\begin{figure}
\par\includegraphics[width=7.5cm]{SN1006_fig7_rev1.eps}\end{figure}](/articles/aa/full/2002/45/aah3593/Timg192.gif) |
Figure 7:
Radial dependence of the  -ray brightness for the -ray brightness for the
 -ray energy -ray energy
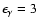 TeV. Thick and thin curves
correspond to the high and low proton injection/acceleration efficiency,
respectively. TeV. Thick and thin curves
correspond to the high and low proton injection/acceleration efficiency,
respectively. |
| Open with DEXTER |
A similar situation is encountered in the X-ray range. An essentially
steeper electron spectrum in the case of efficient CR accelerations much
better fits the nonthermal X-ray data by lying below the total X-ray flux
near the frequency
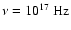 which corresponds to the
photon energy
which corresponds to the
photon energy
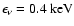 (Fig. 3).
(Fig. 3).
At given number of protons and magnetic field strength an electron to
proton ratio
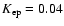 is required in the inefficient case, in
order to reproduce the observed emission.
is required in the inefficient case, in
order to reproduce the observed emission.
Nucleonic CRs absorb in this case only
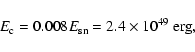 |
(21) |
which is more than an order of magnitude less than the canonically
required
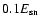 for the Galactic CRs. The electron CR
component contains
for the Galactic CRs. The electron CR
component contains
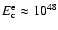 erg. This is
a factor 7 less than what has been obtained by Dyer et al. (2001)
corresponding to their lower downstream magnetic field.
erg. This is
a factor 7 less than what has been obtained by Dyer et al. (2001)
corresponding to their lower downstream magnetic field.
It is important to note that the  -ray brightness of the remnant
-ray brightness of the remnant
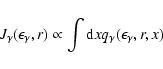 |
(22) |
has a very different dependence upon the distance from its center r in
the two considered cases. The integration of the  -ray emissivity
-ray emissivity
 (which is the number of photons emitted per unit volume per second
in the range
(which is the number of photons emitted per unit volume per second
in the range
 to
to
 )
in the above expression is performed along the line of sight
which intersects the visible remnant surface at the projected distance rfrom its center. In the case of inefficient proton injection TeV
)
in the above expression is performed along the line of sight
which intersects the visible remnant surface at the projected distance rfrom its center. In the case of inefficient proton injection TeV
 -rays are produced by the electrons with the highest energies of
their spectrum
-rays are produced by the electrons with the highest energies of
their spectrum
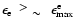 .
These
electrons almost uniformly occupy the entire volume between the shock
surface
.
These
electrons almost uniformly occupy the entire volume between the shock
surface 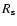 and the contact discontinuity
and the contact discontinuity 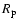 (which
separates the ejecta and swept-up matter) with only a slight increase of
their density toward the shock position. Depending on the turbulence
level near the contact discontinuity they also partially fill the ejecta
volume
(which
separates the ejecta and swept-up matter) with only a slight increase of
their density toward the shock position. Depending on the turbulence
level near the contact discontinuity they also partially fill the ejecta
volume
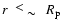 .
Since the upstream
distribution of these electrons is characterized by a diffusive length
which is of the order of
.
Since the upstream
distribution of these electrons is characterized by a diffusive length
which is of the order of
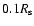 ,
the region
,
the region
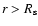 provides a noticeable contribution to the
provides a noticeable contribution to the  -ray brightness.
Therefore the TeV
-ray brightness.
Therefore the TeV  -ray brightness
-ray brightness
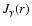 will have a peak
value in the region
will have a peak
value in the region
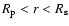 if particle penetration
through the contact discontinuity is strongly suppressed, and at the
center of the remnant r=0 in the opposite case.
A significantly different radial profile
if particle penetration
through the contact discontinuity is strongly suppressed, and at the
center of the remnant r=0 in the opposite case.
A significantly different radial profile
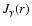 is expected in
the case of efficient proton production. TeV
is expected in
the case of efficient proton production. TeV  -rays are produced in
this case by protons whose energy is considerably lower than the cutoff
energy
-rays are produced in
this case by protons whose energy is considerably lower than the cutoff
energy
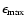 .
Therefore they are concentrated within the
thin region of thickness
.
Therefore they are concentrated within the
thin region of thickness
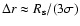 just
behind the shock. The swept-up gas has a similar distribution. Since the
just
behind the shock. The swept-up gas has a similar distribution. Since the
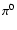 -decay
-decay  -ray luminosity is proportional to the product of
the CR density and the gas number density, the
-ray luminosity is proportional to the product of
the CR density and the gas number density, the  -ray brightness
-ray brightness
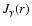 is expected to have a sharp peak close to the shock edge
is expected to have a sharp peak close to the shock edge
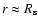 with a considerable decrease at small distances
with a considerable decrease at small distances
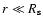 .
The morphological effect of renormalization is to
limit this emission to two polar caps where the interstellar magnetic
field is parallel to the shock normal.
.
The morphological effect of renormalization is to
limit this emission to two polar caps where the interstellar magnetic
field is parallel to the shock normal.
The  -ray brightness calculated for the two different cases is
presented in Fig. 7 for the
-ray brightness calculated for the two different cases is
presented in Fig. 7 for the  -ray energy
-ray energy
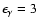 TeV. One can see the essentially different radial
dependence
TeV. One can see the essentially different radial
dependence
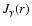 for the two cases. The
for the two cases. The  -rays of
hadronic origin are expected to be concentrated in the postshock region,
whereas the IC
-rays of
hadronic origin are expected to be concentrated in the postshock region,
whereas the IC  -ray brightness, calculated for quite a large level
of turbulence near the contact discontinuity (see Berezhko & Völk
2000 for details), is almost uniformly distributed across the
visible disk of the remnant. As it is seen from Fig. 7, the IC high energy
emission of the inefficient case produces a noticeable halo around the
shock - for SN1006 its size is about 0.1 degrees - that can in principle
be used to discriminate between the
-ray brightness, calculated for quite a large level
of turbulence near the contact discontinuity (see Berezhko & Völk
2000 for details), is almost uniformly distributed across the
visible disk of the remnant. As it is seen from Fig. 7, the IC high energy
emission of the inefficient case produces a noticeable halo around the
shock - for SN1006 its size is about 0.1 degrees - that can in principle
be used to discriminate between the  -ray emissions of hadronic and
leptonic origin.
-ray emissions of hadronic and
leptonic origin.
The reported  -ray flux was detected from the same outer part of
SN 1006 which shows the radio-emission. As it was already pointed out
(Aharonian 1999; Aharonian & Atoyan 1999; Berezhko et al.
1999; Berezhko et al. 2001), this can be considered as an
observational argument favoring a strong role for the nuclear CR
component.
-ray flux was detected from the same outer part of
SN 1006 which shows the radio-emission. As it was already pointed out
(Aharonian 1999; Aharonian & Atoyan 1999; Berezhko et al.
1999; Berezhko et al. 2001), this can be considered as an
observational argument favoring a strong role for the nuclear CR
component.
The nonlinear kinetic model for CR acceleration in SNRs has been applied
to SN 1006 in order to explain its observed properties. We have used
stellar ejecta parameters
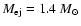 ,
k=7, distance
d=1.8 kpc, and ISM number density
,
k=7, distance
d=1.8 kpc, and ISM number density
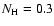 cm-3 from X-ray and
optical imaginary of SN 1006.
For these parameters an explosion energy
cm-3 from X-ray and
optical imaginary of SN 1006.
For these parameters an explosion energy
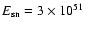 erg is required to fit the observed size
erg is required to fit the observed size 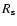 and
expansion speed
and
expansion speed 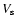 which are determined by the ratio
which are determined by the ratio
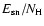 .
.
The number of accelerated electrons required to fit the radio and X-ray
emission of SN 1006, and correspondingly the role of accelerated protons
in  -ray production, depends essentially on the magnetic field
value B0.
-ray production, depends essentially on the magnetic field
value B0.
It was demonstrated that for low magnetic field B0=4 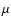 G all the
observed emissions can be dominated by the electron contribution. Protons
are then assumed to be injected into the acceleration much less
efficiently than electrons. For this test particle case the lowest
permitted value of the electron to proton ratio is
G all the
observed emissions can be dominated by the electron contribution. Protons
are then assumed to be injected into the acceleration much less
efficiently than electrons. For this test particle case the lowest
permitted value of the electron to proton ratio is
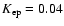 .
It exceeds the canonical value 0.01 observed in situ in the neighborhood
of the Solar System for the Galactic CRs. The maximum energy of
accelerated CRs and their total energy content in this case are only
.
It exceeds the canonical value 0.01 observed in situ in the neighborhood
of the Solar System for the Galactic CRs. The maximum energy of
accelerated CRs and their total energy content in this case are only
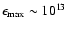 eV and
eV and
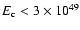 erg respectively. These numbers are too low for such SNRs to be
considered as the main sources of the nucleonic Galactic CRs.
erg respectively. These numbers are too low for such SNRs to be
considered as the main sources of the nucleonic Galactic CRs.
If CRs in SN 1006 are produced due to the diffusive shock acceleration
process, then even in the case of inefficient proton injection quite a
large but plausible downstream magnetic field
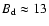
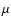 G is required to fit the data. It is several times larger than
assumed in a simple estimate by Tanimori et al. (2001), because
the shock produces in this case an electron spectrum
G is required to fit the data. It is several times larger than
assumed in a simple estimate by Tanimori et al. (2001), because
the shock produces in this case an electron spectrum
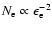 which is significantly harder than the spectrum
assumed in that estimate.
which is significantly harder than the spectrum
assumed in that estimate.
The existing SNR data are better approximated if a significantly larger
upstream magnetic field value B0=20  G and a physically much more
plausible, efficient nucleon injection rate are assumed. Such an ion
injection rate is estimated from injection theory, and consistent with the
observed radio spectral index. The required magnetic field strength, that
is significantly higher than the rms value
G and a physically much more
plausible, efficient nucleon injection rate are assumed. Such an ion
injection rate is estimated from injection theory, and consistent with the
observed radio spectral index. The required magnetic field strength, that
is significantly higher than the rms value  G in the ISM, might be
the result of non-linear amplification near the SN shock by the CR
acceleration process itself.
G in the ISM, might be
the result of non-linear amplification near the SN shock by the CR
acceleration process itself.
The results for this case of efficient proton acceleration are then as
follows:
We find that after adjustment of the predictions of the nonlinear
spherically-symmetric model by a renormalization of the number of
accelerated nuclear CRs to take account of the large area of
quasiperpendicular shock regions in a SNR, good consistency with all
observational data can be achieved, including the reported TeV
 -ray flux. The
-ray flux. The 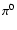 -decay
-decay  -ray flux produced by the
nuclear CR component exceeds the flux of IC
-ray flux produced by the
nuclear CR component exceeds the flux of IC  -rays generated by the
electronic CR component at all energies above about 100 MeV. The theory
did not make use of any knowledge to be derived from
-rays generated by the
electronic CR component at all energies above about 100 MeV. The theory
did not make use of any knowledge to be derived from  -ray
measurements. Therefore the reported TeV flux from SN 1006 supports the
idea that the nuclear CR component is indeed produced in SNRs. The
-ray
measurements. Therefore the reported TeV flux from SN 1006 supports the
idea that the nuclear CR component is indeed produced in SNRs. The
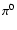 -decay
-decay  -ray flux comes from two polar caps of the remnant.
-ray flux comes from two polar caps of the remnant.
The maximum energy of accelerated protons
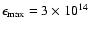 eV and their total energy content
eV and their total energy content
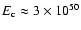 erg, reproduced in this case, are
consistent with the requirements for the Galactic CR sources. The electron
to proton ratio of
erg, reproduced in this case, are
consistent with the requirements for the Galactic CR sources. The electron
to proton ratio of
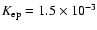 ,
on the other hand,
is lower than the canonical value 0.01.
,
on the other hand,
is lower than the canonical value 0.01.
Comparing the case of efficient proton acceleration with the inefficient
proton acceleration case, we see that the expected  -decay
-decay
 -ray flux
-ray flux
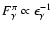 extends up to
almost 100 TeV, whereas the IC
extends up to
almost 100 TeV, whereas the IC  -ray flux reaches less than about
10 TeV. Therefore the detection of
-ray flux reaches less than about
10 TeV. Therefore the detection of  -ray emission above 10 TeV
would imply evidence for a hadronic origin.
-ray emission above 10 TeV
would imply evidence for a hadronic origin.
We therefore conclude that the analysis of SN 1006 on the basis of overall
SNR dynamics and nonlinear diffusive shock acceleration theory results in
a picture where the nuclear component is strongly accelerated, consistent
with all data for this SNR.
The ratio of accelerated electrons to protons comes out lower by a factor
of about 6 than the canonical ratio of 0.01, generally deduced from
observations of the Galactic CRs. If SN 1006 is typical for the nuclear
Galactic CR source population, then other sources like young Pulsars or
Pulsar Nebulae must also significantly contribute to the Galactic CR
electron population. The Crab Nebula is a point in case. Since the
majority of Galactic Supernovae is not of the type Ia to which SN 1006
belongs, but rather occurs as a consequence of core collapse events, there
is the alternative possibility that core collapse Supernovae produce a
higher electron to proton ratio.
Phenomenological studies of the  -ray emission from SN 1006 on the
basis of the observed synchrotron emission have preferred a dominance of
IC emission from electrons in the
-ray emission from SN 1006 on the
basis of the observed synchrotron emission have preferred a dominance of
IC emission from electrons in the  -ray part of the emission
spectrum. This scenario can not explain the apparent bipolar morphology
inferred from the existing
-ray part of the emission
spectrum. This scenario can not explain the apparent bipolar morphology
inferred from the existing  -ray measurements and yields a much
less convincing approximation to the radio and X-ray synchrotron spectrum.
In addition, as we have shown, the IC emission should reach at best about
10 TeV. Apart from future detailed determinations of the
-ray measurements and yields a much
less convincing approximation to the radio and X-ray synchrotron spectrum.
In addition, as we have shown, the IC emission should reach at best about
10 TeV. Apart from future detailed determinations of the  -ray
morphology one therefore needs to precisely measure the
-ray
morphology one therefore needs to precisely measure the  -ray flux
at energies
-ray flux
at energies
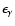 between 100 GeV and 100 TeV, and
preferably even from 10 MeV upwards.
The detailed spectra and in particular the existence of
between 100 GeV and 100 TeV, and
preferably even from 10 MeV upwards.
The detailed spectra and in particular the existence of  -rays with
very high energies above 10 TeV should allow a confirmation, or a
rejection, of CR nucleon production in SN 1006 with an
acceleration efficiency that is consistent with the requirements on the
Galactic CR energy budget.
-rays with
very high energies above 10 TeV should allow a confirmation, or a
rejection, of CR nucleon production in SN 1006 with an
acceleration efficiency that is consistent with the requirements on the
Galactic CR energy budget.
Acknowledgements
This work has been supported in
part by the Russian Foundation for Basic Research (grants 00-02-17728,
99-02-16325). EGB and LTK acknowledge the hospitality of the
Max-Planck-Institut für Kernphysik, where part of this work was
carried out.
-
Aharonian, F. A. 1999, Astropart. Phys., 11, 225
In the text
-
Aharonian, F. A., & Atoyan, A. M. 1999, A&A, 351, 33
In the text
-
Aharonian, F. A., Atoyan, A. M., & Völk, H. J. 1995, A&A, 294, L41
In the text
NASA ADS
-
Allen, W. H, Bond, I. A., Budding, E., et al. 1995, in Proc. 24th ICRC, Paris, 2, 447
In the text
-
Allen, G. E., Gotthelf, E. V., & Petre, R. 1999, in 26th ICRC,
Salt Lake City, 3, 480
In the text
-
Allen, G. E., Petre, R., & Gotthelf, E. V. 2001, ApJ, 558, 739
In the text
NASA ADS
-
Baring, M. G., Ellison, D. C., Reynolds, S. P., et al. 1999, ApJ, 513, 311
In the text
NASA ADS
-
Bennet, L., & Ellison, D. C. 1995, JGR, 100, 3439
In the text
NASA ADS
-
Berezhko, E. G. 1996, Astropart. Phys., 5, 367
In the text
-
Berezhko, E. G., Elshin, V. K., & Ksenofontov, L. T. 1996, JETP, 82, 1
In the text
NASA ADS
-
Berezhko, E. G., & Völk, H. J. 1997, Astropart. Phys., 7, 183
In the text
-
Berezhko, E. G., Ksenofontov, L. T., & Petukhov, S. I. 1999, in Proc.
26th ICRC, Salt Lake City, vol. 3, 431
In the text
-
Berezhko, E. G., & Ksenofontov, L. T. 1999, JETPh, 89, 391
In the text
-
Berezhko, E. G., & Völk, H. J. 2000, A&A, 357, 283
In the text
NASA ADS
-
Berezhko, E. G., Ksenofontov, L. T., & Völk, H. J. 2001,
in 27th ICRC, Hamburg, 5, 2489
In the text
-
Berezinskii, V. S., Bulanov, S. A., Dogiel, V. A., et al. 1990,
Astrophysics of cosmic rays (North-Holland: Publ. Comp.)
In the text
-
Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 236
In the text
-
Chevalier, R. A. 1982, ApJ, 258, 790
In the text
NASA ADS
-
Dermer, C. D. 1986, A&A, 157, 223
In the text
NASA ADS
-
Drury, L. O'C., Aharonian, F. A., & Völk, H. J. 1994, A&A, 287, 959
In the text
NASA ADS
-
Dyer, K. K., Reynolds, S. P., Borkowski, K. J., et al. 2001, ApJ, 551, 439
In the text
NASA ADS
-
Ellison, D. C., Baring, M. G., & Jones, F. C. 1995, ApJ, 453, 873
In the text
NASA ADS
-
Jones, E. M., Smith, B. W., & Straka, W. C. 1981, ApJ, 249, 185
In the text
NASA ADS
-
Hamilton, A. J. S., Sarazin, C. L., & Szymkowiak, A. E. 1986, ApJ, 300, 698
In the text
NASA ADS
-
Koyama, K., Petre, R., Gotthelf, E. V., et al. 1995, Nature, 378, 255
In the text
NASA ADS
-
Lucek, S. G., & Bell, A. R. 2000, MNRAS, 314, 65
In the text
NASA ADS
-
Malkov, M. A. 1998, Phys. Rev. E, 58, 4911
In the text
NASA ADS
-
Malkov, M. A., & Völk, H. J. 1995, A&A, 300, 605
In the text
NASA ADS
-
Malkov, M. A., & Völk, H. J. 1996, Adv. Space Res., 21, No. 4, 551
In the text
-
Malkov, M. A., & Drury, L. O'C. 2001, Rep. Prog. Phys., 64, 429
In the text
-
Malkov, M. A., Diamond, P. H., & Jones, T. W. 2001, ApJ, 571, 856
In the text
NASA ADS
-
Mastichiadis, A. 1996, A&A, 305, L53
In the text
NASA ADS
-
Mastichiadis, A., & de Jager, O. C. 1996, A&A, 311, L5
In the text
NASA ADS
-
Moffett, D. A., Goss, W. M., & Reynolds, S. P. 1993, AJ,
106, 1566
In the text
NASA ADS
-
Naito, T., & Takahara, F. 1994, J. Phys. G: Nucl. Part. Phys., 20, 477
In the text
-
Naito, T., Yoshida, T., Mori, M., & Tanimori, T. 1999,
Astronomische Nachrichten, 320, 205
In the text
NASA ADS
-
Pohl, M. 1996, A&A, 307, L57
In the text
NASA ADS
-
Pohl, M., & Esposito, J. 1998, ApJ, 507, 327
In the text
NASA ADS
-
Reynolds, S. P. 1996, ApJ, 459, L13
In the text
NASA ADS
-
Reynolds, S. P., & Gilmore, D. M. 1993, AJ, 92, 1138
In the text
NASA ADS
-
Scholer, M., Trattner, K. J., & Kucharek, H. 1992, ApJ, 395, 675
In the text
NASA ADS
-
Stecker, F. W. 1971, Cosmic Gamma Rays, NASA SP-249, chapter 5 ff.
In the text
-
Tanimori, T., Hayami, Y., Kamei, S., et al. 1998, ApJ, 497, L25
In the text
NASA ADS
-
Tanimori, T., Naito, T., Yoshida, T., et al. 2001, in 27th ICRC,
Hamburg, vol. 6, 2465
In the text
-
Trattner, K. J., & Scholer, M. 1994, JGR, 99, 6637
In the text
NASA ADS
-
Völk, H. J., et al. 2002, in preparation
In the text
-
Winkler, P. F., & Long, K. S. 1997, ApJ, 491, 829
In the text
NASA ADS
-
Yoshida, T., & Yanagita, S. 1997, in 2nd INTEGRAL Workshop
Transparent Universe (ESA SP-382), 85
In the text
Copyright ESO 2002
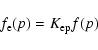
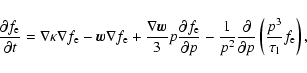
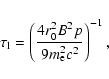
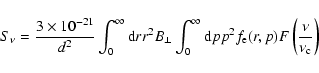
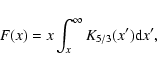
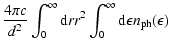
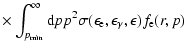
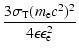
![$\displaystyle \times \left[
2q\ln q+(1+2q)(1-q)+0.5\frac{(\Gamma q)^2(1-q)}{1+\Gamma q}
\right]$](/articles/aa/full/2002/45/aah3593/img57.gif)
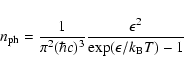
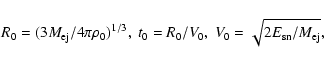
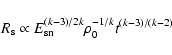
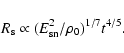
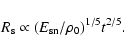
![\begin{figure}
\par\includegraphics[width=7.5cm]{SN1006_fig1.eps}\end{figure}](/articles/aa/full/2002/45/aah3593/Timg78.gif)
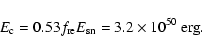
![\begin{figure}
\par\includegraphics[width=7.5cm]{SN1006_fig2_new.eps}\end{figure}](/articles/aa/full/2002/45/aah3593/Timg85.gif)
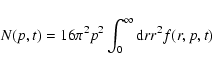
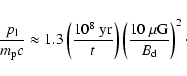
![\begin{figure}
\includegraphics[width=12cm]{SN1006_fig3_color.eps}
\end{figure}](/articles/aa/full/2002/45/aah3593/Timg122.gif)
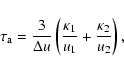
![\begin{displaymath}\tau_{\rm a}(p)^{-1}=\left[\tau_{\rm l}^{-1}(B_0,p)+
\tau_{\r...
...B_2,p)\sigma/\sigma_{\rm B}\right]
/(1+\sigma/\sigma_{\rm B}),
\end{displaymath}](/articles/aa/full/2002/45/aah3593/img133.gif)
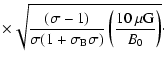
![\begin{figure}
\par\includegraphics[width=7.5cm]{SN1006_fig4_SED.eps}\end{figure}](/articles/aa/full/2002/45/aah3593/Timg160.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm]{SN1006_fig5_SED.epsi}\end{figure}](/articles/aa/full/2002/45/aah3593/Timg168.gif)
![\begin{displaymath}N_{\rm e}\propto
p^{-\gamma}\exp[-\kappa(p)/\kappa(p_{\rm max}^{\rm e})],
\end{displaymath}](/articles/aa/full/2002/45/aah3593/img175.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm]{SN1006_fig6.eps}\end{figure}](/articles/aa/full/2002/45/aah3593/Timg184.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm]{SN1006_fig7_rev1.eps}\end{figure}](/articles/aa/full/2002/45/aah3593/Timg192.gif)