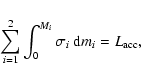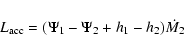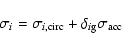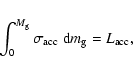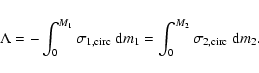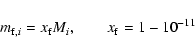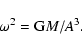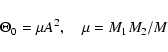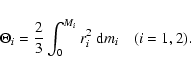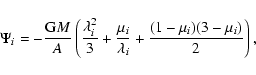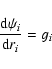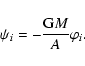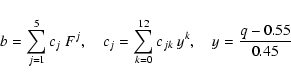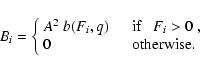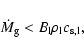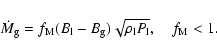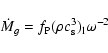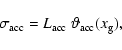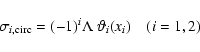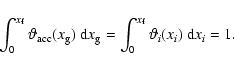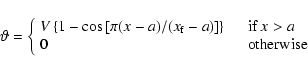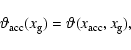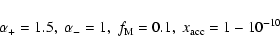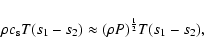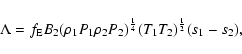A&A 395, 899-905 (2002)
DOI: 10.1051/0004-6361:20021337
The structure equations of contact binaries
H. Kähler
Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg, Germany
Received 3 April 2002 / Accepted 13 September 2002
Abstract
The structure equations of contact binaries are discussed.
An equation for the transfer of mass between the components is derived. Serious uncertainties concern only the transfer of energy.
They are expressed as unknown functions.
An evolution code for contact binaries is presented.
The restrictions imposed by a spherically averaged treatment of the components are discussed. Apart from these restrictions the code can be adapted to any choice of the functions describing the energy transfer. A simple tentative choice for these functions is proposed.
Key words: stars: binaries: close
1 Introduction
Structure and evolution of contact binaries are complex and
by no means well understood (for a review cf. Eggleton 1996).
Sinse theoretical work on early-type systems is almost absent,
the following discussion will be restricted to late-type systems.
Basic observational facts (e.g. Rucinski 1985, 1993) are
the light curves, the period-colour relation, the broad range in mass,
mass ratio and spectral type, the preference for shallow contact,
and the absence of mass ratios close to unity. Most systems appear to be unevolved or slightly evolved only, and some systems are known to be unevolved.
Lucy (1968) had the key idea of a common convective envelope in which the entropy is constant and energy is transferred from the primary to the secondary. Thermal equilibrium turned out to be usually not possible. Lucy (1968) found age zero equilibrium models (violating the period-colour relation) only in a limited mass range and for extreme Population I composition.
Moss & Whelan (1970) and Whelan (1972) encountered similar difficulties. Indeed, in unevolved systems with typical masses and typical composition thermal equilibrium was found to be in conflict with the equal entropy condition (Kähler 1995). If observed systems are assumed to be evolved, thermal equilibrium, when possible, turned out to be unstable (Kähler 1997a).
All these results are based on the assumption that the energy transfer between
the components occurs in the adiabatic part of the common convective envelope
(adiabatic transfer). The modification due to superadiabatic transfer is small
(Whelan 1972; Biermann & Thomas 1973). Extreme superadiabatic
transfer (Moss & Whelan 1973) gives more freedom, but
Hazlehurst (1974) showed that this case must be excluded since the heat capacity of the secondary's subphotospheric layers is too small.
Abandoning the restriction to thermal equilibrium,
Lucy (1976), Flannery (1976), and Robertson &
Eggleton (1977) obtained contact binary solutions evolving in thermal cycles
about a state of marginal contact. The solutions are in the required mass range
and in agreement with the period-colour relation, but they have
bad light curves since for a considerable part of the time
the temperature difference between the components is too large.
In a series of papers Rahunen and Vilhu encountered the same difficulty,
the so-called light curve paradox,
also for systems evolving in cycles without loss of contact. They concluded that the TRO (thermal relaxation oscillation) theory is not able to give a correct description of contact binaries (Rahunen 1983). The cycles investigated by Kähler et al. (1986)
have indeed again bad light curves.
In a recent paper Hazlehurst (2001) confirms the conclusion
that the present theory of cyclic contact binaries is not in a position to resolve the light curve paradox.
As long as a proper hydrodynamic treatment of contact binaries is not possible,
assumptions are necessary in any discussion. The results on thermal cycles
obtained so far are based on few and apparently weak assumptions. The deficiencies of the resulting solutions have led to a number of investigations based on stronger assumptions in order to find contact binary models in
thermal equilibrium which are compatible with the observations and
sound from a theoretical viewpoint. All these attempts failed. In particular,
the contact discontinuity hypothesis (Shu et al. 1976) violates the
second law of thermodynamics (Hazlehurst & Refsdal 1978;
Papaloizou & Pringle 1979), the assumption of an extended turbulent
envelope in the primary (Kähler 1989; Kähler & Fehlberg 1991) is also in conflict with the second law (Hazlehurst 1993),
and the assumption of sufficiently rapid internal mass motions in the
primary's envelope (Kähler 1995) is in conflict with the observations
(Kähler 1997a). For additional arguments against the possibility of
thermal equlibrium see Hazlehurst (1993).
Collecting these results, thermal equilibrium appears to be as impossible as thermal disequilibrium. Nevertheless contact binaries are observed.
We are thus led to the conclusion that the assumptions made so far in the theoretical discussion are not weak but too restrictive. This casts a doubt upon results which have been regarded as reliable for decades. In particular, we expect that if the restrictions are removed the light curve paradox for
thermal cycles can be resolved and/or thermal equilibrium can be shown to be possible.
The purpose of the present paper is to collect the structure equations of contact binaries on the basis of truly weak assumptions, to discuss the remaining uncertainties, and to present an evolution code for contact binaries which is flexible enough to be an appropriate tool when investigating the
theoretical problems and trying to
resolve the conflict between theory and observations.
2 The structure equations of contact binaries
We adopt a self-consistent spherically averaged treatment of the
components (Kähler 1986, 1997b) and assume uniform rotation
and conservation of total mass M=M1+M2 and angular momentum J.
Each component is assumed to be in hydrostatic equation, but the Roche equipotential condition is not assumed to be satisfied.
The system may be either in contact or semi-detached or detached.
2.1 The differential equations
Let 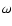 be the angular velocity, mi the mass variable, gi the effective gravity in the component i, and
be the angular velocity, mi the mass variable, gi the effective gravity in the component i, and 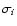 the source (when positive) or sink (when negative) of energy per unit
of mass caused by the interaction of the components. Using standard
notation otherwise, the basic differential equations are
the source (when positive) or sink (when negative) of energy per unit
of mass caused by the interaction of the components. Using standard
notation otherwise, the basic differential equations are
Concerning the temperature gradient, let
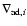 be the
adiabatic gradient,
be the
adiabatic gradient,
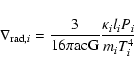 |
(5) |
the radiative gradient, and
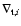 the gradient in the presence
of turbulence. Note that turbulence can be caused by convective instability (
the gradient in the presence
of turbulence. Note that turbulence can be caused by convective instability (
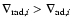 )
as well as by circulation currents.
The gradient
)
as well as by circulation currents.
The gradient
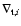 can be obtained from a mixing-length theory if
can be obtained from a mixing-length theory if
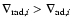 ,
and from a generalised mixing-length theory (Kähler 1989) otherwise. Let
,
and from a generalised mixing-length theory (Kähler 1989) otherwise. Let 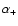 be the mixing length and
be the mixing length and 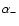 the generalised mixing length, both in units of the pressure scale height. With these definitions we have
the generalised mixing length, both in units of the pressure scale height. With these definitions we have
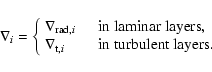 |
(6) |
Convectively stable turbulent layers are expected in the common turbulent envelope of early-type contact binaries, and possibly also in late-type systems.
Concerning the extent of these layers some assumption is necessary, which will
be labeled by the number 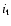 .
We may assume that convectively stable turbulent layers are absent (
.
We may assume that convectively stable turbulent layers are absent (
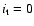 ). Alternatively we may assume
that the extent of these layers is determined by the condition that layers with energy sources and sinks caused by circulation and accretion are turbulent (
). Alternatively we may assume
that the extent of these layers is determined by the condition that layers with energy sources and sinks caused by circulation and accretion are turbulent (
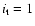 ). Other assumptions (to be labeled with
). Other assumptions (to be labeled with
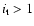 )
are also possible.
)
are also possible.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3582.f1}
\end{figure}](/articles/aa/full/2002/45/aah3582/Timg89.gif) |
Figure 1:
The function 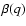 describing the area of the neck in systems
in shallow contact (see text).
describing the area of the neck in systems
in shallow contact (see text). |
| Open with DEXTER |
Since mass M and angular momentum J are conserved, the global balance of energy (Kähler 1997b) requires that
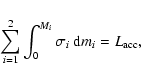 |
(7) |
where
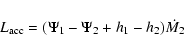 |
(8) |
is the accretion luminosity. The quantities hi and 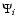 denote, respectively, specific enthalpy and potential at the surface of the component i.
In the presence of mass exchange
(
denote, respectively, specific enthalpy and potential at the surface of the component i.
In the presence of mass exchange
(
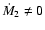 )
let
)
let 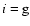 in the gainer (the mass gaining component),
and
in the gainer (the mass gaining component),
and 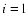 in the loser.
Since the accretion luminosity is caused by energy
sources in the gainer's outermost layers, we can write
in the loser.
Since the accretion luminosity is caused by energy
sources in the gainer's outermost layers, we can write
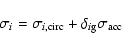 |
(9) |
with
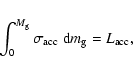 |
(10) |
and the luminosity transferred by circulation currents from the primary
to the secondary is
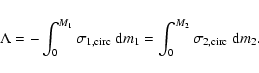 |
(11) |
2.2 The boundary conditions
The central boundary conditions are
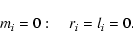 |
(12) |
The outer boundary conditions are in a close approximation
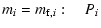 |
= |
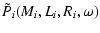 |
(13) |
| Ti |
= |
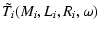 |
(14) |
| ri |
= |
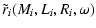 |
(15) |
| li |
= |
Li, |
(16) |
where the functions
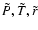 are defined by outer layer integrations, assuming li=Li, and the fitting mass
are defined by outer layer integrations, assuming li=Li, and the fitting mass
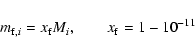 |
(17) |
is very close to the surface, just below the photosphere. This choice makes it possible to treat systems with energy sources or sinks
in the subphotospheric layers.
Total mass M, angular velocity 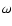 and the separation A of the components are connected by
Kepler's law
and the separation A of the components are connected by
Kepler's law
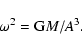 |
(18) |
Conservation of mass requires
and conservation of angular momentum requires
 |
(20) |
with the moments of inertia
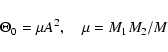 |
(21) |
and
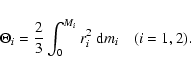 |
(22) |
The components are treated as spherical stars. In addition to the Roche potential we have therefore in each component an effective central potential.
In a self-consistent treatment this potential is well-defined (see Kähler 1986). The surface potential of the component i is
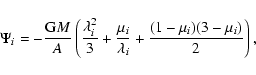 |
(23) |
where 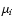 and
and 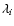 are, respectively, normalised mass and radius
of the component defined by
are, respectively, normalised mass and radius
of the component defined by
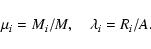 |
(24) |
Note that 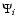 is the average value of the Roche potential over the spherical surface.
The degree of contact Fi of the component i is defined by
is the average value of the Roche potential over the spherical surface.
The degree of contact Fi of the component i is defined by
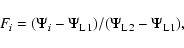 |
(25) |
where
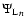 denotes the Roche potential at the Lagrangian point n.
The effective central potential
denotes the Roche potential at the Lagrangian point n.
The effective central potential
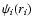 in the component i is
the solution of the differential equation
in the component i is
the solution of the differential equation
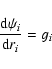 |
(26) |
with the property
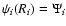 .
In the outermost layers
of the components the effective central potential almost coincides with the
spherically averaged Roche potential. In the interior the two potentials differ and only the effective potential is useful.
We shall also need the normalised potential
.
In the outermost layers
of the components the effective central potential almost coincides with the
spherically averaged Roche potential. In the interior the two potentials differ and only the effective potential is useful.
We shall also need the normalised potential 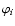 defined by
defined by
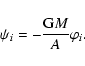 |
(27) |
If a system in contact satisfies the Roche equipotential condition
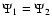 ,
the area B of the neck between the components can be
written in the form
,
the area B of the neck between the components can be
written in the form
where b is a function of mass ratio q=M2/M1 and degree of contact F.
A close approximation for  is
is
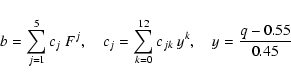 |
(29) |
with coefficients listed in Table 1.
For systems in shallow contact (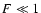 )
we have
)
we have
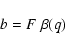 |
(30) |
with the function 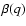 shown in Fig. 1.
shown in Fig. 1.
The area of the neck can be used can be used to derive constraints
for the exchange of mass and energy. We shall need the function Bidefined by
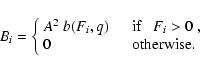 |
(31) |
2.6 The transfer of mass
If the system is semi-detached, matter in the neck is streaming from the loser to the gainer, approximately with the velocity of sound, and through an area which is smaller than 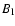 (cf. Fig. 1.6 of Pringle 1985). Accordingly we have
(cf. Fig. 1.6 of Pringle 1985). Accordingly we have
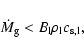 |
(32) |
where
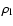 and
and
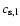 denote, respectively, density and sound
velocity at the loser's inner critical surface. Since
denote, respectively, density and sound
velocity at the loser's inner critical surface. Since
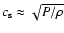 and since
and since
 in semi-detached systems
we can write
in semi-detached systems
we can write
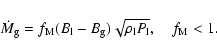 |
(33) |
Following Paczynski & Sienkiewicz (1972),
Pringle (1985) showed that
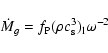 |
(34) |
with 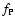 of order unity. As expected, Eqs. (33) and (34) turned out to be roughly equivalent. In most cases investigated
equivalence requires
of order unity. As expected, Eqs. (33) and (34) turned out to be roughly equivalent. In most cases investigated
equivalence requires
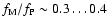 .
.
We need an equation for the rate of mass exchange which depends continuously
on the structure of the system and which is physically plausible in all cases.
Equation (33) has these properties. If matter is streaming almost freely from the loser to the gainer, the rate can be written as the
product of density, sound velocity and effective area in the neck and thus
in the form of Eq. (33). This is the case not only in semi-detached systems but also in systems in contact as long as
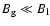 .
In detached systems without mass exchange the equation is trivially valid.
.
In detached systems without mass exchange the equation is trivially valid.
The general case of systems in contact is more complex
since matter is streaming from the loser to the gainer (at the rate
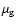 ,
say) as well as from the gainer to the loser (at the rate
,
say) as well as from the gainer to the loser (at the rate
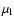 ).
Each rate separately can be approximated by a product of characteristic
values for density, velocity (usually smaller than the sound velocity) and effective area. For the net rate
).
Each rate separately can be approximated by a product of characteristic
values for density, velocity (usually smaller than the sound velocity) and effective area. For the net rate
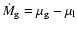 however an expression of this form is not obvious, except for the case (already mentioned) that
however an expression of this form is not obvious, except for the case (already mentioned) that
 ans thus
ans thus
 .
Nevertheless Eq. (33) is plausible as an approximation since
providing fulfilment of the Roche equipotential condition in a close approximation, with the possible exception of short phases during a cycle just before contact is broken or just after contact has been reestablished.
As long as
.
Nevertheless Eq. (33) is plausible as an approximation since
providing fulfilment of the Roche equipotential condition in a close approximation, with the possible exception of short phases during a cycle just before contact is broken or just after contact has been reestablished.
As long as
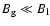 in these phases, Eq. (33)
is certainly adequate. For these reasons Eq. (33), with
in these phases, Eq. (33)
is certainly adequate. For these reasons Eq. (33), with 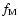 taken in the range
taken in the range
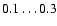 ,
is expected to be reasonable in any system.
,
is expected to be reasonable in any system.
2.7 The transfer of energy
With the rate of mass exchange also the accretion luminosity
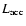 is
known from Eq. (8). The luminosity
is
known from Eq. (8). The luminosity 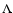 transferred
by circulation currents however is still unknown.
transferred
by circulation currents however is still unknown.
It is convenient to use the variable
xi=mi/Mi and to write
the instantaneous distribution of the energy sources and sinks in the form
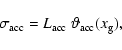 |
(35) |
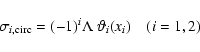 |
(36) |
with normalised functions, i.e.
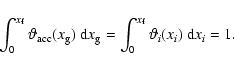 |
(37) |
So far it has almost always been assumed that the energy sources and sinks occur only in the outer layers. For this reason it is useful to introduce a simple and smooth normalised function which is zero in the interior and positive in the outer layers. The function
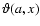 defined by
defined by
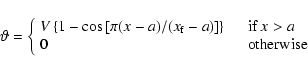 |
(38) |
with
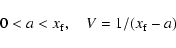 |
(39) |
has these properties.
Since the sources caused by accretion occur in the gainer's surface layers, we may assume that
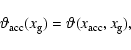 |
(40) |
where
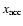 is a number very close to
is a number very close to 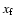 .
.
Sources and sinks caused by circulation currents occur
only in systems in contact. Since the
fitting mass is very close to unity, the contact condition
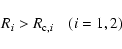 |
(41) |
(where
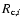 is the inner critical radius of the component i) can be approximated by
is the inner critical radius of the component i) can be approximated by
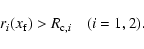 |
(42) |
It is usually assumed that energy sources/sinks occur only in the
secondary's/primary's outer layers. If this assumption is reasonable,
we can approximately write
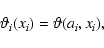 |
(43) |
where ai is a number somewhat smaller than 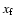 .
The assumption
is however possibly too restrictive. For example, circulation currents deep in the interior of the components as proposed by Webbink (1977) are possibly
associated with energy sources and sinks. As a further example, Martin & Davey (1995) presented arguments for
the existence of additional energy sources/sinks in the primary's/secondary's
layers near the critical surface. If these arguments are valid, the functions
.
The assumption
is however possibly too restrictive. For example, circulation currents deep in the interior of the components as proposed by Webbink (1977) are possibly
associated with energy sources and sinks. As a further example, Martin & Davey (1995) presented arguments for
the existence of additional energy sources/sinks in the primary's/secondary's
layers near the critical surface. If these arguments are valid, the functions
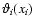 change sign and additional parameters may be necessary.
In any case we may assume that the function
change sign and additional parameters may be necessary.
In any case we may assume that the function
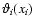 is approximately described by few parameters
is approximately described by few parameters
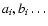
The uncertainties concerning the energy transfer by circulation currents have
been expressed as uncertainties in the quantities 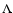 and
and
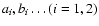 .
We shall assume that these quantities
are (in way so far unknown) determined by the instantaneous spherically averaged structure of both components and thus by the set of functions
.
We shall assume that these quantities
are (in way so far unknown) determined by the instantaneous spherically averaged structure of both components and thus by the set of functions
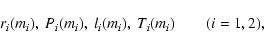 |
(44) |
which will be comprised in the symbol 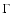 .
This assumption gives the largest freedom within the framework of a spherically averaged description of the components. Symbolically the functionals
.
This assumption gives the largest freedom within the framework of a spherically averaged description of the components. Symbolically the functionals
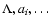 will be written as functions
will be written as functions
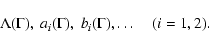 |
(45) |
To be more specific on this point, if the physical parameters (mass, angular momentum and composition) and the functions (44) are given, then from their range of definition also M1 and M2 are known. Since the functions are not independent but coupled by differential equations, also the angular velocity 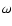 is known from the equation of hydrostatic equilibrium, and the separation A follows from Kepler's law. The instantaneous structure of the
system (within the framework of a spherically averaged description of the components) is therefore completely known. Accordingly,
is known from the equation of hydrostatic equilibrium, and the separation A follows from Kepler's law. The instantaneous structure of the
system (within the framework of a spherically averaged description of the components) is therefore completely known. Accordingly,
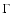 represents the instantaneous structure.
If
represents the instantaneous structure.
If 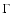 is given, the rate of mass exchange and the effects of accretion are known. The evolution of the system (i.e. the time derivative
is given, the rate of mass exchange and the effects of accretion are known. The evolution of the system (i.e. the time derivative
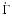 )
however is only determined if in addition the energy sources and sinks associated with circulation currents are given. Assuming that
)
however is only determined if in addition the energy sources and sinks associated with circulation currents are given. Assuming that
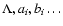 are still unspecified functions of
are still unspecified functions of  we have the largest possible freedom. An example for
functions of this type is the "transport equation''
we have the largest possible freedom. An example for
functions of this type is the "transport equation''
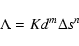 |
(46) |
proposed by Hazlehurst & Refsdal (1980) and adopted by Rahunen
& Vilhu (see Rahunen 1983), where d is the depth of
contact (determined by the radii and the critical radii of the components),
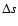 is the entropy difference between the two outer convective zones,
and K,m,n are parameters.
is the entropy difference between the two outer convective zones,
and K,m,n are parameters.
3 Uncertainties in the structure equations
The equations derived in the preceding subsections contain the parameters
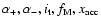 and the unknown functions listed in Eq. (45).
The presence of these parameters and functions reflects the difficulties
of the hydrodynamical problem. Concerning the choice of the parameters there
is little freedom. We decided to use as standard values
and the unknown functions listed in Eq. (45).
The presence of these parameters and functions reflects the difficulties
of the hydrodynamical problem. Concerning the choice of the parameters there
is little freedom. We decided to use as standard values
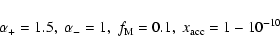 |
(47) |
and to compare results obtained with different values of  .
The uncertainties in the functions however are serious. We have assumed
that the sources and sinks of energy caused by circulation are determined by
the spherically averaged structure of the components. Is this assumption
reasonable from the viewpoint of hydrodynamics? In the general case
(i.e. when considering the evolution of a system starting from
an arbitrarily given initial configuration) the answer is uncertain
since the sources and sinks depend on details of the internal mass motions which escape notice in a spherically averaged description.
.
The uncertainties in the functions however are serious. We have assumed
that the sources and sinks of energy caused by circulation are determined by
the spherically averaged structure of the components. Is this assumption
reasonable from the viewpoint of hydrodynamics? In the general case
(i.e. when considering the evolution of a system starting from
an arbitrarily given initial configuration) the answer is uncertain
since the sources and sinks depend on details of the internal mass motions which escape notice in a spherically averaged description.
When studying the thermal evolution of unevolved systems, however,
we are interested only in the long-time behaviour,
which is expected to be either a stable limit-cycle (i.e. a thermal
cycle) or a fixed point (i.e. a configuration in stable thermal equilibrium).
More complex attractors cannot be excluded, but previous results (Kähler et al. 1986) suggest that they are not realised.
Under these circumstances the problem is less difficult and a spherically averaged treatment of the components is reasonable.
To see this, consider first a given system evolving in relaxed thermal cycles.
All properties (e.g.  )
are periodic functions of the
time t, and t can certainly be eliminated by inverting
functions describing the spherically averaged structure of the components
as a function of t. For example, if the primary's degree of contact F1(t)
is a monotonic function in a certain time interval, then t=t(F1) and
thus
)
are periodic functions of the
time t, and t can certainly be eliminated by inverting
functions describing the spherically averaged structure of the components
as a function of t. For example, if the primary's degree of contact F1(t)
is a monotonic function in a certain time interval, then t=t(F1) and
thus
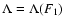 in this interval.
Accordingly, for a given system evolving in cycles the functions (45)
can be defined in a variety of ways. We are interested in a physical
definition which is (approximately) valid not only for the particular system under consideration but for all systems evolving in cycles as well for
all systems in (stable or unstable) thermal equilibrium. Such a definition
can hopefully be obtained in the future from 3-D hydrodynamic calculations.
In the meantime we have to make plausible assumptions and to introduce
free parameters. Equation (46) is an example.
in this interval.
Accordingly, for a given system evolving in cycles the functions (45)
can be defined in a variety of ways. We are interested in a physical
definition which is (approximately) valid not only for the particular system under consideration but for all systems evolving in cycles as well for
all systems in (stable or unstable) thermal equilibrium. Such a definition
can hopefully be obtained in the future from 3-D hydrodynamic calculations.
In the meantime we have to make plausible assumptions and to introduce
free parameters. Equation (46) is an example.
Suppose next that thermal equilibrium can be achieved. In an approximate
discussion the uncertainties in the parameters listed in Eq. (47) can be neglected. The structure of a configuration is then determined by the values of
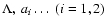 ,
i.e. by few numbers, not functions.
The investigation of possible equilibrium configurations is therefore
much less difficult than the investigation of thermal cycles. In fact,
it is possible to investigate all candidates for reasonable
equilibrium configurations. We are interested in configurations which are dynamically as well as thermally stable. The dynamical stability problem is well determined. More difficult is the thermal stability problem since it involves the change of the quantities
,
i.e. by few numbers, not functions.
The investigation of possible equilibrium configurations is therefore
much less difficult than the investigation of thermal cycles. In fact,
it is possible to investigate all candidates for reasonable
equilibrium configurations. We are interested in configurations which are dynamically as well as thermally stable. The dynamical stability problem is well determined. More difficult is the thermal stability problem since it involves the change of the quantities
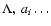 in the course of
thermal perturbations, and thus, if these quantities can be treated as
functions of
in the course of
thermal perturbations, and thus, if these quantities can be treated as
functions of 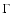 ,
the derivatives of these functions.
,
the derivatives of these functions.
4 A simple model
Some choice of the functions in Eq. (45) being necessary,
here we define a simple model for late-type contact binaries involving
only few parameters in addition to those in Eq. (47).
We assume that the energy flux in the neck is not larger than
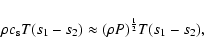 |
(48) |
with all quantities taken at the critical surface and quantities
without index averaged between the components, and that therefore
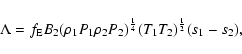 |
(49) |
where 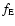 is a parameter not larger than unity.
Concerning the extent of the energy sources and sinks, let
is a parameter not larger than unity.
Concerning the extent of the energy sources and sinks, let
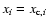 at the critical radius of a system in contact. We assume that Eq. (43)
is valid and that
at the critical radius of a system in contact. We assume that Eq. (43)
is valid and that
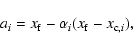 |
(50) |
where 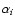 is a parameter. In other words, we make the usual assumption that energy sources/sinks occur only in the secondary's/primary's envelope,
and assume that the extent of the sources or sinks is correlated with the extent of the layers above the inner critical surface.
is a parameter. In other words, we make the usual assumption that energy sources/sinks occur only in the secondary's/primary's envelope,
and assume that the extent of the sources or sinks is correlated with the extent of the layers above the inner critical surface.
In view of the persistent difficulties in the theoretical treatment of contact binaries we cannot expect that this model gives results which are fully
compatible with the observations as well as with theoretical constraints.
We do, however, expect that the deficiencies of the results can be used to
reduce the inconsistencies and to improve the model.
In other words, the model is intended as a starting point in the attempt
to find a consistent description of contact binaries.
5 The evolution code
The equations collected above have been cast into an evolution code
for contact binaries. The structure equations for both components
are solved simultaneously. The code can be adapted to any choice of the
functions in Eq. (45).
The non-Lagrangian mass variables
xi=mi/Mi are used.
Since the components exchange mass, this choice minimises the changes in pressure and temperature at the meshpoints near the surface during a time step.
As expected, numerical stability turned out to be sometimes a serious problem.
While in quiet evolutionary phases time steps of more than 103 years can be used, in some difficult phases steps of 10-4 years are required. We found it necessary to treat the difference equations as proposed by Sugimoto (1970).
A problem with the temperature gradient concerns only the secondary's
envelope. In some phases during a cycle the extent of the convective layers may not converge in the iteration process. Some layers oscillate between radiative transport and convection. This difficulty is removed if the extent of radiative and of turbulent layers is artificially kept fixed after a certain number of iterations.
Concerning the choice of an initial configuration, one of the equations in the Henyey scheme
deals with the exchange of mass between the components. If this equation is replaced by an equation prescribing the mass ratio, and if artificial energy sources/sinks are introduced in the secondary's/primary's interior,
systems in thermal equilibrium with any given mass ratio can easily be
constructed. The energy sources and sinks can be adjusted to obtain a
configuration in contact satisfying the Roche equipotential condition. Switching then off the artificial energy sources and sinks we obtain a contact configuration in thermal disequilibrium which, if dynamically stable, can be used as initial configuration.
6 Concluding remarks
We have collected the equations for zero age contact systems, assuming conservation of angular momentum. (In our opinion it is premature to study the
effects of nuclear evolution and loss of angular momentum as long as the
structure of unevolved systems is not well understood.)
Are these equations based on truly weak assumptions? The continuity equation is beyond doubt. The equation of hydrostatic equilibrium (2) is a very close appoximation in the interior, and a close approximation also in the outer layers if (i) the velocity of the internal mass motions (in a rotating frame) is not larger than the the sound velocity and thus much smaller than the orbital velocity and (ii) the turbulent pressure is unimportant. If the velocity of the
internal mass motions cannot be neglected, modifications of the equation
of hydrostatic equilibrium and of the Roche equipotential condition
will be necessary as described by Kähler (1995), and this
requires a modification of Eq. (33). There are also
uncertainties in the transport equation which can be estimated comparing results
for different assumptions (i.e. different values of 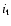 ).
Serious uncertainties concern only the energy balance. Some quantities
decribing the energy transfer between the components are unknown.
When investigating thermal cycles, these quantities can be treated as (so far unknown) functions depending on properties of the spherically averaged
structure of the components.
An evolution code has been presented which can be adapted to any choice of these functions. With this freedom and with the possibility to introduce other modifications (concerning the temperature gradient and departures from hydrostatic equilibrium in the outer layers) the treatment of contact binaries is free from restrictive assumptions.
).
Serious uncertainties concern only the energy balance. Some quantities
decribing the energy transfer between the components are unknown.
When investigating thermal cycles, these quantities can be treated as (so far unknown) functions depending on properties of the spherically averaged
structure of the components.
An evolution code has been presented which can be adapted to any choice of these functions. With this freedom and with the possibility to introduce other modifications (concerning the temperature gradient and departures from hydrostatic equilibrium in the outer layers) the treatment of contact binaries is free from restrictive assumptions.
The transfer of mass and the exchange of energy between the components have been treated separately. In reality these processes are coupled since determined by the internal mass motions. A combined treatment will be possible only when we get more insight into these motions.
A simple model has been proposed as a starting point for more detailed
investigations, and in an accompanying paper first results are presented.
- Biermann, P., & Thomas, H.-C. 1973, A&A, 23, 55
In the text
NASA ADS
- Eggleton, P. P. 1996, in
The Origin, Evolutions, and Destinies of Binary Stars in Clusters,
ed. E. F. Milone, & J.-C. Mermilliod, ASP Conf. Ser., 90
In the text
- Flannery, B. P. 1976, ApJ, 205, 217
In the text
NASA ADS
- Hazlehurst, J. 1974, A&A, 36, 49
In the text
NASA ADS
- Hazlehurst, J. 1993, A&A, 271, 209
In the text
NASA ADS
- Hazlehurst, J. 2001, The Observatory, 121, 86
In the text
NASA ADS
- Hazlehurst, J., & Refsdal, S. 1978, A&A, 62, L9
In the text
NASA ADS
- Hazlehurst, J., & Refsdal, S. 1980, A&A, 84, 200
In the text
NASA ADS
- Kähler, H. 1986, A&A, 157, 329
In the text
NASA ADS
- Kähler, H. 1989, A&A, 209, 67
In the text
NASA ADS
- Kähler, H. 1995, A&A, 294, 497
In the text
NASA ADS
- Kähler, H. 1997a, A&A, 318, 171
In the text
NASA ADS
- Kähler, H. 1997b, A&A, 320, 787
In the text
NASA ADS
- Kähler, H., Matraka, B., & Weigert, A. 1986, A&A, 159, 317
In the text
NASA ADS
- Kähler, H., Matraka, B., & Weigert, A. 1986, A&A, 161, 296
In the text
NASA ADS
- Kähler, H., & Fehlberg, H.-J. 1991, A&A, 252, 137
In the text
NASA ADS
- Lucy, L. B. 1968, ApJ, 151, 1123
In the text
NASA ADS
- Lucy, L. B. 1976, ApJ, 205, 208
In the text
NASA ADS
- Martin, T. J., & Davey, S. C. 1995, MNRAS, 275, 31
In the text
NASA ADS
- Moss, D. L., & Whelan, J. A. J. 1970, MNRAS, 149, 147
In the text
NASA ADS
- Moss, D. L., & Whelan, J. A. J. 1973, MNRAS, 161, 239
In the text
NASA ADS
- Paczynski, B., & Sienkiewicz, R. 1972, Acta Astron., 22, 73
In the text
- Papaloizou, J., & Pringle, J. E. 1979, MNRAS, 189, 5P
In the text
- Pringle, J. E. 1985, in
Interacting binary stars,
ed.
J. E. Pringle, & R. A. Wade (Cambridge Univ. Press, Cambridge)
In the text
- Rahunen, T. 1983, A&A, 117, 235
In the text
NASA ADS
- Robertson, J. A., & Eggleton, P. P. 1977, MNRAS, 179, 359
In the text
NASA ADS
- Rucinski, S. M. 1985, in Interacting binary stars, ed.
J. E. Pringle, & R. A. Wade (Cambridge Univ. Press, Cambridge)
In the text
- Rucinski, S. M. 1993, in
The realm of interacting binary stars, ed. J. Sahade, G. E. Mc Cluskey, & Y. Kondo (Kluwer, Dordrecht)
In the text
- Shu, F. H., Lubow, S. H., & Anderson, L. 1976, ApJ, 209, 536
In the text
NASA ADS
- Sugimoto, D. 1970, ApJ, 159, 619
In the text
NASA ADS
- Webbink, R. F. 1977, ApJ, 215, 851
In the text
NASA ADS
- Whelan, J. A. J. 1972, MNRAS, 156, 115
In the text
NASA ADS
Copyright ESO 2002
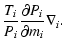
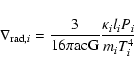
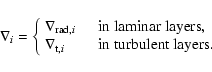
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3582.f1}
\end{figure}](/articles/aa/full/2002/45/aah3582/Timg89.gif)