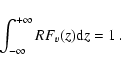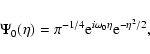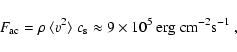A&A 395, L51-L54 (2002)
DOI: 10.1051/0004-6361:20021531

Evidence for short-period acoustic waves in the solar atmosphere

M. Wunnenberg1 - F. Kneer1 - J. Hirzberger2


1 - Universitäts-Sternwarte, Geismarlandstraße 11, 37083 Göttingen, Germany
2 - Institut für Geophysik, Astrophysik und Meteorologie, Universitätsplatz 5, 8010 Graz, Austria

Received 27 September 2002 / Accepted 17 October 2002

Abstract
Short-period acoustic waves are thought to supply the energy for the radiative losses of the non-magnetic chromosphere of the Sun and, in general, of late-type stars. Here, we present evidence for the existence of waves in the solar atmosphere with periods in the range of 50 s <P< 100 s. Two-dimensional time sequences with a cadence of 25 s were obtained from quiet Sun disk center in Fe  I 5434 Å. The observations were performed with the "Göttingen'' Fabry-Perot spectrometer in the Vacuum Tower Telescope at the Observatorio del Teide/Tenerife. They are subjected to speckle reconstruction and to a wavelet analysis. The atmospheric ranges forming the velocity signals are narrowed by linear combinations of Doppler maps from wavelengths near line center. The power in the short-period range is concentrated above intergranular spaces. We estimate an acoustic flux into the chromosphere of approximately 3 $\times10^6$ erg cm-2 s-1, as needed for the chromospheric radiative losses.

Key words: waves - Sun: photosphere - Sun: chromosphere


1 Introduction

The heating of the solar chromosphere, and of stellar chromospheres in general, represents a lively field of research since their detection. This holds for both non-magnetic and magnetic regions on the Sun and on stars. Here, we will only consider the solar heating phenomenon outside active and network regions.

Biermann (1948) and Schwarzschild (1948) suggested that the energy supply stems from acoustic waves generated by the turbulent convection at the bottom and below the photosphere. This mechanism was further investigated by Osterbrock (1961) and Stein (1967, 1968). Following their studies, the solar subphotospheric layers should emit much acoustic energy flux in the form of short-period acoustic waves generated by the Lighthill (1952) mechanism.

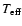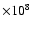On the basis of studies by Musielak et al. (1994) and others, Ulmschneider et al. (1996) and Fawzy et al. (2002) could give estimates of the acoustic wave flux of stars using only few stellar parameters: effective temperature $T_{\rm eff}$, surface gravity g, and metallicity Z. 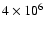For the Sun, one expects an output of 1-3 $\times10^8$ erg cm-2 s-1, sufficient to account for the chromospheric radiative energy losses of 2- $4\times10^6$ erg cm-2 s-1 in non-magnetic areas (Athay 1976). Much of the acoustic energy is lost during the travel from photosphere to chromosphere through radiative damping. 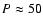The maximum of the wave power is expected at a period of $P\approx50$ s (Ulmschneider et al. 1996; Fawzy et al. 2002). In long-lasting efforts and with increasing realism with regard to the wave spectrum, atmospheric ionization state and radiative transfer, Ulmschneider and his collaborators simulated numerically acoustic shocks running through the solar atmosphere. We refer here to Rammacher & Ulmschneider (2002) where earlier work, also on the heating problem in general, can be traced back.

Carlsson & Stein (1995,1997) demonstrated that the temporal evolution of the Ca  II H and K lines, observed outside the chromospheric network, can be simulated by an excitation with waves from a broad frequency spectrum taken from observations by Lites et al. (1993). Although the latter authors described the velocity signals at periods P<125 s as dominated by noise, Carlsson & Stein (1997) found them as necessary ingredients to simulate the Ca H and K line behaviour. A further result of the simulations by Carlsson & Stein (1995) and Rammacher & Ulmschneider (2002) is that the temperature does not increase with height in the chromosphere when averaged over time. A more accurate notion than heating for the chromospheric problem would thus be the question of energy supply for the radiative emission.

In this letter we present observational evidence for short-period waves. They are difficult to detect for two reasons: 1) they are, very likely, small-scale phenomena, smaller than the granular/intergranular sizes. 2) The large height ranges of spectral line formation reduce the measurable signal which is composed of the contributions from the signal-forming layers along a wave train (cf. Mein & Mein 1980). Early observational studies on short-period waves were either inconclusive (Endler & Deubner 1983) or found no short-period acoustic signal above noise (Lites & Chipman 1979; Mein & Schmieder 1981; Deubner & Fleck 1990; Krijger et al. 2001). Deubner's (1976) interpretation of power showing an interference-like pattern at high frequencies as resonances within response functions has not been verified later on.

We could succeed to detect short-period waves with two-dimensional (2D) spectroscopy using Fabry-Perot interferometers (FPIs). The method has several advantages compared with slit spectroscopy: 1) it allows good feature tracking, after the observations, in a 2D field of view (fov). 2) The repetition rate for a reasonable fov can be short. 3) It allows image reconstruction, thus yields high spatial resolution. The problem of poor differentiation in atmospheric height can partly be overcome by a proper combination of information originating from different height ranges.

Here, we concentrate on the few necessary items of the observations and data analysis and on the communication of first results. A detailed description of the employed methods and of further results will be given in a forthcoming paper.

2 Observations and data reduction

The observations were taken in August 2000 with the "Göttingen'' Fabry-Perot spectrometer (Bendlin et al. 1992) in the Vacuum Tower Telescope at the Observatorio del Teide on Tenerife. The setup was the same as described by Koschinsky et al. (2001) except that we did not use a polarimeter. A 41.25 min time sequence from solar disk center was taken by scanning through the non-magnetic Fe  I line at 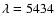$\lambda=5434$ Å with a cadence of 25 s. Thus, the shortest detectable period in the data is P=50 s. The FWHM of the spectrometer and the stepwidth were 32.8 mÅ and 31.9 mÅ, respectively. At each wavelength position 8 frames with an exposure time of 20 ms were taken. Broadband images were taken simultaneously with the narrow-band images.

The data reduction included: subtraction of darks, flat fielding, speckle reconstruction of the broadband images at each time step with the spectral ratio method (von der Lühe 1984) and the speckle masking method (Weigelt 1977), and reconstruction of the narrow-band images as described, e.g., in Krieg et al. (1999) and Hirzberger et al. (2001). A destretching of the broadband granulation time sequence was performed with a code originating from Yi & Molowny Horas (1992). The destretching parameters were then applied as well to the narrow-band time sequences.

Finally, 2D intensity fluctuations at the center of the 5434 Å line and 2D Doppler shift fluctuations from bisectors were determined for all time steps. During each scan of the time series, the images from near line center used for the present study were taken at different times, but with less than 5 s separation. We did not correct for this (by rotating in Fourier space to the same position in time).

3 Velocity response functions

We need the information, at least approximately, about the atmospheric heights contributing to the observed fluctuations. For this purpose we calculate velocity response functions RFv(z) (see, e.g. Pérez Rodríguez & Kneer 2002 and Eibe et al. 2001 as well as references therein). We use the Holweger-Müller (1974) model of the solar atmosphere and calculate the line formation in LTE. It was noted by Shchukina et al. (1997) that especially the strong lines of neutral iron suffer from non-LTE effects in both opacity and source function. Future studies should include these effects. The spectral broadening by the FPI spectrometer is taken into account.


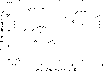 \begin{figure} \resizebox{\hsize}{!}{\includegraphics{Ei271_f1.eps}} \end{figure} Figure 1: Velocity response functions RFv(z) at two intensity positions of the line bisector near line center, curves 1 and 2. The thick solid curve is the linear combination as in Eq. (1).
Open with DEXTER

Figure 1 shows the result for two positions in the bisector near line center, at 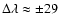$\Delta\lambda\approx\pm29$ mÅ off line center (dashed curve 1) and at 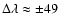$\Delta\lambda\approx\pm49$ mÅ (dash-dotted curve 2), respectively. One notices the very extended height ranges contributing to the velocity signals. By taking the linear combination

RFv(z) = [RFv,1(z) - 0.5*RFv,2(z)]/0.5 (1)

we obtain a substantially narrower height range contributing to the signal. The resulting response function possesses its maximum at 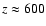$z\approx600$ km and a 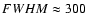$FWHM \approx 300$ km. The response functions are normalized to give

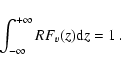\begin{displaymath}\int_{-\infty}^{+\infty}RF_v(z){\rm d}z = 1~. \end{displaymath} (2)

We assume that the signals are small and use the same combination as above to produce new velocity images. The velocities in Fig. 2 below were obtained in this way (while the intensity fluctuations there are the original ones). It turns out that the velocities are of the order of 1 km s-1 (see also Fig. 2). This exceeds slightly the linear regime required by the response functions. Thus, only preliminary estimates of the energy supplied to the chromosphere, calculated from the resulting new velocity signals, can be given (see below, Sect. 5). More accurate determinations must be deferred until we have performed thorough tests with the method. Ultimately, simulations of large amplitude waves and shocks and their expected signals in our apparatus must be performed with correct radiative transfer solutions.

4 Wavelet analysis

The overwhelming signal in the line center intensity and velocity fluctuations stems from the "long-period'' waves with periods around 200 s and from the 5 min p-modes. To extract the short-period waves, a wavelet analysis of the temporal fluctuations was performed with a code by Torrence & Compo (1998). This allows to determine at each time the occurring periods and appertaining amplitudes. We used Morlet wavelets with the mother wavelet

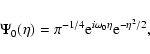\begin{displaymath}\Psi_0(\eta) = \pi^{-1/4}{\rm e}^{i\omega_0\eta}{\rm e}^{-\eta^2/2}, \end{displaymath} (3)

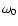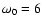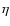where $\omega_0$ is the nondimensional frequency (here $\omega_0=6$) and $\eta$ is the nondimensional time parameter.

Figure 2 depicts in the upper panel the temporal velocity fluctuations, measured near line center, at one point in the fov. They are calculated as linear combinations of velocities at two bisector positions as described above. In the middle panel the appertaining wavelet power in the 50-100 s range is shown. The lower panel gives the velocity and the intensity fluctuations after high-pass filtering, i.e. eliminating signals with periods P>130 s.


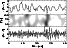 \begin{figure} \resizebox{\hsize}{!}{\includegraphics{Ei271_f2.eps}}\par \end{figure} Figure 2: Upper panel: velocity fluctuations at a single point in the fov measured near line center of Fe  I 5434 Å; middle: wavelet power in the 50-100 s period range; lower: velocity (solid) and relative intensity fluctuations (dotted, arbitrary scale) after high-pass filtering. Upward velocities are positive.
Open with DEXTER

We notice that short-period waves do occur, but with strongly varying amplitude. Shocks, i.e. saw-tooth variations of the velocity, cannot be seen, presumably because the time resolution is not sufficient. Apparently, the intensity fluctuations are only weakly correlated with the velocities, if at all. Naively, one would expect that upward propagating short-period waves have intensity increases (as proxies for temperature increases) at the same time as the upward velocities. This expectation may be misleading because the formation heights of the observed velocities can be much different from the formation heights of the intensity variations for two reasons: 1) we have extracted the velocities from a linear combination of measurements to narrow the height range of the signal forming layers as described above, while the intensity signals are the original values. 2) On grounds of formation of non-LTE lines, it must be expected that the intensities are formed deeper in the atmosphere than the velocities. 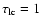The velocity signals from near line center are formed where the (line center) photons can leave the atmosphere, at $\tau_{\rm lc} = 1$. A much wider, essentially deeper atmospheric range contributes to the formation of intensity fluctuations. With this reasoning, one should expect the intensity fluctuations to occur earlier than the velocities, possibly as much as 30 s.

5 Results and conclusion


 \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{Ei271_f3.eps}}\par \end{figure} Figure 3: Two different granulation images of the time series overlayed with the velocity power summed over the 50-100 s period range. The velocity power presentations are from times 75 s later than the granulation images and only the short-period power above 30% of the maximum is shown. The axes are in arcsec.
Open with DEXTER

From the time sequence consisting of 100 steps we show in Fig. 3 two examples from two different times. Represented are the speckle reconstructed broadband granulation images and - overlayed as contours - the areas with velocity power above 30% of the maximum power integrated over periods 50 s <P<100 s. The velocity power is computed from the data obtained three steps later than the underlying granular picture. This 75 s shift corresponds approximately to the travel time from the low photosphere to the layers where the velocity signals are formed, i.e. at 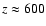$z\approx600$ km (see Fig. 1).

We summarize the results: short-period waves in the range of 50-100 s do exist in the solar atmosphere. (The lower limit of the periods is set by the observational cadence of 25 s.) We found them to be highly intermittent, i.e. they do not occur at any time and at any place. They appear preferentially above intergranular lanes.

Figure 4 gives the short-period power, within the 50-100 s period range and above 30% of the maximum power, vs. the granular intensity for the upper example of Fig. 3. It demonstrates the concentration of acoustic emission in intergranular spaces.


 \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{Ei271_f4.eps}}\par \end{figure} Figure 4: Power in the 50-100 s period range, above 30% of the maximum power, vs. the granular intensity fluctuations.
Open with DEXTER

We consider this non-uniform distribution with respect to the granular intensity pattern as the main evidence for short-period waves. The location above intergranular spaces is similar as found for waves with longer periods (200-300 s) e.g. by Hoekzema et al. (2002 and references therein). The intergranular spaces appear thus as the more dynamic part of the granular convection with more wave emission than the granules. This corresponds well with the interpretation by Nesis et al. (1997) that increased line widths on intergranules are caused by increased turbulence.

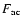We may give a lower limit of the acoustic flux $F_{\rm ac}$ into the chromosphere from the measured velocities in the 50-130 s period range via

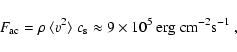\begin{displaymath}F_{\rm ac}=\rho~\langle v^2\rangle~c_{\rm s}\approx9\times10^5~{\rm erg}~{\rm cm}^{-2}{\rm s}^{-1}~, \end{displaymath} (4)

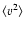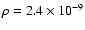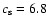where the average $\langle v^2\rangle$ is taken from the whole fov and from the whole time series. We have used the mass density $\rho=2.4\times10^{-9}$ g cm-3 and the sound speed $c_{\rm s}=6.8$ km s-1 at z=600 km from the Holweger-Müller model (1974). We estimate that the true acoustic flux is higher by a factor 3-4: the lower cutoff at 50 s period allows us to see only half of the expected short-period acoustic flux and the wave amplitudes will strongly be diminished by the large extent in height of the layers contributing to the velocity signal (see Introduction and Fig. 1). 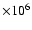The acoustic flux may thus be of the order of 3 $\times10^6$ erg cm-2  s-1, as needed for the chromospheric radiative losses.

Further studies will be concerned with the temporal evolution of the wave emitting structures, with the propagation through the atmosphere by investigating signals at different positions in the spectral line profile, and with estimates of the energy carried by these waves from modelling of wave trains and comparing the measurable signal with the observations. The role of magnetic fields in the heating process by waves is a further important issue which may now be studied observationally.

With future large solar telescopes, we will have more light, thus less noise, and achieve still higher resolution. This will also enable us to distinguish, via combinations of signals from various spectral features, similarly as above, between contributions from different atmospheric heights. New fast detectors will allow to decrease the length of the time step. One will then be able to study waves at the short end of the expected periods, in the range of 20-50 s.

Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft through grant KN 152/24 and by the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (Erwin-Schrödinger-Stipendium J1976-PHY). Wavelet software was provided by C. Torrence and G. Compo, and is available at URL: http://paos.colorado.edu/research/wavelets.

References

 

Copyright ESO 2002