A&A 395, 779-788 (2002)
DOI: 10.1051/0004-6361:20021222

Dark matter revealed

More evidence from faint-star proper-motions for a cool and warm component of the local dark matter in the Galaxy[*]

R. A. Méndez

European Southern Observatory, Casilla 19001, Santiago 19, Chile

Received 24 April 2002 / Accepted 12 July 2002

Abstract
We present new evidence, based on faint HST proper-motions, for a bi-modal kinematic population of old white dwarfs, representative of the Thick-Disk and Halo of our Galaxy. This evidence supports the idea of a massive Halo comprised of faint and old white dwarfs, along with an extant population of Thick-Disk white dwarfs. We show how most of the required dark matter in the solar vicinity can be accounted for by the remnants from these two components together.

Key words: stars: Population II - stars: white dwarfs - stars: kinematics - stars: distances - stars: luminosity function


1 Introduction

The claim by Oppenheimer et al. (2001) that they had found a significant population of Halo stars from a kinematic survey toward the South Galactic Pole opened up an interesting discussion regarding the nature of dark matter in the solar neighborhood. Their discovery seemed to corroborate earlier findings using very deep HST photometry that also pointed out to the existence of an as yet unobserved component to the Halo, identified as very cool and ancient white dwarfs (Méndez & Minniti 2000). However, several authors have indicated that Oppenheimer's sample could be also interpreted as the tail of a "warmer'' white dwarf component (in the sense of having shorter cooling ages and therefore higher surface temperatures), better ascribed to the intermediate Thick-Disk population of the Galaxy (see e.g., Reid et al. 2001; Reylé et al. 2001).

Obviously, disentangling the true nature of Oppenheimer's objects is important to understand their contribution to the dark matter problem in the Galaxy. In this paper we use HST data, deep photometry and proper-motions, to demonstrate that there is indeed a very important population of what appears to be Thick-Disk white dwarfs with a large mass density in the solar vicinity. These Thick-Disk objects could not have been identified before on the Hubble Deep Fields South and North due to their high Galactic latitude ( $\vert b\vert \ge 50^{\rm o}$), which prevented the appearance on these fields-of-view of an important population of these objects, characterized by a steep concentration toward the Galactic plane.

A fundamental discovery presented in this paper is that, regardless of whether the objects found are Thick-Disk or Halo white dwarfs, they together account for most of the dark matter in the solar neighborhood.

2 Description of the photometric and kinematic sample

Our data is based on a proper-motion membership study of the nearest Globular Cluster NGC 6397 by King et al. (1998, KACP98 thereafter). They used HST proper-motions to segregate cluster members from field stars in order to define, characterize, and study the faint end of the main sequence on the cluster, in a seminal paper using HST's WFPC accurate relative astrometry. Since their main science goal was to study the cluster, the field stars received comparatively little attention in that paper. In a previous paper they had also used the first-epoch exposures to study the cluster's white dwarf sequence (Cool et al. 1996).

More recently, Castellani et al. (2001) used King's data set to compare the star- and color-counts with Galactic models, constraining a number of large-scale Galactic parameters, but no attention was given to the kinematic information, as derived from the proper-motions.

In this paper,we use the combined photometric and astrometric information to characterize, specifically, the blue-faint objects found in the field population of the KACP98 sample. The main motivation is the recent discovery of spectroscopically-confirmed old white dwarfs indicative of a rather massive Galactic component comprised of these remnants, as previously suggested by the photometric study of the stellar content on the Hubble Deep Fields South and North by Méndez et al. (1996), and Méndez & Minniti (2000, MM00 henceforth).

Relative proper-motions for all field and cluster stars in a field close to the cluster NGC 6397 were derived by KACP98 using an earlier version of the methods described in Anderson & King (2000, and references therein). The final proper-motions for field stars are motions relative to a reference frame in which the cluster is at rest. Since the internal velocity dispersion for the cluster ($\le$5 km s-1 or 0.4 mas y-1, where mas stands for milli-arcsec) is smaller than the proper-motions detected, at the distance of the cluster, the width of the cluster proper-motion provides a good indication of the uncertainties in the derived relative motions.

The full sample was segregated by KACP98 into three sub-samples, based on a proper-motion and photometric selection criteria: NGC 6397 main-sequence stars (1386 stars), non-main sequence members (64 stars), and generic field stars (929 stars) on a 4.5 arcmin2field-of-view located at $(l,b)=(338.1^\circ, -12.0^\circ)$, encompassing the range $15 \le I \le 25$ and $0 \le V-I \le 4.0$. Here, we will concentrate our attention on the field stars of the KACP98 sample.

The uniqueness of this data set is the availability of proper-motions for a sample of very faint stars in a field with modest Galactic latitude, which then samples a significant path through the Thick-Disk of the Galaxy (Méndez & van Altena 1996). Another fortunate coincidence is that, unlike other studies being carried out with HST on different Globular clusters, which focus on the inner core of the clusters, this field was acquired toward the outer envelope of NGC 6397, some 4.5 arcmin from the cluster center, far from the central 20 arcsec dominated by the cluster's power-law cusp, and therefore minimizing the "contamination'' from cluster stars.

2.1 Photometric calibration

KACP98 published photometry in the F555W and F814W bands of the "flight-system'', as defined by Holtzman et al. (1995, Ho95). In order to compare our photometry with models, we need to convert this photometry to a standard system. However, because we only have magnitudes in two bands we can not apply the iterative method used by Méndez et al. (1996), or MM00, to derive calibrated photometry. Instead, in this paper, the calibration is done on a two-step process, by adjusting the zero-points of the flight-system (Eq. (1) below), then by applying the flight-to-ground transformations (Eq. (2) which yields Eq. (3) below), and then explicitly solving for a quadratic equation on the standard photometry.

Specifically, the mags given by KACP98 are defined by (Eq. (7) of Ho95):

 \begin{displaymath}WFPC2 = -2.5 \log \left(DN ~ {\rm s}^{-1}\right) + Z_{\rm FG} + 2.5 \log GR_i \end{displaymath} (1)

where WFPC2 is the flight magnitude, DN is the measured flux per unit time on the camera, $Z_{\rm FG}$ are the zero-points as given in Table 6 of Ho95, and GRi is the detector's gain (slightly different for all three chips, hence the subscript, in our case this is $\sim $7 e- ADU-1).

On the other hand, the flight-to-ground transformation is accomplished by Eq. (8) on Ho95, which we repeat here for completeness:

 
SMAG=$\displaystyle -2.5 \log (DN ~ {\rm s}^{-1}) + Z_{\rm FS} + 2.5 \log GR_i$
$\displaystyle + T_{1,\rm FS} \times SCOL + T_{2,\rm FS} \times SCOL^2$ (2)

where SMAG and SCOL are the standard-system magnitudes and colors respectively, T1 and T2 are linear and quadratic coefficients determined empirically which, along with the zero-points, are given in Table 7 of Ho95. Combining Eqs. (1) and (2) above thus yields:
 
SMAG=$\displaystyle WFPC2 + (Z_{\rm FS} - Z_{\rm FG}) + 2.5 \log GR_i$
$\displaystyle + T_{1,\rm FS} \times SCOL + T_{2,\rm FS} \times SCOL^2.$ (3)

In our case we have magnitudes in two passbands only, so that SMAG could be either V or I (the closest match to the F555W and F814Wpassbands, see Ho95). Using Eq. (3), and subtracting the terms for the I band from those of the V band, we end up with:
$\displaystyle V-I \cor SCOL$ = (F555W - F814W)  
    $\displaystyle + (T_{1,{\rm FS},F5Q5W} - T_{1,{\rm FS},F814W}) \times SCOL$  
    $\displaystyle + (T_{2,{\rm FS},F555W} - T_{2,{\rm FS},F814W}) \times SCOL^2$  

which is a quadratic equation on SCOL. Solving for SCOL yields thus the standard color, which, combined with Eq. (3) yields also the individual apparent magnitudes. There is no iteration necessary, and the standard magnitudes are uniquely determined (this is not the case if we have more than two bands, in this case the best solution is obtained by the iterative process, which best satisfies (in a minimum-residual sense) Eq. (2) simultaneously, for all passbands). The corrections from the instrumental to the standard system are, in any case, quite small. For example for F14W=15.87, and F555W-F814W=1.03, one finds that I=15.83 and V-I=1.043. Because these corrections are quite small, errors in the transformation (which can be up to 0.1 mag, Ho95) are minimal (i.e., we could have as well used the instrumental magnitudes). The uncertainty in the final calibrated magnitudes is estimated to be less than 0.05 mag (Cool et al. 1996).

  
2.2 Proper-motions

The proper-motions given by KACP98 are actually displacements on a 32-month baseline with respect to the mean displacement of the bona-fide cluster stars. These displacements were converted to actual relative proper-motions using the WFC plate-scale, and the baseline. This proper-motions were then converted to motions in RA and DEC by applying the position angle of the observations. As mentioned before, the motions are measured with respect to a system that has a zero mean motion for the cluster. In order to compute true absolute motions we need to correct for the proper-motion of the cluster, i.e.:

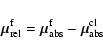
\begin{displaymath}\vec \mu^{\rm f}_{\rm rel} = \vec \mu^{\rm f}_{\rm abs} - \vec \mu^{\rm cl}_{\rm abs} \end{displaymath}

where $\vec \mu^{\rm f}_{\rm rel}$ are the observed relative motions for field stars with respect to the cluster, $\vec \mu^{\rm cl}_{\rm abs}$ is the absolute motion of the cluster, and $\vec \mu^{\rm f}_{\rm abs}$ is the absolute motion of the field stars. Fortunately, the motion for NGC 6397 is known, and it is given in the comprehensive compilation by Dinescu et al. (1999), which has $\mu_{\alpha_{\rm abs}}^{\rm cl} \cos \delta = 3.30 \pm 0.50$ mas y-1, and $\mu_{\delta_{\rm abs}}^{\rm cl} = -15.20 \pm 0.60$ mas y-1. We finally converted the motion to the Galactic system for an easier interpretation of the results. In this system, the mean absolute motion for the cluster would be $\mu_{l_{\rm abs}}^{\rm cl} = -11.46$ mas y-1, and $\mu_{b_{\rm abs}}^{\rm cl} = -10.52$ mas y-1.

3 Analysis of the sample

The vector point diagram (VPD) for the whole sample is shown in Fig. 1. Figure 1a includes all the data, whereas Fig. 1b shows a detail of the inner core of the proper-motion distribution. The pluses indicate the cluster members, whereas the small black dots indicate the non-members. In addition, several other interesting objects have been marked by the solid and open star symbols, as well as the filled square symbol. These objects will be discussed further below. This figure clearly shows that there is a good separation between cluster and field stars, although the boundary, specially in the interface between the two distributions, is somewhat blurry (fortunately this is of no consequence to our analysis).


  \begin{figure} \par\includegraphics[width=14cm]{ms2619f1.eps}\end{figure} Figure 1: Vector point diagram for the whole sample a), and for an enlargement b), showing the most interesting objects found in the field population. The outliers boundary (solid-line polygon) has been drawn by eye. The objects outside the polygon are marked by an open circle in Figs. 2 and 5. Pluses are for cluster stars, dots for field stars. Among these we have the extremely red objects (solid squares), and the blue faint population (filled-star symbol, six stars, and open star symbol, one star). Typical proper-motions uncertainties ($\sim $2 mas y-1) are marked by the large plus symbol in Fig. 1b.
Open with DEXTER

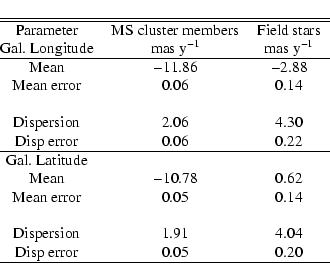
Table 1 indicates the main properties of the proper-motion distributions shown in Fig. 1, split into Main-sequence cluster members, and non-members. The method to compute these parameters, accounting for outliers, has been described in Méndez et al. (2000).


  
Table 1: Properties of the bulk proper-motions in Galactic longitude and latitude for NGC 6397 main-sequence cluster members and field stars.

\begin{displaymath}\begin{tabular}{@{}ccc} \hline \hline Parameter & MS cluster ... ...91 & 4.04 \\ Disp error & 0.05 & 0.20 \\ \hline \end{tabular}\end{displaymath}


From Table 1 we can estimate the accuracy of the proper-motions directly from the dispersion in the cluster members (which should actually have a very small dispersion if there were no observational errors). We obtain an overall uncertainty of about 2.0 mas y-1 in both coordinates. We also note that the mean motion for the cluster is what we would have expected from the absolute motion of the cluster (see Sect. 2.2), after correction from relative to absolute, and within the observational errors as given on the second row of the table above. While the above values are for the entire sample, there is a slight increase in proper-motion errors, as judged from the width of the cluster distribution, when going to fainter magnitudes, for example while the dispersion is 1.99 and 1.88 mas y-1 in $\mu_{\rm l}$ and $\mu_{\rm b}$respectively for $16 \le I < 22$, these values increase to 2.22 and 2.66 mas y-1 respectively for $22 \le I < 24$.

The VPD allows us to mark out some potentially interesting kinematic outliers for further consideration. We have drawn a more or less arbitrary section around the main bulk of the proper-motions for identification in the reduced proper-motion and color-magnitude diagrams (see below). There are, however, other interesting objects that fall within the outliers boundary, and these will be discussed later.

Recently, Oppenheimer et al. (2001) found a large population of white dwarfs with kinematics representative of the Galactic Halo. These objects were pre-selected from a photographic proper-motion survey using UK Schmidt plates. They used the so-called "reduced-proper-motion'' (RPM) parameter H, used for the first time by Luyten many years ago. The interesting property of this parameter is that while it is directly observable once we have proper-motions and photometry, it is mostly an indicator of luminosity for distinct stellar populations. This parameter is defined as:

\begin{displaymath}H_{\rm m} = m + 5 \log \mu + 5 = M + 5 \log V_{\rm tan} - 5 \log K \end{displaymath}

where m and $\mu$ are the apparent magnitude and (absolute) proper-motion, and M and $V_{\rm tan}$ are the absolute magnitude (in the same band) and total tangential velocity for the star, while K is a constant.

As it can be seen from its definition, different stellar populations (with characteristic luminosities and kinematics) will occupy a different locus on, e.g., an H vs. color diagram, hence H can be used to distinguish distinct populations from its position on the RPM diagram.

Figure 2 shows the HV vs. V-I diagram for our HST sample. The same objects found on the VPD have been marked on the RPM. Indeed, the RPM diagram allows us to clearly distinguish some objects that did not stand-out in the VPD (e.g., the red stars or some of the faint blue objects), and vice-versa (the general kinematic outliers). The properties of the most interesting objects found (i.e., the extremely red stars, and the faint blue stars) are given in Table 2.


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms2619f2.eps}}\end{figure} Figure 2: Reduced proper-motion diagram for the field stars toward NGC 6397. Same symbols as for Fig. 1. Solid and dotted lines are the theoretical locus for 0.8 $M_{\odot }$ white dwarfs of different cooling ages, from the models by Chabrier et al. (2000) for a tangential velocity of 60 and 120 km s-1 respectively. The six solid stars match well the theoretical expectation for a population typical of the Thick-Disk, whereas there is one object that seems to have Halo-like kinematics. Size of the errors is marked by the plus sign.
Open with DEXTER

As it can be seen in Fig. 2, there is a group of six very red stars with 21 < I < 24 and colors V-I > 3.6. These objects are interesting because, with their faint magnitudes and red-colors, they could be representatives of a very faint and nearby sample of low-luminosity late-type dwarfs or even brown-dwarfs. There is also a group of six faint blue stars ( $22 \le I < 25$, $V-I \le 1.0$) with intermediate kinematic, and one fainter blue object with even more extreme kinematics (labeled as "Extreme'' in Table 2). These faint blue objects, as will be argued below, are part of two distinct populations, belonging to the Thick-Disk of the Galaxy and to the Halo respectively, and represent the late-stages in the evolution of the precursors of these stars when the Galaxy was formed. The properties of all these objects (i.e., the extremely red stars, and the faint blue stars) are given in Table 2.


  
Table 2: Properties of the red and faint blue stars in the field population.

\begin{displaymath}\begin{tabular}{@{}lccccc} \hline \hline Objects & $I$ & $V-I... ...e & 24.03 & 1.03 & $-$20.07 &$-$24.13 \\ \hline \end{tabular}\end{displaymath}


An inspection of Table 2 indicates that the red stars are actually not very nearby: if they belong to the disk population (as predicted from all Galactic models, see e.g. Castellani et al. 2001), then their kinematics (assuming a tangential velocity of 40 km s-1, typical of this population) indicates distances larger than 600 pc, and absolute magnitudes brighter than $M_I \sim 12.0$, characteristic of M5 to M6-type dwarfs (Gizis 1997; Leggett 1992, her Fig. 1). Their colors also indicate similar distances and luminosities. For example, adopting the color-absolute magnitude relationship given by Gizis (2000, his Table 4 and Fig. 11) or Leggett (1992, her Fig. 15), we have for $V-I \sim 4.0$a typical $M_V \sim 16.5$ or $M_I \sim 12.5$. We conclude that none of these red stars are very nearby nor particularly faint. On the other hand these objects can not be extragalactic, because they exhibit motions that are significantly different from zero, within our estimated 2 mas y-1 error budget (see Table 1).

The object with the most extreme-kinematic (the star far to the left on the VPD, see Fig. 1) has a V-I=2.85 and I=19.56. The absolute magnitude for this color is predicted in the range $12.0 \le M_V \le 13.5$, depending on metallicity (Gizis 1997). Thus, for a total proper-motion of 74.43 mas y-1 one derives a tangential velocity on excess of 200 km s-1, i.e. more than five times the expected tangential velocity of a typical Disk star. This object is thus quite interesting for follow-up spectroscopy as a potential Halo subdwarf (the same is true for the other kinematic outliers, 16 objects in total, located outside the polygon in Fig. 1). Alternatively, if we insist on this object having a tangential velocity of 40 km s-1, one derives a distance of about 120 pc, leading thus to an absolute magnitude of $M_V \sim 17.0$, i.e., more than three magnitudes fainter than normal Disk stars of the same color, an unlikely solution.

The sample of faint blue objects represents an interesting population that deserves further attention, in view of the recent discovery by Oppenheimer et al. (2001) mentioned before. Oppenheimer's study was limited to much brighter magnitudes (with $R \le 19.8$) than our study ( $20 \le I \le 25$, see Fig. 5), but they have spectral confirmation. Our objects are much fainter, and it is unlikely that we will have any confirmatory spectroscopy on them until the large next-generation telescopes of 30 m or more become available. Table 2 shows that all these objects have motions that differ by more than 2.5 times from both the mean motion of the field or the cluster, even considering the large width of the field's proper-motion dispersion of more than 4 mas s-1 given in Table 1.

Even though we can not hope to have spectroscopy on these objects yet, we can use the RPM diagram, along with theoretical models to, at least, compare their position on this diagram with what we would expect for ancient white dwarfs. In Fig. 2 we have superimposed the latest theoretical cooling sequences for old white dwarfs from Chabrier et al. (2000). The continuous line is for a population with a mean tangential speed of 60 km s-1, characteristic of the Thick-Disk (TD model), whereas the dashed line is for a speed of 120 km s-1, typical of the Halo (Halo model). As can be seen the brightest blue stars fall very close to the expected location for old white dwarfs from the Thick-Disk. The faintest point however could, in principle, be fit by either model. However, we argue that this object is better fit by the Halo model rather than the TD model. Indeed, if this was a Thick-Disk star, then the corresponding (cooling) age (i.e., since it left the main-sequence) from the theoretical sequence (almost 14 Gyr), would imply that the Thick-Disk is quite older than what most models predict. It will also imply an absolute magnitude for this object of $M_V \sim 17.6$, thus becoming the faintest degenerate objects ever found (as an example ESO 439-26, the faintest spectroscopically confirmed WD known has $M_V \sim 17.4$, Ruiz et al. 1995). Instead, if this object is placed on the Halo model, then its derived cooling age is 11 Gyr, fully consistent with the age for the Galactic Halo, and with a reasonable luminosity of $M_V \sim 15.8$. We must emphasize here that the derived tangential velocities for these objects are used only as an indication of the population to which they belong, but these velocities are not used to determine distances directly (see Sect. 4).

3.1 Comparison to local and simulated samples


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms2619f3.eps}}\end{figure} Figure 3: Reduced proper-motion diagram for local samples of white dwarfs selected according to different criteria. Small dots are from the Legget et al. (1998) sample with $\mu > 0.8$ arcsec y-1. Plus and solid-square symbols are for the sample from Ruiz & Bergeron (2001) with $\mu > 0.2$ arcsec y-1 and $\mu \le 0.2$ arcsec y-1respectively. Open and solid stars is our sample (same as in Fig. 2), and triangles are the low-luminosty white dwarfs ESO 439-26 and CE 51 with extreme kinematics, as described in the text. Solid and dashed lines are the same as in Fig. 2.
Open with DEXTER

Before we can proceed with any certainty on the probable identification of the faint blue objects as belonging to the stellar Thick-Disk or Halo components of our Galaxy as described in the previous paragraph, we need to compare this sample of putative white dwarfs with the kinematics of local samples of (Disk) white dwarfs. A sample with well defined selection criteria, which has been used for a determination of the (Disk) white dwarf luminosty function is provided by Legget et al. (1998, LRB98 thereafter). Figure 3 shows the locus in the RPM diagram of the LRB stars in comparison with our sample. At first it would seem as if there is no difference between the two samples, thus implying that we are actually looking at normal Disk stars. However, there is a big difference in the two samples: the LRB sample has a strong kinematic bias in favor of stars with quite large proper-motion ($\mu > 0.8$ arcsec y-1), and thus the mean tangential velocity of the LRB89 sample is not representative of the Disk population of white dwarfs as a whole, but rather it overestimates it. This then displaces the mean locus of these objects on the RPM to larger values of HV, making them appear similar to that of our sample (we must note that our sample has not been pre-selected according to a large proper-motion). The mean tangential velocity for the LRB8 sample is 113 km s-1 with a dispersion of 73 km s-1. It would of course be interesting to compare directly our sample with that of Disk white dwarfs that have not been selected according to kinematics. Such a sample does exist (Holberg et al. 2002, HOS01 thereafter), but unfortunately there are no V-I colors available for these stars which would allow us to make a direct comparison with our objects. From HOS01's (volume-limited) complete sample of white dwarfs closer than 13 pc one finds that their mean tangential velocity is only $45 \pm 5$ (m.e.) km s-1 (this is actually based on 43 out of their 49 stars closer than 13 pc due to the lack of proper-motions for a few of them). We note here that volume-limited samples of main-sequence stars from Hipparcos give values close to 40 km s-1 (Dehnen & Binney 1998), i.e., similar to those found for Holberg's sample (actually one would expect white dwarfs to have larger motions since they are older than the disk, and much of the velocity scattering is generated in the first Gyr (Wielen 1977). Indeed, numerical simulations using Reylé's model (private communication, model described in Reylé et al. 2001), for the same Galactic location as our field, and with the same magnitude, color, and error constraints as those of our sample give a $<V_{\rm tan}>~ = 45.8 \pm 1.9$ (m.e.) km s-1, in excellent agreement with the results from HOS01 sample of nearby Disk white dwarfs. From this analysis we see that the mean tangential velocity for our possible Thick-Disk white dwarfs is more than $7 \sigma$ away from the mean of the local (simulated) sample. A further indication of the effect of kinematic selection is provided by the sample of Ruiz & Bergeron (2001, RB01 thereafter). They have published a sample of new nearby spectroscopically confirmed white dwarfs, selected from their own proper-motion survey. For their sample with $\mu > 0.2$ arcsec y-1 one finds $<V_{\rm tan}>~ = 60 \pm 8$ (m.e.) km s-1, while for $\mu \le 0.2$ arcsec y-1 one finds $<V_{\rm tan}>~ = 43 \pm 12$ (m.e.) km s-1 (this last sample is incomplete in proper-motion, so this value is probably an upper limit).

While comparing samples of putative disk white dwarfs to those presented in this paper, one also has to keep in mind that it is not unlikely that a few of the "local'' samples may also have representatives from the Thick-Disk and Halo (Fig. 3). This is the case, for example of ESO439-26 (with MI = 16.29 and $V_{\rm tan} = 78$ km s-1, Ruiz et al. 1995) or CE51 (with MI = 16.47 and $V_{\rm tan} = 68$ km s-1, RB01). The mean tangential velocity estimates derived from these local samples will be biased toward higher values due to these kinematic interlopers. Unfortunately, spectroscopy does not help here because all white dwarfs, irrespective of the metallicity of the parent population, look alike.

We can finally compare the locus of our sample on the RPM diagram to that predicted by Galactic models. Here we use the predictions from the model by Reylé et al. (2001, and private communication) based on the Besançon model of stellar populations in the Milky Way, which has been (succesfully) used to identify the kinematics of Oppenheimer's sample with that of Thick-Disk stars (see also Reid et al. 2001). Model simulations where run for the same Galactic location as that of our sample, with the same magnitude, color and proper-motion limits, as well as the same observational errors in all these quantities. The field-of-view of the simulation was larger than that of our sample in order to have enough (simulated) stars in the comparison. Figure 4 shows the locus for our stars, and those predicted by the model. As it is obvious from this figure, the location of our stars is totally in agreement with the predictions from the model for Thick-Disk stars. Disk stars on the other hand exhibit values with smaller tangential velocity (smaller HV), as it has been discussed before. Of course all this evidence is, in a way, indirect (even if, as dicussed before, we had spectroscopy), and one could still insist that these stars are actually members of the Disk population. But, in this case, how can one explain that they obey such a distint kinematic behavior in the RPM diagram in comparison with the normal Disk stars? This obviously points to these objects as beeing part of a separate higher-velocity component. We thus conclude that, based on the evidence we have, these few blue faint stars are very likely true representatives of the Thick-Disk of our Galaxy. The implications for this will be discussed in the following section.


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms2619f4.eps}}\end{figure} Figure 4: Reduced proper-motion diagram for simulated samples of white dwarfs selected according to the very same criteria as those of our sample. The simulatiosn are based on the Besançon Galactic model of stellar population synthesis (Celine Reylé, private communication). Small dots are (simulated) Disk white dwarfs, plus symbols are (simulated) Thick-Disk stars, and star symbols are the objects found in this study. As it can been seen, our objects trace well the predicted locus for Thick-Disk stars as inferred from the model.
Open with DEXTER

A final point is important when comparing the results from this paper with those found by MM00 for the HDF-S&N. Figure 5 shows the calibrated color-magnitude diagram for our sample. As it can be seen, the faint blue objects are much less well defined, becoming mixed with the rest of the distribution, and making it difficult to distinguish between different kinematic components, a point to which we will come back in the next Section. The outliers on the VPD diagram (open circles) also become well mixed with the rest of the distribution, and only the red objects stand-out by virtue of their color-selection criteria.


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{ms2619f5.eps}}\end{figure} Figure 5: Color-magnitude diagram for the whole sample of field stars, adopting the same symbols as for Figs. 1 and 2. The separation between distinct kinematic groups becomes fuzzy.
Open with DEXTER

4 Discussion

It is interesting to "weight'' (literally) the consequences of the presence of two kinematic components on the faint blue population described above. First of all, is the discovery of one possible truly Halo white dwarf (the open star in Figs. 1 and 2) consistent with previous findings? As it was shown by MM00, the total mass contributed by a Halo-like population is given by:

 
$\displaystyle M(r_{\max})$$\textstyle \cor$$\displaystyle <M_{\rm WD}> \times~ N_{\rm WD}$
=$\displaystyle 8.46 \times 10^{-8} \Omega \times \rho_{\odot} \int_{0}^{r_{\max}} \left( \frac{R_{\odot}}{R} \right)^3 r^2 ~ {\rm d}r$ (4)

where $\rho_{\odot}$ is the local mass density of this component, $\Omega$ is the field-of-view in arcmin2, R is the galactocentric distance (in pc), $R_{\odot}$ is the Solar Galactocentric distance (assumed to be 8500 pc), r is the heliocentric distance (pc), and $M(r_{\max})$ is the mass (in $M_{\odot }$) contributed by this component out to a Heliocentric distance $r_{\max}$ (also in pc), while $N_{\rm WD}$is the number of observed white dwarfs of mean mass $<M_{\rm WD}>$. If we compute the ratio of $M(d_{\max})$ between, e.g., the Hubble Deep fields South and this field close to NGC 6397, then we find that, to the same depth in apparent magnitude, the expected number of Halo white dwarfs would scale as $N_{\rm WD}(N6397) \sim 1.11 \times N_{\rm WD}(HDF-S)$, taken into account the different fields-of-view of the two samples. Now, down to $I \sim 25$ we see from Fig. 3 on MM00 that we have two possible Halo white dwarfs on HDF-S, whereas we have found one based on its kinematic properties on the field of NGC 6397. No doubt, it is small numbers, but at least the two studies (MM00 based only on differential star counts, the present one on kinematics) are consistent with each other. Note also that the HDF images go about 5 mag fainter than the ones on the present study. We conclude thus that there is consistency between these results.

In our study we seem to find a population of stars somewhat brighter than those detected by MM00, with kinematics indicative of the Thick-Disk. However, there is no indication for these objects on the HDF-S&N sample by MM00, which seems to be inconsistent with the findings of the present paper. Here we should point out that there was no kinematic information for the sample used by MM00 and, thus, it was not possible to kinematically distinguish Thick-Disk from Halo-like objects. Therefore, it is in principle possible that some of the blue objects on MM00 could actually be Thick-Disk stars. However, it turns out that the expected density of these latter objects is much smaller in the HDF-S&N because of their spatial location in the Galaxy. If we adopt a density law characteristic of the Thick-Disk of the form:

 \begin{displaymath}\rho(\vec r) = \rho_{\odot} \exp^{-\vert z-z_{\odot}\vert/h_z} \exp^{-(R_{\rm pl}-R_{\odot})/h_{R}} \end{displaymath} (5)

where $\rho(\vec r)$ is the stellar densities at Galactic position $\vec r$ whereas  $\rho_{\odot}$ is the density in the solar neighborhood, hz and hR are the scale height and length of this component respectively, z is the distance from the Galactic plane, $z_{\odot} \sim 7$ (pc) is the Sun displacement with respect to the Galactic plane, and $R_{\rm pl}$ is the distance from the Galactic center, as measured on the plane of the Galaxy, we find, using the analogous of Eq. (4) for this density law, that the ratio between the expected number of objects on the HDF-S&N and the field under consideration is only 0.29 and 0.16 for HDF-S and HDF-N respectively. So, if we have 6 Thick-Disk stars on the N6397 field, we should only expect to see 1 or 2 such objects on HDF-S and 1 or none on HDF-N, for a reasonable choice of hz (760 pc) and hR(2500 pc) in the above equation. It is interesting to notice that, above $V \sim 25$ (i.e. the same magnitude range as our stars, see Fig. 5), there is indeed only one blue object on HDF-N and two blue objects on the HDF-S (see Fig. 3 on MM00). These objects have magnitudes and colors similar to those of our kinematically selected Thick-Disk sample in NGC 6397, and in agreement with the above numbers. However, lacking kinematics for the HDF sample, we can not advance much more in this analysis (see below).

4.1 Density estimates

We can use the six stars identified as members of the Thick-Disk to compute the stellar and mass density associated to this component. For this purpose we use the generalized $1/V_{\rm max}$ method proposed by Tinney et al. (1993). This method extends the classical $1/V_{\rm max}$ to the case of non-(spatially) uniform samples, such as those found here. The method defines a (generalized) density-weighted volume $V_{\rm gen}$ as:

 \begin{displaymath}V_{\rm gen} = \int_{Vol} \frac {\rho(\vec r)}{\rho_{\odot}} ~ {\rm d}Vol \end{displaymath} (6)

where $\rho(\vec r)$ and $\rho_{\odot}$ are the stellar densities at position $\vec r$ and in the solar neighborhood respectively, and the integral is carried out over the volume available to the sample, given the observational constraints.

Then, the total stellar density is given, just as in the classical method, by:

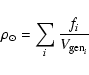
\begin{displaymath}\rho_{\odot} = \sum_{i} \frac{f_i}{V_{{\rm gen}_i}} \end{displaymath}

where the factors fi account for the incompleteness of the sample ($f_i \ge 1$), and the sum is carried over the individual data points. Meanwhile, the standard deviation on the derived overall density is given by:

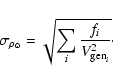
\begin{displaymath}\sigma_{\rho_{\odot}} = \sqrt { \sum_{i} \frac{f_i}{V_{{\rm gen}_i}^2} }\cdot \end{displaymath}

The volume over which the integral in Eq. (6) is to be extended is determined by the minimum and maximum distances ($r_{\min}$ and $r_{\max}$ respectively) over which any star can contribute to the sample (see, e.g., Méndez & Ruiz 2001).

If we have a sample with a lower proper-motion limit $\mu_{\rm l}$ and a faint apparent magnitude $m_{\rm f}$, $r_{\max}$ is given by:

\begin{displaymath}r_{\max} = \min \left[p^{-1} (\mu/\mu_{\rm l}) ; p^{-1} 10^{0.2(m_{\rm f}-m)}\right] \end{displaymath}

where p is the parallax, $\mu$ is the proper-motion and m the apparent magnitude.

Similarly, if the sample is only complete to an upper proper-motion limit $\mu_{\rm u}$ and a bright apparent magnitude $m_{\rm b}$, the minimum distance for inclusion would be:

\begin{displaymath}r_{\min} = \max \left[p^{-1} (\mu/\mu_{\rm u}) ; p^{-1} 10^{0.2(m_{\rm b}-m)}\right]. \end{displaymath}

For our sample, the value for $\mu_{\rm l}$ is determined by the observational errors. As mentioned in Sect. 2.2, our observational errors are on the order of 2 mas y-1. Therefore, one could consider to have a firm detection for, say, three times the error, or 6 mas y-1, which we will adopt as our value for $\mu_{\rm l}$. Objects with motions larger than that would qualify within our selection criteria. Similarly, the fastest-moving object in the sample (see Fig. 1) has a total proper-motion of nearly 75 mas y-1, value thus adopted for $\mu_{\rm u}$. It is very likely that the detection limit is larger than this, and it is determined by the epoch difference used to obtain the proper motions and the confusion limit. However, we have made tests and found that, even if one where to adopt $r_{\min} = 0$, our results will change by less than 0.1%. The apparent magnitude limits were chosen as $m_{\rm b} = 15$ (see Fig. 5), and $m_{\rm f} = 25$ (see Table 1 on KACP98).

For each of the six putative Thick-Disk stars identified in Table 2, we computed their absolute magnitudes in the Ipass-band from their observed V-I color, by interpolation on Table 3 of Chabrier et al. (2000). The I and MI were then used to obtain photometric parallaxes. We must emphasize here that the kinematics of the sample is not used at all to determine photometric distances or absolute magnitudes, rather the kinematics is used as an indication of belonging to a given population, which then allows us to adopt the correspondig density laws (e.g., Eq. (5)) for calculating the effective sampling volume (Eq. (6)). Therefore our results are not dependant on the exact value adopted for $V_{\rm tan}$ on either the Thick-Disk or the Halo.

With the above values, the limiting distances $r_{\rm min}$ and $r_{\max}$ were computed, and the integral on Eq. (6) was evaluated by direct integration, using the adopted Thick-Disk density law, Eq. (5). In this case, Eq. (6) can be written as:

 
$\displaystyle V_{\rm gen}$=$\displaystyle 8.46 \times 10^{-8} \Omega \int_{r_{\min}}^{r_{\max}} \exp^{-\vert z-z_{\odot}\vert/h_z} ~ \exp^{-(R_{\rm pl}-R_{\odot})/h_R} r^2 ~ {\rm d}r$
=$\displaystyle V_{\max} \times \Re.$ (7)

Where $V_{\max}$ is the classical maximum allowed volume for a magnitude and proper-motion selected sample (see, e.g., Méndez & Ruiz 2001), and $\Re $ is a (dimensionless) correction factor which accounts for the non-homogeneous distribution of stars in space (we shall see that, in any case, this correction factor is relatively small, close to one, for our sample). Both terms are given, respectively, by:

 \begin{displaymath}V_{\rm max} = 8.46 \times 10^{-8} \times \Omega \times \left( \frac{r_{\max}^3-r_{\min}^3}{3} \right) \end{displaymath} (8)

and

 \begin{displaymath}\Re = \frac{\int_{r_{\min}}^{r_{\max}} \exp^{-\vert z-z_{\odo... ...\rm d}r}{\left( \frac{r_{\max}^3-r_{\min}^3}{3} \right) }\cdot \end{displaymath} (9)

The density law in Eq. (7) or Eq. (9) has two parameters, namely hz and hR, which introduce some ambiguity in the computation of the integral. We have thus computed the integral (and the corresponding correction factor $\Re $) for several combinations of parameters in the range $760 < h_z < 1300 ~ {\rm pc}$ and $2500 < h_R < 3500 ~{\rm pc}$, and have chosen the extreme values as representative of the 'modeling errors' involved in the computation. Finally, the factors fi have been computed as the reciprocal of the completeness fraction as inferred from the artificial-star experiments reported by KACP98 (their Table 1). Table 3 summarizes all the adopted and derived values for the six Thick-Disk and one Halo stars from Table 2. The cooling age on the second column of Table 3 is the age (since becoming a white dwarf) inferred from the same table on Chabrier et al. (2000) used for determining the absolute magnitudes.

Because of the Galactic location of this field, it is easy to show that, with small errors, the ( $\mu_{\rm l},\mu_{\rm b}$) proper-motions are projected almost directly into the V (along Galactic rotation) and W(towards the North Galactic Pole) velocity components respectively. These velocities, computed using the distance given in the fourth column of Table 3, are indicated, for reference, in the seventh and eigth columns of the same Table. Finally, in the last column we give the approximate tangential velocity (neglecting the small contribution from the U component of the velocity towards the Galactic center). As it can be seen from the Table, the mean tangential velocity is close to 65 km s-1 for the Thick-Disk stars, and more than 100 km s-1 for the one possible Halo white dwarf, in agreement with the value found from Fig. 2, and larger than the value expected for normal nearby Disk white dwarfs, as already discussed in Sect. 3.1.


  
Table 3: Photometric distances and derived parameters for the faint blue stars in Table 2.

\begin{displaymath}\begin{tabular}{@{}lcccccccc} \hline \hline Objects & Age & $... ...702 & 294 & 1097 & $-$67 & $-$80 & 104\\ \hline \end{tabular}\end{displaymath}



  
Table 4: Adopted incompleteness fraction and derived values for $\Re $.

\begin{displaymath}\begin{tabular}{@{}lccc} \hline \hline Objects & $f$ & $\Re_{... ...ine Extreme & 1.153 & 1.3206 & 1.3212 \\ \hline \end{tabular}\end{displaymath}


Equation (9) has thus been integrated using the parameters specified in Table 3. The adopted incompleteness factors and the extreme values derived for the integral in $\Re $ are given in Table 4. $\Re_{\min}$ was derived adopting $h_z =760 ~ {\rm pc}$ and $h_R = 3500 ~ {\rm pc}$, whereas $\Re_{\max}$ was derived using $h_z =1300 ~ {\rm pc}$ and $h_R = 2500 ~ {\rm pc}$. In the case of the Halo star, instead of using a double-exponential density law, we have adopted an R-3 law similar to that used in MM00, which leads to Eq. (4) above (to be more precise $V_{\rm gen}$ is given by Eq. (4) divided by the local stellar density $\rho_{\odot}$, while the definition of $\Re $ is similar to that adopted for a double exponential. In this case however, the free parameter in the density law is the axial ratio of the (flattened) Halo, which was varied in the interval 0.8 (oblate spheroid, $\Re_{\min}$) to 1.0 (round spheroid, $\Re_{\max}$)).

If ( $\rho_{\odot_{\min}}$, $\sigma_{\rho_{\odot_{\min}}}$) and ( $\rho_{\odot_{\max}}$, $\sigma_{\rho_{\odot_{\max}}}$) are the densities and its error derived from $\Re_{\min}$ and $\Re_{\max}$ respectively, then the final value for the total density and its error was calculated from:

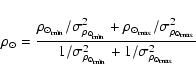
\begin{displaymath}\rho_{\odot} = \frac{\rho_{\odot_{\min}}/\sigma_{\rho_{\odot_... ...ma_{\rho_{\odot_{\min}}}^2 + 1/\sigma_{\rho_{\odot_{\max}}}^2} \end{displaymath}

and,

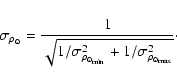
\begin{displaymath}\sigma_{\rho_{\odot}} = \frac{1} {\sqrt {1/\sigma_{\rho_{\odot_{\min}}}^2 + 1/\sigma_{\rho_{\odot_{\max}}}^2} }\cdot \end{displaymath}

With these equations, and the values given in Table 4 we obtain, for the Thick-Disk white dwarf stars a value of:
$\displaystyle \rho_{{\odot}_{\rm WDTD}}$=$\displaystyle (13.82 \pm 4.39) \times 10^{-3} ~ \rm stars/pc^3$
=$\displaystyle (11.06 \pm 3.51) \times 10^{-3} ~ M_{\odot}/\rm pc^3.$  

For the one star that probably belongs to the Halo, the same computation above yields:
$\displaystyle \rho_{{\odot}_{\rm WDH}}$=$\displaystyle (5.31 \pm 3.50) \times 10^{-3} ~ \rm stars/pc^3$
=$\displaystyle (4.25 \pm 2.80) \times 10^{-3} ~ M_{\odot}/\rm pc^3.$  

Obviously, we have much larger errors in this latter case due to the use of only one object. In both cases we have assumed a mean mass per white dwarf of 0.8 $M_{\odot }$.

Because the correction factors $\Re $ given in Table 4 are all close to one, one might as well have computed the stellar densities using the classical $1/V_{\rm max}$method, without correcting for the variation of stellar density as a function of distance away from the Sun. In this case, one does not need to adopt any density law whatsoever, and the method is completely model independent. It is thus interesting to compare the previous values with the ones that one would have derived in this case. Dropping the correction factor $\Re $ in Eq. (7), one finds:

$\displaystyle \rho_{{\odot}_{\rm WDTD}}$=$\displaystyle (19.58 \pm 4.39) \times 10^{-3} ~ \rm stars/pc^3$
=$\displaystyle (15.66 \pm 3.51) \times 10^{-3} ~ M_{\odot}/\rm pc^3.$  

And for the Halo star:
$\displaystyle \rho_{{\odot}_{\rm WDH}}$=$\displaystyle (7.02 \pm 6.54) \times 10^{-3} ~ \rm stars/pc^3$
=$\displaystyle (5.62 \pm 5.23) \times 10^{-3} ~ M_{\odot}/\rm pc^3.$  

As we see, the densities are slightly overestimated, but also the errors are larger. Still, we obtain basically the same results using either method. This is important, because it implies that, regardless of the details of the (model) density law adopted, the stellar and mass densities are indeed quite large. The implications of these results are discussed in the next section.

5 Conclusions

The stellar and mass densities derived above imply that the Thick-Disk white dwarf stars, a population unaccounted for in the Hubble Deep Fields South and North due to their high Galactic latitude, contributes to about 85% of the missing mass in the solar neighborhood, whose density in the solar neighborhood is estimated to be $\rho_{{\odot}_{\rm DM}} \sim 1.26 \times 10^{-2} ~ M_{\odot}/\rm pc^3$.

Additionally, the value derived for only one possibly Halo star, albeit having a large error, is similar to the value derived by MM00 from the larger sample of Halo white dwarfs found in the HDF-S&N. They found a density of $\rho_{{\odot}_{\rm WDH}} = 4.64 \times 10^{-3} ~ M_{\odot}/\rm pc^3$. Their value, however, has to be taken with caution because the lack of kinematic information prevented a clear separation of the populations (compare Figs. 2 and 5 above). It has been mentioned already that one might expect one or two Thick-Disk stars on the HDF-S and one or none in the HDF-N. If these objects were inadvertently identified by MM00 as Halo stars, then the estimated density for these objects on the Halo would have been too large. It is interesting to point out that on HDF-S there are two stars on the WD tracks that are quite a bit brighter than the rest of the blue-faint group. In the HDF-N there seems to be a grouping of faint WDs, and a brighter one, which could also be ascribed to the Thick-Disk (see Fig. 3 on MM00). In any case, proper-motions for both the HDF-S&N sample would help settle this uncertainty.

If we combine the present results for Thick-Disk stars, with the earlier results from MM00 for Halo stars, the overall density on WD stars for both populations seems to be able to account for the whole of the (local) missing mass in the Galaxy. The existence of a massive component of Thick-Disk evolved white dwarfs has been proposed recently by Gates & Gyuk (2001) to help explain some of the (many) difficulties with a massive Halo of ancient stars. However, our results suggest that, in addition to this Thick-Disk component, there would also be a quite massive Halo of remnant stars. Even though their local densities are similar, the mass locked in each population is quite different, in account of their different stellar density functions (double exponential vs. power-law). The simple integration of these density functions over the whole Galaxy lead to masses of:

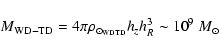
\begin{displaymath}M_{\rm WD-TD} = 4 \pi \rho_{{\odot}_{\rm WDTD}} h_z h_R^3 \sim 10^{9} ~ M_{\odot} \end{displaymath}

and,

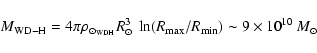
\begin{displaymath}M_{\rm WD-H} = 4 \pi \rho_{{\odot}_{\rm WDH}} R_{\odot}^3 ~ \ln (R_{\max}/R_{\min}) \sim 9 \times 10^{10} ~ M_{\odot} \end{displaymath}

for the Thick-Disk and Halo components respectively. $R_{\max} \sim 20$ kpc and $R_{\min} \sim 1$ kpc in the last equation are the overall extension of the Halo and the Halo core-radius respectively.

The total mass in these components is consistent with the mass required to produce the MACHO events, as indicated by Gates & Gyuk (2001), and is also not inconsistent with the total mass estimates for the Galaxy out to a distance of 20 kpc. We also note that with the small scale height of the Thick-Disk population ( $h_z \leq 1.5$ kpc), their contribution to the optical depth of microlensing events would be quite small, and thus the primary sources of the MACHO events would still be primordially the Halo white dwarfs.

The possibility of a white dwarf dominated (dark) halo has been criticized from many fronts (see e.g. Richer 1999; Gates & Gyuk 2001). Among the most important criticisms is that the precursor of these stars would have produced metals at a rate greater than observed (Gibson & Mould 1997) or that Galaxy halos at high redshift would be brighter than observed due to the the white dwarf precursors (Charlot & Silk 1995). While these are no doubt important issues, Chabrier (1999) and more recently Fontaine et al. (2001, see also Fontaine's C.S. Beals Lecture at http://www.astro.ubc.ca/WD_workshop/talks/index.html) have shown that many of these points can either be overcome, or are doubtful criticisms of this scenario. One example is the chemical evolution problem: the yield of a zero-metallicity stars is largely uknown, nor has there been much modelling of the structure of these stars (e.g., a zero metallicity star never undergoes a helium flash, which must have an effect on the the yield of metals in the PNe phase).

Even if the problems described above with this scenario persist, as pointed out by Lynden-Bell & Tout (2001) in the first "Russell lecture'' of the new millennium, they could be avoided if the objects found are "pristine'' white dwarfs, objects that never underwent nuclear reactions nor followed the "normal'' path of stellar evolution. These objects (with masses in the range $ 0.2 \leq M/M_{\odot} \leq 1.1$) could have formed gradually and very slowly by accretion onto planetary-sized precursor bodies in low-density regions such as cooling flows and galaxy halos. By radiating their energy before collapsing, these bodies would grow in mass resting on the zero-point energy of confined electrons following the uncertainty principle, and never getting a temperature high enough to start nuclear burning. The difficulty with this scenario is that, although theoretically possible, preliminary results suggest that the required accretion rates are too slow to allow the formation of these objects in less than a Hubble time, which keeps the puzzle regarding the origin of these objects still open.

As we have seen before, the assignement of the bulk of the faint blue stars found here to the Thick-Disk is actually irrelevant in the sense that one could as well have used the classical $1/V_{\rm max}$method to derive space densities, without regard to the origin or association to a given stellar population of these stars. This is an important issue in the context of whether some of the stars found by Oppenheimer et al. (2001) are either Thick-Disk or Halo stars. The controversy in this regard seems to come from using white dwarf cooling ages while ignoring the main sequence lifetimes of the progenitors, which for many of these stars will be substantial. Indeed, Oppenheimer's sample seems to come from a population of stars formed in a single burst of stars formation between 11 and 14 Gyr ago, as indicated by the luminosity function of these stars, which is a much more direct indication of the age of the population than the cooling ages (see discussion on http://research.amnh.org/users/bro). Another indication that perhaps most of Oppenheimer's stars actually do belong to the Halo is provided by the recent work of Koopmans & Blanford (2001) that have used a maximum-likelihood analysis to show that these stars are consistent with a kinematically distinct flattend Halo population at the more than 99% confidence level.

Albeit our objects are faint, it would be quite interesting to acquire U-band photometry with HST. In this case, true white dwarfs will stand out from other objects in a UBV diagram. Additionally, at least the two brightest blue objects in Fig. 5 are whithin the capabilities of current 8-m class telescopes for an spectroscopic follow-up. This is an interesting possibility that deserves further work.

Acknowledgements
I thank Ivan King, Jay Anderson and Adrienne Cool for making their data available, and for helping with several questions regarding the nature of the HST observations on NGC 6397. Linda Schmidtobreick, Fernando Comeron, Ivan King, Dante Minniti, Fernando Selman and William F. van Altena have provided valuable input to improve the first draft - I appreciate their help. I want to also thank Celine Reylé for producing the numerical simulations described in the text using the Besançon model of stellar population synthesis (www.obs-besancon.fr/fesg/modele_ang.html). Finally, the referee Dr. B. R. Oppenheimer suggested a number of modifications to the original manuscript that have greatly improved the final version, I am most grateful to him for reading the paper with an open yet rigorous mind.

References

 
Copyright ESO 2002