A&A 395, 557-561 (2002)
DOI: 10.1051/0004-6361:20021278

On the orbital period of the cataclysmic variable V 592 Herculis

R. E. Mennickent 1,[*] - C. Tappert 1 - R. Gallardo 1 - H. W. Duerbeck 2 - T. Augusteijn 3


1 - Universidad de Concepción, Departamento de Física, Casilla 160-C, Concepción, Chile
2 - University of Brussels (VUB), Pleinlaan 2, 1050 Brussels, Belgium
3 - Isaac Newton Group of Telescopes, Apartado 321, 38700 Cruz de La Palma, Canary Islands, Spain

Received 9 July 2002 / Accepted 30 August 2002

Abstract
We present a spectroscopic study of the long-recurrence-time dwarf nova V 592 Herculis based on observations obtained during its August 1998 superoutburst. From the analysis of the radial velocities of the H$\alpha $ emission line we find a most likely orbital period of $85.5 \pm 0.4$ min, but the $91.2 \pm 0.6$ min alias cannot be completely discarded. Both periods imply a very small period excess and supports the brown-dwarf like nature of the secondary star.

Key words: stars: individual: V 592 Her - stars: novae, cataclysmic variables - stars: fundamental parameters - stars: evolution, binaries: general


1 Introduction

Cataclysmic variable stars (CVs) are interacting binaries consisting of a white dwarf accreting matter from a red dwarf donor. In non-magnetic CVs, the transferred gas spirals onto the white dwarf, forming an accretion disk. Due to the partial hydrogen ionization, the disk is thermally unstable, jumping in temperature when a certain critical density is reached. This hot state is accompanied by increased viscosity and a release of luminous energy when the material rapidly drops onto the white dwarf. This event is called an outburst. In some CVs, quasi-periodic humps are seen in the light curve during extended outbursts; they are called superhumps and the outbursts are called superoutbursts. According to current theories, these peculiar CVs, the so-called SU UMa stars, should contain low mass secondaries; some of them could have been eroded after a long time of mass transfer. It is even possible that many of them harbour secondary stars with masses less than the minimum mass needed to sustain hydrogen fusion in their cores (e.g. Howell et al. 2001). Such objects should be found among ultra-short orbital period systems ($P_{\rm o}$ $\sim$ 80 min) with very low mass transfer rates ( $\dot{M} \sim 10^{15}$ g/s), and should be characterized by rare and large-amplitude outbursts. This subgroup of the SU UMa stars is usually called the WZ Sge stars. Until now, a relatively small number of these objects have been studied in detail (Kato et al.  2001), in part due to the fact that their low luminosities make them hard to study in quiescence, even with large aperture telescopes. In this paper we make a contribution to the understanding of these rare objects presenting the first spectroscopic study of V 592 Herculis during superoutburst.

2 Observations and reduction

The third historical outburst of V 592 Her was detected at visual magnitude 12.0 by the Finnish observer Timo Kinnunen on 1998 August 26.835 UT. The outburst was confirmed on August 27.181 UT by Lance Shaw in California (see also Waagen 1998). Observations reported to VSNET (http://www.kusastro.kyoto-u.ac.jp/vsnet/) indicate that the maximum occurred near the day of the detection. We observed V 592 Her both photometrically and spectroscopically. The photometry, obtained 10 days later than the spectroscopy, was already given in Duerbeck & Mennickent (1998), who confirmed the presence of superhumps, and thus the SU UMa star nature of V 592 Her, and constrained the superhump period to SHP $_{1} = 0.06391 \pm 0.00020$ days or SHP $_{2} = 0.06007\pm 0.00020$ days.

We obtained 40 optical spectra of V 592 Herculis with the EMMI spectrograph mounted at the ESO 3.5-m NTT at La Silla Observatory, during 1998 August 29 and 30. 3 spectra were obtained with grating #13, providing a wavelength range of 4010-9420 Å, and 37 spectra were obtained with grating #8, yielding a wavelength range of 4475-7040 Å. We used slit widths of 5 and 1 arcseconds, which yielded spectral resolutions of 5.5 and 2.5 Å, respectively. The standard star LTT 7379 was observed with a 5-arcsecond slit to flux-calibrate the spectra. He-Ar lamp exposures were taken after typically each hour of science exposures. We reduced the images using standard IRAF procedures[*], correcting for bias and flat field. In order to wavelength-calibrate the spectra, we used calibration functions obtained by fitting $\approx$30 He-Ar lines with a typical standard deviation of 0.4 Å  (18 km s-1 at H$\alpha $). An observing log is given in Table 1. The superoutburst light curve, as constructed from the VSNET data archive, is shown in Fig. 1, indicating that our spectroscopic observations were obtained only a few days after the maximum.

  \begin{figure} \par\includegraphics[angle=0,width=8.8cm,clip]{h3824f1.eps} \end{figure} Figure 1: The light curve of the 1998 superoutburst. Data are taken from the VSNET archive. The dates of our observations are indicated by vertical dashed lines.
Open with DEXTER


 
Table 1: Journal of observations. Grating, resolution, exposure time and number of spectra are given. The zero point for Heliocentric Julian Day is HJD0 = 2 451 000.
Grating Res. (Å) exptime (s) HJD N
Gr13 5.5 300 54.4826-4942 3
Gr8 2.5 300 54.4996-5888 18
Gr8 2.5 300 55.4884-5851 19


3 Results

3.1 Spectrum description and variability

The averaged spectrum for grating 13 is shown in the upper panel of Fig. 2. It reveals a steep blue continuum with hydrogen and helium absorption lines. Spectrophotometric magnitude determination of this spectrum yields V = 14.4 and V-R = 0.8. The continuum can be approximated by a function $F_{\lambda} \propto \lambda^{-\alpha}$, with $\alpha = 3.50 \pm 0.01$. This spectral energy distribution is bluer than the expected for an infinitely large steady state disc, i.e. $F_{\lambda}$ $\propto$ $\lambda^{-7/3}$ (Lynden-Bell 1969). It also differs from the observed UV spectra of most dwarf novae during outburst, viz.  $\alpha \approx 2$(Verbunt 1987). A careful examination of the spectrum reveals the presence of emission cores inside the H$\alpha $ and He I absorption lines (Fig. 2, two lower panels).

We measured equivalent widths between two points of the continuum separated by $\pm$2000 (1250) km s-1 from the H$\alpha $ (He I 5875) rest wavelength. In the case of H$\beta $, in order to avoid the blending with He I 4920, we made the measurements between continuum points located at -3500 km s-1 and +2500 km s-1 from the rest wavelength. The averaged equivalent widths and their standard deviations were $1.6 \pm 0.3$, $5.2 \pm 0.5$ and $0.91 \pm 0.15$ Å, for H$\alpha $, H$\beta $ and He 5875 and they did not change during the two nights. The H$\delta$ and H$\gamma$ absorption lines seen in the grating 13 spectra had equivalent widths of 8 and 7 Å, respectively. They were measured as in H$\beta $ but with the upper limit wavelength of 3500 km s-1. In the average grating 8 spectrum we also detected weak lines of He I 4474, He II 4686, He I 4920, He I 5016/5048 and He I 6678 (Fig. 2 middle and bottom panel). The He I 5016/5048 blend shows a central emission at 5027 Å, while He I 4920 and He I 5875 show emission cores at $\lambda$ 4922 and 5874 Å. He II 4686 also shows an emission core at $\lambda$ 4687 Å. The strength of the emission component, relative to their absorption component, is much stronger in the He II line than in the H and He I lines. The FWHM for the double peak H$\alpha $emission core seen in the averaged grating 8 spectrum is 580 km s-1 and the peak separation 270 km s-1.

  \begin{figure} \par\includegraphics[angle=0,width=8.8cm,clip]{h3824f2.eps} \end{figure} Figure 2: Upper graph: flux-calibrated low resolution spectra of V 592 Her. Middle graph: higher resolution normalized spectrum around the H$\beta $ line. Lower graph: same as middle graph but around the H$\alpha $ line.
Open with DEXTER

3.2 Radial velocities and the orbital period

We measured radial velocities for several features in the spectra. We applied the cross correlation technique to the absorption wings and emission lines separately yielding very noise velocity curves. After several trials, we realized that the least noisy radial velocities were obtained by measuring the position of the H$\alpha $ emission core interactively with the cursor in the splot IRAF routine. For that, we used the k key and also choose by eye the position where the intensity was maximum. Both methods yielded similar results. We searched for periodic variations in these velocities using both the Scargle and the AOV algorithm (Scargle 1982; Schwarzenberg-Czerny 1989) implemented in MIDAS. The results in Fig. 3 show possible periods at $P_{1} = 0.0633 \pm 0.0004$ days (91.2 min), $P_{2} =0.0594 \pm 0.0003$ days (85.5 min) and $P_{3} = 0.0561 \pm 0.0004$ days (80.8 min). The errors correspond to the HWHM of the peaks. In order to discriminate between the possible frequencies and to derive the true period, we applied the method described in Mennickent & Tappert (2001). In this method, sets of radial velocity curves are generated with the same noise characteristics and time distribution as the original dataset. These datasets were analyzed with the idea that, after many simulations, the true period emerges like the most recurrent period in the trial periodograms. We fitted the data with a sine function corresponding to the peak frequency (this was done for the three candidate frequencies). Then a Monte Carlo simulation was applied in such a way that a random value from an interval consisting of $\pm$3 times the sigma of the sine fit was added to each data point on the fit function. The Scargle algorithm was applied to the resulting data set and the highest peak was registered. The histogram for these values is shown in Fig. 4. The peak at 0.0594 days shows the narrowest and highest peak, while the other periods have a broader distribution. The total number of maxima is 327, 338 and 335 for periods P1, P2 and P3 respectively. From the above we conclude that P2 is slightly, but not conclusively favoured. However, there is another line of evidence favouring P2. Duerbeck & Mennickent (1998) gave two possible orbital periods, based on the modern calibration of the Schoembs & Stolz relation, namely, P1( ${\it SHP}_{1}$) = 0.06239 $\pm$ 0.00020 and P2( ${\it SHP}_{2}$) = 0.05898 $\pm$0.00020 days. This seems to exclude P3. In addition, the differences between observed and predicted periods are P1 - P1( ${\it SHP}_{1}$) = 0.0009 $\pm$ 0.0004 days and P2 - P2( ${\it SHP}_{2}$) = 0.0004 $\pm$ 0.0004 days. According to Mennickent et al.  (1999), these differences rarely exceed 0.00075 days, so P2 is also favoured in this case. The near coincidence between the superhump and orbital period arises the question if the radial velocity is being modulated by rotation around the center of mass of the binary or, alternatively, by the superhump period. To our knowledge, there is no evidence for "superhump-modulated'' radial velocities in previously published work, so here and thereafter we will assume that the period found really reflects the binary orbital period.

The radial velocities of the H$\alpha $ emission core, folded with the P2 period, are shown in Fig. 4. The ephemeris for the red to blue passing is:

T0 = 2 451 054.4969(12) + 0.0594(3) E. (1)

The figure also shows the best sine fit, with amplitude $179 \pm 11$ km s-1 and zero point $-192 \pm 15$ km s-1. We obtained $161 \pm 39$ km s-1and $217 \pm 22$ km s-1for the amplitudes of first and second night, respectively, and $-165 \pm 28$ km s-1 and $-195 \pm 17$ km s-1 for the corresponding zero points, so we do not find evidence for a $\gamma$ shift like those observed in other dwarf novae during outburst (e.g. in VY Aqr, Augusteijn 1994 derived a shift of 155 km s-1, in TU Men Stolz & Schoembs 1984 derived a full amplitude of $\sim$560 km s-1, in Z Cha Hoeny et al. 1988 derived $\sim$160 km s-1 and in TY PsA, Warner et al.  1989 derived $\sim$600 km s-1). Variations in the system velocity have been explained with the "precessing eccentric disc'' model of Whitehurst (1998) for superhumps. In this model $\gamma$ is expected to change with the precession period of the disc, which is equal to the beat period between the superhump and the orbital period. For V 592 Her the expected precession period of the disc is $\sim$5 or $\sim$7 days. Therefore, the non-detection of a significant $\gamma$ shift during two consecutive nights in V 592 Her could be the result of our very short baseline.

The application of the "double Gaussian'' convolution mask algorithm (Schneider & Young 1980; Shafter 1983) to the radial velocities of the inverted H$\beta $ absorption profile resulted in a large half-amplitude radial velocity near the line center (about $110 \pm 30$ km s-1 between 250 and 1200 km s-1, probably reflecting contamination by unseen emission) and a lower half-amplitude of $46 \pm 25$ km s-1 in the line wings (between 1200-2500 km s-1 from the line center, probably indicating different gas dynamics for the emission and absorption disc regions). The application of period searching algorithms to these datasets yields results which seem to exclude P3 but are not conclusive regarding the other two possible periods. It is generally known for dwarf novae (see, e.g. Warner 1995) that, especially during outburst, the radial velocity half-amplitude does not reflect the white dwarf motion, likely due to the presence of complex gas flow patterns in the accretion disk which are still not well understood. For this reason we do not intend here to constraint the stellar masses using the binary mass function based on the radial velocity half amplitude.

  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{h3824f3.ps} \end{figure} Figure 3: Scargle (top) and AOV (bottom) periodograms of the H$\alpha $radial velocity data. Possible frequencies are labeled.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{h3824f4.ps} \end{figure} Figure 4: Histogram of the maximum-peak frequency.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3824f5.eps} \end{figure} Figure 5: The H$\alpha $ radial velocities folded with the orbital period. Data of the first and the second night are indicated by squares and circles, respectively. The best sine fit is also shown.
Open with DEXTER

4 Discussion

According to Morales-Rueda & Marsh (2002), the presence of He II 4686 emission during high states could be the result of disc irradiation or emission by spiral shocks structures. Therefore, the detection of He II 4686 in V 592 Her could indicate also the presence of spiral shocks in this short orbital period system. Supporting this view is the fact that Baba et al. (2002) imaged the WZ Sge disk during its 2001 superoutburst using the He II 4686 line finding arc-like structures. Higher quality data than currently available are necessary to confirm this suspicion in the case of V 592 Herculis.

The period excess is defined as:

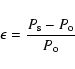\begin{displaymath}\epsilon = \frac{P_{\rm s}-P_{\rm o}}{P_{\rm o}} \end{displaymath} (2)

where $P_{\rm o}$ is the orbital period of the binary and $P_{\rm s}$is the superhump period. The period excess is an important observational parameter in the theory of disk tidal instability, since it can be related to the ratio between the stellar masses q = M2/M1:

\begin{displaymath}1/\epsilon = [0.37q/(1+q)^{1/2}]^{-1}(R_{\rm disk}/0.46a)^{-2.3}-1 \end{displaymath} (3)

where a is the binary separation (Patterson 2001). Here we use Patterson's approximation:

\begin{displaymath}\epsilon = 0.216(\pm0.018)q. \end{displaymath} (4)

Using the orbital period $P_{2} = 85.5 \pm 0.4$ min, along with the superhump period given by Duerbeck & Mennickent (1998), we calculate a period excess of $0.011 \pm 0.006$, one of the shorter among SU UMa stars (Patterson 2001). This period excess implies a mass ratio $q = 0.05 \pm 0.03$. If the white dwarf has a typical mass of $0.7~M_\odot$, we find $M_{2} = 0.035 \pm 0.021~M_{\odot}$. Comparing this value with the Kumar limit for Population I stars ($\approx$ $0.07~M_\odot$, Kumar 1963) we find that the secondary could be a brown dwarf like object. Only if the white dwarf is massive ($\ga$$1~M_\odot$) is the mass ratio consistent with a non-degenerate hydrogen-burning star. On the other hand, if P1 (91.2 min) is the right period, we obtain $\epsilon = 0.0096 \pm 0.0070$ and $q = 0.04 \pm 0.03$. The above shows that our result of a possible brown-dwarf like secondary in V 592 Her is robust against a misidentification of the orbital period. In addition, this finding in agreement with the result of van Teeseling et al.  (1999), who arrived at this conclusion using considerations about magnitudes at outburst and quiescence only.

5 Conclusions

Acknowledgements
We thanks the referee, Dr. Paula Szkody, for useful comments that helped to improve a first version of this paper. This work was supported by Grant Fondecyt 1000324 and DI UdeC 202.011.030-1.0. We are grateful to the VSNET observers and the administrators of the VSNET database for making their data available through the WEB.

References

 

Copyright ESO 2002