Abstract
A sample of Ap and Bp stars have been investigated with respect to their surface magnetic field using synthetic spectrum fitting. The advantage of this technique is the simplicity in determining the surface field strength and the possibility to apply it to objects whose spectrum does not display resolved Zeeman components. We show the usefulness of the method by demonstrations on stellar spectra with resolved Zeeman components, where the results have been compared with values based on measurements of the Zeeman splitting for the magnetically sensitive Fe II $\lambda$ 6149 line. The objects HD 192678 and HD 165474 have been observed over their rotational period to investigate magnetic field variations. The analysis is then extended to objects where no resolved structure is observed. The rapidly rotating stars HD 22316 and HD 10783 are used as examples where this method is useful to achieve a value of the surface field. The relative intensification of the Fe II $\lambda\lambda$ 6147, 6149 lines is investigated in an attempt to understand its relation to the surface magnetic field strength for the stars HD 22316 and HD 10783.

Numerous investigations of stellar magnetic fields have been performed since Babcock (1947) detected the Zeeman effect in the spectrum of 78 Vir. Most of these studies have measured the mean longitudinal field (MLF), which is the averaged magnetic field over the stellar surface in the line-of-sight. An analysis of this kind uses the fact that transitions between magnetic sublevels are differently polarized. Therefore, stellar spectra of opposite circular polarity are used to calculate the Stokes V parameter.

Investigations have also made use of the Stokes I profile to measure the field affecting the atoms in the stellar photosphere (Huchra 1972; Preston 1969a,b; Preston & Wolff 1970; Mathys 1990) and uses the Zeeman splitting of magnetically sensitive spectral lines to measure the surface field, also referred to as the mean field modulus (MFM). This method is restricted to objects with resolved Zeeman components and is not useful for objects whose spectral lines are predominantly broadened by stellar rotation.

The equivalent width, $W_\lambda$ , has been used as a magnetic field indicator for stars with weak field and no observable Zeeman structure (Mathys & Lanz 1992; Lanz & Mathys 1993; Hubrig et al. 1999). Stenflo & Lindegren (1977) developed a method to derive the interdependence of the magnetic field and the equivalent width based on solar observations, a method later refined (Mathys & Lanz 1992) to applications in hotter stars without resolved Zeeman structure. Takeda (1991) investigated the sensitivity of the relative intensification to changes in iron abundance, aspect angle and microturbulence. Unfortunately, the method is highly sensitive to line blending and the method in converting the equivalent width into a magnetic field strength is still not fully developed.

We present an approach to measure magnetic fields, useful for spectra without resolved Zeeman structure, built on synthetic spectrum fitting. Each spectral line shows a characteristic Zeeman pattern when influenced by a magnetic field and through analysis of the line profile information regarding the stellar magnetic field can be obtained. To investigate spectral line profiles, the observed spectrum is compared with a synthetic spectrum including complete Zeeman patterns. The method requires calculated Zeeman patterns and knowledge of the other broadening effects influencing the analyzed spectral line. The first is simplified by assuming pure LS-coupling and a weak magnetic field to avoid partial Paschen-Back effect, which restricts the investigation to objects with surface fields less than 7-8 kG. The measured magnetic field is integrated over the stellar surface and is treated as perpendicular to the line-of-sight. Our approach is capable of investigating line profiles in the absence of resolved Zeeman components and can be used for objects with a weak surface field even if the rotation is the dominating broadening mechanism. Our investigation of the stellar magnetic field using synthetic spectrum fitting does not consider the polarization state of the radiation and the influence on the radiative transfer by the polarized radiation is not included in our synthetic spectrum code.

Table 1: Spectral lines used in the magnetic field analysis.
Ion $\lambda_{\rm air} ({\rm\AA})$ $g_{J_{\rm l}}$ $g_{J_{\rm u}}$ log gf^b

Cr II 6147.154 1.200 1.376 -2.843

Fe II^a 6147.736 1.200 2.700 -2.721

6149.248 0 2.700 -2.724

**Table 1:** Spectral lines used in the magnetic field analysis.
Ion	$\lambda_{\rm air} ({\rm\AA})$	$g_{J_{\rm l}}$	$g_{J_{\rm u}}$	log gf^b
Cr II	6147.154	1.200	1.376	-2.843
Fe II^a	6147.736	1.200	2.700	-2.721
	6149.248	0	2.700	-2.724

Table 2: Observed data.
Object Sp. type V HJD (2 451 700+) S/N^a

HD 2453 A2p 6.91 74.701 173

HD 10783 A2p 6.55 68.736 180

74.680 223

75.682 193

HD 22316 B9p 6.28 65.738 182

66.607 212

67.732 158

HD 165474 A8p 7.50 64.472 193

65.480 190

66.466 176

67.464 175

68.493^b 83^c

68.519 177

69.413 170

70.413 178

70.499^b 139^c

71.426 192

72.419 178

73.421 209

HD 192678 A4p 7.40 64.437 162

65.453 169

66.439 166

67.437 172

68.440 114

68.466^b 105^c

69.466 132

67.464^b 177^c

70.461 139

71.451 164

72.444 151

73.445 151

HD 200311 B9p 7.68 67.490 162

**Table 2:** Observed data.
Object	Sp. type	V	HJD (2 451 700+)	S/N^a
HD 2453	A2p	6.91	74.701	173
HD 10783	A2p	6.55	68.736	180
			74.680	223
			75.682	193
HD 22316	B9p	6.28	65.738	182
			66.607	212
			67.732	158
HD 165474	A8p	7.50	64.472	193
			65.480	190
			66.466	176
			67.464	175
			68.493^b	83^c
			68.519	177
			69.413	170
			70.413	178
			70.499^b	139^c
			71.426	192
			72.419	178
			73.421	209
HD 192678	A4p	7.40	64.437	162
			65.453	169
			66.439	166
			67.437	172
			68.440	114
			68.466^b	105^c
			69.466	132
			67.464^b	177^c
			70.461	139
			71.451	164
			72.444	151
			73.445	151
HD 200311	B9p	7.68	67.490	162

^a: Estimated S/N for the spectral order including Fe II $\lambda\lambda$ 6147, 6149.
^b: Additional observation for less magnetically sensitive lines.
^c: Estimated S/N for the spectral order including Fe II $\lambda\lambda$ 4491, 4508.

2 Observations

All data used in this analysis were obtained with the 2.5 m Nordic Optical Telescope (NOT) at La Palma, Canary Islands, using the SOviet FINish high resolution echelle spectrograph (SOFIN) at a resolving power of $R=\frac{\lambda}{\Delta \lambda}$ =75 000. The data set consists of a sequence of observations for each of two primary targets, HD 192678 and HD 165474 obtained on 10 consecutive nights. In addition, single-phase observations of two stars (HD 2453 and HD 200311) with expected long rotational periods were made with the purpose of testing the magnetic field measurement technique. Two objects, HD 22316 and HD 10783, do not show resolved Zeeman structure and were each observed at three phases. The spectral coverage between 5600 - 7000 Å is not complete and is centered on a spectral region including the magnetically sensitive lines Fe II $\lambda\lambda$ 6147, 6149 and Cr II $\lambda$ 6147 (Table 1). Additional observations for some of the targets were made at shorter wavelengths to cover the less magnetic sensitive lines Fe II $\lambda\lambda$ 4508, 4491 Å. The complete data set is presented in Table 2.

Table 3: Objects used in this analysis with photometric indices, atmospheric parameters and determined value of the surface field.
Object Sp. type V (b-y) m₁ c₁ $\beta$ $T_{\rm eff}$ log g $v~\sin{i}$ $<H>_{\rm av}^{a}$ $<H>_{\rm av}^{b}$

(K) (km s $^{\rm -1}$ ) (kG) (kG)

HD 2453 A2p 6.91 -0.022 0.244 0.887 2.854 9 200 4.1 1.5 3.7 3.7

HD 10783 A2p 6.55 -0.060 0.205 0.864 2.819 11 000 4.1 17 5.0

HD 22316 B9p 6.29 -0.072 0.178 0.614 2.778 12 000 4.2 17 8.5

HD 165474 A8p 7.45 0.167 0.227 0.832 2.856 8 000 4.4 5.0 6.6 6.5

HD 192678 A4p 7.34 -0.043 0.240 0.994 2.872 9 200 4.0 4.8 4.6 4.7

HD 200311 B9p 7.68 -0.044 0.137 0.470 2.718 13 900 4.0 3.5 7.7 8.7

**Table 3:** Objects used in this analysis with photometric indices, atmospheric parameters and determined value of the surface field.
Object	Sp. type	V	(b-y)	m₁	c₁	$\beta$	$T_{\rm eff}$	log g	$v~\sin{i}$	$<H>_{\rm av}^{a}$	$<H>_{\rm av}^{b}$
							(K)		(km s $^{\rm -1}$ )	(kG)	(kG)
HD 2453	A2p	6.91	-0.022	0.244	0.887	2.854	9 200	4.1	1.5	3.7	3.7
HD 10783	A2p	6.55	-0.060	0.205	0.864	2.819	11 000	4.1	17	5.0
HD 22316	B9p	6.29	-0.072	0.178	0.614	2.778	12 000	4.2	17	8.5
HD 165474	A8p	7.45	0.167	0.227	0.832	2.856	8 000	4.4	5.0	6.6	6.5
HD 192678	A4p	7.34	-0.043	0.240	0.994	2.872	9 200	4.0	4.8	4.6	4.7
HD 200311	B9p	7.68	-0.044	0.137	0.470	2.718	13 900	4.0	3.5	7.7	8.7

3 Atmospheric models

The determination of the atmospheric parameters has been accomplished through application of the uvbybeta photometric calibration program uvbybeta developed by Moon & Dworetsky (1985) and later improved by Napiwotzki et al. (1993) based on photometric indices from Hauck & Mermilliod (1980). Stellar atmospheric models have been computed using the LTE approximation with the ATLAS9 code (Kurucz 1993) under the assumption of no turbulent velocity. The rotational velocity, $v~\sin{i}$ , is problematic for magnetic stars unless magnetically unaffected spectral lines can be studied. Stars with resolved magnetic patterns offer the possibility to investigate individual Zeeman components whose line profile is unaffected by the field. A magnetic field shifts the Zeeman components mutually but the line profile for each Zeeman component is preserved. If the field is separating the components enough to make their interdependence negligible, an unaffected profile is offered for determinations of $v~\sin{i}$ . Objects without resolved Zeeman components rely on less magnetically sensitive spectral lines, such as Fe II $\lambda\lambda$ 4491, 4508, with g_J< 0.5 for both the upper and lower level, to place an upper limit on $v~\sin{i}$ . For the included objects with resolved Zeeman structure $v~\sin{i}$ was estimated using iron lines, especially the less magnetically sensitive Fe II $\lambda\lambda$ 4491, 4508 lines, and fine tuned with individual Zeeman component of the Fe II $\lambda$ 6149 line. The rotational velocity for HD 10783 is based on spectrum fitting using a sample of Fe II lines in the blue spectral region while for HD 22316 $v~\sin{i}$ was adopted from Nielsen & Wahlgren (2000). Table 3 presents the photometric indices from Hauck & Mermilliod (1980) for the analyzed objects along with atmospheric parameters determined from photometry and the $v~\sin{i}$ and surface field determined from synthetic spectrum fitting.

4 Analysis

This investigation into stellar magnetic fields is performed by synthetic spectrum fitting using the program SYNTHE (Kurucz 1993) with the Zeeman structure incorporated into the atomic line input. The Zeeman structure is calculated under the assumptions of pure LS-coupling, a weak field (<7-8 kG) and an angle of 90 $^\circ$ between the line-of-sight and the field, which results in an equal visibility of all Zeeman components. Changing the angle between the line-of-sight and the magnetic axis alters the line profile and can give information regarding the field orientation. However, our observed spectra do not show any evidence of "missing'' intensity for the linearly polarized $\pi$ -components, which would be the case when the field is nonperpendicular to the line-of-sight. Our investigation is limited to using a few spectral lines chosen for their atomic characteristics. Spectral lines with a simple and distinct Zeeman pattern and unaffected by other broadening effects such as hyperfine structure (hfs) and isotopic shift (IS) are favorable candidates. A disturbance by an external field causes an energy shift comparable in size with a corresponding shift caused by a net nuclear spin (hfs), whereas the atomic structure becomes difficult to interpret even for a weak external magnetic field. It is advisable to use spectral lines only affected by one of these in a spectral analysis. Different isotopes each generate their own spectrum, which with knowledge of the isotopic composition can be added. Iron and, to some extent chromium, have less significant hfs and IS and are therefore good elements for magnetic field investigations. In this analysis the use of the Fe II $\lambda$ $\lambda$ 6147, 6149 lines is complemented by the Cr II $\lambda$ 6147 line. Fe II $\lambda\lambda$ 6147, 6149 are from the same multiplet ([74], Moore 1972) and are created under similar physical conditions. The Fe II $\lambda$ 6149 transition originates from a magnetically unaffected lower level and since the upper level has J=0.5, this transition will display a double peak structure when resolved Zeeman components are observable. The drawback using these spectral lines is their nearness in energy for the upper levels which might give a slight level mixing due to the magnetic field. A magnetic field of 8 kG give a Zeeman splitting of 1 cm $^{\rm -1}$ for these transition's upper level (( $^{\rm 5}$ D)4p z $^{\rm 4}$ P $_{\rm 1/2}$ ), compared to the fine structure splitting between the lower levels of 4 cm $^{\rm -1}$ . This provides an estimate of the magnetic field, under which the Paschen-Back effect is negligible. IS and hfs were not included in this analysis.

This investigation includes stars with and without resolved Zeeman components. The objects with resolved Zeeman components show the capabilities of the spectrum fitting technique with respect to line profile analysis. The surface magnetic field is derived with the spectrum fitting technique and also calculated based on measurements of the wavelength separation between the Zeeman components of the Fe II $\lambda$ 6149 line (Mathys 1990; Mathys et al. 1997). The wavelength separation is derived by fitting Gaussians to the two resolved Zeeman components. For those spectra where a blend is visible in the blue wing of the short wavelength Zeeman component, an extra Gaussian is included to determine how this component may affect the field measurement.

Stars without resolved Zeeman structure can be investigated from equivalent width measurements, as for example with the Fe II lines at 6147 and 6149 Å. Mathys & Lanz investigated magnetic fields in sharp-lined stars without resolved Zeeman components by computing the relative intensification, defined as

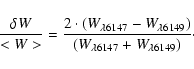$\begin{displaymath}\nonumber \frac{\delta W}{<W>}=\frac{2\cdot(W_{\rm\lambda6147... ...m\lambda6149})}{(W_{\rm\lambda6147}+W_{\rm\lambda6149})}\cdot \end{displaymath}$

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{H3792F1.ps}\end{figure}$	Figure 1: $W_\lambda$ as function of the magnetic field strength. Plus signs: Fe II $\lambda$ 6149. Diamonds: Fe II $\lambda$ 6147. Calculations based on a stellar atmosphere model where $T_{\rm eff}=11~000$ K, $\log~g=4.1$ , $\xi _{\rm t}=0$ km s $^{\rm -1}$ , ${\rm [Fe/H]}=0.5$ and $v~\sin~i = 20$ km s $^{\rm -1}$ .
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{H3792F2.ps} \end{figure}$	Figure 2: The relative intensification for the choice of atmospheric parameters: $T_{\rm eff}=11~000$ K, $\log~g=4.1$ , $\xi _{\rm t}=0$ km s $^{\rm -1}$ and ${\rm [Fe/H]}=0.5$ . Plus signs: investigation based on $v~\sin~i = 0$ . Diamonds: investigation based on $v~\sin~i = 20$ km s $^{\rm -1}$ .
Open with DEXTER

Based on this quotient they empirically identified a linear relationship between the relative intensification and the magnetic field strength for fields between 3 and 5 kG.

We have measured $W_{\rm\lambda}$ for the Fe II $\lambda\lambda$ 6147, 6149 lines for a range of magnetic field strengths from synthetically generated line profiles. The synthetic spectral lines were created with a stellar atmosphere model with $T_{\rm eff}=11~000$ K, $\log~g=4.1$ , $\xi _{\rm t}=0$ km s $^{\rm -1}$ and ${\rm [Fe/H]}=0.5$ . This model is similar to the atmospheric models for the observed objects (HD 10783, HD 22316) and is applicable to our analysis. In Fig. 1 it is shown how $W_{\rm\lambda}$ becomes greater with an increasing magnetic field and the how the increase in $W_\lambda$ is different for the two Fe II $\lambda\lambda$ 6147, 6149 lines. The Fe II $\lambda$ 6149 line, which has the simpler Zeeman structure of the two, becomes "saturated'' more quickly. Based on the values presented in Fig. 1 the relative intensification is calculated and presented in Fig. 2. Below a field value of 6.0 kG the relative intensification seems independent of small variations of the rotational velocity. Furthermore, we note the linear behavior between 3 and 5 kG as observed by Mathys & Lanz (1992). The magnetic "curve-of-growths'' are different for the two iron lines, even for weak magnetic field strengths. The relative intensification is a negative value when the field is below 2.5 kG. In the case, when the field strength is above 6 kG the equivalent width is constant for both lines and no information regarding the magnetic field can be obtained with this method. The relationship between the relative intensification and the magnetic field strength is dependent on $T_{\rm eff}$ , [Fe/H] and the angle between the line-of-sight, which is a problem previously been partly investigated by Takeda (1991). We have investigated the objects with no resolved Zeeman structure using the equivalent width technique and compared the results with values obtained with synthetic spectrum fitting.

The field measurements will be discussed for each star individually, starting with those stars whose spectrum displays resolved Zeeman structure. The objects HD 192678 and HD 165474 were investigated over their expected rotational period in an attempt to find the magnetic maxima and minima. The targets without observed Zeeman structure, where the surface field cannot be measured with other methods, are discussed last. In this analysis the objects HD 22316 and HD 10783 are examples of stars where the Zeeman effect is smeared out due to stellar rotation.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{H3792F3.ps}\end{figure}$	Figure 3: Determination of the surface field using the spectrum fitting technique. Solid line: observed spectrum of the Ap star HD 192678. Dotted line: synthetic spectrum generated with a surface field of 4.7 G.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{H3792F4.ps} \end{figure}$	Figure 4: Determination of the surface field for HD 192678 based on the separation of the Zeeman components of the Fe II $\lambda$ 6149. Solid line: observed spectrum. Dotted line fitted Gaussians for the two Zeeman components. Dashed line: fitted Gaussians including the unknown blend in the blue wing.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{H3792F5.ps} \end{figure}$	Figure 5: Magnetic field determination for HD 192678 as a function of the time. Upper figure: field determined with the spectrum fitting technique. Lower figure: field based on separation of the Fe II $\lambda$ 6149 Zeeman doublet.
Open with DEXTER

4.1 HD 192678

The stellar magnetic field for the A4p star HD 192678 has previously been analyzed regarding its longitudinal field (Leroy 1995) and the mean field modulus (Mathys et al. 1997). These two investigations are in agreement on a value of a rotational period of $6\hbox{$.\!\!^{\rm d}$ }4185$ , with a magnetic maximum at $\phi= 0.00$ and minimum at $\phi=0.50$ . Mathys et al. (1997) determined a MFM of 4831 G, based on 34 field determinations using the Fe II $\lambda$ 6149 Zeeman doublet. An investigation of the field geometry was made by Wade et al. (1996), who determined the angle between the rotational and the magnetic axes to be ( $120\pm7$ ) $\hbox{$^\circ$ }$ with an inclination between the rotational axes and the line of sight of ( $173\pm5$ ) $\hbox{$^\circ$ }$ , based on an oblique dipole model. HD 192678 is a photometric variable (Adelman & Rice 1999) in the u and b bands. The flux variation is related to the previously mentioned period, with a flux maximum occurring when the field is weakest. The flux variations are calculated to give a difference in $T_{\rm eff}$ of less than 100 K which is within our estimated error margin for the determination of $T_{\rm eff}$ .

This analysis covers 10 observations/phases of the magnetic sensitive lines Fe II $\lambda\lambda$ 6147, 6149 complemented with spectra of the less magnetically sensitive lines Fe II $\lambda$ 4491, 4508 used for preliminary investigations of $v~\sin{i}$ . The rotational velocity was fine tuned, using individual Zeeman components of the Fe II $\lambda$ 6149 line, to be $\leq$ $4.8 \pm 0.4$ km s ^-1. This value is an average over the rotational period with an error corresponding to one standard deviation. The magnetic field is determined with the Fe II $\lambda\lambda$ 6147, 6149 lines supplemented with the Cr II $\lambda$ 6147 line at all 10 phases. A determination of the magnetic field by the synthetic spectrum fitting technique is presented in Fig. 3. The accuracy of the magnetic field determination using spectrum fitting is estimated to be $\pm$ 100 G based on the line profile fitting. The result from the synthetic spectrum fitting procedure is compared with calculations based on measurements of the wavelength separation of the two Fe II $\lambda$ 6149 Zeeman components. This Zeeman doublet is disturbed by an unknown feature in the blue wing, which has been considered in the fitting procedure. The magnetic field determination using Gauss fitting of the Zeeman doublet is presented in Fig. 4. The result of the magnetic field varies by 100 - 150 G, dependent upon whether the unknown component is included. We estimate the accuracy of the magnetic field determination using the wavelength separation of the Fe II $\lambda$ 6149 Zeeman doublet to be $\pm$ 100 G if the unknown component is included. The results obtained with the spectrum fitting technique agree with the results obtained by measurements of the Zeeman separation (Fig. 5). Our result for the averaged surface field over the rotational period is presented in Table 3 and is in agreement with the corresponding value for the average MFM determined by Mathys et al. (1997). Ten phase points are too few in order to investigate the rotational period independently since the accuracy of the field determination is of the same order as the amplitude of the field variations. When the value of the rotational period, 6 $.\!\!^{\rm d}$ 4185, obtained by Mathys et al. (1997) is adopted and our results are added to the data points in their analysis (Fig. 6), it appears that the two datasets are in agreement.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{H3792F6.ps} \end{figure}$	Figure 6: Surface field variations for HD 192678, based on a rotational period of $6\hbox{$.\!\!^{\rm d}$ }4185$ . Plus signs: data points from Mathys et al. (1997). Triangles: measurements in this analysis.
Open with DEXTER

A small wavelength shift relative to the Fe II lines is observable for Cr II $\lambda$ 6147. The shift is phase dependent with a minimum phase shift at magnetic maximum. A possible explanation for this could be a difference in the distribution of chromium relative to iron over the stellar surface.

4.2 HD 165474

HD 165474 has previously been investigated with respect to its rotational period but with contradicting results. Babcock (1958), Mathys (1991) and Leroy (1995) have investigated the longitudinal magnetic field for HD 165474. The last determined the rotational period to be either 12 $.\!\!^{\rm d}$ 02 or 23 $.\!\!^{\rm d}$ 38. Later, Mathys et al. (1997) investigated the rotational period using measurements of the MFM with the result of a period of 2 $.\!\!^{\rm d}$ 54065.

Our analysis for HD 165474 is performed in a similar manner as for HD 192678 with an identical set of observational data. The surface magnetic field is measured with the synthetic spectrum technique at all 10 observations/phase points and compared with the calculated field value based on the wavelength separation of the Fe II $\lambda$ 6149 Zeeman doublet. $v~\sin{i}$ is determined using the less magnetically sensitive Fe II $\lambda\lambda$ 4491, 4507 lines and fine tuned with individual Zeeman components of Fe II $\lambda$ 6149 at each phase. A value of the rotational velocity of ( $5.0 \pm 0.2$ ) km s ^-1 was derived. The magnetic field strength obtained with the spectrum fitting technique is in agreement with those based on measurements of the separation of the Fe II $\lambda$ 6149 doublet within 100 G (Fig. 7). An average magnetic field, based on the 10 field measurements, gives a value of 6.6 kG which is in agreement with the value obtained by Mathys et al. to within 100 G. If a rotational period of 2 $.\!\!^{\rm d}$ 54065 is assumed, our values are shifted in phase compared to the results from Mathys et al. (1997). In Fig. 8 the result from Mathys et al. is presented together with our phase shifted values. The error for the rotational period is set to be 0 $.\!\!^{\rm d}$ 0020 (Mathys et al. 1997). The time difference between their first and our last data point can account for a phase difference of 0.375. If this shift is adopted to our observations, the two datasets are in good agreement. This would imply a slightly longer rotational period than previously proposed. The new value would then be, $P=2\hbox{$.\!\!^{\rm d}$ }54085$ .

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{H3792F7.ps} \end{figure}$	Figure 7: Magnetic field determination for HD 165474 as a function of time. Upper figure: field determined with synthetic fitting. Lower figure: field based on separation of the Fe II $\lambda$ 6149 Zeeman doublet.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{H3792F8.ps} \end{figure}$	Figure 8: Comparison of our field values for HD 165474 with results obtained by Mathys et al. (1997). The phase is based on a rotational period of 2 $.\!\!^{\rm d}$ 54065. Plus signs: data points from Mathys et al. Triangles: measurements in this analysis where the phase is shifted 0.375 compared to the ephemeris from Mathys et al.
Open with DEXTER

4.3 HD 2453

HD 2453 has earlier been analyzed with respect to its photometric variation (Wolff 1975) resulting in a value of the rotational period of 523 $^{\rm d}$ , later refined by Mathys & Hubrig (1997) to 521 $^{\rm d}$ . We have investigated this object at a single phase, $\phi=0.209$ ( $\phi_0=0.283$ at HJD = 2448166.502, Mathys et al. 1997). The field was determined to be $3.7 \pm 0.1$ kG, obtained with spectrum fitting of the Fe II $\lambda\lambda$ 6147, 6149 lines (Fig. 9) with $v~\sin{i} = 1.5$ km s $^{\rm -1}$ . The surface field determination using the splitting of the Fe II $\lambda$ 6149 Zeeman doublet results in a field value of 3.6 kG, which is in agreement with the result obtained with synthetic spectrum fitting. Both values are in good agreement with the result from Mathys et al. (1997) at this phase.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{H3792F9.ps} \end{figure}$	Figure 9: Surface field measured for HD 2453 using the spectrum fitting technique. Solid line: observed spectrum. Dashed line: synthetic spectrum created with H=3.7 kG.
Open with DEXTER

4.4 HD 200311

This object was investigated by Adelman (1974) regarding line identification and magnetic field measurements. The magnetic field was determined to be $8.4 \pm 0.6$ kG using spectral lines with partially resolved Zeeman components in the spectral region 3761 - 4915 Å. The investigation was redone by Mathys et al. 1997, who also determined the rotational period to be 51 $.\!\!^{\rm d}$ 75. Our analysis is restricted to a single observation ( $\phi=0.875$ ). The field was determined using the spectrum fitting technique to be 7.7 kG, which is a weaker field compared to the value obtained by Mathys et al. (1997), who is observing a field exceeding 9.0 kG at this phase. The difference is most likely a result of the magnetic field strength which is on the limit where Paschen-Back effect could be observed. It is not possible to fit the Fe II $\lambda$ 6149 Zeeman doublet with two Gaussians, hence it is not possible to measure the magnetic field using the separation between the Zeeman components with reasonably good accuracy. If the technique is used with the poorly fitted line profiles a field value of 8.2 kG is obtained.

4.5 HD 22316

HD 22316 is an object with a spectrum not showing resolved Zeeman structure. Hill & Blake (1996) measured the longitudinal field and determined its rotational period to be $2 \hbox{$.\!\!^{\rm d}$ }9761 \pm 0 \hbox{$.\!\!^{\rm d}$ }0014$ . To our knowledge the surface field has never been measured. Our observations of HD 22316 were limited to three phases and it is not possible to independently determine the rotational period, so the ephemeris of Hill & Blake (1996) is applied. The spectrum of HD 22316 shows a large line density caused by a peculiar chemical composition, and with a rotational velocity of 17 km s $^{\rm -1}$ (Nielsen & Wahlgren 2000) the spectrum becomes difficult to analyze. The Fe II $\lambda$ 6147 and the Cr II $\lambda$ 6147 lines are due to the large rotational velocity not resolved, hence the magnetic field measurement has to be made by synthetic spectrum fitting using this complex and the Fe II $\lambda$ 6149 line. No strong blends are evident, but a blend on the blue side of the Fe II $\lambda$ 6149 line might be suspected since this feature often is observed in other Ap/Bp star spectra. A synthetic spectrum using a single magnetic field value can mimic the line profile of the Cr II/Fe II $\lambda$ 6147 complex, but the generated spectral feature for Fe II $\lambda$ 6149 is broad and cannot fill out the observed line core.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{H3792F10.ps} \end{figure}$	Figure 10: Measurements of the surface field for HD 22316. Solid line: observed spectrum. Dashed line: synthetic spectrum including a zero field model and a field of 9.5 kG. Dotted line: synthetic spectrum based on a single magnetic field value (9.5 kG).
Open with DEXTER

The magnetic field strength is in a regime where Paschen-Back effect may be observable. When the magnetic field is strong the LS-coupling rules are not applicable and consequently a new set of magnetic components will be observed with a slightly different intensity distribution. The spectral line core for the Fe II $\lambda$ 6149 line in Fig. 10 can not be reproduced by the Paschen-Back effect alone. Therefore, another explanation is needed to reproduce the triangular profile of the Fe II $\lambda$ 6149 line.

An alternative explanation is local magnetic field variations in the stellar plasma. A complicated field structure may affect atoms in the stellar photosphere with different magnetic field strengths. Using a model with two field values, it is possible to achieve a better spectrum fitting as shown in Fig. 10. The line wings are created by the stronger magnetic field while the line core requires a much weaker magnetic field strength. In Fig. 10 the synthetic spectrum is generated as a sum of two spectra created with field strengths of zero and 9.5 kG, respectively, and weighted equally. A model including more than one field value increases the complexity of the analysis considerably, and it is not possible to obtain an unique combination of magnetic field values. The application of two fields might imply a still more complicated field structure than first assumed, with local field variations between 0 and 10 kG.

At present time we are limited to use a model based on a single field value. Our measurement then give a variation of the surface field between 7.0 and 9.5 kG over the rotational period, obtained with synthetic spectrum fitting of the Fe II/Cr II complex and presented in Table 4. The accuracy of each measurement of approximately $\pm$ 400 G is based on line profile fitting. The spectral line profile for the Fe II/Cr II complex is less sensitive to variations of the field affecting the line core, due to a larger number of close located Zeeman components.

The magnetic field has also been investigated by measuring equivalent widths of the iron lines near 6150 Å. The measurements at all three phases give values exceeding the level at which the relative intensification becomes insensitive to magnetic field strength. The large relative intensification implies a field exceeding 5.0 kG, which is in agreement with the results obtained with spectrum fitting. The surface field shows similar variations as the ephemeris obtained by Hill & Blake (1996) but, as shown in Fig. 11, shifted in phase by $\delta \phi =0.29$ . Based on the minimum phase shift of the ephemeris to match our data points, we can revise the rotational period from 2 $.\!\!^{\rm d}$ 9761 derived by Hill & Blake (1996) to a value of 2 $.\!\!^{\rm d}$ 9770.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{H3792F11.ps} \end{figure}$	Figure 11: Crosses: measurements of the surface field strength for HD 22316 in our analysis. Dotted line: ephemeris based on a mean surface field of 8.5 kG with an amplitude of 1.4 kG and a rotational period of 2 $.\!\!^{\rm d}$ 9761 (Hill & Blake 1996). Solid line: identical with the dotted line but with a phase shift of $\delta \phi =0.29$ to fit our measurements.
Open with DEXTER

4.6 HD 10783

The longitudinal magnetic field has previously been determined to vary between -1.2 and 2.2 kG (Babcock 1958). The light variability has been investigated by van Genderen (1971) and Preston & Stepien (1968) who determined a value for the rotational period of 4 $.\!\!^{\rm d}$ 1327, which later was refined by Hardie et al. (1990) to 4 $^{\rm d}$ .13281. The magnetic and the light variations coincide in phase. The star has $v~\sin{i}<15$ km s $^{\rm -1}$ and a suggested value of the microturbulent velocity of 2 km s $^{\rm -1}$ (Preston & Stepien 1968). Our analysis finds a slighter higher value of the rotational velocity (<17 km s $^{\rm -1}$ ) under the assumption of no microturbulence.

We have observed HD 10783 at three phases, $\phi = 0.079$ , 0.320, 0.648, based on the ephemeris given by Hardie et al. (1990). The surface field is determined to vary between 4.5 and 5.6 kG at these phases (Table 4). Even if the line profiles do not imply the same magnetic field complexity as for HD 22316, it is possible that a single field solution is a simplification of a complicated problem.

The magnetic field has also been investigated using the relative intensification. However, the spectrum line density is high and both of the Fe II lines near 6150 Å seem blended and we do not get any further information using equivalent width measurements.

Table 4: Comparison of results using different methods for stars without resolved Zeeman structure.
Object phase, $\phi$ $<H>_{\rm av}^{a}$ $\frac{\delta W_{\rm\lambda}}{<W_{\rm\lambda}>}$ <H $>_{\rm av} ^{b}$

(kG) (kG)

HD 22316^c 0.098 9.0 0.298 >5.0

0.440 9.5 0.271 >5.0

0.767 7.0 0.349 >5.0

HD 10783^d 0.079 5.6 0.045 2.9

0.320 4.5 0.105 3.4

0.648 5.0 0.220 4.4

**Table 4:** Comparison of results using different methods for stars without resolved Zeeman structure.
Object	phase, $\phi$	$<H>_{\rm av}^{a}$	$\frac{\delta W_{\rm\lambda}}{<W_{\rm\lambda}>}$	<H $>_{\rm av} ^{b}$
		(kG)		(kG)
HD 22316^c	0.098	9.0	0.298	>5.0
	0.440	9.5	0.271	>5.0
	0.767	7.0	0.349	>5.0
HD 10783^d	0.079	5.6	0.045	2.9
	0.320	4.5	0.105	3.4
	0.648	5.0	0.220	4.4

^a: Surface field obtained with spectrum fitting.
^b: Surface field based on relative intensification.
^c: Phase derived with ephemeris from Hill & Blake (1996).
^d: Phase derived with ephemeris from Hardie et al. (1990).

5 Discussion

Measuring the separation between the Fe II $\lambda$ 6149 Zeeman doublet provides a simple method to achieve a value of the surface field. However, the technique is not applicable to stars with unresolved Zeeman patterns and is sensitive to blending features. It is found that the equivalent width provides a field value over a limited range of magnetic fields strength, roughly over a range 3-6 kG in our example. Measurements of equivalent widths can also be limited by blending spectral features, especially the Cr II $\lambda$ 6147 line and for cooler stars the Fe I $\lambda$ 6147 line.

For stars without resolved components with magnetic fields outside the range between 3 and 6 kG, another method is needed to measure the surface field. The synthetic spectrum technique is shown to have advantages for measurement of the surface magnetic field. The method is insensitive to known line blends and is also useful for objects with and without resolved Zeeman structure. For objects with resolved components the method gives accurate results. The average surface fields for the Ap stars HD 192678, HD 165474, HD 2453 and HD 200311 were measured and for the first two targets we have tracked the field variation over their rotational periods.

A useful application of the synthetic spectrum method is its extension to more rapidly rotating stars. HD 10783 and HD 22316 have been analyzed and the average surface field has been measured. The measurements for HD 22316 have been compared with the ephemeris from Hill & Blake (1996) where a phase shift has been observed. Based on the shift a revision of the rotational period is calculated to be $P=2\hbox{$.\!\!^{\rm d}$ }9770$ , under the assumption of an equal variation for the surface field as for the longitudinal.

The complexity of the viewed magnetic field is most likely correlated to the rotational velocity. Stars with low values of the rotational velocity are most likely observed pole-on with the consequence of a simpler magnetic field structure when the angle between the magnetic and the rotational axis is small. The large difference between the strength of the surface and the longitudinal field for HD 10783 and HD 22316 implies a great inclination between the magnetic axis and the line-of-sight for those objects. If the angle between the rotational axis and the line-of-sight is great the projected rotational velocity will be larger and the observed field structure of the photosphere could very well appear more complicated since the object then is observed at the equator instead of the pole. Observations of HD 22316 and HD 10783 confirm Zeeman patterns not reproducible with a model based on a single value of the magnetic field.

Measurements of stellar magnetic fields using synthetic spectrum fitting

1 Introduction