A&A 395, 587-593 (2002)
DOI: 10.1051/0004-6361:20021317

Long-term photometry of the near-contact detached binary GR Tauri[*]

X. B. Zhang - R. X. Zhang - M. J. Fang

National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, PR China

Received 3 June 2002 / Accepted 9 September 2002

Abstract
We present photometric observations of the eclipsing binary GR Tau made in 1985, 1993, 1998, 2000 and 2001. New times of minima and ephemerides are given. Based on a statistical analysis of the times of minima obtained by photoelectric and CCD photometry, the orbital period of the system is found to be decreasing with a rate of $\Delta P/P = 3.27 \times10^{-10}$ during the past decades. An assumed hot spot on the trailing hemisphere of the secondary enables us to reconstruct the peculiar asymmetry of the distorted light curves. The photometric solution with the Wilson-Devinney code reveals that GR Tau is a near-contact detached system with the two components almost filling their respective critical Roche lobes. The photometric mass ratio turns out to be q=0.22, and the masses and radii are derived for the components as $M_{1}=1.42\pm 0.18~ M_{\odot}$, $M_{2}=0.31\pm 0.04~ M_{\odot}$, $R_{1}=1.47\pm 0.19~ R_{\odot}$ and $R_{2}=0.70\pm 0.09~ R_{\odot}$. The authors discuss the possible evolutionary status of the component stars and the probable nature of the assumed hot spot.

Key words: stars: binaries: eclipsing - stars: individual: GR Tau


1 Introduction

GR Tau (=BD + $20^{\circ}$0685) was discovered to be an eclipsing binary by Strohmeier et al. (1957) from their photographic survey for variable stars. The subsequent observations of Strohmeier et al. (1963) gave the first photographic light curve and a period of 0.474022 days for the system. Gotz & Wenzel (1962) assigned a spectral type of A9 for the primary component. Yamasaki et al. (1984) published the first photoelectric and spectroscopic observations of the binary. The spectral type of GR Tau was suggested to be about A5. They obtained a small mass function of 0.0101 $M_{\odot}$ and a revised orbital period of 0.4298525 days. From the analysis of the light curves, they determined the first photometric solution of the system. Their solutions showed that GR Tau is a near-contact system, but their photometric mass ratio of q=m2/m1=0.32 leads to a mass of the primary component unacceptably small for an A5V star.

Lázaro et al. (1995) observed the system with visual and infrared photometry, and obtained B, V, J and K light curves. The near-contact configuration of GR Tau was confirmed by their Roche model photometric solution. From the analysis of the colours of GR Tau, however, they showed that the primary component's spectral type could be about A9V, instead of A5V as classified by Yamasaki et al. (1984). The orbital period was refined to be 0.42985060 days.

The asymmetry of the light curves of GR Tau has been noted by most of the previous studies since Yamasaki et al. (1984). It is also found that the light curve of the system changes frequently with time as it presents always an asymmetry with Max I brighter than Max II. It may be due to the so-called O'Connell effect, as is widely found among the V1010 Oph type binaries. However, no detailed analysis in modeling the asymmetry as well as its variations has yet been made.

Because of the peculiar asymmetric feature of the light curve and the near-contact configuration, GR Tau has been listed as one of the programming targets for our long-term photometric observations. We have observed the system in five runs since 1985. In this paper, we report the long-term photometric observations made in the past 17 years. The light curves are analyzed using the W-D code (Wilson & Devinney 1971; Wilson 1979, 1990). The asymmetry and the changes of the light curves are discussed on the basis of a model with an assumed hot spot possibly caused by mass transfer between the component stars.

2 Observations and data reduction

The star GR Tau was observed in five runs made in the observing seasons of 1985, 1993, 1998, 2000 and 2001. The observations were all made at the Xinglong station of Beijing Astronomical Observatory. Table 1 gives relevant information on the observations.

The 1985 and 1993 observations were both carried out with the 60 cm reflector. The star BD +20$^{\circ}$0684 was employed as the comparison, and BD +19$^{\circ}$0642, as the check star. The differences in magnitude between the variable and comparison stars were corrected for differential extinction and transformed into the UBV system. The BV light curves obtained in 1993 have been reported by Fang et al. (1994).

The observations in 1998 were made on the 85 cm Cassegrain telescope. In this run, the comparison star was BD +19$^{\circ}$0642 and the check star was BD +20$^{\circ}$0684. Data reduction was done in the same way as the 1985 and 1993 observations.

The 2000 observations were carried out on the 85 cm reflector with a red-sensitive Thomson TH7882 576$\times$384 CCD photometer (Wei et al. 1990; Zhou et al. 2001) which provides a field of view of about $12'\times 8'$. Five stars in the field around GR Tau were selected as reference stars. We finally chose the star GSC 1258-171 as the comparison star through a try during the data reduction. Sky extinction was not taken into account in view of the close proximity of the program stars. The exposure times were 30 s. A single V filter was employed.

The 2001 observations were made on the 85 cm telescope with a 3-channel photometer. On the first two nights (Oct. 28 and 29, 2001), we obtained a completely covered light curve with V filter. The observations in the B passband made on Oct. 31 and Nov. 1 have not recorded a complete light curve but did cover two primary eclipses. The comparison star was the same as that used for the 2000 CCD observations. The exposure times ranged from 10 to 15 s depending on the weather conditions.

All measurements of the 1985, 1993 and 1998 photoelectric observations are given in the appendix. For the 2000 CCD and 2001 fast photometry observations we list only the normal points in the appendix in the form of phase vs. relative magnitude, as the amount of individual data is too large.


 

 
Table 1: Information on the observations of GR Tau.
Year Telescope Photometer Filter Comparison star

1985

 60 cm single channel B, V BD +20$^{\circ}$0684
1993 60 cm single channel B, V BD +20$^{\circ}$0684
1998 85 cm single channel B, V BD +19$^{\circ}$0642
2000 85 cm CCD V GSC 1258-171
2001 85 cm three channel B, V GSC 1258-171


3 The period of GR Tau

By using the K-W method (Kwee & van Woerden 1956), 13 new times of minima were derived from our data. They are given in Table 2 along with previously published times of photoelectric and CCD minima collected since Yamasaki et al. (1984). These minimum times with a time-base of about 30 years enable us to discuss the long-term variations of the orbital period of GR Tau. Analyzing with the least square method, the following new ephemerides are derived:

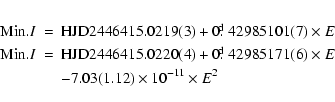
\begin{eqnarray*}{\rm Min}.I&=&{\rm HJD} 244 6415.0219(3) + 0\hbox{$.\!\!^{\rm d... ...85171(6) \times E \\ &&- 7.03(1.12)\times 10^{-11} \times E^{2} \end{eqnarray*}


As shown in Fig. 1 the quadratic ephemeris gives much better fitting to the observations than the linear ephemeris. The O-C values calculated from the second ephemeris above for each minimum time are given in Table 2. It is obvious that the period of GR Tau appears to show appreciable decreasing trend in the past decades. The rate of the period decrease turns out to be $\Delta P/P = 3.27 \times10^{-10}$ ($\sim$0.01 s yr-1).

Yamasaki et al. (1984) concluded that the orbital period of GR Tau was unlikely to have any obvious long-term variation based on a statistical study of the times of minima observed over 15 years before 1980. The large scattering of their statistical data caused by the uncertainties in visual and photographic observations does not exclude the possibility of long-term changes of the orbital period as indicated by recent photoelectric and CCD photometry.


 

 
Table 2: Times of photoelectric and CCD minima of GR Tau.
HJD E O-C source
2 400 000+      

44544.3075

 -4352.0 -.0011 Yamasaki & Okazaki (1984)
44573.1074 -4285.0 -.0020 Yamasaki & Okazaki (1984)
44578.2643 -4273.0 -.0013 Yamasaki & Okazaki (1984)
44579.1252 -4271.0 .0002 Yamasaki & Okazaki (1984)
46414.1619 -2.0 -.0022 Present study
46415.0209 .0 -.0025 Present study
46438.6622 55.0 -.0019 Mullis & Faulkner (1991)
47821.4944 3272.0 -.0056 Wunder et al. (1992)
47827.5148 3286.0 -.0008 Hanzl (1990)
47849.4363 3337.0 -.0012 Hanzl (1990)
47881.6752 3412.0 -.0006 Mullis & Faulkner (1991)
47889.4089 3430.0 -.0052 Hanzl (1990)
47945.2937 3560.0 -.0032 Hanzl (1990)
48288.3122 4358.0 -.0042 Agerer (1991)
48619.2973 5128.0 -.0074 Hanzl (1995)
48936.5294 5866.0 -.0019 Lázaro et al. (1995)
48938.6757 5871.0 -.0040 Lázaro et al. (1995)
48952.4314 5903.0 -.0022 Lázaro et al. (1995)
48953.2915 5905.0 -.0015 Lázaro et al. (1995)
48953.5019 5905.5 -.0059 Lázaro et al. (1995)
48954.3659 5907.5 -.0013 Lázaro et al. (1995)
49334.1394 6791.0 -.0012 Present study
49368.3190 6870.5 .0026 Agerer (1994)
49368.3199 6870.5 .0035 Agerer(1994)
49734.3334 7722.0 -.0025 Agerer (1996)
49760.3440 7782.5 .0042 Agerer (1996)
49760.3490 7782.5 .0092 Agerer (1996)
50013.5295 8371.5 .0061 Agerer et al. (1999)
50422.5188 9323.0 -.0046 Agerer & Hübscher (1998)
51139.5145 10 991.0 -.0011 Agerer et al. (1999)
51173.0380 11 069.0 -.0050 Present study
51176.0496 11 076.0 .0002 Present study
51198.4049 11 128.0 -.0014 Agerer et al. (1999)
51486.3991 11 798.0 -.0032 Agerer et al. (2001)
51571.0834 11 995.0 .0014 Present study
51573.0238 11 999.5 .0082 Present study
51574.0894 12 002.0 -.0044 Present study
52211.1277 13 484.0 -.0051 Present study
52211.3454 13 484.5 -.0023 Present study
52214.1353 13 491.0 -.0053 Present study
52220.1553 13 505.0 -.0049 Present study



  \begin{figure} \par\includegraphics[angle=-90,width=7.98cm,clip]{ms2755f1.eps} \end{figure} Figure 1: The O-C diagram of the observed times photoelectric and CCD minima. The solid line represents the quadratic fitting curve.
Open with DEXTER

4 The light curves and photometric analysis

4.1 The asymmetry and variations of the light curves

Using the above quadratic ephemeris, phases are computed for all the observations and the corresponding light curves are displayed in Figs. 3-7. It is clear that all the light curves obtained in the five observing seasons show marked asymmetry with Max. I brighter than Max. II. The general features are closely similar to those of the light curves previously obtained by Yamasaki et al. (1984). In Table 3 we list the main feature parameters of V-band light curves in the five different epochs. Since the secondary minima are not completely covered in the 1998 light curves, the corresponding values of Max. I-Min. II and Max. II-Min. II remain unknown.

The asymmetry of the light curve of GR Tau seems to be fixed in phase and not to migrate with phase like the photometric waves exhibited by the RS CVn stars. But the amplitude of asymmetry changed with time. From Table 3 we find that the amplitude Max. I-Min. I varied obviously with time, while the value of Max. II-Min. I seems to remain nearly constant. Thus the difference of brightness between Max. I and Max. II appears to depend primarily on the former.


 

 
Table 3: Main feature parameters of the V band light curves obtained in the five epochs.
Epoch 1985 1993 1998 2000 2001

Max. I-Min. I		 -0.51 -0.50 -0.53 -0.53 -0.50
Max. I-Min. II -0.22 -0.20 ... -0.23 -0.23
Max. II-Min. I -0.44 -0.45 -0.44 -0.45 -0.43
Max. II-Min. II -0.15 -0.15 ... -0.15 -0.16
Max. I-Max. II -0.07 -0.05 -0.09 -0.08 -0.07


4.2 The hot spot assumption

The peculiar asymmetry of the light curve seems to be something like the case in the stream-distorted light curves observed frequently in Algol-type systems with diminution of light in the phase interval 0.5-1.0, but for GR Tau there is no evidence of mass transfer from the secondary to the primary and, moreover, the near-contact configuration revealed by Yamasaki et al. (1984) and Lázaro et al. (1995) implies that there will be no space between the stellar surface and Roche lobe to allow the formation of an optically thick stream layer that would affect the brightness of the system.

On the other hand, the photometric asymmetry of GR Tau appears unlikely to be caused by the dark spot activity as is the case in RS CVn systems. The primary component of GR Tau has a spectral type of A, which is much earlier than that of active stars. The secondary component is ascribed to be a late K or M dwarf star, but it contributes only a few percent to the total brightness (Yamasaki et al. 1984; Lázaro et al. 1995). In any dark spot model assumed for the system the photometric analysis will always produce an unrealistically low spot temperature.

In order to model the asymmetric light curves of GR Tau, a natural alternative is to try the hot spot assumption. Shaw (1990) found that such asymmetry of light curves with Max. I brighter than Max. II appears to occur regularly in the V1010 Oph-type near-contact systems. From the IUE satellite observations of V1010 Oph, Shaw & Guinan (1990) found that there is an additional thermal source responsible for the Lyman $\alpha $ emission from the trailing hemisphere of the secondary component. They suggested further that the photometric asymmetry of V1010 Oph may also be caused by the additional thermal source, a phenomenon which could be typical for the V1010 Oph-type stars. For a similar, near-contact binary V361 Lyr, Zhai & Fang (1995) used a hot-spot model and gave a thorough treatment of its striking asymmetric light curves. In the case of GR Tau, we find rapid decrease of the system orbital period. This implies there could be mass transfer from the hot primary onto the hemisphere of the cool secondary component causing extra light emitted from the later type star. Thus a hot-spot model could well be the most preferable one to describe the light-curve asymmetry of GR Tau.

By assuming the existence of a hot spot on the trailing hemisphere of the secondary, the W-D synthetic light-curve program is employed to carry out the photometric analysis of the observed light curves.

4.3 Photometric solutions


  \begin{figure} \par\includegraphics[angle=-90,width=7.98cm,clip]{ms2755f2.eps} \end{figure} Figure 2: The diagram of $\sum w^{2}(\rm O{-}C)^{2}$ vs. q for the determination of solutions of the 1985, 1993, 2000 and 2001 light curves of GR Tau.
Open with DEXTER

The 1992 version of the Wilson-Devinney code (Wilson 1990) was employed for our light curve analysis. All the individual light curves were combined into normal points and were used to compute the solutions. In deriving the photometric solution, we made an un-spotted synthesis for the light curves of 1985, 1993, 2000 and 2001 at the first stage. Since 1998 light curves do not completely cover the secondary eclipse, they are not included in the test calculation. The following assumptions are made for the light-curve analysis: temperature of the primary component is set at T1=7500 K according to Lázaro et al. (1995); gravity exponents and albedos are taken to be g1=1.0 and A1=1.0 for the primary (radiative envelope) and g2=0.32 and A2=0.5 for the secondary (convective envelope); the limb darkening coefficients, according to Al-Naimiy (1978), are assigned as x1=0.60, x2=0.73 in V and x1=0.79, x2=0.92 in B, respectively.

The adjustable parameters are the phase shift $\phi _{0}$, the orbital inclination i, the temperature T2, the luminosity L1 and L2, the surface potentials $\Omega _{1}$ and $\Omega _{2}$, and the mass ratio q=m2/m1. According to the analysis of Lázaro et al. (1995), the mass ratio of GR Tau should be around 0.22 from its small mass function $f(m)=0.0101~M_{\odot}$. On the other hand Yamasaki et al. (1984) derived a mass ratio of 0.32. We just fix the mass ratio at a series of values of 0.18, 0.20, 0.22, 0.24, 0.26, 0.28, 0.30, 0.32, 0.34, 0.36, 0.40 and 0.50. All the test solutions started from Mode 2. In this way, the initial solutions are carried out at each assumed mass ratio for each light curve.


 

 
Table 4: Photometric solutions of the 1985, 1993, 1998, 2000 and 2001 light curves.
Parameter LC 1985 LC 1993 LC 1998 LC 2000 LC 2001

i (degrees)		 87.68$~\pm~ $0.52 87.15$~\pm~ $0.73 . 87.42$~\pm~ $0.18 87.58$~\pm~ $0.26
q=m2/m1 0.215$~\pm~ $0.003 0.222$~\pm~ $0.002 . 0.219$~\pm~ $0.001 0.246$~\pm~ $0.002
T1 (K)* 7500 7500 . 7500 7500
T2 (K) 3682$~\pm~ $109 3624$~\pm~ $82 . 3641$~\pm~ $32 3650$~\pm~ $27
g1* 1.0 1.0 . 1.0 1.0
g2* 0.32 0.32 . 0.32 0.32
A1* 1.0 1.0 . 1.0 1.0
A2* 0.5 0.5 . 0.5 0.5
x1B* 0.73 0.73 .    
x1V* 0.60 0.60 . 0.60 0.60
x2B* 0.92 0.92 .    
x2V* 0.79 0.79 . 0.79 0.79
$\Omega _{1}$ 2.3050$~\pm~ $0.0122 2.3132$~\pm~ $0.0074 . 2.2912$~\pm~ $0.0040 2.3555$~\pm~ $0.0058
$\Omega _{2}$ 2.2930$~\pm~ $0.0080 2.3060$~\pm~ $0.0043 . 2.2848$~\pm~ $0.0030 2.4770$~\pm~ $0.0096
r1 (pole) 0.4737$~\pm~ $0.0018 0.4731$~\pm~ $0.0011 . 0.4777$~\pm~ $0.0008 0.4691$~\pm~ $0.0011
r1 (point) 0.5887$~\pm~ $0.0063 0.5918$~\pm~ $0.0041 . 0.6156$~\pm~ $0.0062 0.6071$~\pm~ $0.0083
r1 (side) 0.5116$~\pm~ $0.0023 0.5108$~\pm~ $0.0015 . 0.5173$~\pm~ $0.0012 0.5062$~\pm~ $0.0015
r1 (back) 0.5324$~\pm~ $0.0026 0.5322$~\pm~ $0.0016 . 0.5398$~\pm~ $0.0014 0.5295$~\pm~ $0.0017
r2 (pole) 0.2319$~\pm~ $0.0106 0.2340$~\pm~ $0.0049 . 0.2380$~\pm~ $0.0036 0.2197$~\pm~ $0.0037
r2 (point) 0.2988$~\pm~ $0.0392 0.3025$~\pm~ $0.0235 . 0.3282$~\pm~ $0.0296 0.2534$~\pm~ $0.0078
r2 (side) 0.2405$~\pm~ $0.0125 0.2428$~\pm~ $0.0058 . 0.2475$~\pm~ $0.0043 0.2258$~\pm~ $0.0042
r2 (back) 0.2686$~\pm~ $0.0210 0.2711$~\pm~ $0.0097 . 0.2791$~\pm~ $0.0075 0.2430$~\pm~ $0.0059
L1/(L1+L2)B 0.996$~\pm~ $0.003 0.997$~\pm~ $0.002 .    
L1/(L1+L2)V 0.992$~\pm~ $0.004 0.993$~\pm~ $0.002 . 0.994$~\pm~ $0.001 0.994$~\pm~ $0.001
$\Omega _{in}$ 2.2696 2.2866 . 2.2793 2.3436

Spot model		          
co-latitude* 90.00 90.00 90.00 90.00 90.00
co-longitude 270.40$~\pm~ $0.87 272.10$~\pm~ $1.25 272.80$~\pm~ $1.57 271.82$~\pm~ $0.46 270.95$~\pm~ $0.42
$r_{\rm spot}$ 25.73$~\pm~ $0.48 25.64$~\pm~ $0.35 27.60$~\pm~ $0.44 27.48$~\pm~ $0.30 28.60$~\pm~ $0.28
$T_{\rm spot}/T_{2}$ 2.040$~\pm~ $0.027 1.928$~\pm~ $0.032 2.150$~\pm~ $0.045 2.038$~\pm~ $0.025 2.100$~\pm~ $0.028
$\sum w^{2}(\rm O{-}C)^{2}$ 0.0263 0.0167 . 0.0024 0.0090


* Assumed.



  \begin{figure} \par\includegraphics[angle=-90,width=7.98cm,clip]{ms2755f3.eps} \end{figure} Figure 3: The BV light curves of GR Tau obtained in 1985. Dots present the observations and the solid lines the theoretical light curves.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=-90,width=7.98cm,clip]{ms2755f4.eps} \end{figure} Figure 4: The same as Fig. 3, but for the year 1993.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=-90,width=7.98cm,clip]{ms2755f5.eps} \end{figure} Figure 5: The BV light curves of GR Tau in 1998.
Open with DEXTER

After that, the hot-spot assumption mentioned above is employed to perform a further analysis for all the observations of the light curves. The spot parameters are the spot temperature $T_{\rm s}$ (given as a fraction of the surrounding photospheric temperature), the spot radius (defined as half of the angular radius subtended by the spot at the stellar center), the spot latitude (0-180$^{\circ}$, measured from the north to the south pole of star) and spot longitude (0-360$^{\circ}$, measured for each star counterclockwise from the meridian at the substellar point to the other component). In our hot-spot model, the spot latitude is fixed at $90^{\circ}$. The preliminary spot longitude could be found approximately from the phase of the maximum brightness of the light hump caused by the hot spot on the secondary component. The other two spot parameters, $T_{\rm s}$ and $r_{\rm s}$, are calculated by adjusting the theoretical light curves to fit approximately the observed distorted light curves. After several runs, the parameters of both the Roche-model and the spot model are corrected alternately and best solution is derived for each assumed mass ratio. By referring to the distributions of $\sum w^{2}(\rm O{-}C)^{2}$ vs. qi for each program light curve as shown in Fig. 2, it is found that the most probable solution would be at around q=0.22 for the 1985, 1993 and 2000 light curves and at q=0.24 for the 2001 light curve. The final convergent solution of the photometric mass ratio is derived to be $q=0.215\pm 0.003$ for the 1985, $q=0.222\pm 0.002$ for the 1993, $q=0.219\pm 0.001$ for the 2000, and $q=0.245\pm 0.002$ for the 2001 light curve, respectively. The solutions are given in Table 4. As for the 1998 light curves, no Roche solution could be found from the above analysis. Here we adopt the Roche parameters for the 1993 light curve to fit the 1998 light curves. Subsequently the parameters of the hot-spot model for the 1998 light curves are derived through synthesis of the residual distortions.

5 Discussion and conclusions

We have presented a long-term photometric study of GR Tau. The results of period analysis and light-curve synthesis allow us to draw the following conclusions.

1) GR Tau appears to be a near-contact detached binary with the two components each almost filling its Roche lobe. Such a near-contact configuration has already been reported by Yamasaki et al. (1984), but that is based on the photometric solution of part of their 1980 light curves. The solution of Lázaro et al.'s (1995) resulted in a near-contact semi-detached configuration for the system with the secondary filling its Roche lobe. However, being taken from an average Roche model solution of their 1992 light curves, the distortion of the light curves, albeit slight, has not been taken into account. In our analysis all the observations of the light curves have been used to perform the photometric solution. By adopting a hot-spot model, our theoretical light curves give much better fittings to the observations of all the 1985, 1993, 2000 and 2001 light curves without all-phase systematic deviations. Furthermore, such a near-contact status of GR Tau is supported by the fact of orbital period decrease as evidenced by O-C analysis.

2) The W-D approach in the analysis of light curves with total eclipses can in general yield a reliable mass ratio for the binary systems under study. If we take the average values of the mass ratio $\-{q} =0.22$ and orbital inclination $\-{i} =87\hbox{$.\!\!^\circ$ }42$ obtained from the photometric solutions for the four light curves, and combine them with the spectroscopic mass function $f(m)=0.0101~M_{\odot}$ (Yamasaki et al. 1984), we can derive the absolute dimensions of GR Tau as:

\begin{eqnarray*}\begin{array}{ll} M_{1} = 1.42\pm0.18~ M_{\odot} \quad R_{1} =... ... \\ \hspace*{5cm} L_{2} = 0.08\pm0.02~ L_{\odot}.\\ \end{array}\end{eqnarray*}


From their photometric solution, Yamasaki et al. (1984) deduced an unacceptably small mass and radius for the primary component. Our results have greatly reduced the discrepancy of the derived mass and radius compared with the spectral type. However, the new values of mass and radius deduced for the primary are still somewhat small when compared to its spectral type of A9V.

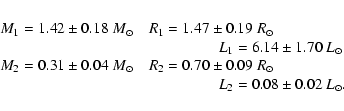
If the primary component of GR Tau is a normal main sequence star, for a spectral type A9V, its mass and radius should be about $M_{1} = 1.68~M_{\odot}$ and $R_{1} = 1.54~R_{\odot}$ according to the calibration from Schmidt-Kaler (1982). To match the deduced mass for the primary with its spectral type, an assumed mass ratio of q=0.206 would be appropriate for the mass function of $f(m)=0.0101~M_{\odot}$, or else, the mass function should be taken to be about 0.0120 with our photometric mass ratio q=0.22. Since we know that the mass ratios derived from all the photometric solutions to date (Yamasaki et al. 1984; Lázaro et al. 1995 and present work) are all larger than 0.22, we suggest that the discrepancy of the deduced mass in relation to the spectral type of GR Tau mentioned above might be due to the slight underestimation of the mass function if the photometric mass ratio is more reliable. A new high-precision radial velocity study based on high S/N spectroscopy is especially desirable to settle the problem.


  \begin{figure} \par\includegraphics[angle=-90,width=7.98cm,clip]{ms2755f6.eps} \end{figure} Figure 6: The V light curve of GR Tau observed in 2000.
Open with DEXTER

Another possibility is that, in such a near-contact binary system, the primary of GR Tau might be a low-mass and low-luminosity star as suggested by Yamasaki et al. (1984). In our results, the secondary has a temperature of about 3640 K, which corresponds to a spectral type of M1-2 if it is a dwarf star. Taking the values of absolute dimensions deduced for GR Tau, we plot the two components on the mass-radius diagram and find that the primary is still on the main sequence while the secondary is evidently an evolved star far away from the main sequence. The evolutionary status of GR Tau is something like that in other near-contact detached systems with the less massive secondary actually more evolved than the primary. It is suggested that the evolved secondary component should have been the more massive component but is now the less massive one after losing a considerable part of its original mass through Roche lobe overflow. And at present, the secondary could have just shrunken back from its Roche lobe making the system a near-contact detached system. The present massive primary component would have gained additional mass from the secondary. This could explain why it looks strange with respect to its spectral type.

3) The hot spot assumption gives a good description of the asymmetry of the light curves of GR Tau. The photometric solutions indicate that the hot spot remains at nearly the same position, with almost the same temperature and size in both epochs of 1985, 1993, 1998, 2000 and 2001. Taking the average value of $T_{\rm spot}/T_{2} = 2.05$ and $r_{\rm spot} = 27\hbox{$.\!\!^\circ$ }01$, the additional luminosity emitted by the hot spot can be calculated as:

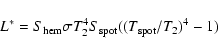
\begin{displaymath}L^{*} = S_{\rm hem}\sigma T^{4}_{2}S_{\rm spot}((T_{\rm spot}/T_{2})^{4}-1)\end{displaymath}

where $S_{\rm spot}=1-{\rm cos}~r_{\rm spot}$ is the spot area as a fraction of the hemispheric area $S_{\rm hem}$ of the star.
  \begin{figure} \par\includegraphics[angle=-90,width=7.98cm,clip]{ms2755f7.eps} \end{figure} Figure 7: The same as Fig. 6, but observed in 2001.
Open with DEXTER

The physical nature of the hot spot is still open for discussion. In view of the probable mass transfer in the system revealed by the period changes observed, we suggest that the hot spot on the secondary could be caused by the mass accreted from the primary component. Suppose that the accreting mass falls from the inner Lagrange point L1 directly onto the surface of the secondary, the luminosity caused by the accreting mass would be approximately represented by the following expressing according to Zhai & Fang (1995):

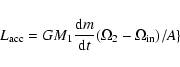
\begin{displaymath}L_{\rm acc}=GM_{1} \frac{{\rm d}m}{{\rm d}t} ( \Omega _{2}- \Omega _{\rm in})/A\}\end{displaymath}

where G is the gravitation constant, $\frac{{\rm d}m}{{\rm d}t}$ is the mass-accretion rate, A is the distance between the two components, $\Omega _{2}$ and $\Omega _{\rm in}$ are the dimensionless potentials of the stellar surface and the critical Roche lobe, respectively. If $L^{*}=L_{\rm acc}$, or we assume that the enhanced luminosity of the secondary component is entirely from the mass accretion, we find the mass-accretion rate to be $\frac{{\rm d}m}{{\rm d}t} = 1.86\times 10^{-7}~ M_{\odot}/\rm yr$, which corresponds to a period-change rate of $\Delta P/P = -1.34\times 10^{-9}$.

The observed period-change rate is about $\Delta P/P = -3.27\times 10^{-10}$, the absolute value of which is much less than what we predicted. This implies that the possible mass transfer we infer from our photometry is not strong enough to create the spot luminosity unless some additional energy, besides the potential energy which we have taken into account, has also been released by the mass flow. Usually the original velocity of the accreting mass around the Lagrange point is not equal to zero as we have assumed, thus the original kinetic energy of the mass flow could probably serve as part of the additional energy released. Another possible energy source might be the thermal energy brought about directly by the mass flow through the high temperature plasma wind from the primary component. A satisfactory model should be carefully constructed in order to give an comprehensive description of the mass accretion and the physical nature of the hot spot, but this goes beyond the scope of the present work.

4) All the light curves of GR Tau obtained by us in the five epochs are asymmetric. They are basically similar to the 1980 light curves published by Yamasaki et al. (1984). On the other hand, Hanzl (1990) and Lázaro et al. (1995) report nearly symmetric light curves of the system. The light curve of GR Tau seems to vary between asymmetric and symmetric forms on a time scale of several years. Comparing the symmetric light curves with the asymmetric ones, we notice that the asymmetric light curves always have deeper primary minima (Max. I-Min. I) than the symmetric light curves. It is suggested that the variation in the light curves of the system could be due to changes of the hot spot in the secondary component. Well-planned observational studies in the future are needed to understand better the true nature and behaviour of the binary system including the hot spot deduced by conventional theory.



Appendix

Table A.4: Normal points of the 2000 V light curve.
Phase $\Delta V$ Phase $\Delta V$ Phase $\Delta V$ Phase $\Delta V$ Phase $\Delta V$

0.0082		 -2.2208 0.2203 -2.7435 0.4172 -2.5931 0.6182 -2.5919 0.8197 -2.6381
0.0200 -2.2286 0.2298 -2.7478 0.4317 -2.5786 0.6336 -2.6060 0.8351 -2.6165
0.0309 -2.2355 0.2436 -2.7484 0.4468 -2.5597 0.6495 -2.6236 0.8484 -2.5975
0.0463 -2.2675 0.2571 -2.7489 0.4621 -2.5480 0.6610 -2.6329 0.8618 -2.5808
0.0606 -2.3318 0.2713 -2.7469 0.4736 -2.5441 0.6723 -2.6365 0.8728 -2.5612
0.0718 -2.3866 0.2877 -2.7383 0.4855 -2.5354 0.6837 -2.6521 0.8865 -2.5388
0.0861 -2.4440 0.2984 -2.7303 0.5009 -2.5317 0.6990 -2.6605 0.9010 -2.4926
0.1117 -2.5775 0.3131 -2.7149 0.5152 -2.5301 0.7133 -2.6730 0.9140 -2.4509
0.1242 -2.6061 0.3280 -2.7024 0.5298 -2.5287 0.7256 -2.6712 0.9272 -2.4081
0.1378 -2.6373 0.3403 -2.6906 0.5406 -2.5271 0.7370 -2.6845 0.9407 -2.3410
0.1506 -2.6644 0.3498 -2.6804 0.5529 -2.5326 0.7518 -2.6801 0.9541 -2.2866
0.1664 -2.6888 0.3648 -2.6683 0.5672 -2.5375 0.7672 -2.6785 0.9644 -2.2521
0.1823 -2.7112 0.3806 -2.6492 0.5819 -2.5483 0.7821 -2.6742 0.9786 -2.2289
0.1961 -2.7208 0.3958 -2.6278 0.5963 -2.5655 0.7935 -2.6667 0.9959 -2.2205
0.2096 -2.7385 0.4067 -2.6099 0.6072 -2.5758 0.8043 -2.6648    


 
Table A.5: Normal points of the 2001 V light curve.
Phase $\Delta V$ Phase $\Delta V$ Phase $\Delta V$ Phase $\Delta V$ Phase $\Delta V$

0.0061		 -2.0066 0.2062 -2.4743 0.4064 -2.3365 0.6056 -2.3070 0.8072 -2.3947
0.0214 -2.0121 0.2199 -2.4774 0.4199 -2.3171 0.6199 -2.3247 0.8211 -2.3843
0.0330 -2.0326 0.2344 -2.4873 0.4333 -2.3010 0.6327 -2.3383 0.8330 -2.3666
0.0465 -2.0754 0.2464 -2.4856 0.4468 -2.2864 0.6461 -2.3495 0.8465 -2.3507
0.0599 -2.1339 0.2594 -2.4872 0.4603 -2.2731 0.6596 -2.3609 0.8600 -2.3288
0.0734 -2.1884 0.2728 -2.4869 0.4729 -2.2677 0.6731 -2.3771 0.8733 -2.3050
0.0869 -2.2400 0.2873 -2.4803 0.4878 -2.2634 0.6866 -2.3844 0.8861 -2.2781
0.1004 -2.2862 0.3002 -2.4724 0.4981 -2.2613 0.7000 -2.3922 0.8996 -2.2404
0.1138 -2.3219 0.3134 -2.4628 0.5136 -2.2537 0.7102 -2.3998 0.9130 -2.1938
0.1273 -2.3526 0.3278 -2.4457 0.5279 -2.2492 0.7260 -2.4109 0.9210 -2.1714
0.1401 -2.3755 0.3404 -2.4274 0.5410 -2.2506 0.7400 -2.4159 0.9412 -2.0598
0.1534 -2.3990 0.3535 -2.4122 0.5533 -2.2591 0.7533 -2.4162 0.9533 -2.0322
0.1662 -2.4235 0.3663 -2.3964 0.5613 -2.2595 0.7668 -2.4147 0.9668 -2.0114
0.1793 -2.4497 0.3798 -2.3754 0.5802 -2.2774 0.7802 -2.4119 0.9798 -2.0075
0.1934 -2.4649 0.3932 -2.3586 0.5938 -2.2926 0.7937 -2.4029 0.9933 -2.0053


Acknowledgements
This work is partly supported by the Chinese National Science Foundation (CNNSF) through grant 10173013. The authors are grateful to Prof. Shen Liangzhao for his suggestions and help. Thanks are also given to the refree, Dr. P. Niarchos for his careful reviewal.

References

 
Copyright ESO 2002