We deal with granular intensity fluctuations in the Sun and how they are caused by temperature fluctuations. We calculate temperature response functions
A&A 395, 279-284 (2002)
DOI: 10.1051/0004-6361:20021239
E. Pérez Rodríguez - F. Kneer
Universitäts-Sternwarte, Geismarlandstraße 11, 37083 Göttingen, Germany
Received 24 June 2002 / Accepted 27 August 2002
Abstract
We deal with granular intensity fluctuations in the Sun and
how they are caused by temperature fluctuations. We calculate
temperature response functions
![]() in the solar
photosphere. We apply the Diagonal Element Lambda Operator (DELO) method
to calculate the response functions for the continuum (
in the solar
photosphere. We apply the Diagonal Element Lambda Operator (DELO) method
to calculate the response functions for the continuum (
![]() nm-2.5
nm-2.5 ![]() ).
LTE is assumed throughout. It is demonstrated that, within the framework of the linear approximation, the H- continuum absorption plays an important rôle for the formation of the fluctuations in continuum images. It counteracts substantially the intensity fluctuations caused by variations of the Planck function. The temperature response functions are used to calculate, for three models of temperature fluctuations, the continuum intensity contrasts and their formation height for the above wavelength range.
).
LTE is assumed throughout. It is demonstrated that, within the framework of the linear approximation, the H- continuum absorption plays an important rôle for the formation of the fluctuations in continuum images. It counteracts substantially the intensity fluctuations caused by variations of the Planck function. The temperature response functions are used to calculate, for three models of temperature fluctuations, the continuum intensity contrasts and their formation height for the above wavelength range.
Key words: Sun: photosphere - Sun: granulation - radiative transfer
It is a widespread believe that the fluctuation of the granular intensity pattern on the Sun can be approximated by the simple relation
![]() with
with ![]() being the Planck function. Thus, in the linear approximation with
being the Planck function. Thus, in the linear approximation with
![]() ,
the observation of
,
the observation of
![]() would give a good proxy to
would give a good proxy to ![]() at some optical depth
at some optical depth
![]() ,
the latter according to the Eddington-Barbier relation.
,
the latter according to the Eddington-Barbier relation.
Such reasonning falls short on two grounds: 1) It neglects the opacity
changes due to temperature changes. 2) Simulations of the granular convection (e.g. Solanki et al. 1996; Stein & Nordlund 1998,2000; Steffen & Holweger 2002, and references therein) demonstrate that the excursions ![]() can be very large and thus
can be very large and thus
![]() is no longer valid and that the continuous optical depth
is no longer valid and that the continuous optical depth
![]() is very rugged. Beyond the granular intensity contrast, Steffen & Holweger (2002) have demonstrated with numerical simulations that the equivalent widths of spectral lines depend non-linearly on the temperature fluctuations.
is very rugged. Beyond the granular intensity contrast, Steffen & Holweger (2002) have demonstrated with numerical simulations that the equivalent widths of spectral lines depend non-linearly on the temperature fluctuations.
We shall not discuss non-linearities here. We aim at discussing the influence of the continuum opacity and its temperature sensitivity on the fluctuation of the emergent intensities. In the solar atmosphere, as in atmospheres of late-type stars, the continuum opacity in the visible and infra-red spectral range is mainly due to the H- ion. We restrict ourselves to the linear regime from which one can already gain insight into the formation of intensity fluctuations, without the need to refer to complex non-linear calculations.
For this purpose, it is appropriate to calculate temperature response functions
![]() for a given mean solar atmospheric model.
for a given mean solar atmospheric model.
Response functions are a means to obtain a first order (linear) approximation on the height range in the solar atmosphere in which fluctuations of certain atmospheric parameters (temperature, velocity, ...) influence observed fluctuations. They were introduced by Mein (1971) and are widely in use nowadays (see e.g. Eibe et al. 2001 and references therein and references in Kneer & Nolte 1991). In addition, response functions are applied in inversion codes to obtain heights of formation in which the atmospheric model parameters are to be tuned iteratively for a best fit of modelled, synthetic intensities to the observations (e.g. Ruiz Cobo & del Toro Iniesta 1994; Bellot Rubio et al. 2000; Borrero & Bellot Rubio 2002 and references there).
We will outline the method of the calculations of temperature response functions in the next section. This will include both continuum and line opacities. Some results concerning the formation of continuum fluctuations upon temperature variations will be presented in Sect. 3. Section 4 conludes the paper.
Given an average atmosphere, one asks, very generally, how big the change
![]() of the average intensity
of the average intensity ![]() would be if a certain atmospheric parameter P(z), e.g. the temperature T(z), is changed by a small amount
would be if a certain atmospheric parameter P(z), e.g. the temperature T(z), is changed by a small amount
![]() in the height range
in the height range
![]() .
In the linear regime, one has
.
In the linear regime, one has
![]() and the response function can be defined as
and the response function can be defined as
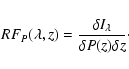 |
(1) |
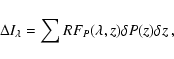 |
(2) |
We shall deal with the solar photosphere up to a height of approximately 500 km (above
![]() ). We will assume LTE throughout. Thus, the atomic level populations and the ionization equilibria follow from the Boltzmann-Saha statistics and the source function is given by the Planck function,
). We will assume LTE throughout. Thus, the atomic level populations and the ionization equilibria follow from the Boltzmann-Saha statistics and the source function is given by the Planck function,
![]() .
As a consequence, the changes of the source function and of the opacities upon a (small) temperature perturbation can be evaluated analytically, to a wide extent. A detailed description of the assumptions and the calculations is found in Pérez Rodríguez (2001).
.
As a consequence, the changes of the source function and of the opacities upon a (small) temperature perturbation can be evaluated analytically, to a wide extent. A detailed description of the assumptions and the calculations is found in Pérez Rodríguez (2001).
The average solar atmosphere is represented by the model C of Vernazza et al. (1981), commonly named VAL C model. The temperature T(m), with m = column mass density, and the microturbulent velocity
![]() serve as input for a selfconsistent calculation of the complete model in hydrostatic equilibrium, i.e. fulfilling
serve as input for a selfconsistent calculation of the complete model in hydrostatic equilibrium, i.e. fulfilling
| (3) |
For solar abundances, the gas pressure and the mass density are calculated from an initial guess of the electron pressure with the procedure given by Mihalas (1970). The electron pressure is iterated with the secant method until the hydrostatic equilibrium, Eq. (3), is fulfilled to a relative accuracy of 10-5 yielding the gas pressure and mass density to the same accuracy.
The geometric height, z, is then obtained from
| (4) |
In the solar photosphere, in the wavelength range of interest here,
![]() nm-2.5
nm-2.5 ![]() ,
the continuum absorption is overwhelmingly due to H- bound-free and free-free transitions. The small contributions from H free-free transitions and from the Paschen-, Bracket- and Pfund bound-free transitions of hydrogen are also included. We use the routines from the LINEAR-A code by Auer et al. (1972). There polynomial fits in wavelength
,
the continuum absorption is overwhelmingly due to H- bound-free and free-free transitions. The small contributions from H free-free transitions and from the Paschen-, Bracket- and Pfund bound-free transitions of hydrogen are also included. We use the routines from the LINEAR-A code by Auer et al. (1972). There polynomial fits in wavelength ![]() and temperature T, sometimes also in
and temperature T, sometimes also in
![]() ,
to the opacities are taken from Carbon & Gingerich (1969). The Gaunt factors are calculated, also via analytical expressions in
,
to the opacities are taken from Carbon & Gingerich (1969). The Gaunt factors are calculated, also via analytical expressions in ![]() and
and ![]() ,
following Mihalas (1967).
With known continuum opacities it is now easy to locate the position in the atmosphere where
,
following Mihalas (1967).
With known continuum opacities it is now easy to locate the position in the atmosphere where
![]() .
Following common use we define z=0 at this position by shifting the geometric height from Eq. (4) by an appropriate amount.
.
Following common use we define z=0 at this position by shifting the geometric height from Eq. (4) by an appropriate amount.
The present contribution is embedded in a broader work which includes the treatment of spectral lines. We therefore comment on line opacities. They are calculated using the (solar) abundance of the element of the line under consideration, the lower level excitation energy, the partition functions of the relevant ionization states, the oscillator strength, and the collisional damping. For the latter we use van der Waals damping according to Unsöld (1955). As Borrero & Bellot Rubio (2002) we include enhancement factors to the damping constants to fit the calculated wings to those of the Fourier Transform Spectrometer Atlas by Brault & Neckel (cited by Neckel 1999) The absorption profile is given by the Voigt function calculated from the complex error function after Hui et al. (1978). The partition functions are considered, as an approximation for the response functions of lines, independent of temperature.
We solve the radiative transfer equation for the specific intensity ![]() in a plane parallel atmosphere
in a plane parallel atmosphere
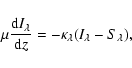 |
(5) |
The emergent intensity is
| = | 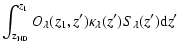 |
||
| (6) |
We omit, for brevity, the index for the wavelength dependence. ![]() are the optical depths on the corresponding geometric grid
are the optical depths on the corresponding geometric grid
![]() .
We use the notations
.
We use the notations
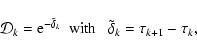 |
(7) |
![\begin{displaymath}S(\tau) = [(\tau_{k+1}-\tau)S_k + (\tau-\tau_k)S_{k+1}]/\tilde\delta_k.
\end{displaymath}](/articles/aa/full/2002/43/aah3789/img52.gif) |
(8) |
| (9) |
| (10) |
| (11) |
![\begin{displaymath}G_k = \left[1-\left(1+\tilde\delta_k\right){\cal D}_k\right]/\tilde\delta_k.
\end{displaymath}](/articles/aa/full/2002/43/aah3789/img57.gif) |
(12) |
We introduce a small perturbation ![]() of an atmospheric parameter P and linearize the transfer equation Eq. (5) (for
of an atmospheric parameter P and linearize the transfer equation Eq. (5) (for ![]() )
which gives
)
which gives
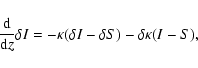 |
(13) |
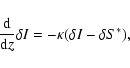 |
(14) |
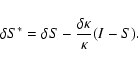 |
(15) |
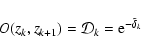 |
(16) |
| (17) |
| (18) |
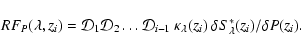 |
(19) |
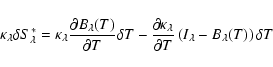 |
(20) |
![$\displaystyle RF_{\rm T}(\lambda,z_i) = O_\lambda(z_1, z_i)\Bigl[\kappa_\lambda...
...partial\kappa_\lambda\over\partial T}\left(I_\lambda-B_\lambda(T)\right)\Bigr].$](/articles/aa/full/2002/43/aah3789/img68.gif) |
(21) |
We note:
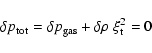 |
(22) |
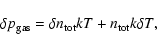 |
(23) |
The variation of the mass density is expressed by
| (24) |
In the VAL C model, up to the temperature minimum, the electron density ![]() is approximated, within 20% accuracy in high layers and within 1% accuracy in deep layers, by the formula
is approximated, within 20% accuracy in high layers and within 1% accuracy in deep layers, by the formula
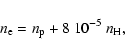 |
(25) |
Although we shall not expand on temperature response functions for spectral lines below, we give here for completeness the temperature derivatives of the Voigt function H(a,v), where
![]() and
and
![]() .
.
![]() is the damping constant and
is the damping constant and
![]() is the Doppler width, expressed in frequencies. We have
is the Doppler width, expressed in frequencies. We have
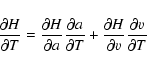 |
(26) |
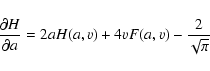 |
(27) |
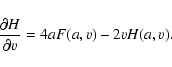 |
(28) |
In this Section, we present results for continuum intensity fluctuations
in a wide spectral range, 380 nm to 2.5 ![]() .
We have extended
the calculations into the IR region because there too, as in
the visible,
spectral features with excellent diagnostic
properties can be observed. We mention the He I line at
1.083
.
We have extended
the calculations into the IR region because there too, as in
the visible,
spectral features with excellent diagnostic
properties can be observed. We mention the He I line at
1.083 ![]() ,
the two Zeeman sensitive Fe I lines at
1.565
,
the two Zeeman sensitive Fe I lines at
1.565 ![]() ,
the H- opacity minimum at 1.655
,
the H- opacity minimum at 1.655 ![]() ,
and the CO
rotation-vibration band with
,
and the CO
rotation-vibration band with
![]() (v = vibration quantum
number) at 2.3
(v = vibration quantum
number) at 2.3 ![]() .
The capability of IR observations will be much
improved with new, large
solar telescopes and with new detectors.
.
The capability of IR observations will be much
improved with new, large
solar telescopes and with new detectors.
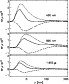 |
Figure 1:
Temperature response functions
|
| Open with DEXTER | |
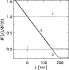 |
Figure 2: Three models of the (rms) temperature fluctuation. |
| Open with DEXTER | |
To obtain intensity fluctuations we apply height dependent temperature fluctuations
![]() according to Eq. (2). Since the emergent intensity fluctuations depend linearly on
according to Eq. (2). Since the emergent intensity fluctuations depend linearly on
![]() its actual amplitude is of no importance. Figure 2 gives three "models'': (1) with
its actual amplitude is of no importance. Figure 2 gives three "models'': (1) with ![]() independent of atmospheric height, (2) with
independent of atmospheric height, (2) with
![]() above 150 km and increasing below 150 km linearly towards subphotospheric layers, and (3) similar as (2) but decreasing to a minimum of
above 150 km and increasing below 150 km linearly towards subphotospheric layers, and (3) similar as (2) but decreasing to a minimum of
![]() for z>150 km. All three models possess the same
for z>150 km. All three models possess the same ![]() at z=0.
at z=0.
Model 2, which we consider more realistic than model 1, is suggested by the work of Komm et al. (1990). They find that the intensity contrast measured in the wings of strong absorption lines looses its coherence with continuum contrasts in the mid-photosphere. Temperature inversions in higher layers, as in the third model of Fig. 2, are found by, e.g., Holweger & Kneer (1989), Ruiz Cobo et al. (1996), Gadun et al. (2000), and Borrereo & Bellot Rubio (2002).
Figure 3, then, gives the contrasts
![]() as
functions of wavelength for models 1 and 2. The results for model 3 are
few percent lower than those for model 2, but otherwise very
similar. Thus, we do not show them here. All the contrasts are normalized such that we have the value of 0.15 at 550 nm from model 2 (indicated by
as
functions of wavelength for models 1 and 2. The results for model 3 are
few percent lower than those for model 2, but otherwise very
similar. Thus, we do not show them here. All the contrasts are normalized such that we have the value of 0.15 at 550 nm from model 2 (indicated by ![]() in Fig. 3). This contrast comes close to that measured in speckle reconstructions by de Boer (1995).
in Fig. 3). This contrast comes close to that measured in speckle reconstructions by de Boer (1995).
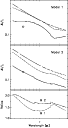 |
Figure 3:
Wavelength dependence of continuum intensity contrasts
|
| Open with DEXTER | |
To demonstrate the influence of the opacity changes upon temperature fluctuations we give in Fig. 3 the contrasts separately for the fluctuations of the source function alone (dashed curves) and including the opacity effects (solid curves). The dotted curves represent the wavelength dependence of
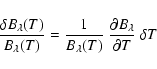 |
(29) |
Apart from short wavelengths, the contrasts in model 1 are larger than those in model 2 because in the former the atmospheric layers above z=0 km contribute stronger than in the latter. Especially above z=150 km, model 1 together with the extended response functions gives high contrasts. It is also due to these high reaching response functions that the contrasts for model 1 increase above 1.655 ![]() towards still longer wavelengths. We note in passing that one sees in the contrasts, which include the opacity effects, the Paschen- and Bracket boundaries of the hydrogen bound-free transitions at 821 nm and at 1.459
towards still longer wavelengths. We note in passing that one sees in the contrasts, which include the opacity effects, the Paschen- and Bracket boundaries of the hydrogen bound-free transitions at 821 nm and at 1.459 ![]() ,
respectively.
,
respectively.
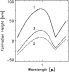 |
Figure 4:
Wavelength dependence of the average formation heights |
| Open with DEXTER | |
We may now ask at which average height
![]() in the atmosphere the intensity fluctuations (in the continuum) are formed. We use two definitions, one which includes the structure of the temperature fluctuations and one which does not, i.e.
in the atmosphere the intensity fluctuations (in the continuum) are formed. We use two definitions, one which includes the structure of the temperature fluctuations and one which does not, i.e.
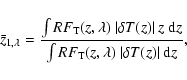 |
(30) |
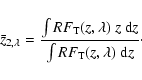 |
(31) |
Figure 4 depicts the formation heights of continuum intensity fluctuations for the three models. The wavelength dependence shows clearly the opacity dependence. We consider the formation heights of models 2 and 3 (between approximately -35 km and +25 km) as more realistic than those of model 1 because the latter are just centers of gravity of very extended contribution functions. Yet, generally, the formation heights should not be taken too literally. Even in this limited context of linear approximations, it is better to test models of (granular) temperature fluctuations by calculating the emergent intensities by means of the response functions and compare them with observations.
We have presented temperature response functions
![]() for the continua in the wavelength range of 380 nm-2.5
for the continua in the wavelength range of 380 nm-2.5![]() .
They were calculated from the VAL C solar photospheric model (Veranzza et al. 1981) and by linearizing the transfer equation using LTE. The differentiation of the opacities with respect to temperature could be performed analytically. The response functions were used to calculate, in linear approximation, granular intensity contrasts and formation heights in the above wavelength range. We emphasized the importance of opacities, especially that of the H- ion, which reduce the intensity contrast by up to a factor of two compared to calculations which neglect the opacity effects.
.
They were calculated from the VAL C solar photospheric model (Veranzza et al. 1981) and by linearizing the transfer equation using LTE. The differentiation of the opacities with respect to temperature could be performed analytically. The response functions were used to calculate, in linear approximation, granular intensity contrasts and formation heights in the above wavelength range. We emphasized the importance of opacities, especially that of the H- ion, which reduce the intensity contrast by up to a factor of two compared to calculations which neglect the opacity effects.
Response functions neglect non-linear effects which occur when the temperature fluctuations are large. We thus reiterate that such calculations can give only first order impressions of the correct fluctuations of atmospheric parameters which cause the granular intensity pattern. Yet, response functions are often helpful in preparing and analysing observations to have a first order conception where and how spectral features are formed and how they react on fluctuations of the atmospheric structure.
Acknowledgements
Most of this work was performed while EPR was studying at the Göttingen University with support from the ERASMUS program of the European Union.