The spatial-mark product-density
Mark correlation functions (MCFs) have been used for the characterization of marked point sets for quite some time (see Stoyan & Stoyan 1994 for an instructive introduction and overview). Beisbart & Kerscher (2000) introduced MCFs to cosmology and used them to quantify the luminosity and morphology dependent clustering in the observed galaxy distribution (see also Szapudi et al. 2000). Gottlöber et al. (2002) discussed the correlations of galaxy sized halos depending on the merging history with MCFs (see also Gottlöber et al. 2001). In a recent review Beisbart et al. (2002) show other physical applications of the MCFs and also how the MCFs can be calculated from stochastic models. To make this article self contained, we repeat briefly the basics of MCFs and then extend the formalism to allow for vector marks:
Consider the set of N points
![]() and attach a mark
mi to each point
and attach a mark
mi to each point
![]() resulting in the marked point set
resulting in the marked point set
![]() (Stoyan 1984; Stoyan & Stoyan 1994). In the following we
use a variety of marks: the mass, the absolute value of the angular
momentum, the spin parameter
(Stoyan 1984; Stoyan & Stoyan 1994). In the following we
use a variety of marks: the mass, the absolute value of the angular
momentum, the spin parameter ![]() ,
and as vector valued marks,
the principal axes of the second moment of the mass distribution and
the angular momentum. Let
,
and as vector valued marks,
the principal axes of the second moment of the mass distribution and
the angular momentum. Let ![]() be the mean number density of the
points in space and
be the mean number density of the
points in space and ![]() the probability density of the mark
distribution. The mean mark is then
the probability density of the mark
distribution. The mean mark is then
![]() ,
and the variance is
,
and the variance is
![]() .
We assume that the joint probability
.
We assume that the joint probability
![]() of finding a point at position
of finding a point at position ![]() with mark M,
splits into a space-independent mark probability and the constant mean
density:
with mark M,
splits into a space-independent mark probability and the constant mean
density:
![]() .
.
The spatial-mark product-density
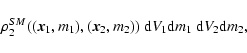 |
(2) |
| = | |||
| = | (3) |
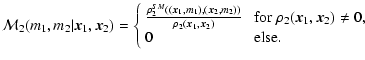 |
(4) |
| (5) |
Starting from these definitions, especially using the conditional mark
density
![]() ,
one may construct several mark-correlation
functions sensitive to different aspects of mark-segregation
(Beisbart & Kerscher 2000). The basic idea was to consider
weighted correlation functions conditional that two points can be
found at a distance r.
For a non-negative weighting function
f(m1,m2) we define the
average over pairs with separation r:
,
one may construct several mark-correlation
functions sensitive to different aspects of mark-segregation
(Beisbart & Kerscher 2000). The basic idea was to consider
weighted correlation functions conditional that two points can be
found at a distance r.
For a non-negative weighting function
f(m1,m2) we define the
average over pairs with separation r:
To calculate such mark correlation functions from the cluster data we use an estimator taking into account the periodic boundaries of the simulation box. We obtain virtually identical results for the estimator without boundary corrections (Beisbart & Kerscher 2000).
For scalar marks the following mark correlation functions have proven to be useful (Beisbart & Kerscher 2000):
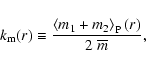 |
(7) |
To study the alignment effects between the clusters we attach to each
cluster the orientation as a vector mark ![]() with
with
![]() .
The
orientation is either given by the direction of the major half-axis of
the mass ellipsoid, or the direction of the angular momentum. The
distance vector between two clusters is
.
The
orientation is either given by the direction of the major half-axis of
the mass ellipsoid, or the direction of the angular momentum. The
distance vector between two clusters is ![]() ,
and the normalized
direction is
,
and the normalized
direction is
![]() .
We consider the following MCFs:
.
We consider the following MCFs:
Copyright ESO 2002