A&A 395, 321-338 (2002)
DOI: 10.1051/0004-6361:20021071
Gravitational collapse of nonsingular logatropic spheres
L. Di G. Sigalotti1 -
F. de Felice2 -
E. Sira1
1 - Instituto Venezolano de Investigaciones Científicas, IVIC,
Apartado 21827, Caracas 1020A, Venezuela
2 -
Dipartimento di Fisica Galileo Galilei, Università di Padova,
via Marzolo n. 8, 35131 Padova, Italy
Received 2 May 2002 / Accepted 19 July 2002
Abstract
We present the results of high-resolved, hydrodynamic calculations
of the spherical gravitational collapse and subsequent accretion of nonsingular
subcritical and critical A=0.2 logatropes, starting with initial configurations
close to hydrostatic equilibrium. Two sequences of models with varying masses and
the same central temperature
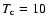 K are defined, which differ only in the
fiducial value of the truncation pressure (
K are defined, which differ only in the
fiducial value of the truncation pressure (
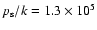 cm-3 K and
cm-3 K and
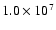 cm-3 K). In all cases, we follow the calculations
until the central protostar has accreted 99% of the total available mass. Thus,
the models may be indicative of early evolution from the Class 0 to the Class I
protostellar phase. We find that the approach to the singular density profile is
never entirely subsonic. In the lower
cm-3 K). In all cases, we follow the calculations
until the central protostar has accreted 99% of the total available mass. Thus,
the models may be indicative of early evolution from the Class 0 to the Class I
protostellar phase. We find that the approach to the singular density profile is
never entirely subsonic. In the lower  sequence, about 6% of the mass
collapses supersonically in a
sequence, about 6% of the mass
collapses supersonically in a
 sphere, while only
sphere, while only  0.02% behaves
this way in a critical (
0.02% behaves
this way in a critical (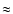 92.05
92.05 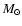 )
logatrope. In the high
)
logatrope. In the high  sequence the same trend is observed, with
sequence the same trend is observed, with  0.7% of the mass now infalling
supersonically at the time of singularity formation in a
0.7% of the mass now infalling
supersonically at the time of singularity formation in a
 sphere.
Immediately after singularity formation, the accretion rate rises steeply in all
cases, reaching a maximum value when the central protostar has accreted
sphere.
Immediately after singularity formation, the accretion rate rises steeply in all
cases, reaching a maximum value when the central protostar has accreted  40%
of its final mass. Thereafter, it decreases monotonically for the remainder
of the evolution. Our models predict peak values of
40%
of its final mass. Thereafter, it decreases monotonically for the remainder
of the evolution. Our models predict peak values of
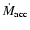 as
high as
as
high as 
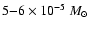 yr-1 for logatropes close to the
critical mass. In contrast, a subcritical
yr-1 for logatropes close to the
critical mass. In contrast, a subcritical
 logatrope reaches a maximum
value of
logatrope reaches a maximum
value of 
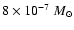 yr-1 for the lower
yr-1 for the lower  sequence
compared to
sequence
compared to 
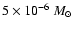 yr-1 for the higher
yr-1 for the higher  case.
The results also imply that the accretion lifetimes are longer in logatropes with
lower
case.
The results also imply that the accretion lifetimes are longer in logatropes with
lower  ,
consistent with the observational evidence that star formation
in clumped regions occurs on shorter timescales compared to more isolated
environments.
,
consistent with the observational evidence that star formation
in clumped regions occurs on shorter timescales compared to more isolated
environments.
Key words: hydrodynamics -
methods: numerical -
stars: formation -
circumstellar matter
Despite recent progress in the field of star formation, the exact way by which stars
form out of a molecular cloud is still unclear. The early stages of star
formation, which observationally correspond to the gap separating starless cloud
cores from young embedded protostars, bracket in time the onset of protostellar
collapse within star-forming regions. A correct theory of star formation must
therefore give a complete description of the gravitational collapse of molecular
cloud cores. We adopt herein the
terminology employed by Reid et al. (2002, hereafter RPW), in
which a molecular cloud is referred to as an extended region containing gas
condensations called clumps. In turn, the clumps may contain dense cores, or cloud
cores, from which single and binary stars may form. The central, densest part of a
core shall be denoted as a protostellar object or protostar.
The isothermal collapse of uniform-density spheres was first described by
Bodenheimer & Sweigart (1968), Larson (1969) and Penston
(1969), who performed hydrodynamical collapse calculations over density
ranges relevant to the initial stages of star formation. Larson and Penston also
derived semianalytically similarity solutions for the isothermal
collapse in which both the density and velocity profiles approach invariant
forms. At large radii, or at times close enough to the upper limit t=0, the
Larson-Penston (LP) solution approaches a singular r-2 density profile
with a constant inflow velocity equal to
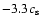 ,
where
,
where 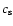 is the isothermal sound speed. The limit t=0, also referred to as the core
formation time, is exactly the time at which the density profile becomes
singular everywhere. Hunter (1977) extended the LP solution through
t=0 and found that for t>0, the flow approaches a free-fall collapse
with the velocity varying as r-1/2 and the density approaching an
r-3/2 profile. In a further paper, Shu (1977) derived a separate set
of self-similar solutions for the isothermal collapse of a sphere. In particular,
one of his solutions - the so-called expansion wave - has played a central
role in the development of the standard theory of star formation (Shu et al.
1987). This solution begins at t=0 with a singular isothermal
sphere (SIS) of density
is the isothermal sound speed. The limit t=0, also referred to as the core
formation time, is exactly the time at which the density profile becomes
singular everywhere. Hunter (1977) extended the LP solution through
t=0 and found that for t>0, the flow approaches a free-fall collapse
with the velocity varying as r-1/2 and the density approaching an
r-3/2 profile. In a further paper, Shu (1977) derived a separate set
of self-similar solutions for the isothermal collapse of a sphere. In particular,
one of his solutions - the so-called expansion wave - has played a central
role in the development of the standard theory of star formation (Shu et al.
1987). This solution begins at t=0 with a singular isothermal
sphere (SIS) of density
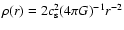 in
hydrostatic equilibrium, where G is the gravitational constant. The sphere
first collapses at the center and then the infall gradually propagates outwards.
This is precisely the inside-out collapse or expansion-wave solution. However,
the SIS model is not applicable to more realistic clouds with
finite central densities such as the marginally stable Bonnor-Ebert sphere
(Ebert 1955; Bonnor 1956). It also predicts
a time-independent central protostellar accretion rate which seems to be
inconsistent with the observed luminosities of young stars
(Kenyon et al. 1994). Such a constant rate is, however, too low
to form massive stars on the timescales suggested by observations (Caselli
& Myers 1995; McLaughlin & Pudritz 1997, hereafter MP97).
in
hydrostatic equilibrium, where G is the gravitational constant. The sphere
first collapses at the center and then the infall gradually propagates outwards.
This is precisely the inside-out collapse or expansion-wave solution. However,
the SIS model is not applicable to more realistic clouds with
finite central densities such as the marginally stable Bonnor-Ebert sphere
(Ebert 1955; Bonnor 1956). It also predicts
a time-independent central protostellar accretion rate which seems to be
inconsistent with the observed luminosities of young stars
(Kenyon et al. 1994). Such a constant rate is, however, too low
to form massive stars on the timescales suggested by observations (Caselli
& Myers 1995; McLaughlin & Pudritz 1997, hereafter MP97).
Hydrodynamic calculations of the collapse of critically stable Bonnor-Ebert
spheres were made by Foster & Chevalier (1993), who showed that
only the innermost 0.05% of the mass follows the LP solution just prior to
the singularity formation (t=0). They also found that about 44% of the
mass falls supersonically with a velocity of
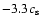 at the time of
singularity formation. One problem with this picture is that such high infall
velocities has never been detected. Magnetic fields offer a way to slow down
the collapse prior to singularity formation, but rapid infall may still occur
thereafter. However, observational evidence in support of the isothermal models
has recently been given by Bacmann et al. (2000) and Alves et al.
(2001), who found, respectively, that the starless core L1544 in Taurus
and the dark cloud Barnard 68 can be very well fitted by the structure of
pressure-bounded Bonnor-Ebert spheres. On the other hand, there is strong evidence
that the nonthermal component of the total velocity dispersion dominates over the
thermal one in massive cores (Caselli & Myers 1995). Significant
nonthermal motion has also been detected in low-mass cores (Fuller & Myers
1992). The properties of such cores cannot be explained by a simple
isothermal equation of state (EOS).
at the time of
singularity formation. One problem with this picture is that such high infall
velocities has never been detected. Magnetic fields offer a way to slow down
the collapse prior to singularity formation, but rapid infall may still occur
thereafter. However, observational evidence in support of the isothermal models
has recently been given by Bacmann et al. (2000) and Alves et al.
(2001), who found, respectively, that the starless core L1544 in Taurus
and the dark cloud Barnard 68 can be very well fitted by the structure of
pressure-bounded Bonnor-Ebert spheres. On the other hand, there is strong evidence
that the nonthermal component of the total velocity dispersion dominates over the
thermal one in massive cores (Caselli & Myers 1995). Significant
nonthermal motion has also been detected in low-mass cores (Fuller & Myers
1992). The properties of such cores cannot be explained by a simple
isothermal equation of state (EOS).
As an alternative to the isothermal EOS, McLaughlin & Pudritz (1996,
hereafter MP96) introduced a pure logatropic EOS in which the pressure depends
on density logarithmically. MP96 showed that the logatropic EOS provides
the best available phenomenological description of the internal structure and
average properties of both molecular clouds and cores of low and high mass. In
particular, a logatrope is consistent with the observed internal
velocity-dispersion profiles of cloud cores and clumps from a variety of
environments. This relation is meant to account for all contributions of the
total gas pressure, including the effects of disordered magnetic fields
(MHD turbulence). MP96 and MP97 also derived solutions for the equilibrium
and self-similar collapse of logatropic spheres. In the limit of large radii,
or small positive times, they found an entire family of singular solutions.
At 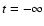 ,
the cloud is nonsingular with
,
the cloud is nonsingular with
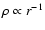 in the outer layers. As it collapses, it approaches a singular profile
in the outer layers. As it collapses, it approaches a singular profile
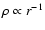 everywhere by t=0. At this time, the solution
coincides with the analytical singular solution to the equation of
hydrostatic equilibrium for a self-gravitating logatrope (MP96). In the
singular logatropic sphere (SLS), the inflow velocity vanishes in accordance
with the physical picture at t<0 of quasistatic evolution towards the
singular profile. This situation is in clear contrast with the Bonnor-Ebert
sphere, where the flow approaches the
everywhere by t=0. At this time, the solution
coincides with the analytical singular solution to the equation of
hydrostatic equilibrium for a self-gravitating logatrope (MP96). In the
singular logatropic sphere (SLS), the inflow velocity vanishes in accordance
with the physical picture at t<0 of quasistatic evolution towards the
singular profile. This situation is in clear contrast with the Bonnor-Ebert
sphere, where the flow approaches the
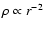 profile with
supersonic velocities. In the opposite limit of small radii, or large
positive times (t>0), the density and velocity near the center tend
to
profile with
supersonic velocities. In the opposite limit of small radii, or large
positive times (t>0), the density and velocity near the center tend
to
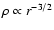 and
and
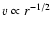 ,
respectively, similar to
the LP solution. The unstable singular equilibrium with
,
respectively, similar to
the LP solution. The unstable singular equilibrium with
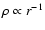 everywhere is the analogous of Shu's (1977) unstable SIS solution,
while the stable nonsingular equilibrium solution is the counterpart of the
hydrostatic Bonnor-Ebert sphere.
everywhere is the analogous of Shu's (1977) unstable SIS solution,
while the stable nonsingular equilibrium solution is the counterpart of the
hydrostatic Bonnor-Ebert sphere.
Recently, RPW performed three-dimensional hydrodynamic calculations of the
collapse of both singular and nonsingular logatropic spheres with a choice of
the kinetic temperature and surface pressure appropriate for isolated star
formation (MP97). They were able to follow the collapse and subsequent
accretion phase of only low-mass logatropes because of limited spatial resolution
in their calculations.
In this paper, we extend the work of RPW by conducting one-dimensional (1D),
hydrodynamic simulations with high spatial resolution to follow the collapse
and subsequent accretion of massive, nonsingular logatropes using the same
fiducial central temperature and truncation pressure employed by MP97 and RPW.
A set of calculation models with a much higher surface pressure representative
of clustered star formation is also presented. In Sect. 2, we outline some
relevant aspects of the logatropic collapse theory introduced by MP96 and MP97.
The initial conditions and methods employed in our model calculations are
described in Sects. 3 and 4. Section 4 also contains the results of some
comparison test cases, including the collapse of a singular
 logatrope. The results of our collapse calculations for both subcritical and
critical nonsingular logatropes are described in Sects. 5 and 6. Finally,
in Sect. 7 we compare our predictions with observations and discuss our
results, while Sect. 8 contains the conclusions.
logatrope. The results of our collapse calculations for both subcritical and
critical nonsingular logatropes are described in Sects. 5 and 6. Finally,
in Sect. 7 we compare our predictions with observations and discuss our
results, while Sect. 8 contains the conclusions.
In this section we briefly review the theory of MP96 and MP97
to facilitate discussion throughout the paper.
MP96 introduced the "pure'' logatropic EOS
![\begin{displaymath}p=p_{\rm c}\left[1+A\ln\left(\frac{\rho}{\rho _{\rm c}}\right)\right]
,
\end{displaymath}](/articles/aa/full/2002/43/aah3666/img46.gif) |
(1) |
where 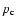 and
and
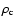 are, respectively, the central cloud
pressure and density, and A is a positive, free parameter. This relation was
formulated to provide a unified treatment of both molecular clouds and cores
of low and high mass. In particular, it guarantees that the total
velocity dispersion
are, respectively, the central cloud
pressure and density, and A is a positive, free parameter. This relation was
formulated to provide a unified treatment of both molecular clouds and cores
of low and high mass. In particular, it guarantees that the total
velocity dispersion
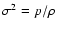 increases with decreasing density
and increasing radius, in accordance with observations that indicate that
the line widths are essentially thermal near the center of real cloud cores
and nonthermal on larger scales. In this way, the central velocity dispersion
in a logatrope is identified with the thermal value
increases with decreasing density
and increasing radius, in accordance with observations that indicate that
the line widths are essentially thermal near the center of real cloud cores
and nonthermal on larger scales. In this way, the central velocity dispersion
in a logatrope is identified with the thermal value
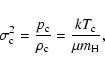 |
(2) |
where k is the Boltzmann constant, 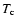 is the central temperature
of the cloud core and
is the central temperature
of the cloud core and 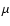 is the mean molecular weight. Note that when
is the mean molecular weight. Note that when
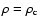 ,
Eq. (1) reduces to
,
Eq. (1) reduces to
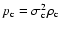 .
The sound speed in a logatrope
is given by
.
The sound speed in a logatrope
is given by
 |
(3) |
except at the center, where
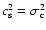 .
Thus, it is
precisely at the center that a correspondence between the isothermal and
logatropic EOS is established. The best fit of Eq. (1) to the observed
internal velocity-dispersion profiles for low mass (Fuller & Myers 1992)
and high mass (Caselli & Myers 1995) cores was obtained for
.
Thus, it is
precisely at the center that a correspondence between the isothermal and
logatropic EOS is established. The best fit of Eq. (1) to the observed
internal velocity-dispersion profiles for low mass (Fuller & Myers 1992)
and high mass (Caselli & Myers 1995) cores was obtained for
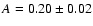 (MP96). For the calculations of this paper we use A=0.2.
(MP96). For the calculations of this paper we use A=0.2.
Once the value of A is specified, we can determine the equilibrium structure
of a logatropic sphere by using Eq. (1) along with the differential equations
governing the motion of a self-gravitating fluid. Under the assumption of
spherical symmetry, these are: the equation of continuity
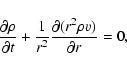 |
(4) |
Euler's equation of motion
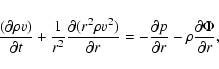 |
(5) |
and Poisson's equation
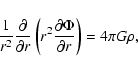 |
(6) |
where
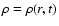 is the mass-density, v=v(r,t) is the fluid velocity,
p=p(r,t) is the gas pressure and
is the mass-density, v=v(r,t) is the fluid velocity,
p=p(r,t) is the gas pressure and
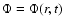 is the gravitational
potential.
is the gravitational
potential.
In a state of exact hydrostatic equilibrium, the velocity v and the temporal
derivatives in Eqs. (4) and (5) vanish. Using Eqs. (1) and (6), the equation
for the balance of forces can be solved analytically to yield the singular
density profile
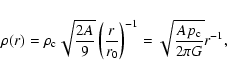 |
(7) |
where
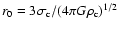 is the
characteristic or scale radius of the spherical core. This solution, which is
the analogous of the SIS solution, defines an unstable equilibrium for the
SLS. A second solution can also be obtained which represents a
pressure-bounded sphere of finite central density. This solution can only be
found through numerical integration of the hydrostatic equation (see Sect. 3)
and is the logatropic analogous of the Bonnor-Ebert sphere.
is the
characteristic or scale radius of the spherical core. This solution, which is
the analogous of the SIS solution, defines an unstable equilibrium for the
SLS. A second solution can also be obtained which represents a
pressure-bounded sphere of finite central density. This solution can only be
found through numerical integration of the hydrostatic equation (see Sect. 3)
and is the logatropic analogous of the Bonnor-Ebert sphere.
MP97 also derived self-similar solutions for the collapse of logatropic spheres
in terms of the similarity variable
x=r/(a) and the dimensionless
density, velocity and mass variables
respectively, where M(r,t) is the total mass within a radius r at time t
and at is a normalization velocity given by
![$a_{t}=[Ap_{\rm c}(4\pi Gt^{2})]^{1/2}$](/articles/aa/full/2002/43/aah3666/img69.gif) .
Here,
.
Here, 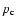 refers to the central
pressure in the initial, precollapse core (
refers to the central
pressure in the initial, precollapse core (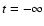 ). For large radii,
or small positive times, MP97 obtained analytically a family of singular
solutions having the form
). For large radii,
or small positive times, MP97 obtained analytically a family of singular
solutions having the form
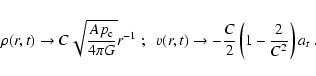 |
(9) |
The core starts to collapse at 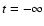 with a density profile at large
radii given by Eq. (9). For inflow v<0, and hence
with a density profile at large
radii given by Eq. (9). For inflow v<0, and hence
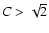 .
When
.
When
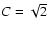 ,
the similarity solution reduces to the analytic singular
profile (7) with v=0. This means that the core is essentially at rest at
the time of singularity formation (t=0). On the other hand, at small
radii (
,
the similarity solution reduces to the analytic singular
profile (7) with v=0. This means that the core is essentially at rest at
the time of singularity formation (t=0). On the other hand, at small
radii (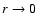 ), or large times (
), or large times (
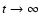 ), the solution becomes
), the solution becomes
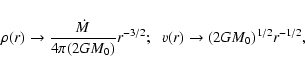 |
(10) |
where
M0=M(0,t) is the mass of the central accreting protostar and
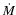 is the accretion rate. These solutions are only valid near
the center and after the singularity formation time. The r-3/2 and r-1/2 scalings for
is the accretion rate. These solutions are only valid near
the center and after the singularity formation time. The r-3/2 and r-1/2 scalings for 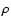 and v, respectively, are
similar to the LP solution and Shu's (1977) SIS collapse. The more
significative
difference between the SIS and SLS solutions lies in the form of the
central accretion rate. From Eqs. (8), it follows that
and v, respectively, are
similar to the LP solution and Shu's (1977) SIS collapse. The more
significative
difference between the SIS and SLS solutions lies in the form of the
central accretion rate. From Eqs. (8), it follows that
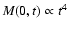 ,
yielding a central accretion rate
,
yielding a central accretion rate
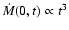 .
In particular, the time-varying central
protostellar accretion rate takes the form
.
In particular, the time-varying central
protostellar accretion rate takes the form
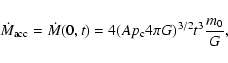 |
(11) |
where m0 is the reduced (dimensionless) mass of the collapsing core.
For the singular logatrope (
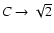 ),
),
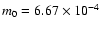 (MP97). The primary function of m0 for a given SLS collapse is just
to set the central mass accretion rate.
(MP97). The primary function of m0 for a given SLS collapse is just
to set the central mass accretion rate.
The collapse of the SLS is qualitatively similar to that of the SIS model.
In both cases, the solution is characterized by an expansion wave
propagating from the origin (r=0). That is, the mass shells of a
collapsing SIS or SLS do not all fall in together, as in homologous
collapse, but in sequence, from the inside out. Each collapsing shell
removes the pressure support from the next, so the instantaneous locus
where collapse starts is an expansion wave moving outwards at the sound
speed. The fractional mass of the central accreting protostar
varies as
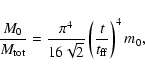 |
(12) |
where
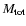 is the total mass of the collapsing core and
is the total mass of the collapsing core and
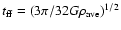 is the mean free-fall
time of the initial (
is the mean free-fall
time of the initial (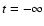 )
core defined in terms of the average
density. The expansion wave reaches the outer surface of the collapsing
core at
)
core defined in terms of the average
density. The expansion wave reaches the outer surface of the collapsing
core at
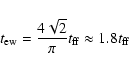 |
(13) |
after which the total mass of the core is collapsing inwards. At this point,
the similarity solution of MP97 predicts that the central protostar
contains only 3% of the total available mass. Thereafter, the expansion
wave is reflected and driven back into the core as a compression wave.
Hence further accretion will no longer obey Eqs. (11) and (12) as was
demonstrated by the numerical calculations of RPW. We defer discussion of
this point to Sect. 4.5, where the collapse of a singular
 logatrope is presented as a comparison test.
logatrope is presented as a comparison test.
There is some direct evidence that the internal structure of turbulent cores
matches the predictions of logatropic equilibrium spheres. This justifies
in part the use of numerical hydrodynamic calculations to examine the
collapse of nonsingular logatropes of both low and high mass.
For example, André et al. (1996) and
Ward-Thompson et al. (1999) reported radial density gradients
approaching
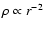 for
for
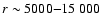 AU, and flattening
to
AU, and flattening
to
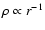 for
for
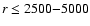 AU in individual cores.
Convincing evidence has been given by Colomé et al. (1996)
and Henning et al. (1998), who detected radial density
gradients consistent with
AU in individual cores.
Convincing evidence has been given by Colomé et al. (1996)
and Henning et al. (1998), who detected radial density
gradients consistent with
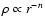 for
for
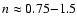 in
the envelopes of massive Herbig Ae/Be stars. Envelopes matching the density
profile of collapsing logatropic spheres have also been reported by Osorio
et al. (1999), who studied the dust thermal spectra of
a number of hot cloud cores, which are thought to be the sites of massive
star formation. More recently, van der Tak et al. (2000) studied the
structure of the envelopes around 14 massive young stars, finding density
profiles consistent with
in
the envelopes of massive Herbig Ae/Be stars. Envelopes matching the density
profile of collapsing logatropic spheres have also been reported by Osorio
et al. (1999), who studied the dust thermal spectra of
a number of hot cloud cores, which are thought to be the sites of massive
star formation. More recently, van der Tak et al. (2000) studied the
structure of the envelopes around 14 massive young stars, finding density
profiles consistent with
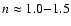 .
Imaging of submillimeter dust
emission from the envelopes of individual young protostars in Taurus and
Perseus by Chandler & Richer (2000) also revealed density variations
consistent with
.
Imaging of submillimeter dust
emission from the envelopes of individual young protostars in Taurus and
Perseus by Chandler & Richer (2000) also revealed density variations
consistent with
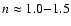 for the youngest sources (Class 0
protostars) in their sample.
for the youngest sources (Class 0
protostars) in their sample.
The above observational results point towards a prevalence of nonthermal
support in massive young stellar objects, yielding power-law density
variations that match the internal structure of both equilibrium (n=1.0)
and collapsing (n=1.5) logatropic spheres. Thus, in contrast with most
previous studies, the present logatropic collapse model calculations will
apply to massive star formation.
The properties of A=0.2 pressure-bounded logatropes have been calculated by
MP97, assuming fiducial values of the central temperature (
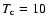 K)
and surface pressure (
K)
and surface pressure (
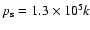 cm-3 K) appropriate
for isolated star formation. For convenience in establishing the initial
conditions and parameters used in our collapse calculations, we have
recalculated the internal structure of A=0.2 pressure-truncated logatropes.
cm-3 K) appropriate
for isolated star formation. For convenience in establishing the initial
conditions and parameters used in our collapse calculations, we have
recalculated the internal structure of A=0.2 pressure-truncated logatropes.
The initial core model is chosen to be a logatrope close to hydrostatic
equilibrium. For pressure-bounded spheres, the core properties are set by
the central temperature 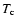 ,
surface pressure
,
surface pressure  and the
truncation radius R at which the internal pressure equals a confining
pressure. For all models,
we use A=0.2,
and the
truncation radius R at which the internal pressure equals a confining
pressure. For all models,
we use A=0.2,
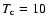 K and
K and 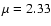 .
Two sequences of nonsingular collapse models with varying core mass and
truncation radius are defined which differ only in the fiducial value of
the surface pressure
.
Two sequences of nonsingular collapse models with varying core mass and
truncation radius are defined which differ only in the fiducial value of
the surface pressure  .
The first sequence of models use
.
The first sequence of models use
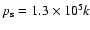 cm-3 K as in MP97 and RPW, while the
second sequence employs
cm-3 K as in MP97 and RPW, while the
second sequence employs
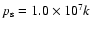 cm-3 K, which
is more representative of the conditions observed in regions of clustered
star formation.
cm-3 K, which
is more representative of the conditions observed in regions of clustered
star formation.
For any of these sequences, we solve numerically the equation of hydrostatic
equilibrium, as obtained from Eq. (5) by setting terms in v and
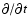 to zero, coupled with the logatropic EOS (1) and
Poisson's Eq. (6). Defining the dimensionless radius
to zero, coupled with the logatropic EOS (1) and
Poisson's Eq. (6). Defining the dimensionless radius 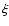 and
gravitational potential
and
gravitational potential 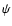 as (see Appendix A of MP97)
as (see Appendix A of MP97)
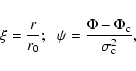 |
(14) |
where
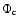 denotes the gravitational potential at the core
center, the equation of hydrostatic equilibrium integrates to
denotes the gravitational potential at the core
center, the equation of hydrostatic equilibrium integrates to
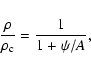 |
(15) |
and the Poisson equation transforms into the Lane-Emden type equation
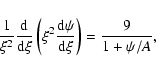 |
(16) |
with boundary conditions such that at 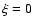 ,
,
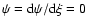 and for
and for 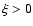 ,
,
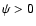 .
For given A, the
solution of Eq. (16) determines the density profile of equilibrium
nonsingular logatropes. The radial integration of this equation was started
from
.
For given A, the
solution of Eq. (16) determines the density profile of equilibrium
nonsingular logatropes. The radial integration of this equation was started
from 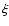 sufficiently close to the origin using an appropriate series
expansion for
sufficiently close to the origin using an appropriate series
expansion for 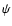 valid when
valid when 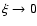 .
In all cases, we defined a
sphere of maximum truncation radius
.
In all cases, we defined a
sphere of maximum truncation radius
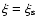 and subdivided its
volume into N concentric shells of uniform width
and subdivided its
volume into N concentric shells of uniform width 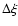 .
The value
of
.
The value
of 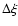 was chosen such that the starting radius was always at a
distance <<0.01 from the origin in order to get expansion values for
was chosen such that the starting radius was always at a
distance <<0.01 from the origin in order to get expansion values for
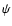 and
and
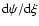 satisfying Eq. (16) within less than 10-8%.
In practice, a value of
satisfying Eq. (16) within less than 10-8%.
In practice, a value of
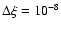 has been used yielding a
solution for
has been used yielding a
solution for 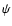 accurate within one part in 8.
accurate within one part in 8.
Table 1 lists the properties of the first calculated sequence of
equilibria (see Table 1 of MP97) using fiducial values of  representative of isolated star-forming regions. The properties of
equilibria using
representative of isolated star-forming regions. The properties of
equilibria using  consistent with cluster-forming regions
are given in Table 2. The entries in each table specify, starting from
the first column, the dimensionless truncation radius R/r0, the
central density and pressure contrasts, the ratios of mean density and
mass averaged line width to the central values, the mass of the core in
solar mass units and the mean free-fall time. The last row in each
table lists the properties of the critically stable core with truncation
radius given by (MP96)
consistent with cluster-forming regions
are given in Table 2. The entries in each table specify, starting from
the first column, the dimensionless truncation radius R/r0, the
central density and pressure contrasts, the ratios of mean density and
mass averaged line width to the central values, the mass of the core in
solar mass units and the mean free-fall time. The last row in each
table lists the properties of the critically stable core with truncation
radius given by (MP96)
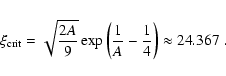 |
(17) |
The critical radius is not affected by changing the surface pressure
because for any given value of A, a pressure-bounded logatrope admits
only one critical mode. MP96 also gave an expression for the critical
mass of an A=0.2 logatrope, namely
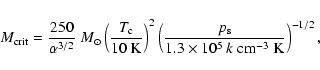 |
(18) |
where 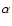 is a parameter that depends on the strength of any
magnetic field threading the core. In the absence of any magnetic
field, MP97 gives the value
is a parameter that depends on the strength of any
magnetic field threading the core. In the absence of any magnetic
field, MP97 gives the value
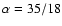 .
Using this value in Eq. (18)
with
.
Using this value in Eq. (18)
with
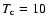 K and
K and
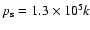 cm-3 K
yields a critical mass
cm-3 K
yields a critical mass
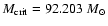 slightly larger
than the value of
slightly larger
than the value of
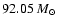 in Table 1. This value is consistent
with having
in Table 1. This value is consistent
with having
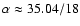 in Eq. (18). Since
in Eq. (18). Since
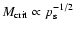 ,
an increase of
,
an increase of  by
two orders of magnitude lowers the critical mass by a factor of
by
two orders of magnitude lowers the critical mass by a factor of
 10 (see Table 2). Furthermore, in accordance with the stability
criteria derived by MP96, nonsingular logatropes of total mass
10 (see Table 2). Furthermore, in accordance with the stability
criteria derived by MP96, nonsingular logatropes of total mass
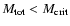 ,
or equivalently of radius
,
or equivalently of radius
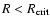 ,
will be stable against collapse. Cores with
,
will be stable against collapse. Cores with
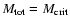 ,
or
,
or
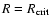 ,
will be marginally stable, while for
,
will be marginally stable, while for
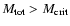 ,
or
,
or
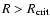 ,
the cores will always
be unstable to collapse.
,
the cores will always
be unstable to collapse.
In Fig.1 we show the singular and nonsingular density profiles for the
critically stable logatrope in the sequence of Table 1. We see that
the nonsingular profile follows the singular behavior closely over a
broad range of outer radii.
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f1.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg130.gif) |
Figure 1:
Density profile of the A=0.2 critically stable logatrope
of Table 1. Both the singular and nonsingular profiles are shown. |
| Open with DEXTER |
As a suitable comparison test case, we present high-resolution
calculations of the collapse of a singular
 logatrope.
The same model was previously calculated by RPW using 3D hydrodynamics.
This test also allows for a direct comparison with the self-similar
solutions of MP97.
logatrope.
The same model was previously calculated by RPW using 3D hydrodynamics.
This test also allows for a direct comparison with the self-similar
solutions of MP97.
The singular equilibrium density profile is given by Eq. (7). This
form corresponds to
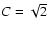 and
and
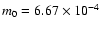 ,
in
the terminology of MP97. Since at r=0, the density becomes infinite
care must be taken in handling the central region containing the
singularity. One trivial way of skipping over this problem is to assign
a finite density to this region by integrating Eq. (7) over a small
radius and then dividing the result by the volume of the region. A
similar approach was used by RPW to truncate the singular profile in
their Cartesian-coordinate based calculations. This method yields for
the central finite density the expression
,
in
the terminology of MP97. Since at r=0, the density becomes infinite
care must be taken in handling the central region containing the
singularity. One trivial way of skipping over this problem is to assign
a finite density to this region by integrating Eq. (7) over a small
radius and then dividing the result by the volume of the region. A
similar approach was used by RPW to truncate the singular profile in
their Cartesian-coordinate based calculations. This method yields for
the central finite density the expression
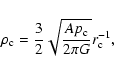 |
(19) |
where  is chosen such that
is chosen such that
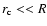 .
The smaller the
value of
.
The smaller the
value of  ,
the more singular will appear the profile in the
proximity of the center. If the surface density
,
the more singular will appear the profile in the
proximity of the center. If the surface density  and radius
R of the singular core are set by the corresponding values in a
nonsingular sphere, use of Eq. (7) gives a relation for the central
pressure of the form
and radius
R of the singular core are set by the corresponding values in a
nonsingular sphere, use of Eq. (7) gives a relation for the central
pressure of the form
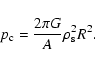 |
(20) |
This can be inserted in Eqs. (7) and (19) to completely determine the
singular density distribution. Thus, using the parameters in Table 1
for a
 nonsingular sphere, the best fit to a corresponding
nonsingular sphere, the best fit to a corresponding
 SLS can be obtained by choosing
SLS can be obtained by choosing 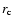 in Eq. (19)
as small as possible. With this choice of
in Eq. (19)
as small as possible. With this choice of
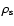 and R,
the mass of the resulting SLS will be slightly higher than that of the
corresponding nonsingular sphere because the inner singular density region
contributes with a small mass excess (see Fig. 1). For a
and R,
the mass of the resulting SLS will be slightly higher than that of the
corresponding nonsingular sphere because the inner singular density region
contributes with a small mass excess (see Fig. 1). For a
 SLS,
this excess is only about 1% of the total mass of the nonsingular
sphere (see Sect. 4.5).
SLS,
this excess is only about 1% of the total mass of the nonsingular
sphere (see Sect. 4.5).
For the calculations of this paper we have used a 1D hydrodynamics
code based on an extension of the Lagrangian-remap scheme originally
developed by Lufkin & Hawley (1993). In its complete version,
the code solves the equations of hydrodynamics for a self-gravitating,
reacting fluid including the effects of viscosity, thermal conduction,
cooling and heating, generation of chemical species and net reaction
rate. Here we shall only briefly describe the methods employed in a
simplified version of the code for solving Eqs. (4)-(6), coupled to
the logatropic EOS (1).
The code solves Eqs. (4) and (5) written in Lagrangian integral form
through the use of second-order, finite-difference (FD) methods on a
staggered spherical mesh in which scalar quantities, such as the
density and pressure, are assigned to the volume centers of
concentric shells and vector quantities, such as the velocity, are
centered at the surfaces between adjacent shells. Temporal
second-order accuracy is also enforced by solving the Lagrangian
equations in a predictor-corrector fashion. For problems involving
more complicated physics, both the predictor and corrector steps
rely on a multistep procedure to advance the solution. This
amounts to operationally splitting the source contributions in the
momentum and energy equations so that the final update after a given
time step involves a sequence of separate substeps. For the present
case, where the only sources in Eq. (5) are the pressure and
gravitational forces, the predictor-corrector scheme reduces to a
single-step procedure for solving the equation
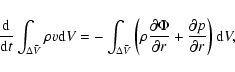 |
(21) |
where the spatial integration is over the volume
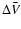 of the shifted vector shells. The continuity Eq. (4) reduces
to the mass conservation statement
of the shifted vector shells. The continuity Eq. (4) reduces
to the mass conservation statement
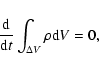 |
(22) |
where now the integration is taken over the volume 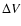 of
scalar shells.
of
scalar shells.
In this way, Eq. (21) is solved explicitly by evaluating the fluid
acceleration according to
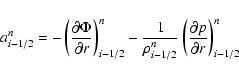 |
(23) |
so that new Lagrangian radii and velocities are obtained using the
following simple scheme
rn+1i-1/2=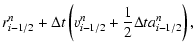 |
vn+1i-1/2=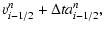 |
(24) |
where the superscripts denote the time level
(
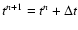 )
and the subscripts are used to label the
shell interfaces defined at half the distance between consecutive
zone-centered positions, i.e.,
)
and the subscripts are used to label the
shell interfaces defined at half the distance between consecutive
zone-centered positions, i.e.,
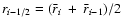 .
Because of the assumption of spherical symmetry, the Poisson Eq. (6) can be
integrated once to give
.
Because of the assumption of spherical symmetry, the Poisson Eq. (6) can be
integrated once to give
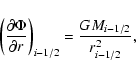 |
(25) |
where Mi-1/2 is the mass interior to ri-1/2. In order to
accommodate the logatropic EOS (1), we have modified the calculation
of the pressure gradient term in Eq. (23) following the method
suggested by RPW, which relies on the observation that the radial
derivative of the logatropic pressure can be expressed as
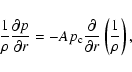 |
(26) |
which in FD form becomes
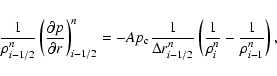 |
(27) |
where
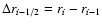 is the interdistance between
consecutive volume shell-centers, where scalar variables are
defined.
is the interdistance between
consecutive volume shell-centers, where scalar variables are
defined.
An identical sequence to (24) is employed in the corrector part
with the only change being that
ani-1/2 is now replaced
with its time-centered value
an+1/2i-1/2. Because of mass
conservation during the Lagrangian step, time-centered values of
the potential gradients follows directly from use of the
time-centered radii
rn+1/2i-1/2=(rni-1/2+rn+1i-1/2)/2 in Eq. (25).
Similarly, time-centered values of the pressure forces are obtained
from the time-centered densities using
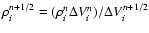 ,
where
,
where 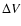 is the volume of a particular concentric shell.
is the volume of a particular concentric shell.
After completion of the Lagrangian step, the solution is remapped
back onto an Eulerian grid, which can be either fixed or moving, by
assuming piecewise-linear representations of the density and
velocity to preserve the second-order accuracy of the Lagrangian
solution. The remap equations for the density and velocity are
constructed directly from the laws of mass and momentum conservation.
A detailed account of the remap formulation is given by Lufkin &
Hawley (1993) and so it will not be repeated here. Since the
Eulerian grid is allowed to follow the Lagrangian distortions, the
remap procedure is adaptive in nature. In order to guarantee
entropy generation in the presence of shocks and spread them over
a fixed number of zones, the code employs a scalar formulation for
the artificial viscosity. However, for the present collapse
calculations the artificial viscosity has never been used to
mediate the arising shocks.
In addition to this spherical-coordinate based version of the code,
a Cartesian-like version has also been written. Both versions have
been tested on a variety of problems including the standard
Riemann shock tube (Sod 1978), the propagation of a shock
wave in both planar and spherical geometry (Noh 1987), the
collapse of a pressureless sphere and of a protostellar gas cloud
to stellar densities (Sigalotti & Klapp 2001) and the
implosion of a neutron star (May & White 1966). In
particular, the results of Noh's problem and the collapse of
a neutron star are described in Sigalotti & Mendoza-Briceño
(2002), where the code has been applied to hydrodynamic
models of solar coronal loops.
Under the assumption of spherical symmetry, the velocity goes to
zero at the origin (r=0), which then allows the use of a reflecting
inner boundary condition. Starting with a nonsingular density profile,
the collapse towards singularity formation is followed with the
Lagrangian version of the code, i.e., without repositioning the fluid
elements after a time step. This allows to better resolve the fluid's
behavior near the origin. However, close to singularity formation, the
central core regions develop extremely high densities and velocities,
causing a computational block when the Lagrangian version of the code
is used. At this time, the innermost shells shrink to practically zero
width, making the time step to become extremely small. Even if the
Eulerian remap procedure is activated before singularity formation,
this will not be of help because the infalling material may shock as
it encounters the singularity. When this happens, high velocities
develop behind the shock also leading to a drastic reduction of the
time step. To avoid these problems, an inflow/outflow boundary
condition is enforced away from the origin at the time of singularity
formation. This is done by lopping off the smallest grid shells into
a sink cell. This boundary condition, modelled after that of Boss &
Black (1982), is here implemented following a treatment very
similar to that of Foster & Chevalier (1993).
The use of a central sink cell effectively removes from the calculation
the details of the flow around the singularity and isolates it from
the rest of the grid. In this way, we can maintain a reasonably large
time step and follow the accretion of the core envelope over its own
collapse timescale. Because the flow across the sink cell boundary
is supersonic off the grid, the inflow/outflow does not affect the
calculation. Once the sink cell is activated, the subsequent collapse is
followed using the Eulerian version of the code. The activation is
done automatically in the course of the calculation by monitoring the
size of the time step. Roughly independently of the initial spatial
resolution, the time of singularity formation is achieved when the
ratio of the current time step to the initial one becomes less than
10-3. At this point, the sink cell is activated. For runs with
400 radial points, the central regions are highly resolved at the time
of singularity formation so that the sink cell usually occupies a very
small spherical volume with the first 10 - 20 computational shells
merging into the sink region.
The mass which enters the sink is assumed to be condensed into a
central point mass located at the origin. This mass will no longer
interact hydrodynamically with the rest of the grid, but only
gravitationally via a point mass potential (Boss & Black 1982;
RPW). In this way, the gravitational acceleration term in Eq. (25)
is modified according to
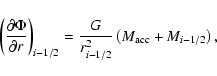 |
(28) |
where
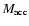 is the mass within the sink region. Its time
evolution is calculated by subtracting to the rest of the grid the
mass that has crossed the sink boundary after a time step and adding
it to the central point mass. For convenience, the density of material
within the sink is set to a spatially uniform value and reset after
each time step to the density of the first adjacent grid shell. Since
the sink density determined this way is not related to the true density
in that region, the pressure gradients at the sink surface are
determined by linear extrapolation from the pressure gradients in the
adjacent two shell surfaces. This inflow/outflow boundary condition
effectively separates hydrodynamically the mass within the sink cell
(protostar) from the rest of the collapsing core (envelope), while
maintaining the gravitational interaction between the two regions as
the dominant coupling process (Boss & Black 1982).
is the mass within the sink region. Its time
evolution is calculated by subtracting to the rest of the grid the
mass that has crossed the sink boundary after a time step and adding
it to the central point mass. For convenience, the density of material
within the sink is set to a spatially uniform value and reset after
each time step to the density of the first adjacent grid shell. Since
the sink density determined this way is not related to the true density
in that region, the pressure gradients at the sink surface are
determined by linear extrapolation from the pressure gradients in the
adjacent two shell surfaces. This inflow/outflow boundary condition
effectively separates hydrodynamically the mass within the sink cell
(protostar) from the rest of the collapsing core (envelope), while
maintaining the gravitational interaction between the two regions as
the dominant coupling process (Boss & Black 1982).
Activation of the sink cell before singularity formation makes no
difference in the results provided that a supersonic inflow has
already been established in the central regions. The sink cell can
then be viewed as a useful numerical tool to alleviate the problem
of increasingly small time steps, permitting in this way to record
the mass accretion history of the central protostar.
The outer core surface is handled by means of a constant-pressure
boundary condition, in which the pressure there is kept in time
at a constant value equal to the initial truncation pressure
 .
This boundary condition was developed by Boss &
Black (1982) and thereafter used widely in many collapse
calculations (e.g., Foster & Chevalier 1993; RPW).
Although the velocity immediately outside the external surface is
zeroed such that there is no mass entering the grid, the velocity
at the core surface can vary in such a way as to keep the pressure
there at a constant value. In this way, the outer boundary is
strictly outflow allowing mass to leave the grid as needed. For
a typical calculation, the amount of mass that leaves the grid this
way is negligible and so the total mass is essentially conserved.
Physically, this
is consistent with having a growing central protostar accreting
from a finite mass reservoir.
.
This boundary condition was developed by Boss &
Black (1982) and thereafter used widely in many collapse
calculations (e.g., Foster & Chevalier 1993; RPW).
Although the velocity immediately outside the external surface is
zeroed such that there is no mass entering the grid, the velocity
at the core surface can vary in such a way as to keep the pressure
there at a constant value. In this way, the outer boundary is
strictly outflow allowing mass to leave the grid as needed. For
a typical calculation, the amount of mass that leaves the grid this
way is negligible and so the total mass is essentially conserved.
Physically, this
is consistent with having a growing central protostar accreting
from a finite mass reservoir.
The ability of the code to maintain the equilibrium of a
stable logatropic sphere was tested for both the Lagrangian and the
Eulerian mode. Referring to the equilibrium models of Table 1, we
followed the evolution of subcritical logatropes
(
R/r0<24.367) of mass 1, 10, 50 and 90 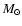 for more
than 100
for more
than 100
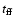 .
The calculations were made using initial
grid resolutions corresponding to 200 and 400 uniformly spaced
radial points. The
.
The calculations were made using initial
grid resolutions corresponding to 200 and 400 uniformly spaced
radial points. The
 logatrope with 200 zones oscillated
about equilibrium with deviations from the initial density profile
of
logatrope with 200 zones oscillated
about equilibrium with deviations from the initial density profile
of  0.02% over periods of about 20
0.02% over periods of about 20
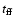 and velocities
never exceeding
and velocities
never exceeding
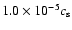 .
The 400 zones calculation
produced oscillations in the density of
.
The 400 zones calculation
produced oscillations in the density of  0.009% and maximum
velocities less than
0.009% and maximum
velocities less than
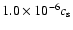 .
For comparison RPW,
reported velocities less than
.
For comparison RPW,
reported velocities less than 
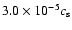 for the same model calculation at roughly comparable grid resolutions.
for the same model calculation at roughly comparable grid resolutions.
The code was also able to maintain the equilibrium structure of more
massive logatropes for both types of calculations (Lagrangian and
Eulerian). The 10, 50 and 90 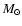 cores with 200 radial zones,
experienced oscillations about the equilibrium density with deviations of
cores with 200 radial zones,
experienced oscillations about the equilibrium density with deviations of
 0.06, 0.1 and 0.35%, respectively. Much lower deviations were
obtained in the high-resolution (400 zones) calculations. For the more
critical (90
0.06, 0.1 and 0.35%, respectively. Much lower deviations were
obtained in the high-resolution (400 zones) calculations. For the more
critical (90 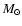 )
case, the maximum velocities achieved never
surpassed peaks of
)
case, the maximum velocities achieved never
surpassed peaks of 
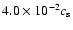 .
These results
show that the code is making a good job in maintaining for long times
the equilibrium of stable logatropes even for masses close to the
critical value.
.
These results
show that the code is making a good job in maintaining for long times
the equilibrium of stable logatropes even for masses close to the
critical value.
In this subsection, we describe the results obtained for the collapse of
a singular
 logatrope using the Eulerian version of the
code. This test calculation provides direct comparison with the
theoretical self-similar solution of MP97 and the numerical calculations
of RPW.
logatrope using the Eulerian version of the
code. This test calculation provides direct comparison with the
theoretical self-similar solution of MP97 and the numerical calculations
of RPW.
In contrast with the nonsingular collapse cases, the singular collapse
is started in the presence of a central sink cell. The initial profile
is mapped onto a spherical grid of 200 uniformly spaced radial points
as described in Sect. 3.2. The sink cell is chosen such that its
boundary is made to coincide with the second shell interface from the
origin, of radius
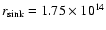 cm and corresponding
to a small fraction (
cm and corresponding
to a small fraction (
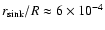 )
of the total
truncated core radius. We assign to the sink region an initial density
given by Eq. (19) with
)
of the total
truncated core radius. We assign to the sink region an initial density
given by Eq. (19) with
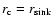 and
and 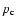 as
defined by Eq. (20). As in RPW, an initial 25% enhancement is applied
to the sink density so that the core is slightly out of hydrostatic
balance and begins to collapse slowly. With this choice of the initial
parameters, the mass at t=0 within the sink boundary is
as
defined by Eq. (20). As in RPW, an initial 25% enhancement is applied
to the sink density so that the core is slightly out of hydrostatic
balance and begins to collapse slowly. With this choice of the initial
parameters, the mass at t=0 within the sink boundary is
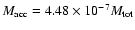 ;
a very small fraction of the
total core mass (
;
a very small fraction of the
total core mass (
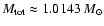 ). Compared
to a
). Compared
to a
 nonsingular logatrope, the SLS will be in excess of
nonsingular logatrope, the SLS will be in excess of
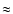 0.0143
0.0143 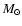 due to the inner singular density region.
due to the inner singular density region.
Figure 2 shows the radial velocity profiles at different times during the
initial collapse phase. The solid lines in the figure correspond to the
analytic MP97's expansion-wave solution. The sequence of times was chosen
to facilitate comparison with the results of RPW (their Fig. 5). The
maximum deviations from the SLS collapse solutions of MP97 occur at early
times (0.35 and 0.5
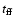 )
as shown in Fig. 2. This is a
reflection of the initial density distribution near the center not being
exactly singular as in the analytic case. Later on in the collapse the
numerical and analytic solutions achieve a much better agreement. Also
note that at
)
as shown in Fig. 2. This is a
reflection of the initial density distribution near the center not being
exactly singular as in the analytic case. Later on in the collapse the
numerical and analytic solutions achieve a much better agreement. Also
note that at
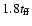 ,
when the expansion wave reaches the surface
of the collapsing core, the numerical results agree with the analytic
predictions. Figure 3a depicts the density profiles throughout the core
size for the same times of Figs. 2 and 3b shows a central
amplification of the same data. We see that the numerical
solution closely follows the analytic predictions of MP97 at all radii
up to
,
when the expansion wave reaches the surface
of the collapsing core, the numerical results agree with the analytic
predictions. Figure 3a depicts the density profiles throughout the core
size for the same times of Figs. 2 and 3b shows a central
amplification of the same data. We see that the numerical
solution closely follows the analytic predictions of MP97 at all radii
up to
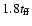 .
After this time, the expansion wave leaves the
core and we can no longer follow its behavior. This is more clearly
seen in Fig. 2, where at
.
After this time, the expansion wave leaves the
core and we can no longer follow its behavior. This is more clearly
seen in Fig. 2, where at
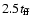 the numerical solution matches
the analytic velocity profile only within the truncation radius. However,
we can follow the subsequent collapse of the core and track the central
protostellar accretion for sufficiently long times. After
the numerical solution matches
the analytic velocity profile only within the truncation radius. However,
we can follow the subsequent collapse of the core and track the central
protostellar accretion for sufficiently long times. After
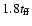 ,
the outer core regions become more and more depleted
during further collapse. Meanwhile the inner regions achieve progressively
higher densities as more matter is being condensed by the collapse itself.
This behavior can be interpreted as a result of the expansion wave being
reflected and then driven back into the core as a compression wave.
,
the outer core regions become more and more depleted
during further collapse. Meanwhile the inner regions achieve progressively
higher densities as more matter is being condensed by the collapse itself.
This behavior can be interpreted as a result of the expansion wave being
reflected and then driven back into the core as a compression wave.
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f2.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg165.gif) |
Figure 2:
Radial velocity profiles (filled circles) compared with the
analytic expansion-wave solution of MP97 (solid lines) for the collapse
of a singular
 logatrope, as obtained using the Eulerian
version of the code with 200 radial points. The sequence of times,
starting from the lowest curves, is
logatrope, as obtained using the Eulerian
version of the code with 200 radial points. The sequence of times,
starting from the lowest curves, is
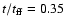 ,
0.5, 1.0,
1.25, 1.8 and 2.5. The dashed vertical line marks the truncation
radius of the core. ,
0.5, 1.0,
1.25, 1.8 and 2.5. The dashed vertical line marks the truncation
radius of the core. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f3a.eps}\par\includegraphics[width=8.8cm]{h3666f3b.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg166.gif) |
Figure 3:
a) Density profiles through the entire radius of the core
compared with the analytic expansion-wave solution of MP97 (solid lines)
for the collapse of a singular
 logatrope, as obtained using
the Eulerian version of the code with 200 radial points. In b) an
amplification of the central core regions is shown for the same data.
A sequence of times is presented, corresponding to
logatrope, as obtained using
the Eulerian version of the code with 200 radial points. In b) an
amplification of the central core regions is shown for the same data.
A sequence of times is presented, corresponding to
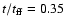 (filled cicles), 0.5 (plus signs), 1.0 (asterisks), 1.25 (open circles)
and 1.8 (crosses). The dashed vertical line in a) marks the truncation
radius of the core. (filled cicles), 0.5 (plus signs), 1.0 (asterisks), 1.25 (open circles)
and 1.8 (crosses). The dashed vertical line in a) marks the truncation
radius of the core. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f4.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg167.gif) |
Figure 4:
Time evolution of the central mass accretion for the
collapse of a singular
 logatrope (solid line) compared
with a fit to the analytic self-similar prediction of MP97 (dashed
line) as obtained using Eq. (29). Each curve refers to the logarithm
of the central protostellar mass in units of the total core mass.
logatrope (solid line) compared
with a fit to the analytic self-similar prediction of MP97 (dashed
line) as obtained using Eq. (29). Each curve refers to the logarithm
of the central protostellar mass in units of the total core mass. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f5.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg168.gif) |
Figure 5:
Time evolution of the central mass accretion and central mass
accretion rate for the collapse of a singular
 logatrope.
The solid lines show the variation of
logatrope.
The solid lines show the variation of
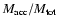 (thin line) and d (thin line) and d
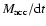 in units of
in units of
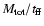 (thick line). The dashed line is the fit
to the analytical prediction of MP97 given by Eq. (29).
(thick line). The dashed line is the fit
to the analytical prediction of MP97 given by Eq. (29). |
| Open with DEXTER |
Figure 4 shows the time evolution of the mass contained within the sink
cell,
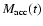 ,
in units of the total core mass. The evolution
of the
,
in units of the total core mass. The evolution
of the
 singular collapse was continued until about
singular collapse was continued until about
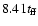 by which time more than 90% of the available core
mass has accreted onto the central protostar. Also shown in the figure
is a two-parameter fit to the anlytical solution given by
by which time more than 90% of the available core
mass has accreted onto the central protostar. Also shown in the figure
is a two-parameter fit to the anlytical solution given by
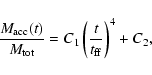 |
(29) |
where
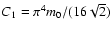 is a scaling factor given by
the constant coefficient in Eq. (12). The second fitting parameter
is a scaling factor given by
the constant coefficient in Eq. (12). The second fitting parameter
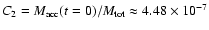 accounts
for the fact that the singularity which is numerically represented by
the sink cell has initially a small, but finite mass. The use of Eq. (29)
tells us in which measure and how long the numerical solution follows
the analytic prediction
accounts
for the fact that the singularity which is numerically represented by
the sink cell has initially a small, but finite mass. The use of Eq. (29)
tells us in which measure and how long the numerical solution follows
the analytic prediction
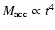 .
By
.
By
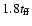 ,
when the expansion wave leaves the core
,
when the expansion wave leaves the core
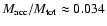 ,
which is very close to the
analytically predicted value of 0.03 (see Sect. 2.1). Accretion onto
the central protostar follows the t4 behavior until approximately
,
which is very close to the
analytically predicted value of 0.03 (see Sect. 2.1). Accretion onto
the central protostar follows the t4 behavior until approximately
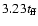 by which time about 32% of the total mass has fallen
into the central sink. For comparison, RPW found that their solution
followed the t4 behavior until
by which time about 32% of the total mass has fallen
into the central sink. For comparison, RPW found that their solution
followed the t4 behavior until 
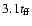 ,
at which time
the central protostar has accreted 35% of the total core mass. Figure 5
also shows the time variation of
,
at which time
the central protostar has accreted 35% of the total core mass. Figure 5
also shows the time variation of
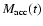 along with that of
the central accretion rate
along with that of
the central accretion rate
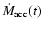 .
We see that all curves,
including the fit given by Eq. (29), intersects at
.
We see that all curves,
including the fit given by Eq. (29), intersects at 
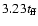 .
After this time, the accretion rate increases a little bit more reaching
a maximum value
.
After this time, the accretion rate increases a little bit more reaching
a maximum value
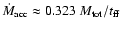 by
by
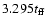 ,
and then slows down for the remainder of the evolution.
As was outlined by RPW, this behavior is expected because the accreting
central protostar is drawing mass from a finite reservoir. Once the
expansion wave reaches the outer boundary, it will not set new mass into
collapse and so the flow of inward-moving material cannot be maintained
at the same rate. Further, on comparing with the results of RPW, we see
that Fig. 5 reproduces very well the results in their Fig. 8. By extending
the validity of the self-similar solution beyond
,
and then slows down for the remainder of the evolution.
As was outlined by RPW, this behavior is expected because the accreting
central protostar is drawing mass from a finite reservoir. Once the
expansion wave reaches the outer boundary, it will not set new mass into
collapse and so the flow of inward-moving material cannot be maintained
at the same rate. Further, on comparing with the results of RPW, we see
that Fig. 5 reproduces very well the results in their Fig. 8. By extending
the validity of the self-similar solution beyond
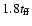 ,
MP97
predicted that 100% of the mass in a SLS collapse would be accreted by
,
MP97
predicted that 100% of the mass in a SLS collapse would be accreted by
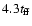 .
Because of the decline of the accretion rate, the present
calculations show that more than twice this time is actually required by
the central protostar to accrete
.
Because of the decline of the accretion rate, the present
calculations show that more than twice this time is actually required by
the central protostar to accrete  90% of the total mass. This
result also follows the predictions made by RPW.
90% of the total mass. This
result also follows the predictions made by RPW.
![\begin{figure}
\par\includegraphics[width=8.3cm]{h3666f6a.eps}\includegraphics[width=8.3cm]{h3666f6b.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg182.gif) |
Figure 6:
a) Density and b) radial velocity profiles in the collapse of
a perturbed nonsingular
 core with initial parameters as
given in Table 1. The sequence of times, starting from the lowest curves,
is
core with initial parameters as
given in Table 1. The sequence of times, starting from the lowest curves,
is
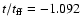 (initial density profile) in a), and -0.189,
(initial density profile) in a), and -0.189,
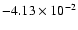 , ,
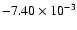 , ,
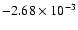 , ,
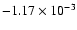 and 0 (time of singularity formation) in a) and
b), respectively.
In a), the inclined dashed line indicates a
and 0 (time of singularity formation) in a) and
b), respectively.
In a), the inclined dashed line indicates a
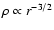 variation and the vertical one marks the scale radius r0 of the
core. The better inner resolution shown in b) is an effect of the
density being staggered with respect to the velocity in the present
calculations. variation and the vertical one marks the scale radius r0 of the
core. The better inner resolution shown in b) is an effect of the
density being staggered with respect to the velocity in the present
calculations. |
| Open with DEXTER |
In this section, we describe the results of the collapse of nonsingular
spheres, starting with initial parameters as listed in Table 1. We
define a sequence of seven model calculations with both subcritical
(1, 10, 50, 60, 80 and 90 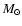 )
and critical
(
)
and critical
(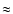 92.05
92.05 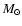 )
masses. All these models have the same
fiducial truncation pressure
)
masses. All these models have the same
fiducial truncation pressure
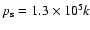 cm-3 K
and so they may be representative of star-forming cloud cores in an
isolated environment.
If we increase the equilibrium density
profile
cm-3 K
and so they may be representative of star-forming cloud cores in an
isolated environment.
If we increase the equilibrium density
profile
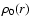 of a subcritical sphere of mass M by a small
fraction
of a subcritical sphere of mass M by a small
fraction 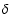 such that
such that
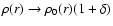 ,
its
mass and pressure will also be enhanced by the same fractional
amount. A simple linear analysis can be done to demonstrate that this
small mass excess will bring the sphere out of equilibrium, causing a
self-gravitational acceleration, given by
,
its
mass and pressure will also be enhanced by the same fractional
amount. A simple linear analysis can be done to demonstrate that this
small mass excess will bring the sphere out of equilibrium, causing a
self-gravitational acceleration, given by
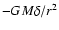 ,
at every
radius within the sphere. For all cases, the collapse of the nonsingular
sphere is initiated by adding a 5% density enhancement (
,
at every
radius within the sphere. For all cases, the collapse of the nonsingular
sphere is initiated by adding a 5% density enhancement (
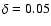 )
to the equilibrium profile throughout the core, which is the same
perturbation employed by RPW in their calculations.
)
to the equilibrium profile throughout the core, which is the same
perturbation employed by RPW in their calculations.
We separate the discussion of the
 collapse from that of the
more massive cases because: (a) this model provides a further direct
comparison with the results of RPW and (b) it is used to check the
effects of increasing the initial spatial resolution from 200 to 400
radial zones.
collapse from that of the
more massive cases because: (a) this model provides a further direct
comparison with the results of RPW and (b) it is used to check the
effects of increasing the initial spatial resolution from 200 to 400
radial zones.
![\begin{figure}
\par\includegraphics[width=8.3cm]{h3666f7a.eps}\includegraphics[width=8.3cm]{h3666f7b.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg188.gif) |
Figure 7:
a) Time evolution of the central mass accretion and b) central
mass accretion rate in the collapse of a nonsingular
 core
with initial parameters as given in Table 1 at high (400 radial zones,
thick solid line) and low (200 radial zones, thin solid line) resolution.
In a) the vertical dashed line marks the time at which the density profile
becomes singular and the time is represented in terms of
core
with initial parameters as given in Table 1 at high (400 radial zones,
thick solid line) and low (200 radial zones, thin solid line) resolution.
In a) the vertical dashed line marks the time at which the density profile
becomes singular and the time is represented in terms of
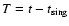 ,
where ,
where
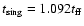 .
To facilitate comparison with the
results of RPW, the vertical dashed lines in b) indicate the transition
from the protostellar collapse phase (PC) to the Class 0 stage (t=0) and
from the Class 0 to the Class I stage ( .
To facilitate comparison with the
results of RPW, the vertical dashed lines in b) indicate the transition
from the protostellar collapse phase (PC) to the Class 0 stage (t=0) and
from the Class 0 to the Class I stage (
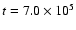 yr),
respectively. Note that during the whole accretion phase the high- and
low-resolution runs produce essentially the same solution.
yr),
respectively. Note that during the whole accretion phase the high- and
low-resolution runs produce essentially the same solution. |
| Open with DEXTER |
The details of the collapse preceding the time of singularity formation are
shown in Fig. 6 for the 400 zones case. This figure depicts the shape of
both the density (Fig. 6a) and radial infall velocity (Fig. 6b) profiles
for a sequence of times, including that of singularity formation
(
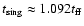 ). Here, we adopt the same convention
of RPW, in which t=0 marks the instant at which the density profile
becomes singular. In this way, all intermediate adjustments from the
nonsingular to the singular configuration occur at negative times (t<0).
The core collapses to progressively higher densities through a sequence
of profiles with decreasing inner, flat-topped regions. The evolution of
the density is qualitatively similar in form to the collapse of the
Bonnor-Ebert sphere (Foster & Chevalier 1993). In the logatropic
case, however, the flat-topped region approaches an approximately
r-3/2 density profile by t=0 as shown in Fig. 6a. This singular
region extends in radius up to
). Here, we adopt the same convention
of RPW, in which t=0 marks the instant at which the density profile
becomes singular. In this way, all intermediate adjustments from the
nonsingular to the singular configuration occur at negative times (t<0).
The core collapses to progressively higher densities through a sequence
of profiles with decreasing inner, flat-topped regions. The evolution of
the density is qualitatively similar in form to the collapse of the
Bonnor-Ebert sphere (Foster & Chevalier 1993). In the logatropic
case, however, the flat-topped region approaches an approximately
r-3/2 density profile by t=0 as shown in Fig. 6a. This singular
region extends in radius up to
 ,
while for r>r0 the
profile matches the
,
while for r>r0 the
profile matches the
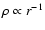 power-law. The co-existence of
two distinct density gradients at the time of singularity formation is
not seen in the collapse of the Bonnor-Ebert sphere, where at t=0 the
inner, flat region approaches the same r-2 variation of the rest of
the sphere (Foster & Chevalier 1993). The velocity profiles also
evolve self-similarly with the peak in the infall velocity moving inwards
(Fig. 6b). The run with 200 zones produced essentially the same results
displayed in Fig. 6, except that within a radius of
power-law. The co-existence of
two distinct density gradients at the time of singularity formation is
not seen in the collapse of the Bonnor-Ebert sphere, where at t=0 the
inner, flat region approaches the same r-2 variation of the rest of
the sphere (Foster & Chevalier 1993). The velocity profiles also
evolve self-similarly with the peak in the infall velocity moving inwards
(Fig. 6b). The run with 200 zones produced essentially the same results
displayed in Fig. 6, except that within a radius of
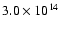 cm during the rapid transition to the
SLS-like collapse, the velocities were a factor of
cm during the rapid transition to the
SLS-like collapse, the velocities were a factor of  2 lower
than in the 400 zones calculation. This clearly implies that the lack of
sufficient spatial resolution in the vecinity of the singularity may
lead to an underestimate of the supersonic character of the flow
in pure hydrodynamic calculations.
2 lower
than in the 400 zones calculation. This clearly implies that the lack of
sufficient spatial resolution in the vecinity of the singularity may
lead to an underestimate of the supersonic character of the flow
in pure hydrodynamic calculations.
A central sink cell is activated at the precise time of singularity
formation and thereafter the evolution is continued using the Eulerian
version of the code. Since prior to t=0, the calculation is made in
Lagrangian form we monitor the temporal variation of
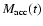 only after the sink cell is activated (t>0). Figure 7 shows the mass
accretion profile for the nonsingular
only after the sink cell is activated (t>0). Figure 7 shows the mass
accretion profile for the nonsingular
 collapse (Fig. 7a)
along with the form of the accretion rate as expressed in physical
units (Fig. 7b). These figures compare very well with the results of
RPW (see their Figs. 7 and 11b, respectively). We see that the accretion
rate increases steeply just after singularity formation. By the time,
the sink contains
collapse (Fig. 7a)
along with the form of the accretion rate as expressed in physical
units (Fig. 7b). These figures compare very well with the results of
RPW (see their Figs. 7 and 11b, respectively). We see that the accretion
rate increases steeply just after singularity formation. By the time,
the sink contains  2% of the total core mass,
2% of the total core mass,
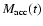 grows with time more slowly. During this period
(
grows with time more slowly. During this period
(
 ), the sink cell accretes more
than 60% of the total available mass. Thereafter, the central accretion
enters a slow phase of relatively steady growth in which the remaining
40% core mass is accreted. This last phase occurs on a much longer
timescale. The calculation was terminated at
), the sink cell accretes more
than 60% of the total available mass. Thereafter, the central accretion
enters a slow phase of relatively steady growth in which the remaining
40% core mass is accreted. This last phase occurs on a much longer
timescale. The calculation was terminated at
 (
(
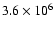 yr),
when
yr),
when  99% of the total mass has been accreted by the central
protostar.
99% of the total mass has been accreted by the central
protostar.
RPW studied the collapse of nonsingular logatropic spheres for masses
 5
5 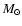 .
They found that by increasing the subcritical mass
from
.
They found that by increasing the subcritical mass
from
 to
to
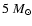 ,
the adjustment of the nonsingular configuration to a singular density
profile occurs with a decreasing fractional amount of the infalling
supersonic mass at t=0. They also extrapolated this trend to higher mass
collapses, arguing that a critical nonsingular logatrope may approach
the singular profile in an entirely subsonic manner in accordance with
the theoretical predictions of MP96 and MP97. With the purpose of
verifying these trends, we have performed high-resolved calculations
of massive subcritical (10-90
,
the adjustment of the nonsingular configuration to a singular density
profile occurs with a decreasing fractional amount of the infalling
supersonic mass at t=0. They also extrapolated this trend to higher mass
collapses, arguing that a critical nonsingular logatrope may approach
the singular profile in an entirely subsonic manner in accordance with
the theoretical predictions of MP96 and MP97. With the purpose of
verifying these trends, we have performed high-resolved calculations
of massive subcritical (10-90
 )
and critical
(
)
and critical
( 92.05
92.05  )
spheres (see Table 1). Since the primary goal
of these calculations is to study the purely hydrodynamical behavior of
the collapse of massive logatropes, we obviate the effects of magnetic
fields and radiative transfer (see Sect. 7 for a discussion).
)
spheres (see Table 1). Since the primary goal
of these calculations is to study the purely hydrodynamical behavior of
the collapse of massive logatropes, we obviate the effects of magnetic
fields and radiative transfer (see Sect. 7 for a discussion).
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f8a.eps}\par\includegraphics[width=8.8cm]{h3666f8b.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg210.gif) |
Figure 8:
a) Density and b) radial velocity profiles during the collapse
of a nonsingular critical (
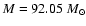 )
core (Table 1) preceding
the time of singularity formation (t=0). The sequence of times,
starting from the lowest curves, is )
core (Table 1) preceding
the time of singularity formation (t=0). The sequence of times,
starting from the lowest curves, is
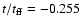 (initial
density profile) in a), and
(initial
density profile) in a), and
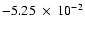 , ,
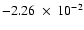 , ,
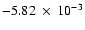 , ,
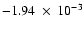 , ,
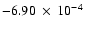 and
0 (time of singularity formation) in a) and b), respectively.
In a), the inclined dashed
line indicates a
and
0 (time of singularity formation) in a) and b), respectively.
In a), the inclined dashed
line indicates a
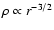 variation and the vertical one marks
the scale radius r0 of the core. The better inner resolution shown in
b) is an effect of the density being staggered with respect to the
velocity in the present calculations.
variation and the vertical one marks
the scale radius r0 of the core. The better inner resolution shown in
b) is an effect of the density being staggered with respect to the
velocity in the present calculations. |
| Open with DEXTER |
For all masses considered here, the initial collapse phase prior to
singularity formation is qualitatively similar to that of the
 case described above. This is shown in Fig. 8, which
depicts the time evolution of the density (Fig. 8a) and radial infall
velocity (Fig. 8b) profiles for the collapse of the critical
case described above. This is shown in Fig. 8, which
depicts the time evolution of the density (Fig. 8a) and radial infall
velocity (Fig. 8b) profiles for the collapse of the critical
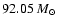 logatrope up to t=0. Table 3 lists for all models
the time of singularity formation in years and in units of
the sound crossing time
logatrope up to t=0. Table 3 lists for all models
the time of singularity formation in years and in units of
the sound crossing time
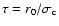 interior to r0 and the free-fall
time
interior to r0 and the free-fall
time
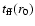 of the initial flat-topped region (r<r0),
respectively, the percentage of the total core mass that undergoes
supersonic infall at t=0 and the fractional radius containing that
mass. As the mass of the logatrope is increased, the timescale of
singularity formation decreases. This is understandable because cores
of higher mass exhibit larger central condensations, and consequently,
higher average densities. The results in Table 3 also confirm the
finding of RPW that the time elapsed between the initiation of collapse
and the formation of the density singularity obeys the approximate
scaling
of the initial flat-topped region (r<r0),
respectively, the percentage of the total core mass that undergoes
supersonic infall at t=0 and the fractional radius containing that
mass. As the mass of the logatrope is increased, the timescale of
singularity formation decreases. This is understandable because cores
of higher mass exhibit larger central condensations, and consequently,
higher average densities. The results in Table 3 also confirm the
finding of RPW that the time elapsed between the initiation of collapse
and the formation of the density singularity obeys the approximate
scaling
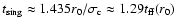 for all masses, including the critical one. Most
importantly, the amount of mass falling supersonically at t=0 as well
as its volume drop by increasing the mass of the logatropic core.
About 6% of the total core mass collapses supersonically in a
for all masses, including the critical one. Most
importantly, the amount of mass falling supersonically at t=0 as well
as its volume drop by increasing the mass of the logatropic core.
About 6% of the total core mass collapses supersonically in a
 core, while only 0.02% behaves this manner in a critical
logatrope. Although this result is in agreement with the trends found
by RPW, the approach to the singularity is never entirely subsonic at
least in a pure hydrodynamical scenario. The Mach number of the
supersonic flow also decreases as R/r0, or equivalently
core, while only 0.02% behaves this manner in a critical
logatrope. Although this result is in agreement with the trends found
by RPW, the approach to the singularity is never entirely subsonic at
least in a pure hydrodynamical scenario. The Mach number of the
supersonic flow also decreases as R/r0, or equivalently
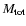 ,
increases towards the critical value. The calculations
predict maximum Mach numbers between
,
increases towards the critical value. The calculations
predict maximum Mach numbers between  26 (critical mass) and
26 (critical mass) and
 116 (
116 (
 ), which are by far much higher than those
reported by RPW. An explanation for this is the much higher central
resolution achieved in the present models, which allows to go much
deeper into the singular region than the calculations of RPW did.
However, the presence of such extremely high velocities in the
supersonic region may be indicative of the physical limitations of
purely hydrodynamical models. For instance, under the action of a
mean magnetic field these velocities should be substantially lowered.
In addition, higher densities in more massive cores lead to greater
optical depths and hence to increasingly higher pressures at t=0,
which should also work on reducing the Mach number to physically
realistic values. Future simulations of the collapse of massive cores
must therefore include the effects of magnetic fields and radiative
transfer to correctly describe the collapse of logatropic configurations.
), which are by far much higher than those
reported by RPW. An explanation for this is the much higher central
resolution achieved in the present models, which allows to go much
deeper into the singular region than the calculations of RPW did.
However, the presence of such extremely high velocities in the
supersonic region may be indicative of the physical limitations of
purely hydrodynamical models. For instance, under the action of a
mean magnetic field these velocities should be substantially lowered.
In addition, higher densities in more massive cores lead to greater
optical depths and hence to increasingly higher pressures at t=0,
which should also work on reducing the Mach number to physically
realistic values. Future simulations of the collapse of massive cores
must therefore include the effects of magnetic fields and radiative
transfer to correctly describe the collapse of logatropic configurations.
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f9a.eps}\includegraphics[width=8.8cm]{h3666f9b.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg213.gif) |
Figure 9:
a) Central mass accretion and b) central mass accretion rate
expressed in physical units as a function of time for all of the
nonsingular collapses of Sect. 5. In all cases, the evolution is
shown up to the point where 99% of the total core mass has been
accreted by the central protostar. |
| Open with DEXTER |
The main goal of pursuing the evolution farther in time after singularity
formation is to track the central protostellar accretion history. Figure
9 displays the time evolution of the central mass accretion (Fig. 9a)
and central mass accretion rate (Fig. 9b) in physical units
for all models. In all cases, the evolution is shown up to the point
where  99% of the total mass has been accreted. The
99% of the total mass has been accreted. The
 core is the first to complete its accretion phase. The accretion
timescale then increases with increasing mass of the core up to about
core is the first to complete its accretion phase. The accretion
timescale then increases with increasing mass of the core up to about
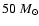 .
For masses higher than this, the trend reverses and the
accretion timescale decreases as the total core mass approaches
criticality. This dependence of the overall accretion lifetime on core
mass is expected because the mean free-fall time has also a similar
dependence on total mass (see Table 1). This is in contrast with the
singular logatropic collapse theory of MP97, where more massive stars
take longer to form in the logatrope. The results imply that stars of
mass
.
For masses higher than this, the trend reverses and the
accretion timescale decreases as the total core mass approaches
criticality. This dependence of the overall accretion lifetime on core
mass is expected because the mean free-fall time has also a similar
dependence on total mass (see Table 1). This is in contrast with the
singular logatropic collapse theory of MP97, where more massive stars
take longer to form in the logatrope. The results imply that stars of
mass
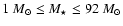 all tend to form
within 3.6-
all tend to form
within 3.6-
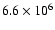 yr. This small spread in
star-formation times is due to the t4 variation of the mass
accretion and also to the weak dependence of the mean free-fall time
on mass. In terms of Fig. 9b, the accretion phase in a logatrope can
be subdivided into three main stages. The first one, which marks the
transition from the collapse phase into an SLS-like accretion phase,
is the shortest one and is characterized by an abrupt increase of the
mass accretion rate immediately after singularity formation. Note that
cores of higher mass experience a steeper accretion rate during this
first stage. During
the second stage, the accretion rate grows more slowly until it reaches
a maximum value. At this epoch, about 40% of the total mass has been
accreted by the central protostar. After this point, a third stage
starts in which the accretion rate declines for the remainder of the
evolution until 100% of the total core mass is condensed into the
central object. The higher is the mass of the core, the larger is the
size of the accretion rate. In particular, our models predict peak
values of
yr. This small spread in
star-formation times is due to the t4 variation of the mass
accretion and also to the weak dependence of the mean free-fall time
on mass. In terms of Fig. 9b, the accretion phase in a logatrope can
be subdivided into three main stages. The first one, which marks the
transition from the collapse phase into an SLS-like accretion phase,
is the shortest one and is characterized by an abrupt increase of the
mass accretion rate immediately after singularity formation. Note that
cores of higher mass experience a steeper accretion rate during this
first stage. During
the second stage, the accretion rate grows more slowly until it reaches
a maximum value. At this epoch, about 40% of the total mass has been
accreted by the central protostar. After this point, a third stage
starts in which the accretion rate declines for the remainder of the
evolution until 100% of the total core mass is condensed into the
central object. The higher is the mass of the core, the larger is the
size of the accretion rate. In particular, our models predict peak
values of
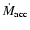 as high as
as high as
 5-
5-
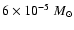 yr-1 for cores close to the
critical mass. These are about two orders of magnitude larger than the
peak value achieved by the highly subcritical
yr-1 for cores close to the
critical mass. These are about two orders of magnitude larger than the
peak value achieved by the highly subcritical
 core
(
core
(
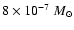 yr-1).
yr-1).
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f10.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg218.gif) |
Figure 10:
Central mass accretion rate as a function of the
central accreted mass in dimensionless units for all of the
nonsingular collapses of Sect. 5. |
| Open with DEXTER |
The dependence of the central mass accretion rate on the
central accreted mass in dimensionless units is shown in Fig. 10
for all models. When expressed in dimensionless units, the
accretion rate of the
 core looks higher than that
of the more massive cores. This trend is expected because for
the
core looks higher than that
of the more massive cores. This trend is expected because for
the
 core to be the first to accrete 99% of its
total mass (see Fig. 9a), it must effectively accrete a larger fraction
of its mass compared to the more massive cores. For cores of mass
core to be the first to accrete 99% of its
total mass (see Fig. 9a), it must effectively accrete a larger fraction
of its mass compared to the more massive cores. For cores of mass
 50
50 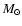 the curves in Fig. 10 overlap, with all of
these cores showing a lower accretion rate compared to the 1 and
the curves in Fig. 10 overlap, with all of
these cores showing a lower accretion rate compared to the 1 and
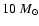 cores. A feature common to all curves is a
maximum when the central protostar has accreted about 40% of
the available mass. For higher fractions of the accreted mass,
the accretion rate declines in all cases. When the accretion
rate is plotted as a function of time in dimensionless units,
the variation of the accretion rate has a form very similar
to that shown in Fig. 10. This suggests an approximate linear
dependence of the accreted mass on time. Such rough linear variation
is effectively observed when
cores. A feature common to all curves is a
maximum when the central protostar has accreted about 40% of
the available mass. For higher fractions of the accreted mass,
the accretion rate declines in all cases. When the accretion
rate is plotted as a function of time in dimensionless units,
the variation of the accretion rate has a form very similar
to that shown in Fig. 10. This suggests an approximate linear
dependence of the accreted mass on time. Such rough linear variation
is effectively observed when
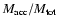 is
plotted as a function of
is
plotted as a function of
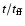 and it is maintained
until the accretion rate starts to decline. This is in stark
contrast with the SLS case, where
and it is maintained
until the accretion rate starts to decline. This is in stark
contrast with the SLS case, where
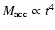 .
.
So far we have scaled our collapse models to central temperatures and
truncation pressures representative of isolated star-forming regions.
We now describe the results obtained for a new set of nonsingular
collapse models in which the surface pressure is chosen to be
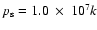 cm-3 K, in keeping with observations
of clustered star-forming regions such as
cm-3 K, in keeping with observations
of clustered star-forming regions such as  Oph (André et al.
2000). The initial parameters for these
model calculations are listed in Table 2. Here, we consider spheres with
0.5, 1, 2, 5, 8 (subcritical cases) and
Oph (André et al.
2000). The initial parameters for these
model calculations are listed in Table 2. Here, we consider spheres with
0.5, 1, 2, 5, 8 (subcritical cases) and
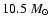 (critical case).
As before, in each case the collapse is initiated by adding throughout
the core a 5% overdensity.
(critical case).
As before, in each case the collapse is initiated by adding throughout
the core a 5% overdensity.
For all models, the initial collapse phase towards the singular density
profile proceeds as in the previous cases. Table 4 lists the times of
singularity formation and the properties of the infalling mass at
t=0. An inspection of this table shows that the data along the
columns follow essentially the same trends seen in Table 3. In view of
this and of the qualitative similar behavior of the models with those
described in the preceding section, we shall discuss the results in terms
of the main differences between both sets of calculations.
One effect of increasing the surface pressure is to shorten the time
of collapse to singularity formation. Subcritical cores of equal mass
and varying  will reach the singular state more rapidly for
larger values of
will reach the singular state more rapidly for
larger values of  .
In addition, for highly subcritical cores,
the percentage of mass collapsing supersonically at t=0 decreases as
.
In addition, for highly subcritical cores,
the percentage of mass collapsing supersonically at t=0 decreases as
 is increased, while for critical cores the relative amount
of supersonic mass is independent of
is increased, while for critical cores the relative amount
of supersonic mass is independent of  .
A similar trend is
also observed for the fractional volume occupied by the supersonic flow.
Furthermore, increasing
.
A similar trend is
also observed for the fractional volume occupied by the supersonic flow.
Furthermore, increasing  also results in supersonic inflow
of much lower Mach numbers, with maximum values ranging from
also results in supersonic inflow
of much lower Mach numbers, with maximum values ranging from  19
(
19
(
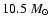 )
to
)
to  38 (
38 (
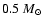 ). Thus, in a purely
hydrodynamical scenario, the general effect of increasing the bounding
pressure in the collapse of a logatrope is to produce a less supersonic
approach to the singularity.
). Thus, in a purely
hydrodynamical scenario, the general effect of increasing the bounding
pressure in the collapse of a logatrope is to produce a less supersonic
approach to the singularity.
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f11a.eps}\par\includegraphics[width=8.8cm]{h3666f11b.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg225.gif) |
Figure 11:
a) Central mass accretion and b) central mass accretion rate
expressed in physical units as a function of time for all of the
nonsingular collapses of Sect. 6. In all cases, the evolution is
shown up to the point where 99% of the total core mass has been
accreted by the central protostar. |
| Open with DEXTER |
For all cases, the accretion history is displayed in Fig. 11, where the
time evolution of the central mass accretion (Fig. 11a) and the central
mass accretion rate (Fig. 11b) are depicted in terms of physical units.
As before, the
accretion has been followed to the point where  99% of the total
core mass has fallen into the sink cell. It is evident from Fig. 11a
that the accretion timescale is longer for the
99% of the total
core mass has fallen into the sink cell. It is evident from Fig. 11a
that the accretion timescale is longer for the
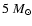 collapse
case. Starting from this mass, the accretion timescale shortens towards
increasing and decreasing masses. Again, this is a consequence of the
mean free-fall time being longer for subcritical masses around
collapse
case. Starting from this mass, the accretion timescale shortens towards
increasing and decreasing masses. Again, this is a consequence of the
mean free-fall time being longer for subcritical masses around
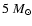 (see Table 2). For fixed A, increasing the fiducial value
of
(see Table 2). For fixed A, increasing the fiducial value
of  has little effect on the size of the accretion rate in
critical logatropes. This can be seen by comparing Figs. 9b and 11b,
where the accretion rate peaks at
has little effect on the size of the accretion rate in
critical logatropes. This can be seen by comparing Figs. 9b and 11b,
where the accretion rate peaks at 
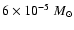 yr-1 for both the critical 10.5 and
yr-1 for both the critical 10.5 and
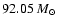 logatropes.
However, the same is not true for subcritical logatropes sharing the
same mass. For instance, a
logatropes.
However, the same is not true for subcritical logatropes sharing the
same mass. For instance, a
 core with
core with
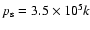 cm-3 K experiences a maximum accretion
rate of
cm-3 K experiences a maximum accretion
rate of 
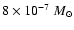 yr-1 compared to
yr-1 compared to

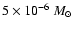 yr-1 achieved in a
yr-1 achieved in a
 core with
core with
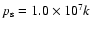 cm-3 K. Thus, for comparable
subcritical masses, the size of the accretion rate is smaller in cores having
lower values of
cm-3 K. Thus, for comparable
subcritical masses, the size of the accretion rate is smaller in cores having
lower values of  .
On the other hand, by comparing Figs. 9a and 11a, we see that the accretion lifetimes are considerably longer in cores
with lower
.
On the other hand, by comparing Figs. 9a and 11a, we see that the accretion lifetimes are considerably longer in cores
with lower  ,
implying that star formation in clustered regions
occurs on shorter timescales (
,
implying that star formation in clustered regions
occurs on shorter timescales ( 5.4-
5.4-
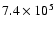 yr as
predicted for these models) compared to more isolated environments.
yr as
predicted for these models) compared to more isolated environments.
We have presented high-resolved calculations of the spherically symmetric
collapse and subsequent accretion of nonsingular A=0.2 logatropic cores
with varied masses and values of the fiducial external
bounding pressure. For all cases, the evolution has been followed to the
point where nearly all of the finite core mass has fallen into the central
protostar. Thus, the models are indicative of the early star-formation
stages, including: (a) the protostellar collapse (PC) phase, (b) the Class 0
stage, in which the central protostar accretes  50%
of the total core mass (André et al. 1993) and
(c) the Class I stage, in which the protostar accretes the remainder of the
final stellar mass, leading to the formation of a Class II object of mass
50%
of the total core mass (André et al. 1993) and
(c) the Class I stage, in which the protostar accretes the remainder of the
final stellar mass, leading to the formation of a Class II object of mass
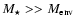 .
These very young stellar objects are known to be
optically visible and possess emission lines characteristic of classical
T-Tauri stars (Adams et al. 1987). We can therefore compare
the various predicted lifetimes with those derived observationally from
statistical arguments and theoretically from other proposed models.
.
These very young stellar objects are known to be
optically visible and possess emission lines characteristic of classical
T-Tauri stars (Adams et al. 1987). We can therefore compare
the various predicted lifetimes with those derived observationally from
statistical arguments and theoretically from other proposed models.
Based on a total starless core lifetime of a few 106 yr, as derived
from the survey of Beichman et al. (1986), Ward-Thompson et al.
(1994) estimated the lifetime of prestellar cores detected in the
submm continuum to be  106 yr. More recently, Lee et al.
(1999) found evidence for collapse in seven out of 220
cores surveyed, implying that the PC phase lasts
106 yr. More recently, Lee et al.
(1999) found evidence for collapse in seven out of 220
cores surveyed, implying that the PC phase lasts  3% of the total
starless core phase, or
3% of the total
starless core phase, or  3-
3-
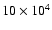 yr. Furthermore,
Gregersen & Evans (2000) discovered six more sources undergoing
collapse from the catalog of 50 starless cores listed by Beichman et al.
(1986). Their results imply a lifetime for the PC phase of a
few 105 yr. While these estimates carry large inherent uncertainties,
we note that our calculations predict lifetimes for this phase of
yr. Furthermore,
Gregersen & Evans (2000) discovered six more sources undergoing
collapse from the catalog of 50 starless cores listed by Beichman et al.
(1986). Their results imply a lifetime for the PC phase of a
few 105 yr. While these estimates carry large inherent uncertainties,
we note that our calculations predict lifetimes for this phase of
 1.5-
1.5-
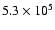 yr for the
yr for the
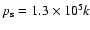 cm-3 K
nonsingular collapses (see Table 3), consistent with the
estimates of Gregersen & Evans (2000). For models with
cm-3 K
nonsingular collapses (see Table 3), consistent with the
estimates of Gregersen & Evans (2000). For models with
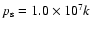 cm-3 K, the predicted lifetimes are
cm-3 K, the predicted lifetimes are
 1.7-
1.7-
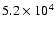 yr (see Table 4), which are more consistent
with the ages suggested by Lee et al. (1999). However, the
detection of much larger samples of contracting sources along with more
accurate estimates of their PC lifetimes, would be required to confirm
the validity of our predictions. The logatropic PC lifetimes listed
in Table 3 are an order of magnitude longer than
the prediction of
yr (see Table 4), which are more consistent
with the ages suggested by Lee et al. (1999). However, the
detection of much larger samples of contracting sources along with more
accurate estimates of their PC lifetimes, would be required to confirm
the validity of our predictions. The logatropic PC lifetimes listed
in Table 3 are an order of magnitude longer than
the prediction of 
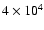 yr made
by Whitworth & Ward-Thompson (2001), who proposed a simple
analytic model for the protostellar collapse of the isolated core
L1544 based on a Plummer-like radial density profile as its initial
condition.
yr made
by Whitworth & Ward-Thompson (2001), who proposed a simple
analytic model for the protostellar collapse of the isolated core
L1544 based on a Plummer-like radial density profile as its initial
condition.
At the end of the PC phase, the density distribution becomes singular
everywhere and a central point-mass forms. This transition to a
SLS-like collapse marks the beginning of the Class 0 stage and is
characterized by a steep increase of the mass accretion rate. This
is shown schematically in Fig. 7b for the
 collapse case with
collapse case with
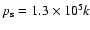 cm-3 K. During this stage,
the accretion rate reaches a maximum value and the protostar accretes
half of the mass of the envelope on a timescale of
cm-3 K. During this stage,
the accretion rate reaches a maximum value and the protostar accretes
half of the mass of the envelope on a timescale of 
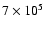 yr, which marks the transition to the Class I protostellar phase. Class
0 objects are good candidates of very young accreting protostars in
which a hydrostatic object has already formed but not yet accreted the
majority of its final mass. Most of the final stellar mass is still in
the form of a dense circumstellar envelope. About 30-40 confirmed
Class 0 objects have been identified up to now (André et al.
2000), mostly in regions of multiple star formation. For instance,
in the
yr, which marks the transition to the Class I protostellar phase. Class
0 objects are good candidates of very young accreting protostars in
which a hydrostatic object has already formed but not yet accreted the
majority of its final mass. Most of the final stellar mass is still in
the form of a dense circumstellar envelope. About 30-40 confirmed
Class 0 objects have been identified up to now (André et al.
2000), mostly in regions of multiple star formation. For instance,
in the 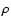 Oph main cloud, there have been reported only two good
Class 0 candidates, suggesting a Class 0 lifetime of
Oph main cloud, there have been reported only two good
Class 0 candidates, suggesting a Class 0 lifetime of
 1-
1-
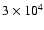 yr compared to
yr compared to 
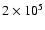 yr for
the Class I sources (e.g., Greene et al. 1994). It then appears on
observational grounds that the lifetime of the Class 0 phase is short
compared to both the PC phase and the Class I near-IR phase. Tables 5
and 6 contain the predicted lifetimes for both the Class 0 and Class I
phases from the sequences of logatropic collapse calculations with
yr for
the Class I sources (e.g., Greene et al. 1994). It then appears on
observational grounds that the lifetime of the Class 0 phase is short
compared to both the PC phase and the Class I near-IR phase. Tables 5
and 6 contain the predicted lifetimes for both the Class 0 and Class I
phases from the sequences of logatropic collapse calculations with
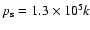 cm-3 K and
cm-3 K and
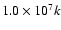 cm-3 K, respectively. These values are
cm-3 K, respectively. These values are  1-2 orders of magnitude larger
than those inferred observationally for the Class 0 phase, and about an
order of magnitude larger than
1-2 orders of magnitude larger
than those inferred observationally for the Class 0 phase, and about an
order of magnitude larger than 
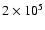 yr for the Class I
stage in the models with lower
yr for the Class I
stage in the models with lower  (see Table 5). The models with
(see Table 5). The models with
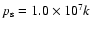 cm-3 K are more
representative of cloud cores contracting in a clustered environment, and
as shown in Table 6, their lifetimes for the Class I stage are
comparable to the observational estimates for the
cm-3 K are more
representative of cloud cores contracting in a clustered environment, and
as shown in Table 6, their lifetimes for the Class I stage are
comparable to the observational estimates for the 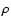 Oph main cloud.
Here, we have adopted the widely accepted convention that the borderline
between Class 0 and Class I sources occurs when
Oph main cloud.
Here, we have adopted the widely accepted convention that the borderline
between Class 0 and Class I sources occurs when
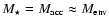 ,
while that between Class I and
Class II sources occurs when 99% of the total core mass has been delivered
(
,
while that between Class I and
Class II sources occurs when 99% of the total core mass has been delivered
(
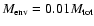 ), which allows for residual accretion
during the (Class II) pre-main-sequence evolution (Henriksen et al.
1997). For further comparison, the analytic collapse
model of Whitworth & Ward-Thompson (2001) predict that L1544
should have accumulated about 50% of its mass in
), which allows for residual accretion
during the (Class II) pre-main-sequence evolution (Henriksen et al.
1997). For further comparison, the analytic collapse
model of Whitworth & Ward-Thompson (2001) predict that L1544
should have accumulated about 50% of its mass in 
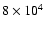 yr. In the logatropic scenario, both the Class 0 and Class I lifetimes
depend weakly on the total core mass and are about an order of magnitude
larger in regions of isolated star formation than in cluster-forming
environments.
yr. In the logatropic scenario, both the Class 0 and Class I lifetimes
depend weakly on the total core mass and are about an order of magnitude
larger in regions of isolated star formation than in cluster-forming
environments.
The timescales in Tables 5 and 6 for the transition from Class 0/I to
Class I/II have been determined under the assumptions that there is no mass
disruption mechanism operating during the protostellar evolution and that
the final stellar mass is determined by the total core mass, which have no
observational support. For instance, there is confirmed evidence that
NH3 cloud cores are much more massive than the embedded young stars
formed at their centers (Jijina et al. 1999). Furthermore, it is
well-known that star formation within molecular cloud cores is accompanied
by some degree of outflow activity (see discussion below). Such protostellar
outflows have been indicated as a mechanism to remove gas from star-forming
regions (e.g., Bally et al. 1999) and from protostellar cores (e.g.,
Velusamy & Langer 1998; Ladd et al. 1998). Mass disruption
by bipolar outflows then limits the fraction of mass that can accrete
and therefore the efficiency of star formation in a protostellar core
(Matzner & MacKee 2000). Thus, more accurate predictions of the
Class 0 and Class I lifetimes would evidently require a solution to the
problem of simultaneous infall and outflow.
Most, if not all, Class 0 protostars drive highly collimated or "jet-like''
CO molecular outflows (Bachiller 1996). In contrast, the CO
outflows from Class I sources are much less powerful and collimated. In
particular, Bontemps et al. (1996) analyzed a set of CO(2-1) outflow
data around a large sample of embedded young stellar objects, including 9
Class 0 sources and 36 Class I sources. They found that the outflow phase and
the infall/accretion phase coincide for the entire sample of sources
examined, thereby suggesting that outflows are directly powered by
accretion. In addition, magneto-centrifugal accretion/ejection models of
bipolar outflows (Ouyed & Pudritz 1997; Kudoh & Shibata
1997) predict a direct proportionality between accretion and
ejection. This implies that the observed decline of outflow power must
be accompanied by a corresponding decline of the mass accretion rate
from the Class 0 to the Class I stage (Bontemps et al. 1996).
The results of Bontemps et al. (1996) further indicate that the
ejected mass
 declines from
declines from  10
10
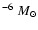 yr-1
for the youngest Class 0 protostars to
yr-1
for the youngest Class 0 protostars to

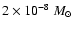 yr-1 for the most evolved Class I
objects. Realistic jet models give the relation
yr-1 for the most evolved Class I
objects. Realistic jet models give the relation
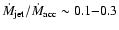 between the
accretion and ejection rates (André et al. 2000). This implies
that
between the
accretion and ejection rates (André et al. 2000). This implies
that
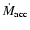 decreases from
decreases from
 0.3-
0.3-
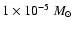 yr-1 for Class 0 objects to
yr-1 for Class 0 objects to
 0.7-
0.7-
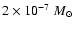 yr-1 for evolved Class I
protostars.
yr-1 for evolved Class I
protostars.
In Tables 7 and 8 we list the maximum values of
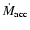 along
with its values at the borderlines between Class 0 and Class I sources
(
along
with its values at the borderlines between Class 0 and Class I sources
(
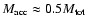 )
and between Class I and Class
II sources (
)
and between Class I and Class
II sources (
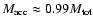 ), as predicted by our
logatropic collapse models. In all cases,
), as predicted by our
logatropic collapse models. In all cases,
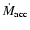 reaches
a peak value when the protostar contains
reaches
a peak value when the protostar contains  40% of its final mass.
We see that the predicted
40% of its final mass.
We see that the predicted
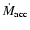 agrees with the
observational estimates for cores with
agrees with the
observational estimates for cores with
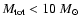 in the
sequence of calculations with
in the
sequence of calculations with
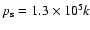 cm-3 K
(Table 7) and for cores with
cm-3 K
(Table 7) and for cores with
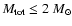 in the higher
in the higher
 sequence (Table 8). For logatropes of higher mass in both
sequences, the accretion rates are higher than the observational estimates
by factors of
sequence (Table 8). For logatropes of higher mass in both
sequences, the accretion rates are higher than the observational estimates
by factors of  2-7. Furthermore, the logatropic models predict
values of
2-7. Furthermore, the logatropic models predict
values of
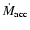 which are factors of
which are factors of  40 larger for Class 0
sources than for Class I sources, implying much higher accretion luminosities
for the former than for the latter. This factor is 4 times higher than
that proposed by Henriksen et al. (1997). However, both factors
seem to be in apparent contradiction with observations which suggest that
Class 0 sources are not significantly over-luminous compared to the more
evolved Class I objects. In particular, the embedded source sample of
Bontemps et al. (1996) indicates an estimated ratio of the average
bolometric luminosities between Class 0 and Class I sources of
40 larger for Class 0
sources than for Class I sources, implying much higher accretion luminosities
for the former than for the latter. This factor is 4 times higher than
that proposed by Henriksen et al. (1997). However, both factors
seem to be in apparent contradiction with observations which suggest that
Class 0 sources are not significantly over-luminous compared to the more
evolved Class I objects. In particular, the embedded source sample of
Bontemps et al. (1996) indicates an estimated ratio of the average
bolometric luminosities between Class 0 and Class I sources of  1.6.
However, this estimate can be affected by the observational uncertainty of
the typical luminosity of Class 0 sources due to the rarity of these
objects. Recently, Eisner et al.
(2002) estimated the mass ejection rate from a high-mass
protostar in W51-IRS 2 due to a bipolar outflow associated with it to be
1.6.
However, this estimate can be affected by the observational uncertainty of
the typical luminosity of Class 0 sources due to the rarity of these
objects. Recently, Eisner et al.
(2002) estimated the mass ejection rate from a high-mass
protostar in W51-IRS 2 due to a bipolar outflow associated with it to be
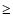
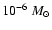 yr-1, which according to the relationship
yr-1, which according to the relationship
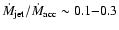 would correspond
to an accretion rate
would correspond
to an accretion rate 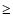 10
10
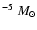 yr-1; a value which
is consistent with our predicted Class 0 lifetimes for high-mass logatropes
(see Tables 7 and 8).
yr-1; a value which
is consistent with our predicted Class 0 lifetimes for high-mass logatropes
(see Tables 7 and 8).
We have considered a set of calculations starting with initial conditions
appropriate for contracting cores within a high-pressure
environment (
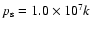 cm-3 K; see Table 2).
Such a high surface pressure is consistent with the expected average
pressure in the
cm-3 K; see Table 2).
Such a high surface pressure is consistent with the expected average
pressure in the 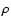 Oph main body region. That is, given the
Oph main body region. That is, given the  1 pc extent of the
1 pc extent of the 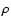 Oph central region, the average number density is
expected to be
Oph central region, the average number density is
expected to be
 cm-3 and so the
corresponding average pressure is
cm-3 and so the
corresponding average pressure is
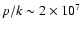 cm-3 K.
Johnstone et al. (2000) identified 55 independent cores in the
central region of the
cm-3 K.
Johnstone et al. (2000) identified 55 independent cores in the
central region of the 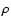 Oph molecular cloud and fitted them to
Bonnor-Ebert spheres, suggesting internal temperatures of 10 - 30 K and
surface pressures in the range between
Oph molecular cloud and fitted them to
Bonnor-Ebert spheres, suggesting internal temperatures of 10 - 30 K and
surface pressures in the range between  106 and
106 and  107k cm-3 K for the 55 cores sampled. As was argued by RPW, these surface
pressures depend on the assumption that all of these cores could be well-fit
by Bonnor-Ebert spheres, and hence
107k cm-3 K for the 55 cores sampled. As was argued by RPW, these surface
pressures depend on the assumption that all of these cores could be well-fit
by Bonnor-Ebert spheres, and hence
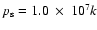 cm-3 K cannot necessarily be considered reflective of the values that
would be required to truncate nonsingular logatropic spheres in a
cluster-forming environment. In the lack of convincing evidence confirming
this point, the present calculations represent a step
forward in studying the protostellar evolution of logatropes under
conditions appropriate for star formation in clustered environments.
cm-3 K cannot necessarily be considered reflective of the values that
would be required to truncate nonsingular logatropic spheres in a
cluster-forming environment. In the lack of convincing evidence confirming
this point, the present calculations represent a step
forward in studying the protostellar evolution of logatropes under
conditions appropriate for star formation in clustered environments.
The primary goal of these calculations is to study the dynamical aspects
of logatropic collapse, and so we have obviated the effects of
rotation, magnetic fields and radiative transfer. While logatropic models
are able to fit the observed line width-size data well (MP96), they do
not specify the physical basis of the nonthermal motions. The coupling
of the magnetic field to the neutrals seems to be necessary to keep the
amplitude of the observed nonthermal motions. Estimates of the
ionization in molecular cloud cores suggest that ion-neutral coupling is
sufficient to support MHD waves, even in the densest cores (Myers &
Khersonsky 1995). Further, the relatively shallow dependence of
the kinetic pressure on radius,
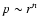 ,
with 0<n<1, from the
line width-size relations, combined with the evidence for similarity of
magnetic and kinetic energy density in some clouds (Myers & Goodman
1988), suggest that the magnetic field must also vary slowly
within dense cores. If the line width-size relations originate in
nonlinear MHD turbulence, it will take substantial computational power
to simulate these phenomena for a compressible, self-gravitating medium
in three dimensions. The magnetic field offers a way to slow down the
prestellar collapse, leading to a much gentler approach towards the
singular density profile compared to a pure hydrodynamical scenario,
where unreasonably high supersonic infall velocities may eventually
develop in a small central region. However, it is important to stress
that the logatrope already incorporates a mean magnetic field as a
virial parameter and so it accounts for some measure of both magnetic
and turbulent support (MP97, RPW).
,
with 0<n<1, from the
line width-size relations, combined with the evidence for similarity of
magnetic and kinetic energy density in some clouds (Myers & Goodman
1988), suggest that the magnetic field must also vary slowly
within dense cores. If the line width-size relations originate in
nonlinear MHD turbulence, it will take substantial computational power
to simulate these phenomena for a compressible, self-gravitating medium
in three dimensions. The magnetic field offers a way to slow down the
prestellar collapse, leading to a much gentler approach towards the
singular density profile compared to a pure hydrodynamical scenario,
where unreasonably high supersonic infall velocities may eventually
develop in a small central region. However, it is important to stress
that the logatrope already incorporates a mean magnetic field as a
virial parameter and so it accounts for some measure of both magnetic
and turbulent support (MP97, RPW).
The inclusion of rotation is a further step towards improving the picture
of logatropic collapse. In particular, this will ensure that protostellar
accretion does proceed in an anisotropic manner, i.e., through the
formation of a circumstellar accretion disk. Such a process is also likely
to affect the spherically symmetric timescales listed in Tables 5 and 6,
which will still apply to the limiting case of very slow rotation. A
consistent treatment of contracting, rotating logatropes will demand
calculating appropriate equilibria from which to start the collapse. The
calculation of such rotating equilibrium sequences is mandatory for
future work wherein we will generalize the present approach to the
two-dimensional collapse of rotating, logatropic cores. Furthermore, a
careful treatment of radiative transfer is essential for realistic
simulations of the formation of massive stars. Because of their high
luminosities, we expect that radiative acceleration will contribute
significantly to the dynamical evolution of high-mass cores. Moreover,
evidence for high-luminosity far-IR sources, which are known to be suspected
embedded young OB stars, shows that they have powerful bipolar outflows
associated with them (e.g., Shepherd et al. 2000). Such massive
outflows are probably powered by disk accretion and, similarly to their
low-mass counterparts, the flow energetics appear to scale with the
luminosity of the source (Richer et al. 2000). Recently,
Yorke & Sonnhalter (2002) have calculated the collapse of
slowly rotating, massive molecular cores, including the effects of
frequency-dependent radiation transfer and grain opacity contribution.
Although their initial conditions correspond to a r-2 SIS model, they
predict a time-dependent accretion which follows qualitatively the
behavior shown in Figs. 9 and 11. For the particular case of a
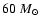 core model, they report a maximum value of the accretion rate of
core model, they report a maximum value of the accretion rate of

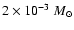 yr-1 which is achieved after
yr-1 which is achieved after

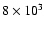 yr in the collapse. This value of
yr in the collapse. This value of
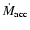 is significantly higher compared to the predictions of our logatropic
collapse models. In the same way, the timescale of
is significantly higher compared to the predictions of our logatropic
collapse models. In the same way, the timescale of 
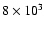 yr
is much shorter than those marking the temporal position of the
yr
is much shorter than those marking the temporal position of the
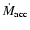 peaks in Figs. 9 and 11. Clearly these results show that
radiative transfer may strongly influence the evolution of high-mass cores,
and also limit the amount of mass that will end into the form of stars.
peaks in Figs. 9 and 11. Clearly these results show that
radiative transfer may strongly influence the evolution of high-mass cores,
and also limit the amount of mass that will end into the form of stars.
In this paper, we have presented solutions for the spherical collapse and
subsequent accretion of nonsingular (subcritical and critical) logatropic
spheres, starting with initial conditions close to hydrostatic equilibrium.
Two sequences of calculations have been conducted by increasing the
fiducial truncation pressure from
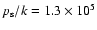 cm-3 K,
representative of the conditions in relatively isolated star-forming regions,
to
cm-3 K,
representative of the conditions in relatively isolated star-forming regions,
to
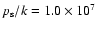 cm-3 K, as would be appropriate to
clustered environments. The main conclusions of this study can be summarized
in the following points:
cm-3 K, as would be appropriate to
clustered environments. The main conclusions of this study can be summarized
in the following points:
(i) The initial collapse phase preceding the time (t=0) of singularity
formation is qualitatively similar for all models. At t=0, the density
profile becomes singular everywhere, matching an approximate r-3/2variation for all radii within
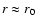 .
For r>r0, however,
the density follows the initial
.
For r>r0, however,
the density follows the initial
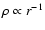 power-law.
Along each sequence of calculations, the time of singularity formation
decreases with increasing mass of the core. For logatropic spheres of
mass ranging from 1 (highly subcritical) to
power-law.
Along each sequence of calculations, the time of singularity formation
decreases with increasing mass of the core. For logatropic spheres of
mass ranging from 1 (highly subcritical) to 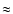 92.05
92.05 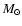 (critical mass) in the lower
(critical mass) in the lower  sequence, the predicted lifetimes
for the prestellar collapse phase are
sequence, the predicted lifetimes
for the prestellar collapse phase are  1.5-
1.5-
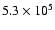 yr,
compared to
yr,
compared to  1.7-
1.7-
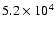 yr for the higher
yr for the higher  sequence involving masses from 0.5 to
sequence involving masses from 0.5 to  10.5
10.5 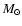 (critical case).
(critical case).
(ii) The approach to the singular density profile never occurs in an entirely
subsonic fashion, as was suggested by RPW. Referring to the lower  models, about 6% of the total core mass collapses supersonically in a
models, about 6% of the total core mass collapses supersonically in a
 ,
while only
,
while only  0.02% behaves this manner in a critical
(
0.02% behaves this manner in a critical
(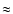 92.05
92.05  )
logatrope. In the higher
)
logatrope. In the higher  sequence
the same trend is observed, with
sequence
the same trend is observed, with  0.7% of the mass now infalling
supersonically at t=0 in a
0.7% of the mass now infalling
supersonically at t=0 in a
 sphere. Thus, the effect of
increasing the fiducial truncation pressure is to produce a gentler
adjustment from the nonsingular to the singular collapse stage. The
time elapsed between the initiation of collapse and the singularity
formation obeys the approximate scaling
sphere. Thus, the effect of
increasing the fiducial truncation pressure is to produce a gentler
adjustment from the nonsingular to the singular collapse stage. The
time elapsed between the initiation of collapse and the singularity
formation obeys the approximate scaling
 (first noted by RPW) for
all masses, including the critical one.
(first noted by RPW) for
all masses, including the critical one.
(iii) Immediately after singularity formation, a phase of vigorous accretion
follows in which the accretion rate rises steeply, reaching a maximum value
precisely when the central protostar has already accreted  40% of
its final mass. Thereafter, it decreases steadily for the remainder of the
evolution. In all cases, we have continued the calculations until the core
has delivered 99% of its mass to the central protostar. Thus, the models
may be indicative of the early star formation stages, including the Class 0
(
40% of
its final mass. Thereafter, it decreases steadily for the remainder of the
evolution. In all cases, we have continued the calculations until the core
has delivered 99% of its mass to the central protostar. Thus, the models
may be indicative of the early star formation stages, including the Class 0
(
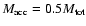 )
and the Class I (
)
and the Class I (
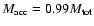 )
accretion phase.
)
accretion phase.
(iv) In particular, our models predict peak values of
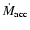 as high as
as high as
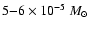 yr-1 for cores close to the
critical mass, independently of the fiducial value of the truncation pressure.
These are from
yr-1 for cores close to the
critical mass, independently of the fiducial value of the truncation pressure.
These are from  1 to 2 orders of magnitude larger than the peak values
achieved by a highly subcritical
1 to 2 orders of magnitude larger than the peak values
achieved by a highly subcritical
 core
(
core
(
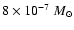 and
and 
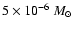 for the
lower and higher
for the
lower and higher  cases, respectively). At the borderline indicative
of the transition between Class 0 and Class I sources, the logatropic models
predict
cases, respectively). At the borderline indicative
of the transition between Class 0 and Class I sources, the logatropic models
predict
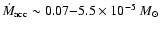 yr-1for the lower
yr-1for the lower  sequence and
sequence and
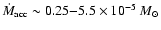 yr-1 for the
higher
yr-1 for the
higher  cases. Similarly, the corresponding values at the
borderline indicative of the transition between Class I and Class II
protostars are
cases. Similarly, the corresponding values at the
borderline indicative of the transition between Class I and Class II
protostars are
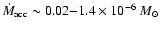 yr-1 and
yr-1 and
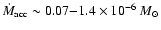 yr-1 for the
lower and higher
yr-1 for the
lower and higher  sequences, respectively. These results imply
a factor of
sequences, respectively. These results imply
a factor of
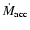 between Class 0 and Class I of
between Class 0 and Class I of  40,
which is at least 4 times higher than that inferred observationally.
40,
which is at least 4 times higher than that inferred observationally.
(v) For masses in the range
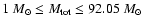 (lower
(lower  sequence), the accretion timescale increases with mass
up to about
sequence), the accretion timescale increases with mass
up to about
 .
For
.
For
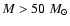 ,
the trend reverses and
the accretion timescale decreases as the total mass core approaches
criticality. Similarly, for the higher
,
the trend reverses and
the accretion timescale decreases as the total mass core approaches
criticality. Similarly, for the higher  sequence with core
masses between 0.5 and
sequence with core
masses between 0.5 and  10.5
10.5 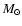 ,
the accretion timescale
is longer for subcritical masses around
,
the accretion timescale
is longer for subcritical masses around
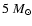 .
In particular,
our models predict Class 0 lifetimes of
.
In particular,
our models predict Class 0 lifetimes of  0.7-
0.7-
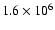 yr
(for lower
yr
(for lower  )
and
)
and  1.1-
1.1-
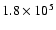 yr (for
higher
yr (for
higher  )
and Class I lifetimes of
)
and Class I lifetimes of
 2.9-
2.9-
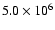 yr (for lower
yr (for lower  )
and
)
and
 4.2-
4.2-
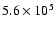 yr (for higher
yr (for higher  ), implying
that star formation in clustered regions occurs on shorter timescales
compared to more isolated environments. The predicted lifetimes for
the higher
), implying
that star formation in clustered regions occurs on shorter timescales
compared to more isolated environments. The predicted lifetimes for
the higher  sequence are comparable with the observationally
inferred Class I lifetime of
sequence are comparable with the observationally
inferred Class I lifetime of 
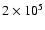 yr in the
yr in the 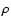 Oph
cluster-forming cloud.
Oph
cluster-forming cloud.
(vi) More realistic simulations of the formation of massive stars must
include the effects of radiative transfer. Because of the high luminosities
of young embedded massive stars, we expect that radiative acceleration
will contribute significantly to the dynamical evolution of high-mass
cores, probably producing larger sizes of the maximum accretion rate,
shorter lifetimes and smaller final stellar masses than predicted by the
present purely hydrodynamic logatropic collapse models. An improved
picture of the logatropic collapse must then necessarily require the
inclusion of the effects of radiative transfer along with the effects
of rotation and magnetic fields.
Acknowledgements
We thank the referee for a number of very helpful comments and
suggestions that have improved the quality of the manuscript.
The calculations of this paper were made using the facilities of the
Laboratory of Computational Physics at the IVIC Center of Physics.
-
Adams, F. C., Lada, C. J., & Shu, F. H. 1987, ApJ, 312, 788
In the text
NASA ADS
-
Alves, J. F., Lada, C. J., & Lada, E. A. 2001, Nature, 409,
159
In the text
NASA ADS
-
André, P., Ward-Thompson, D., & Motte, F. 1996, A&A, 314,
625
In the text
NASA ADS
-
André, P., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406,
122
In the text
NASA ADS
-
André, P., Ward-Thompson, D., & Barsony, M. 2000, in
Protostars and Planets IV, ed. V. G. Mannings, A. P. Boss, &
S. S. Russell (Tucson: Univ. Arizona Press), 59
In the text
-
Bacmann, A., André, P., Puget, J.-L., et al. 2000, A&A,
361, 555
In the text
NASA ADS
-
Bachiller, R. 1996, ARA&A, 34, 111
In the text
NASA ADS
-
Bally, J., Reipurth, B., Lada, C. J., & Billawala, Y. 1999,
AJ, 117, 410
In the text
NASA ADS
-
Beichman, C. A., Myers, P. C., Emerson, J. P., et al. 1986,
ApJ, 307, 337
In the text
NASA ADS
-
Bodenheimer, P., & Sweigart, A. 1968, ApJ, 152, 515
In the text
NASA ADS
-
Bonnor, W. B. 1956, MNRAS, 116, 351
In the text
NASA ADS
-
Bontemps, S., André, P., Terebey, S., & Cabrit, S. 1996,
A&A, 311, 858
In the text
NASA ADS
-
Boss, A. P., & Black, D. C. 1982, ApJ, 258, 270
In the text
NASA ADS
-
Caselli, P., & Myers, P. C. 1995, ApJ, 446, 665
In the text
NASA ADS
-
Chandler, C. J., & Richer, J. S. 2000, ApJ, 530, 851
In the text
NASA ADS
-
Colomé, C., di Francesco, J., & Harvey, P. M. 1996, ApJ, 461,
909
In the text
NASA ADS
-
Ebert, R. 1955, Z. Astrophys., 37, 217
In the text
NASA ADS
-
Eisner, J. A., Greenhill, L. J., Herrnstein, J. R., Moran, J. M.,
& Menten, K. M. 2002, ApJ, 569, 334
In the text
NASA ADS
-
Foster, P. N., & Chevalier, R. A. 1993, ApJ, 416, 303
In the text
NASA ADS
-
Fuller, G. A., & Myers, P. C. 1992, ApJ, 384, 523
In the text
NASA ADS
-
Greene, T. P., Wilking, B. A., André, P., Young, E. T., &
Lada, C. J. 1994, ApJ, 434, 614
In the text
NASA ADS
-
Gregersen, E. M., & Evans, N. J. 2000, ApJ, 538, 260
In the text
NASA ADS
-
Henning, T., Burkert, A., Launhardt, R., Leinert, Ch., & Stecklum,
B. 1998, A&A, 336, 565
In the text
NASA ADS
-
Henriksen, R., André, P., & Bontemps, S. 1997, A&A, 323, 549
In the text
NASA ADS
-
Hunter, C. 1977, ApJ, 218, 834
In the text
NASA ADS
-
Jijina, J., Myers, P. C., & Adams, F. C. 1999, ApJS, 125, 161
In the text
NASA ADS
-
Johnstone, D., Wilson, C. D., Moriarty-Schieven, G., et al.
2000, ApJ, 545, 327
In the text
NASA ADS
-
Kenyon, S. J., Gomez, M., Marzke, R. O., & Hartmann, L. 1994,
AJ, 108, 251
In the text
NASA ADS
-
Kudoh, T., & Shibata, K. 1997, ApJ, 476, 632
In the text
NASA ADS
-
Ladd, E. F., Fuller, G. A., & Deane, J. R. 1998, ApJ, 495, 871
In the text
NASA ADS
-
Larson, R. B. 1969, MNRAS, 145, 271
In the text
NASA ADS
-
Lee, C. W., Myers, P. C., & Tafalla, M. 1999, ApJ, 526, 788
In the text
NASA ADS
-
Lufkin, E. A., & Hawley, J. F. 1993, ApJS, 88, 569
In the text
NASA ADS
-
McLaughlin, D. E., & Pudritz, R. E. 1996, ApJ, 469, 194 (MP96)
In the text
NASA ADS
-
McLaughlin, D. E., & Pudritz, R. E. 1997, ApJ, 476, 750 (MP97)
In the text
NASA ADS
-
Matzner, C. D., & McKee, C. F. 2000, ApJ, 545, 364
In the text
NASA ADS
-
May, M. M., & White, R. H. 1966, Phys. Rev., 141(4), 1232
In the text
-
Myers, P. C., & Goodman, A. A. 1988, ApJ, 329, 392
In the text
NASA ADS
-
Myers, P. C., & Khersonsky, V. K. 1995, ApJ, 442, 186
In the text
NASA ADS
-
Noh, W. F. 1987, J. Comput. Phys., 72, 78
In the text
-
Osorio, M., Lizano, S., & D'Alessio, P. 1999, ApJ, 525, 808
In the text
NASA ADS
-
Ouyed, R., & Pudritz, R. E. 1997, ApJ, 482, 712
In the text
NASA ADS
-
Penston, M. V. 1969, MNRAS, 144, 425
In the text
NASA ADS
-
Reid, M. A., Pudritz, R. E., & Wadsley, J. 2002, ApJ, in press
[arXiv:astro-ph/0201261] v1 16 Jan. 2002 (RPW)
In the text
-
Richer, J. S., Shepherd, D. S., Cabrit, S., Bachiller, R., &
Churchwell, E. 2000, in Protostars and Planets IV, ed. V. G.
Mannings, A. P. Boss, & S. S. Russell (Tucson: Univ. Arizona Press),
867
In the text
-
Shepherd, D. S., Yu, K. C., Bally, J., & Testi, L. 2000, ApJ,
535, 833
In the text
NASA ADS
-
Shu, F. H. 1977, ApJ, 214, 488
In the text
NASA ADS
-
Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23
In the text
NASA ADS
-
Sigalotti, L. di G., & Klapp, J. 2001, IJMP D, 10(2), 115
In the text
-
Sigalotti, L. di G., & Mendoza-Briceño, C. A. 2002, A&A,
submitted
In the text
-
Sod, G. A. 1978, J. Comput. Phys., 27, 1
In the text
-
van der Tak, F. F. S., van Dishoeck, E. F., Evans, N. J. II, &
Blake, G. A. 2000, ApJ, 537, 283
In the text
NASA ADS
-
Velusamy, T., & Langer, W. D. 1998, Nature, 392, 685
In the text
NASA ADS
-
Ward-Thompson, D., Scott, P. F., Hills, R. E., & André, P.
1994, MNRAS, 268, 276
In the text
NASA ADS
-
Ward-Thompson, D., Motte, F., & André, P. 1999, MNRAS, 305,
143
In the text
NASA ADS
-
Whitworth, A. P., & Ward-Thompson, D. 2001, ApJ, 547, 317
In the text
NASA ADS
-
Yorke, H. W., & Sonnhalter, C. 2002, ApJ, 569, 846
In the text
NASA ADS
Copyright ESO 2002
![\begin{displaymath}p=p_{\rm c}\left[1+A\ln\left(\frac{\rho}{\rho _{\rm c}}\right)\right]
,
\end{displaymath}](/articles/aa/full/2002/43/aah3666/img46.gif)
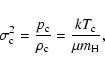

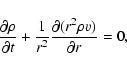
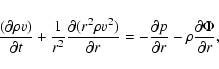
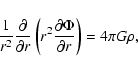
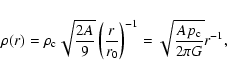
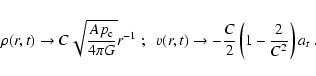
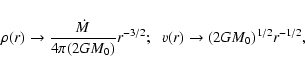
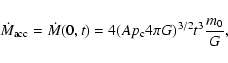
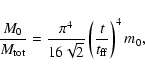
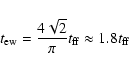
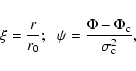
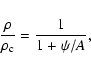
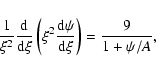
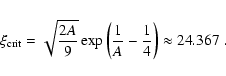
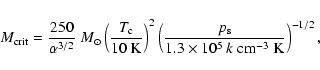
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f1.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg130.gif)
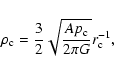
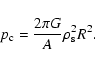
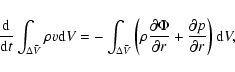
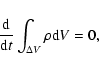
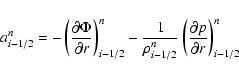
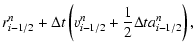
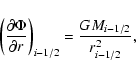
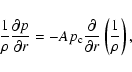
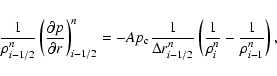
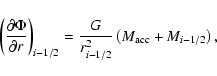
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f2.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg165.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f3a.eps}\par\includegraphics[width=8.8cm]{h3666f3b.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg166.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f4.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg167.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f5.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg168.gif)
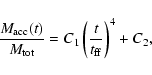
![\begin{figure}
\par\includegraphics[width=8.3cm]{h3666f6a.eps}\includegraphics[width=8.3cm]{h3666f6b.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg182.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm]{h3666f7a.eps}\includegraphics[width=8.3cm]{h3666f7b.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg188.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f8a.eps}\par\includegraphics[width=8.8cm]{h3666f8b.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg210.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f9a.eps}\includegraphics[width=8.8cm]{h3666f9b.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg213.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f10.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg218.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3666f11a.eps}\par\includegraphics[width=8.8cm]{h3666f11b.eps}\end{figure}](/articles/aa/full/2002/43/aah3666/Timg225.gif)