

Up: On the theory of
We confine our attention to an isothermal atmosphere
with a vertical magnetic field which is unbounded in the
horizontal direction. Using a fluid description and assuming an ideal plasma,
we write the energy equation as,
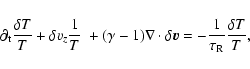 |
(1) |
where
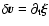 is the velocity
perturbation, T is the temperature of the gas and
is the velocity
perturbation, T is the temperature of the gas and 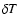 the temperature perturbation.
We assume the Lagrangian displacement
the temperature perturbation.
We assume the Lagrangian displacement
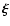 varies as
varies as 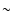
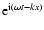 ,
where
,
where 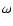 is the angular frequency and k is the horizontal wave number.
We allow for radiative losses, approximating them by Newton's law
of cooling (e.g. Spiegel 1957; Mihalas & Mihalas 1984),
which assumes that the temperature fluctuations are damped
radiatively on a time scale
is the angular frequency and k is the horizontal wave number.
We allow for radiative losses, approximating them by Newton's law
of cooling (e.g. Spiegel 1957; Mihalas & Mihalas 1984),
which assumes that the temperature fluctuations are damped
radiatively on a time scale
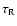 ,
given by
,
given by
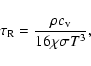 |
(2) |
where 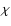 is the mean absorption coefficient per unit length,
is the mean absorption coefficient per unit length,
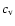 the specific heat per unit volume,
and
the specific heat per unit volume,
and 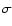 the Stefan-Boltzmann constant.
For simplicity, we assume that
the Stefan-Boltzmann constant.
For simplicity, we assume that
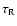 is constant over the atmosphere.
If the vertical dimension
of the perturbation is small compared to the local scale height,
the relation between the Lagrangian perturbations in pressure p
and density
is constant over the atmosphere.
If the vertical dimension
of the perturbation is small compared to the local scale height,
the relation between the Lagrangian perturbations in pressure p
and density 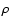 is then approximately given by
is then approximately given by
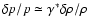 ,
where
,
where
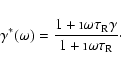 |
(3) |
With these assumptions,
the linearized
equations for MAG waves are given by a system of two coupled
differential equations (Banerjee et al. 1997),
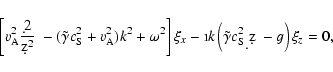 |
(4) |
![\begin{displaymath}\left[\tilde{\gamma} c_{\rm S}^2 {\d^2\over \d z^2} - \tilde{...
...2{\d\over \d z }-(\tilde{\gamma}\gamma -1)g\right]
\xi_x =0 ,
\end{displaymath}](/articles/aa/full/2002/43/aa2813/img31.gif) |
(5) |
where 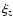 and
and 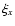 are the amplitudes of the vertical and
horizontal components of the displacement,
g is the acceleration due to gravity,
and
are the amplitudes of the vertical and
horizontal components of the displacement,
g is the acceleration due to gravity,
and
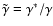 .
The adiabatic sound speed and the Alfvén speed are given, respectively, by
.
The adiabatic sound speed and the Alfvén speed are given, respectively, by
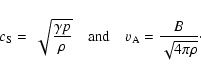 |
(6) |
We should point out here that the equation governing the propagation of the
purely transverse Alfvén waves is decoupled from Eqs. (4)
and (5) and will not be considered in the present investigation.
We have implicitly assumed that the propagation and the motions of the
MAG modes are confined to the x-z plane. This involves no loss of generality.
Equations (4) and (5) have the same structure as the
linearized wave equation for adiabatic perturbations
(see Eqs. (1), (2) of Hasan & Christensen-Dalsgaard 1992), apart
from the appearance of the parameter
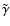 ,
which
incorporates radiative cooling.
In non-dimensional form Eq. (3) can be written as
,
which
incorporates radiative cooling.
In non-dimensional form Eq. (3) can be written as
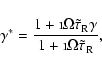 |
(7) |
where the dimensionless relaxation time scale is given by
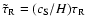 ,
where
,
where
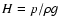 is the scale height of
the atmosphere, which is constant for an isothermal medium and the dimensionless frequency,
is the scale height of
the atmosphere, which is constant for an isothermal medium and the dimensionless frequency,
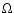 ,
is given by expression (9).
As
,
is given by expression (9).
As
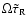 varies from 0 to
varies from 0 to 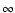 ,
,
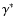 describes a semi-circle in the complex plane
(see Bünte & Bogdan 1994).
describes a semi-circle in the complex plane
(see Bünte & Bogdan 1994).
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{MS2813f2.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg42.gif) |
Figure 2:
The variation of the real part (solid line)
and the imaginary part (dashed line) of the effective
Brunt-Väisälä frequency
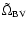 ,
(in
dimensionless units) as a function of ,
(in
dimensionless units) as a function of
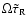 . . |
Figures 1a, b show the variation of the real and
imaginary parts of
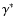 respectively as a function of
respectively as a function of
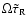 .
We find that for
.
We find that for
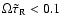 ,
,
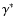 approaches the isothermal limit,
and
approaches the isothermal limit,
and
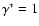 .
For
.
For
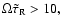 Re(
Re(
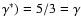 .
Thus in the limit
.
Thus in the limit
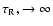 i.e. in the limit of
adiabatic perturbations,
i.e. in the limit of
adiabatic perturbations,
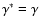 and
and
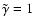 .
Letting
.
Letting
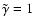 in Eqs. (4) and (5) we recover the linearized
equations given by Hasan & Christensen-Dalsgaard (1992).
The imaginary contribution to
in Eqs. (4) and (5) we recover the linearized
equations given by Hasan & Christensen-Dalsgaard (1992).
The imaginary contribution to
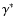 is maximal for
is maximal for
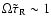 .
Thus to study the maximal effect
of radiative heat exchange we choose our parametric
values such that
.
Thus to study the maximal effect
of radiative heat exchange we choose our parametric
values such that
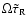 becomes close to 1.
In order to obtain a dimensionless wave equation we introduce three
dimensionless parameters,
becomes close to 1.
In order to obtain a dimensionless wave equation we introduce three
dimensionless parameters,
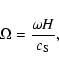 |
(9) |
and the dimensionless vertical coordinate
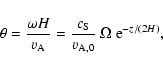 |
(10) |
where vA,0 is the Alfvén speed at z=0.
In terms of the variables defined by Eqs. (8)-(10),
Eqs. (4) and (5) can be combined into
a fourth-order differential equation for 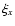 ,
,
where
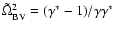 is the square of the effective Brunt-Väisälä frequency (in
dimensionless units). This Brunt-Väisälä frequency is a
function of frequency in the non-adiabatic case.
is the square of the effective Brunt-Väisälä frequency (in
dimensionless units). This Brunt-Väisälä frequency is a
function of frequency in the non-adiabatic case.
Figure 2 shows the dependence of
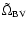 on
the radiative relaxation time
on
the radiative relaxation time
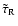 .
The solid line depicts
the real part whereas the dashed line represents the imaginary
part of
.
The solid line depicts
the real part whereas the dashed line represents the imaginary
part of
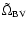 .
Note that for
.
Note that for
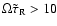 ,
,
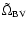 reaches a constant value of 0.5 (corresponding
to the adiabatic limit). On the other hand, as
reaches a constant value of 0.5 (corresponding
to the adiabatic limit). On the other hand, as
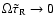 ,
Re(
,
Re(
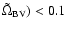 .
Thus, in the isothermal
limit,
.
Thus, in the isothermal
limit,
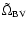 ,
which is the higher cutoff frequency for the
g-modes, is very low. The consequences of this will be taken
up again when we discuss the properties of g-modes in
detail. Figure 2 also reveals that the imaginary
part of
,
which is the higher cutoff frequency for the
g-modes, is very low. The consequences of this will be taken
up again when we discuss the properties of g-modes in
detail. Figure 2 also reveals that the imaginary
part of
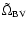 is significant only for
is significant only for
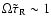 .
.
The general solution of Eq. (11)
can be expressed in terms of Meijer functions (Zhugzhda 1979) as
follows:
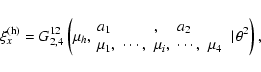 |
(12) |
where
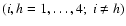 and
and
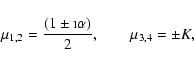 |
(13) |
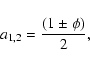 |
(14) |
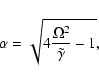 |
(15) |
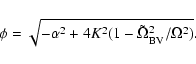 |
(16) |
These solutions are very similar in nature to the purely
adiabatic case (see Banerjee et al. 1995).
Once
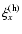 is known, it is fairly straightforward to
determine the corresponding solutions
is known, it is fairly straightforward to
determine the corresponding solutions
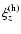 from either of
Eqs. (4) or (5). The complete solutions
satisfying the required
boundary conditions can be constructed as linear combinations of
from either of
Eqs. (4) or (5). The complete solutions
satisfying the required
boundary conditions can be constructed as linear combinations of
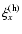 and
and
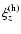 .
.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS2813f3a.eps}\\ [4mm]
\includegraphics[width=7cm,clip]{MS2813f3b.eps}
\end{figure}](/articles/aa/full/2002/43/aa2813/Timg69.gif) |
Figure 3:
Diagnostic diagram for non adiabatic modes. Panel a)
for g1-mode and b) for p1-mode. Different line styles
correspond to different radiative relaxation time
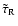 as
labelled.
as
labelled. |


Up: On the theory of
Copyright ESO 2002
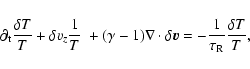
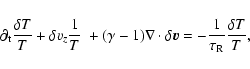
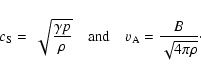
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{MS2813f2.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg42.gif)
![]() on
the radiative relaxation time
on
the radiative relaxation time
![]() .
The solid line depicts
the real part whereas the dashed line represents the imaginary
part of
.
The solid line depicts
the real part whereas the dashed line represents the imaginary
part of
![]() .
Note that for
.
Note that for
![]() ,
,
![]() reaches a constant value of 0.5 (corresponding
to the adiabatic limit). On the other hand, as
reaches a constant value of 0.5 (corresponding
to the adiabatic limit). On the other hand, as
![]() ,
Re(
,
Re(
![]() .
Thus, in the isothermal
limit,
.
Thus, in the isothermal
limit,
![]() ,
which is the higher cutoff frequency for the
g-modes, is very low. The consequences of this will be taken
up again when we discuss the properties of g-modes in
detail. Figure 2 also reveals that the imaginary
part of
,
which is the higher cutoff frequency for the
g-modes, is very low. The consequences of this will be taken
up again when we discuss the properties of g-modes in
detail. Figure 2 also reveals that the imaginary
part of
![]() is significant only for
is significant only for
![]() .
.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS2813f3a.eps}\\ [4mm]
\includegraphics[width=7cm,clip]{MS2813f3b.eps}
\end{figure}](/articles/aa/full/2002/43/aa2813/Timg69.gif)