A&A 395, 263-277 (2002)
DOI: 10.1051/0004-6361:20021257
On the theory of MAG waves and a comparison with sunspot observations
from CDS/SoHO
D. Banerjee1 - E. O'Shea2 - M. Goossens 1 - J. G. Doyle 3 - S. Poedts 1
1 - Centre for Plasma Astrophysics, Katholieke Universiteit
Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
2 -
Instituto de Astrofisica de Canarias, C/ Vía Láctea s/n, 38200 La Laguna, Tenerife, The Canary Islands, Spain
3 -
Armagh Observatory, College Hill, Armagh BT61
9DG, N. Ireland
Received 18 June 2002 / Accepted 23 August 2002
Abstract
We examine the influence of non-adiabatic effects on the modes of an isothermal
stratified magnetic atmosphere. We present new solutions for
magneto-acoustic-gravity (or MAG) waves in the presence of a radiative heat
exchange based on Newton's law of cooling. An analytic expression for the
dispersion relation is derived, which allows the effect of a weak magnetic field
on the modes to be studied. The insight so gained proves useful in extending
the computations to the moderate-high field case. In the second part we
present observations of two sunspots obtained in the EUV wavelength range with
the Coronal Diagnostic Spectrometer ( CDS) on SoHO. We examine the time
series for the line intensities and relative velocities and calculate their
power spectra using wavelet transforms. We find oscillations in the
chromosphere and transition region above the sunspots in the temperature range
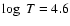 -5.4 K. Most of the spectral power above the umbra is contained in the
5-7 mHz frequency range. When the CDS slit crosses the sunspot umbra a
clear 3 min oscillation is observed. The observed oscillation frequencies are
compared with the computed frequencies and the observations
are interpreted in terms of the slow magneto-acoustic waves.
-5.4 K. Most of the spectral power above the umbra is contained in the
5-7 mHz frequency range. When the CDS slit crosses the sunspot umbra a
clear 3 min oscillation is observed. The observed oscillation frequencies are
compared with the computed frequencies and the observations
are interpreted in terms of the slow magneto-acoustic waves.
Key words: Sun: atmosphere - Sun: magnetic fields - Sun: sunspots - Sun: UV radiation
In the past thirty years, observations of oscillations with periods around 3 min have been widely reported in the atmosphere of sunspots (see reviews by Lites
1992; Bogdan 2000; Fludra 1999, 2001; Brynildsen et al. 1999a,b, 2000, 2002; Maltby et al. 1999,
2001; Tziotziou et al. 2002; O'Shea et al. 2002). It is widely believed that these oscillations are the signatures of waves propagating in the sunspot atmosphere. A study of these oscillations can
therefore be used to reveal information about the form of the waves and the structure and nature
of the sunspot. The aim of the present study is to
contribute towards developing a theory of such wave motions and to compare them
with observations performed by the Coronal Diagnostic Spectrometer ( CDS)
on SoHO. The waves that we consider here are magneto-acoustic-gravity
( MAG for short) waves. We study the physical nature of the MAG
oscillations and try to understand the cause for the existence of different types
of elementary wave modes in a magnetized radiative isothermal atmosphere,
subject to different sets of boundary conditions. The present investigation is a
continuation of earlier work by Hasan & Christensen-Dalsgaard (1992) and
Banerjee et al. (1995), who examined the effects of a weak vertical magnetic
field on the normal adiabatic modes of an isothermal atmosphere by combining a
semi-analytic approach, based on asymptotic dispersion relations, with numerical
solutions. However, oscillations in a realistic solar atmosphere are affected by radiative
dissipation and energy losses at the boundaries. Thus the modes are damped and have
complex frequencies. In this paper, we examine the influence of non-adiabatic effects on
the modes of an isothermal stratified magnetized atmosphere. The
inclusion of radiative dissipation based on Newton's law of
cooling demonstrates the importance of this effect in the study
of magneto-atmospheric waves.
It was pointed out by Bünte & Bogdan (1994) that Newtonian cooling
can be incorporated in the solution of the isothermal magneto-atmospheric wave
problem by replacing 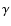 ,
the ratio of specific heats, by a complex
frequency-dependent quantity.
This procedure permits one to generalize easily the previous
calculations to include radiative dissipation.
Bünte & Bogdan treated a planar,
isothermal and stratified atmosphere in the presence of a horizontal magnetic
field, whereas in this study we consider a vertical magnetic field.
Babaev et al. (1995) derived an exact solution of the MAG waves in the
case of oblique propagation with respect to the magnetic field. The solutions
are expressed in terms of the generalized Meijer's hypergeometric G functions.
Their solutions are very similar to our analytical results. We further perform a
normal mode analysis subject to different sets of boundary conditions and
compare our analytical results with full numerical solutions.
,
the ratio of specific heats, by a complex
frequency-dependent quantity.
This procedure permits one to generalize easily the previous
calculations to include radiative dissipation.
Bünte & Bogdan treated a planar,
isothermal and stratified atmosphere in the presence of a horizontal magnetic
field, whereas in this study we consider a vertical magnetic field.
Babaev et al. (1995) derived an exact solution of the MAG waves in the
case of oblique propagation with respect to the magnetic field. The solutions
are expressed in terms of the generalized Meijer's hypergeometric G functions.
Their solutions are very similar to our analytical results. We further perform a
normal mode analysis subject to different sets of boundary conditions and
compare our analytical results with full numerical solutions.
We consider wave damping by radiative energy
exchange, which is likely to be efficient in the solar photosphere, where the radiative relaxation
times are very short compared to the typical wave periods. By comparison, damping of
hydro-magnetic waves due to viscous
dissipation and particle conduction is entirely negligible in
those layers of the solar atmosphere where small amplitude disturbances are likely to occur.
As we will see later, the
condition for the propagation of gravity waves, which depends on
the existence of the buoyancy force, is more stringent in the
presence of radiative damping than in its absence (Bray &
Loughhead 1974).
The radiative damping of oscillatory modes in a optically thin, isothermal,
unmagnetized medium was studied by several authors (Stix 1970; Souffrin
1972; Mihalas & Mihalas 1984). Bogdan & Knölker (1989) obtained the
dispersion relation for linear compressive plane waves in a homogeneous,
unstratified, uniformly magnetized radiating fluid. Here we consider
the propagation of optically thin MAG waves in a stratified, uniformly
magnetized medium in which the
radiative energy exchange occurs through Newton's law of cooling. The main
effect of radiation is to damp the waves.
The plan of the paper is as follows: in Sect. 2, the basic wave equations
are presented, including Newton's law of cooling.
In Sects. 3 and 4 we present the dispersion
relation for a weak field followed by numerical results in the form of a
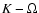 diagram. In Sect. 5 we treat the strong field case which will be more
relevant for comparison with our observations.
This is followed by an observational report of sunspot oscillation studies
by CDS in Sects. 6 and 7.
A discussion of the observational results and a comparison with the theoretical
results are taken up in Sect. 8 and finally the conclusions are drawn in Sect. 9.
diagram. In Sect. 5 we treat the strong field case which will be more
relevant for comparison with our observations.
This is followed by an observational report of sunspot oscillation studies
by CDS in Sects. 6 and 7.
A discussion of the observational results and a comparison with the theoretical
results are taken up in Sect. 8 and finally the conclusions are drawn in Sect. 9.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{MS2813f1a.eps}\\ [4mm]
\includegraphics[width=7.4cm,clip]{MS2813f1b.eps}
\end{figure}](/articles/aa/full/2002/43/aa2813/Timg14.gif) |
Figure 1:
The complex parameter
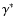 as a function of
as a function of
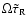 .
Panels a) represents the variation of the real
part and b) represents the variation of the imaginary
part. .
Panels a) represents the variation of the real
part and b) represents the variation of the imaginary
part. |
| Open with DEXTER |
We confine our attention to an isothermal atmosphere
with a vertical magnetic field which is unbounded in the
horizontal direction. Using a fluid description and assuming an ideal plasma,
we write the energy equation as,
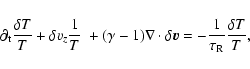 |
(1) |
where
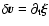 is the velocity
perturbation, T is the temperature of the gas and
is the velocity
perturbation, T is the temperature of the gas and 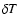 the temperature perturbation.
We assume the Lagrangian displacement
the temperature perturbation.
We assume the Lagrangian displacement
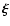 varies as
varies as 
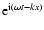 ,
where
,
where 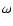 is the angular frequency and k is the horizontal wave number.
We allow for radiative losses, approximating them by Newton's law
of cooling (e.g. Spiegel 1957; Mihalas & Mihalas 1984),
which assumes that the temperature fluctuations are damped
radiatively on a time scale
is the angular frequency and k is the horizontal wave number.
We allow for radiative losses, approximating them by Newton's law
of cooling (e.g. Spiegel 1957; Mihalas & Mihalas 1984),
which assumes that the temperature fluctuations are damped
radiatively on a time scale
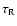 ,
given by
,
given by
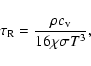 |
(2) |
where 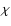 is the mean absorption coefficient per unit length,
is the mean absorption coefficient per unit length,
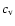 the specific heat per unit volume,
and
the specific heat per unit volume,
and 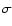 the Stefan-Boltzmann constant.
For simplicity, we assume that
the Stefan-Boltzmann constant.
For simplicity, we assume that
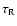 is constant over the atmosphere.
If the vertical dimension
of the perturbation is small compared to the local scale height,
the relation between the Lagrangian perturbations in pressure p
and density
is constant over the atmosphere.
If the vertical dimension
of the perturbation is small compared to the local scale height,
the relation between the Lagrangian perturbations in pressure p
and density 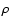 is then approximately given by
is then approximately given by
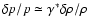 ,
where
,
where
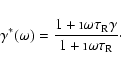 |
(3) |
With these assumptions,
the linearized
equations for MAG waves are given by a system of two coupled
differential equations (Banerjee et al. 1997),
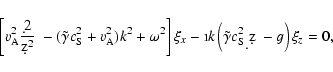 |
(4) |
![\begin{displaymath}\left[\tilde{\gamma} c_{\rm S}^2 {\d^2\over \d z^2} - \tilde{...
...2{\d\over \d z }-(\tilde{\gamma}\gamma -1)g\right]
\xi_x =0 ,
\end{displaymath}](/articles/aa/full/2002/43/aa2813/img31.gif) |
(5) |
where 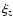 and
and 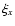 are the amplitudes of the vertical and
horizontal components of the displacement,
g is the acceleration due to gravity,
and
are the amplitudes of the vertical and
horizontal components of the displacement,
g is the acceleration due to gravity,
and
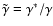 .
The adiabatic sound speed and the Alfvén speed are given, respectively, by
.
The adiabatic sound speed and the Alfvén speed are given, respectively, by
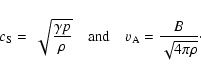 |
(6) |
We should point out here that the equation governing the propagation of the
purely transverse Alfvén waves is decoupled from Eqs. (4)
and (5) and will not be considered in the present investigation.
We have implicitly assumed that the propagation and the motions of the
MAG modes are confined to the x-z plane. This involves no loss of generality.
Equations (4) and (5) have the same structure as the
linearized wave equation for adiabatic perturbations
(see Eqs. (1), (2) of Hasan & Christensen-Dalsgaard 1992), apart
from the appearance of the parameter
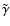 ,
which
incorporates radiative cooling.
In non-dimensional form Eq. (3) can be written as
,
which
incorporates radiative cooling.
In non-dimensional form Eq. (3) can be written as
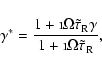 |
(7) |
where the dimensionless relaxation time scale is given by
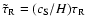 ,
where
,
where
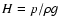 is the scale height of
the atmosphere, which is constant for an isothermal medium and the dimensionless frequency,
is the scale height of
the atmosphere, which is constant for an isothermal medium and the dimensionless frequency,
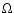 ,
is given by expression (9).
As
,
is given by expression (9).
As
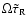 varies from 0 to
varies from 0 to 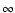 ,
,
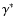 describes a semi-circle in the complex plane
(see Bünte & Bogdan 1994).
describes a semi-circle in the complex plane
(see Bünte & Bogdan 1994).
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{MS2813f2.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg42.gif) |
Figure 2:
The variation of the real part (solid line)
and the imaginary part (dashed line) of the effective
Brunt-Väisälä frequency
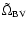 ,
(in
dimensionless units) as a function of ,
(in
dimensionless units) as a function of
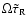 . . |
| Open with DEXTER |
Figures 1a, b show the variation of the real and
imaginary parts of
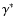 respectively as a function of
respectively as a function of
 .
We find that for
.
We find that for
 ,
,
 approaches the isothermal limit,
and
approaches the isothermal limit,
and
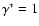 .
For
.
For
 Re(
Re(
 .
Thus in the limit
.
Thus in the limit
 i.e. in the limit of
adiabatic perturbations,
i.e. in the limit of
adiabatic perturbations,
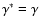 and
and
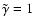 .
Letting
.
Letting
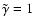 in Eqs. (4) and (5) we recover the linearized
equations given by Hasan & Christensen-Dalsgaard (1992).
The imaginary contribution to
in Eqs. (4) and (5) we recover the linearized
equations given by Hasan & Christensen-Dalsgaard (1992).
The imaginary contribution to
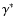 is maximal for
is maximal for
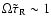 .
Thus to study the maximal effect
of radiative heat exchange we choose our parametric
values such that
.
Thus to study the maximal effect
of radiative heat exchange we choose our parametric
values such that
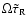 becomes close to 1.
In order to obtain a dimensionless wave equation we introduce three
dimensionless parameters,
becomes close to 1.
In order to obtain a dimensionless wave equation we introduce three
dimensionless parameters,
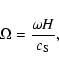 |
(9) |
and the dimensionless vertical coordinate
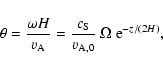 |
(10) |
where vA,0 is the Alfvén speed at z=0.
In terms of the variables defined by Eqs. (8)-(10),
Eqs. (4) and (5) can be combined into
a fourth-order differential equation for 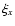 ,
,
where
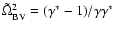 is the square of the effective Brunt-Väisälä frequency (in
dimensionless units). This Brunt-Väisälä frequency is a
function of frequency in the non-adiabatic case.
is the square of the effective Brunt-Väisälä frequency (in
dimensionless units). This Brunt-Väisälä frequency is a
function of frequency in the non-adiabatic case.
Figure 2 shows the dependence of
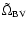 on
the radiative relaxation time
on
the radiative relaxation time
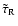 .
The solid line depicts
the real part whereas the dashed line represents the imaginary
part of
.
The solid line depicts
the real part whereas the dashed line represents the imaginary
part of
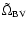 .
Note that for
.
Note that for
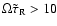 ,
,
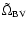 reaches a constant value of 0.5 (corresponding
to the adiabatic limit). On the other hand, as
reaches a constant value of 0.5 (corresponding
to the adiabatic limit). On the other hand, as
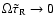 ,
Re(
,
Re(
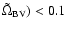 .
Thus, in the isothermal
limit,
.
Thus, in the isothermal
limit,
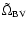 ,
which is the higher cutoff frequency for the
g-modes, is very low. The consequences of this will be taken
up again when we discuss the properties of g-modes in
detail. Figure 2 also reveals that the imaginary
part of
,
which is the higher cutoff frequency for the
g-modes, is very low. The consequences of this will be taken
up again when we discuss the properties of g-modes in
detail. Figure 2 also reveals that the imaginary
part of
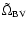 is significant only for
is significant only for
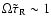 .
.
The general solution of Eq. (11)
can be expressed in terms of Meijer functions (Zhugzhda 1979) as
follows:
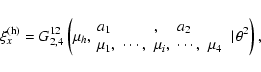 |
(12) |
where
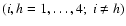 and
and
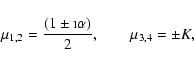 |
(13) |
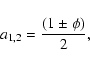 |
(14) |
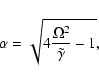 |
(15) |
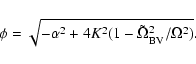 |
(16) |
These solutions are very similar in nature to the purely
adiabatic case (see Banerjee et al. 1995).
Once
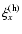 is known, it is fairly straightforward to
determine the corresponding solutions
is known, it is fairly straightforward to
determine the corresponding solutions
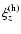 from either of
Eqs. (4) or (5). The complete solutions
satisfying the required
boundary conditions can be constructed as linear combinations of
from either of
Eqs. (4) or (5). The complete solutions
satisfying the required
boundary conditions can be constructed as linear combinations of
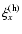 and
and
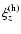 .
.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS2813f3a.eps}\\ [4mm]
\includegraphics[width=7cm,clip]{MS2813f3b.eps}
\end{figure}](/articles/aa/full/2002/43/aa2813/Timg69.gif) |
Figure 3:
Diagnostic diagram for non adiabatic modes. Panel a)
for g1-mode and b) for p1-mode. Different line styles
correspond to different radiative relaxation time
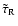 as
labelled.
as
labelled. |
| Open with DEXTER |
We now examine the asymptotic properties of waves and
normal modes of a stratified atmosphere with a weak magnetic
field (corresponding to the limit of small 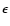 ,
where
,
where
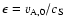 ).
The analytical results are used for the interpretation of
the numerical solutions presented in Sect. 4.
In order to get a physical picture of the solution, we consider the
upward propagation of a wave, excited from below at z=0, in an
isothermal atmosphere. It is well known
that acoustic modes are easily reflected if the temperature of
the medium changes with height (for a good discussion see Leibacher & Stein
1981). The slow mode can be reflected due to the increasing Alfvén speed with
height from layers where
).
The analytical results are used for the interpretation of
the numerical solutions presented in Sect. 4.
In order to get a physical picture of the solution, we consider the
upward propagation of a wave, excited from below at z=0, in an
isothermal atmosphere. It is well known
that acoustic modes are easily reflected if the temperature of
the medium changes with height (for a good discussion see Leibacher & Stein
1981). The slow mode can be reflected due to the increasing Alfvén speed with
height from layers where
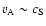 ,
through
conversion into a fast mode (e.g. Zhugzhda et al. 1984).
We implicitly assume that the properties of the
atmosphere change abruptly at the top boundary, resulting in downward
reflection of the waves. The lower boundary condition is chosen to
simulate a forcing layer. This permits standing wave solutions.
It should, however, be kept in mind that an isothermal atmosphere by itself
does not trap modes, rather we use this assumption to understand the
physical properties of the modes in a stratified atmosphere with a
vertical field. Let us now derive approximate dispersion relations for
various boundary conditions.
,
through
conversion into a fast mode (e.g. Zhugzhda et al. 1984).
We implicitly assume that the properties of the
atmosphere change abruptly at the top boundary, resulting in downward
reflection of the waves. The lower boundary condition is chosen to
simulate a forcing layer. This permits standing wave solutions.
It should, however, be kept in mind that an isothermal atmosphere by itself
does not trap modes, rather we use this assumption to understand the
physical properties of the modes in a stratified atmosphere with a
vertical field. Let us now derive approximate dispersion relations for
various boundary conditions.
Let us first consider rigid boundary conditions, viz.
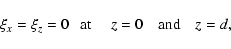 |
(17) |
here d is the height of the upper boundary, and D = d/His the dimensionless height.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{MS2813f4.eps}
\end{figure}](/articles/aa/full/2002/43/aa2813/Timg74.gif) |
Figure 4:
Variation of the imaginary part of 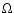 with
K for
with
K for
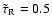 .
The different line styles corresponds to
different .
The different line styles corresponds to
different 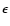 values (which is a measure of magnetic field
strength) as labelled.
values (which is a measure of magnetic field
strength) as labelled. |
| Open with DEXTER |
The asymptotic properties of the solution in the purely
adiabatic limit are presented in Hasan & Christensen-Dalsgaard (1992).
Following the same line of treatment using Eqs. (12)-(16) and applying the boundary
conditions given by Eq. (17) one can derive
the following dispersion relation in the weak field limit
where
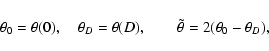 |
(19) |
and Kz2 is given by
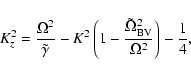 |
(20) |
and
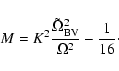 |
(21) |
For
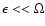 ,
the dispersion relation to lowest order
in
,
the dispersion relation to lowest order
in
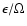 becomes
becomes
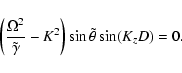 |
(22) |
Equation (22) admits the following solutions
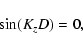 |
(23) |
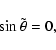 |
(24) |
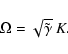 |
(25) |
We first consider the solution given by Eq. (23) which
implies that
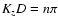 ,
where n is an integer and denotes the
order of the mode. Using this condition Eq. (20) yields,
,
where n is an integer and denotes the
order of the mode. Using this condition Eq. (20) yields,
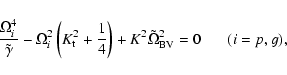 |
(26) |
where
Kt2 = Kz2 + K2.
Note that Eq. (26) looks very similar to the
usual relation for p- and g-modes (see Banerjee et al. 1995)
apart from the factor
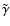 and modified
and modified
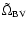 .
Because
of the presence of these two factors, the properties of these modes
change drastically. Figures 3a, b give an overview
of the behaviour of the g- and p-type modes respectively. Their
properties are reflected in these two
.
Because
of the presence of these two factors, the properties of these modes
change drastically. Figures 3a, b give an overview
of the behaviour of the g- and p-type modes respectively. Their
properties are reflected in these two 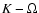 diagrams produced by
solving Eq. (26) for different values of the relaxation time
diagrams produced by
solving Eq. (26) for different values of the relaxation time
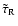 .
Figure 3a clearly shows that the
g1-mode has been pushed down to the low frequency part of the
diagnostic diagram with decreasing value of
.
Figure 3a clearly shows that the
g1-mode has been pushed down to the low frequency part of the
diagnostic diagram with decreasing value of
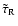 .
As
.
As
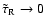 ,
the g1-mode tends to disappear, because
,
the g1-mode tends to disappear, because
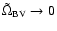 .
On the other hand,
Fig. 3b shows that the inclusion of radiative
exchange has not greatly changed the behaviour of the p1-mode, apart from
a decrease of the acoustic cutoff frequency.
.
On the other hand,
Fig. 3b shows that the inclusion of radiative
exchange has not greatly changed the behaviour of the p1-mode, apart from
a decrease of the acoustic cutoff frequency.
The solution corresponding to Eq. (25) can be
recognized as a modified Lamb mode (compare with
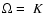 ,
for pure Lamb
mode). Thus we expect a frequency shift of the adiabatic Lamb mode.
Turning our attention to the solution given by
Eq. (24), we find that these modes are the same
magnetic modes present in the adiabatic conditions,
which arise solely due to the presence of the magnetic field.
The magnetic modes, hereafter referred to as m-modes, have frequencies
,
for pure Lamb
mode). Thus we expect a frequency shift of the adiabatic Lamb mode.
Turning our attention to the solution given by
Eq. (24), we find that these modes are the same
magnetic modes present in the adiabatic conditions,
which arise solely due to the presence of the magnetic field.
The magnetic modes, hereafter referred to as m-modes, have frequencies
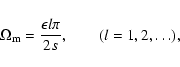 |
(27) |
where
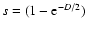 .
These modes are approximately transverse (it has be shown by Banerjee et al. (1995) that
.
These modes are approximately transverse (it has be shown by Banerjee et al. (1995) that
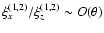 ).
Physically, these modes can be interpreted as gravity-modified slow modes
in a weak magnetic field. Thus these slow
modes are not affected by the inclusion of radiative losses in
the weak field limit. This result complements the result of Bogdan &
Knölker (1989), where it was conjectured that the uniform magnetic field
reduces the temperature perturbations associated with these waves and
therefore suppresses the radiative damping of these disturbances.
This aspect will be taken up later when we discuss the numerical solutions.
).
Physically, these modes can be interpreted as gravity-modified slow modes
in a weak magnetic field. Thus these slow
modes are not affected by the inclusion of radiative losses in
the weak field limit. This result complements the result of Bogdan &
Knölker (1989), where it was conjectured that the uniform magnetic field
reduces the temperature perturbations associated with these waves and
therefore suppresses the radiative damping of these disturbances.
This aspect will be taken up later when we discuss the numerical solutions.
If we use zero-gradient boundary conditions
at the top and bottom of the layer,
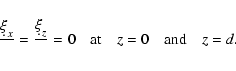 |
(28) |
In addition to the modes discussed previously, we find another wave mode,
namely the gravity-Lamb mode. The dispersion relation for this mode is given by
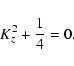 |
(29) |
Combining Eqs. (29) with (20) yields
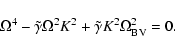 |
(30) |
This equation has the solution
![\begin{displaymath}\Omega ^2 = {\tilde\gamma K^2 \over 2} \left[ 1 \pm
\left(1 ...
...\rm BV}^2 \over K^2 \tilde\gamma }
\right)^{1/2} \right] \cdot
\end{displaymath}](/articles/aa/full/2002/43/aa2813/img101.gif) |
(31) |
The solution resembles a modified
gravity mode on the lower branch and a Lamb mode on the upper branch.
In order to see this, consider
the limit
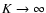 .
The smaller solution in Eq. (31) has the limit
.
The smaller solution in Eq. (31) has the limit
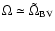 ,
which is the dispersion relation for a
modified g-mode for large K;
the larger solution has the limit
,
which is the dispersion relation for a
modified g-mode for large K;
the larger solution has the limit
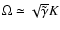 for large K,
which shows that the mode behaves like a modified Lamb wave.
for large K,
which shows that the mode behaves like a modified Lamb wave.
Thus the separate modes have changed their behavior in the diagnostic
diagram in the non-adiabatic case. It is important to know how
these modified modes interact with one another in the presence of radiative
losses. Mode coupling in the non adiabatic case will be different as
compared to the adiabatic case studied by Banerjee et al. (1995) (the
right hand side of Eq. (18) contributes to the coupling).
The behavior of the MAG waves is reflected in their properties in the
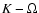 diagram namely the variation of the real and imaginary
part of the complex frequency with the horizontal wave number
K. The solutions were obtained by solving
Eq. (11) numerically, using a complex
version of the Newton-Raphson-Kantorovich scheme (Cash & Moore 1980) subject
to a different sets of boundary conditions. Banerjee et al. (1997) presented
the numerical solutions for the weak field case subjected to rigid boundary
conditions. In this paper we would like to compare our theoretical results with
some observational results so we concentrate here on higher magnetic field strengths.
diagram namely the variation of the real and imaginary
part of the complex frequency with the horizontal wave number
K. The solutions were obtained by solving
Eq. (11) numerically, using a complex
version of the Newton-Raphson-Kantorovich scheme (Cash & Moore 1980) subject
to a different sets of boundary conditions. Banerjee et al. (1997) presented
the numerical solutions for the weak field case subjected to rigid boundary
conditions. In this paper we would like to compare our theoretical results with
some observational results so we concentrate here on higher magnetic field strengths.
First we show the effect of the strength of the magnetic
field on the damping of these waves. To delineate the influence of the
magnetic field, we choose the m2-mode, which is predominantly
magnetic in nature. Figure 4 shows the
variation of the imaginary part of the frequency (which is a measure of the
damping) with K for fixed
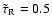 ,
D=1, and
,
D=1, and
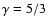 (for rigid boundary conditions). The different line
styles correspond to different
(for rigid boundary conditions). The different line
styles correspond to different 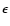 values. It clearly reveals
that as we increase the value of
values. It clearly reveals
that as we increase the value of 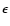 (increasing magnetic field
strength) the imaginary part reduces, indicating less damping of these
wave modes. This result is in agreement with the conclusions drawn by
Bogdan & Knölker (1989), that the magnetic field suppresses
radiative damping. For horizontal magnetic field Bünte & Bogdan
(1994) also reported a
"stiffening'' of the atmosphere with increasing
(increasing magnetic field
strength) the imaginary part reduces, indicating less damping of these
wave modes. This result is in agreement with the conclusions drawn by
Bogdan & Knölker (1989), that the magnetic field suppresses
radiative damping. For horizontal magnetic field Bünte & Bogdan
(1994) also reported a
"stiffening'' of the atmosphere with increasing 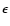 values.
values.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{MS2813f5.eps}
\end{figure}](/articles/aa/full/2002/43/aa2813/Timg106.gif) |
Figure 5:
Region in the diagnostic diagram for moderate
field strength (
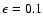 )
and )
and
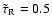 ,
where the
modified Lamb mode, magnetic modes and the gravity-Lamb mode are present.
These results are for zero gradient boundary conditions. ,
where the
modified Lamb mode, magnetic modes and the gravity-Lamb mode are present.
These results are for zero gradient boundary conditions. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=4.2cm,clip]{MS2813f6a.eps}\hspace*{4mm}\includegraphics[width=4.2cm,clip]{MS2813f6b.eps}
\end{figure}](/articles/aa/full/2002/43/aa2813/Timg107.gif) |
Figure 6:
Variation of the imaginary part of 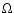 with K for the same set of parameters as in Fig. 5.
Panel a) shows the m1-mode and panel b) the m2-mode.
with K for the same set of parameters as in Fig. 5.
Panel a) shows the m1-mode and panel b) the m2-mode. |
| Open with DEXTER |
Let us now consider a moderate magnetic field strength.
Figure 5 shows a region in the diagnostic diagram for
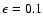 (
(
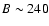 G) and
G) and
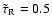 ,
subject to the zero-gradient
boundary conditions. The mode coupling
in this case is much more complicated because we have three mode interaction
regions as indicated.
As K increases, the m1-mode begins to acquire the character of
a modified Lamb mode. Figure 6a, which shows
the variation of imaginary part of the frequency of the m1-mode
with K also reveals that, there is an enhancement as it approaches
an avoided crossing (near K=0.8) followed by a suppression due to
mode transformation. Up to K=0.8 this mode behaves as a magnetic Lamb
mode and after the mode transformation it becomes a magnetic type.
This process is repeated at higher frequency (around K=2). Note the large
drop due to magnetic field suppression.
Figure 6b shows the variation of the imaginary part of the
frequency for the m2-mode (Fig. 5) with K. The two peaks
correspond to modified Lamb and m-mode coupling and modified gravity-Lamb
(gL-) and m-mode coupling respectively. Note the steep rise of the imaginary
part after the avoided crossing which indicates the effect of the gravity
mode. Figure 5 also shows the lower branch of the modified
gravity-Lamb mode (indicated as
,
subject to the zero-gradient
boundary conditions. The mode coupling
in this case is much more complicated because we have three mode interaction
regions as indicated.
As K increases, the m1-mode begins to acquire the character of
a modified Lamb mode. Figure 6a, which shows
the variation of imaginary part of the frequency of the m1-mode
with K also reveals that, there is an enhancement as it approaches
an avoided crossing (near K=0.8) followed by a suppression due to
mode transformation. Up to K=0.8 this mode behaves as a magnetic Lamb
mode and after the mode transformation it becomes a magnetic type.
This process is repeated at higher frequency (around K=2). Note the large
drop due to magnetic field suppression.
Figure 6b shows the variation of the imaginary part of the
frequency for the m2-mode (Fig. 5) with K. The two peaks
correspond to modified Lamb and m-mode coupling and modified gravity-Lamb
(gL-) and m-mode coupling respectively. Note the steep rise of the imaginary
part after the avoided crossing which indicates the effect of the gravity
mode. Figure 5 also shows the lower branch of the modified
gravity-Lamb mode (indicated as
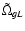 )
which was absent in
the purely adiabatic case.
)
which was absent in
the purely adiabatic case.
We now consider a situation which is more realistic as far as
the solar atmosphere is concerned. We consider an isothermal
atmosphere extending over several scale heights for which
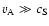 over most of the atmosphere. This situation is somewhat
similar to the atmosphere in sunspots. We consider the solution for small K.
There are three types of wave modes present in this situation, the slow, fast
and magneto-gravity-Lamb (MgL) modes. The gL-mode acquires a more pronounced magnetic
behavior because of the higher magnetic field strength and so we call them MgL-mode (see
Banerjee et al. 1995 for further details). From a study of the energy density
variation of these modes we find that the fast and MgL-modes are essentially
confined to photospheric regions (i.e. the lower part of the atmosphere), whereas the
wave energy density of the slow waves is spread over the entire extension of the
cavity. As far as the wave heating is concerned the slow modes appear to be a
more promising candidate than the other two type of modes.
over most of the atmosphere. This situation is somewhat
similar to the atmosphere in sunspots. We consider the solution for small K.
There are three types of wave modes present in this situation, the slow, fast
and magneto-gravity-Lamb (MgL) modes. The gL-mode acquires a more pronounced magnetic
behavior because of the higher magnetic field strength and so we call them MgL-mode (see
Banerjee et al. 1995 for further details). From a study of the energy density
variation of these modes we find that the fast and MgL-modes are essentially
confined to photospheric regions (i.e. the lower part of the atmosphere), whereas the
wave energy density of the slow waves is spread over the entire extension of the
cavity. As far as the wave heating is concerned the slow modes appear to be a
more promising candidate than the other two type of modes.
The frequencies of the slow magneto-acoustic modes or p-modes
can be found from Eq. (26) with K = 0, i.e.
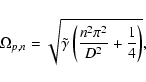 |
(32) |
where n denotes the order.
Following Scheuer & Thomas (1981) let us treat the
sunspot umbra as a cylinder of radius a. It can easily be shown that
our analysis for a plane can be carried over in a straightforward way to
cylindrical geometry, by treating axisymmetric modes and regarding
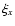 and k as the radial displacement and wave number respectively.
Assuming that the radial component of the displacement vanishes at r=a,
we find that k takes discrete values given by
and k as the radial displacement and wave number respectively.
Assuming that the radial component of the displacement vanishes at r=a,
we find that k takes discrete values given by
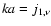 ,
where
,
where
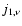 denotes the zero of the Bessel function J1 of order
denotes the zero of the Bessel function J1 of order 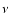 .
We consider the lowest-order mode (where order refers to the horizontal
direction) corresponding to
.
We consider the lowest-order mode (where order refers to the horizontal
direction) corresponding to 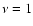 .
This provides us with a relation
between the horizontal wave number and the radius of the spot.
Table 1 represents the eigenfrequencies of
different order p-modes from our model atmosphere with D =
10,
.
This provides us with a relation
between the horizontal wave number and the radius of the spot.
Table 1 represents the eigenfrequencies of
different order p-modes from our model atmosphere with D =
10,
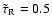 and
and
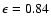 (
(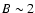 KG).
Table 1 reveals that radiative cooling
shifts the eigenfrequencies away from the real axis. Note that
the computed frequencies match very well with the ones
calculated from expression (32).
KG).
Table 1 reveals that radiative cooling
shifts the eigenfrequencies away from the real axis. Note that
the computed frequencies match very well with the ones
calculated from expression (32).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2813f7.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg121.gif) |
Figure 7:
MDI intensity-gram showing the location of the slit of the
s19332r00 dataset, relative to the sunspot umbra and penumbra. The over-plotted black rectangles are the locations of the slit at the start (right) and at the end time (left) of the observations. Pixel number 67 is marked with a white box. |
| Open with DEXTER |
Radiative cooling leads to a temporal decay of oscillations
of the form exp(
 ). The frequency eigenvalues of the
four modes are listed in Table 2 for a typical sunspot with radius
of 5000 km (K=0.06) together with the ratio of characteristic
decay time
). The frequency eigenvalues of the
four modes are listed in Table 2 for a typical sunspot with radius
of 5000 km (K=0.06) together with the ratio of characteristic
decay time
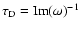 and oscillation period =
and oscillation period =
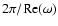 .
In the presence of Newtonian cooling all four modes are damped
by a factor e-1 within two oscillation periods.
.
In the presence of Newtonian cooling all four modes are damped
by a factor e-1 within two oscillation periods.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{MS2813f8.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg125.gif) |
Figure 8:
CDS raster images for the s19331r00 dataset,
in different temperature lines (as labeled),
and the Kitt peak magnetogram.
The over-plotted white rectangles are the locations of the slit for the s19332r00 dataset at the start (right) and the end time (left).
Pixel 67 is marked as a black box on the images. The contours indicate the
location of the umbra and penumbra. |
| Open with DEXTER |
Table 3:
A log of the datasets used in this paper obtained during April 2000.
| Active |
Date |
Dataset |
Type of |
Pointing |
Starting time |
Lines used |
| region |
|
|
observation |
(X, Y) |
UT |
|
| AR 8951 |
14 April 2000 |
s19331r00 |
Raster |
(116, 277) |
04:25 |
O III,
O V, He I, Mg IX, Ca X |
| |
|
s19332r00 |
Temporal |
(122, 277) |
04:48 |
O III,
O V, He I |
| |
|
s19333r00 |
Raster |
(135, 277) |
06:14 |
O III,
O V, He I, Mg IX, Ca X |
| |
|
s19334r00 |
Temporal |
(136, 277) |
06:37 |
O III,
O V, He I |
| |
|
s19335r00 |
Raster |
(152, 276) |
08:02 |
O III,
O V, He I, Mg IX, Ca X |
| |
|
s19336r00 |
Temporal |
(153, 275) |
08:26 |
O III,
O V, He I |
| AR 8963 |
19 April 2000 |
s19377r00 |
Raster |
(-1, 418) |
18:21 |
O III,
O V, He I, Mg IX, Ca X |
| |
|
s19378r00 |
Temporal |
(4, 412) |
18:45 |
O III,
O V, He I |
| |
|
s19379r00 |
Raster |
(18, 416) |
20:10 |
O III,
O V, He I, Mg IX, Ca X |
| |
|
s19380r00 |
Temporal |
(20, 415) |
20:34 |
O III,
O V, He I |
| |
|
s19381r00 |
Raster |
(33, 416) |
21:59 |
O III,
O V, He I, Mg IX, Ca X |
| |
|
s19382r00 |
Temporal |
(32, 414) |
22:23 |
O III,
O V, He I |
| AR 8963 |
20 April 2000 |
s19387r00 |
Raster |
(204, 402) |
18:00 |
O III,
O V, He I, Mg IX, Ca X |
| |
|
s19388r00 |
Temporal |
(204, 402) |
18:24 |
O III,
O V, He I |
| |
|
s19389r00 |
Raster |
(217, 401) |
19:49 |
O III,
O V, He I, Mg IX, Ca X |
| |
|
s19390r00 |
Temporal |
(218, 401) |
20:13 |
O III,
O V, He I |
| |
|
s19391r00 |
Raster |
(232, 401) |
21:38 |
O III,
O V, He I, Mg IX, Ca X |
| |
|
s19392r00 |
Temporal |
(233, 401) |
22:02 |
O III,
O V, He I |
For these observations we have used the normal incidence spectrometer ( NIS)
(Harrison et al. 1995), which is one of the components of the Coronal Diagnostic
Spectrometer ( CDS) on-board the Solar Heliospheric Observatory (SoHO).
The data discussed here were selected from the observing period 14 April and
19-20 April 2000. The observations were performed for two different active
regions. The details of the observations including pointing and start
times are summarized in Table 3. Two different
CDS sequences were run, one temporal series sequence called CHROM-N6 and
another raster sequence called CHROM-N5.
Temporal series datasets of 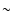 85 min duration were obtained for the three
lines of He I 584 Å (
85 min duration were obtained for the three
lines of He I 584 Å (
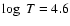 ), O III 599 Å (
), O III 599 Å (
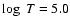 )
and
O V 629 Å (
)
and
O V 629 Å (
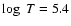 )
using exposure times of 25 s and the
)
using exposure times of 25 s and the
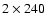 arcsec2 slit. The
CDS pixels in the y direction (i.e. spatial resolution) are of size 1.68 arcsec. In the raster sequence the
arcsec2 slit. The
CDS pixels in the y direction (i.e. spatial resolution) are of size 1.68 arcsec. In the raster sequence the
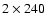 slit was moved 30 times in steps
of 2 arcsec so as to build up
slit was moved 30 times in steps
of 2 arcsec so as to build up
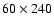 arcsec2 raster images within a duration of 24 min. For
this sequence the lines used were: He I 584 Å (
arcsec2 raster images within a duration of 24 min. For
this sequence the lines used were: He I 584 Å (
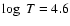 ),
O III 599 Å (
),
O III 599 Å (
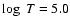 ), O V 629 Å (
), O V 629 Å (
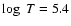 ),
Ca X 574 Å (
),
Ca X 574 Å (
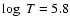 ), and Mg IX 368 Å (
), and Mg IX 368 Å (
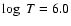 ).
).
In order
to get good time resolution the rotational compensation was switched off
(sit-and-stare mode) and so it becomes important to calculate the lowest possible
frequency we can detect from this long time sequence after taking the solar rotation
into account (see Doyle et al. 1998 for details). We estimate that the maximum effect of
the sit and stare mode on the resulting power, for all datasets would be a spreading of the frequencies by around
1.5 mHz, depending on the size of the source. For all our sunspots, whose sizes
are several arcsec and which have (well-defined) primary oscillating frequencies much above 3 mHz,
the effect of the sit and stare is not considered to be important.
The fitting of the different CDS lines was done using a single Gaussian as the
lines were found to be generally symmetric. Details on the CDS reduction
procedure, plus the wavelet
analysis, may be found in O'Shea et al. (2001). Before applying the wavelet
analysis we first removed the trend of the data (i.e. the very lowest frequency
oscillations) using a 30 point running average. By dividing the results of this
running average (or trend) into the original data and subtracting a value of
one we obtained the resulting detrended data used in the analysis. Fludra
(2001) have shown that this method is very efficient in removing the low
frequency background oscillation.
The statistical significance of the observed oscillations was estimated
using a Monte Carlo or randomization method. The advantage of using a
randomization test is that it is distribution free or nonparametric, i.e. it
is not limited or constrained by any specific noise models, such as Poisson,
Gaussian etc. We follow the method of Fisher randomization as outlined in
Nemec & Nemec (1985), performing 250 random permutations to calculate the
probability levels. The levels displayed here are the values of
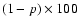 ,
where p is the proportion of the permutations that show a null test
result (see O'Shea et al. 2001). We choose a value of 95% as the lowest
acceptable probability level. Occasionally the estimated p value can
have a value of zero, i.e. there being an almost zero chance that the observed
time series oscillations could have occurred by chance. In this case, and
following Nemec & Nemec (1985), the 95% confidence interval can be obtained
using the binomial distribution, and is given by
0.0 < p < 0.01, that is,
the probability (
,
where p is the proportion of the permutations that show a null test
result (see O'Shea et al. 2001). We choose a value of 95% as the lowest
acceptable probability level. Occasionally the estimated p value can
have a value of zero, i.e. there being an almost zero chance that the observed
time series oscillations could have occurred by chance. In this case, and
following Nemec & Nemec (1985), the 95% confidence interval can be obtained
using the binomial distribution, and is given by
0.0 < p < 0.01, that is,
the probability (
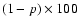 )
in this case is between 99-100%.
The velocity values presented in this paper are relative velocities, that is,
they are calculated relative to an averaged profile, obtained by summing over
all pixels along the slit and all time frames.
)
in this case is between 99-100%.
The velocity values presented in this paper are relative velocities, that is,
they are calculated relative to an averaged profile, obtained by summing over
all pixels along the slit and all time frames.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{MS2813f9a.eps}\\ [4mm]
\includegraphics[angle=90,width=8.8cm,clip]{MS2813f9b.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg133.gif) |
Figure 9:
Frequencies measured as a function of spatial position along the slit
(X-F slice) for the O V 629 Å line (left panels) and the s19332r00
dataset. The right panels show
the total number of counts in a pixel (summed counts) over the observation
time. |
| Open with DEXTER |
We first present results from the sunspot in active region 8951 as
observed on 14 April 2000. In Fig. 7, using an MDI intensity-gram image, we show
an enlarged region around the sunspot together with an overlay of a portion of
the slit from the temporal series dataset s19932r00 showing its location at the beginning and end times of the observation. The MDI intensity-gram used was obtained from the file
fd-Ic-01h.63844.0048.fits. The MDI intensity-gram observations were
performed at 04:47:33, the same time approximately as the start time of the
CDS temporal series observations of dataset s19332r00.
In Fig. 8 we show CDS intensity rasters of size
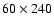 arcsec2 for different temperature lines along with a (low
resolution) Kitt peak magnetogram. The CDS rasters were obtained from dataset
s19331r00, with a starting time of 04:25 on the 14 April 2000. The low
resolution Kitt Peak magnetogram (resolution
arcsec2 for different temperature lines along with a (low
resolution) Kitt peak magnetogram. The CDS rasters were obtained from dataset
s19331r00, with a starting time of 04:25 on the 14 April 2000. The low
resolution Kitt Peak magnetogram (resolution  4 arcsec) with a start-time
of 14:26:31 on the same day was thus obtained about 10 hours after the CDS
observations. The thin rectangles over-plotted
on these images show the location of the slit (for the s19332r00 dataset) at
the beginning (the right one) and end of the temporal sequence (the left one).
Pixel 67 is marked as a black box in all the images. The CDS rasters shown are
the square-root images (i.e. the square root of the intensities has been taken
to reduce the contrast between the most bright and dark values). A comparison
of the raster images and the magnetogram clearly reveals that all the
intensity enhancements are closely related with concentrated magnetic field
regions.
4 arcsec) with a start-time
of 14:26:31 on the same day was thus obtained about 10 hours after the CDS
observations. The thin rectangles over-plotted
on these images show the location of the slit (for the s19332r00 dataset) at
the beginning (the right one) and end of the temporal sequence (the left one).
Pixel 67 is marked as a black box in all the images. The CDS rasters shown are
the square-root images (i.e. the square root of the intensities has been taken
to reduce the contrast between the most bright and dark values). A comparison
of the raster images and the magnetogram clearly reveals that all the
intensity enhancements are closely related with concentrated magnetic field
regions.
The contours for the umbra and penumbra (in Figs. 7, 8) are plotted using the average value for the whole MDI
intensity-gram as a guide. The penumbra is defined as the parts of the
MDI intensity where the intensity falls below a factor of 1.5 that
of the average, i.e. it is the average/1.5. The outer contour around the sunspot shows
the contour of the average value, while the inner contour shows the contour of the
average/1.5 values. The umbra is then defined as anything that is contained within this average/1.5
contour.
![\begin{figure}
\par\includegraphics[angle=90,width=15cm,clip]{MS2813f10.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg134.gif) |
Figure 10:
Wavelet results corresponding to the
He I 584 Å line in the s19332r00 dataset at pixel 67. Panels a) and
b) represent intensity and velocity results respectively. The middle row left
panels show the time
frequency phase plot corresponding to the variations shown in the
top panels. The middle row right hand panels show the average of the wavelet power
spectrum over time, i.e. the global wavelet spectrum. The continuous dashed
horizontal lines in the wavelet spectra indicate the lower cut off frequency.
The lowest panels
show the variation of the probability with time from the randomization test,
with the dot-dash line indicating the 95% significance level. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=90,width=15.3cm,clip]{MS2813f11.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg135.gif) |
Figure 11:
Wavelet results corresponding to the
O V 629 Å line in the s19332r00 dataset at pixel 67. Representations are
same as Fig. 10. |
| Open with DEXTER |
In order to show the spatial variation of the observed oscillation frequencies across
the sunspot region we select the strongest line, i.e. O V 629 Å. In
Fig. 9 we plot the variation of the frequencies over a section of
the observing slit. This section includes the umbra, penumbra and the adjacent regions.
The top panel shows a contrast enhanced intensity map (X-T slice), obtained by
removing the low frequency trend of the oscillations for each of the positions along
the slit. The lower two left panels show the measured frequencies as a
function of position along the slit (X-F slice) for velocity and intensity
respectively. The crosses correspond to the primary maxima in the global
wavelet spectra. The total number of counts in a pixel (summed counts) during
the observation is shown in the right columns and is useful in identifying the location of the
umbra of the sunspot. Note that pixel 67 is the brightest pixel across our slit
(see right panel of Fig. 9). This pixel may correspond to a
plume region. According to Maltby et al. (1999), locations that show
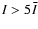 ,
where
,
where 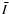 is the average intensity in the sunspot area being
investigated, can be considered as plumes in the sunspot umbra, if they also coincide with the location of an umbral region seen in, for example, a MDI intensity-gram. In
the X-T slice, for portions of the image, roughly from 50-60 and then between
80-90 pixels along the slit there are brightenings and darkenings, representing
longer period oscillations, which correspond to the penumbra and adjacent
regions. The frequencies in these regions are typically in the 2-4 mHz range,
whereas for the central part of the slit, roughly from pixels 60-75, there
are many alternate dark and bright ridges, corresponding to the umbral
oscillations, with frequencies of oscillation in the range 5.5-7 mHz, with most
peaks at 6.2 mHz. Another point to note in the X-T image is that there
is a drift in the ridges, a slanting from top to bottom, which is due to the
solar rotational drift (i.e. a sit and stare effect), that is, the oscillating umbra source moves down along the slit as the Sun rotates under the slit. As mentioned before, the peak counts occur at pixel 67. Below
we investigate this pixel in all three spectral lines, He I, O III and O V.
is the average intensity in the sunspot area being
investigated, can be considered as plumes in the sunspot umbra, if they also coincide with the location of an umbral region seen in, for example, a MDI intensity-gram. In
the X-T slice, for portions of the image, roughly from 50-60 and then between
80-90 pixels along the slit there are brightenings and darkenings, representing
longer period oscillations, which correspond to the penumbra and adjacent
regions. The frequencies in these regions are typically in the 2-4 mHz range,
whereas for the central part of the slit, roughly from pixels 60-75, there
are many alternate dark and bright ridges, corresponding to the umbral
oscillations, with frequencies of oscillation in the range 5.5-7 mHz, with most
peaks at 6.2 mHz. Another point to note in the X-T image is that there
is a drift in the ridges, a slanting from top to bottom, which is due to the
solar rotational drift (i.e. a sit and stare effect), that is, the oscillating umbra source moves down along the slit as the Sun rotates under the slit. As mentioned before, the peak counts occur at pixel 67. Below
we investigate this pixel in all three spectral lines, He I, O III and O V.
![\begin{figure}
\par\includegraphics[angle=90,width=15.3cm,clip]{MS2813f12.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg138.gif) |
Figure 12:
Wavelet results corresponding to the
O V 629 Å line in the s19336r00 dataset at pixel 67. Representations are
the same as Fig. 10. |
| Open with DEXTER |
In Fig. 10 we show as a representative umbral oscillation,
the power spectra analysis corresponding to the
He I 584 Å line at pixel location 67 (marked as a box in
Fig. 8). In the wavelet
spectrum, the dark contour regions show the locations of the highest powers.
Only locations that have a probability greater than 95% are regarded as
being real, i.e. not due to noise. Cross-hatched regions, on either side of the
wavelet spectrum, indicate the "cone of influence'' (COI), where edge effects
become important (see Torrence & Compo 1998). The dashed horizontal lines in
the wavelet spectra indicate the lower frequency cut-off, in this instance
1.5 mHz.
The results from the phase plots show that the He I 584 Å intensity and
velocity both show significant power in the 6.0-7.0 mHz range, for the periods
between the 20-30th and 40-65th minutes of the observing sequence. From
the overlay of the MDI intensity-gram and the slit location
(Fig. 7) one can clearly see that this particular pixel was
over the sunspot umbra between the time interval 20-65th minute of the observing
sequence (for a total of 45 min). We should point out that the
wavelet analysis has been carried out on relative intensity and velocity values and
hence there is a lack of low frequency power in the wavelet spectrum plots.
The global wavelet spectra (on the right of
Figs. 10a, b, which are the average of the wavelet power spectrum over the
entire observing period, show the strongest intensity and velocity power at
6.2 mHz ( 161 s). This is printed out in Fig. 10 above the
global wavelet plots, together with the probability estimate for the global
wavelet power spectrum. In the lowest panels we show the variation of the
probability level as estimated from the randomization test. Note that the
statistical significance is calculated only for the maximum powers in the
wavelet spectrum marked by the dotted white line in the dark patches. From these
panels we can clearly see that the oscillations were significant in the period between the 20-30
and 40-65 min of the time sequence.
161 s). This is printed out in Fig. 10 above the
global wavelet plots, together with the probability estimate for the global
wavelet power spectrum. In the lowest panels we show the variation of the
probability level as estimated from the randomization test. Note that the
statistical significance is calculated only for the maximum powers in the
wavelet spectrum marked by the dotted white line in the dark patches. From these
panels we can clearly see that the oscillations were significant in the period between the 20-30
and 40-65 min of the time sequence.
The O III 599 Å line formed in the low-to-mid transition region, is rather faint and to increase the signal to noise ratio we binned over two
pixels (67-68). The intensity wavelet shows power around 5.6 mHz and also some
strong power around 3 mHz for the first 20 min. The slit was not positioned
over the sunspot umbra for the first 20 min of the observing sequence and thus
the first 20 min power corresponds to the umbra boundary. In the global
wavelet the main power peak is at 5.6 mHz, but there is also a strong peak
around 3 mHz, which corresponds to the first 20 min during which the
penumbra rotates under the slit. The most significant oscillations take place
during the time intervals between 20-25 and 45-50 min. For the
O III 599 Å line the velocity signal is too weak and hence the
oscillations for this component are not reliable and so are not included in
this analysis.
Now we turn our attention to the transition region O
V 629 Å line. Figure 11 shows the wavelet results for the
same pixel location, 67, and dataset, s19332r00. Intensity and velocity both shows
strong power around 6.7 mHz in the phase and global wavelet spectra. The O V oscillation is strong for the same time interval (as in He
I and O III), namely between the 20-65 min, with a drop in significance for the time interval between 30-40 min of the sequence. From this one pixel located in the
sunspot umbra we thus find that the average frequency of oscillation
over the entire observing time for the O V line is at 6.7 mHz (165 s), as
estimated from the global wavelet spectrum.
Using the same techniques as before, we also examine
the same sunspot  30 min later using dataset s19334r00. The results
from this temporal series dataset are summarized in Table 4. For the central
portion of the umbra we find that the global peaks show frequencies in the
range 5.2-5.7 mHz for all the three lines observed and the lifetimes of the
oscillations are between 10-20 min, very similar to the previous case of
s19332r00.
We concentrate on the same single pixel as before, namely pixel 67, in the
umbra of the sunspot (plume). From Fig. 12 it is clear that
the main oscillations in intensity and velocity, take place in a 5-60 min
interval in the observing sequence, with most significant oscillations
occurring in the 5-15 and 25-65 min intervals for intensity and the 20-55 min interval for the velocity (this can be confirmed by looking at
the variation of probability in the lowest panels). The global peak for the
intensity and velocity both appear at 6.2 mHz with a very high probability
level. The results from the other lines from this dataset are given in Table 4.
In Fig. 13, we show the overall spatial variations of the
oscillations in O V. In the X-T slice we can see faint light and dark
ridges in the interval between pixels 60-75, where the central part, roughly
between pixels 66-68 corresponds to the plume (where
30 min later using dataset s19334r00. The results
from this temporal series dataset are summarized in Table 4. For the central
portion of the umbra we find that the global peaks show frequencies in the
range 5.2-5.7 mHz for all the three lines observed and the lifetimes of the
oscillations are between 10-20 min, very similar to the previous case of
s19332r00.
We concentrate on the same single pixel as before, namely pixel 67, in the
umbra of the sunspot (plume). From Fig. 12 it is clear that
the main oscillations in intensity and velocity, take place in a 5-60 min
interval in the observing sequence, with most significant oscillations
occurring in the 5-15 and 25-65 min intervals for intensity and the 20-55 min interval for the velocity (this can be confirmed by looking at
the variation of probability in the lowest panels). The global peak for the
intensity and velocity both appear at 6.2 mHz with a very high probability
level. The results from the other lines from this dataset are given in Table 4.
In Fig. 13, we show the overall spatial variations of the
oscillations in O V. In the X-T slice we can see faint light and dark
ridges in the interval between pixels 60-75, where the central part, roughly
between pixels 66-68 corresponds to the plume (where
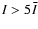 ,
see
rightmost panels). Once again a slow downward drift of the bright ridges may be
seen in the X-T slice, which is a rotational effect due to the movement of the
oscillating source down relative to the slit with time. The frequency
distribution shows that the umbra oscillates in intensity and velocity in the
5-6.5 mHz range, with most oscillations occurring at 6.2 mHz.
,
see
rightmost panels). Once again a slow downward drift of the bright ridges may be
seen in the X-T slice, which is a rotational effect due to the movement of the
oscillating source down relative to the slit with time. The frequency
distribution shows that the umbra oscillates in intensity and velocity in the
5-6.5 mHz range, with most oscillations occurring at 6.2 mHz.
Now we turn our attention to the study of the other active region, AR8963 over
the period 19-20 April 2000 (see Table 3 for details). To save space, we do not show here detailed wavelet plots for
individual dataset, rather we choose some selective pixel locations in each
dataset (corresponding to the umbra of a sunspot) and summarize our results
in the form of Table 4. We also list the duration of the oscillations,
estimated as the periods of time different oscillation packets showed
significant oscillations above the 95% significance level. This can be easily
measured from a comparison of the wavelet phase plots and the variation of the
probability level in the wavelet analysis (e.g. in Fig. 12).
We just point out here some of the other additional features which we noticed
for this active region. Firstly we should point out that this active region was
much larger compared to the previous one with 12 beta type spots. In certain
cases we found that the oscillation frequency changed during the observation
which might indicate that a new oscillating region was rotating into the field
of view of the CDS slit. For 20 April 2000 dataset, we also encountered
a small flaring event which interfered with the measurement of the underlying
higher frequency oscillations. It was noted that active region AR8963 had
slightly evolved in comparison with the previous day (the flare was a result of
that). In all the datasets corresponding to 20th April we find a wider
distribution of frequency measured from the peak of the global wavelet
spectrum, so we have listed the range of frequency over which the oscillation
was most significant.
Using UVSP data obtained in emission lines formed at temperature of
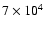 K to
K to
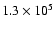 K, Gurman et al. (1982) observed transition
region oscillations in sunspots with frequencies in the range of 5.8-7.8 mHz.
Their in-phase intensity and velocity oscillations lead them to interpret the
oscillations in terms of upward propagating acoustic waves. For the first time
Thomas et al. (1987) made simultaneous detection of umbral oscillation at
different heights, starting from the chromosphere to the transition region. Their power
spectra of intensity and velocity both show multiple peaks at the 3 min band.
K, Gurman et al. (1982) observed transition
region oscillations in sunspots with frequencies in the range of 5.8-7.8 mHz.
Their in-phase intensity and velocity oscillations lead them to interpret the
oscillations in terms of upward propagating acoustic waves. For the first time
Thomas et al. (1987) made simultaneous detection of umbral oscillation at
different heights, starting from the chromosphere to the transition region. Their power
spectra of intensity and velocity both show multiple peaks at the 3 min band.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{MS2813f13a.eps}\\ [4mm]
\includegraphics[angle=90,width=8.8cm,clip]{MS2813f13b.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg141.gif) |
Figure 13:
Frequencies measured as a function of spatial position along the slit
(X-F slice) for the O V 629 Å line (left panels) and the s19336r00
dataset. |
| Open with DEXTER |
Table 4:
Summary of the oscillation frequencies observed corresponding to
the different dataset.
| Dataset |
Lines |
Pixel |
Intensity results |
Velocity results |
| |
|
|
Freq. maxima |
Prob. level |
Duration |
Freq. maxima |
Prob. level |
Duration |
s19332r00 |
He I |
67 |
6.2 mHz |
99-100% |
20-30, 40-65 |
6.2 mHz |
99-100% |
20-25, 40-65 |
| |
O III |
67-68 |
5.6 mHz |
99.2% |
20-25, 45-50 |
|
|
|
| |
O V |
67 |
6.7 mHz |
99-100% |
20-30, 40-65 |
6.7
mHz |
99-100% |
20-30, 40-50, 60-65 |
| s19334r00 |
He I |
66 |
5.7 mHz |
99-100% |
10-30, 40-50 |
5.2 mHz |
98.8% |
15-30, 40-50 |
| |
O III |
66-67 |
5.2 mHz |
95.6% |
15-20, 45-55 |
|
|
|
| |
O V |
66 |
5.7 mHz |
99-100% |
15-30, 40-55 |
5.7
mHz |
99-100% |
15-30, 40-50 |
| s19336r00 |
He I |
67 |
6.2 mHz |
99-100% |
5-10, 20-30, 40-60 |
|
|
|
| |
O III |
66-67 |
5.7 mHz |
98.4% |
5-10, 40-50 |
|
|
|
| |
O V |
67 |
6.2 mHz |
99-100% |
5-15, 25-60 |
6.2 mHz |
99-100% |
20-55 |
| s19378r00 |
He I |
20 |
4.8 mHz |
99-100% |
5-20, 25-45 |
|
|
|
| |
O III |
21-22 |
4.8 mHz |
99-100% |
10-20, 25-50 |
4.8 mHz |
98.8% |
10-20, 40-50 |
| |
O V |
21 |
4.8 mHz |
99-100% |
10-20, 25-45 |
4.8 mHz |
99-100% |
0-20 |
| s19380r00 |
He I |
21 |
4.8 mHz |
99-100% |
5-20, 25-30, 45-55 |
|
|
|
| |
O III |
21-22 |
5.2 mHz |
99-100% |
5-20, 45-55 |
|
|
|
| |
O V |
21 |
4.8 mHz |
99-100% |
5-20, 45-55 |
4.0 mHz |
99.8% |
5-20 |
| s19382r00 |
He I |
21 |
5.2 mHz |
99-100% |
45-70 |
|
|
|
| |
O III |
21-22 |
5.6 mHz |
99-100% |
45-60 |
|
|
|
| |
O V |
21 |
5.2 mHz |
99-100% |
10-20, 25-35, 45-65 |
4.0 mHz |
99-100% |
25-35 |
| s19388r00 |
He I |
33 |
3.5-5.0 mHz |
99-100% |
0-35 |
3.5-5.0 mHz |
99-100% |
5-35 |
| |
O III |
32-33 |
4.0-5.0 mHz |
99-100% |
0-45 |
5.7 mHz |
95.0% |
5-10, 35-45 |
| |
O V |
33 |
4.0-5.0 mHz |
99-100% |
5-20, 35-55 |
5.2 mHz |
99-100% |
40-55 |
| s19390r00 |
He I |
33 |
3.5-5.0 mHz |
99-100% |
5-35 |
4.5-5.0 mHz |
95.0% |
0-20 |
| |
O III |
32-33 |
3.5-5.0 mHz |
95.0% |
5-10, 25-30 |
|
|
|
| |
O V |
33 |
3.0-5.0 mHz |
99-100% |
10-45 |
|
|
|
| s19392r00 |
He I |
32 |
3.0-6.0 mHz |
99-100% |
30-75 |
4.4 mHz |
99.2% |
10-20, 40-45 |
| |
O III |
31-32 |
4.8 mHz |
98.4% |
30-40 |
|
|
|
| |
O V |
32 |
3.0-5.0 mHz |
99-100% |
0-10, 35-50, 65-70 |
3.5-5.0 mHz |
99-100% |
0-20, 40-45 |
With the launch of SoHO there has been renewed interest in the study of umbral
oscillations. Fludra (1999, 2001) investigated 3 min intensity oscillations with
CDS by observing the chromospheric line He I and several transition
region lines. He concluded that the 3 min umbral oscillations can occur both in
the so called sunspot plumes (bright features seen in the transition region
above sunspot) or in the lower intensity plasma closely adjacent to the plumes.
He found the spectral power to be contained in the 5.55-6.25 mHz range. No
oscillations were detected by him in the Mg IX 368 Å line, suggesting that the
3 min oscillation does not propagate into the corona. Tziotziou et al. (2002) have
presented two-dimensional intensity and Doppler shift images computed at
different wavelengths within the Ca II 8542 Å line. Their power
spectrum analysis shows a 6 mHz frequency, for the standing umbral oscillations
only for the upper half part of the umbra. For the penumbra they report a 3 mHz
frequency. They also conclude that the umbral oscillations are a localized
phenomena. SUMER observations (in both intensity and velocity) have confirmed that the sunspot oscillations are
prominent in transition region lines above the umbra (Maltby et al. 2001). They also
state that the umbral oscillations are a localized phenomenon and that the 3 min
oscillations fill the sunspot umbra in the transition region and tends to
stop at the umbral rim. Support
for the acoustic wave hypothesis was presented by Brynildsen et al. (1999a,b).
They observed oscillations in intensity and velocity to test the hypothesis
and found the oscillations to be compatible with upwardly propagating waves.
More recently O'Shea et al. (2002) and Brynildsen et al. (2002) have both presented
joint observations of the 3 min umbral oscillations with TRACE and
CDS. O'Shea et al. (2002) find oscillations at all temperatures from the
temperature minimum, as observed by TRACE 1700 Å up to the upper corona, as
measured by the Fe XVI 335 Å line with CDS. Both these authors report
that the oscillation amplitude above the umbra increases with increasing
temperature, reaches a maximum in the transition region and decreases for higher
temperature lines, though O'Shea et al. (2002) finds evidence for another increase in
amplitude for lines formed above 1 MK. O'Shea et al. interpreted their
observations in terms of slow magneto-acoustic waves propagating upwards (as
confirmed from their time delays) along magnetic field lines. In a recent
theoretical paper, Zhukov (2002) calculated the spectrum of eigenmodes of
umbral oscillations. It was shown that the 3 min umbral oscillations are the p-modes modified by the magnetic field.
The salient feature of our observation is that we have detected both intensity
and velocity oscillations in chromospheric and transition region lines as
observed by CDS. We should point out that the velocity resolution of
CDS is, at best, 5 km s-1, and generally it is quite difficult to detect velocity
oscillations with any confidence from noisy data. But with inclusion of a
reliable probability test and wavelet technique we were able to extract velocity
information in most of the cases with a 95% confidence level or higher. Most of
the earlier work on sunspot oscillations with CDS (Fludra et al.
1999, 2001; Brynildsen et al. 2002; O'Shea et al. 2002) presented only
intensity results. Our results clearly show that the 3 min intensity and velocity
oscillations are a property of the umbra, and not just the sunspot plume
(Figs. 9 and 13, shows that power peak
around 6 mHz is present over several pixels in the umbra). We also detect 3 mHz
oscillations corresponding to the penumbra, which supports the recent
observation by THEMIS, Tziotziou et al. (2002). We should point out
that the He I line is thought to have a complex formation history and its
emission may not correspond to that which one might expect from a chromospheric
line. It is believed that there are two main mechanisms by which He I can
form (Andretta & Jones 1997); either by collisional excitation in the lower
transition region from electrons with kinetic temperature higher than the local
temperature of the helium atom or by a process in which coronal photons
penetrate into the chromosphere and photoionize helium atoms which then
recombine to form He I. Thus the emission from He I can reflect
conditions at temperatures above that of its putative formation temperature.
Furthermore, the definition of where the
chromosphere ends and transition region begins is a bit arbitrary. Thus there
exists an uncertainty and controversy over the He I formation height.
Moreover, the O III and O V lines are formed close to each other in
temperature. This does not allow us to make a time-delay analysis for the
calculation of the wave propagation speed using this data.
There exists several observational reports of umbral oscillations in the
literature and there have been several theoretical attempts to explain them. However,
no generally accepted model exists for the understanding of these mechanical
structures, their physical mechanisms and energy transport to the surroundings. In
this paper we presented new solutions for magneto-atmospheric waves
in an isothermal atmosphere with a vertical magnetic field in the presence of radiative heat
exchange based on Newton's law of cooling. Radiation can radically alter the dynamical properties of wave
modes in a fluid. This radiative heat exchange gives
rise to a temporal decay of oscillations with a
characteristic dimensionless decay time
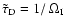 ,
where
,
where
 is the imaginary part of
is the imaginary part of 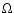 .
Depending on the value of the radiative relaxation time
.
Depending on the value of the radiative relaxation time
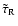 ,
the modes are effectively damped by the radiative dissipation
in as short a time as two oscillation periods;
however, in the limits of very large or very small
,
the modes are effectively damped by the radiative dissipation
in as short a time as two oscillation periods;
however, in the limits of very large or very small
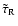 ,
corresponding to nearly adiabatic or nearly isothermal oscillations,
the modes are essentially undamped. We would also like to point out
the merits and demerits of using
Newton's law to model heat exchange. At sufficiently low frequencies,
the wavelength of a disturbance is so long, that it becomes optically
thick (no matter how transparent the material is), and the Newtonian
cooling approximation no longer holds. Conversely, at high
frequencies the wavelength of a disturbance becomes so small that it
is optically thin (no matter how opaque the material) and the
Newtonian approximation holds good. Bünte & Bogdan (1994) have
already pointed out that radiative effects on oscillations in
photospheric and higher layers are clearly important.
Radiative dissipation based upon Newton's cooling law
is clearly an oversimplification of the problem;
nevertheless it allows us to assess the effects of radiative damping on the
modal structure. It also enables us to look at the full frequency spectrum
and the interaction amongst various modes.
Our treatment of the weak field limit has
permitted an analysis of the
,
corresponding to nearly adiabatic or nearly isothermal oscillations,
the modes are essentially undamped. We would also like to point out
the merits and demerits of using
Newton's law to model heat exchange. At sufficiently low frequencies,
the wavelength of a disturbance is so long, that it becomes optically
thick (no matter how transparent the material is), and the Newtonian
cooling approximation no longer holds. Conversely, at high
frequencies the wavelength of a disturbance becomes so small that it
is optically thin (no matter how opaque the material) and the
Newtonian approximation holds good. Bünte & Bogdan (1994) have
already pointed out that radiative effects on oscillations in
photospheric and higher layers are clearly important.
Radiative dissipation based upon Newton's cooling law
is clearly an oversimplification of the problem;
nevertheless it allows us to assess the effects of radiative damping on the
modal structure. It also enables us to look at the full frequency spectrum
and the interaction amongst various modes.
Our treatment of the weak field limit has
permitted an analysis of the 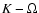 diagram in terms of asymptotic
approximations; this has allowed us to understand the nature of the modes in a
vertical magnetic field in the presence of radiative exchange. The insight so gained
has proved useful in extending the computation to the moderate to strong field
case. The transition region lines as observed by CDS on SoHO
are capable of diagnosing, Alfven, slow and fast magnetoacoustic waves.
The Alfvenic oscillations are
essentially velocity oscillations and do not cause any density
fluctuations. The compressional modes may however reveal
themselves in the form of intensity oscillations through a
variation in the emission measure. This fact, together with the
oscillations in intensity, allows us to interpret the waves as
slow magneto-acoustic in nature.
We have computed the frequencies of the modes from the full MAG equation
(see Eq. (11)) and found out that for our model atmosphere they correspond to the
slow magneto-acoustic modes. The p1 and p2 mode frequencies fall
very well within the observed range (compare Tables 2 and 4).
Our observational results
very much complement earlier results and provide additional input for the study
of the characteristics of the wave modes.
Our observations reveal that umbral oscillations are a localized phenomenon,
where intensity and velocity both shows a clear peak around 6 mHz.
In all the wavelet plots, we also notice a smaller peak in the
global wavelet spectra and some power in the phase plot around 3 mHz, for part of the time sequence, which corresponds to the penumbra.
In the theory part of this paper we have shown that the life time of the oscillations are dependent on the
relaxation time scale and in some cases these oscillations could be damped within a few oscillations periods as well. Our observations also indicate that the
oscillations seems to come in packets with life times of
diagram in terms of asymptotic
approximations; this has allowed us to understand the nature of the modes in a
vertical magnetic field in the presence of radiative exchange. The insight so gained
has proved useful in extending the computation to the moderate to strong field
case. The transition region lines as observed by CDS on SoHO
are capable of diagnosing, Alfven, slow and fast magnetoacoustic waves.
The Alfvenic oscillations are
essentially velocity oscillations and do not cause any density
fluctuations. The compressional modes may however reveal
themselves in the form of intensity oscillations through a
variation in the emission measure. This fact, together with the
oscillations in intensity, allows us to interpret the waves as
slow magneto-acoustic in nature.
We have computed the frequencies of the modes from the full MAG equation
(see Eq. (11)) and found out that for our model atmosphere they correspond to the
slow magneto-acoustic modes. The p1 and p2 mode frequencies fall
very well within the observed range (compare Tables 2 and 4).
Our observational results
very much complement earlier results and provide additional input for the study
of the characteristics of the wave modes.
Our observations reveal that umbral oscillations are a localized phenomenon,
where intensity and velocity both shows a clear peak around 6 mHz.
In all the wavelet plots, we also notice a smaller peak in the
global wavelet spectra and some power in the phase plot around 3 mHz, for part of the time sequence, which corresponds to the penumbra.
In the theory part of this paper we have shown that the life time of the oscillations are dependent on the
relaxation time scale and in some cases these oscillations could be damped within a few oscillations periods as well. Our observations also indicate that the
oscillations seems to come in packets with life times of 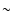 10-20 min, which
matches fairly well with the damping behavior of our MAG waves.
We should also point out that the envelope of these packets do not show
exponential decay, as one would expect from the theory, rather the intensity
amplitude usually remain sinusoidal. An alternative explanation for the
appearance of the packets could be due to the rotation of
the sun under the slit than the actual length of the oscillations. We see
oscillations for only 20 min as that may be the time necessary for a
source of say, 2 arcsec wide in the 2 arcsec wide slit, to rotate out of the
field of view, if the sun is rotating at say, 6 arcsec/hour. In general we
find good agreement between the model and observations as far as the duration
of oscillation and range of frequency is concerned.
10-20 min, which
matches fairly well with the damping behavior of our MAG waves.
We should also point out that the envelope of these packets do not show
exponential decay, as one would expect from the theory, rather the intensity
amplitude usually remain sinusoidal. An alternative explanation for the
appearance of the packets could be due to the rotation of
the sun under the slit than the actual length of the oscillations. We see
oscillations for only 20 min as that may be the time necessary for a
source of say, 2 arcsec wide in the 2 arcsec wide slit, to rotate out of the
field of view, if the sun is rotating at say, 6 arcsec/hour. In general we
find good agreement between the model and observations as far as the duration
of oscillation and range of frequency is concerned.
Acknowledgements
DB expresses his gratitude to Profs. S. S. Hasan and Joergen Christensen-Dalsgaard
for many valuable discussions which has enabled to develop the
theory of the MAG waves.
DB wishes to thank the FWO for a fellowship (G.0344.98).
EOS is a member of the European PLATON Network.
We would like to thank the CDS and EIT
teams at Goddard Space Flight Center for their help in obtaining the present
data. CDS and EIT are part of SoHO, the Solar and Heliospheric Observatory,
which is a mission of international cooperation between ESA
and NASA. Research at Armagh Observatory is grant-aided by the N. Ireland Dept.
of Culture, Arts and Leisure. This work was supported by PPARC grant
PPA/G/S/1999/00055. The original wavelet software was provided
by C. Torrence and G. Compo, and is available at
URL: http://paos.colorado.edu/research/wavelets/.
- Andretta, V., & Jones, H. P. 1997, ApJ, 489, 375
In the text
NASA ADS
- Babaev, E. S., Dahalilov, N. S., & Zhugzhda, Yu. D. 1995, Astron.
Rep., 39(2), 211
In the text
- Banerjee, D., Hasan, S. S., & Christensen-Dalsgaard, J. 1995, ApJ,
451, 825
In the text
NASA ADS
- Banerjee, D., Hasan, S. S., & Christensen-Dalsgaard, J. 1997,
Sol. Phys., 172, 53
In the text
NASA ADS
- Bogdan, T. J., & Knölker, M. 1989, ApJ, 339, 579
In the text
NASA ADS
- Bogdan, T. J. 2000, Sol. Phys., 192, 373
In the text
NASA ADS
- Bray, R. J., & Loughhead, R. E. 1974, in The Solar
Chromosphere (Chapman & Hall: London).
In the text
- Brynildsen, N., Leifsen, T., Kjeldseth-Moe, O., Maltby, P.,
& Wilhelm, K. 1999a, ApJ, 511, L121
In the text
NASA ADS
- Brynildsen, Kjeldseth-Moe, O., Maltby, P.,
& Wilhelm, K. 1999b, ApJ, 517, L159
NASA ADS
- Brynildsen, N., Maltby, P., Leifsen, T., Kjeldseth-Moe, O.,
& Wilhelm, K. 2000, Sol. Phys., 191, 129
In the text
NASA ADS
- Brynildsen, N., Maltby, P., Fredvik, T., & Kjeldseth-Moe, O.,
2002, Sol. Phys., 207, 259
In the text
NASA ADS
- Bünte, M., & Bogdan, T. J. 1994, A&A, 283, 642
In the text
NASA ADS
- Cash, J. R., & Moore, D. R. 1980, BIT, 20, 44
In the text
NASA ADS
- Doyle, J. G., van den Oord, G. H. J., O'Shea, E., & Banerjee,
D. 1998, Sol. Phys., 181, 51
In the text
NASA ADS
- Fludra, A. 1999, A&A, 344, L75
In the text
NASA ADS
- Fludra, A. 2001, A&A, 368, 639
In the text
NASA ADS
- Harrison, Sawyer, E. C., Carter, M. K., et al. 1995, Sol. Phys., 162, 233
In the text
NASA ADS
- Gurman, J. B., Leibacher, J. W., Shine, R. A., Woodgate, B. E., & Henze,
W. 1982, ApJ, 253, 939
In the text
NASA ADS
- Hasan, S. S., & Christensen-Dalsgaard, J. 1992, ApJ, 396, 311
In the text
NASA ADS
- Leibacher, J. W., & Stein, R. F. 1981, in The Sun as a star
(NASA), 263
In the text
- Lites, B. W. 1992, in Sunspots: Theory and observations,
ed. J. H. Thomas, & N. O. Weiss (Dordrecht: Kluwer), 261
In the text
- Maltby, P., Brynildsen, N., Fredvik, T., Kjeldseth-Moe, O.,
& Wilhelm, K. 1999, Sol. Phys., 190, 437
In the text
NASA ADS
- Maltby, P., Brynildsen, N., Kjeldseth-Moe, O.,
& Wilhelm, K. 2001, A&A, 373, L1
In the text
NASA ADS
- Mihalas, D., & Mihalas, B. W. 1984, in
Foundations of Radiation Hydrodynamics (Oxford University Press,
New York)
In the text
- Nemec, A. F., & Nemec, J. M. 1985, AJ, 90, 2317
In the text
NASA ADS
- O'Shea, E., Banerjee, D., Doyle, J. G., Fleck, B., & Murtagh, F. 2001,
A&A, 368, 1095
In the text
NASA ADS
- O'Shea, E., Muglach, K., & Fleck, B. 2002, A&A, 387, 642
In the text
NASA ADS
- Scheuer, M. D., & Thomas, J. H. 1981, Sol. Phys., 71, 21
In the text
NASA ADS
- Souffrin, P. 1972, A&A, 17, 458
In the text
NASA ADS
- Spiegel, E. A. 1957, ApJ, 126, 202
In the text
NASA ADS
- Stix, M. 1970, A&A, 4, 189
In the text
NASA ADS
- Torrence, C., & Compo, G. P. 1998, Bull. Amer. Meteor. Soc.,
79, 61
In the text
- Thomas, J. H., Lites, B. W., Gurman, J. B., & Ladd, E. F. 1987, ApJ,
312, 457
In the text
NASA ADS
- Tziotziou, K., Tsiropoula, G., & Mein, P. 2002, A&A, 381, 279
In the text
NASA ADS
- Zhugzhda, Yu. D. 1979, Soviet Astron., 23, 42
In the text
- Zhugzhda, Yu. D., Staude, J., & Locans, V. 1984, Sol. Phys., 91, 219
In the text
NASA ADS
- Zhukov, V. I. 2002, A&A, 386, 653
In the text
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{MS2813f1a.eps}\\ [4mm]
\includegraphics[width=7.4cm,clip]{MS2813f1b.eps}
\end{figure}](/articles/aa/full/2002/43/aa2813/Timg14.gif)
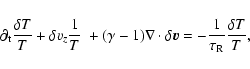
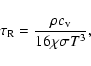
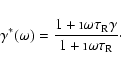
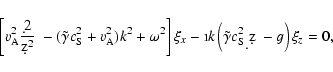
![\begin{displaymath}\left[\tilde{\gamma} c_{\rm S}^2 {\d^2\over \d z^2} - \tilde{...
...2{\d\over \d z }-(\tilde{\gamma}\gamma -1)g\right]
\xi_x =0 ,
\end{displaymath}](/articles/aa/full/2002/43/aa2813/img31.gif)
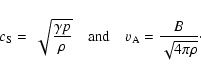
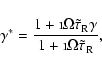
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{MS2813f2.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg42.gif)
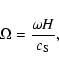
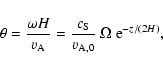
![$\displaystyle \left\{ \theta^4 {\d^4\over \d\theta ^4}
+ 4\theta ^3 {\d ^3\over...
...gamma}} -K^2\right)+4\theta ^2 \right]
\theta^2 {\d ^2\over \d\theta^2} \right.$](/articles/aa/full/2002/43/aa2813/img53.gif)
![$\displaystyle -\left[ 1-4\left({\Omega^2 \over \tilde{\gamma}} +K^2\right)-12\theta ^2 \right]
\theta {\d \over \d\theta }$](/articles/aa/full/2002/43/aa2813/img54.gif)
![$\displaystyle +\left.16\left[\left({\Omega^2 \over \tilde{\gamma}} +K^2\left({\...
...ight) \theta ^2
- {\Omega^2K^2 \over \tilde{\gamma}} \right] \right\} \xi_x=0 ,$](/articles/aa/full/2002/43/aa2813/img55.gif)
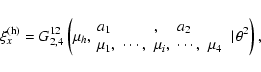
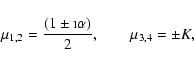
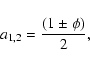
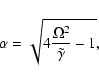
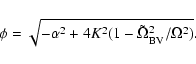
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS2813f3a.eps}\\ [4mm]
\includegraphics[width=7cm,clip]{MS2813f3b.eps}
\end{figure}](/articles/aa/full/2002/43/aa2813/Timg69.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{MS2813f4.eps}
\end{figure}](/articles/aa/full/2002/43/aa2813/Timg74.gif)
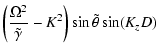
![$\displaystyle =2\sqrt{\tilde\gamma} {\epsilon\over\Omega}{\rm e}^{D/4} \bigg\{ K_z K^2
\bigl[\cosh(D/4)\cos \tilde\theta \cos(K_zD) - 1\bigr]$](/articles/aa/full/2002/43/aa2813/img76.gif)
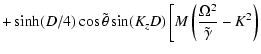
![$\displaystyle \left.\left.
-K^2\left(\frac 1{\gamma\tilde\gamma} -\frac 12\right)\right]\right\}
+ O\left({\epsilon^2\over\Omega^2}\right),$](/articles/aa/full/2002/43/aa2813/img78.gif)
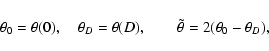
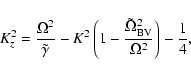
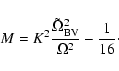
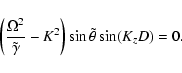
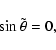
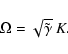
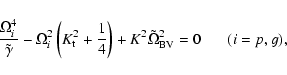
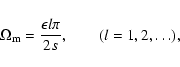
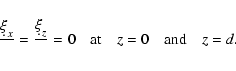
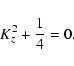
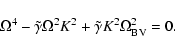
![\begin{displaymath}\Omega ^2 = {\tilde\gamma K^2 \over 2} \left[ 1 \pm
\left(1 ...
...\rm BV}^2 \over K^2 \tilde\gamma }
\right)^{1/2} \right] \cdot
\end{displaymath}](/articles/aa/full/2002/43/aa2813/img101.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{MS2813f5.eps}
\end{figure}](/articles/aa/full/2002/43/aa2813/Timg106.gif)
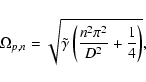
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2813f7.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg121.gif)
![\begin{figure}
\par\includegraphics[width=18cm,clip]{MS2813f8.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg125.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{MS2813f9a.eps}\\ [4mm]
\includegraphics[angle=90,width=8.8cm,clip]{MS2813f9b.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg133.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=15cm,clip]{MS2813f10.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg134.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=15.3cm,clip]{MS2813f11.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg135.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=15.3cm,clip]{MS2813f12.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg138.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{MS2813f13a.eps}\\ [4mm]
\includegraphics[angle=90,width=8.8cm,clip]{MS2813f13b.eps}\end{figure}](/articles/aa/full/2002/43/aa2813/Timg141.gif)