A&A 395, 357-371 (2002)
DOI: 10.1051/0004-6361:20021277

Reconstructing reality: Strategies for sideband deconvolution

C. Comito - P. Schilke

Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany

Received 11 June 2002 / Accepted 30 August 2002

Abstract
We present a study aimed at optimizing the observing strategy for double-sideband molecular line surveys, in order to achieve, for this kind of data, the best possible single-sideband reconstruction. The work is based on simulations of the acquisition of spectral line surveys with the HIFI instrument on board the Herschel Space Observatory, but our results can be applied to the general case. The reconstruction of the simulated data is obtained through the Maximum Entropy Method. The main factors responsible for degrading the quality of the reconstruction are taken into account: high rms noise in the data, pointing errors (particularly in the presence of intrinsic chemical structure in the source) and sideband imbalances. The presented results will allow the users of the new powerful submillimeter and THz telescopes, such as APEX, ALMA and Herschel, to make the most efficient use of their instruments for line survey work.

Key words: surveys - submillimeter - line: identification - molecular data - methods: data analysis - methods: numerical


  
1 Introduction

Line surveys provide, in any given frequency range and for any given source, an unbiased and complete inventory of molecular emission. On the one hand, the great number of very chemically different species, observed at once, sets very tight constraints on the chemical modeling of the source, and therefore clears the path to understanding its chemical history. On the other hand, the availability of spectral lines emitted by many different transitions of the same molecule and its isotopomers allows a reliable determination of physical parameters such as, for example, temperatures and densities of the studied object.

So far, efforts have been mainly addressed to surveying a few sources considered as representative of a class of objects, e.g. the evolved star IRC+10216 (Groesbeck et al. 1994and references therein), or the prototypical hot core source Orion-KL (Schilke et al. 1997,2001and references therein). Particularly, the molecular emission towards Orion-KL has been sampled through virtually all the frequency windows currently accessible from ground-based observatories, up to $\sim$900 GHz (Comito et al. in preparation).

New powerful instruments are being built in the attempt to explore the high-frequency end of the radio spectrum. The Atacama Pathfinder EXperiment (APEX) will be able, starting from 2004, to carry out spectral surveys up to THz frequencies. The Atacama Large Millimeter Array (ALMA) will, in its single-dish mode, produce DSB line surveys up to 900 GHz, while imaging line surveys in its interferometric mode will allow sideband separation in the hardware, making any deconvolution unnecessary. Finally, the Herschel Space Observatory, which is expected to be launched in 2007, will be able to explore, with its HIFI instrument, the whole frequency range between 480 and 1250 GHz, plus a window from 1410 to 1910 GHz. High-frequency line surveys are, and will even more be in the future, an incomparable tool to study the hottest and densest regions of molecular clouds. In fact, one of the candidate key projects for the HIFI facility is a whole-band line survey of about 25 sources, chosen among a sample of "shocked molecular clouds, dense Photon-Dominated Regions (PDRs), diffuse atomic clouds, hot cores and proto-planetary disks around newly formed stars, winds from dying stars and toroids interacting with AGN engines'' (de Graauw & Helmich 2001). Such an extensive project will require a significant amount of the total HIFI observing time.

In the submillimeter wavelength range, data are mostly acquired in double-sideband (DSB) form. The contribution to a DSB scan comes from equally weighted lower and upper sidebands, separated from each other by an interval equal to twice the intermediate frequency (IF): consequently, for each channel the intensity cannot be unambiguously associated either to the lower-sideband or to the upper-sideband frequency. The rejection of one of the sidebands would resolve this ambiguity. Unfortunately, no intrinsically single-sideband devices exist at submillimeter wavelengths, and mechanical sideband filters are not often used. For spaceborne instruments, sideband rejection with interference filters has the additional disadvantage of depending on moving mechanical parts that, for example for Herschel, which will be orbiting around the Earth-Moon Lagrangian point L2, would constitute single points of failure for the whole instrument.

Proper line identification requires spectra to be analyzed in their single-sideband (SSB) form. The conversion from DSB to SSB is obtained by software deconvolution, and its quality depends on several free parameters, such as spacing between contiguous DSB scans in the coverage of the band, pointing errors and sideband imbalances. Any intrinsic chemical structure of the source, in conjunction with pointing errors, also plays a role. In the worst scenario, the deconvolved SSB spectrum will contain spurious lines, which do not exist in the data but are created in the deconvolution process, and which are, for their shapes and intensities, virtually indistinguishable from actual features.

About 4% of the detected lines in Groesbeck et al.'s (1994) survey of IRC+10216 (from 330 to 358 GHz) are unidentified. This percentage grows as the frequency and density of lines increase, as in the Orion-KL surveys of Schilke et al. (1997 and 2001, from 325 to 360 and from 607 to 725 GHz), where the unidentified features are 6% and 14% of the total, respectively. This is partly due to the fact that laboratory measurements of the rest frequencies of high-energy transitions from many known molecules, at this stage, simply do not exist. Some of these unidentified features may be emitted by as yet completely unknown molecules. It is not unlikely, though, that a number of them are artifacts produced during the deconvolution, although care has been taken in identifying spurious lines.

In view of the future applications of the forthcoming instruments in the field of astrochemistry, we believe it is worthwhile to work on optimizing the observing procedures for spectral surveys, in order to minimize the effects introduced by the above mentioned factors in the reconstructed data. With this in mind, we have performed simulations of line surveys, in order to test the capability of single-sideband reconstruction from double-sideband data in presence of various quality-deteriorating factors. As a case study, we have simulated the reconstruction of DSB data acquired with HIFI, but our results are applicable to the general case.

The study has been mainly carried out from an observer's point of view. The question we want to answer is: given the technical characteristics of Herschel in general and of HIFI in particular, and given that the data will be acquired in DSB mode, what can the observers do to improve the quality of the reconstruction of their line surveys? Quantitatively, our results depend very much on the technical specifications of the telescope we have decided to simulate; from a qualitative point of view, though, they will allow the users of all telescopes to plan the observations for their double-sideband spectral surveys with a greater awareness of how the data reconstruction is affected, in practice, by the adopted observing strategy as well as by the characteristics of the instrument.

The paper is structured as follows: Sect. 2 gives a summary of the factors that play a role in determining the quality of the reconstruction of a SSB spectrum from a DSB line survey, and it illustrates the deconvolution scheme. Section 3 describes the details of the simulations, analyzing the effects introduced, in the reconstruction, by the variation of a few free parameters, such as the redundancy of information in the data, the presence of pointing errors and sideband imbalances, and finally the presence of intrinsic chemical structure in the surveyed source. A short paragraph is also dedicated to the possibility of carrying out spectral surveys in frequency-switching mode. The final goal is to make the simulated observations as close as possible to reality. Finally, in Sect. 4 we discuss the results and draw the conclusions. The concept of intrinsic confusion limit of a source, mentioned in Sect. 2 and in Sect. 3, is briefly illustrated in Appendix A.

  
2 The simulation approach

The first DSB-to-SSB deconvolution algorithm was of the CLEAN type, as modified for line deconvolution by Sutton et al. (1985) and applied by Blake et al. (1986), Groesbeck et al. (1994) and Schilke et al. (1997). More recently, the Maximum Entropy Method (MEM), as implemented by Sutton et al. (1995, hereafter S95) and Schilke et al. (2001), has been used. The Maximum Entropy Method seems to "offer greater freedom from instrumental artifacts'' (S95), and it also has the great advantage of allowing the sideband gain ratios to be treated as free parameters, whereas they have to be provided as an input when using the CLEAN algorithm (this feature will be further discussed in Sect. 3.3). In what follows, the deconvolution from the DSB data to a SSB spectrum will always be meant as obtained through the Maximum Entropy Method. The application of MEM to the reconstruction of double-sideband spectral surveys has been thoroughly discussed by S95 and all the MEM-related definitions and notation in this work refer to their paper.

During a line survey, a selected frequency band is covered by a series of DSB spectra of given bandwidth. A proper analysis of the data (identification of the lines, abundance measurements, determination of physical parameters in the source) can be performed only if they are displayed in SSB form. The quality of a SSB reconstruction is mainly affected by the following factors:

a)
the spacing, in frequency, between the scans. This parameter determines the redundancy of the collected information, the redundancy being minimum when the spacing corresponds to the bandwidth of the scans, so that every line is observed twice (once in the lower and once in the upper sideband)[*]. An optimal reconstruction requires the redundancy to be as high as possible (i.e. the spacing must be as small as possible). On the other hand, by employing a smaller spacing, the dead times get longer because of the increase of the required number of tunings, hence a greater amount of time will be necessary to reach the desired level of rms noise. Looking at it from a different perspective, we can say that, for a given amount of observing time, the spacing between the DSB scans determines the rms noise in the scans, because it determines the percentage of time that will be available for on-source integration. To this end, it is desirable to perform the lowest number of tunings in order to increase the signal-to-noise ratio in the data.
b)
the pointing errors for each DSB scan: every on-source scan is affected by a pointing error, and this causes spectral lines to show different intensities in different spectra. As a result of the ambiguous information contained in the DSB scans, spurious lines might exist in the deconvolved spectrum. Figure 1 shows a simplified sketch describing the mechanism of ghost lines production during the reconstruction of the SSB spectrum. This has very nasty effects on the quality of the deconvolution as well as on the interpretation of the data. If pointing errors cause the line intensities to vary by 10% from a DSB scan to another, then a 50 K line will produce a 5 K ghost. This means that, for their intensity and shape, the artifacts can easily be taken for real features; on the other hand, the identification and subtraction of the spurious features is possible knowing the position, in the spectrum, of the strongest emission lines (or of the deepest absorption features). Unfortunately, once created the ghosts propagate, in the fashion explained in Fig. 1, throughout the reconstructed spectrum, blending with other (real or fake) lines, therefore the subtraction of a line that has been identified as a ghost would necessarily cause the weakest lines possibly "hidden'' below the ghost to disappear. Hence, spurious features modify the scientific output of the survey in an unrecoverable way. This kind of error must be avoided as far as possible, and it can only be countered by a high redundancy of information in the data (cf. Sect. 3.3). It should also be kept in mind that this effect is enhanced for sources structured on scales which are comparable to the beam size (see Sect. 3.4).
c)
the sideband gain ratio: the sideband balance of the receiver is unlikely to be perfect, and the value of the sideband gain ratio (ideally equal to 1) will be different for every tuning. The effects of a sideband imbalance are in practice similar to those produced by pointing errors (see above), and again they will be reduced by minimizing the distance, in frequency, between close-by DSB scans as the data are acquired.

  \begin{figure} \par\includegraphics[angle=-90,width=13cm,clip]{MS2791f1.eps}\\ [... ...s}\\ [5mm] \includegraphics[angle=-90,width=13cm,clip]{MS2791f3.eps}\end{figure} Figure 1: Production of spurious features during the reconstruction of a single-sideband spectrum from double-sideband data: in this very simple sketch, our source radiates, in the frequency range of interest, one single line at frequency $\nu _l=987.6$ GHz (fourth panel, from left to right, in row a)). No background continuum emission is considered. The rest of the spectrum is flat. Row b) shows a DSB coverage of the band. The DSB scans are spaced by twice the IF, where ${\rm IF=6}$ GHz (see Table 1). Our line shows up twice, once in the upper sideband (USB, third panel of row b)) and again in the lower sideband (LSB, fourth panel of row b)). All DSB scans are affected by pointing errors and/or sideband imbalances: in the USB, the intensity of the line is 20% lower than it is in the LSB. During the reconstruction (row c)), the algorithm assigns the correct frequency and the highest observed intensity to the actual line (fourth panel in row c)), and it interprets the missing flux in the USB with the presence of an absorption feature, of depth equal to the missing intensity of our line, lying at a frequency of $\nu _{\rm l}-2 {\rm IF}$. If supported by the data, such absorption line should show up in the second DSB scan of row b) as a contribution from the USB. Its absence will be interpreted by the algorithm with the presence of an emission feature at the frequency corresponding to the LSB of the same scan ( $\nu _{\rm l}-4 {\rm IF}$, second panel in row c)). The absorption line at frequency $\nu _{\rm l}-6 {\rm IF}$ (first panel in row c)) is produced in the same way. The DSB spectra produced by this SSB reconstruction match the observations perfectly: in this fashion, ghost emission and absorption features propagate throughout the reconstructed spectrum.
Open with DEXTER

In order to achieve the best possible data reconstruction, an optimal balance must be found between the attempt to increase the signal-to-noise ratio in the data, and the attempt to prevent the propagation of spurious lines throughout the reconstruction. As already mentioned, for any given telescope with given technical specifications, the only quantity that the observer can actively modify to improve the quality of the data is the frequency spacing in the DSB coverage. Therefore, our aim is to determine the spacing by which the reconstruction of the HIFI data will be less affected by both rms noise and spurious lines. Because of the non-linear nature of the MEM reconstruction (see Eq. (2) of this paper, and Sect. 3.1 of S95), its response to the variation of any of the parameters above cannot be derived analytically, and simulations have to be performed.

We proceed as follows: using the XCLASS software, developed by one of us (PS) on the basis of the GILDAS CLASS package, we have produced a spectrum representing the 800-960 GHz band, which corresponds to HIFI's Band 3. The modeling of the molecular emission in the selected frequency range is based on the molecular abundances and source sizes derived by fitting, with XCLASS, the Orion-KL line survey published by Schilke et al. (2001), and making use of the molecular data from the JPL catalog. The frequency resolution is set to 1 MHz, and the diameter of the telescope (3.5 m) is also taken into account in order to reproduce the correct beam filling factor. The resulting spectrum (Fig. 2) contains 14 643 transitions from 31 molecular species. Note that the actual number of detectable lines is about an order of magnitude smaller, due to confusion induced by such a high density of lines. A brief discussion on the intrinsic confusion limit of our model source is given in Appendix A.


  \begin{figure} \par\includegraphics[angle=-90,width=13cm,clip]{MS2791f4.eps}\end{figure} Figure 2: Simulation of the molecular emission towards Orion-KL, in the frequency range between 800 and 960 GHz. The spectrum displays, with a frequency resolution of 1 MHz, 14 643 emission lines from 31 molecular species. It will be used as the starting point for all the simulations of DSB line surveys in this paper (except when surveys of a source with intrinsic chemical structure are simulated, cf. Sect. 3.4).
Open with DEXTER


   
Table 1: Setup values on which all the simulations presented in this work are based. References: van Leeuwen et al. (2001a) (vL01); N. Whyborn, priv. comm. (NW); our assumption (CS).
    Ref.
Covered band 800-960 GHz CS
DSB Bandwidth (B) 4 GHz vL01
Intermediate frequency (IF) 6 GHz vL01
Frequency resolution ( $\Delta \nu$) 1 MHz vL01
Dead time $^{{\rm a}}$ ( $t_{\rm dead}$) 10 $\div$ 60 s NW
Receiver temperature $^{{\rm b}}$ ( $T_{\rm rec}$) 170 K vL01
HPBW $^{{\rm c}}$ 25 $\hbox {$^{\prime \prime }$ }$ vL01
Pointing error (HPW) 3 $\hbox {$^{\prime \prime }$ }$ CS
Sideband ratio (HPW) $1\pm 0.2$ CS
Integration time $^{{\rm d}}$ ( $t_{\rm tot}$) 5 hrs CS
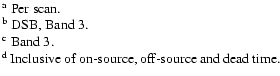
$\textstyle \parbox{7cm}{ $^{{\rm a}}$\space Per scan.\\ $^{{\rm b}}$\space DSB... ...and 3.\\ $^{{\rm d}}$\space Inclusive of on-source, off-source and dead time.}$


A DSB coverage of the initial spectrum in Fig. 2 is then simulated, assuming our target source to be point-like. The coverage is repeated several times, each time letting the spacing, or the pointing errors, or the sideband imbalances, or a combination of the three, vary. The details, case by case, are discussed in Sect. 3. However, it is useful, at this point, to recall how the MEM reconstruction works. As discussed by S95, during the MEM deconvolution every channel of (what will be) the reconstructed SSB spectrum is treated as a free parameter. The algorithm produces a SSB spectrum, creates DSB scans from it and finally compares them to the data, trying to minimize the quantity $\chi_{\nu}^2 - \lambda F_1$. Here, $\chi^2_{\nu}$ is the reduced $\chi^2$ over $\nu$ degrees of freedom ($\nu=$ number of channels in the reconstructed SSB spectrum):

 \begin{displaymath}\chi_{\nu}^2 = \frac{1}{\nu} \sum_k \frac{1}{\sigma^2_k} (y_k^0 - y_k)^2, \end{displaymath} (1)

where $\{y_k^0\}$ are the DSB data, $\{\sigma^2_k\}$ the data variances, and $\{y_k\}$ represent the hypothetical DSB spectra determined on the basis of the SSB reconstruction. F1 is the entropy of the spectrum, which is maximum when the spectrum is flat (also cf. Gull & Skilling 1984):

 \begin{displaymath}F_1 = - \sum_{i} \frac{x_i}{x_{\rm s}} \log \frac{x_i}{x_{\rm s}}, \end{displaymath} (2)

where $\{x_i\}$ are the reconstructed single-sideband data, and $x_{\rm s} = \sum_i x_i$. The parameter $\lambda$ is used to balance the flatness of the spectrum, due to the entropy term, with the fidelity of the reconstruction to the data set by the $\chi^2$term.

Since the MEM reconstructed spectrum cannot be negative (see Eq. (2)), a constant continuum offset is added to the DSB data, prior to the deconvolution, in order to allow the MEM algorithm to reconstruct absorption lines. In fact, although we know that no negative feature is given in our initial spectrum, such a priori information is usually not known to the observer. Many sources (e.g. SgrB2) actually display quite prominent absorption lines, and even objects so far observed, throughout the radio band, in molecular emission only, such as Orion-KL, are likely to present absorption features at frequencies higher than THz.

We then quantitatively compare the reconstructed SSB spectrum with the initial one, using the absolute value of the area of the difference between the two spectra averaged by the number of channels, hereafter $\langle A_{\rm diff}\rangle$, as a fidelity parameter (the smaller the value of $\langle A_{\rm diff}\rangle$, the more accurate the deconvolution):

 \begin{displaymath}\langle A_{\rm diff}\rangle = \frac{{\sum_{i=1}^{n_{\rm c}} \vert I_{\rm R}(i)-I_{\rm O}(i)\vert }}{n_{\rm c}}, \end{displaymath} (3)

where $I_{\rm R}(i)$ and $I_{\rm O}(i)$ are, respectively, the value of the intensity of the reconstruction and of the original spectrum, measured at the ith channel. The number of channels, $n_{\rm c}$, equals $1.6 \times 10^5$ in the initial spectrum, and it is always somewhat lower in the reconstruction. The value of $n_{\rm c}$ in Eq. (3) is to be understood as the number of channels in the reconstructed SSB. The use of the absolute value in Eq. (3) makes our $\langle A_{\rm diff}\rangle$ more robust than the standard deviation, since it is less affected by outlying points.

The reconstructions are achieved through the XCLASS software mentioned above. It must be pointed out that no unique solution can be obtained for systems of non-linear equations (cf. Sect. 9.6 of Press et al. 1992), and the procedure to achieve SSB reconstructions of satisfactory quality has to be empirically determined taking into account, for example, the quality of the data and the available computational resources. The reconstructions of our simulated line surveys are not, in general, the result of a single plain deconvolution. In fact, as the complexity of the data grows (i.e., more sources of error are added), it is necessary to introduce some degree of iteration in the data processing.

In order to be able to compare results from different simulations, all the reconstructions are achieved following the same iteration scheme (see Fig. 3), which can be roughly described as follows:

I.
The simulated DSB data are reconstructed for the first time. The algorithm is given no first-guess input for the first iteration, which is equivalent to assuming that the initial intensity of each channel of the SSB deconvolution is zero (Fig. 3, panel Ia). Typically, at this stage, the reconstruction (Fig. 3, panel Ib) is already very similar to the initial spectrum (Fig. 3, top panel). It looks noisy, though, and spurious absorption and emission features show up in some parts.
II.
We are not happy with the result, and go through a second deconvolution of the data. This time we can improve the output of the deconvolution by using the first reconstruction (Fig. 3, panel Ib) as a model for the algorithm. In this case, the entropy of the reconstructed spectrum is written as

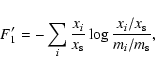\begin{displaymath}F_1^{\prime} = - \sum_{i} \frac{x_i}{x_{\rm s}}\log \frac{x_i/x_{\rm s}}{m_i/m_{\rm s}}, \end{displaymath} (4)

where $\{m_i\}$ is our model spectrum and $m_{\rm s} = \sum_i m_i$(see S95 for a thorough discussion on the use of a model within the Maximum Entropy Method). The algorithm will therefore try to minimize the quantity $\chi_{\nu}^2 - \lambda F_1^{\prime}$ instead of $\chi_{\nu}^2 - \lambda F_1$. Using spectrum Ib as it is would perpetuate the presence of noise and spurious lines in the reconstruction: therefore, the model should be made up of the strongest features in the spectrum only. This is achieved by cutting off everything below three times the rms noise of the spectrum, which, in our specific example, is of about 2 K. It is necessary to adopt such a severe cut-off limit (indicated by the dashed line in panel Ib), in order to be sure that only the lines that are supported by the data are selected as a model for the next iteration. The derived model features are shown in panel IIa.
III.
We go on iterating in the same fashion, using the strongest lines of IIb as a model for the next recursion (panel IIIa). Making use of the information derived from the previous iteration, this time we can set the cut-off limit (dashed line in panel IIb) to three times the rms noise of the difference between IIb and IIa. The resulting higher number of features in the model (panel IIIa) allows a better-quality reconstruction of the SSB spectrum, as shown in panel IIIb. The difference between initial spectrum and deconvolution is smaller for every successive iteration.
Our reconstruction scheme involves ten such recursions. The described loop is slightly different for the deconvolution of data affected by sideband imbalances (see Sect. 3.3). In fact, the MEM algorithm allows the treatment of the sideband ratios as free parameters, but the use of this option during the first iteration leads to a completely unreliable result, due to the fact that the algorithm tends to minimize the $\chi^2$ and maximize the entropy terms by wildly varying the gain ratios. This happens because the variation of the gain ratios impacts a whole spectrum (4000 channels) and thus has a greater effect on the $\chi^2$ term than varying the intensity of a single channel. In our experience, this kind of data should first be deconvolved keeping the gain ratios fixed and equal to 1. This reconstruction should then be used as first guess for a second one, during which the ratios are let free to vary. This procedure produces reasonable values for the gain ratios, and SSB deconvolutions that are very close to the initial spectrum (see Sect. 3.3).


  \begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{MS2791f5.eps}\\ [5mm] \includegraphics[angle=-90,width=10cm,clip]{MS2791f6.eps}\end{figure} Figure 3: Sketch representing the applied scheme of reconstruction of a SSB spectrum from our simulated DSB data. The scheme is discussed at the end of Sect. 2.
Open with DEXTER

  
3 Simulations

First of all, it is useful to quantify the effect that the increase of redundancy in the data has on the signal-to-noise ratio in the single DSB scans. A high-redundancy set of data involves more frequent tunings of the receiver, hence higher overhead times, hence a significantly longer observing time, or, alternatively, a significantly lower signal-to-noise ratio in the data. Let us consider the radiometer equation that defines the rms noise per channel for data acquired in position-switching mode:

 \begin{displaymath}\sigma_{\rm rms} = \frac{2 \cdot T_{\rm sys}}{\sqrt{\Delta \nu \cdot (t_{\rm on}+t_{\rm off})}}, \end{displaymath} (5)

where $T_{\rm sys}$ is the system temperature in K, $\Delta \nu$ is the frequency resolution in Hz, $t_{\rm on}$ and $t_{\rm off}$are respectively the on-source an off-source integration times, for a single scan, in seconds. For a DSB coverage,
$\displaystyle t_{\rm on} = \frac{t_{\rm tot}-(t_{\rm off}+t_{\rm dead}) \cdot n_{\rm scans}}{n_{\rm scans}},$      

where $t_{\rm tot}$ is the total time available for the observing run, $t_{\rm dead}$ includes the dead times resulting, for each scan, from tuning the receiver and moving the telescope (when needed), and $n_{\rm scans}$ is the number of DSB scans needed to obtain a complete coverage of the band. We can assume $t_{\rm off} = t_{\rm on}$, so

 \begin{displaymath}t_{\rm on} = \frac{t_{\rm tot}-(t_{\rm dead} \cdot n_{\rm scans})}{2 \cdot n_{\rm scans}}\cdot \end{displaymath} (6)

The value of $n_{\rm scans}$ can be easily calculated knowing the spacing, $\Delta x$, between two contiguous DSB spectra. We define $\Delta x$ as a fraction of the bandwidth, B, of a single DSB scan,

 \begin{displaymath}\Delta x = \frac{B}{N}, \end{displaymath} (7)

with N integer. Thus, an increase of the redundancy of information in the data is obtained by increasing the value of N. We will hereafter refer to N as to the degree of redundancy of the survey.

For spaceborne observations such as those that will be performed by HIFI, as a first approximation the only contribution to the system temperature comes from the receiver temperature, $T_{\rm rec}$, which, for Band 3, is expected to be around 170 K (double-sideband, van Leeuwen et al. 2001a). The bandwidth of the DSB scans, B, is expected to be of 4 GHz in wide-band mode, and $t_{\rm dead}$, is expected to be between 10 and 60 s (N. Whyborn, priv. comm.; also cf. Ossenkopf 2002). Such values have been used as a setup in order to simulate a set of data as close as possible to what real HIFI data could be like in this frequency range. The frequency resolution, $\Delta \nu$, is again 1 MHz as in the initial spectrum (cf. Sect. 2), and the total observing time is set to five hours. In fact, a shorter time would not be long enough for a full coverage in the high-redundancy, long-dead-time case, whereas a longer total time would make it more difficult to really appreciate the effect of an increase of the noise in the deconvolution. A summary of the technical specifications used throughout this work is given in Table 1. By substituting the above values into Eqs. (7), (6) and (5), the increase of $\sigma_{\rm rms}$ as a function of N can be quantitatively estimated. One should take into account, though, that all channels but those at the edges of the band (the first and last $2 \times{\rm IF}$ GHz of the surveyed frequency range) are covered $2\times N$ times (N times per sideband). A consistent value of $\sigma_{\rm rms}$ is then obtained by increasing the quantity ( $t_{\rm on}+t_{\rm off}$accordingly in Eq. (5)). Table 2 lists the effective rms noise per channel, $\sigma _{\rm rms\_eff}$, for the channels lying in the fully-covered region of the band, calculated as N increases from 1 to 7, for $t_{\rm dead}=10$ and 60 s. The effective on-time per channel, $t_{\rm on\_eff}$, is also listed. In the worst case (N = 7 and $t_{\rm dead}=60$ s), the effective rms noise per channel will be of about 30 mK. Note that the desired value of $\sigma _{\rm rms\_eff}$ must be ultimately determined taking into account the intrinsic confusion limit of the source, which mostly depends on the density of features in the spectrum, hence on the chemical and physical characteristics of the object (see Appendix A). Attempting to achieve a lower rms noise level than the confusion limit would be futile.

Table 2 also lists the variation of the "observing efficiency'', $ \eta = n_{\rm scans} \cdot t_{\rm on}/t_{\rm tot}$, as a function of N and of $t_{\rm dead}$. Note that $\eta $ is a function of the nominal on-time as defined by Eq. (6), and that in the highest-redundancy, longest-dead-time case here considered, only 8% of the total observing time is spent on source.


 

 
Table 2: Variation of the number of DSB scans needed for a full coverage of the selected band, $n_{\rm scans}$, of the effective rms noise per channel, $\sigma _{\rm rms\_eff}$, of the effective on-time per channel, $t_{\rm on\_eff}$, and of the observing efficiency, $\eta $, as a function of the degree of redundancy N. The values of $\sigma _{\rm rms\_eff}$ and $t_{\rm on\_eff}$ only apply to the fully-covered section of the band (see Sect. 3).
      $t_{\rm dead}=10$ s   $t_{\rm dead}=60$ s
N $n_{\rm scans}$   $\sigma _{\rm rms\_eff}$ $t_{\rm on\_eff}$ $\eta $   $\sigma _{\rm rms\_eff}$ $t_{\rm on\_eff}$ $\eta $
      (10-3 K) (s)     (10-3 K) (s)  
1 37   11.0 476.5 0.49   11.6 426.5 0.44
2 73   11.1 473.2 0.48   12.4 373.2 0.38
3 109   11.1 465.4 0.47   13.5 315.4 0.32
4 145   11.3 456.6 0.46   15.0 256.6 0.26
5 181   11.4 447.2 0.45   17.1 197.2 0.20
6 217   11.5 437.7 0.44   20.5 137.7 0.14
7 253   11.6 428.0 0.43   27.2 78.0 0.08



  \begin{figure} \par\includegraphics[angle=-90,width=15.5cm,clip]{MS2791f7.eps}\end{figure} Figure 4: Section of the plot of the residuals, obtained by subtracting the initial spectrum in Fig. 2 from the SSB reconstructed after a regularly spaced DSB coverage carried out with a degree of redundancy of 5. The residuals show that periodic structures are introduced during the reconstruction. Such structure disappears in the DSB spectra, and therefore it is not constrained by the data.
Open with DEXTER

  
3.1 Regular or irregular spacing?

In the previous paragraph, we have defined $\Delta x$ as a fraction of the bandwidth of the scans. Therefore, the spacing is so far assumed to be constant throughout the coverage. In fact, regular spacing proves not to be the ideal tool for a DSB spectral line survey.

Figure 4 shows a 12-GHz section of the difference between the initial spectrum, reproduced in Fig. 2, and the SSB spectrum reconstructed from a DSB coverage with a degree of redundancy of 5. No quality-deteriorating factors have been included in the simulation, and with a redundancy as high as 5 we expect a perfect reconstruction of the data. The plot, however, shows regular patterns that do not exist in the original spectrum and must therefore be artifacts introduced by the deconvolution.

We find that such patterns are only produced when $\Delta x$ is regular throughout the survey. The reason why periodic structures arise, during the reconstruction of the data, only if the DSB scans are regularly spaced, is fairly simple to understand. At some point of the deconvolution, some artifacts may be created which are not supported by the data. In spite of this, a very low value for $\chi_{\nu}^2 - \lambda F_1$ can be obtained if these artifacts are periodic, and if their period is such that they cancel out in the DSB scans calculated from the reconstructed SSB ($\{y_k\}$ in Eq. (1)), which are the only product of the deconvolution that can actually be compared with the data. In order to check if this is the case, we have simulated a N=5 DSB coverage of the spectrum in Fig. 4. The resulting DSB scans appear to be absolutely flat on the scale of the periodic structures. So, basically for the same reason which causes spurious features to propagate throughout the reconstructed SSB (see Fig. 1), such artifacts propagate in regular patterns, with a period that depends on the distance, in frequency, between lower and upper sideband (twice the IF), and on the value of $\Delta x$ used for the coverage.

The maximization of the entropy term should in principle help to eliminate this kind of structures, since the flatter the deconvolved spectrum, the higher the value of the entropy. A reduction of the amplitude of the patterns in Fig. 4 might then be obtained by increasing the value of the parameter $\lambda$, hence the weight of the entropy term in the minimization of the quantity $\chi_{\nu}^2 - \lambda F_1$. However, instead of making assumptions about the data and forcing them into the reconstruction, which is what the maximization of the entropy term does, it is better to design the experiment in a way that eliminates these structures without a priori knowledge of the result.

The best solution seems to be that of using irregular spacing. The spacing between the jth and the (j-1)th DSB scan is then:

 \begin{displaymath}\Delta x_{j,j-1} = \frac{B}{N} + \delta x_{j}. \end{displaymath} (8)

We choose random values of $\delta x_{j}$ so that they belong to a normalized Gaussian distribution of half power width 200 MHz. No periodic structure is present in the SSB reconstruction when $\Delta x$ is irregular.

This is a very important result: first of all, the Maximum Entropy Method shows all its efficacy by demonstrating that perfect data can be perfectly reconstructed; second, an easy-to-implement tool is now available that, if used, will produce a significant improvement in the quality of the reconstruction of DSB line surveys.

In the following, all the presented results refer to irregularly-spaced coverages.

  
3.2 Noise

The effect produced, by an increase of the degree of redundancy in the data, on the signal-to-noise ratio in the single DSB scans has already been discussed at the beginning of Sect. 3. We now want to investigate how the decrease of the signal-to-noise in the raw data, due to a decrease of $\Delta x$ in the coverage and/or to an increase of $t_{\rm dead}$, affects the quality of the deconvolved SSB spectrum. Pointing errors and sideband imbalances are not included in this simulation.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2791f8.eps}\end{figure} Figure 5: Variation, as a function of the degree of redundancy N, of the fidelity parameter, $\langle A_{\rm diff}\rangle$, relative to the reconstruction of simulated DSB line surveys affected by rms noise only. Two simulations have been carried out: one, represented by the solid curve, assumes a (relatively) short dead time per scan ( $t_{\rm dead}=10$ s); the other one (dashed curve) assumes a long dead time ( $t_{\rm dead}=60$ s). The effects of an increase of the rms noise due to the higher degree of redundancy are clearly visible in the long-dead-time case, whereas they are almost absent when the dead time is short. Note that the scale for $\langle A_{\rm diff}\rangle$ is logarithmic.
Open with DEXTER

Figure 5 shows the variation of the fidelity parameter described in Sect. 2, $\langle A_{\rm diff}\rangle$, as a function of the degree of redundancy N. A minimum in the variation curve corresponds to the degree of redundancy that allows the best possible MEM deconvolution, within the considered range of values for N. The DSB coverages have been simulated in the extreme cases of lowest and highest expected dead time, 10 and 60 s respectively. The plot clearly shows that, if the dead times are kept low ( $t_{\rm dead}=10$ s, solid curve), the quality of the reconstructed spectrum improves dramatically when going from N = 1 to N = 2, then it settles to a nearly constant value. Increasing the degree of redundancy in the data, in this case, would only marginally improve the quality of the reconstruction. The dashed curve representing the long-dead-time case ( $t_{\rm dead}=60$ s) shows a minimum for N=2, but then it grows as N increases: the higher rms noise in the data, due to a combination of longer dead times per tuning and larger number of tunings, degrades the quality of the deconvolved single-sideband spectrum, overriding the improvement due to a higher N. In both cases, however, a degree of redundancy as low as 2 would be sufficient to achieve a satisfactory reconstruction of a Band 3 HIFI double-sideband line survey into a SSB spectrum. This should not surprise us, since a high degree of redundancy is mainly needed to counter the presence, in the reconstructed SSB, of artifacts caused by pointing errors or sideband imbalances (cf. Sects. 2 and 3.3).

Since we already know that, even in presence of the rms noise alone, long dead times cause more damage than a high degree of redundancy can fix, every effort should be made, at a hardware development level, in order to minimize such overhead for the Herschel/HIFI instrument. In what follows we will drop the long-dead-time option and will only concentrate on the very desirable short-dead-time one. As a consequence of this choice, all our simulations illustrate high signal-to-noise ratio cases. Although it would be very interesting to study how the optimal value of N varies as the noise in the data increases, no HIFI time is likely to be spent on high-noise line surveys. Thus, this case is, at the moment, of little interest to us.

  
3.3 Pointing errors and sideband imbalances

Let us now consider spectral surveys in which the DSB data are made non-perfect by two factors: a), rms noise plus pointing errors, and b), rms noise plus sideband imbalances.

a)
Prior to the MEM deconvolution, every simulated DSB scan is assigned a random pointing error belonging to a Gaussian distribution of half power width 3 $\hbox {$^{\prime \prime }$ }$, which is quite a conservative assumption if compared to the present goal for Herschel ($\sim$ $ 1\hbox{$.\!\!^{\prime\prime}$ }5$, van Leeuwen et al. 2001b). The intensity of each scan is then corrected for its distance from the nominal pointing position, taking into account that, in the range of frequencies belonging to HIFI's Band 3, Herschel is expected to have a HPBW of 25 $\hbox {$^{\prime \prime }$ }$.
b)
In this case, the gain of the upper sideband, $g_{\rm USB}$, of every simulated DSB spectrum is assigned, before the reconstruction, a random percentage of deviation from its ideal value of 1. Such deviation is assumed to have a Gaussian distribution of half power width 0.2. If $g_{\rm LSB}$ is the gain of the lower sideband, its deviation from 1 is such that

 \begin{displaymath}g_{\rm LSB}+g_{\rm USB}=2, \end{displaymath} (9)

since this is the assumption under which the spectra are calibrated.
Afterwards, the DSB data are reconstructed in the usual fashion. Again, the coverage is repeated with increasing degree of redundancy, leaving $t_{\rm dead}$ unchanged and equal to 10 s. The calculation of the fidelity parameter requires, this time, an intermediate step before subtracting the initial spectrum from the MEM deconvolution. In fact, the pointing errors introduced in the simulation correspond, on average, to a larger beam, and hence to weaker features for non-beam-filling sources. The area of the reconstructed spectrum will then naturally be smaller than that of the original one. A similar effect is introduced by sideband imbalances. Since our measure of the fidelity of the reconstruction does not aim at the absolute calibration but at quantifying the presence of artifacts and spurious features, it would be of no use, in this case, to calculate $\langle A_{\rm diff}\rangle$ as in Eq. (3), since its value would be dominated by the difference in area introduced by the pointing and sideband corrections. A significant value of the fidelity parameter is obtained if, prior to the calculation of the difference spectrum, the reconstructed SSB is multiplied by the ratio between its area and that of the initial spectrum. The normalized fidelity parameter calculated in this fashion will be named $\langle A_{\rm diff}\rangle_{\rm norm}$.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2791f9.eps}\end{figure} Figure 6: Variation, as a function of the degree of redundancy N, of the normalized fidelity parameter, $\langle A_{\rm diff}\rangle_{\rm norm}$, relative to the reconstruction of SSB spectra from simulated DSB line surveys affected by pointing errors (solid curve) and sideband imbalances (dashed curve).
Open with DEXTER

Figure 6 plots the trend of variation of $\langle A_{\rm diff}\rangle_{\rm norm}$ as a function of N. A comparison between the plot in Fig. 6 and that in Fig. 5 immediately shows that, when pointing errors and sideband imbalances are present in the DSB data, the quality of the reconstruction is worse (the fidelity parameter has on average higher values, in spite of the normalization described above): the MEM deconvolution has, in this case, spawned an unknown number of spurious features, that are now responsible for the larger difference between the area of the original and that of the reconstructed spectrum. Such artifacts are prominent for low degrees of redundancy, and, as expected, they become less and less important for higher values of N.

The trend displayed in Fig. 6 seems to suggest that, within the technical specifications so far assumed for HIFI, a proper reconstruction of DSB spectral surveys will need the data to be acquired with a degree of redundancy at least as high as 4. An example of the improvement introduced by increasing the degree of redundancy of the coverage is illustrated in Fig. 7. The upper panel represents, in grey, a section of the MEM reconstruction of a SSB spectrum from set of DSB data affected by rms noise and sideband imbalances. The simulated coverage has a degree of redundancy of 1. In the lower panel, the coverage (again in grey) has instead been carried out with N=7. Overlaid is the original spectrum (black solid curve). The low-redundancy deconvolution shows a large number of artifacts, both in emission and in absorption. Particularly striking is the 4-K feature at 944.3 GHz: for its intensity and shape, it could well be interpreted as a real emission line, either from some unlikely transition of an already known molecule, or even from an as yet unknown species. Although it is possible to discern between real and "fake'' features through a "by-eye'' analysis of the DSB scans, this approach is prohibitively time-consuming, particularly if we consider the huge amount of data that will be produced by the HIFI line-survey key project. Moreover, the mere identification of a ghost line does not help to recover the spectral information likely to be obliterated by such ghost. In our example, an increase of the degree of redundancy to 7 inhibits the production of artifacts: although the 944.3-GHz ghost feature is still present, its intensity is drastically reduced, and the reconstruction matches very well with the original spectrum.


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS2791f10.eps}\end{figure} Figure 7: Section of two SSB spectra (in grey), reconstructed from simulated DSB coverages of the 800-960 GHz band affected by sideband imbalances, and carried out with N=1 (upper panel) and N=7 (lower panel). The corresponding section of the initial spectrum (cf. Fig. 2) is overlaid in black.
Open with DEXTER

Another issue has to be addressed that is connected to the reconstruction of a SSB spectrum from DSB data affected by sideband imbalances. As anticipated in Sect. 2, MEM allows one to treat the sideband ratios as free parameters. The question has arisen whether it is possible to use the MEM algorithm to measure the HIFI sideband ratio curve throughout the band. In order to check this possibility, for every scan of each simulation we compare the input values ( $g_{\rm in}$) of the sideband gains to the output ( $g_{\rm out}$) from the deconvolution. The $g_{\rm in}/g_{\rm out}$ ratio should, ideally, be equal to 1. The two examples given in Fig. 8 derive from the deconvolution of DSB data with degree of redundancy 1 (upper panel) and 7 (lower panel). The plots of $g_{\rm in}/g_{\rm out}$ in Fig. 8 give us at least two important pieces of information: i), the output does not equal the input, although it gets very close to it (the standard deviation from 1 is $\sigma_{N=1}=0.14$ and $\sigma_{N=7}=0.03$); ii), the ratio is closer to 1 as the degree of redundancy grows. Note that the sideband gains fitted, for each DSB scan, by the algorithm, are not bound to satisfy the condition expressed by Eq. (9). In this way, the correction for the sideband imbalances can also incorporate a correction for the pointing errors. After the deconvolution, the condition in Eq. (9) can be imposed to recover, for every DSB scan, the pointing error as it has been estimated by the algorithm.

The results illustrated in Fig. 8 show that the input values of the sideband gains can be recovered reasonably well through the MEM deconvolution. Still, we believe that the accuracy achieved is not high enough to satisfy HIFI requirements: the calibration of the sideband gains based on processing one single line survey is inadequate to reach, for each DSB scan, the HIFI goal for the calibration accuracy (better than 10%, van Leeuwen et al. 2001a). However, if the sideband gains are reproducible, processing several surveys will enhance the accuracy of the reconstruction (hence of the gains determination) significantly. Our results will also be improved by any constraint coming from laboratory measurements of the gains.


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS2791f11.eps}\end{figure} Figure 8: Plot of the ratio between the input value of the sideband gains ( $g_{\rm in}$) assigned to each scan during the simulation of the DSB coverage, and the output value fitted by the MEM algorithm ( $g_{\rm out}$). The upper panel refers to the reconstruction of a minimum-redundancy survey, while the lower panel refers to a coverage with a degree of redundancy of 7. The left side of the panels displays values relative to the lower sideband, the right side refers to the image upper sideband. Each value of the plots represents the $g_{\rm in}/g_{\rm out}$ ratio for a single scan. A section of the corresponding reconstructed SSB spectra is shown in Fig. 7.
Open with DEXTER


  \begin{figure} \includegraphics[angle=-90,width=11.8cm,clip]{MS2791f12.eps}\end{figure} Figure 9: Model of chemically structured source. The model is inspired by Orion-KL, where O-bearing and N-bearing molecules peak at different positions (towards the Compact Ridge and the Hot Core, respectively). We must stress, though, that this sketch has been obtained by simply producing, in the same fashion as for the spectrum in Fig. 2, separated spectra for O-bearing species and N-bearing species, and therefore it does not represent Orion-KL. The HPBW of the HIFI instrument at 800 GHz (25 $\hbox {$^{\prime \prime }$ }$) is displayed in the bottom right corner of the plot.
Open with DEXTER

  
3.4 Making it realistic

Having separately analyzed the three main sources of noise in the reconstruction of a DSB line survey, we now want our simulation to get as close as possible to reality. Our data will therefore be affected by all of the following quality-degrading factors:

i)
rms noise, increasing as $\Delta x$ decreases (cf. Sect. 3.2);
ii)
different pointing errors in each DSB scan (cf. Sect. 3.3);
iii)
different sideband imbalances in each DSB scan (cf. Sect. 3.3);
iv)
moreover, we introduce some intrinsic chemical structure in our source, as schematically illustrated in Fig. 9. The simulated spectra are supposed to be emitted from two point-like sources with different chemical composition. Drawing inspiration from the chemical differentiation in Orion-KL, where oxygen-bearing molecules are most abundant towards the so-called Compact Ridge, whereas nitrogen-bearing species peak towards the Hot Core (cf. Blake et al. 1987), we have differentiated the emission from the two sub-sources by assigning to source 1 all the N-bearing molecules used in the modeling of the Band 3 spectrum, and to source 2 all the O-bearing species (see Fig. 9). The distance between the two objects is of about 7 $\hbox {$^{\prime \prime }$ }$, and it is therefore comparable to the projected distance of the Orion Hot Core from the Compact Ridge. The nominal pointing position corresponds to source 1: the initial spectrum will, in this case, be given by the sum of the emission towards source 1 (spectrum in the top right corner of Fig. 9) and of the emission towards source 2 (bottom left corner in Fig. 9), as corrected for the distance from the center of the Gaussian beam. The beam size (25 $\hbox {$^{\prime \prime }$ }$) is displayed in the bottom right corner for comparison.
The chemical differentiation within the source enhances the effects of pointing errors. A "worse'' pointing will not necessarily correspond to the lines being weaker than they would be if the pointing was correct. In fact, features radiated from O-bearing molecules will, in this example, be stronger when the pointing drifts from the nominal position towards south-east. Thus, we would expect ghost features to be more abundant in the "structured-source'' rather than in the "non-structured-source'' case. The solid curve in Fig. 10 shows instead that the quality of the reconstruction of the 25 $\hbox {$^{\prime \prime }$ }$ surveys is quantitatively comparable to that of the surveys in which pointing errors and sideband imbalances have been separately taken into account (see Fig. 6). In fact, there is one more factor that must be considered when discussing the degrading effects of pointing errors on the deconvolution of DSB line surveys of structured sources, namely the separation between the different components of the observed object relative to the beam size. As shown in Fig. 9, the separation between source 1 and source 2 of our model is more than 3 times smaller than the HPBW of Herschel at 800 GHz. It is no surprise, then, that the intrinsic source structure has no dramatic effects on the quality of the reconstructions. It can be easily foreseen that such effects will become more important as the beam size of the telescope becomes smaller. The dashed curve in Fig. 10 represents the variation of $\langle A_{\rm diff}\rangle_{\rm norm}$ as a function of N, for simulated surveys where the HPBW has been reduced to 13 $\hbox {$^{\prime \prime }$ }$. The comparison between the 25 $\hbox {$^{\prime \prime }$ }$ and the $13\hbox{$^{\prime\prime}$ }$ curve shows that the reconstructions of the 13 $\hbox {$^{\prime \prime }$ }$-resolution surveys are from about 2 (low N) to about 4 (high N) times worse than the lower-spatial-resolution ones. This result will have to be taken into account, especially for instruments able to span wide frequency ranges. In the very particular case of a HIFI all-band line survey (from 480 to 1250 and from 1410 to 1910 GHz), the HPBW shrinks from a maximum size of 39 $\hbox {$^{\prime \prime }$ }$ (Band 1) to a minimum of 13 $\hbox {$^{\prime \prime }$ }$ (Band 6), therefore the observing procedures (i.e., the degree of redundancy) needed to achieve a proper data reconstruction will vary as the observing frequency increases.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2791f13.eps}\end{figure} Figure 10: Variation, as a function of the degree of redundancy N, of the normalized fidelity parameter, $\langle A_{\rm diff}\rangle_{\rm norm}$, relative to the reconstruction of simulated DSB line surveys of a chemically structured source (see Fig. 9), where the data are affected by rms noise, pointing errors and sideband imbalances. The simulations have been carried out for two different values of the beam size (25 $\hbox {$^{\prime \prime }$ }$ and 13 $\hbox {$^{\prime \prime }$ }$, solid and dashed curve respectively).
Open with DEXTER

  
3.5 Frequency switching

As discussed in Sect. 3.2, a good reconstruction of a DSB spectral line survey does not depend on the degree of redundancy in the data only. A great effort must be made in order to keep the dead times, naturally associated to the data acquisition, as short as possible. One possibility to achieve this goal is offered by the frequency-switching (FSW) observing mode, which enables the observer to reduce the off-source time to zero. Equation (6) then becomes

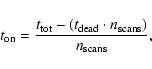\begin{displaymath}t_{\rm on} = \frac{t_{\rm tot}-(t_{\rm dead} \cdot n_{\rm scans})}{n_{\rm scans}}, \end{displaymath} (10)

that is, the time available, per scan, for on-source integration is a factor of two longer with respect to the position-switching (PSW) mode. It is therefore interesting to test the possibility of reconstructing DSB line surveys carried out in FSW mode.

Frequency-switching data are such that the measured intensity, $I(\nu_i)$, at the frequency $\nu_i$, corresponding to the ith channel of the scan, is given by:

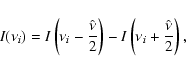\begin{displaymath}I(\nu_i)=I\left(\nu_i- \frac{\hat{\nu}}{2}\right)-I\left(\nu_i+\frac{\hat{\nu}}{2}\right), \end{displaymath} (11)

where $\hat{\nu}$ is the frequency throw of the scan. So, while for PSW observations the subtraction of the background radiation is achieved by taking an off-source scan and then subtracting it from the on-source data, with FSW this is done by taking two on-source scans, respectively at frequencies $\nu_0-\hat{\nu}$ and $\nu_0+\hat{\nu}$where $\nu_0$ is the nominal observing frequency, and then by subtracting them from each other. One major drawback of this technique is that the baseline of the acquired scans is far from being flat, mainly due to the bandpass of the receiver which varies with time and frequency. While FSW can be reliably and successfully used for single-line observations, where even higher order baseline subtraction is made relatively easy by the fact that rest frequency and (hyperfine) structure of the observed transition are already known or can at least be guessed, the introduction of such technique for DSB line surveys produces a dramatic increase in the complexity of the data. A comparison between a DSB scan acquired in FSW mode and one acquired in PSW mode is shown in Fig. 11.


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS2791f14.eps}\end{figure} Figure 11: a) example of a DSB scan acquired in frequency-switching mode. The center frequency (LSB) is 810.3 GHz, the frequency throw is of 10 MHz. As a comparison, a coverage carried out in position-switching mode (leaving all the other conditions unchanged) would produce, at 810.3 GHz, the DSB scan shown in panel  b). No receiver bandpass structure is taken into account.
Open with DEXTER

In order to quantitatively estimate whether the improvement due to the longer integration time available overrules the downgrade due to the increased complexity, many specific technical informations about the observing instrument would be needed, for example:

These informations relative to the HIFI instrument are, as yet, not available. Nonetheless, we are interested in testing, from a merely qualitative point of view, the capabilities of the MEM algorithm to reconstruct DSB/FSW data. Therefore, we have simulated a frequency-switching coverage of the target source described in Sect. 3.4 and Fig. 9, across the 800-960 GHz band, and taking into account the effects introduced in the data by rms noise, pointing errors and sideband imbalances. As for the additional complications introduced, in FSW mode, by possible receiver bandpass variations, we believe it is impossible to deal with it via MEM reconstruction. Frequency switching DSB line surveys will only be feasible if such structures can be calibrated out at the DSB stage. Therefore, we have not included residual bandpass structure in the simulation. Also, this time the degree of redundancy in the data has not been increased by increasing N, but by applying four different frequency throws (10, 20, 40 and 80 MHz) to each LO setting. We assume that, for frequency throws as small as 80 MHz, a re-tuning of the receiver is not necessary, so the total tuning time is only depending on the number of LO settings, hence on N. In this way we can achieve an effective degree of redundancy higher than 1, while maximizing the on-source integration time.
  \begin{figure} \par\includegraphics[angle=-90,width=12cm,clip]{MS2791f15.eps}\end{figure} Figure 12: a) Section of the SSB reconstruction of a simulated DSB coverage of the emission, in the 800-960 GHz band, towards the chemically structured source in Fig. 9, where the simulated observations have been carried out in frequency-switching mode; b) section of the original spectrum used as a basis to simulate the coverage; c) difference between a) and b).
Open with DEXTER

It is hard to quantify the effective degree of redundancy for such a simulation: the frequency ranges that are closer to the LO settings of the DSB scans are definitely covered four times in each sideband (once for each value of the frequency throw), while in many regions the coverage might only achieve a degree of redundancy of 1. However, the results of the MEM deconvolution are quite encouraging. Figure 12 shows, in the upper panel, a section of the SSB spectrum reconstructed on the basis of the DSB simulated survey of a structured source (see Fig. 9), carried out in FSW mode in the fashion clarified above. Pointing errors and sideband imbalances are included in the simulation as well. The reconstruction is indeed very similar to the original spectrum (panel b)). Panel c) shows the difference between reconstruction and original: although some residuals are present, the quality of the deconvolution proves to be high in spite of the increased complexity of the DSB data.

  
4 Conclusions

Upcoming submillimeter and THz telescopes (APEX, ALMA, Herschel) will be invaluable tools to study the chemistry of the densest and hottest regions of molecular gas. Unbiased line surveys of several key objects will be, for this purpose, the most powerful instrument available.

For the time being, the technology nowadays available does not allow intrinsic sideband rejection at wavelengths smaller than one millimeter. The reconstruction of line surveys from the double-sideband (DSB) form in which they are acquired, to the single-sideband (SSB) form in which they can be analyzed, is dramatically affected by a handful of factors, namely spacing, pointing errors and sideband imbalances, as illustrated in Sect. 2.

We have produced simulations of DSB line surveys in order to elaborate an observing strategy capable of minimizing the quality-deteriorating effects that the combined action of the above-mentioned factors have on the data and on their reconstruction. In particular, we have simulated the MEM reconstruction of DSB data acquired with the HIFI instrument on board the Herschel Space Observatory. The main results of this work can be summarized as follows:

Observing strategy
$\bullet$
The spacing must be irregular: in Sect. 3.1 we have shown that surveying a frequency band by means of regularly-spaced DSB scans gives rise, in the reconstructed SSB spectrum, to periodic structures of random amplitude and period depending on the values of the IF and of the spacing. Such structures could be artificially "flattened out'' by increasing the weight of the Maximum Entropy term in the deconvolution, but a proper observing strategy involving irregular spacing solves the problem by inhibiting the production of such artifacts.
$\bullet$
The degree of redundancy in the data must be high: the plots in Figs. 6 and 10 show that the quality of the data reconstruction improves dramatically if the degree of redundancy of the coverage increases. This is especially true only if the data are affected by pointing errors and/or sideband imbalances (that is, in all "real life'' cases). Thus, a high degree of redundancy is advisable for a double-sideband line survey to be properly reconstructed. The optimum value is a function of many parameters, and has to be explicitly determined for each specific survey.
$\bullet$
Finally, we have shown that the most complex and "realistic'' sets of data can be satisfactorily reconstructed through the Maximum Entropy Method. In particular, frequency-switching DSB line surveys can be properly deconvolved.

System requirements
$\bullet$
The tuning time per LO setting must be as short as possible: if the dead times per tuning are too long, the improvement brought in by increasing the redundancy of information in the survey will be obliterated by the high rms noise in the data. Since, as explained above, a high degree of redundancy is necessary to avoid the presence of spurious features due to pointing errors and sideband imbalances (see Sect. 3.3), for any instrument planned to be used for line surveys, the tuning time must be kept as low as possible. The tuning times of order 1 min considered in Sect. 3.2 are not acceptable.
$\bullet$
The tunings of the receiver should be highly reproducible, and in particular the sideband imbalances as a function of the observing frequency should be parametrizable. This would allow us to get rid of one of the free parameters playing a key role in the deconvolution, the sideband gain ratios, thus making the reconstruction more reliable. From this point of view, lab measurements of the gain ratios, throughout the observable frequency range of the instrument, would be highly desirable.
$\bullet$
The great advantages offered by the possibility of carrying out frequency-switching DSB line surveys (Sect. 3.5) can only be exploited if the shape of the receiver bandpass is known a priori, or can be calibrated out without adding much overhead time. Should the bandpass variations be reproducible and parametrizable, frequency switching will be a powerful option to scan through large frequency bands in a (relatively) short observing time.

Acknowledgements
The authors would like to thank V. Ossenkopf, D. Teyssier, M. Walmsley, N. Whyborn, H. Beuther, and above all the referee T. G. Phillips, for their valuable comments and constructive questions. Also, we are grateful to all the colleagues in the Submillimeter Astronomy Group at MPIfR for letting us use, without too much grumbling, their CPU time to run the simulations. Special thanks to Dirk Muders for taking good care of the MPIfR Linux cluster.

  
Appendix A: Confusion limit

The term "confusion'' has been mentioned, in Sect. 2 of this work, to explain the fact that only about 12% of the transitions included in our initial spectrum (Fig. 2) are actually visible.

  \begin{figure} \par\includegraphics[width=7.1cm,clip]{MS2791f16.eps}\end{figure} Figure A.1: Variation, as a function of the intensity S0, of the number of lines/GHz showing, in our model spectrum (Fig. 2), an intensity S > S0. The solid curve refers to the total number of features in the model, whereas the dashed curve is based on the detected (because non-blended) lines. The tags indicate the flux values at which 70 to 11.8% of the features are non-blended and hence counted among the "detected'' ones (see Table A.1).

The term was first introduced to define, in the two-dimensional case, the effect by which the presence of a high number of sources in the observed field would not allow their reliable identification (cf. Scheuer 1956). Such definition can be easily applied to our (one-dimensional) case. Here, the confusion is determined by a high density of features in the spectrum, which leads to severe line blending. This affects both weak and strong lines: in fact, while it precludes the very identification of most weak lines, confusion also affects the measured intensity of stronger features by creating a "pseudo-continuum'' due to the superposition of a great number of weak ones. Particularly in the presence of non-Gaussian line wings, the contribution of the pseudo-continuum to the continuum emission could produce significant deviations of the measured continuum level from the actual value.

An analytical determination of the confusion limit (i.e., the flux threshold below which identifications are questionable) in unbiased line surveys is beyond the scope of this paper. Nevertheless, it is useful to illustrate how such limit can be determined for our model spectrum. Note that the rms noise does not enter in what follows: what we want to estimate is the intrinsic confusion limit of our model source, independent of the sensitivity of the instrument through which we will perform the observations.

The two curves in Fig. A.1 represent the variation of the density of lines, per GHz, stronger than S0, as a function of the intensity S0. The distribution is calculated over all the 14 643 transitions included in the model (solid curve), and over the 1935 lines actually visible in the spectrum (dashed curve). The latter number has been obtained by simply counting the intensity maxima.

The tags in Fig. A.1 indicate the flux at which the number of detected (because non-blended) features, $N_{\rm d}$, is 70 to 11.8% of the total. Table A.1 lists the flux values and line densities corresponding to each $N_{\rm d}$.


 

 
Table A.1: Flux values and line densities corresponding to a percentage of detected lines/GHz ($N_{\rm d}$) of 70 to 11.8% (see Fig. A.1).
S0 N(S > S0) $N_{\rm d}$
(K) (lines/GHz)  

$1.4\times10^{-1}$		 7 $70\%$
$7.1\times10^{-2}$ 10 $60\%$
$3.1\times10^{-2}$ 16 $50\%$
$1.8\times10^{-2}$ 22 $40\%$
$4.4\times10^{-3}$ 34 $30\%$
$5.7\times10^{-4}$ 58 $20\%$
$4.6\times10^{-7}$ 104 $11.8\%$


Figure A.1 and Table A.1 can be used to estimate the intrinsic confusion limit for a high-line-density source. Such limit depends on a somewhat arbitrary definition of the confusion threshold, but if we set it to 50% of the lines being lost to blending, then the confusion will dominate at a line density of 16 lines per GHz, which in our case corresponds to an intensity level of about 30 mK. The line density limit is more fundamental, since it varies only with frequency and line width as

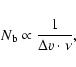\begin{displaymath}N_{\rm b} \propto \frac{1}{\Delta v \cdot \nu}, \end{displaymath} (A.1)

while the intensity limit depends additionally on the line intensities and beam filling factor.

References

 
Copyright ESO 2002