A&A 395, 45-67 (2002)
DOI: 10.1051/0004-6361:20021283

Integrated spectroscopy of bulge globular clusters and fields

I. The data base and comparison of individual Lick indices
in clusters and bulge

T. H. Puzia ¹ - R. P. Saglia ¹ - M. Kissler-Patig ² - C. Maraston ³ - L. Greggio ^1,4 - A. Renzini ² - S. Ortolani⁴

1 - Sternwarte der Ludwig-Maximilians-Universität, Scheinerstrasse 43, 81679 München, Germany
2 - European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
3 - Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstrasse, 85748 Garching bei München, Germany
4 - Università di Padova, Dept. di Astronomia, Vicolo dell'Osservatorio 2, 35122 Padova, Italy

Received 7 June 2002 / Accepted 23 August 2002

Abstract
We present a comprehensive spectroscopic study of the integrated light of metal-rich Galactic globular clusters and the stellar population in the Galactic bulge. We measure line indices which are defined by the Lick standard system and compare index strengths of the clusters and Galactic bulge. Both metal-rich globular clusters and the bulge are similar in most of the indices, except for the CN index. We find a significant enhancement in the CN $/\langle$ Fe $\rangle$ index ratio in metal-rich globular clusters compared with the Galactic bulge. The mean iron index $\langle$ Fe $\rangle$ of the two metal-rich globular clusters NGC 6528 and NGC 6553 is comparable with the mean iron index of the bulge. Index ratios such as Mgb $/\langle$ Fe $\rangle$ , Mg $_2/\langle$ Fe $\rangle$ , Ca 4227 $/\langle$ Fe $\rangle$ , and TiO $/\langle$ Fe $\rangle$ , are comparable in both stellar population indicating similar enhancements in individual elements which are traced by the indices. From the globular cluster data we fully empirically calibrate several metallicity-sensitive indices as a function of [Fe/H] and find tightest correlations for the Mg₂ index and the composite [MgFe] index. We find that all indices show a similar behavior with galactocentric radius, except for the Balmer series, which show a large scatter at all radii. However, the scatter is entirely consistent with the cluster-to-cluster variations in the horizontal branch morphology.

Key words: Galaxy: globular clusters: general - Galaxy: abundances - Galaxy: formation - stars: abundances

1 Introduction

Stars in globular clusters are essentially coeval and - with very few exceptions - have all the same chemical composition, with only few elements breaking the rule. As such, globular clusters are the best approximation to simple stellar populations (SSP), and therefore offer a virtually unique opportunity to relate the integrated spectrum of stellar populations to age and chemical composition, and do it in a fully empirical fashion. Indeed, the chemical composition can be determined via high-resolution spectroscopy of cluster stars, the age via the cluster turnoff luminosity, while integrated spectroscopy of the cluster can also be obtained without major difficulties. In this way, empirical relations can be established between integrated-light line indices (e.g. Lick indices as defined by Faber et al. 1985) of the clusters, on one hand, and their age and chemical composition on the other hand (i.e., [Fe/H], [ $\alpha$ /Fe], etc.).

These empirical relations are useful in two major applications: 1) to directly estimate the age and chemical composition of unresolved stellar populations for which integrated spectroscopy is available (e.g. for elliptical galaxies and spiral bulges), and 2) to provide a basic check of population synthesis models.

Today we know of about 150 globular clusters in the Milky Way (Harris 1996), and more clusters might be hidden behind the high-absorption regions of the Galactic disk. Like in the case of many elliptical galaxies (e.g. Harris 2001), the Galactic globular cluster system shows a bimodal metallicity distribution (Freeman & Norris 1981; Zinn 1985; Ashman & Zepf 1998; Harris 2001) and consists of two major sub-populations, the metal-rich bulge and the metal-poor halo sub-populations.

The metal-rich ( ${\rm [Fe/H]}>-0.8$ dex) component was initially referred to as a "disk'' globular cluster system (Zinn 1985), but it is now clear that the metal-rich globular clusters physically reside inside the bulge and share its chemical and kinematical properties (Minniti 1995; Barbuy et al. 1998; Côté 1999). Moreover, the best studied metal-rich clusters (NGC 6528 and NGC 6553) appear to have virtually the same old age as both the halo clusters and the general bulge population (Ortolani et al. 1995a; Feltzing & Gilmore 2000; Ortolani et al. 2001; Zoccali et al. 2001,2002; Feltzing et al. 2002), hence providing important clues on the formation of the Galactic bulge and of the whole Milky Way galaxy.

Given their relatively high metallicity (up to ${\sim} Z_\odot$ ), the bulge globular clusters are especially interesting in the context of stellar population studies, as they allow comparisons of their spectral indices with those of other spheroids, such as elliptical galaxies and spiral bulges. However, while Lick indices have been measured for a representative sample of metal-poor globular clusters (Burstein et al. 1984; Covino et al. 1995; Cohen et al. 1998; Trager et al. 1998), no such indices had been measured for the more metal-rich clusters of the Galactic bulge. It is the primary aim of this paper to present and discuss the results of spectroscopic observations of a set of metal-rich globular clusters that complement and extend the dataset so far available only for metal-poor globulars.

Substantial progress has been made in recent years to gather the complementary data to this empirical approach: i.e. ages and chemical composition of the metal-rich clusters. Concerning ages, HST/WFPC2 observations of the clusters NGC 6528 and NGC 6553 have been critical to reduce to a minimum and eventually to eliminate the contamination of foreground disk stars (see references above), while HST/NICMOS observations have started to extend these studies to other, more heavily obscured clusters of the bulge (Ortolani et al. 2001).

High spectral-resolution studies of individual stars in these clusters is still scanty, but one can expect rapid progress as high multiplex spectrographs become available at 8-10 m class telescopes. A few stars in NGC 6528 and NGC 6553 have been observed at high spectral resolution, but with somewhat discrepant results. For NGC 6528, Carretta et al. (2001) and Coelho et al. (2001) report respectively $\rm [Fe/H]=+0.07$ and -0.5 dex (the latter value coming from low-resolution spectra). For [M/H] the same authors derive +0.17 and -0.25 dex, respectively. For NGC 6553 Barbuy et al. (1999) give $\rm [Fe/H] =-0.55$ dex and $\rm [M/H] =-0.08$ dex, while Cohen et al. (1999) report $\rm [Fe/H] =-0.16$ dex, and Origlia et al. (2002) give $\rm [Fe/H] =-0.3$ dex, with [ $\alpha$ /Fe] =+0.3 dex. Some $\alpha$ -element enhancement has also been found among bulge field stars, yet with apparently different element-to-element ratios (McWilliam & Rich 1994).

Hopefully these discrepancies may soon disappear, as more and better quality high-resolution data are gathered at 8-10 m class telescopes. In summary, the overall metallicity of these two clusters (whose color magnitude diagrams are virtually identical, Ortolani et al. 1995a) appears to be close to solar, with an $\alpha$ -element enhancement [ $\alpha$ /Fe] $\simeq +0.3$ dex.

The $\alpha$ -element enhancement plays an especially important role in the present study. It is generally interpreted as the result of most stars having formed rapidly (within less than, say $\sim$ 1 Gyr), thus having had the time to incorporate the $\alpha$ -elements produced predominantly by type II supernovae, but failing to incorporate most of the iron produced by the longer-living progenitors of type Ia supernovae. Since quite a long time, an $\alpha$ -element enhancement has been suspected for giant elliptical galaxies, inferred from the a comparison of Mg and Fe indices with theoretical models (Peletier 1989; Worthey et al. 1992; Davies et al. 1993; Greggio 1997). This interpretation has far-reaching implications for the star formation timescale of these galaxies, with a fast star formation being at variance with the slow process, typical of the current hierarchical merging scenario (Thomas & Kauffmann 1999). However, in principle the apparent $\alpha$ -element enhancement may also be an artifact of some flaws in the models of synthetic stellar populations, especially at high metallicity (Maraston et al. 2001). The observations presented in this paper are also meant to provide a dataset against which to conduct a direct test of population synthesis models, hence either excluding or straightening the case for an $\alpha$ -element enhancement in elliptical galaxies. This aspect is extensively addressed in an accompanying paper (Maraston et al. 2002).

The main goal of this work is the measurement of the Lick indices for the metal-rich globular clusters of the bulge and of the bulge field itself. Among others, we measure line indices of Fe, Mg, Ca, CN, and the Balmer series which are defined in the Lick standard system (Worthey & Ottaviani 1997; Trager et al. 1998). In Sect. 2 we describe in detail the observations and our data reduction which leads to the analysis and measurement of line indices in Sect. 3. Index ratios in globular clusters and the bulge are presented in Sect. 4. Index-metallicity relations are calibrated with the new data in Sect. 5 and Sect. 6 discusses the index variations as a function of galactocentric radius. Section 7 closes this work with the conclusions followed by a summary in Sect. 8.

**Table 1:** General properties of sample Globular Clusters. If not else mentioned, all data were taken from the 1999 update of the McMaster catalog of Milky Way Globular Clusters (Harris 1996). $R_{\rm gc}$ is the globular cluster distance from the Galactic Center. $r_{\rm h}$ is the half-light radius. E_(B-V) and (m-M)_V are the reddening and the distance modulus. $v_{\rm rad}$ the heliocentric radial velocity. Note, that our radial-velocity errors are simple *internal* errors which result from the fitting of the cross-correlation peak. The real *external* errors are a factor $\sim$ 2-4 larger. HBR is the horizontal-branch morphology parameter (e.g. Lee et al. 1994).
GC	$R_{\rm gc}$ [kpc]	[Fe/H]	$r_{\rm h}$ [arcmin]	E_(B-V)^a	(m-M)_V	$v_{\rm rad}^{b}$ [km s^-1]	$v_{\rm rad}$ [km s^-1]	HBR^c

NGC 5927	4.5	-0.37	1.15	0.45	15.81	$-130\pm12$	$-107.5\pm 1.0$	-1.00^d
NGC 6218 (M 12)	4.5	-1.48	2.16	0.40	14.02	$-46\pm23$	$-42.2\pm 0.5$	0.97^d
NGC 6284	6.9	-1.32	0.78	0.28	16.70	$8\pm16$	$27.6\pm 1.7$	1.00^e
NGC 6356	7.6	-0.50	0.74	0.28	16.77	$35\pm12$	$27.0\pm 4.3$	-1.00^d
NGC 6388	4.4	-0.60	0.67	0.40	16.54	$58\pm10$	$81.2\pm 1.2$	-0.70^e
NGC 6441	3.5	-0.53	0.64	0.44	16.62	$-13\pm10$	$16.4\pm 1.2$	-0.70^f
NGC 6528	1.3	-0.17	0.43	0.56	16.53	$180\pm10$	$184.9\pm 3.8$	-1.00^d
NGC 6553	2.5	-0.34	1.55	0.75	16.05	$-25\pm16$	$-6.5\pm 2.7$	-1.00^d
NGC 6624	1.2	-0.42	0.82	0.28	15.37	$27\pm12$	$53.9\pm 0.6$	-1.00^d
NGC 6626 (M 28)	2.6	-1.45	1.56	0.43	15.12	$-15\pm15$	$17.0\pm 1.0$	0.90^d
NGC 6637 (M 69)	1.6	-0.71	0.83	0.16	15.16	$6\pm12$	$39.9\pm 2.8$	-1.00^d
NGC 6981 (M 72)	12.9	-1.40	0.88	0.05	16.31	$-360\pm18$	$-345.1\pm 3.7$	0.14^d

^a: Taken from Harris (1996).
^b: This work.
^c: Horizontal branch parameter, (B-R)/(B+V+R), for details see e.g. Lee et al. (1994).
^d: Taken from Harris (1996).
^e: Taken from Zoccali et al. (2000).
^f: Due to very similar HB morphologies in CMDs of NGC 6388 and NGC 6441 (see Rich et al. 1997), we assume that the HBR parameter is similar for both globular clusters and adopt $\rm HBR=-0.70$ for NGC 6441.

2 Observations and data reduction

2.1 Observations

We observed 12 Galactic globular clusters, 9 of which are located close to the Milky-Way bulge (see Fig. 1). Four globular clusters belong to the halo sub-population with a mean metallicity $\rm [Fe/H]\leq-0.8$ dex (Harris 1996). The other globular clusters with higher mean metallicities are associated with the bulge. Our sample includes the well-studied metal-rich clusters NGC 6553 and NGC 6528, which is located in Baade's Window. Several relevant cluster properties are summarized in Table 1. Our cluster sample was selected to maximize the number of high-metallicity clusters and to ensure a high enough signal-to-noise ratio (S/N) of the resulting spectra.

Long-slit spectra were taken on three nights in July 5th to 7th 1999 with the Boller & Chivens Spectrograph of ESO's 1.52 m on La Silla. We used grating #23 with 600 grooves per mm yielding a dispersion of 1.89 Å/pix with a spectral range from $\sim$ 3400 Å to $\sim$ 7300 Å. We used the detector CCD #39, a Loral $2048\times2048$ pix² chip, with a pixel size of 15 $\mu$ m and a scale of 0.82 $^{\prime\prime}$ /pix. Its readout noise is 5.4 e^- and the gain was measured with 1.2 e^-/ADU. In order to check the dark current we also obtained dark images which resulted in a negligible average dark current of 0.0024 e $^{-}~{\rm s}^{-1}~{\rm pix}^{-1}$ . The total slit length of the spectrograph covers 4.5 $^\prime$ on the sky. For the benefit of light sampling the slit width was fixed at 3 $^{\prime\prime}$ , which guarantees an instrumental resolution ( $\sim$ 6.7 Å) which is smaller than the average resolution ( $\ga$ 8 Å) of the Lick standard system (Worthey et al. 1994; Trager et al. 1998). The mean seeing during the observing campaign varied between 0.8 $^{\prime\prime}$ and 1.6 $^{\prime\prime}$ , resulting in seeing-limited spectra. Consequently, the stellar disks are smeared over 1-2 pixel along the spatial axis.

To ensure a representative sampling of the underlying stellar population we obtained several spectra with slightly offset pointings. In general three long-slit spectra were taken for each of our target clusters (see Table 2 for details). The observing pattern was optimized in time (i.e. in airmass) to obtain one spectrum of the nuclear region and spectra of adjacent fields by shifting the telescope a few arc seconds (i.e. $\sim$ 2 slit widths) to the North and South. Exposure times were adjusted according to the surface brightness of each globular cluster to reach an statistically secure luminosity sampling of the underlying stellar population. Before and after each block of science exposures, lamp spectra were taken for accurate wavelength calibration.

In addition to the globular cluster data, we obtained long-slit spectra of three stellar fields near the Galactic center (see Fig. 1). Two of them are located in Baade's Window. The exposure time for a single bulge spectrum is 1800 s. Five slightly offset pointings have been observed in each field resulting in 15 exposures of 30 min each.

During each night Lick and flux standard stars were observed for later index and flux calibrations. Table 2 shows the observing log of all three nights. Figure 1 gives the positions of all observed globular clusters (filled dots) and bulge fields (open squares) in the galactic coordinate system.

$\begin{figure} \includegraphics[width=16.1cm,clip]{2781f1.eps} \end{figure}$

Figure 1: Distribution of galactic globular clusters as seen in the galactic coordinate system. The filled circles are the observed sample globular clusters while open circles mark the position of other known Milky Way globular clusters. All observed globular clusters are appropriately labeled. The positions were taken from the Globular Cluster Catalog by Harris (1996). Large squares show the positions of our three bulge fields for which spectroscopy is also available. Note that two of the three fields almost overlap in the plot.

Table 2: Journal of all performed observations.
Night Targets Exptime RA(J2000) Dec (J2000) l[ $^{\circ}$ ] b[ $^{\circ}$ ]

5.7.1999 NGC 5927 3 $~\times~$ 600 s 15h 28m 00.5 s $-50^{\circ}40'22''$ 326.60 4.86

NGC 6388 3 $~\times~$ 600 s 17h 36m 17.0 s $-44^{\circ}44'06''$ 345.56 -6.74

NGC 6528 3 $~\times~$ 600 s 18h 04m 49.6 s $-30^{\circ}03'21''$ 1.14 -4.17

NGC 6624 3 $~\times~$ 600 s 18h 23m 40.5 s $-30^{\circ}21'40''$ 2.79 -7.91

NGC 6981 1 $~\times~$ 1320 s 20h 53m 27.9 s $-12^{\circ}32'13''$ 35.16 -32.68

Bulge1 5 $~\times~$ 1800 s 18h 03m 12.1 s $-29^{\circ}52'06''$ 1.13 3.78

6.7.1999 NGC 6218 3 $~\times~$ 1200 s 16h 47m 14.5 s $-01^{\circ}56'52''$ 15.72 26.31

NGC 6441 3 $~\times~$ 600 s 17h 50m 12.9 s $-37^{\circ}03'04''$ 353.53 -5.01

NGC 6553 3 $~\times~$ 720 s 18h 09m 15.6 s $-25^{\circ}54'28''$ 5.25 -3.02

NGC 6626 3 $~\times~$ 600 s 18h 24m 32.9 s $-24^{\circ}52'12''$ 7.80 -5.58

NGC 6981 1 $~\times~$ 1800 s 20h 53m 27.9 s $-12^{\circ}32'13''$ 35.16 -32.68

Bulge2 5 $~\times~$ 1800 s 18h 05m 21.3 s $-29^{\circ}58'38''$ 1.26 4.23

7.7.1999 NGC 6284 3 $~\times~$ 600 s 17h 04m 28.8 s $-24^{\circ}45'53''$ 358.35 9.94

NGC 5927 2 $~\times~$ 600 s 15h 28m 00.5 s $-50^{\circ}40'22''$ 326.60 4.86

NGC 6356 3 $~\times~$ 900 s 17h 23m 35.0 s $-17^{\circ}48'47''$ 6.72 10.22

NGC 6637 3 $~\times~$ 900 s 18h 31m 23.2 s $-32^{\circ}20'53''$ 1.72 -10.27

NGC 6981 1 $~\times~$ 1800 s 20h 53m 27.9 s $-12^{\circ}32'13''$ 35.16 -32.68

Bulge3 5 $~\times~$ 1800 s 17h 58m 38.3 s $-28^{\circ}43'33''$ 1.63 2.35

**Table 2:** Journal of all performed observations.
Night	Targets	Exptime	RA(J2000)	Dec (J2000)	l[ $^{\circ}$ ]	b[ $^{\circ}$ ]
5.7.1999	NGC 5927	3 $~\times~$ 600 s	15h 28m 00.5 s	$-50^{\circ}40'22''$	326.60	4.86
	NGC 6388	3 $~\times~$ 600 s	17h 36m 17.0 s	$-44^{\circ}44'06''$	345.56	-6.74
	NGC 6528	3 $~\times~$ 600 s	18h 04m 49.6 s	$-30^{\circ}03'21''$	1.14	-4.17
	NGC 6624	3 $~\times~$ 600 s	18h 23m 40.5 s	$-30^{\circ}21'40''$	2.79	-7.91
	NGC 6981	1 $~\times~$ 1320 s	20h 53m 27.9 s	$-12^{\circ}32'13''$	35.16	-32.68
	Bulge1	5 $~\times~$ 1800 s	18h 03m 12.1 s	$-29^{\circ}52'06''$	1.13	3.78
6.7.1999	NGC 6218	3 $~\times~$ 1200 s	16h 47m 14.5 s	$-01^{\circ}56'52''$	15.72	26.31
	NGC 6441	3 $~\times~$ 600 s	17h 50m 12.9 s	$-37^{\circ}03'04''$	353.53	-5.01
	NGC 6553	3 $~\times~$ 720 s	18h 09m 15.6 s	$-25^{\circ}54'28''$	5.25	-3.02
	NGC 6626	3 $~\times~$ 600 s	18h 24m 32.9 s	$-24^{\circ}52'12''$	7.80	-5.58
	NGC 6981	1 $~\times~$ 1800 s	20h 53m 27.9 s	$-12^{\circ}32'13''$	35.16	-32.68
	Bulge2	5 $~\times~$ 1800 s	18h 05m 21.3 s	$-29^{\circ}58'38''$	1.26	4.23
7.7.1999	NGC 6284	3 $~\times~$ 600 s	17h 04m 28.8 s	$-24^{\circ}45'53''$	358.35	9.94
	NGC 5927	2 $~\times~$ 600 s	15h 28m 00.5 s	$-50^{\circ}40'22''$	326.60	4.86
	NGC 6356	3 $~\times~$ 900 s	17h 23m 35.0 s	$-17^{\circ}48'47''$	6.72	10.22
	NGC 6637	3 $~\times~$ 900 s	18h 31m 23.2 s	$-32^{\circ}20'53''$	1.72	-10.27
	NGC 6981	1 $~\times~$ 1800 s	20h 53m 27.9 s	$-12^{\circ}32'13''$	35.16	-32.68
	Bulge3	5 $~\times~$ 1800 s	17h 58m 38.3 s	$-28^{\circ}43'33''$	1.63	2.35

2.2 Data reduction

We homogeneously applied standard reduction techniques to the whole data set using the IRAF platform (Tody 1993). The basic data reduction was performed for each night individually. In brief, a masterbias was subtracted from the science images followed by a division by a normalized masterflat spectrum which has been created from five quarz-lamp exposures. The quality, i.e. the flatness, of the spectra along the spatial axis was checked on the sky spectra after flatfielding. Any gradients along the spatial axis were found to be smaller than $\lesssim$ 5%.

He-Ne-Ar-Fe lines were used to calibrate all spectra to better than 0.13 Å (rms). Unfortunately, the beam of the calibration lamp covers only the central 3.3 $^\prime$ along the slit's spatial axis (perpendicular to the dispersion direction), which allows no precise wavelength calibration for the outer parts close to the edge of the CCD chip. We tried, however, to extrapolate a 2-dim. $\lambda$ -calibration to the edges of the long-slit and found a significant increase in the rms up to an unacceptable 0.7 Å. Hence, to avoid calibration biases we use data only from regions which are covered by the arc lamp beam. Our effective slit length is therefore 3.3 $^\prime$ with a slit width of 3 $^{\prime\prime}$ . For each single pixel row along the dispersion axis an individual wavelength solution was found and subsequently applied to each object, bulge, and sky spectrum. After wavelength calibration the signal along the spatial axis was averaged in $\lambda$ -space, i.e. the flux of 3.3 $^\prime$ was averaged to obtain the final spectrum of a single pointing.

Finally, spectrophotometric standard stars, Feige 56, Feige 110, and Kopff 27 (Stone & Baldwin 1983; Baldwin & Stone 1984) were used to convert counts into flux units.

2.3 Radial velocities

All radial velocity measurements were carried out after the subtraction of a background spectrum (see Sect. 3.1) using cross-correlation with high-S/N template spectra of two globular clusters in M 31 (i.e. 158-213 and 225-280, see Huchra et al. 1982 for nomenclature). Both globular clusters have metallicities which match the average metallicity of our globular cluster sample. We strictly followed the recipe of the Fourier cross-correlation which is implemented in the FXCOR task of IRAF (see IRAF manual for details). Table 1 summarizes the results including the internal uncertainties of our measurements resulting from the fitting of the cross-correlation peak.

Following the rule of thumb, by which 1/10 of the instrumental resolution ( $\sim$ 6.7 Å) transforms into the radial velocity resolution, we estimate for our spectra a resolution of $\sim$ 40 km s^-1. In order to estimate the real uncertainty we compare the radial velocity measurements of one globular cluster (NGC 6981) which was observed in all three nights. We find a dispersion in radial velocity $\sigma_{\rm v}\approx17$ km s^-1 and a maximal deviation of 32.4 km s^-1. A comparison of measured radial velocities of all our Lick standard stars with values taken from the literature gives a dispersion of $\sigma_{\rm v}\approx40$ km s^-1 which matches the earlier rough estimate. In the case of NGC 6981, the internal error estimate ( $\Delta_{\rm cc} v_{\rm rad}=18.4$ km s^-1) underestimates the real radial velocity uncertainty assumed to be of the order of $\sim$ 40 km s^-1 by a factor of $\sim$ 2. Note however, that data of lower S/N will produce larger radial velocity uncertainties. Moreover, taking into account the slit width of 3 $^{\prime\prime}$ the maximum possible radial velocity error for a star positioned at the edge of the slit is $\sim$ 200 km s^-1. For high surface-brightness fluctuations inside the slit, this would inevitably result in larger radial velocity errors than originally expected from the calibration quality. Since we sum up all the flux along the slit, we most effectively eliminate this surface-brightness fluctuation effect. In fact, after a check of all our single spectra, we find no exceptionally bright star inside the slit aperture, which could produce a systematic deviation from the mean radial velocity.

After all, we estimate that our real radial velocity uncertainties are larger by a factor $\sim$ 2-4 than the values given in Table 1.

2.4 Transformation to the lick system

The Lick standard system was initially introduced by Burstein et al. (1984) in order to study element abundances from low-resolution integrated spectra of extragalactic stellar systems. It has recently been updated and refined by several authors (González 1993; Worthey et al. 1994; Worthey & Ottaviani 1997; Trager et al. 1998). The Lick system defines line indices for specific atomic and molecular absorption features, such as Fe, Mg, Ca and CN, CH, TiO, in the optical range from $\sim$ 4100 Å to $\sim$ 6100 Å. The definitions of a line index are given in Appendix A. We implemented the measuring procedure in a software and tested it extensively on original Lick spectra (see Appendix A for details). This code is used for all further measurements.

The Lick system provides two sets of index passband definitions. One set of 21 passband definitions was published in Worthey et al. (1994) to which we will refer as the old set. A new and refined set of passband definitions is given in Trager et al. (1998) which is supplemented by the Balmer index definitions of Worthey & Ottaviani (1997). This new set of 25 indices is used throughout the subsequent analysis. However, we also provide Lick indices based on the old passband definitions (see Appendix D) which enable a consistent comparison with predictions from SSP models which make use of fitting functions based on the old set of passband definitions. Note that indices and model predictions which use two different passband definition sets are prone to systematic offsets. This point will be discussed in the second paper of the series (Maraston et al. 2002).

Before measuring indices, one has carefully to degrade spectra with higher resolution to adapt to the resolution of the Lick system. We strictly followed the approach of Worthey & Ottaviani (1997) and degraded our spectra to the wavelength-dependent Lick resolution ( $\sim$ 11.5 Å at 4000 Å, 8.4 Å at 4900 Å, and 9.8 Å at 6000 Å). The effective resolution (FWHM) of our spectra has been determined from calibration-lamp lines and isolated absorption features in the object spectra. The smoothing of our data is done with a wavelength-dependent Gaussian kernel with the width

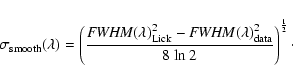$\begin{displaymath}\sigma_{\rm smooth}(\lambda)=\left(\frac{{\it FWHM}(\lambda)_... ...ambda)_{\rm data}^2}{8~ {\rm ln}~2}\right)^{\frac{1}{2}}\cdot \end{displaymath}$

(1)

We tested the shape of absorption lines in our spectra and found that they are very well represented by a Gaussian. Worthey & Ottaviani tested the shape of the absorption lines in the Lick spectra and found also no deviation from a Gaussian. Both results justify the use of a Gaussian smoothing kernel.

The smoothing kernel for the bulge stellar fields is generally narrower since one has to account for the non-negligible velocity dispersion of bulge field stars. A typical line-of-sight velocity dispersion $\sigma_{\rm LOS}\approx 100$ km s^-1 was assumed for the bulge data (e.g. Spaenhauer et al. 1992). We do not correct for the mean velocity dispersion of the globular clusters ( $\sigma_{\rm LOS}\approx 10$ km s^-1 Pryor & Meylan 1993).

Another point of concern for low-S/N spectra ( $S/N\lesssim10$ per resolution element) is the slope of the underlying continuum (see Beasley et al. 2000, for detailed discussion of this effect) which influences the pseudo-continuum estimate for broad features and biases the index measurement. However, since all our spectra are of high S/N( $\gtrsim$ 50 per resolution element), we are not affected by a noisy continuum.

After taking care of the resolution corrections, one has to correct for systematic, higher-order effects. These variations are mainly due to imperfect smoothing and calibration of the spectra. To correct the small deviations 12 index standard stars from the list of Worthey et al. (1994) have been observed throughout the observing run. Figure 2 shows the comparison between the Lick data and our index measurements for all passbands. Least-square fits using a $\kappa$ - $\sigma$ -clipping (dashed lines) are used to parameterize the deviations from the Lick system as a function of wavelength. The functional form of the fit is

$\begin{displaymath}{EW}_{\rm cal} = \alpha + (1+\beta)\cdot{EW}_{\rm raw},\end{displaymath}$

where ${EW}_{\rm cal}$ and ${EW}_{\rm raw}$ are the calibrated and raw indices, respectively. Table 3 summarizes the individual coefficients $\alpha$ and $\beta$ . This correction functions are applied to all further measurements. The corresponding coefficients for index measurements using the old passband definitions are documented in Table D.1.

Table 3: Summary of the coefficients $\alpha$ and $\beta$ for all 1st and 2nd-order index corrections.
index $\alpha$ $\beta$ rms units

CN₁ -0.0017 -0.0167 0.0251 mag

CN₂ -0.0040 -0.0389 0.0248 mag

Ca 4227 -0.2505 -0.0105 0.2582 Å

G4300 0.6695 -0.1184 0.4380 Å

Fe 4384 -0.5773 0.0680 0.2933 Å

Ca 4455 -0.1648 0.0249 0.4323 Å

Fe 4531 -0.3499 0.0223 0.1566 Å

Fe 4668 -0.8643 0.0665 0.5917 Å

H $\beta$ 0.0259 0.0018 0.1276 Å

Fe 5015 1.3494 -0.2799 0.3608 Å

Mg₁ 0.0176 -0.0165 0.0160 mag

Mg₂ 0.0106 0.0444 0.0112 mag

Mgb 0.0398 -0.0392 0.1789 Å

Fe 5270 -0.3608 0.0514 0.1735 Å

Fe 5335 -0.0446 -0.0725 0.3067 Å

Fe 5406 -0.0539 -0.0730 0.2054 Å

Fe 5709 -0.5416 0.3493 0.1204 Å

Fe 5782 -0.0610 -0.0116 0.2853 Å

NaD 0.3620 -0.0733 0.2304 Å

TiO₁ 0.0102 0.2723 0.0133 mag

TiO₂ -0.0219 0.1747 0.0342 mag

H $\delta _{\rm A}$ -0.1525 -0.0465 1.5633 Å

H $\gamma_{\rm A}$ 0.4961 0.0117 0.6288 Å

H $\delta_{\rm F}$ -0.1127 -0.0639 0.4402 Å

H $\gamma _{\rm F}$ -0.0062 -0.0343 0.1480 Å

**Table 3:** Summary of the coefficients $\alpha$ and $\beta$ for all 1st and 2nd-order index corrections.
index	$\alpha$	$\beta$	rms	units
CN₁	-0.0017	-0.0167	0.0251	mag
CN₂	-0.0040	-0.0389	0.0248	mag
Ca 4227	-0.2505	-0.0105	0.2582	Å
G4300	0.6695	-0.1184	0.4380	Å
Fe 4384	-0.5773	0.0680	0.2933	Å
Ca 4455	-0.1648	0.0249	0.4323	Å
Fe 4531	-0.3499	0.0223	0.1566	Å
Fe 4668	-0.8643	0.0665	0.5917	Å
H $\beta$	0.0259	0.0018	0.1276	Å
Fe 5015	1.3494	-0.2799	0.3608	Å
Mg₁	0.0176	-0.0165	0.0160	mag
Mg₂	0.0106	0.0444	0.0112	mag
Mgb	0.0398	-0.0392	0.1789	Å
Fe 5270	-0.3608	0.0514	0.1735	Å
Fe 5335	-0.0446	-0.0725	0.3067	Å
Fe 5406	-0.0539	-0.0730	0.2054	Å
Fe 5709	-0.5416	0.3493	0.1204	Å
Fe 5782	-0.0610	-0.0116	0.2853	Å
NaD	0.3620	-0.0733	0.2304	Å
TiO₁	0.0102	0.2723	0.0133	mag
TiO₂	-0.0219	0.1747	0.0342	mag
H $\delta _{\rm A}$	-0.1525	-0.0465	1.5633	Å
H $\gamma_{\rm A}$	0.4961	0.0117	0.6288	Å
H $\delta_{\rm F}$	-0.1127	-0.0639	0.4402	Å
H $\gamma _{\rm F}$	-0.0062	-0.0343	0.1480	Å

Note, that most passbands require only a small linear offset, but no offset as a function of index strength. While the former is simply due to a small variation in the wavelength calibration, the latter is produced by over/under-smoothing of the spectra. Absorption lines for which the smoothing pushes the wings outside narrowly defined feature passbands are mostly affected by this non-linear effect. However, for passbands of major interest (such as CN, H $\beta$ , Fe 5270, Fe 5335, Mgb, and Mg₂) the Lick indices are satisfactorily reproduced by a simple offset (no tilt) in the index value (see Fig. 2).

$\begin{figure} \par\includegraphics[width=13.5cm,clip]{2781f2.eps} \end{figure}$

Figure 2: Comparison of passband measurements from our spectra and original Lick data for 12 Lick standard stars. The dotted line shows the one-to-one relation, whereas the dashed line is a least-square fit to the filled squares. Data, which have been discarded from the fit because of too large errors or deviations, are shown as open squares. Bold frames indicate some of the widely used Lick indices which are also analysed in this work.

3 Analysis of the spectra

3.1 Estimating the background light

Long-slit spectroscopy of extended objects notoriously suffers from difficulties in estimating the contribution of the sky and background light. Since we observe globular clusters near the Galactic Bulge, their spectra will be contaminated by an unknown fraction of the bulge light, depending on the location on the sky (see Fig. 1). In order to estimate the contribution of the background, two different approaches have been applied. The first approach was to estimate the sky and bulge contribution from separately taken sky and bulge spectra (hereafter "background modeling''). The other technique was to extract the total background spectrum from low-intensity regions at the edges of the spatial axis in the object spectrum itself (henceforth "background extraction''). While the first technique suffers from the unknown change of the background spectrum between the position of the globular clusters and the background fields, the second one suffers from lower S/N. However, tests have shown that the "background extraction'' allows a more reliable estimate of the background spectrum.

We compare both background subtraction techniques in Table B.1. We find that the "background modeling'' systematically overestimates the background light contribution as one goes to larger galactocentric radii. The index differences increase between spectra which have been cleaned using "background modeling'' and "background extraction''. This is basically due to an overestimation of the background light from single background spectra which were taken at intermediate galactocentric radii. We, therefore, drop the "background modeling'' and proceed for all subsequent analyses with the "background extraction'' technique. In summary, the crucial drawback of the "background modeling'' is that it requires a prediction of the bulge light fraction from separate spectra which is strongly model-dependent. The bulge light contains changing scale heights for different stellar populations (see Frogel 1988; Wyse et al. 1997, and references therein). The background light at the cluster position includes an unknown mix of bulge and disk stellar populations (Frogel 1988; Frogel et al. 1990; Feltzing & Gilmore 2000), an unknown contribution from the central bar (Unavane & Gilmore 1998; Unavane et al. 1998), and is subject to differential reddening on typical scales of $\sim$ 90 $^{\prime\prime}$ (Frogel et al. 1999) which complicates the modeling. Clearly, with presently available models (e.g. Kent et al. 1991; Freudenreich 1998) it is impossible to reliably predict a spectrum of the galactic bulge as a function of galactic coordinates. The "background extraction'' technique naturally omits model predictions and allows to obtain the total background spectrum, including sky and bulge light, from the object spectrum itself.

We selected low-luminosity outer sections in the slit's intensity profile (see Fig. 3) to derive the background spectrum for each globular cluster. Only those regions which show flat and locally lowest intensities and are located outside the half-light radius $r_{\rm h}$ (Trager et al. 1995) are selected. We sum the spectra of the background light of all available pointings to create one high-S/Nbackground spectrum for each globular cluster. All globular clusters were corrected using this background spectrum. The background-to-cluster light ratio depends on galactic coordinates, and is $\la$ 0.1 for NGC 6388 and $\sim$ 1 for NGC 6528. In order to lower this ratio, only regions inside $r_{\rm h}$ are used to create the final globular-cluster spectrum. This restriction decreases the background-to-cluster ratio by a factor of $\ga$ 2. In the case of NGC 6218, NGC 6553, and NGC 6626 the half-light diameter $2r_{\rm h}$ is larger or comparable to the spatial dimensions of the slit, so that no distinct background regions can be defined. For these clusters we estimate the background from flat, low-luminosity parts along the spatial axis inside $r_{\rm h}$ but avoid the central regions (see Fig. 3).

3.2 Contamination by bright objects

To check if bright foreground stars inside the slit contaminate the globular cluster light, we plot the intensity profile along the slit's spatial axis. The profiles of each pointing are documented in Fig. 3. Since we use the light only inside one half-light radius (indicated by the shaded region) and therefore maximize the cluster-to-background ratio, the probability for a significant contamination by bright non-member objects is very low. Even very bright foreground stars will contribute only a small fraction to the total light.

$\begin{figure} \par\includegraphics[width=7cm,clip]{2781f3a.eps}\hspace*{0.45cm}... ...eps}\hspace*{0.45cm} \includegraphics[width=7cm,clip]{2781f3f.eps} \end{figure}$

Figure 3: Intensity profiles of each pointing for all sample globular clusters. The fraction of the profile which was used to create the final globular cluster spectrum is shaded. Each cluster has at least three pointings which are shifted by a few slit widths to the north and south. Note that clusters with a sampled luminosity less than $10^4 L_\odot$ and relatively large half-light radii (i.e. see Sect. 3.4 and Table 1) have strongly fluctuating profiles.

$\begin{figure} \par\includegraphics[width=7.3cm,clip]{2781f3g.eps}\hspace*{0.45c... ...}\hspace*{0.45cm} \includegraphics[width=7.3cm,clip]{2781f3l.eps} \end{figure}$

Figure 3: continued.

However, three of our sample globular clusters (NGC 6218, NGC 6553, and NGC 6626) are extended and their half-light diameter are just or not entirely covered by the slit. The low radial velocity resolution of our spectra does not allow to distinguish between globular cluster stars and field stars inside the slit. Galactic stellar-population models (e.g. Robin et al. 1996) predict a maximum cumulative amount of 4 stars with magnitudes down to V=19.5 (all stars with V=18.5-19.5 mag) towards the Galactic center inside the equivalent of three slits. This maximum estimate applies only to the Baade's Window globular clusters NGC 6528 and NGC 6553. All other fields have effectively zero probability to be contaminated by foreground stars. Nonetheless, even in the worst-case scenario, if 4 stars of 19th magnitude would fall inside one slit, their fractional contribution to the total light would be ${\la}1.2\times 10^{-4}$ . For globular clusters at larger galactocentric radii this fraction is even lower. Hence, we do not expect a large contamination by foreground disk stars.

One critical case is the northern pointing of NGC 6637 in which a bright star falls inside the half-light radius (see upper panel of the NGC 6637 profile in Fig. 3). This star contributes $\la$ 10% to the total light of the sampled globular cluster and its radial velocity is indistinguishable from the one of NGC 6637. An inspection of DSS images shows that the NGC 6637 field contains more such bright stars which are concentrated around the globular cluster center and are therefore likely to be cluster members. We therefore assume that the star is a member of NGC 6637 and leave it in the spectrum.

3.3 Comparison with previous measurements

Lick indices are available in the literature for a few globular clusters in our sample, as we intentionally included these clusters for comparison. The samples of Trager et al. (1998) and Covino et al. (1995) and Cohen et al. (1998) have, respectively, three, six, and four clusters in common with our data. Note that the indices of Covino et al. (1995) and Cohen et al. (1998) were measured with the older passband definitions of Burstein et al. (1984) and are subject to potential systematic offsets. Where necessary we also converted the values of Covino et al. to the commonly used Å-scale for atomic indices and kept the magnitude scale for molecular bands. Table A.1 summarizes all measurements, including our data. Figure 4 shows the comparison of some indices between the previously mentioned data sets and ours. The mean offset in the sense $EW_{\rm data}$ - $EW_{\rm lit.}$ and the dispersion are given in Table 4. Most indices agree well with the literature values and have offsets smaller than the dispersion.

Only the Fe 5270 index is $0.75~ \sigma$ higher for our data compared with the literature. This is likely to be due to imperfect smoothing of the spectra in the region of $\sim$ 5300 Å. Our smoothing kernel is adjusted according to the Lick resolution given by the linear relations in Worthey & Ottaviani (1997). This relations are fit to individual line resolution data which show a significant increase in scatter in the spectral range around 5300 Å (see Fig. 7 in Worthey & Ottaviani 1997). Hence even if our smoothing is correctly applied, the initial fitting of the Lick resolution data by Worthey & Ottaviani might introduce biases which cannot be accounted for a posteriori. However, the offset between the literature and our data is reduced by the use of the synthetic $\langle$ Fe $\rangle$ index which is a combination of the Fe 5270 and Fe 5335 index. The $\langle$ Fe $\rangle$ index partly cancels out the individual offsets of the former two indices.

Table 4: Offsets and dispersion of the residuals between our data and the literature. Dispersions are 1 $\sigma$ scatter of the residuals.
index offset dispersion units

G4300 0.45 0.70 Å

H $\beta$ 0.27 0.57 Å

Mg₂ 0.009 0.014 mag

Mgb -0.01 0.27 Å

Fe 5270 -0.33 0.44 Å

Fe 5335 0.12 0.27 Å

**Table 4:** Offsets and dispersion of the residuals between our data and the literature. Dispersions are 1 $\sigma$ scatter of the residuals.
index	offset	dispersion	units
G4300	0.45	0.70	Å
H $\beta$	0.27	0.57	Å
Mg₂	0.009	0.014	mag
Mgb	-0.01	0.27	Å
Fe 5270	-0.33	0.44	Å
Fe 5335	0.12	0.27	Å

$\begin{figure} \includegraphics[width=13.2cm,clip]{2781f4.eps} \end{figure}$

Figure 4: Comparison of index measurements of Trager et al. (1998), marked by squares, Cohen et al. (1998), marked by circles (without errors for the Cohen et al. data), and Covino et al. (1995), indicated by triangles, with our data. Solid lines mark the one-to-one relation and dashed lines the mean offsets.

3.4 Estimating the sampled luminosity

The spectrograph slit samples only a fraction of the total light of a globular cluster's stellar population. The less light is sampled the higher the chance that a spectrum is dominated by a few bright stars. In general, globular cluster spectra of less than $10^4~L_\odot$ are prone to be dominated by statistical fluctuations in the number of high-luminosity stars (such as RGB and AGB stars, etc.). For a representative spectrum it is essential to adequately map all evolutionary states in a stellar population, such that no large statistical fluctuations for the short-living phases are expected. We therefore estimate the total sampled luminosity of the underlying stellar population 1) from spectrophotometry of the flux-calibrated spectra and 2) from the integration of globular cluster surface brightness profiles.

As a basic condition of the first method we confirm that all three nights have had photometric conditions using the ESO database for atmospheric conditions at La Silla. We use the flux at 5500 Å in the co-added and background-subtracted spectra and convert it to an apparent magnitude with the relation

$\displaystyle m_V = -2.5\cdot\log(F_\lambda) - (19.79\pm0.24)$

(2)

where $F_\lambda$ is the flux in erg cm^-2 s^-1 Å^-1. The zero point was determined from five flux-standard spectra, which have been observed in every night. Its uncertainty is the 1 $\sigma$ standard deviation of all measurements. After correcting for the distance, the absolute magnitudes were de-reddened using the values given in Harris (1996). The reddening values are given in Table 1 along with the distance modulus (Harris 1996). Using the absolute magnitude of the combined globular cluster spectrum, we calculate the total sampled luminosity

$\displaystyle L_{\rm T}=BC_V\cdot10^{-0.4\cdot\left(m_V-(m-M)_V-M_\odot-3.1\cdot{E}_{(B-V)}\right)}$

(3)

where $M_\odot=4.82$ mag is the absolute solar magnitude in the V band (Hayes 1985; Neckel 1986a,1986b). With the bolometric correction BC_V (Renzini 1998; Maraston 1998) we obtain the total bolometric luminosity $L_{\rm T}$ . The total globular cluster luminosity is compared to the sampled flux and tabulated in Table 5 as $L_{\rm slit}$ .

**Table 5:** Sampled and total luminosities of observed globular clusters and bulge. All values have been determined from the co-added spectra of all available pointings. For the co-added bulge spectrum we adopted a mean metallicity of $\rm [Fe/H]\approx~ -0.33$ dex (Zoccali et al. 2002).
cluster	$F_\lambda$ (@5500 Å)^a	M_V^b	M_V^c	$BC_{\rm V}^{d}$	$L_{{\rm prof}}^{e}$	$L_{{\rm slit}}^{f}$	$L_{{\rm GC}}^{g}$	$\frac{L_{{\rm slit}}}{L_{{\rm GC}}}$	$N_{\rm RGB}^{h}$	$N_{\rm uRGB}^{i}$

NGC 5927	$(3.6\pm0.2)\times10^{-13}$	-5.88	-7.80	1.57	$1.7\times10^4$	$(3.0\pm0.8)\times10^4$	$1.8\times10^5$	0.171	359	9
NGC 6218	$(2.0\pm0.1)\times10^{-13}$	-2.65	-7.32	1.29	$4.0\times10^3$	$(1.3\pm0.3)\times10^3$	$9.3\times10^4$	0.014	15	0
NGC 6284	$(3.7\pm0.1)\times10^{-13}$	-6.27	-7.87	1.32	$1.9\times10^4$	$(3.6\pm0.9)\times10^4$	$1.6\times10^5$	0.230	435	11
NGC 6356	$(6.4\pm0.1)\times10^{-13}$	-6.94	-8.52	1.51	$4.8\times10^4$	$(7.6\pm1.8)\times10^4$	$3.3\times10^5$	0.233	913	23
NGC 6388	$(2.8\pm0.1)\times10^{-12}$	-8.68	-9.82	1.47	$1.6\times10^5$	$(3.7\pm1.0)\times10^5$	$1.1\times10^6$	0.351	4430	111
NGC 6441	$(2.0\pm0.1)\times10^{-12}$	-8.52	-9.47	1.49	$1.3\times10^5$	$(3.2\pm0.9)\times10^5$	$7.8\times10^5$	0.417	3894	97
NGC 6528	$(4.9\pm0.2)\times10^{-13}$	-7.28	-6.93	1.66	$2.3\times10^4$	$(1.1\pm0.3)\times10^5$	$8.3\times10^4$	1.376 $^{{\rm j}}$	1376	34
NGC 6553	$(2.0\pm0.1)\times10^{-13}$	-6.41	-7.99	1.59	$1.5\times10^4$	$(4.9\pm1.4)\times10^4$	$2.1\times10^5$	0.234	593	15
NGC 6624	$(8.0\pm0.7)\times10^{-13}$	-5.78	-7.50	1.54	$1.8\times10^4$	$(2.7\pm0.8)\times10^4$	$1.3\times10^5$	0.205	322	8
NGC 6626	$(5.6\pm0.1)\times10^{-13}$	-5.61	-8.33	1.30	$1.4\times10^4$	$(1.9\pm0.5)\times10^4$	$2.4\times10^5$	0.082	231	6
NGC 6637	$(8.0\pm1.4)\times10^{-14}$	-2.70	-7.52	1.43	$1.5\times10^4$	$(1.5\pm0.6)\times10^3$	$1.2\times10^5$	0.012	17	0
NGC 6981	$(1.2\pm0.1)\times10^{-13}$	-3.95	-7.04	1.31	$7.7\times10^3$	$(4.2\pm1.3)\times10^3$	$7.3\times10^4$	0.058	50	1
Bulge	$(4.0\pm0.3)\times10^{-13}$	-5.14	...	1.59	...	$(1.5\pm0.7)\times10^4$	...	...	180	5

^a: Sampled flux at 5500 Å in erg cm^-2 s^-1 Å^-1.
^b: Absolute magnitude of the sampled light.
^c: Absolute globular cluster magnitude (Harris 1996).
^d: V-band bolometric correction for a 12 Gyr old stellar population calculated for the according cluster metallicity (see Table 1). The values were taken from Maraston (1998,2002).
^e: Sampled bolometric luminosity $L_{\rm T}$ in $L_\odot$ from the integration of King surface brightness profiles of Trager et al. (1995).
^f: Sampled bolometric luminosity $L_{\rm T}$ in $L_\odot$ calculated from the total light sampled by all slit pointings.
^g: Globular cluster's total bolometric luminosity $L_{\rm T}$ in $L_\odot$ .
^h: Expected number of RGB stars contributing to the sampled luminosity.
ⁱ: Expected number of upper RGB stars ( $\Delta M_{\rm Bol}\leq 2.5$ mag down from the tip of the RGB) contributing to the sampled luminosity.
^j: See Sect. 3.4.

For the integration of the surface brightness profiles we use the data from Trager et al. (1995) who provide the parameters of single-mass, non-rotating, isotropic King profiles (King 1966) for all sample globular clusters. The integrated total V-band luminosities have been transformed to $L_{\rm T}$ and are included in Table 5 as $L_{\rm prof}$ . Note that for most globular clusters the results from both techniques agree well. However, for some globular clusters the integration of the surface brightness profile gives systematically larger values. This is due to the fact that the profiles were calculated from the flux of all stars in a given radial interval whereas the slits sample a small fraction of the flux at a given radius. Hence, the likelihood to sample bright stars which dominate the surface brightness profile falls rapidly with radius. Since bright stars are point sources the slit will most likely sample a smaller total flux than predicted by the surface brightness profile. This effect is most prominent for globular clusters with relatively large half-light radii and waggly intensity profiles (cf. Fig. 3).

Among the values reported in Table 5, the case of NGC 6528 is somewhat awkward, as the estimated luminosity sampled by the slit is apparently higher than the total luminosity of the cluster, which obviously cannot be. This cluster projects on a very dense bulge field, and therefore the inconsistency probably arises from either an underestimate of the field contribution that we have subtracted from the cluster+field co-added spectrum, or to an underestimate of the total luminosity of the cluster as reported in Harris (1996), or from a combination of these two effects.

From the sampled flux $L_{\rm slit}$ we estimate the number of red giant stars contributing to the total light. Renzini (1998) gives the expected number of stars for each stellar evolutionary phase of a $\sim$ 15 Gyr old, solar-metallicity simple stellar population. In general, in this stellar population the brightest stars which contribute a major fraction of the flux to the integrated light are found on the red giant branch (RGB) which contributes $\sim$ 40% (Renzini & Fusi Pecci 1988) to the total light. The last two columns of Table 5 give the expected number of RGB and upper RGB stars in the sampled light. Upper RGB stars are defined here as those within 2.5 bolometric magnitudes from the RGB tip. The RGB and upper RGB lifetimes are ${\sim}6\times 10^8$ and ${\sim}1.5\times 10^7$ years, respectively.

Due to the small expected number of RGB and upper RGB stars contributing to the spectra of NGC 6218 and NGC 6637, both spectra are prone to be dominated by a few bright stars. In fact, for both clusters the intensity profiles (see Fig. 3) show single bright stars. However, the contribution of the brightest single object is $\la$ 10% (see Sect. 3.2) for all spectra. All other spectra contain enough RGB stars to be unaffected by statistical fluctuations in the number of bright stars.

The sampled luminosity of the bulge fields is more difficult to estimate. Uncertain sky subtraction (see problems with "background modeling'' in Sect. 3.1), and patchy extinction in combination with the bulge's spatial extension along the line of sight make the estimate of the sampled luminosity quite uncertain. Here we simply give upper and lower limits including all available uncertainties. The average extinction in Baade's Window is $\langle A_V\rangle\approx1.7$ mag and varies between 1.3 and 2.8 mag (Stanek 1996). The more recent reddening maps of Schlegel et al. (1998) confirm the previous measurements and give for our three Bulge fields the extinction in the range $1.6\la A_{V}\la 2.1$ mag. We adopt a distance of 8-9 kpc to the Galactic center and use the faintest and brightest sky spectrum to estimate the flux at 5500 Å. The total sampled luminosity $L_{\rm T}$ of the final co-added Bulge spectrum is $(1.3{-}2.6)\times 10^4~ L_\odot$ . Our value is in good agreement with the sampled luminosity derived from surface brightness estimates in Baade's Window and several fields at higher galactic latitudes by Terndrup (1988). According to his V-band surface brightness estimates for Baade's Window and a field at the galactic coordinates $l=0.1^{\circ}$ and $b=-6^{\circ}$ , the sampled luminosity in an area equivalent to all our bulge-field pointings in one of the two fields is $(2.6\pm0.5)\times 10^4~ L_\odot$ and $(1.2\pm0.3)\times10^4~L_\odot$ , respectively.

4 Index ratios in globular clusters and bulge fields

Figure 5 shows two representative spectra of a metal-poor (NGC 6626) and a metal-rich (NGC 6528) globular cluster, together with the co-added spectrum from the 15 bulge pointings.

$\begin{figure} \par\includegraphics[width=13.7cm,clip]{2781f5.eps} \end{figure}$

Figure 5: Representative spectra of two globular clusters, i.e. NGC 6626 and NGC 6528, and the Galactic bulge. The two clusters represent the limits of the metallicity range which is covered by our sample. NGC 6626 has a mean metallicity $\rm [Fe/H]=-1.45$ dex. NGC 6528, on the other hand, has a mean metallicity $\rm [Fe/H]=-0.17$ dex (Harris 1996). Note the similarity between the bulge and the NGC 6528 spectrum. Important Lick-index passbands are indicated at the bottom of the panel.

In the following we focus on the comparison of index ratios between globular clusters and the field stellar population in the Galactic bulge. We include the data of Trager et al. (1998) who measured Lick indices for metal-poor globular clusters and use our index measurements (due to higher S/N) whenever a globular cluster is a member of both data sets.

All Lick indices are measured on the cleaned and co-added globular-cluster and bulge spectra. Statistical uncertainties are determined in bootstrap tests (see Appendix A.2 for details). We additionally determine the statistical slit-to-slit variations between the different pointings for each globular cluster and estimate the maximum systematic error due to the uncertainty in radial velocity. All line indices and their statistical and systematic uncertainties are documented in Table C.1.

It is worth to mention that the slit-to-slit fluctuations of index values, which are calculated from different pointings (3 and 5 for globular clusters and 15 for the bulge), are generally larger than the Poisson noise of the co-added spectra. Such variations are expected from Poisson fluctuations in the number of bright stars inside the slit and the sampled luminosities of the single spectra correlate well with the slit-to-slit index variations for each globular cluster. More pointings are required to solidify this correlation and to search for other effects such as radial index changes.

4.1 The $\alpha$ -element sensitive indices vs. $\mathsfsl{\langle}$ Fe $\mathsfsl{\rangle}$

$\begin{figure} \includegraphics[width=8.4cm,clip]{2781f6a.eps}\hspace*{0.5cm}... ...eps}\hspace*{0.5cm} \includegraphics[width=8.4cm,clip]{2781f6d.eps}\end{figure}$

Figure 6: Lick-index ratios for Mg₂, Mgb, NaD, H $\beta$ versus the mean iron index $\langle$ Fe $\rangle=({\rm Fe~5270} + {\rm Fe~5335})/2$ . Filled dots show the index measurements of our sample globular clusters, whilst open circles show the data of Trager et al. (1998). A solid star indicates the index values derived from the co-added spectrum of the Galactic bulge. Solid error bars show bootstrap errors which represent the total uncertainty due to the intrinsic noise of the co-added spectra. Statistical slit-to-slit fluctuations between different pointings are shown as dotted error bars. Systematic radial velocity errors are not plotted, but given in Table C.1. For clarity reasons no error bars are plotted for the Trager et al. sample which are generally an order of magnitude larger than the intrinsic noise of our spectra. The mean errors of the Trager et al. data are 0.3 Å for the $\langle$ Fe $\rangle$ index, 0.01 mag for Mg₂, and 0.3 Å for Mgb, NaD, and H $\beta$ .

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{2781f6e.eps}\hspace*{0.5cm... ...s}\hspace*{0.5cm} \includegraphics[width=8.4cm,clip]{2781f6h.eps} \end{figure}$

Figure 6: continued. G4300, CN₁, TiO₂, and Ca 4227 versus $\langle$ Fe $\rangle$ . The mean errors of the Trager et al. data are 0.3 Å for the $\langle$ Fe $\rangle$ index, and 0.4 Å, 0.03 mag, 0.01 mag, and 0.4 Å for the G4300, CN₁, TiO₂, and Ca 4227 index, respectively.

$\alpha$ -particle capture elements with even atomic numbers (C, O, Mg, Si, Ca, etc.) are predominantly produced in type II supernovae (Tsujimoto et al. 1995; Woosley & Weaver 1995; Thomas et al. 1998). The progenitors of SNe II are massive stars, which explode and pollute the interstellar medium after their short lifetime of some 10⁷ years. The ejecta of SNe II have a mean [ $\alpha$ /Fe] $~~\sim 0.4$ dex. On the other hand, type Ia supernovae eject mainly iron-peak elements ([ $\alpha$ /Fe] $~~\sim -0.3$ dex) $\sim$ 1 Gyr after the formation of their progenitor stars. Stellar populations which have been created on short timescales are likely to show [ $\alpha$ /Fe] enhancement. The [ $\alpha$ /Fe] ratio is therefore potentially a strong discriminator of star-formation histories. Alternative explanations, however, include a changing IMF slope and/or a changing binary fraction.

Such enhancements have already been suspected and observed in the stellar populations in giant elliptical galaxies (Worthey et al. 1992), the Galactic bulge (McWilliam & Rich 1994), and for disk and halo stars in the Milky Way (Edvardsson et al. 1993; Fuhrmann 1998). A detailed discussion of the [ $\alpha$ /Fe] ratio in our sample globular clusters and their assistance to parameterize simple stellar population models for varying [ $\alpha$ /Fe] ratios will be presented in the second paper of this series (Maraston et al. 2002).

To search for any trends in the index( $\alpha$ )/index(Fe) ratio in the globular cluster population and the bulge we plot supposedly $\alpha$ -element sensitive indices against the mean iron index $\langle$ Fe $\rangle$ . Figure 6 shows some representative index measurements for globular clusters and bulge fields. Generally, all the correlations between $\alpha$ -sensitive indices and the mean iron index are relatively tight. For our sample globular clusters a Spearman rank test yields values between 0.87 and 0.97 (1 indicates perfect correlation, -1 anti-correlation) for the indices CN₁, TiO₂, Ca 4227, Mgb, Mg₂. The CN₁ and TiO₂indices show the tightest correlation with $\langle$ Fe $\rangle$ , followed by Mg₂ and Ca 4227. All correlations are linear (no higher-order terms are necessary) and hold to very high metallicities of the order of the mean bulge metallicity (filled star in Fig. 6). The three most metal-rich globular clusters in our sample, i.e. NGC 5927, NGC 6528, and NGC 6553, have roughly the same mean iron index as the stellar populations in the Galactic bulge indicating similar [Fe/H]. This was also found in recent photometric CMD studies of the two latter globular clusters and the bulge (Ortolani et al. 1995b; Zoccali et al. 2002). Ranking by the $\langle$ Fe $\rangle$ and Mg indices, which are among the best metallicity indicators in the Lick sample of indices (see Sect. 5), the most metal-rich globular cluster in our sample is NGC 6553, followed by NGC 6528 and NGC 5927.

The comparison of some $\alpha$ -sensitive indices of globular clusters and the bulge requires some further words. The Ca 4227, Mgb, and Mg₂index of the bulge light is in good agreement with the sequence formed by globular clusters. All deviations from this sequence are of the order of ${\la}1\sigma$ according to the slit-to-slit variations. One exception is the CN index which is significantly higher in metal-rich globular clusters than in the bulge. We discuss this important point in Sect. 4.2. In general, our data show that the ratio of $\alpha$ -sensitive to iron-sensitive indices is comparable in metal-rich globular clusters and in the stellar population of the Galactic bulge.

Likely super-solar [ $\alpha$ /Fe] ratios in globular clusters and the bulge were shown in numerous high-resolution spectroscopy studies. From a study of 11 giants in Baade's window McWilliam & Rich (1994) report an average [Mg/Fe] $~~\approx 0.3$ dex, while Barbuy et al. (1999) and Carretta et al. (2001) find similar [Mg/Fe] ratios in two red giants in NGC 6553 and in four red horizontal branch stars in NGC 6528. Similarly, McWilliam & Rich find [Ca/Fe] $~~\approx0.2$ dex, which is reflected by the former observations in globular clusters. Although the studied number of stars is still very low, the first high-resolution spectroscopy results point to a similar super-solar $\alpha$ -element abundance in both Milky Way globular clusters and the bulge which is supported by our data.

4.2 CN vs. $\mathsfsl{\langle}$ Fe $\mathsfsl{\rangle}$

The CN index measures the strength of the CN absorption band at 4150 Å. The Lick system defines two CN indices, CN₁ and CN₂ which differ slightly in their continuum passband definitions. The measurements for both indices give very similar results, but we prefer the CN₁ index due to its smaller calibration biases (see Fig. 2) and refer in the following to CN₁ as the CN index.

Like for most other indices, the CN index of globular clusters correlates very tightly with the $\langle$ Fe $\rangle$ index, following a linear relation (see Fig. 6). A Spearman rank test yields 0.97 as a correlation coefficient. The apparent gap at $\rm CN\sim0$ mag is a result of the bimodal distribution of metallicity in our cluster sample, and similar gaps are recognizable in all other index vs. $\langle$ Fe $\rangle$ diagrams.

Quite striking is the comparison of the bulge value of the CN index with that of globular clusters at the same value of the $\langle$ Fe $\rangle$ index: the CN index of the bulge is significantly offset to a lower value by $\sim$ 0.05 mag, corresponding to at least a 2 $\sigma$ effect. This is also evident from Fig. 5, showing that the CN feature is indeed much stronger in the cluster NGC 6528 than in the bulge spectrum. We also note that the CN index of NGC 6528 and NGC 6553 is as strong as in the most metal-rich clusters in M 31 studied by Burstein et al. (1984).

It is well known that globular cluster stars often exhibit so-called CN anomalies, with stars in a cluster belonging either to a CN-strong or a CN-weak group (see Kraft 1994 for an extended review). Among the various possibilities to account for these anomalies, accretion of AGB ejecta during the early phases of the cluster evolution appears now the most likely explanation (Kraft 1994; Ventura et al. 2001), as originally proposed by D'Antona et al. (1983) and Renzini (1983). In this scenario, some ${\sim} 30\times 10^6$ years after cluster formation (corresponding to the lifetime of ${\sim} 8~ M_\odot$ stars) the last type II supernovae explode and AGB stars begin to appear in the cluster. Then the low-velocity AGB wind and super-wind materials may accumulate inside the potential well of the cluster, and are highly enriched in carbon and/or nitrogen from the combined effect of the third dredge-up and envelope-burning processes (Renzini & Voli 1981). Conditions are then established for the low-mass stars (now still surviving in globular clusters) having a chance to accrete carbon and/or nitrogen-enriched material, thus preparing the conditions for the CN anomalies we observe in today clusters. One of the arguments in favor of the accretion scenario is that field stars do not share the CN anomalies of their cluster counterparts (Kraft et al. 1982). Indeed, contrary to the case of clusters, in the field no localized, high-density accumulation of AGB ejecta could take place, and low-mass stars would have not much chance to accrete AGB processed materials. In the case of the bulge, its much higher velocity dispersion ( $\sim$ 100 km s^-1) compared to that of clusters (few km s^-1) would make accretion even less likely. In conclusion, we regard the lower CN index of the bulge relative to metal-rich globular clusters as consistent with - and actually supporting - the accretion scenario already widely entertained for the origin of CN anomalies in globular-cluster stars.

4.3 H $\beta$ vs. $\mathsfsl{\langle}$ Fe $\mathsfsl{\rangle}$

Figure 6 shows a plot of H $\beta$ vs. $\langle$ Fe $\rangle$ . The Spearman rank coefficient for the globular cluster sequence is -0.52 indicating a mild anti-correlation. At high $\langle$ Fe $\rangle$ , the H $\beta$ index of globular clusters is slightly stronger than that of the bulge field. However, the values are consistent with each other within ${\sim}1\sigma$ , with the large slit-to-slit variations exhibited by the bulge spectra being a result of the lower luminosity sampling due to the lower surface brightness in Baade's Window compared to globular clusters.

The two clusters NGC 6441 and NGC 6388 show somewhat stronger H $\beta$ compared to clusters with similar $\langle$ Fe $\rangle$ index. This offset is probably caused by the conspicuous blue extension of the HB of these two clusters, a so far unique manifestation of the "second parameter'' effect among the metal-rich population of bulge globular clusters (Rich et al. 1997). Contrary to NGC 6441 and NGC 6388, the other globular clusters with comparable $\langle$ Fe $\rangle$ indices (i.e. NGC 5927, NGC 6356, NGC 6624, and NGC 6637) have without exception purely red horizontal branches ( $\rm HBR=-1.0$ ).

Also the two most metal-rich clusters in our sample, NGC 6553 and NGC 6528, appear to have a somewhat stronger H $\beta$ compared to a linear extrapolation of the trend from lower values of the $\langle$ Fe $\rangle$ index. In this case, however, the relatively strong H $\beta$ cannot be ascribed to the HB morphology, since the HB of these two clusters is purely red (Ortolani et al. 1995a; Zoccali et al. 2001). In principle, a younger age would produce a higher H $\beta$ index, but optical and near-infrared HST color-magnitude diagrams of these two clusters indicate they are virtually coeval with halo clusters (Ortolani et al. 1995a,2001; Zoccali et al. 2001; Feltzing et al. 2002). So, we are left without an obvious interpretation of the relatively strong H $\beta$ feature in the spectra of these clusters. Perhaps the effect is just due to insecure sampling, i.e., to statistical fluctuations in the stars sampled by the slit in either the cluster or in the adjacent bulge field used in the background subtraction. Another reason for the offset might be the increasing dominance of metallic lines inside the H $\beta$ feature passband which could artificially increase the index value.

$\begin{figure} \includegraphics[width=12.8cm,clip]{2781f7.eps} \end{figure}$

Figure 7: Line indices as a function of mean globular cluster metallicity. Our sample globular clusters are shown as filled circles while the open circles denote the globular cluster data of Trager et al. (1998).

4.4 Other Indices vs. $\mathsfsl{\langle}$ Fe $\mathsfsl{\rangle}$

NaD - The correlation coefficient for this index pair is 0.94. Globular clusters and bulge compare well within the errors. Both stellar populations follow, within their uncertainties, the same trend. A clear exception from this correlation is NGC 6553, which shows a significantly lower NaD index for its relatively high $\langle$ Fe $\rangle$ than the sequence of all other globular clusters. The reason for this offset is unclear.

G4300 - The G4300 index predominantly traces the carbon abundance in the G band. For giants, its sensitivity to oxygen is about 1/3 of that to carbon (Tripicco & Bell 1995). The metal-rich globular clusters fall in the same region as the bulge data. In combination with the CN index which mainly traces the CN molecule abundance, this implies that the offset between bulge and globular clusters in the CN vs. $\langle$ Fe $\rangle$ plot is most likely due to an offset in the nitrogen abundance between bulge and clusters.

TiO - The TiO abundance is measured by the TiO₁ and TiO₂indices. Both indices do not differ in their correlation with the mean iron index (Spearman rank coefficient 0.96), but we use TiO₂because of its better calibration. In Fig. 6 we plot TiO₂ vs. $\langle$ Fe $\rangle$ which shows the strongest indices for NGC 6553 and NGC 6528, followed by NGC 5927 and the bulge.

The absorption in the TiO band sensitively depends on $T_{\rm eff}$ which is very low for very metal-rich RGB stars. While the strongest TiO bands are observed in metal-rich M-type giants almost no absorption is seen in metal-rich K-type RGB stars. As $T_{\rm eff}$ decreases towards the RGB tip, a large increase in the TiO-band absorption occurs which drives the observed bending of the upper RGB in color-magnitude diagrams, in particular those which use V-band magnitudes (Carretta & Bragaglia 1998; Saviane et al. 2000). In fact, the most metal-rich globular clusters in the Milky Way, e.g. NGC 6553 and NGC 6528, show the strongest bending of the RGBs (e.g. Ortolani et al. 1991; Cohen & Sleeper 1995). Figure 6 shows that the slit-to-slit scatter is extremely large for the metal-rich data. This is likely reflecting the sparsely populated upper RGB. In other words, for metal-rich stellar populations the TiO index is prone to be dominated by single bright stars which increase the slit-to-slit scatter due to statistically less significant sampling (see also the high slit-to-slit scatter of NGC 6218 due to its small luminosity sampling). Another Ti-sensitive index in the Lick system is Fe 4531 (Gorgas et al. 1993). It shows similar behaviour as a function of $\langle$ Fe $\rangle$ .

Table 6: Coefficients of the index vs. [Fe/H] relations. The rms ( $\sqrt {\chi ^2 /n}$ ) is given in the units of the parameterization (in dex in equation 4 and in Å or mag in Eq. (5)).
index a b c rms d e f rms

Mg₂ $-2.46\pm0.10$ $16.24\pm1.81$ $-29.88\pm6.52$ 0.151 $0.29\pm0.01$ $0.22\pm0.02$ $0.05\pm0.01$ 0.016

Mgb $-2.53\pm0.14$ $1.11\pm0.16$ $-0.14\pm0.04$ 0.182 $4.46\pm0.19$ $3.51\pm0.35$ $0.79\pm0.14$ 0.254

$\langle$ Fe $\rangle$ $-2.83\pm0.21$ $1.91\pm0.36$ $-0.35\pm0.13$ 0.199 $2.68\pm0.12$ $1.85\pm0.23$ $0.39\pm0.09$ 0.167

[MgFe] $-2.76\pm0.14$ $1.59\pm0.20$ $-0.26\pm0.06$ 0.150 $3.45\pm0.13$ $2.55\pm0.24$ $0.55\pm0.10$ 0.173

H $\beta$ $-1.99\pm2.26$ $2.09\pm2.24$ $-0.78\pm0.54$ 0.384 $1.55\pm0.20$ $-0.33\pm0.37$ $0.08\pm0.15$ 0.271

CN₁ $-0.83\pm0.11$ $6.84\pm0.86$ $-17.12\pm13.47$ 0.314 $0.16\pm0.02$ $0.26\pm0.04$ $0.06\pm0.02$ 0.032

**Table 6:** Coefficients of the index vs. [Fe/H] relations. The rms ( $\sqrt {\chi ^2 /n}$ ) is given in the units of the parameterization (in dex in equation 4 and in Å or mag in Eq. (5)).
index	a	b	c	rms	d	e	f	rms
Mg₂	$-2.46\pm0.10$	$16.24\pm1.81$	$-29.88\pm6.52$	0.151	$0.29\pm0.01$	$0.22\pm0.02$	$0.05\pm0.01$	0.016
Mgb	$-2.53\pm0.14$	$1.11\pm0.16$	$-0.14\pm0.04$	0.182	$4.46\pm0.19$	$3.51\pm0.35$	$0.79\pm0.14$	0.254
$\langle$ Fe $\rangle$	$-2.83\pm0.21$	$1.91\pm0.36$	$-0.35\pm0.13$	0.199	$2.68\pm0.12$	$1.85\pm0.23$	$0.39\pm0.09$	0.167
[MgFe]	$-2.76\pm0.14$	$1.59\pm0.20$	$-0.26\pm0.06$	0.150	$3.45\pm0.13$	$2.55\pm0.24$	$0.55\pm0.10$	0.173
H $\beta$	$-1.99\pm2.26$	$2.09\pm2.24$	$-0.78\pm0.54$	0.384	$1.55\pm0.20$	$-0.33\pm0.37$	$0.08\pm0.15$	0.271
CN₁	$-0.83\pm0.11$	$6.84\pm0.86$	$-17.12\pm13.47$	0.314	$0.16\pm0.02$	$0.26\pm0.04$	$0.06\pm0.02$	0.032

5 Index-metallicity relations

We use the mean [Fe/H] values from the 1999 update of the McMaster catalog (Harris 1996) to create parabolic relations between line indices and the globular cluster metallicity as expressed by [Fe/H], based on the Zinn-West scale (Zinn & West 1984). Together with the globular cluster data of Trager et al. (1998) the sample comprises 21 Galactic globular cluster with metallicities $-2.29\leq$ [Fe/H] $\leq-0.17$ . Figure 7 shows six indices as a function of [Fe/H] most of which show tight correlations. Least-square fitting of second-order polynomials

$\displaystyle {\rm [Fe/H]}$	=	$\displaystyle a + b\cdot (EW) + c\cdot(EW)^2$	(4)
EW	=	$\displaystyle d + e\cdot {\rm [Fe/H]} + f\cdot{\rm [Fe/H]}^2$	(5)

where EW is the index equivalent width in Lick units, allows a simple parameterization of these sequences as index vs. [Fe/H] and vice versa. The obtained coefficients are summarized in Table 6. Higher-order terms improve the fits only marginally and are therefore unnecessary.

These empirical relations represent metallicity calibrations of Lick indices with the widest range in [Fe/H] ever obtained. Note that the best metallicity indicators in Table 6 are the [MgFe] and Mg₂ indices both with a rms of 0.15 dex. Leaving out globular clusters with poor luminosity sampling and relatively uncertain background subtraction (i.e. NGC 6218, NGC 6553, NGC 6626, and NGC 6637) changes the coefficients only little within their error limits. In particular, the high-metallicity part of all relations is not driven by the metal-rich globular cluster NGC 6553.

We point out that all relations could be equally well fit by first-order polynomials if the metal-rich clusters are excluded. Consequently, such linear relations would overestimate the metallicity for a given index value at high metallicities (except for H $\beta$ which would underestimate [Fe/H]; however, H $\beta$ is anyway not a good metallicity indicator). This clearly emphasizes the caution one has to exercise when deriving mean metallicities from SSP models which have been extrapolated to higher metallicities. The current sample enables a natural extension of the metallicity range for which Lick indices can now be calibrated. In the second paper of the series (Maraston et al. 2002) we compare the data with the predictions of SSP models.

We also point out that the fitting of the CN index improves when $\rm CN>0$ and $\rm CN<0$ data are fit separately by first-order polynomials. The lines are indicated in Fig. 7. Their functional forms are

$\begin{eqnarray*}{\rm CN} =& (0.14\pm0.03)+(0.17\pm0.06)\cdot {\rm [Fe/H]}{:} ~{... ...=& (-0.04\pm0.02)+(0.03\pm0.01)\cdot {\rm [Fe/H]}{:} ~{\rm CN}<0 \end{eqnarray*}$

with reduced $\chi^2$ of 0.025 and 0.023. The inverse relations are

$\begin{eqnarray*}{\rm [Fe/H]} =& (-0.69\pm0.09)+(3.54\pm1.18)\cdot EW{:} ~{\rm C... ... [Fe/H]} =& (-0.86\pm0.32)+(8.10\pm3.86)\cdot EW{:} ~{\rm CN}<0 \end{eqnarray*}$

with a rms of 0.115 and 0.380. The change in the slope occurs at $\rm [Fe/H]\sim-1.0$ dex and is significant in both parameterizations. The metallicity sensitivity in the metal-poor part is around six times smaller than in the metal-rich part. Only the inclusion of metal-rich bulge globular clusters allows the sampling of the transition region between the shallow and the steep sequence of the CN vs. [Fe/H] relation.

6 Galactocentric index variations

$\begin{figure} \includegraphics[width=13.1cm,clip]{2781f8.eps} \end{figure}$

Figure 8: Various line indices as a function of galactocentric radius $R_{\rm GC}$ . Filled dots show our sample globular clusters. Their error bars are split into the Poisson error (solid error bars which are very small) and slit-to-slit variations (dashed error bars) Open circles mark the globular clusters from Trager et al. (1998).

In Fig. 8 we plot some Lick indices as a function of galactocentric radius $R_{\rm GC}$ . To increase the range in radius, we again merge our sample with the data for metal-poor halo globular cluster of Trager et al. (1998). The galactocentric radius was taken from the 1999 update of the McMaster catalog of Milky Way globular clusters (Harris 1996). Our compilation includes now both bulge and halo globular clusters and spans a range $\sim$ 1-40 kpc in galactocentric distance.

All metal indices show a gradually declining index strength as a function of $R_{\rm GC}$ . The inner globular clusters show a strong decrease in each index out to $\sim$ 10 kpc. The sequence continues at apparently constant low values out to large radii. Furthermore, some indices (CN, Mgb, and $\langle$ Fe $\rangle$ ) show a dichotomy between the bulge and the halo globular cluster system. While the Mgb and $\langle$ Fe $\rangle$ indices clearly reflect the bimodality in the metallicity distribution of Milky Way globular clusters, the striking bimodality in the CN index is more difficult to understand. In the context of Sect. 4.2 this may well be explained by evolutionary differences between metal-rich bulge and metal-poor halo globular clusters.

The behavior of H $\beta$ differs from that of the other indices. There is no clear sequence of a decreasing index as a function of $R_{\rm GC}$ , as for the metal-sensitive indices. Instead we measure a mean H $\beta$ index with $2.1\pm0.5$ Å. The strength of the Balmer series is a function of $T_{\rm eff}$ . In old stellar populations, relatively hot stars, which contribute significantly to the Balmer-line strength of the integrated light, are found at the main sequence turn-off and on the horizontal branch. The temperature of the turn-off is a function of age and metallicity while the temperature of the horizontal branch is primarily a function of metallicity and, with exceptions, of the so-called "second parameter''.

In the following we focus on the correlation of the horizontal branch morphology on the H $\beta$ index. We use the horizontal branch ratio HBR from the McMaster catalog ( ${\rm HBR} = (B-R)/(B+V+R)$ : B and R are the number of stars bluewards and redwards of the instability strip; V is the number of variable stars inside the instability strip) to parameterize the horizontal branch morphology. Figure 9 shows that the HBR parameter vs. $R_{\rm GC}$ follows a similar trend as H $\beta$ vs. $R_{\rm GC}$ in Fig. 8. This supports the idea that the change in H $\beta$ (as a function of $R_{\rm GC}$ ) is mainly driven by the change of the horizontal branch morphology as one goes to more distant halo globular clusters with lower metallicities. Indeed, the lower panel in Fig. 9 shows that HBR is correlated with the H $\beta$ index (Spearman rank coefficient 0.77). The functional form of this correlation is

$\displaystyle {\rm HBR} = (-3.71\pm0.41) + (1.75\pm0.19)\cdot{\rm H}\beta$

(6)

with an rms of 0.39 which is marginally larger than the mean measurement error (0.36). That is, the scatter found can be fully explained by observational uncertainties. Note that according to this relation the H $\beta$ index can vary by $\sim$ 1 Å when changing the horizontal branch morphology from an entirely red to an entirely blue horizontal branch (see also de Freitas Pacheco & Barbuy 1995). This behaviour is also predicted by previous stellar population models (e.g. Lee et al. 2000; Maraston & Thomas 2000).

Figure 9 implies that the change of H $\beta$ is mainly driven by the horizontal branch morphology which itself is influenced by the mean globular cluster metallicity. However, we know of globular cluster pairs - so-called "second parameter'' pairs -, such as the metal-poor halo globular clusters NGC 288 and NGC 362 ( $\rm [Fe/H]\approx-1.2$ , Catelan et al. 2001) and the metal-rich bulge clusters NGC 6388 and NGC 6624 ( $\rm [Fe/H]\approx-0.5$ , Rich et al. 1997; Zoccali et al. 2000), with very similar metallicities and different horizontal branch morphologies. In fact, NGC 6388 (and NGC 6441, another metal-rich cluster in our sample also featuring a blue horizontal branch) shows a stronger H $\beta$ index than other sample globular clusters at similar metallicities (see Sect. 4.3). Clearly, metallicity cannot be the only parameter which governs the horizontal branch morphology. In the context of the "second-parameter effect'' other global and non-global cluster properties (Freeman & Norris 1981) impinging on the horizontal branch morphology have been discussed of which the cluster age and/or several other structural and dynamical cluster properties are suspected to be the best candidates (e.g. Fusi Pecci et al. 1993; Rich et al. 1997). Our sample does not contain enough "second parameter'' pairs to study the systematic effects these "second parameters'' might have on H $\beta$ , such as the correlation of the residuals of the HBR-H $\beta$ relation as a function of globular cluster age or internal kinematics. A larger data set would help to solve this issue.

$\begin{figure} \includegraphics[width=8.8cm,clip]{2781f9a.eps} \includegraphics[width=8.8cm,clip]{2781f9b.eps} \end{figure}$

Figure 9: Horizontal branch morphology in terms of the HBR parameter as a function of galactocentric radius $R_{\rm GC}$ (upper panel) and H $\beta$ (lower panel). Filled and open circles show our globular cluster data and the data of Trager et al. (1998), respectively.

7 Conclusions

For the first time the complete set of Lick indices have been measured for a sample of metal-rich globular clusters belonging to the Galactic bulge. In combination with data for metal-poor globular clusters this data set has allowed us to establish an empirical calibration of the Lick indices of old stellar populations from very low metallicities all the way to near solar metallicity. On the one hand, these empirical relations can be directly used to get age and chemical composition information for the stellar populations of unresolved galaxies. On the other hand, they can be used to submit to most stringent tests of population synthesis models, an aspect which is the subject of an accompanying paper (Maraston et al. 2002).

The comparison of the Lick indices for the Galactic bulge with those of globular clusters shows that the bulge and the most metal-rich globular clusters have quite similar stellar populations, with the slightly deviating values of some of the bulge indices being the likely result of the metallicity distribution of bulge stars, which extends down to $\rm [Fe/H]\simeq -1.0$ (McWilliam & Rich 1994; Zoccali et al. 2002). Within the uncertainties, both the metal-rich clusters and the bulge appear to have also the same index ratios, in particular those sensitive to [ $\alpha$ /Fe]. This implies similar enhancements for individual $\alpha$ -elements in clusters as in the field. Existing spectroscopic determinations of the $\alpha$ -element enhancement in clusters and bulge field stars are still scanty, but extensive high-resolution spectroscopy at 8-10 m class telescopes will soon provide data for a fully empirical calibration of the Lick indices at the [ $\alpha$ /Fe] values of the bulge and bulge globular clusters.

Some other line index ratios, such as CN $/\langle$ Fe $\rangle$ , show clear exceptions. In these cases the bulge indices are definitely below the values for the metal-rich clusters. Several possibilities have been discussed for the mechanism responsible for the CN index offset between the bulge and the clusters, the environmental-pollution being active in clusters (but not in the field) appearing as the most likely explanation. In this scenario, globular cluster stars would have experienced accretion of materials lost by cluster AGB stars, early in the history of the clusters (i.e., when clusters were ${\sim} 10^8{-}10^9$ years old).

8 Summary

1.: We present for the first time the full set of Lick indices for a sample of metal-rich globular clusters in the Galactic bulge.
2.: The Mg₂ and $\langle$ Fe $\rangle$ indices of the most metal-rich globular clusters (NGC 5927, NGC 6528, and NGC 6553) are similar to those of the bulge, indicating that cluster and bulge fields have a similar [Fe/H] ratio.
3.: The CN index is clearly stronger in metal-rich globular clusters, compared to the stellar population in the Galactic bulge.
4.: All the metallicity-sensitive indices are tightly correlated with the $\langle$ Fe $\rangle$ index (Spearman rank coefficient $\geq$ 0.87).
5.: We provide empirical calibrations of several indices versus [Fe/H] in the range $-2.29\leq\rm [Fe/H]\leq-0.17$ . We find that the Mg₂ and the [MgFe] index are the best metallicity indicators with a rms of 0.15 dex.
6.: The H $\beta$ index shows a large scatter as a function of galactocentric distance which can be explained by the changing horizontal branch morphology.
7.: All other indices decrease with galactocentric radius and have constant low values beyond the radius of $\sim$ 10 kpc.

Acknowledgements

We acknowledge the use of the Lick standard star database which is maintained by Guy Worthey. THP gratefully acknowledges the support of the German Deutsche Forschungsgemeinschaft, DFG under the project number Be 1091/10-1. We would like to thank the anonymous referee for a careful and constructive report.

Appendix A: Description and performance tests of the index-measuring routine

The Lick/IDS standard system is briefly described in Sect. 2.4. The passband definitions of line indices and the index measuring prescriptions were implemented in a code, which performs a full statistical error treatment (see Sect. A.2 for details). In summary, a line index is defined as the missing/additional flux between the spectrum and a pseudo-continuum which is defined by two continuum passbands on either side of the feature passband. Trager et al. (1998) defines a line index as

$\displaystyle {EW}_{\circ}=\int_{\lambda_{\min}}^{\lambda_{\max}} \left(1-\frac{F_{\rm l}(\lambda)}{F_{\rm c}(\lambda)}\right)~{\rm d}\lambda,$

(A.1)

where $F_{\rm l}(\lambda)$ and $F_{\rm c}(\lambda)$ is the flux of the feature passband and the pseudo-continuum, respectively. However, González (1993) gives another definition of a line index

$\begin{displaymath} {EW}_{\rm t}=\left(1-\frac{\int_{\lambda_{\min}}^{\lambda_{\... ...F_{\rm c}(\lambda)~{\rm d}\lambda}\right)~\cdot\Delta\lambda. \end{displaymath}$

(A.2)

While the former is an integral of the flux ratio the latter is the ratio of the flux integrals. We refer to the former as the observer's definition ( ${EW}\rm _o$ ) and to the latter as the theorist's definition ( ${EW}\rm _t$ ). For high-S/N spectra the difference between the two definitions is negligible. ${EW}\rm _t$ is a more global definition and is, therefore, more robust for low-S/N spectra. However, since most literature uses the observer's definition, all the measurements which are given in this paper are ${EW}\rm _o$ (Eq. (A.1)). To check for systematic offsets and/or different error patterns, our code performes index measurements with both definitions. Without exception, we find no systematic offset between the measurements and a value-to-value scatter of less than 0.1%. In particular, this causes no problems between theoretical predictions from SSP models, which synthesise line indices using the $EW_{\rm t}$ definition, and measurements.

A.1 Accuracy tests

$\begin{figure} \includegraphics[width=8.8cm,clip]{2781fa1.eps} \end{figure}$

Figure A.1: Comparison of index measurements of Worthey and from our code. The upper panel shows the direct comparison between our and the Worthey data. Each single point gives the measurement for one star in one single passband. Residuals are plotted in the lower panel. The measurements of passbands which are defined in magnitudes have been previously transformed to the Å-scale. From the lower panel we determine the average statistical scatter with 0.0034 Å and a zero offset $0.0037\pm 2\times 10^{-5}$ Å.

The whole measurement procedure was tested on original Lick spectra available from the database of Guy Worthey. Applying our code to 6 original Lick spectra (HYA VB 112/sdr310007, HYA VB 111/sdr310010, HYA VB 103 (R)/sdr310017, HYA VB 103 (R+L)/sdr310019, HYA VB 95/sdr320230, and HR 7429/sdr370421) and comparing the results of 150 line index measurements (using the ${EW}\rm _o$ definition, see above) with the original data provided by Guy Worthey, we find excellent agreement between the Lick datasets and ours. After transformation of molecular-band indices, which are usually given in magnitudes, to a uniform Å-scale, we determine an average scatter of 0.0034 Å, which is most likely due to the different treatment of sub-pixels at the edges of passbands. The average systematic zero offset between the two datasets was found $0.0037\pm 2\times 10^{-5}$ Å. Figure A.1 shows a comparison between measurements performed by Worthey and us based on the same data. Since the offset between the two datasets is of the order of the scatter of all index values, we do not consider any correction for all measurements performed in this work. Moreover, the offset is significantly smaller than the errors which result from Poisson noise of the spectra themselves.

A.2 Error estimation

The main purpose of implementing a new code for index measurements, was the need for a robust error estimate of the indices. Since we deal with CCD data, as opposed to the Lick spectra, which are digitized images of a phosphor screen, we can determine the contribution of the flux Poisson noise of each spectrum to the total error budget. Note that due to the scanning of a spectrum off a phosphor screen the photo-tube suffers from the correlation of photon-noise errors over a wide wavelength range. Moreover, the photo-tube increases the noise due to statistical fluctuations in the amplification process (Robinson & Wampler 1972). The data used in this work is entirely free from these effects.

Since we need to subtract background spectra from our science spectra it is necessary to estimate the contribution of errors introduced by the subtraction and any radial velocity uncertainties to the total error budget. Both background and science spectra are included in the estimation of the total index uncertainty. Radial velocity errors are considered as systematic errors and are not included in the statistical error budget, but listed in the paper.

The code determines the total line-index uncertainty in 100 Monte Carlo simulations. Each simulation creates a new object and background spectrum by adding noise according to the Poisson statistics taking into account the detector noise. Line indices are measured on each noise-added spectrum. Since a Monte Carlo test naturally takes into account all possible error correlations in the line-index measurement process (such as the correlation of errors in the background passbands with the errors in the feature passband), the scatter in all simulated line indices is the best estimate for their total uncertainty. We therefore use the 1- $\sigma$ standard deviation of all Monte-Carlo line-index measurements as the best guess for the final index uncertainty.

The variations due to uncertain radial velocities are given separately. They are calculated as the deviation of the initial line index by changing the radial velocity within its error limits.

References

Ashman, K. M., & Zepf, S. E. 1998, Globular cluster systems (Cambridge University Press) In the text
Baldwin, J. A., & Stone, R. P. S. 1984, MNRAS, 206, 241 In the text NASA ADS
Barbuy, B., Bica, E., & Ortolani, S. 1998, A&A, 333, 117 In the text NASA ADS
Barbuy, B., Renzini, A., Ortolani, S., Bica, E., & Guarnieri, M. D. 1999, A&A, 341, 539 In the text NASA ADS
Beasley, M. A., Sharples, R. M., Bridges, T. J., et al. 2000, MNRAS, 318, 1249 In the text NASA ADS
Bica, E., & Alloin, D. 1986, A&A, 162, 21 NASA ADS
Burstein, D., Faber, S. M., Gaskell, C. M., & Krumm, N. 1984, ApJ, 287, 586 In the text NASA ADS
Carretta, E., & Bragaglia, A. 1998, A&A, 329, 937 In the text NASA ADS
Carretta, E., Cohen, J. G., Gratton, R. G., & Behr, B. B. 2001, AJ, 122, 1469 In the text NASA ADS
Catelan, M., Bellazzini, M., Landsman, W. B., et al. 2001, AJ, 122, 3171 In the text NASA ADS
Coelho, P., Barbuy, B., Perrin, M.-N., et al. 2001, A&A, 376, 136 In the text NASA ADS
Cohen, J. G., & Sleeper, C. 1995, AJ, 109, 242 In the text NASA ADS
Cohen, J. G., Blakeslee, J. P., & Ryzhov, A. 1998, ApJ, 496, 808 In the text NASA ADS
Cohen, J. G., Gratton, R. G., Behr, B. B., & Carretta, E. 1999, ApJ, 523, 739 In the text NASA ADS
Côté, P. 1999, AJ, 118, 406 In the text NASA ADS
Covino, S., Galletti, S., & Pasinetti, L. E. 1995, A&A, 303, 79 In the text NASA ADS
D'Antona, F., Gratton, R., & Chieffi, A. 1983, Mem. della Soc. Astron. Ital., 54, 173 In the text
Davies, R. L., Sadler, E. M., & Peletier, R. F. 1993, MNRAS, 262, 650 In the text NASA ADS
Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 In the text NASA ADS
Faber, S. M., Friel, E. D., Burstein, D., & Gaskell, C. M. 1985, ApJS, 57, 711 In the text NASA ADS
Feltzing, S., & Gilmore, G. 2000, A&A, 355, 949 In the text NASA ADS
Feltzing, S., Johnson, R. A., & de Cordova, A. 2002, A&A, 385, 67 In the text NASA ADS
Freeman, K. C., & Norris, J. 1981, ARA&A, 19, 319 In the text NASA ADS
de Freitas Pacheco, J. A., & Barbuy, B. 1995, A&A, 302, 718 In the text NASA ADS
Freudenreich, H. T. 1998, ApJ, 492, 495 In the text NASA ADS
Frogel, J. A. 1988, ARA&A, 26, 51 In the text NASA ADS
Frogel, J. A., Terndrup, D. M., Blanco, V. M., & Whitford, A. E. 1990, ApJ, 353, 494 In the text NASA ADS
Frogel, J. A., Tiede, G. P., & Kuchinski, L. E. 1999, AJ, 117, 2296 In the text NASA ADS
Fuhrmann, K. 1998, A&A, 338, 161 In the text NASA ADS
Fusi Pecci, F., Ferraro, F. R., Bellazzini, M., et al. 1993, AJ, 105, 1145 In the text NASA ADS
González, J. J. 1993, Ph.D. Thesis, 172 In the text
Gorgas, J., Faber, S. M., Burstein, D., et al. 1993, ApJS, 86, 153 In the text NASA ADS
Greggio, L. 1997, MNRAS, 285, 151 In the text NASA ADS
Grundahl, F., Briley, M. M., Nissen, P. E., & Feltzing, S. 2002, A&A, 385, L14 NASA ADS
Harris, W. E. 1996, AJ, 112, 1487, for the 1999 update see In the text http://physun.physics.mcmaster.ca/~harris/mwgc.dat
Harris, W. E. 2001, in Star Clusters, ed. L. Labhardt, & B. Binggeli (Springer-Verlag, Berlin), 22 In the text
Hayes, D. S. 1985, in Calibration of fundamental stellar quantities, IAU Symp., 111, 225 In the text
Huchra, J., Stauffer, J., & van Speybroeck, L. 1982, ApJ, 259, L57 In the text NASA ADS
Kent, S. M., Dame, T. M., & Fazio, G. 1991, ApJ, 378, 131 In the text NASA ADS
King, I. R. 1966, AJ, 71, 64 In the text NASA ADS
Kraft, R. P. 1994, PASP, 106, 553 In the text NASA ADS
Kraft, R. P., Suntzeff, N. B., Langer, G. E., et al. 1982, PASP, 94, 55 In the text NASA ADS
Lee, Y., Demarque, P., & Zinn, R. 1994, ApJ, 423, 248 In the text NASA ADS
Lee, H., Yoon, S., & Lee, Y. 2000, AJ, 120, 998 In the text NASA ADS
Maraston, C. 1998, MNRAS, 300, 872 In the text NASA ADS
Maraston, C. 2002, in preparation In the text
Maraston, C., & Thomas, D. 2000, ApJ, 541, 126 In the text NASA ADS
Maraston, C., Greggio, L., & Thomas, D. 2001, Ap&SS, 276, 893 In the text NASA ADS
Maraston, C., et al. 2002, A&A, submitted In the text
McWilliam, A., & Rich, R. M. 1994, ApJS, 91, 749 In the text NASA ADS
Minniti, D. 1995, AJ, 109, 1663 In the text NASA ADS
Neckel, H. 1986, A&A, 159, 175 In the text NASA ADS
Neckel, H. 1986, A&A, 167, 97 In the text NASA ADS
Origlia, L., Rich, R. M., & Castro, S. 2002, AJ, 123, 1559 In the text NASA ADS
Ortolani, S., Barbuy, B., & Bica, E. 1991, A&A, 249, L31 In the text NASA ADS
Ortolani, S., Renzini, A., Gilmozzi, R., et al. 1995b, Nature, 377, 701 In the text NASA ADS
Ortolani, S., Bica, E., & Barbuy, B. 1995a, A&A, 296, 680 In the text NASA ADS
Ortolani, S., Barbuy, B., Bica, E., et al. 2001, A&A, 376, 878 In the text NASA ADS
Peletier, R. 1989, Ph.D. Thesis, Rijksuniv. Groningen In the text
Pryor, C., & Meylan, G. 1993, in Structure and Dynamics of Globular Clusters, ASP Conf. Ser., 50, 357 In the text
Renzini, A. 1983, Mem. della Soc. Astron. Ital., 54, 335 In the text
Renzini, A. 1998, AJ, 115, 2459 In the text NASA ADS
Renzini, A., & Voli, M. 1981, A&A, 94, 175 In the text NASA ADS
Renzini, A., & Fusi Pecci, F. 1988, ARA&A, 26, 199 In the text NASA ADS
Rich, R. M., et al. 1997, ApJ, 484, L25 In the text NASA ADS
Robin, A. C., Haywood, M., Crézé, M., Ojha, D. K., & Bienaymé, O. 1996, A&A, 305, 125 In the text NASA ADS
Robinson, L. B., & Wampler, E. J. 1972, PASP, 84, 161 In the text NASA ADS
Saviane, I., Rosenberg, A., Piotto, G., & Aparicio, A. 2000, A&A, 355, 966 In the text NASA ADS
Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 In the text NASA ADS
Spaenhauer, A., Jones, B. F., & Whitford, A. E. 1992, AJ, 103, 297 In the text NASA ADS
Stanek, K. Z. 1996, ApJ, 460, L37 In the text NASA ADS
Stone, R. P. S., & Baldwin, J. A. 1983, MNRAS, 204, 347 In the text NASA ADS
Terndrup, D. M. 1988, AJ, 96, 884 In the text NASA ADS
Thomas, D., Greggio, L., & Bender, R. 1998, MNRAS, 302, 537 In the text NASA ADS
Thomas, D., & Kauffmann, G. 1999, in Spectrophotometric Dating of Stars and Galaxies, ASP Conf. Ser., 192, 261 In the text
Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, ed. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 173 In the text
Trager, S. C., King, I. R., & Djorgovski, S. 1995, AJ, 109, 218 In the text NASA ADS
Trager, S. C., Worthey, G., Faber, S. M., Burstein, D., & Gonzalez, J. J. 1998, ApJS, 116, 1 In the text NASA ADS
Tripicco, M. J., & Bell, R. A. 1995, AJ, 110, 3035 In the text NASA ADS
Tsujimoto, T., Nomoto, K., Yoshii, Y., et al. 1995, MNRAS, 277, 945 In the text NASA ADS
Unavane, M., & Gilmore, G. 1998, MNRAS, 295, 145 In the text NASA ADS
Unavane, M., Gilmore, G., Epchtein, N., et al. 1998, MNRAS, 295, 119 In the text NASA ADS
Ventura, P., D'Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 In the text NASA ADS
Worthey, G., Faber, S. M., & Gonzalez, J. J. 1992, ApJ, 398, 69 In the text NASA ADS
Worthey, G., Faber, S. M., Gonzalez, J. J., & Burstein, D. 1994, ApJS, 94, 687 In the text NASA ADS
Worthey, G., & Ottaviani, D. L. 1997, ApJS, 111, 377 In the text NASA ADS
Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 In the text NASA ADS
Wyse, R. F. G., & Gilmore, G. 1993, in The Globular Cluster-Galaxy Connection, ASP Conf. Ser., 48, 727
Wyse, R. F. G., Gilmore, G., & Franx, M. 1997, ARA&A, 35, 637 In the text NASA ADS
Zinn, R. 1985, ApJ, 293, 424 In the text NASA ADS
Zinn, R., & West, M. J. 1984, ApJS, 55, 45 In the text NASA ADS
Zoccali, M., Cassisi, S., Bono, G., et al. 2000, ApJ, 538, 289 In the text NASA ADS
Zoccali, M., Renzini, A., Ortolani, S., Bica, E., & Barbuy, B. 2001, AJ, 121, 2638 In the text NASA ADS
Zoccali, M., et al. 2002, A&A, in preparation In the text

Online Material

Appendix B: Comparison with the literature

Table B.1: Comparison of Lick indices CN1 to Fe 5015 for our sample globular clusters with data taken from literature. The according errors are given in Table C.1. Our index measurements and the indices of Trager et al. use the new passband definitions of Trager et al. (1998). Cohen et al. and Covino et al. use old passband definitions of Burstein et al. (1984).
GC bkg mode^a CN1 CN2 Ca 4227 G4300 Fe 4383 Ca 4455 Fe 4531 Fe 4668 H $\beta$ Fe 5015

mag mag A A A A A A A A

NGC 6624 BE 0.0497 0.0739 0.4889 4.8910 2.4023 0.5065 2.2739 1.4643 1.6502 4.1850

w/o 0.0635 0.0856 0.6070 5.0023 2.8872 0.5122 2.9936 1.6337 1.5347 4.1861

BM 0.0692 0.0907 0.6064 5.0702 2.7295 0.5335 3.1087 1.0489 1.4807 4.1552

Trager et al. (1998) ... ... ... ... ... ... ... ... ... ...

Covino et al. (1995) 0.02 0.02 ... 4.758 ... ... ... ... 2.535 ...

Cohen et al. (1998) ... ... ... ... ... ... ... ... 1.69 ...

NGC 6218 BE -0.0763 -0.0596 0.0586 2.7004 -0.1175 -0.0055 0.9504 -0.6060 2.7147 2.7170

w/o -0.0711 -0.0550 0.0688 2.6871 -0.1207 0.0536 0.8507 -0.7686 2.5817 2.6896

BM -0.0820 -0.0661 -0.0429 2.4039 -0.8066 0.0178 0.5669 -1.7789 2.8366 2.2599

Trager et al. (1998) -0.0910 -0.0490 0.6300 1.8700 0.0000 0.1000 1.6900 -1.3200 2.2800 2.1100

Covino et al. (1995) ... ... ... ... ... ... ... ... 1.214 ...

Cohen et al. (1998) ... ... ... ... ... ... ... ... ... ...

NGC 6626 BE -0.0455 -0.0259 0.1473 3.1433 0.5716 0.0926 1.2946 -0.0206 2.2747 3.1826

w/o -0.0425 -0.0245 0.1859 3.1207 0.7364 0.1256 1.3939 0.1220 2.1582 3.1877

BM -0.0459 -0.0277 0.1428 3.0243 0.4942 0.1222 1.3238 -0.2020 2.2132 3.0836

Trager et al. (1998) ... ... ... ... ... ... ... ... ... ...

Covino et al. (1995) -0.052 -0.052 ... 2.713 ... ... ... ... 2.443 ...

Cohen et al. (1998) ... ... ... ... ... ... ... ... ... ...

NGC 6284 BE -0.0417 -0.0227 0.1551 3.1957 0.6659 0.1992 1.4645 -0.1003 2.4274 3.1553

w/o -0.0347 -0.0155 0.2107 3.3368 0.7969 0.2928 1.4811 0.1469 2.2370 3.2056

BM -0.0507 -0.0277 0.0278 2.9414 -0.5049 0.0494 1.0449 -2.3533 2.8913 2.2407

Trager et al. (1998) ... ... ... ... ... ... ... ... ... ...

Covino et al. (1995) -0.082 -0.082 ... 1.785 ... ... ... ... 2.764 ...

Cohen et al. (1998) ... ... ... ... ... ... ... ... ... ...

NGC 6356 BE 0.0450 0.0648 0.5079 5.0611 2.3472 0.5334 2.2955 1.3231 1.6341 4.0541

w/o 0.0432 0.0626 0.4911 4.8895 2.3269 0.5481 2.1968 1.4871 1.6190 4.1296

BM 0.0561 0.0788 0.4667 5.1272 2.0202 0.5053 2.1965 0.5297 1.7782 3.9587

Trager et al. (1998) 0.0237 0.0726 1.3270 4.8180 3.9220 1.6030 2.6900 2.9720 1.4680 4.2980

Covino et al. (1995) ... ... ... ... ... ... ... ... 1.646 ...

Cohen et al. (1998) ... ... ... ... ... ... ... ... 1.62 ...

NGC 6637 BE 0.0248 0.0438 0.4009 5.1912 2.0615 0.4497 2.1725 1.3150 1.6224 3.9535

w/o 0.0223 0.0412 0.3859 5.1082 2.1333 0.3674 2.0921 1.2860 1.5773 3.8951

BM 0.0258 0.0459 0.3493 5.2617 1.9243 0.2976 2.0623 0.7096 1.6590 3.7375

Trager et al. (1998) -0.0125 0.0048 1.0560 5.0490 0.2010 1.1300 3.4870 1.5220 0.8980 4.6420

Covino et al. (1995) ... ... ... ... ... ... ... ... 1.15 ...

Cohen et al. (1998) ... ... ... ... ... ... ... ... ... ...

NGC 6553 BE 0.1378 0.1619 1.0915 5.4464 4.0079 0.8316 3.0767 3.4849 1.8881 5.7254

w/o 0.0699 0.0842 0.7192 5.0248 4.2101 0.9686 2.5541 3.5774 1.1596 4.9798

BM 0.1107 0.1243 0.7044 5.4233 4.5439 1.3630 2.7317 3.5390 1.0138 5.2232

Trager et al. (1998) ... ... ... ... ... ... ... ... ... ...

Covino et al. (1995) ... ... ... ... ... ... ... ... ... ...

Cohen et al. (1998) ... ... ... ... ... ... ... ... 1.63 ...

NGC 6528 BE 0.0959 0.1174 0.9089 5.2218 4.7754 0.8794 2.7074 4.2181 1.7745 5.1531

w/o 0.0696 0.0877 0.6629 5.1257 4.4139 0.5266 2.7904 4.0300 1.5097 5.0032

BM 0.1229 0.1569 1.3493 6.2741 6.1253 1.4228 3.7042 4.5434 1.0913 6.1269

Trager et al. (1998) ... ... ... ... ... ... ... ... ... ...

Covino et al. (1995) ... ... ... ... ... ... ... ... ... ...

Cohen et al. (1998) ... ... ... ... ... ... ... ... 1.80 ...

**Table B.1:** Comparison of Lick indices CN1 to Fe 5015 for our sample globular clusters with data taken from literature. The according errors are given in Table C.1. Our index measurements and the indices of Trager et al. use the *new* passband definitions of Trager et al. (1998). Cohen et al. and Covino et al. use *old* passband definitions of Burstein et al. (1984).
GC	bkg mode^a	CN1	CN2	Ca 4227	G4300	Fe 4383	Ca 4455	Fe 4531	Fe 4668	H $\beta$	Fe 5015
		mag	mag	A	A	A	A	A	A	A	A
NGC 6624	BE	0.0497	0.0739	0.4889	4.8910	2.4023	0.5065	2.2739	1.4643	1.6502	4.1850
	w/o	0.0635	0.0856	0.6070	5.0023	2.8872	0.5122	2.9936	1.6337	1.5347	4.1861
	BM	0.0692	0.0907	0.6064	5.0702	2.7295	0.5335	3.1087	1.0489	1.4807	4.1552
	Trager et al. (1998)	...	...	...	...	...	...	...	...	...	...
	Covino et al. (1995)	0.02	0.02	...	4.758	...	...	...	...	2.535	...
	Cohen et al. (1998)	...	...	...	...	...	...	...	...	1.69	...
NGC 6218	BE	-0.0763	-0.0596	0.0586	2.7004	-0.1175	-0.0055	0.9504	-0.6060	2.7147	2.7170
	w/o	-0.0711	-0.0550	0.0688	2.6871	-0.1207	0.0536	0.8507	-0.7686	2.5817	2.6896
	BM	-0.0820	-0.0661	-0.0429	2.4039	-0.8066	0.0178	0.5669	-1.7789	2.8366	2.2599
	Trager et al. (1998)	-0.0910	-0.0490	0.6300	1.8700	0.0000	0.1000	1.6900	-1.3200	2.2800	2.1100
	Covino et al. (1995)	...	...	...	...	...	...	...	...	1.214	...
	Cohen et al. (1998)	...	...	...	...	...	...	...	...	...	...
NGC 6626	BE	-0.0455	-0.0259	0.1473	3.1433	0.5716	0.0926	1.2946	-0.0206	2.2747	3.1826
	w/o	-0.0425	-0.0245	0.1859	3.1207	0.7364	0.1256	1.3939	0.1220	2.1582	3.1877
	BM	-0.0459	-0.0277	0.1428	3.0243	0.4942	0.1222	1.3238	-0.2020	2.2132	3.0836
	Trager et al. (1998)	...	...	...	...	...	...	...	...	...	...
	Covino et al. (1995)	-0.052	-0.052	...	2.713	...	...	...	...	2.443	...
	Cohen et al. (1998)	...	...	...	...	...	...	...	...	...	...
NGC 6284	BE	-0.0417	-0.0227	0.1551	3.1957	0.6659	0.1992	1.4645	-0.1003	2.4274	3.1553
	w/o	-0.0347	-0.0155	0.2107	3.3368	0.7969	0.2928	1.4811	0.1469	2.2370	3.2056
	BM	-0.0507	-0.0277	0.0278	2.9414	-0.5049	0.0494	1.0449	-2.3533	2.8913	2.2407
	Trager et al. (1998)	...	...	...	...	...	...	...	...	...	...
	Covino et al. (1995)	-0.082	-0.082	...	1.785	...	...	...	...	2.764	...
	Cohen et al. (1998)	...	...	...	...	...	...	...	...	...	...
NGC 6356	BE	0.0450	0.0648	0.5079	5.0611	2.3472	0.5334	2.2955	1.3231	1.6341	4.0541
	w/o	0.0432	0.0626	0.4911	4.8895	2.3269	0.5481	2.1968	1.4871	1.6190	4.1296
	BM	0.0561	0.0788	0.4667	5.1272	2.0202	0.5053	2.1965	0.5297	1.7782	3.9587
	Trager et al. (1998)	0.0237	0.0726	1.3270	4.8180	3.9220	1.6030	2.6900	2.9720	1.4680	4.2980
	Covino et al. (1995)	...	...	...	...	...	...	...	...	1.646	...
	Cohen et al. (1998)	...	...	...	...	...	...	...	...	1.62	...
NGC 6637	BE	0.0248	0.0438	0.4009	5.1912	2.0615	0.4497	2.1725	1.3150	1.6224	3.9535
	w/o	0.0223	0.0412	0.3859	5.1082	2.1333	0.3674	2.0921	1.2860	1.5773	3.8951
	BM	0.0258	0.0459	0.3493	5.2617	1.9243	0.2976	2.0623	0.7096	1.6590	3.7375
	Trager et al. (1998)	-0.0125	0.0048	1.0560	5.0490	0.2010	1.1300	3.4870	1.5220	0.8980	4.6420
	Covino et al. (1995)	...	...	...	...	...	...	...	...	1.15	...
	Cohen et al. (1998)	...	...	...	...	...	...	...	...	...	...
NGC 6553	BE	0.1378	0.1619	1.0915	5.4464	4.0079	0.8316	3.0767	3.4849	1.8881	5.7254
	w/o	0.0699	0.0842	0.7192	5.0248	4.2101	0.9686	2.5541	3.5774	1.1596	4.9798
	BM	0.1107	0.1243	0.7044	5.4233	4.5439	1.3630	2.7317	3.5390	1.0138	5.2232
	Trager et al. (1998)	...	...	...	...	...	...	...	...	...	...
	Covino et al. (1995)	...	...	...	...	...	...	...	...	...	...
	Cohen et al. (1998)	...	...	...	...	...	...	...	...	1.63	...
NGC 6528	BE	0.0959	0.1174	0.9089	5.2218	4.7754	0.8794	2.7074	4.2181	1.7745	5.1531
	w/o	0.0696	0.0877	0.6629	5.1257	4.4139	0.5266	2.7904	4.0300	1.5097	5.0032
	BM	0.1229	0.1569	1.3493	6.2741	6.1253	1.4228	3.7042	4.5434	1.0913	6.1269
	Trager et al. (1998)	...	...	...	...	...	...	...	...	...	...
	Covino et al. (1995)	...	...	...	...	...	...	...	...	...	...
	Cohen et al. (1998)	...	...	...	...	...	...	...	...	1.80	...

^a: BE: background extraction; w/o: without background subtraction; BM: background modeling. See Sect. 3.1 for details.

Table B.1: continued. Comparison of Lick indices Mg₁ - TiO₂.
GC bkg mode^a Mg₁ Mg₂ Mgb Fe 5270 Fe 5335 Fe 5406 Fe 5709 Fe 5782 Na 5895 TiO₁ TiO₂

mag mag A A A A A A A mag mag

NGC 6624 BE 0.0707 0.1721 2.7280 1.8158 1.6403 0.9789 0.5009 0.6411 2.7063 0.0470 0.0628

w/o 0.0696 0.1758 2.6730 1.7832 1.7237 0.9738 0.5322 0.6349 3.8927 0.0542 0.0658

BM 0.0642 0.1669 2.6254 1.6564 1.6780 0.9527 0.4837 0.5945 3.4454 0.0572 0.0719

Trager et al. (1998) ... ... ... ... ... ... ... ... ... ... ...

Covino et al. (1995) 0.05 0.15 2.486 2.117 1.812 ... ... ... 2.881 ... ...

Cohen et al. (1998) 0.048 0.163 2.94 2.09 1.78 ... ... ... 2.20 0.035 ...

NGC 6218 BE 0.0268 0.0672 1.0628 0.7687 0.8935 0.2246 -0.1909 0.2025 1.2915 0.0182 0.0040

w/o 0.0293 0.0675 1.4179 0.7036 0.7692 0.2148 -0.1939 0.2421 1.2410 0.0059 -0.0067

BM 0.0132 0.0256 1.0507 0.2819 0.4167 -0.1026 -0.5354 0.0523 -0.2041 -0.0222 -0.0679

Trager et al. (1998) -0.0060 0.0690 1.2800 1.3400 0.5000 0.0600 -0.0600 0.0000 1.6300 0.0020 0.0000

Covino et al. (1995) 0.02 0.07 1.68 1.125 0.8472 ... ... ... ... ... ...

Cohen et al. (1998) ... ... ... ... ... ... ... ... ... ... ...

NGC 6626 BE 0.0415 0.0919 1.3679 1.0900 0.9747 0.5413 0.1846 0.4735 2.1005 0.0288 0.0382

w/o 0.0424 0.0956 1.3511 1.1049 1.0347 0.5392 0.1824 0.4674 2.2341 0.0299 0.0385

BM 0.0382 0.0841 1.2213 1.0144 0.9603 0.4811 0.1324 0.4479 1.9655 0.0245 0.0274

Trager et al. (1998) ... ... ... ... ... ... ... ... ... ... ...

Covino et al. (1995) -0.002 0.063 1.103 1.539 1.229 ... ... ... 2.565 ... ...

Cohen et al. (1998) ... ... ... ... ... ... ... ... ... ... ...

NGC 6284 BE 0.0427 0.0966 1.4403 0.8563 1.0216 0.5178 0.1110 0.3141 2.3978 0.0159 0.0039

w/o 0.0463 0.1064 1.3460 1.0142 1.0683 0.5497 0.1973 0.3497 2.1540 0.0137 0.0023

BM 0.0063 0.0180 0.0513 -0.3341 0.2294 -0.1227 -0.0984 -0.3166 -2.1392 -0.0380 -0.1080

Trager et al. (1998) ... ... ... ... ... ... ... ... ... ... ...

Covino et al. (1995) 0.027 0.077 1.075 1.505 1.091 ... ... ... 2.433 ... ...

Cohen et al. (1998) ... ... ... ... ... ... ... ... ... ... ...

NGC 6356 BE 0.0728 0.1773 2.7863 1.7187 1.6597 0.9557 0.4067 0.5493 3.2660 0.0333 0.0531

w/o 0.0773 0.1851 2.5857 1.9996 1.4993 0.8985 0.3764 0.5451 3.6050 0.0390 0.0579

BM 0.0666 0.1656 2.3420 1.7049 1.2805 0.7273 0.3410 0.3598 2.2064 0.0327 0.0408

Trager et al. (1998) 0.0404 0.1700 2.9800 1.9940 1.4010 1.3970 0.6640 0.6200 3.3290 0.0369 0.0460

Covino et al. (1995) 0.062 0.179 2.776 2.352 1.125 ... ... ... ... ... ...

Cohen et al. (1998) 0.070 0.169 3.09 2.00 1.69 ... ... ... 3.00 0.029 ...

NGC 6637 BE 0.0567 0.1542 2.5420 1.6335 1.3969 0.8222 0.3565 0.4906 2.6053 0.0381 0.0441

w/o 0.0562 0.1541 2.4696 1.5448 1.4297 0.8195 0.3538 0.4789 2.9313 0.0418 0.0464

BM 0.0461 0.1369 2.3096 1.2681 1.2806 0.6971 0.3144 0.3349 1.9320 0.0359 0.0310

Trager et al. (1998) 0.0384 0.1433 2.3720 1.9470 0.9590 0.8580 0.3850 0.1100 3.2550 0.0498 0.0000

Covino et al. (1995) 0.05 ... 2.671 1.642 1.539 ... ... ... ... ... ...

Cohen et al. (1998) ... ... ... ... ... ... ... ... ... ... ...

NGC 6553 BE 0.1002 0.2552 3.8961 2.6091 2.2654 1.2371 0.7744 1.0970 3.8792 0.0689 0.1420

w/o 0.0949 0.2513 3.6472 2.4476 2.1073 1.3023 0.7823 1.0423 4.1967 0.0640 0.1245

BM 0.0972 0.2606 3.9386 2.5740 2.2081 1.3565 0.8161 1.1643 3.9533 0.0640 0.1262

Trager et al. (1998) ... ... ... ... ... ... ... ... ... ... ...

Covino et al. (1995) ... ... ... ... ... ... ... ... ... ... ...

Cohen et al. (1998) 0.110 0.249 3.88 3.11 2.51 ... ... ... 3.40 0.044 ...

NGC 6528 BE 0.1149 0.2615 3.7413 2.3673 2.2777 1.5499 0.8223 0.7987 5.1366 0.0750 0.1268

w/o 0.1109 0.2573 3.4276 2.3885 2.0133 1.3893 0.7406 0.6816 5.5471 0.0714 0.1183

BM 0.1248 0.2928 4.1444 2.6491 2.4803 1.7290 0.9335 0.8722 5.4463 0.0939 0.1696

Trager et al. (1998) ... ... ... ... ... ... ... ... ... ... ...

1995 ... ... ... ... ... ... ... ... ... ... ...

Cohen et al. (1998) 0.097 0.247 3.89 2.96 2.45 ... ... ... 4.93 0.046 ...

**Table B.1:** continued. Comparison of Lick indices Mg₁ - TiO₂.
GC	bkg mode^a	Mg₁	Mg₂	Mgb	Fe 5270	Fe 5335	Fe 5406	Fe 5709	Fe 5782	Na 5895	TiO₁	TiO₂
		mag	mag	A	A	A	A	A	A	A	mag	mag
NGC 6624	BE	0.0707	0.1721	2.7280	1.8158	1.6403	0.9789	0.5009	0.6411	2.7063	0.0470	0.0628
	w/o	0.0696	0.1758	2.6730	1.7832	1.7237	0.9738	0.5322	0.6349	3.8927	0.0542	0.0658
	BM	0.0642	0.1669	2.6254	1.6564	1.6780	0.9527	0.4837	0.5945	3.4454	0.0572	0.0719
	Trager et al. (1998)	...	...	...	...	...	...	...	...	...	...	...
	Covino et al. (1995)	0.05	0.15	2.486	2.117	1.812	...	...	...	2.881	...	...
	Cohen et al. (1998)	0.048	0.163	2.94	2.09	1.78	...	...	...	2.20	0.035	...
NGC 6218	BE	0.0268	0.0672	1.0628	0.7687	0.8935	0.2246	-0.1909	0.2025	1.2915	0.0182	0.0040
	w/o	0.0293	0.0675	1.4179	0.7036	0.7692	0.2148	-0.1939	0.2421	1.2410	0.0059	-0.0067
	BM	0.0132	0.0256	1.0507	0.2819	0.4167	-0.1026	-0.5354	0.0523	-0.2041	-0.0222	-0.0679
	Trager et al. (1998)	-0.0060	0.0690	1.2800	1.3400	0.5000	0.0600	-0.0600	0.0000	1.6300	0.0020	0.0000
	Covino et al. (1995)	0.02	0.07	1.68	1.125	0.8472	...	...	...	...	...	...
	Cohen et al. (1998)	...	...	...	...	...	...	...	...	...	...	...
NGC 6626	BE	0.0415	0.0919	1.3679	1.0900	0.9747	0.5413	0.1846	0.4735	2.1005	0.0288	0.0382
	w/o	0.0424	0.0956	1.3511	1.1049	1.0347	0.5392	0.1824	0.4674	2.2341	0.0299	0.0385
	BM	0.0382	0.0841	1.2213	1.0144	0.9603	0.4811	0.1324	0.4479	1.9655	0.0245	0.0274
	Trager et al. (1998)	...	...	...	...	...	...	...	...	...	...	...
	Covino et al. (1995)	-0.002	0.063	1.103	1.539	1.229	...	...	...	2.565	...	...
	Cohen et al. (1998)	...	...	...	...	...	...	...	...	...	...	...
NGC 6284	BE	0.0427	0.0966	1.4403	0.8563	1.0216	0.5178	0.1110	0.3141	2.3978	0.0159	0.0039
	w/o	0.0463	0.1064	1.3460	1.0142	1.0683	0.5497	0.1973	0.3497	2.1540	0.0137	0.0023
	BM	0.0063	0.0180	0.0513	-0.3341	0.2294	-0.1227	-0.0984	-0.3166	-2.1392	-0.0380	-0.1080
	Trager et al. (1998)	...	...	...	...	...	...	...	...	...	...	...
	Covino et al. (1995)	0.027	0.077	1.075	1.505	1.091	...	...	...	2.433	...	...
	Cohen et al. (1998)	...	...	...	...	...	...	...	...	...	...	...
NGC 6356	BE	0.0728	0.1773	2.7863	1.7187	1.6597	0.9557	0.4067	0.5493	3.2660	0.0333	0.0531
	w/o	0.0773	0.1851	2.5857	1.9996	1.4993	0.8985	0.3764	0.5451	3.6050	0.0390	0.0579
	BM	0.0666	0.1656	2.3420	1.7049	1.2805	0.7273	0.3410	0.3598	2.2064	0.0327	0.0408
	Trager et al. (1998)	0.0404	0.1700	2.9800	1.9940	1.4010	1.3970	0.6640	0.6200	3.3290	0.0369	0.0460
	Covino et al. (1995)	0.062	0.179	2.776	2.352	1.125	...	...	...	...	...	...
	Cohen et al. (1998)	0.070	0.169	3.09	2.00	1.69	...	...	...	3.00	0.029	...
NGC 6637	BE	0.0567	0.1542	2.5420	1.6335	1.3969	0.8222	0.3565	0.4906	2.6053	0.0381	0.0441
	w/o	0.0562	0.1541	2.4696	1.5448	1.4297	0.8195	0.3538	0.4789	2.9313	0.0418	0.0464
	BM	0.0461	0.1369	2.3096	1.2681	1.2806	0.6971	0.3144	0.3349	1.9320	0.0359	0.0310
	Trager et al. (1998)	0.0384	0.1433	2.3720	1.9470	0.9590	0.8580	0.3850	0.1100	3.2550	0.0498	0.0000
	Covino et al. (1995)	0.05	...	2.671	1.642	1.539	...	...	...	...	...	...
	Cohen et al. (1998)	...	...	...	...	...	...	...	...	...	...	...
NGC 6553	BE	0.1002	0.2552	3.8961	2.6091	2.2654	1.2371	0.7744	1.0970	3.8792	0.0689	0.1420
	w/o	0.0949	0.2513	3.6472	2.4476	2.1073	1.3023	0.7823	1.0423	4.1967	0.0640	0.1245
	BM	0.0972	0.2606	3.9386	2.5740	2.2081	1.3565	0.8161	1.1643	3.9533	0.0640	0.1262
	Trager et al. (1998)	...	...	...	...	...	...	...	...	...	...	...
	Covino et al. (1995)	...	...	...	...	...	...	...	...	...	...	...
	Cohen et al. (1998)	0.110	0.249	3.88	3.11	2.51	...	...	...	3.40	0.044	...
NGC 6528	BE	0.1149	0.2615	3.7413	2.3673	2.2777	1.5499	0.8223	0.7987	5.1366	0.0750	0.1268
	w/o	0.1109	0.2573	3.4276	2.3885	2.0133	1.3893	0.7406	0.6816	5.5471	0.0714	0.1183
	BM	0.1248	0.2928	4.1444	2.6491	2.4803	1.7290	0.9335	0.8722	5.4463	0.0939	0.1696
	Trager et al. (1998)	...	...	...	...	...	...	...	...	...	...	...
	1995	...	...	...	...	...	...	...	...	...	...	...
	Cohen et al. (1998)	0.097	0.247	3.89	2.96	2.45	...	...	...	4.93	0.046	...

^a: BE: background extraction; w/o: without background subtraction; BM: background modeling. See Sect. 3.1 for details.