Based on detailed 2D and 3D numerical radiation-hydrodynamics (RHD) simulations of time-dependent compressible convection, we have studied the dynamics and thermal structure of the convective surface layers of a prototypical late-type M-dwarf (
A&A 395, 99-115 (2002)
DOI: 10.1051/0004-6361:20021153
H.-G. Ludwig1,2 - F. Allard2 - P. H. Hauschildt3,2
1 - Lund Observatory, Box 43, 22100 Lund, Sweden
2 -
C.R.A.L., École Normale Supérieure, 69365 Lyon Cedex 7, France
3 -
Dept. of Physics and Astronomy & Center for Simulational Physics,
University of Georgia,
Athens, GA 30602-2451, Greece
Received 17 January 2002 / Accepted 1 August 2002
Abstract
Based on detailed 2D and 3D numerical
radiation-hydrodynamics (RHD) simulations of time-dependent
compressible convection, we have studied the dynamics and thermal
structure of the convective surface layers of a prototypical late-type
M-dwarf (
![]() ,
,
![]() ,
solar chemical
composition). The RHD models predict stellar granulation
qualitatively similar to the familiar solar pattern. Quantitatively, the granular
cells show a convective turn-over time scale of
,
solar chemical
composition). The RHD models predict stellar granulation
qualitatively similar to the familiar solar pattern. Quantitatively, the granular
cells show a convective turn-over time scale of ![]()
![]() ,
and a horizontal scale of
,
and a horizontal scale of
![]() ;
the relative intensity
contrast of the granular pattern amounts to 1.1%, and
root-mean-square vertical velocities reach 240 m s-1 at
maximum. Deviations from radiative equilibrium in the higher, formally
convectively stable atmospheric layers are found to be insignificant
allowing a reliable modeling of the atmosphere with 1D standard model
atmospheres. A mixing-length parameter of
;
the relative intensity
contrast of the granular pattern amounts to 1.1%, and
root-mean-square vertical velocities reach 240 m s-1 at
maximum. Deviations from radiative equilibrium in the higher, formally
convectively stable atmospheric layers are found to be insignificant
allowing a reliable modeling of the atmosphere with 1D standard model
atmospheres. A mixing-length parameter of
![]() = 2.1 provides the
best representation of the average thermal structure of the RHD model
atmosphere while alternative values are found when fitting the
asymptotic entropy encountered in deeper layers of the stellar
envelope (
= 2.1 provides the
best representation of the average thermal structure of the RHD model
atmosphere while alternative values are found when fitting the
asymptotic entropy encountered in deeper layers of the stellar
envelope (
![]() = 1.5), or when matching the vertical velocity (
= 1.5), or when matching the vertical velocity (
![]() = 3.5). The close correspondence between RHD and
standard model atmospheres implies that presently existing
discrepancies between observed and predicted stellar colors in the
M-dwarf regime cannot be traced back to an inadequate treatment of
convection in the 1D standard models. The RHD models predict a modest
extension of the convectively mixed region beyond the formal
Schwarzschild stability boundary which provides hints for the
distribution of dust grains in cooler (brown dwarf) atmospheres.
= 3.5). The close correspondence between RHD and
standard model atmospheres implies that presently existing
discrepancies between observed and predicted stellar colors in the
M-dwarf regime cannot be traced back to an inadequate treatment of
convection in the 1D standard models. The RHD models predict a modest
extension of the convectively mixed region beyond the formal
Schwarzschild stability boundary which provides hints for the
distribution of dust grains in cooler (brown dwarf) atmospheres.
Key words: convection - hydrodynamics - radiative transfer - stars: atmospheres - stars: late-type
Late-type M-dwarfs are fully convective stars where the convective flows penetrate far into the atmospheres reaching optical depths as low as 10-3 (Allard & Hauschildt 1995). Allard et al. (1997) have reviewed the physical, spectroscopic, and photometric properties of these objects. In the past, model atmospheres have typically failed to reproduce their spectroscopic and photometric properties in two respects: i) the near-IR spectral distribution (JHK colors) where, independent of the source of water vapor line data used, models all agree to predict an underluminous K-band (relative to J), and ii) the optical MV vs. V-I color-magnitude relation, where all models systematically predict bluer colors (i.e. being overluminous in V) than observed.
Brett (1995) raised the possibility that this near-IR problem was due to models being "too cool in the upper photospheric layers'', and suggested two possible causes: chromospheric heating and/or the treatment of convection based on mixing-length theory (MLT).
Hydrodynamical simulations of solar and stellar granulation including a realistic description of radiative transfer have become an increasingly powerful and handy instrument for studying the influence of convective flows on the the structure of late-type stellar atmospheres as well as on the formation of their spectra (e.g. Nordlund & Dravins 1990; Steffen & Freytag 1991; Ludwig et al. 1994; Freytag et al. 1996; Stein & Nordlund 1998; Asplund et al. 2000). Hitherto, model calculations have been exclusively performed for atmospheres where atomic lines are dominating the line blanketing. A possible next step in the development of hydrodynamical models is towards cooler atmospheres where molecular absorption dominates the atmospheric energy balance. Constructing hydrodynamical model atmospheres for cooler stars can shed light on the presently pressing shortcomings of the classical models mentioned above. Regarding the considerable improvements in the quality of the molecular opacities and related atmospheric models, it becomes more and more important to determine whether the treatment of convection by MLT is at the origin of the observed discrepancies.
The basic questions we want to answer in this theoretical
investigation are: Is mixing-length theory adequate to handle
convection in the atmospheres of M-dwarfs? And if so, which
mixing-length parameter
![]() is necessary to reproduce the various
thermal and dynamical properties of an atmosphere (temperature profile
in the line forming region, surface boundary condition connecting to
stellar evolution models, convective velocities)? We start by
describing some methodological aspects and the applied computer codes,
in particular discuss the critical question of how accurately we can
describe the complex radiative transfer within the hydrodynamical
simulations. We continue by presenting our results which give some
insight in what granulation looks like on the surface of an M-dwarf. We proceed with quantitative estimates of the mixing-length
parameter, and discuss the consequences for conventional atmosphere
modeling. Finally, we extrapolate slightly beyond the existing
hydrodynamical models proper, and suggest a scenario for the transport
of dust grains in brown dwarf atmospheres due to convective overshoot
which is motivated from our present simulations at hotter
temperatures. Often we refer to the Sun as our benchmark for
comparison and assume some familiarity with its atmospheric
properties.
is necessary to reproduce the various
thermal and dynamical properties of an atmosphere (temperature profile
in the line forming region, surface boundary condition connecting to
stellar evolution models, convective velocities)? We start by
describing some methodological aspects and the applied computer codes,
in particular discuss the critical question of how accurately we can
describe the complex radiative transfer within the hydrodynamical
simulations. We continue by presenting our results which give some
insight in what granulation looks like on the surface of an M-dwarf. We proceed with quantitative estimates of the mixing-length
parameter, and discuss the consequences for conventional atmosphere
modeling. Finally, we extrapolate slightly beyond the existing
hydrodynamical models proper, and suggest a scenario for the transport
of dust grains in brown dwarf atmospheres due to convective overshoot
which is motivated from our present simulations at hotter
temperatures. Often we refer to the Sun as our benchmark for
comparison and assume some familiarity with its atmospheric
properties.
The aim is to model the atmospheric structure of a prototypical late M-dwarfs as realistically as possible, with a focus on the interplay of convective flows and radiative transfer. Being well aware of the limitations in our models, we took, whenever possible, a differential approach in trying to reduce the influence of systematic uncertainties on the outcome of our investigation. This concerned mostly the dimensionality of the problem: the multi-dimensional, time dependent approach adopted in the hydrodynamical simulations versus the one-dimensional, time independent approach adopted in classical stellar atmospheres. We ensured that the numerical treatment (i.e. implemented microphysics, representation of radiative energy transport) in the two "worlds'' was as similar as possible. We employed various computer codes whose names and main characteristics we introduce below. We elaborate on specific aspects critical for the investigation in more detail later.
RHD: A radiation-hydrodynamics code developed by Å. Nordlund and R. F. Stein (see Stein & Nordlund 1998, and references therein) for modeling stellar atmospheres in two or three spatial dimensions. It implements a consistent treatment of compressible gas flows together with non-local radiative energy exchange. The radiative transfer is treated in LTE approximation, the wavelength dependence of the radiation field is represented by a small number of wavelength bins (see below). Open lower and upper boundaries, as well as periodic lateral boundaries are assumed. The effective temperature of a model (i.e. the average emergent radiative flux) is controlled indirectly by prescribing the entropy of inflowing material at the lower boundary. Magnetic fields are neglected.
LHD: A 1D Lagrangian hydrodynamics code developed by one of the authors (HGL) used to calculate standard stellar atmospheres which can be compared with results obtained with RHD. Besides the reduced dimensionality, the adopted physics (equation of state, radiative transfer scheme) is the same as in RHD. The convective energy transport is based on MLT. In this paper we adopt the MLT formulation of Mihalas (1978). Excluding one exception, all values of the mixing-length parameter are given with reference to Mihalas' formulation.
PHOENIX: A 1D model atmosphere code developed by two of the authors (PHH & FA, for a detailed description see Hauschildt & Baron 1999). It implements a treatment of the wavelength dependence of the radiation field with high resolution based on direct opacity sampling. In this investigation PHOENIX served as opacity data base, and was used for assessing the quality of the simplified radiative transfer employed in the hydrodynamics codes.
ATLAS6: A version of the 1D model atmosphere code developed by R. Kurucz (Kurucz 1979). It served as additional opacity data base.
| Name | Dim. | Mesh | Size [km] | Opacities |
|
|
|
Modelcode |
| A-3D | 3 | 125 |
250 |
PHOENIX | 4 |
|
5.0 | d3gt30g50n18 |
| B-3D | 3 | 250 |
500 |
PHOENIX | 4 |
|
5.0 | d3gt30g50n19 |
| S-3D | 3 | 125 |
6.0 |
Uppsala | 4 |
|
4.44 | sun3d |
| C-2D | 2 | 125 |
250 |
ATLAS6 | 1 |
|
5.0 | d2gt30g50n8 |
| D-2D | 2 | 251 |
250 |
ATLAS6 | 1 |
|
5.0 | d2gt30g50n9 |
Table 1 summarizes the properties of the hydrodynamical models discussed in the paper. Model A-3D is our M-dwarf reference model. The twice as large model B-3D was primarily calculated for checking effects of the domain size, the solar model S-3D was added for assessing scaling properties with effective temperature and gravitational acceleration. We note that the solar model is not strictly differentially comparable to the M-dwarf models since it is employing different opacity sources and equation of state which stem from the Uppsala stellar atmosphere package (Gustafsson et al. 1975). We do not consider this as particularly critical since the physical conditions in the atmospheres of M-dwarfs and the Sun are so different that one looses the advantages of a differential approach anyway. The 2D models C-2D and D-2D are models which were considered in the forefield to investigate effects of the numerical resolution. They are based on ATLAS6 opacities without contributions of molecular lines and employ grey radiative transfer. Due to the different input physics their behavior is qualitatively different from the more realistic 3D models. Despite their shortcomings, they are of interest for qualitatively understanding the interplay of convection and radiative transfer in optically thin regions, and therefore will be discussed in more detail. As is apparent from the table, all hydrodynamical M-dwarf models show very small fluctuations around their average effective temperature. This reflects the fact that the horizontal and temporal fluctuations of all quantities are small compared to the Sun - a central feature of the atmospheres of late-type M-dwarfs.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f1.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg41.gif) |
Figure 1:
Comparison of the specific heat at constant pressure from various
equations of state in a representative M-dwarf: RHD (solid), and PHOENIX (dash-dotted). If one
artificially removes the contribution of |
| Open with DEXTER | |
Figure 1 shows that the equation of state (EOS) which is
employed in the hydrodynamical simulations and LHD models is very
similar to the PHOENIX EOS. We do not expect significant systematic
differences by applying these two different equations of state in our
various model calculations. The equations of state of RHD and
PHOENIX treat ionization and molecular formation assuming
Saha-Boltzmann statistics. Since non-ideal effects are not pronounced
in atmospheres of M-dwarfs the inclusion of ![]() molecular
formation is the main ingredient required to obtain a realistic
description of the thermodynamics of the stellar plasma.
molecular
formation is the main ingredient required to obtain a realistic
description of the thermodynamics of the stellar plasma.
Indeed, Fig. 1 demonstrates that in the M-dwarf atmosphere
![]() molecular formation is the most important contributor
for increasing the specific heat above the value associated with the
purely translatorial degrees of freedom. In the Sun the dominant
contributor is the hydrogen ionization which has an even more dramatic
effect on the heat capacity of the stellar plasma. I.e. from the
perspective of the content of latent heat in the gas flows M-dwarf
atmospheres are not particularly extreme objects.
molecular formation is the most important contributor
for increasing the specific heat above the value associated with the
purely translatorial degrees of freedom. In the Sun the dominant
contributor is the hydrogen ionization which has an even more dramatic
effect on the heat capacity of the stellar plasma. I.e. from the
perspective of the content of latent heat in the gas flows M-dwarf
atmospheres are not particularly extreme objects.
An important problem when modeling M-dwarf envelopes is the
treatment of the large number of absorption lines in their atmospheres
which are mostly of molecular origin. The complex wavelength
dependence of the radiation field is illustrated in
Fig. 2. While it is already a formidable task to treat the
frequency dependence of the radiation field in 1D model atmospheres,
this is even more the case in hydrodynamical models where one has to
account for the 3D geometry of the flow field and its temporal
evolution. Present computer capacity allows only for a very modest
number of frequency points to be included in the modeling of the
radiation field within a hydrodynamical simulation. However, the
situation is somewhat alleviated. For the interaction of
hydrodynamics and radiative transfer only the frequency integrated
net amount of radiative heating (or cooling if negative)
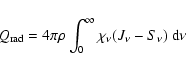 |
(1) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f2.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg47.gif) |
Figure 2:
Scatter plot of standard optical depth where the monochromatic optical
depth reaches unity as a function of wavelength in a PHOENIX model
atmosphere with
|
| Open with DEXTER | |
It is clear that the sorting procedure described before is specific to
the stellar atmosphere under consideration and has to be repeated as
soon as the atmospheric parameters differ widely from the one where
the sorting was done. We used a model atmosphere calculated with
PHOENIX at
![]() and
and
![]() as reference
atmosphere for the grouping. It is sufficiently close to the
atmospheric parameters of the hydrodynamical models.
This has been checked by studying the performance of the sorting when
applied to differing atmospheric parameters (
as reference
atmosphere for the grouping. It is sufficiently close to the
atmospheric parameters of the hydrodynamical models.
This has been checked by studying the performance of the sorting when
applied to differing atmospheric parameters (
![]() down to
3.0, and
down to
3.0, and
![]() up to 3300 K).
up to 3300 K).
The sorting criterion that
![]() should fall within a
certain depth range in the atmosphere does not guarantee that the
overall depth dependence of
should fall within a
certain depth range in the atmosphere does not guarantee that the
overall depth dependence of
![]() is similar for all
frequencies grouped together - a condition for allowing the
interchange of the solution of the transfer equation with the
frequency integration when evaluating
is similar for all
frequencies grouped together - a condition for allowing the
interchange of the solution of the transfer equation with the
frequency integration when evaluating
![]() .
In particular,
the simultaneous presence of atomic and molecular lines can lead to
significantly different functional forms of the monochromatic optical
depth at different frequencies: deeper regions of the atmosphere too
hot to allow for molecule formation might be dominated by atomic lines
while higher and cooler regions which allow for molecule formation
might be dominated by molecular lines. If the atomic and molecular
lines emerge from different elements there is no physical
connection between them leading to an uncorrelated behavior in optical
depth of deeper and higher layers with frequency. Such a situation
would be unfavorable for the OBM. However, the OBM is rather
successful in reproducing the heat exchange between radiation and
matter - as evident from Fig. 3.
This is linked to the statistical dominance of molecular
absorption in all radiative layers of the rather cool
atmosphere under consideration.
.
In particular,
the simultaneous presence of atomic and molecular lines can lead to
significantly different functional forms of the monochromatic optical
depth at different frequencies: deeper regions of the atmosphere too
hot to allow for molecule formation might be dominated by atomic lines
while higher and cooler regions which allow for molecule formation
might be dominated by molecular lines. If the atomic and molecular
lines emerge from different elements there is no physical
connection between them leading to an uncorrelated behavior in optical
depth of deeper and higher layers with frequency. Such a situation
would be unfavorable for the OBM. However, the OBM is rather
successful in reproducing the heat exchange between radiation and
matter - as evident from Fig. 3.
This is linked to the statistical dominance of molecular
absorption in all radiative layers of the rather cool
atmosphere under consideration.
Another point concerning the present implementation of the
OBM is our usage of global Rosseland means - i.e. Rosseland averages
over the whole frequency range - for representing the average
opacity in each bin. For the the continuum we took the Rosseland means
themselves while we scaled them by factors of 101, 102 , and
103 for the bins representing the successively stronger lines. The
scaling factors correspond to the factors of 10 in optical depth
selected as thresholds for the sorting procedure which are
![]() -0.5, -
-0.5, -
![]() -2.5(see Fig. 2). The basic assumption behind this approach is
that the line opacity scales with temperature and pressure like the
continuous opacity. The source function has been integrated over the
frequency ranges of the individual bins. While it is certainly not the
optimal representation of the opacities it was dictated by the lack of
a detailed tabulation of the monochromatic opacities over the full
temperature-pressure range of interest. Work is presently under way to
generate such tabulation which is a non-trivial task due to the
enormous amount of line data which need to be processed.
Considering the various approximations described before one
might ask whether the OBM is a real improvement beyond a grey
description. Eventually, this can be tested quantitatively by
comparing 1D atmospheres computed with high frequency resolution or
the OBM. Such a comparison serves as ultimate indicator of the
performance of the OBM.
-2.5(see Fig. 2). The basic assumption behind this approach is
that the line opacity scales with temperature and pressure like the
continuous opacity. The source function has been integrated over the
frequency ranges of the individual bins. While it is certainly not the
optimal representation of the opacities it was dictated by the lack of
a detailed tabulation of the monochromatic opacities over the full
temperature-pressure range of interest. Work is presently under way to
generate such tabulation which is a non-trivial task due to the
enormous amount of line data which need to be processed.
Considering the various approximations described before one
might ask whether the OBM is a real improvement beyond a grey
description. Eventually, this can be tested quantitatively by
comparing 1D atmospheres computed with high frequency resolution or
the OBM. Such a comparison serves as ultimate indicator of the
performance of the OBM.
Figure 3 shows a comparison of 1D model atmospheres
calculated with PHOENIX employing opacity sampling with a wavelength
resolution of ![]()
![]() ,
and LHD employing the OBM as
described before. Comparing flux constant models in radiative and
radiative-convective equilibrium shows a good correspondence of the
resulting equilibrium temperature profiles. While the radiative
equilibrium models are less important for the investigation of M-dwarf
atmospheres, they were added to the comparison to show the similarity
in the radiative transport properties independent of influences of the
convective transport. More important are the models in
radiative-convective equilibrium since they are closer to the actual
physical situation. For judging the correspondence between opacity
sampling and OBM models one should take the grey model as benchmark
which represents a strongly simplified (equivalent to one frequency
bin) description of radiative transfer. Clearly, the OBM matches much
more closely the PHOENIX opacity sampling model. The cooling of the
higher atmosphere by lines is reasonably represented as well as the
backwarming of the deeper layers.
,
and LHD employing the OBM as
described before. Comparing flux constant models in radiative and
radiative-convective equilibrium shows a good correspondence of the
resulting equilibrium temperature profiles. While the radiative
equilibrium models are less important for the investigation of M-dwarf
atmospheres, they were added to the comparison to show the similarity
in the radiative transport properties independent of influences of the
convective transport. More important are the models in
radiative-convective equilibrium since they are closer to the actual
physical situation. For judging the correspondence between opacity
sampling and OBM models one should take the grey model as benchmark
which represents a strongly simplified (equivalent to one frequency
bin) description of radiative transfer. Clearly, the OBM matches much
more closely the PHOENIX opacity sampling model. The cooling of the
higher atmosphere by lines is reasonably represented as well as the
backwarming of the deeper layers.
The most important deviation between opacity sampling and OBM model
occurs in the layers where the transition from convectively to
radiatively dominated energy transport takes place (around
![]() ). The OBM stratification becomes noticeably cooler. This was
traced back to an insufficient heating of the gas in the OBM continuum
bin. This in turn is probably related to the use of Rosseland averages
for the continuum opacity in these optically thin regions. Planck
averages would be more suitable. But again, at the time this work was
performed only globally averaged opacities were available. Rosseland
and Planck averages differ by at least a factor of 100 in these
regions, making an ad hoc switching from one to the other
problematic. However, we consider the remaining deviations not as
vital, in particular with respect to the calibration of the
mixing-length parameter which we describe later in this paper. The
calibration is a result of a differential comparison of models which
all base on the OBM.
). The OBM stratification becomes noticeably cooler. This was
traced back to an insufficient heating of the gas in the OBM continuum
bin. This in turn is probably related to the use of Rosseland averages
for the continuum opacity in these optically thin regions. Planck
averages would be more suitable. But again, at the time this work was
performed only globally averaged opacities were available. Rosseland
and Planck averages differ by at least a factor of 100 in these
regions, making an ad hoc switching from one to the other
problematic. However, we consider the remaining deviations not as
vital, in particular with respect to the calibration of the
mixing-length parameter which we describe later in this paper. The
calibration is a result of a differential comparison of models which
all base on the OBM.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f3.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg57.gif) |
Figure 3:
Comparison of 1D standard model atmospheres (
|
| Open with DEXTER | |
For completeness, we finally remark that only the exchange of energy was considered within the radiative transfer. The exchange of momentum was neglected; the prevailing relatively high mass densities combined with low radiative fluxes render radiation pressure unimportant for the structure of M-dwarf atmospheres.
To get an overview of the problem Fig. 4 shows various
characteristic time scales in a representative M-dwarf model ( LHD model with
![]() = 2790 K,
= 2790 K,
![]() = 5.0,
= 5.0,
![]() = 1.0). The expressions
which we applied in the calculation of the time scales are summarized
in the appendix. The time scales have been evaluated under simplifying
assumptions, and should therefore be taken as order of magnitude
estimates only.
= 1.0). The expressions
which we applied in the calculation of the time scales are summarized
in the appendix. The time scales have been evaluated under simplifying
assumptions, and should therefore be taken as order of magnitude
estimates only.
The radiative time scales based on ATLAS6 and PHOENIX Rosseland mean opacities are rather similar in the deeper layers while being very different in the optically thin regime. This emphasizes the great influence of molecular absorption which becomes important at cooler temperatures and which is not included in the ATLAS6 opacities. The radiative time scales from PHOENIX Rosseland and Planck opacities differ also significantly. Comparing the radiative time scales to a dynamical or convective time scale as given by the Brunt-Väisälä period leads us to expect that one gets a qualitatively different behavior depending on the treatment of the radiative transfer. We will see that models based on a frequency-independent Rosseland opacities show significant deviations from radiative equilibrium conditions. A more realistic treatment - in the optically thin regions more closely represented by the Planck mean opacities - results in an atmospheric structure closer to radiative equilibrium. In all cases, one expects an almost adiabatic structure in the deeper layers since the radiative relaxation time is much longer than the convective time scale.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f4.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg58.gif) |
Figure 4: Various characteristic time scales as a function of pressure in an M-dwarf model: Brunt-Väisälä period (solid), Kelvin-Helmholtz time scale (dashed), radiative relaxation time based on ATLAS6 Rosseland opacities (dotted), PHOENIX Rosseland (dashed-dotted), and PHOENIX Planck (triple-dot-dashed) opacities. A logarithmic Rosseland optical depth scale is indicated by the tick marks near the abscissa. The kink in the run of the Brunt-Väisälä period is located at the boundary between the convectively stable and unstable part of the model. |
| Open with DEXTER | |
RHD uses an explicit numerical scheme for advancing the solution in
time. It is well known that in an explicit scheme the time step is
limited to a fraction of the dynamical time scale, more precisely to
the limit given by the Courant-Friedrichs-Levy stability
condition. Together with the amount of available computer - and
wallclock - time, this limits the time interval which can be covered
by a 3D RHD model to about
![]() of stellar time.
Figure 4 seemingly implies that it is impossible to
obtain a thermally relaxed hydrodynamical model within this time
interval since the Kelvin-Helmholtz time scale of the deeper layers is
at least an order of magnitude larger. Contrary to the impression
given in Fig. 4, in the multi-dimensional hydrodynamical
simulations this does not pose a problem since the thermal relaxation
of the model is not governed by the time scale for the
exchange of energy as expressed by the Kelvin-Helmholtz time. In fact,
the thermal evolution of the deeper layers of the RHD models is
governed by the time scale for the exchange of mass in these layers
which is much shorter (as quantified below, see
Fig. 16). Due to the exponential run in density of the
atmosphere the mass exchange consists primarily of the replacement of
mass by fresh material stemming from deeper layers. In the
hydrodynamical model it is ultimately fed into the computational
domain at the lower boundary.
The convective energy flux is the net effect of the energy
transported by counteracting, opposing mass currents in and out of a
test volume. The advective - as opposed to diffusive - nature of
the mass transport leads to a situation where there can be a large
imbalance in the energy content of the mass currents: the in-coming
mass elements carry the energy (strictly speaking the specific
entropy) of much deeper layers (in the hydrodynamical model the
entropy at the lower boundary), while the out-going elements just
carry the local energy density. This implies an energy flux much
larger than the one close to equilibrium conditions. The system is
driven much faster towards equilibrium than implied by the
classical Kelvin-Helmholtz time scale, which assumes an energy flux
as encountered close to equilibrium conditions.
of stellar time.
Figure 4 seemingly implies that it is impossible to
obtain a thermally relaxed hydrodynamical model within this time
interval since the Kelvin-Helmholtz time scale of the deeper layers is
at least an order of magnitude larger. Contrary to the impression
given in Fig. 4, in the multi-dimensional hydrodynamical
simulations this does not pose a problem since the thermal relaxation
of the model is not governed by the time scale for the
exchange of energy as expressed by the Kelvin-Helmholtz time. In fact,
the thermal evolution of the deeper layers of the RHD models is
governed by the time scale for the exchange of mass in these layers
which is much shorter (as quantified below, see
Fig. 16). Due to the exponential run in density of the
atmosphere the mass exchange consists primarily of the replacement of
mass by fresh material stemming from deeper layers. In the
hydrodynamical model it is ultimately fed into the computational
domain at the lower boundary.
The convective energy flux is the net effect of the energy
transported by counteracting, opposing mass currents in and out of a
test volume. The advective - as opposed to diffusive - nature of
the mass transport leads to a situation where there can be a large
imbalance in the energy content of the mass currents: the in-coming
mass elements carry the energy (strictly speaking the specific
entropy) of much deeper layers (in the hydrodynamical model the
entropy at the lower boundary), while the out-going elements just
carry the local energy density. This implies an energy flux much
larger than the one close to equilibrium conditions. The system is
driven much faster towards equilibrium than implied by the
classical Kelvin-Helmholtz time scale, which assumes an energy flux
as encountered close to equilibrium conditions.
We have argued from the perspective of our hydrodynamical models. But the fast thermal relaxation is driven by a physical mechanism implying that a real stellar convection zone does not operate any differently. Hence, we want to stress that to our understanding the thermal relaxation of a convective layer is generally not governed by the classical Kelvin-Helmholtz time scale but by the usually shorter time scale of mass exchange.
In the one-dimensional LHD models no mass exchange takes place and the convective energy flux is computed from MLT, in which convection is modeled as diffusion process. Under such circumstances the time scale of the thermal evolution of the convective layers is indeed comparable to the Kelvin-Helmholtz time scale as shown in Fig. 4. Of course, covering the time interval necessary for the slower thermal relaxation in a 1D model run poses no problems due to the largely reduced computational costs.
Models C-2D and D-2D are 2D models (see Table 1) which were constructed to gain experience regarding the size of the computational domain and grid resolution. They are based on grey radiative transfer utilizing ATLAS6 opacities which do not include contributions of molecular lines. The choice of the ATLAS6 opacities was dictated by the lack of more realistic opacities during the initial phase of the project. From Fig. 4 one might readily conclude that their atmospheric structure will be dominated by convection since the radiative relaxation times in the atmosphere are long as compared to the dynamical time scale. Indeed, when starting from a temperature structure taken from a LHD model based on MLT, we find a rapid cooling of the originally radiatively stratified atmospheric layers by convective overshooting (see Fig. 5). Convection tends to transform the stratification into a purely adiabatic one since the radiative heating is too weak to keep the temperature close to the radiative equilibrium value. The transformation into an almost adiabatic stratification takes too long to be covered within the multi-dimensional hydrodynamical simulations. However, we conducted numerical experiments with LHD where an ad hoc velocity field mimicking the convective overshoot was put into the atmospheric regions which are formally stable according to the Schwarzschild criterion. The LHD models indicate that the asymptotic temperature profile tends to a fully adiabatic stratification.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f5.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg61.gif) |
Figure 5:
Temporal evolution of the average temperature profile of model C-2D in steps of 5 ks showing a successive cooling of the layers
around
|
| Open with DEXTER | |
Due to the unrealistic opacities, the models cannot give a good
representation of a real M-dwarf atmosphere. They are nevertheless
interesting from a numerical point of view. The resolution of the less
resolved model C-2D is already sufficient to represent the
convective transport properties, in particular in the important
transition region from convectively to radiatively dominated energy
transport: after an initial relaxation phase we find in both models
that the minimum temperature drops linearly with a rate of
![]() .
Looking at further diagnostics at comparable instances
during the secular evolution of the model runs we observe that RMS
velocities are similar within a 20% level. The higher resolved
model shows somewhat more small-scale features, and its downflows
appear more concentrated. However, we are primarily interested in the
balance of convective to radiative energy transport. The temperature
drop rate is a convenient measure of the relative efficiency of both
processes. Hence, we conclude from the similarity of the drop rates
that the resolution of the less resolved model applied in 3D
simulations is sufficient to model the transport properties of the
convective flows.
.
Looking at further diagnostics at comparable instances
during the secular evolution of the model runs we observe that RMS
velocities are similar within a 20% level. The higher resolved
model shows somewhat more small-scale features, and its downflows
appear more concentrated. However, we are primarily interested in the
balance of convective to radiative energy transport. The temperature
drop rate is a convenient measure of the relative efficiency of both
processes. Hence, we conclude from the similarity of the drop rates
that the resolution of the less resolved model applied in 3D
simulations is sufficient to model the transport properties of the
convective flows.
Another conclusion which can be drawn from these models is that standard MLT models can give quite misleading predictions of the atmospheric temperature structure if the radiative relaxation time is long in comparison to convective time scales. In other words, one should be cautious when the coupling of the temperature structure to the radiative equilibrium temperature is so weak that overshoot of low amplitude happens essentially adiabatically. In the following we shall see that M-dwarf atmospheres are unlikely to exhibit such conditions.
Figure 6 shows a typical snapshot of the emergent intensity
during the temporal evolution of model B-3D. For comparison,
Fig. 7 shows a similar snapshot from the solar
run S-3D. Note, that the spatial and intensity scaling is very
different in the reproductions, hence, only relative geometrical
properties should be directly compared. The average relative RMS
intensity contrast of the granular pattern amounts to 1.1% in
the M-dwarf as opposed to 16% in the solar case. The first
thing to note is that surface convection in an M-dwarf produces a
granular pattern qualitatively resembling solar granulation: bright
extended regions of upwelling material which are surrounded by dark
concentrated lanes of downflowing material. The dark lanes form an
interconnected network. Looking more closely, granules are less
regularly delineated in M-dwarfs, the inter-granular lanes show a
higher degree of variability in terms of their strength. A feature
which is uncommon in the solar granulation pattern are the dark
"knots'' (e.g. at
![]() and
and
![]() in
Fig. 6) found in or attached to the inter-granular
lanes. The knots are associated with strong downdrafts which carry a
significant vertical component of angular momentum. The width of the
inter-granular lanes to the typical granular size is smaller in
M-dwarfs. Inspecting the velocity field (not shown) in vicinity of the
continuum forming layers shows less pronounced size differences. This
indicates that the relatively broader lanes in the solar case are the
result of a stronger smoothing of the temperature field due to a more
intense radiative energy exchange, i.e. the effective Peclét
number of the flow is larger around optical depth unity in M-dwarfs.
in
Fig. 6) found in or attached to the inter-granular
lanes. The knots are associated with strong downdrafts which carry a
significant vertical component of angular momentum. The width of the
inter-granular lanes to the typical granular size is smaller in
M-dwarfs. Inspecting the velocity field (not shown) in vicinity of the
continuum forming layers shows less pronounced size differences. This
indicates that the relatively broader lanes in the solar case are the
result of a stronger smoothing of the temperature field due to a more
intense radiative energy exchange, i.e. the effective Peclét
number of the flow is larger around optical depth unity in M-dwarfs.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f6.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg65.gif) |
Figure 6:
Typical snapshot of emergent intensity during the evolution of
model B-3D. The intensity contrast amounts to
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f7.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg66.gif) |
Figure 7:
Like Fig. 6, but for the solar model S-3D. The
intensity contrast amounts to
|
| Open with DEXTER | |
The different magnitude of the intensity contrast already indicates
that horizontal fluctuations of the thermodynamic quantities are small
in M-dwarf atmospheres. Figure 8 shows the run of the
relative temperature and pressure fluctuations in
model A-3D. Plotted are long term temporal and horizontal![]() rms averages. As we will argue later, the fluctuations in the higher
atmosphere are likely to be overestimated in the model. But even taken
at face value they are quite modest. The low level of fluctuations in
the thermodynamic quantities is accompanied by small flow velocities,
the maximum Mach number amounts to 6.5% in model A-3D. MLT
models show that Mach numbers drop to even lower values as one goes to
lower effective temperatures which are encountered in the regime of
brown dwarfs. Our findings may have a direct bearing on the dust
formation conditions in such objects. Our hydrodynamical simulations
support the view that dust forming layers in cool main sequence
objects experience only small variations around their mean
thermodynamic state. This view is clearly at odds with the scenario
discussed by Helling et al. (2001) who study the dust formation in
turbulent brown dwarf atmospheres. Helling et al. assume thermodynamic
fluctuations of order unity.
rms averages. As we will argue later, the fluctuations in the higher
atmosphere are likely to be overestimated in the model. But even taken
at face value they are quite modest. The low level of fluctuations in
the thermodynamic quantities is accompanied by small flow velocities,
the maximum Mach number amounts to 6.5% in model A-3D. MLT
models show that Mach numbers drop to even lower values as one goes to
lower effective temperatures which are encountered in the regime of
brown dwarfs. Our findings may have a direct bearing on the dust
formation conditions in such objects. Our hydrodynamical simulations
support the view that dust forming layers in cool main sequence
objects experience only small variations around their mean
thermodynamic state. This view is clearly at odds with the scenario
discussed by Helling et al. (2001) who study the dust formation in
turbulent brown dwarf atmospheres. Helling et al. assume thermodynamic
fluctuations of order unity.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f8.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg68.gif) |
Figure 8:
Relative horizontal temperature (solid) and pressure
(dashed) fluctuations of model A-3D. The fluctuations in the
region
|
| Open with DEXTER | |
Another important feature, which distinguishes M-dwarf atmospheric
conditions from solar ones, is the extent of the convective layers. As
evident from Figs. 11 and 12, the
convective motions reach much lower optical depth
(
![]()
![]() -1.5) in the M-dwarf than in the
Sun (
-1.5) in the M-dwarf than in the
Sun (
![]() ). Two factors contribute
to this behavior. The temperature gradient in non-grey radiative
equilibrium is significantly steeper in the M-dwarf than in the Sun,
presumably due to efficient cooling of the atmospheric layers by
molecular lines. Furthermore, the
). Two factors contribute
to this behavior. The temperature gradient in non-grey radiative
equilibrium is significantly steeper in the M-dwarf than in the Sun,
presumably due to efficient cooling of the atmospheric layers by
molecular lines. Furthermore, the ![]() molecule formation
reduces the adiabatic gradient in the M-dwarf atmosphere, while in the
Sun the hydrogen recombination is essentially completed in
subphotospheric layers. The different radiative and thermodynamic
conditions favor the presence of convection in M-dwarf atmospheres.
molecule formation
reduces the adiabatic gradient in the M-dwarf atmosphere, while in the
Sun the hydrogen recombination is essentially completed in
subphotospheric layers. The different radiative and thermodynamic
conditions favor the presence of convection in M-dwarf atmospheres.
In the deeper layers we observe the tendency - also known from solar simulations (see Stein & Nordlund 1998) - that the granular network of downflows decays into isolated downdrafts. Our models are rather shallow reaching only 2.3 pressure scale heights below optical depth unity. Thus we cannot follow the change of flow topology as far as has been done for solar models, but within the limited depth range comprised by our models we do not see indications of a qualitatively different behavior as found in the Sun.
In the following we shall discuss spatial power spectra of intensity and vertical velocity. Note, that in the Figs. 9 and 10 we display power per logarithmic wavenumber interval and not per unit wavenumber - the more common choice. This allows visually for a more direct identification of the power carrying scales. However (in humble respect of Kolmogorov's achievements), we labeled the power laws drawn for comparison with the familiar spectral index of power per unit wavenumber. The spectra are temporal averages over one to a few convective turn-over times and many convective cells, so that they are statistically representative.
Figure 9 shows a comparison of power spectra of the emergent intensity (more precisely: the intensity in the OBM continuum bin in vertical direction at the upper boundary of the computational volume) for the models A-3D, and B-3D as well as the solar model. Figure 10 shows a corresponding comparison of the vertical velocity component measured at the layer where its RMS value reaches the maximum. To facilitate a comparison between the M-dwarf models and the solar model, the solar model was arbitrarily scaled in power and wavenumber so that the maxima and position of the power distributions matched. For the M-dwarf models the hump in power at the highest wavenumbers is likely an artifact of an imperfect choice of parameters controlling the small scale dissipation and should be ignored.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f9.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg73.gif) |
Figure 9:
Power spectrum of the emergent intensity pattern for model A-3D (solid), and B-3D (dashed), as well as the solar
model S-3D (dotted). The spectrum of the solar model was
scaled in power as well as wavenumber to match the peak of power in
the M-dwarf models. Lines with slopes
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8.8cm,clip]{ms2282f10.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg74.gif) |
Figure 10:
Power spectrum of the vertical velocity pattern, line styles as in
Fig. 9. The solar power spectrum was scaled to match the
peak of power of the M-dwarf models. The velocity pattern was
taken from the layer where the RMS vertical velocity reaches its
maximum, with absolute values of
|
| Open with DEXTER | |
Fluctuations in the Sun are an order of magnitude larger and had to be reduced accordingly in order to match the height of the maxima in the M-dwarf models, while the horizontal scale of the solar model had to be shrunk by a factor of 15. This factor closely corresponds to variation of the pressure scale height at the surface (factor 12.5) and follows the scaling found for hotter models by Freytag et al. (1997). Different from Freytag et al., we accounted for the change of the mean molecular weight of the stellar gas since the H2 molecular formation leads to a significant increase in M-dwarf atmospheres. The peak power of the M-dwarf models is located at an absolute scale of 80 km for intensity and 63 km for velocity structures.
Comparing the width of the power distribution at 1 dex below peak level, the M-dwarf model B-3D displays a range of scales of 1.4 dex, the solar model of 1.1 dex. As is evident from the figures, the solar scale distribution is slightly but noticeably narrower. This might be traced back to the lower Péclet number of the plasma encountered at the surface of an M-dwarfs as opposed to solar conditions. The formation of small scale structures is more strongly suppressed by the radiation field under solar conditions, leading to an overall narrower power distribution. Model A-3D apparently lacks some larger scale power indicating that the computational box is somewhat too small in this case. However, since the total fluctuations are very similar in the models we conclude that the relevant structures are captured in model A-3D which serves as our standard model.
Towards high wavenumbers the M-dwarf spectra do not show a clear power law behavior. In any case, they cannot be fitted with a -5/3 slope, and are at best roughly compatible with a -17/3 slope. We would like to emphasize that despite the very different physical parameters of M-dwarf atmospheres this is qualitatively what was already found in solar models, and is at odds with expectations for homogeneous and isotropic turbulence. While smaller scales in the hydrodynamical models are definitely influenced by the artificial viscosity, it is still somewhat surprising that the asymptotic behavior in the Sun as well as in the M-dwarf is so similar despite their quite different characteristic flow speeds (i.e. Mach numbers). While our present models cannot make definite statements about the properties of small scale turbulence, a "non-Kolmogorov'' behavior cannot be ruled out neither. See Nordlund et al. (1997) for an in-depth discussion of this issue in a solar context.
Figures 11-13 show a comparison of the thermal structure of our "best'' hydrodynamical model A-3D with standard 1D atmosphere models computed with LHD. Again, we point out that the treatment of the microphysics (equation of state and opacities) is equivalent between RHD and LHD models. Differences lie mainly in the dimensionality of the models - 3D versus 1D - and the related MLT treatment of the convective energy transport in LHD. In LHD effects of the turbulent pressure due to convective velocities computed from MLT are neglected. This approximation is well justified since the turbulent pressure - as found in the RHD simulations - nowhere exceeds 0.5% of the gas pressure.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f11.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg77.gif) |
Figure 11:
Overview of the temperature-pressure relation of hydrodynamical
model A-3D (solid) and three standard mixing-length model
atmospheres (dash-dotted) with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f12.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg78.gif) |
Figure 12:
Temperature-pressure relations like in Fig. 11 but
focusing on the transition region from convective to radiative energy
transport. In this region the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f13.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg80.gif) |
Figure 13:
Entropy-pressure relation of hydrodynamical model A-3D (solid) and three standard mixing-length model atmospheres
(dash-dotted) with
|
| Open with DEXTER | |
For the hydrodynamical model we have plotted in fact six different
mean stratifications in the afore mentioned figures, each one a
horizontal and temporal average over a 250 s time interval -
comparable to the turn-over time of the convective cells. The
statistical variations are so small that the profiles are virtually
indistinguishable on the scale of the plots demonstrating again that
we are dealing with atmospheres showing little temporal and horizontal
fluctuations. Figure 11 shows that the mean thermal
structure of the hydrodynamical model corresponds closely to those of
mixing-length models. The mixing-length models themselves do not show
a strong dependence on the mixing-length. In the deeper, convective
layers small horizontal entropy fluctuations
are sufficient to carry the convective flux, and the radiative energy
transport is unimportant. Here the stratification has to follow
essentially an adiabat in the pressure-temperature plane. The same
reasoning holds for the hydrodynamical as well as MLT models. The
situation is somewhat different in the radiative layers. By
construction, the mixing-length models have to approach a temperature
profile corresponding to radiative equilibrium conditions. Since the
differences among the mixing-length models in the convective region
are small the radiative equilibrium profiles are almost identical as
well. In the hydrodynamical model the temperature of the higher
atmospheric layers (
![]() )
is controlled by a competition of
radiative heating and adiabatic cooling of material which overshoots
into regions with formally stable entropy gradient
)
is controlled by a competition of
radiative heating and adiabatic cooling of material which overshoots
into regions with formally stable entropy gradient
![]() (see Fig. 13), and, analogously, the radiative cooling and
adiabatic heating of downflowing material. The relative time scales
involved in adiabatic and radiative temperature changes determine how
the temperature will adjust between the upper extreme - the
radiative equilibrium temperature - and the lower extreme - the
temperature achieved during adiabatic expansion of a rising mass
element in the higher atmosphere.
(see Fig. 13), and, analogously, the radiative cooling and
adiabatic heating of downflowing material. The relative time scales
involved in adiabatic and radiative temperature changes determine how
the temperature will adjust between the upper extreme - the
radiative equilibrium temperature - and the lower extreme - the
temperature achieved during adiabatic expansion of a rising mass
element in the higher atmosphere.
Obviously, in the present case, radiative processes dominate and the hydrodynamical model closely follows the radiative equilibrium temperature. As we have seen in the context of the hydrodynamical models adopting grey ATLAS6 opacities this is not necessarily so. In fact, we trace back the short radiative time scales (see Fig. 4) to the presence of molecular absorption which provides the close coupling of the stratification to the radiative equilibrium temperature. We speculate here that the situation might change significantly when one goes to metal poor objects. Convective velocities are likely not to be reduced as dramatically as the atmospheric opacities, shifting the relative importance towards adiabatic cooling. This might lead to a significant deviation from radiative equilibrium in the atmospheric layers of such objects. Indeed, for metal poor dwarfs at about solar effective temperatures such effects are found in hydrodynamical models (e.g. Asplund & Garcia Perez 2001).
Quantitatively, there are small differences in the thermal structure
between the hydrodynamical model and the mixing-length models. As one
can expect the differences are most pronounced in the transition
region between convectively and radiatively dominated energy transport
where the detailed balance between both processes decides about the
resulting temperature profile. Figures 12
and 13 show that the hydrodynamical model has a mean
thermal structure which is close to the profiles of the mixing-length
models but cannot be matched exactly. This certainly comes not as a
big surprise when one considers the simplistic nature of mixing-length
theory. However, certain aspects of the hydrodynamical model can be
matched by choosing a mixing-length model from the set which are parameterized
by
![]() .
This is most easily done considering the entropy since it
emphasizes model differences (see Fig. 13). The entropy of
inflowing material of the hydrodynamical model which we interpret as
the entropy of material located in the deep almost perfectly
adiabatically stratified part of the stellar envelope is matched best
by a mixing-length model of
.
This is most easily done considering the entropy since it
emphasizes model differences (see Fig. 13). The entropy of
inflowing material of the hydrodynamical model which we interpret as
the entropy of material located in the deep almost perfectly
adiabatically stratified part of the stellar envelope is matched best
by a mixing-length model of
![]() .
In global
stellar structure models the entropy of the envelope controls to some
extent the radius of a star, making
.
In global
stellar structure models the entropy of the envelope controls to some
extent the radius of a star, making
![]() most relevant
for evolutionary models - hence, our naming "evo''. For
further justification and discussion of our interpretation see
Steffen (1993) and Ludwig et al. (1999).
most relevant
for evolutionary models - hence, our naming "evo''. For
further justification and discussion of our interpretation see
Steffen (1993) and Ludwig et al. (1999).
If one wants to match the entropy jump of the hydrodynamical model
![]() provides the closest fit. The entropy jump is the
entropy difference between the atmospheric entropy minimum and the
asymptotic entropy of the deeper layers. The entropy jump
provides a qualitative measure of the overall available convective
driving, and in the present case also gives a match to the
temperature gradient of the deeper photosphere with
provides the closest fit. The entropy jump is the
entropy difference between the atmospheric entropy minimum and the
asymptotic entropy of the deeper layers. The entropy jump
provides a qualitative measure of the overall available convective
driving, and in the present case also gives a match to the
temperature gradient of the deeper photosphere with
![]() .
The internal uncertainties in the determination of
.
The internal uncertainties in the determination of
![]() and
and
![]() are small (
are small (![]()
![]() )
as estimated from the statistical fluctuations observed in the
models.
However, in the present M-dwarf model small deviations from
equilibrium conditions determine the mixing-length parameters. This
is a challenging situation for any numerical scheme, and we consider
it possible that the actual calibration errors are dominated by
related systematic uncertainties.
)
as estimated from the statistical fluctuations observed in the
models.
However, in the present M-dwarf model small deviations from
equilibrium conditions determine the mixing-length parameters. This
is a challenging situation for any numerical scheme, and we consider
it possible that the actual calibration errors are dominated by
related systematic uncertainties.
Throughout this paper mixing-length parameters are given with respect to the formulation of MLT according Mihalas (1978) (see Ludwig et al. 1999 for details of the implementation). The formulation of Mihalas is widely used, in particular in the context of stellar atmosphere work. But it is by far not the only MLT "dialect'' around. Another widely used formulation is the original one by Böhm-Vitense (1958) which is often encountered in the context of stellar evolution work. We would like to emphasize that generally the details in the MLT implementation have a direct and significant influence on the calibration of the mixing-length parameter. This is particularly true in the present case where convection penetrates far into optically thin regions. Typically it is the treatment of the radiative energy exchange of the convective elements in the optically thin limit that distinguishes the various MLT formulations. For enabling inter-comparison in other context, we like to mention that the MLT formulation in PHOENIX is similar but slightly different from the Mihalas formulation. However, test calculations have shown that numerical differences are negligible in the M-dwarf regime. Furthermore, in the ATLAS6 stellar atmosphere code the Mihalas formulation is implemented. MLT formulations as given by Kippenhahn & Weigert (1991) and Stix (1989) are identical to the Böhm-Vitense formulation.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f14.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg88.gif) |
Figure 14:
Entropy-pressure relation of hydrodynamical model A-3D (solid) and standard mixing-length model atmospheres with
|
| Open with DEXTER | |
Figure 14 shows a comparison of the entropy profiles of
standard mixing-length models of the same
![]() based on
the the Mihalas and Böhm-Vitense formulation.
We concentrate on the entropy jump since it is sensitive to
the convective transport in the optically thick and thin layers. The
asymptotic entropy level of the deeper layers is largely controlled by
the entropy change over the optically thick layers only. Mihalas and
Böhm-Vitense formulation differ little here, implying the rather
similar outcome. The formulations differ significantly in the
optically thin layers. Clearly, the entropy jump comes out to be
almost a factor of 2 larger in the Böhm-Vitense formulation! To
reduce the entropy jump to a level comparable as obtained from the
Mihalas formulation, one had to increase the mixing-length parameter
noticeably. Again, this emphasizes that
based on
the the Mihalas and Böhm-Vitense formulation.
We concentrate on the entropy jump since it is sensitive to
the convective transport in the optically thick and thin layers. The
asymptotic entropy level of the deeper layers is largely controlled by
the entropy change over the optically thick layers only. Mihalas and
Böhm-Vitense formulation differ little here, implying the rather
similar outcome. The formulations differ significantly in the
optically thin layers. Clearly, the entropy jump comes out to be
almost a factor of 2 larger in the Böhm-Vitense formulation! To
reduce the entropy jump to a level comparable as obtained from the
Mihalas formulation, one had to increase the mixing-length parameter
noticeably. Again, this emphasizes that
![]() is only well defined
with reference to a specific MLT formulation.
is only well defined
with reference to a specific MLT formulation.
The Böhm-Vitense formulation assumes optically thick convective elements throughout. Their radiative energy exchange is described in diffusion approximation. It might be surprising that the entropy jump obtained from the Böhm-Vitense formulation is larger than from the Mihalas formulation which distinguishes between optically thick and thin elements. The optically thin elements loose (or gain) energy in a non-diffusive fashion. A larger entropy jump implies larger radiative losses of the convective elements. Intuitively, one would expect that a diffusive transport is rather inefficient, implying a smaller energy exchange and smaller entropy jump. However, Eq. (A.3) shows that the situation is reversed: the thermal adjustment time of convective elements becomes independent of their optical thickness in the optically thin limit, while the diffusion approximation predicts (inaccurately) a decrease of the adjustment time with decreasing optical thickness. Since the optical thickness becomes very small in the optically thin limit, the diffusion approximation underestimates the thermal relaxation time, and overestimates the radiative losses which leads to a larger entropy jump.
While it appears at first glance arbitrary which MLT formulation one
chooses, Fig. 14 also shows that in the present case the
formulation of Mihalas is perhaps superior to the formulation of
Böhm-Vitense. The shape of the entropy profile of the Mihalas model
resembles the result of the hydrodynamical model more closely. This
comes at no surprise since the formulation of Mihalas considers
optically thick and thin convective elements - i.e. better
represents the actual situation. Of course, our choice of relating our
![]() to the formulation of Mihalas was motivated by this property.
to the formulation of Mihalas was motivated by this property.
It is interesting to compare equivalent mixing-length parameters
derived for the thermal structure of the hydrodynamical models with
other ones found in hotter objects, especially the Sun. Using the MLT
formulation of Böhm-Vitense, Ludwig et al. (1999) found in a study of
the convective efficiency based on 2D hydrodynamical models
![]() for the Sun which has likely to be corrected to
for the Sun which has likely to be corrected to
![]() if one
considers 3D models. In the Sun no distinction needed to be made
between fitting the entropy jump or the asymptotic entropy. The solar
mixing-length models match the photospheric entropy minimum found in
the hydrodynamical models quite well. This is a consequence of the
fact that convection does not reach very far up into optically
thin regions. Together with the relatively large entropy jump which
makes the exact value of the entropy minimum less important this leads
to the "one
if one
considers 3D models. In the Sun no distinction needed to be made
between fitting the entropy jump or the asymptotic entropy. The solar
mixing-length models match the photospheric entropy minimum found in
the hydrodynamical models quite well. This is a consequence of the
fact that convection does not reach very far up into optically
thin regions. Together with the relatively large entropy jump which
makes the exact value of the entropy minimum less important this leads
to the "one
![]() fits both'' situation. Contrary to the situation
in M-dwarfs differences between the Böhm-Vitense's and Mihalas' MLT
formulation are small in the Sun, again, a consequence of the
confinement of convection to optically thick regions. This allows us
to inter-compare the mixing-length parameter obtained by
Ludwig et al. (1999) for the Sun with the values derived here.
fits both'' situation. Contrary to the situation
in M-dwarfs differences between the Böhm-Vitense's and Mihalas' MLT
formulation are small in the Sun, again, a consequence of the
confinement of convection to optically thick regions. This allows us
to inter-compare the mixing-length parameter obtained by
Ludwig et al. (1999) for the Sun with the values derived here.
The mixing-length parameter of 1.8 for the Sun and 1.5 (matching
the asymptotic entropy) or 2.1 (matching the entropy jump) for the
M-dwarf are not vastly different, the solar value even falls within
the range spanned by the M-dwarf values. In MLT the convective flux
scales as the square of
![]() ,
hence we are considering a flux
variation within a factor of 2 only. Convection is efficient in
M-dwarfs in the sense that the whole envelope is almost adiabatically
stratified. The convective energy transport process itself does not
work much differently than in the solar case - taking the similar
mixing-length parameters as a measure. The adiabatic behavior follows
mostly from the reduction of the transported flux which can be
accommodated with smaller horizontal entropy fluctuations. This
ultimately leads to the smaller entropy jump which amounts to
,
hence we are considering a flux
variation within a factor of 2 only. Convection is efficient in
M-dwarfs in the sense that the whole envelope is almost adiabatically
stratified. The convective energy transport process itself does not
work much differently than in the solar case - taking the similar
mixing-length parameters as a measure. The adiabatic behavior follows
mostly from the reduction of the transported flux which can be
accommodated with smaller horizontal entropy fluctuations. This
ultimately leads to the smaller entropy jump which amounts to
![]() ,
or only
,
or only ![]()
![]() of the
solar entropy jump. This is remarkable since as evident from
Fig. 13 about half of the entropy jump happens to take
place in the optically thin region which is qualitatively different
from the Sun. Moreover, the MLT captures surprisingly well the
convective transport properties under such conditions.
of the
solar entropy jump. This is remarkable since as evident from
Fig. 13 about half of the entropy jump happens to take
place in the optically thin region which is qualitatively different
from the Sun. Moreover, the MLT captures surprisingly well the
convective transport properties under such conditions.
We note that an extrapolation of the entropy jump as found by
Ludwig et al. (1999) (their Fig. 4) for F-, G-, and K-dwarfs leads to a significant overestimation of the entropy jump for M-dwarfs. This
means that the trend in the entropy jump found in hotter objects
changes at some point when moving towards lower
![]() .
This, again, is
plausible because the dominant atmospheric opacity source as well as
contributors to the specific heat change in the M-dwarf regime.
.
This, again, is
plausible because the dominant atmospheric opacity source as well as
contributors to the specific heat change in the M-dwarf regime.
| Model |
|
V-I | R-I | J-K | J-H |
| [K] | [mag] | [mag] | [mag] | [mag] | |
| RHD, A-3D | 2754 | 3.651 | 1.974 | 0.749 | 0.455 |
| LHD,
|
2743 | 3.733 | 2.010 | 0.739 | 0.449 |
| LHD,
|
2744 | 3.701 | 1.996 | 0.746 | 0.452 |
| LHD,
|
2745 | 3.686 | 1.989 | 0.749 | 0.454 |
Table 2 provides synthetic optical and near-infrared
colors for the models discussed before and shown in
Fig. 11. The colors of the hydrodynamical model have been
calculated from the average pressure-temperature structure. In the
calculation of the colors the radiation field has been sampled with a
resolution of 2 Å, i.e. the treatment of frequency dependence
is different and more detailed than the OBM used in the models
proper. Here we are concerned with the relative behavior among the
models. For the V-I and J-K colors appreciable
discrepancies exist between observations and model predictions by
PHOENIX (" NEXTGEN'' model grid) in the
![]() -range
-range
![]() (Chabrier et al. 2000; Allard et al. 2001). In V-I the offset amounts to
(Chabrier et al. 2000; Allard et al. 2001). In V-I the offset amounts to
![]() 0.2-0.3 mag in the sense that the NEXTGEN models
are too blue. In J-K the offset amounts to
0.2-0.3 mag in the sense that the NEXTGEN models
are too blue. In J-K the offset amounts to ![]() 0.2-0.5 mag depending on the source of water line opacity data
used in the models. The treatment of the convective energy transport
in the MLT framework - employing a standard
0.2-0.5 mag depending on the source of water line opacity data
used in the models. The treatment of the convective energy transport
in the MLT framework - employing a standard
![]() of 1.0 - was
suspected to be one possible reason for the
discrepancy. Table 2 shows that a detailed treatment of
convection does not remedy the situation. The difference between the
V-I color of the hydrodynamical model to the LHD
of 1.0 - was
suspected to be one possible reason for the
discrepancy. Table 2 shows that a detailed treatment of
convection does not remedy the situation. The difference between the
V-I color of the hydrodynamical model to the LHD
![]() amounts to 82 mmag only. Moreover, the hydrodynamical model is
even bluer than the mixing-length model, i.e. when assuming the same
differential behavior for models employing detailed radiative
transfer, the discrepancy between theory and observations gets even
slightly worse. As expected from the thermal structure
amounts to 82 mmag only. Moreover, the hydrodynamical model is
even bluer than the mixing-length model, i.e. when assuming the same
differential behavior for models employing detailed radiative
transfer, the discrepancy between theory and observations gets even
slightly worse. As expected from the thermal structure
![]() gives the closest match in color among the three LHD models.
gives the closest match in color among the three LHD models.
Our results strengthen those of Allard et al. (2000) and Chabrier et al. (2000) who explain most of the visual discrepancy in terms of missing opacities. We would also like to emphasize that an optical color mismatch of this magnitude does not indicate a major shortcoming of the PHOENIX models. The V-band, which is likely to be responsible for the color mismatch, is formed high up in the atmosphere. The radiative energy flux in the V-band is a small fraction of the total radiative output of the star. Hence, the problem of the optical colors is related to a part of the atmosphere that is of minor importance for the overall energetics.
Similarly, the discrepancies between observed and predicted near-infrared colors cannot be traced back to an inadequate treatment of convection with MLT. Possible differences between MLT and hydrodynamical models amount to 10 mmag only.
Table 2 allows us to address a side point, namely the
question of how the hydrodynamical model A-3D and the mixing-length
models shown in Fig. 11 can have the same effective
temperature (2790 K) despite the fact that the hydrodynamical
model is almost always noticebly hotter than the mixing-length
models. Indeed, when calculating the total flux within the detailed
spectral synthesis the corresponding effective temperature
![]() of the hydrodynamical model appears to be slightly
(
of the hydrodynamical model appears to be slightly
(![]()
![]() )
hotter than the one of the mixing-length models
- with an offset to the nominal
)
hotter than the one of the mixing-length models
- with an offset to the nominal
![]() due to the more detailed
treatment of the radiative transfer. We interpret this as an effect of
the small remaining non-linearities when interchanging the averaging
of the temperature-pressure structure with the solution of the
radiative transfer. Strictly speaking, in order to determine the
colors of the hydrodynamical model one must perform the detailed
calculation of the 3D radiation field for many instances in time and
had to average subsequently horizontally and temporally. However, in
the present context, the smallness of the effects did not appear worth
the dramatically increased computational effort.
due to the more detailed
treatment of the radiative transfer. We interpret this as an effect of
the small remaining non-linearities when interchanging the averaging
of the temperature-pressure structure with the solution of the
radiative transfer. Strictly speaking, in order to determine the
colors of the hydrodynamical model one must perform the detailed
calculation of the 3D radiation field for many instances in time and
had to average subsequently horizontally and temporally. However, in
the present context, the smallness of the effects did not appear worth
the dramatically increased computational effort.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f15.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg96.gif) |
Figure 15:
Velocity-pressure relation of hydrodynamical model A-3D (solid) and five standard mixing-length model atmospheres
(dash-dotted) with
|
| Open with DEXTER | |
In the previous sections we discussed mixing-length parameters
associated with the thermal properties of our hydrodynamical
models. We now want to turn to a dynamical feature - the velocity
profile. Figure 15 shows a comparison of velocities of
hydrodynamical model A-3D with convective velocities from
mixing-length models. In the case of the hydrodynamical model RMS
fluctuations of the vertical velocity, for the mixing-length models
the MLT convective velocity are displayed. Six different temporal
windows (each 250 s in length) have been used for averaging the
hydrodynamical data, showing noticable variations of the mean velocity
particularly in the higher atmospheric layers.
The velocity plateau in the uppermost layers is an
artifact of the upper boundary condition which stipulates the same
velocity at the boundary and the grid points next to the boundary.
In order to match the
convective velocities in the convectively unstable layers we find that
![]() gives a reasonable match around the velocity
maximum. The hydrodynamical model has the tendency to retain higher
velocities towards smaller atmospheric pressure as compared to the MLT
models. The behavior of the velocities towards high pressure shows a
faster decline than the MLT models. The deeper hydrodynamical
model B-3D (not shown) exhibits a similar velocity maximum as
model A-3D but a decline which is not as fast. We conclude that the
decline in model A-3D is to some extend influenced by the lower
boundary condition and an asymptotic behavior towards high pressure
closer to MLT predictions is likely.
gives a reasonable match around the velocity
maximum. The hydrodynamical model has the tendency to retain higher
velocities towards smaller atmospheric pressure as compared to the MLT
models. The behavior of the velocities towards high pressure shows a
faster decline than the MLT models. The deeper hydrodynamical
model B-3D (not shown) exhibits a similar velocity maximum as
model A-3D but a decline which is not as fast. We conclude that the
decline in model A-3D is to some extend influenced by the lower
boundary condition and an asymptotic behavior towards high pressure
closer to MLT predictions is likely.
The hydrodynamical model shows an appreciable amount of overshoot into the formally stable atmospheric regions. Of course, by construction, standard MLT is unable to make any predictions about velocity amplitudes there. Two different components contribute to the velocities in the higher atmosphere: one contribution are waves excited by the stochastical fluid motions in the deeper layers and travelling upwards, the other contributions are advective motions overshooting into the stably stratified layers (see also Ludwig & Nordlund 2000).
Qualitatively, we expect that velocity fluctuations ![]() associated with advective motions decay with increasing distance from
the Schwarzschild boundary, roughly
associated with advective motions decay with increasing distance from
the Schwarzschild boundary, roughly
![]() where f is a positive parameter of order unity. For undamped sound
waves we would expect a height dependence of roughly
where f is a positive parameter of order unity. For undamped sound
waves we would expect a height dependence of roughly
![]() .
This means that the relative importance of
both contributions shifts from advection dominated motions to wave
dominated motions with increasing height. If the wave motions are not
strongly damped we would ultimately expect an increase of the velocity
fluctuations with height. Indeed, according to Fig. 15
this is what we observe in our model. The wave motions mostly arise
from standing waves - i.e. excited acoustic eigenmodes of the
computational box. The detailed run of the velocity in the overshoot
layers reflects the location of nodes and anti-nodes of the eigenmodes
in vertical direction which explains the non-monotonic behavior of the
atmospheric velocity amplitude.
.
This means that the relative importance of
both contributions shifts from advection dominated motions to wave
dominated motions with increasing height. If the wave motions are not
strongly damped we would ultimately expect an increase of the velocity
fluctuations with height. Indeed, according to Fig. 15
this is what we observe in our model. The wave motions mostly arise
from standing waves - i.e. excited acoustic eigenmodes of the
computational box. The detailed run of the velocity in the overshoot
layers reflects the location of nodes and anti-nodes of the eigenmodes
in vertical direction which explains the non-monotonic behavior of the
atmospheric velocity amplitude.
The spectrum and the structure of the eigenmodes are to some extent determined by the geometry of the computational domain. This means that the velocities in the higher atmosphere where the velocity amplitude is wave dominated are model dependent and should not taken for real without skepticism. In the next sections we will even argue that the velocity amplitudes of the acoustic modes observed in our particular models are probably strongly influenced by the numerics, and in this sense are mostly artificial. In order to study the transport properties of the atmospheric velocity field we will try to filter out as much of the acoustic contribution to the velocity field as possible.
Stellar atmospheres around
![]() are too hot to
allow for a significant formation of dust grains. However, already at
slightly cooler effective temperatures, grain formation sets in and
dust grains become major opacity contributors, i.e. an important
factor in determining the thermal structure of the atmosphere. In
fact, the spectral energy distribution in the range of effective
temperatures
are too hot to
allow for a significant formation of dust grains. However, already at
slightly cooler effective temperatures, grain formation sets in and
dust grains become major opacity contributors, i.e. an important
factor in determining the thermal structure of the atmosphere. In
fact, the spectral energy distribution in the range of effective
temperatures
![]() is crucially linked
to the distribution of dust grains in the atmosphere
(Allard et al. 2000). The amount of dust which is present is determined
by chemical condensation and evaporation processes as sources and
sinks, as well as macroscopic transport processes which carry dust
grains away from their sites of formation. In M-dwarf
atmospheres the transport is dominated by two opposing processes:
gravitational settling of dust grains and their mixing due to the
presence of velocity fields, either related to convection or global
circulations induced by rotation (T. Guillot 2000, private
communication). In our models, no dust formation takes place but we
nevertheless find it worthwhile to give a characterization of the
atmospheric mixing due to convection and convective overshoot. This
can give at least a first order approximation of how convective mixing
might operate when dust is actually present. The basic question which
we want to address is whether convective overshoot can provide enough
mixing to prevent dust grains from being completely removed from the
atmosphere by gravitational settling.
is crucially linked
to the distribution of dust grains in the atmosphere
(Allard et al. 2000). The amount of dust which is present is determined
by chemical condensation and evaporation processes as sources and
sinks, as well as macroscopic transport processes which carry dust
grains away from their sites of formation. In M-dwarf
atmospheres the transport is dominated by two opposing processes:
gravitational settling of dust grains and their mixing due to the
presence of velocity fields, either related to convection or global
circulations induced by rotation (T. Guillot 2000, private
communication). In our models, no dust formation takes place but we
nevertheless find it worthwhile to give a characterization of the
atmospheric mixing due to convection and convective overshoot. This
can give at least a first order approximation of how convective mixing
might operate when dust is actually present. The basic question which
we want to address is whether convective overshoot can provide enough
mixing to prevent dust grains from being completely removed from the
atmosphere by gravitational settling.
Formally, we are interested in a statistical representation of the mean transport properties of the convective velocity field in vertical direction. The horizontal advection of dust grains by the convective velocity field probably produces horizontal inhomogeneities in the dust distribution. We neglect these here since i) we are targeting at the application of our results in standard 1D stellar atmosphere models, ii) the horizontal inhomogeneities are small scale (the size of a convective cell), i.e. hardly observable and iii) the uncertainties in our understanding of the dust formation process itself perhaps limits the achievable accuracy anyway. In view of the last point we present a proxy of the convective mixing only, without trying to derive a detailed statistical description of the transport properties of the convective velocity field, i.e. extracting its effective transport coefficients (cf. Miesch et al. 2000, as an example of a more stringent treatment).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2282f16.eps}
\end{figure}](/articles/aa/full/2002/43/aa2282/Timg103.gif) |
Figure 16:
Mass exchange frequency as a function of pressure for various degrees
of subsonic filtering. The solid curves from top to bottom
correspond to no filtering,
|
| Open with DEXTER | |
Figure 16 shows the mass exchange frequency
![]() which
provides an approximate measure of the convective mixing. We define
this quantity as
which
provides an approximate measure of the convective mixing. We define
this quantity as
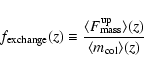 |
(2) |
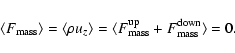 |
(3) |
As mentioned previously, the atmospheric velocity field has strong contributions of acoustic waves generated in the deeper layers of the models. From the comparison (not shown) of the hydrodynamical models A-3D and B-3D - which has a slightly greater extent in depth - we concluded that instabilities associated with the lower boundary condition contribute to the excitation of waves, i.e. the waves are mostly a numerical artifact. We could not trace down the responsable process, but the behavior was apparently related to the high degree of adiabaticity the stratification exhibits close to the lower boundary. In the Sun the boundary condition operated stably. Besides the numerical findings, from a purely theoretical point of view one would expect that the generation of acoustic energy is rather inefficient in a flow with as low a Mach number (few percent) as in the present case. Finally, it turns out that the Richardson number associated with the horizontal shear introduced by the acoustic modes in the atmosphere is not low enough to render the shear flow unstable. No small scale turbulence is induced by the waves and their oscillatory velocity fields do not contribute significantly to the mixing of material. Hence, we concluded that the wave contribution to the velocity field should be discarded if one wants to measure its mixing efficiency.
We therefore removed the contribution of waves before evaluating the
average mass flux by subsonic filtering - a technique invented in
the context of solar observations for cleaning images from "noise''
stemming from the 5 min oscillations (Title et al. 1989). In
short, one considers a time sequence of images and removes features
with horizontal phase speeds greater than a prescribed threshold. This
is achieved by Fourier filtering of the spatial-temporal data in the
k-![]() domain. In our case we worked with 150 snapshots of the
flow field sampled at 10 s time intervals. The total length of
the sequence was long in comparison to the periods of the excited
acoustic modes. For every depth layer we performed a 3D Fourier
analysis (one temporal, two spatial dimensions) of the vertical mass
flux. We selected velocity thresholds
domain. In our case we worked with 150 snapshots of the
flow field sampled at 10 s time intervals. The total length of
the sequence was long in comparison to the periods of the excited
acoustic modes. For every depth layer we performed a 3D Fourier
analysis (one temporal, two spatial dimensions) of the vertical mass
flux. We selected velocity thresholds
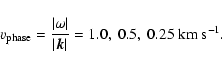 |
(4) |
Figure 16 shows the resulting mass exchange
frequency
![]() as a function of height (expressed in terms of the
mean pressure) for our hydrodynamical model A-3D. Lowering the
threshold
as a function of height (expressed in terms of the
mean pressure) for our hydrodynamical model A-3D. Lowering the
threshold
![]() leads to a significant decrease of the
mass exchange frequency in the atmospheric layers while the deeper
layers remain essentially unaffected by the subsonic filtering. This
again shows that the velocity field of the higher atmospheric layers
stems primarily from wave motions. Only the lowest threshold of
0.25 km s-1 starts to affect the deeper layers since also
convective flow features reach such velocities. The dashed line in
Fig. 16 indicates our extrapolation of what to expect in
case of a perfect removal of the acoustic contribution. Its slope is
given by the envelope of the sequence of curves for increasing degree
of subsonic filtering.
We want to emphasize that by the very nature of the problem
the filtering procedure does not apply a small correction to the
signal but removes even most of the original signal in some layers.
Wave motions almost inevitably dominate the flow velocity above a
certain atmospheric level. Large corrections as exhibited in
Fig. 16 are to be expected, but do not pose particular
problems so that we are confident about the filtering procedure.
leads to a significant decrease of the
mass exchange frequency in the atmospheric layers while the deeper
layers remain essentially unaffected by the subsonic filtering. This
again shows that the velocity field of the higher atmospheric layers
stems primarily from wave motions. Only the lowest threshold of
0.25 km s-1 starts to affect the deeper layers since also
convective flow features reach such velocities. The dashed line in
Fig. 16 indicates our extrapolation of what to expect in
case of a perfect removal of the acoustic contribution. Its slope is
given by the envelope of the sequence of curves for increasing degree
of subsonic filtering.
We want to emphasize that by the very nature of the problem
the filtering procedure does not apply a small correction to the
signal but removes even most of the original signal in some layers.
Wave motions almost inevitably dominate the flow velocity above a
certain atmospheric level. Large corrections as exhibited in
Fig. 16 are to be expected, but do not pose particular
problems so that we are confident about the filtering procedure.
As an additional check of our approach we calculated for an LHD
mixing-length model with
![]() linear eigenmodes describing the
growth of a perturbation under the action of the convective
instability.
linear eigenmodes describing the
growth of a perturbation under the action of the convective
instability.
![]() was chosen since the model gave among the
available mixing-length models the closest match to the thermal
structure of the hydrodynamical model. As horizontal wavelength of the
pertubation we chose the horizontal extent of model A-3D of
250 km, i.e. the largest horizontal wavelength which could be
accomodated in this hydrodynamical model. Freytag et al. (1996) showed
that the velocity field of convective eigenmodes gives a reasonable
representation of the velocity field in the overshoot region as long
as the horizontal wavelength is chosen in the vicinity of the actually
present convective scales. The dash-dotted line in Fig. 16
shows the shape of
was chosen since the model gave among the
available mixing-length models the closest match to the thermal
structure of the hydrodynamical model. As horizontal wavelength of the
pertubation we chose the horizontal extent of model A-3D of
250 km, i.e. the largest horizontal wavelength which could be
accomodated in this hydrodynamical model. Freytag et al. (1996) showed
that the velocity field of convective eigenmodes gives a reasonable
representation of the velocity field in the overshoot region as long
as the horizontal wavelength is chosen in the vicinity of the actually
present convective scales. The dash-dotted line in Fig. 16
shows the shape of
![]() associated with the linear eigenmode. The
velocity amplitude was scaled to match the maximum of
associated with the linear eigenmode. The
velocity amplitude was scaled to match the maximum of
![]() in the
deeper layers of the hydrodynamical model. Besides a systematic shift
the functional behavior predicted by the mode is quite similar to the
one of the hydrodynamical simulation. Moreover, the time scale for the
growth of the perturbation comes out to 120 s which is of the
same order as the convective turn-over time scale. The similar rate
of decline of
in the
deeper layers of the hydrodynamical model. Besides a systematic shift
the functional behavior predicted by the mode is quite similar to the
one of the hydrodynamical simulation. Moreover, the time scale for the
growth of the perturbation comes out to 120 s which is of the
same order as the convective turn-over time scale. The similar rate
of decline of
![]() in the atmospheric layers strengthens our
confidence in the robustness of our extrapolation procedure. However,
changing the horizontal wavelength of the perturbation within
reasonable limits as well as experimenting with different background
models did not improve the correspondence between linear modes and
non-linear hydrodynamical model beyond the quality shown in
Fig. 16.
in the atmospheric layers strengthens our
confidence in the robustness of our extrapolation procedure. However,
changing the horizontal wavelength of the perturbation within
reasonable limits as well as experimenting with different background
models did not improve the correspondence between linear modes and
non-linear hydrodynamical model beyond the quality shown in
Fig. 16.
Strictly speaking, the mixing frequency displayed in Fig. 16 is a lower limit since we removed all contributions associated with waves. However, the arguments given before make it very likely that the contributions of wave motions to the mixing are negligible: the Mach number of the flow is low, and the weak waves motions which may be excited are associated with little turbulence. Therefore we believe that the derived mixing efficiency is close to what is encountered in a real M-dwarf atmosphere.
What are the possible consequences of the exponential decline of the
mixing time scale due to convective overshoot? Following the work of
Rossow (1978), one arrives at an estimate of about
![]() for the typical time scale of dust sedimentation in M-dwarf
atmospheres. According to our hydrodynamical models the convective
mixing could counteract the sedimentation up to a layer of about two
pressure scale heights above the formally convectively unstable
layers. The convective turn-over time scale is of the order of
for the typical time scale of dust sedimentation in M-dwarf
atmospheres. According to our hydrodynamical models the convective
mixing could counteract the sedimentation up to a layer of about two
pressure scale heights above the formally convectively unstable
layers. The convective turn-over time scale is of the order of
![]() .
This is slow enough to allow for dust nucleation in the
upper regions of the convective envelopes of M-dwarfs - provided
that the thermodynamic conditions allow for nucleation in the first
place. From these considerations we would expect that dust clouds
in M-dwarf (and brown dwarf) atmospheres are confined to layers in the
vicinity of the upper Schwarzschild boundary of the convective
envelope.
.
This is slow enough to allow for dust nucleation in the
upper regions of the convective envelopes of M-dwarfs - provided
that the thermodynamic conditions allow for nucleation in the first
place. From these considerations we would expect that dust clouds
in M-dwarf (and brown dwarf) atmospheres are confined to layers in the
vicinity of the upper Schwarzschild boundary of the convective
envelope.
We used elaborate 2D and 3D radiation-hydrodynamics simulations to
study properties of convection on the surface of a prototypical late
M-dwarf (
![]() ,
,
![]() ,
solar chemical
composition). Despite the significant differences in the physical
conditions encountered in the solar and an M-dwarf atmosphere we
obtained the striking result that M-dwarf granulation does not look
qualitatively different from what is familiar from the Sun (see Fig. 6). Quantitative differences (intensity contrast
1.1%, horizontal scales
,
solar chemical
composition). Despite the significant differences in the physical
conditions encountered in the solar and an M-dwarf atmosphere we
obtained the striking result that M-dwarf granulation does not look
qualitatively different from what is familiar from the Sun (see Fig. 6). Quantitative differences (intensity contrast
1.1%, horizontal scales ![]()
![]() ,
maximum RMS
velocities
,
maximum RMS
velocities ![]()
![]() ,
convective turn-over time scale
,
convective turn-over time scale
![]()
![]() )
remain within the expectations derived from
mixing-length theory.
)
remain within the expectations derived from
mixing-length theory.
Connected to this basic finding is the - for practical purposes - perhaps most important result that the temperature structure of the higher atmospheric layers is determined by the condition of radiative equilibrium, and is not very much affected by processes usually not accounted for in standard stellar atmosphere models. Convective overshoot as well as energy transport by waves do not significantly affect the temperature structure outside of the region of convective instability. We expect that this finding also holds for main-sequence objects of higher effective temperature where radiation becomes relatively more important.
Answering the questions posed in the introduction we confirm that in late M-dwarfs mixing-length theory can be applied to obtain a realistic description of the convective energy transport in a 1D stellar atmosphere code, provided one can remove uncertainties related to the choice of the mixing-length parameter. If an independent calibration is available we expect that 1D atmosphere models allow reasonable accurate predictions (on a level as displayed in Fig. 13) of the atmospheric temperature structure and ultimately the stellar spectrum to be made. Effects on the stellar spectrum related to horizontal temperature inhomogeneities are expected to be very small in the M-dwarf studied here, primarily due to the small horizontal fluctuations of the thermodynamic variables. Even in the Sun - with the much higher temperature contrast present at its surface - effects related to horizontal temperature inhomogeneities are rather subtle (cf. Steffen & Ludwig 1999). We expect that 1D stellar atmosphere models provide an acceptable overall approximation to the spectrum of main-sequence objects between the Sun and late M-dwarfs. Only if one demands for a precision exceeding commonly adopted levels or desires to study effects in principle not included in standard model atmospheres (e.g. spectral line shifts and asymmetries), one has to go to more sophisticated modeling. We emphasize that this refers to objects at solar metallicity. For metal poor objects the situation is clearly different (see Asplund et al. 1999).
A downside of our findings is that we cannot trace back the remaining differences between theoretical and observed colors for M-dwarfs to shortcomings in the treatment of the convective energy transport. The resolution of the problem has to be found elsewhere, as pointed out earlier, deficiencies in the molecular opacities are still a possible option.
We are left with the problem of finding an adequate value of the
mixing-length parameter to obtain a description of the vertical
temperature run in the superadiabatic layers. In the present case we
find a mixing-length parameter
![]() (
(![]() ) = 2.1 which
gives a match to the entropy jump and the temperature gradient of the
deeper atmospheric layers (see Fig. 13). Despite perhaps
the best value to be employed in stellar atmosphere calculations, for
global stellar structure models a value of
) = 2.1 which
gives a match to the entropy jump and the temperature gradient of the
deeper atmospheric layers (see Fig. 13). Despite perhaps
the best value to be employed in stellar atmosphere calculations, for
global stellar structure models a value of
![]() (
(![]() ) = 1.5
would be more appropriate since it ensures to find the correct
asymptotic entropy in the convective envelope which is important for
obtaining the correct stellar radius. To complete the "zoo'' of
mixing-length parameters, we get a value of
) = 1.5
would be more appropriate since it ensures to find the correct
asymptotic entropy in the convective envelope which is important for
obtaining the correct stellar radius. To complete the "zoo'' of
mixing-length parameters, we get a value of
![]() (v) = 3.5 when
matching the convective velocities predicted in our hydrodynamical
models. We reiterate that all values are given with reference to the
formulation of MLT by Mihalas (1978).
(v) = 3.5 when
matching the convective velocities predicted in our hydrodynamical
models. We reiterate that all values are given with reference to the
formulation of MLT by Mihalas (1978).
The various values of the mixing-length parameter point towards the
deeper rooted problem that MLT can give a reasonable but not exact
description of the average convective properties. Even calibrating one
aspect does not ensure the overall correct functional form of, say,
the temperature profile. We have seen that different formulations of
MLT can give quite different functional dependencies. They offer the
possibility to improve fits beyond the quality limited by fitting the
mixing-length parameter only. For late M-dwarfs all this does not
matter much since the differences of the atmospheric structure for
various values of
![]() are small. However, we stress that this
statement refers to cooler M-dwarfs on or close to the
main-sequence. For pre-main-sequence (PMS) objects the situation is
markedly different (Baraffe et al. 2002). There the specific choice of
are small. However, we stress that this
statement refers to cooler M-dwarfs on or close to the
main-sequence. For pre-main-sequence (PMS) objects the situation is
markedly different (Baraffe et al. 2002). There the specific choice of
![]() has a large impact on the resulting atmospheric structure. Work
is underway to extend the present study into this regime which may
also allow us to find the most suitable MLT formulation.
has a large impact on the resulting atmospheric structure. Work
is underway to extend the present study into this regime which may
also allow us to find the most suitable MLT formulation.
A result beyond the scope of classical model atmospheres is the
derivation of a proxy of atmospheric mixing-time scales (see Fig. 16) due to convective overshoot. We find an
exponential "leaking'' of the convective velocity field into the
formally stably stratified layers. Depending on the exact criterion,
overshooting extends the efficiently mixed regions about 2 pressure
scale heights beyond the Schwarzschild boundary. We suggest that the
mixing found in the
![]() model studied here,
takes place in an analogous fashion in brown dwarfs, and provides the
mixing which counteracts dust sedimentation. Hydrodynamical models can
be used to address this problem more directly by performing
simulations including the formation and transport of dust which we
consider as an interesting challenge for the future.
model studied here,
takes place in an analogous fashion in brown dwarfs, and provides the
mixing which counteracts dust sedimentation. Hydrodynamical models can
be used to address this problem more directly by performing
simulations including the formation and transport of dust which we
consider as an interesting challenge for the future.
Last but not least we would like to point out the two weakest points of our investigation. While the precision of the radiative transfer in the hydrodynamical calculations is sufficient to address the questions discussed here there is certainly room for improvement of the OBM to get an even closer agreement with detailed spectral synthesis calculations. Secondly, the models presented here are rather shallow. Improvements in the formulation of the lower boundary condition would perhaps allow the use of deeper computational domains, and would reduce the influence of the specific formulation of the lower boundary conditions.
Acknowledgements
The authors are indebted to Isabelle Baraffe and Gilles Chabrier for their supportive enthusiasm during the course of the project, and their scientific input during many discussions. HGL would like to thank Åke Nordlund and Robert Stein for making available a version of their hydrodynamical atmosphere code. PHH acknowledges support by "Pôle Scientifique de Modélisation Numérique'' (PSMN) at the École Normale Supérieure de Lyon, NSF grants AST-9720704 and AST-0086246, NASA grants NAG5-8425, NAG5-9222, as well as NASA/JPL grant 961582 to the University of Georgia (UGA), Athens. The calculations presented in this paper were performed on machines operated by the PSMN, on the NEC-SX5 at the "Institut du Développement et des Ressources en Informatique Scientifique'' (IDRIS), Paris, on the IBM SP2 of the UGA UCNS, on the IBM SP "Blue Horizon'' of the San Diego Supercomputer Center (SDSC) with support from the National Science Foundation, and on the IBM SP of the NERSC with support from the US Department of Energy. We thank all these institutions for a generous allocation of computer time.
The radiative time scales shown in Fig. 4 were
evaluated in Eddington approximation (see e.g. Edwards 1990)
according
| (A.2) |
The (adiabatic) Brunt-Väisälä period
![]() was
calculated according
was
calculated according
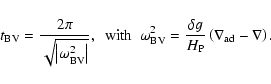 |
(A.4) |
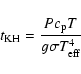 |
(A.5) |