3 Data quality and error estimation

3.1 Spectral resolution

Figure 2 shows the observed spectral lines. The "+''-symbol corresponds to the mean spectrum of normal granulation in the data set. The spectrum represented by the "$\triangle$''-symbol is based on the atlas profile, adapted to the spectral resolution of TESOS. The distance between two "$\triangle$''-symbols corresponds to the selected step size used for the observations. The comparison between the observed and the "simulated'' profile demonstrates the high spectroscopic quality of our G-band data.

Figure 2: "+'' represents the observed profile, "$\triangle$'' the "simulated'' profile and the dashed curve the atlas spectra. For clarity the observed data is shifted by +0.05 and the simulated data by -0.05 intensity units. The curve below represents the normalized difference $(I^{+}-I^{\triangle })/(I^{+}+I^{\triangle })$ of the data and the simulation (scale to the right).

   
3.2 Seeing effects

TESOS obtains 2D-spectra by scanning through the spectral line. Since the images are not taken simultaneously the line profiles are influenced by seeing effects. As described by Schlichenmaier & Schmidt (2000), the variable seeing conditions can induce shifts of the line profiles. This is a potential error source when calculating e.g. velocity maps from the data. Figure 3 shows the rms-intensity contrast for the broadband channel during the scan as a function of time. The rms-intensity contrast is calculated in each frame in a region of normal granulation, located in the upper right corner of the field of view, as indicated in Fig. 1. The contrast is varying between 5 and 6.8% (rms). On average the seeing conditions during the Fe II-line scan are better than for the CH-line scan.

Figure 3: The solid curve represents the course of rms-intensity contrast of normal granulation (see Fig. 1) in the broadband channel during the scan. The dashed line shows the mean intensity in normal granulation of the filtergram channel. The given wavelength range corresponds to the 34 steps of the scan.

To estimate the errors, we produce a synthetic filtergram scan, $I_{{\rm syn}}^i$, making use of the simultaneously observed broadband images and a mean line profile, based on the filtergrams. For each step i we multiply the broadband image, $I_{{\rm bb}}^i$, with the quotient of mean filtergram intensity $\left\langle I_{{\rm nb}}^i \right\rangle$ and mean broadband intensity $\left\langle I_{{\rm bb}}^i \right\rangle$ , each calculated for the region of normal granulation:

$$\begin{eqnarray*}I_{{\rm syn}}^i = I_{{\rm bb}}^i \cdot \frac{\left\langle I_{{\... ...le} {\left\langle I_{{\rm bb}}^i \right\rangle}~~~~~ i=0,...,33, \end{eqnarray*}$$

where brackets denote spatial average over the "reference region'' as indicated in Fig. 1. In this way, we replace the original observed line profile at each spatial position by a spatially unresolved "synthetic'' line profile. This scan does not bear any physical information, like line shifts due to flows on the solar surface, but only the mean line profile weakened or strengthened by the varying intensity of the broadband image due to seeing.

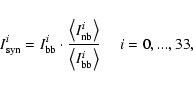
In a next step we calculate maps (line core intensity, velocity, etc.) from this synthetic scan. An example of a resulting error map is shown in Fig. 4 to the right. The image visualizes the error due to seeing for the velocity map (Fe II-line, Fourier method). In the example the rms-value of the map is 26 m s^-1 and the maximum deviation amounts to 215 m s^-1 (peak-to-peak). The spatial error is not distributed homogeneously. However, the rms-value of these maps provides a good estimation of the error due to seeing variation. Compared to the seeing error, numerical errors - as they occur e.g. at line shift determination - are negligible. In the following analysis we give the $2\sigma$-level based on this rms-calculation.

Figure 4: Velocity maps. From left to right: map based on CH-line shift determination (Fourier method), map based on Fe II-line shift determination (polynomial fit around line core), map of seeing error for the map based on Fe II-line shift determination. The contour lines mark $I=0.58\cdot\left\langle I_{G-{\rm band}}\right\rangle$ and indicate the location of the pores.