A&A 394, 769-789 (2002)
DOI: 10.1051/0004-6361:20020976
I. García-Ruiz1 - R. Sancisi2,1 - K. Kuijken1
1 - Kapteyn Astronomical Institute, Postbus 800, 9700 AV,
Groningen, The Netherlands
2 -
Osservatorio Astronomico di Bologna, Via Ranzani 1, 40127
Bologna, Italy
Received 21 December 2001 / Accepted 28 June 2002
Abstract
We present 21-cm HI line and optical R-band observations for a sample
of 26 edge-on galaxies. The HI observations were obtained with the
Westerbork Synthesis Radio Telescope, and are part of the WHISP
database (Westerbork HI Survey of Spiral and Irregular Galaxies). We
present HI maps, optical images, and radial HI density profiles. We have also
derived the rotation curves and studied the warping and lopsidedness
of the HI disks. 20 out of the 26 galaxies of our sample are warped, confirming that
warping of the HI disks is a very common phenomenon in disk
galaxies. Indeed, we find that all galaxies that have an extended HI disk with
respect to the optical are warped. The warping usually starts around the
edge of the optical disk. The degree of warping varies considerably
from galaxy to galaxy. Furthermore, many warps are asymmetric, as they
show up in only one side of the disk or exhibit large
differences in amplitude in the approaching and receding sides of the
galaxy. These asymmetries are more pronounced in rich environments, which may
indicate that tidal interactions are a source of warp asymmetry. A
rich environment tends to produce larger warps as well.
The presence of lopsidedness seems to be related to the
presence of nearby companions.
Key words: galaxies: kinematics and dynamics - galaxies: structure
It has long been known that many galaxies have warped disks. The phenomenon occurs at large galactocentric radii, starting close to the edge of the optical disk. This makes 21-cm line observations essential for the study of warps: there are galaxies that have no optical warp and yet exhibit extraordinary warps in their outer HI layers.
The first indication that the HI distribution of disk galaxies was sometimes bent or warped came in 1957 from observations of our own Galaxy (Burke 1957; Kerr 1957). Early calculations showed that the tidal field due to the Magellanic Clouds was unable to account for the warp of the Galaxy (Burke 1957; Kerr 1957; Hunter & Toomre 1969), and so it was regarded as a rare, uncommon phenomenon. Later on, Sancisi (1976) studied the HI layer of 5 edge-on galaxies and discovered 4 of them to have warps. This result indicated that warps are very common among galaxies. This discovery was not expected, because three of Sancisi's galaxies were quite isolated and thus presented a problem with the tidal-warp scenario. The high incidence of warps among spiral galaxies has later been confirmed with larger samples both in the optical (Sánchez-Saavedra et al. 1990),(Reshetnikov & Combes 1998) and the HI (Bosma 1991). The ubiquity of warps means that either warps are long-lasting phenomena or they are transient but easily and often excited. Neither of these has been proven and no satisfactory explanation has been found yet. A study by Briggs (1990) of a sample of 12 galaxies showed that: (1) warps start around R25-RH0; (2) the line of nodes of the warp is straight inside R25, and is a leading spiral outside.
The absence of a mechanism that would regularly generate warps and the fact that the line of nodes of the observed warps does not show a severe winding effect (Briggs 1990) suggest that warps are long-lived. The main issue in trying to explain a long lasting warp is differential precession, which in a few rotation periods will destroy the coherent warp pattern (this is similar to the winding problem of material spiral arms). The differential precession arises from the non-sphericity of the potential (Avner & King 1967). However, the survival time of a coherent warp pattern can be larger if the halo in which the disk is embedded deviates only slightly from spherical symmetry (Tubbs & Sanders 1979). Likewise, a halo with a flattening that decreases outwards in the right way would be able to maintain a coherent warped disk for a Hubble time (Petrou 1980).
Extending the work of Hunter & Toomre (1969), Sparke & Casertano (1988) studied long-lived warping modes of a galactic disk inside an oblate halo potential, where no winding occurs. They found that the combined torque from a halo and a self-gravitating disk allows a configuration in which the precession frequency of the warp is the same at all radii, thus allowing the warp to maintain its shape unchanged for many rotation periods. One of their assumptions was that of a fixed halo potential that does not react to the potential of the disk.
The back-reaction of the precessing disk onto the halo, analogous to dynamical
friction, was investigated by Dubinski & Kuijken (1995), Nelson &
Tremaine (1995), and Binney et al. (1998) after an earlier investigation
in terms of WKB density waves by Bertin & Mark (1980). It turns out
that it has a very strong influence on the evolution of the warp,
causing the disk and halo to reorient to a common plane of symmetry in
a few orbital times, and making the warp decay.
| UGC | NGC | type | R25 |
|
i | PA |
|
|||
| ' | ' | Mpc | Mpc | |||||||
| 1281 | Sc | 2.23 | 2.59 | 90.0 | 38 | 10.95 | 0.11 | 5.4 | 5.1 | |
| 2459 | Scd | 1.24 | 2.02 | 90.0 | 62 | - | - | 36.3 | 36.3 | |
| 3137 | Sbc | 1.78 | 2.66 | 90.0 | 74 | 13.61 | 1.00 | 18.3 | 33.8 | |
| 3909 | SBc | 1.32 | 1.39 | 90.0 | 82 | 13.57 | 0.77 | 17.7 | 24.5 | |
| 4278 | SBc | 2.27 | 2.69 | 90.0 | 172 | 11.09 | 0.23 | 10.4 | 8.1 | |
| 4806 | 2770 | Sc | 1.83 | 2.41 | 77.0 | 148 | 11.62 | 0.07 | 29.6 | 21.0 |
| 5452 | 3118 | Sc | 1.26 | 1.41 | 90.0 | 41 | 12.88 | 1.00 | 22.1 | 21.7 |
| 5459 | SBc | 2.38 | 2.67 | 90.0 | 132 | 11.58 | 0.11 | 19.6 | 15.9 | |
| 5986 | 3432 | SBd | 3.44 | 3.52 | 81.2 | 38 | 10.36 | 0.08 | 8.9 | 8.5 |
| 6126 | 3510 | SBcd | 2.03 | 2.13 | 90.0 | 163 | 11.17 | 0.33 | 8.8 | 8.8 |
| 6283 | 3600 | Sab | 2.03 | 2.15 | 87.0 | 3 | 11.51 | 0.59 | 11.4 | 11.3 |
| 6964 | 4010 | SBcd | 2.10 | 2.13 | 85.5 | 66 | 11.79 | 0.10 | 16.6 | 16.9 |
| 7089 | Sc | 1.61 | 2.73 | 87.2 | 36 | 12.29 | 0.14 | 13.2 | 11.6 | |
| 7090 | 4096 | SBc | 3.30 | 3.96 | 80.9 | 20 | 10.16 | 0.19 | 9.4 | 10.2 |
| 7125 | SBd | 2.35 | 2.26 | 90.0 | 85 | 12.44 | 0.92 | 19.6 | 12.6 | |
| 7151 | 4144 | SBc | 3.06 | 3.34 | 81.6 | 104 | 10.72 | 0.16 | 4.3 | 6.0 |
| 7321 | Sc | 2.78 | 2.91 | 90.0 | 82 | 11.99 | 0.16 | 4.0 | 14.9 | |
| 7483 | 4359 | SBc | 1.75 | 2.49 | 80.8 | 108 | 12.31 | 0.80 | 22.4 | 17.6 |
| 7774 | Sc | 1.75 | 1.90 | 90.0 | 102 | 12.98 | 0.86 | 7.3 | 20.6 | |
| 8246 | SBc | 1.71 | 1.86 | 90.0 | 83 | 13.62 | 1.00 | 11.7 | 19.4 | |
| 8286 | 5023 | Sc | 3.03 | 3.58 | 90.0 | 28 | 11.09 | 0.13 | 6.3 | 8.0 |
| 8396 | 5107 | SBc | 0.84 | 0.90 | 77.3 | 128 | 13.89 | 1.45 | 17.4 | 27.5 |
| 8550 | 5229 | SBc | 1.67 | 2.10 | 90.0 | 167 | 12.97 | 1.00 | 6.3 | 13.2 |
| 8709 | 5297 | SBbc | 2.72 | 3.02 | 83.6 | 148 | 11.13 | 0.21 | 37.3 | 19.8 |
| 8711 | 5301 | SBc | 2.02 | 2.49 | 87.2 | 151 | 11.98 | 0.22 | 25.8 | 22.5 |
| 9242 | Sc | 2.51 | 3.04 | 90.0 | 71 | 11.86 | 0.07 | 24.7 | 12.6 |
More recently, several other mechanisms have been investigated. Debattista & Sellwood (1999) studied the warps generated by a disk embedded in a halo whose angular momentum vector is misaligned with that of the disk, and Ing-Guey & Binney (1999) built a model of a warp caused by a disk embedded in a halo which is constantly accreting material of angular momentum misaligned with that of the disk. Magnetic fields have also been proposed as a cause for warps. This hypothesis is mainly based on the alignment of the warps of different galaxies that are close in space (Battaner et al. 1990). Such alignment would be hard to explain in a warping model that is based only on the interaction of a disk and a halo of an individual galaxy without involving the surroundings.
In spite of the several models proposed, none is fully convincing, and many questions remain. Observationally the main problem lies in the fact that the current sample of warped galaxies is very small and inhomogeneous, and often the resolution of the data is poor. Furthermore, in many cases the warps are inferred by modeling the HI kinematics, using assumptions like axisymmetry and circularity of the orbits, which may be not completely correct.
Although most of the warps start outside the optical disk, optical warps do exist. In fact, Sanchez-Saavedra et al. (1990) claimed that the majority of galaxies have optical warps. A study by Reshetnikov & Combes (1998) on optical warps showed the influence of the environment, in the sense that there are more optically warped galaxies in dense environments than in low-density regions. The relation between the optical and HI warps is not clear yet. There have been claims based on near infrared data (DIRBE) that the Galactic warp is more pronounced in the HI than in the old stellar population (Porcel et al. 1997), but an early cutoff of the old stellar disk (Robin et al. 1992) can also explain the data. If magnetic fields have some influence in exciting and/or maintaining warps, the old stellar disk is expected to have a milder warp than the HI disk at every radius (Porcel et al. 1997).
Our goal in this paper is to present an analysis of a sample of late-type spiral galaxies to determine the occurrence rate of warps, and to study their properties (symmetry, dependence on environment, etc.). We have selected a sample of edge-on galaxies that have been observed with the Westerbork Synthesis Radio Telescope (WSRT) for the WHISP project (Swaters et al. 2001). We have used optical R-band data as well (Swaters & Balcells 2002), to explore possible links between the optical properties and the warps of our galaxies. These images also serve to study the environment of our sample galaxies and to identify possible satellite dwarf galaxies that may be orbiting them.
The WHISP sample (Swaters et al. 2001) was selected from the Uppsala
General Catalogue of Galaxies (Nilson 1973). Only the galaxies north of
20![]() declination and with blue diameters larger than 1.5'were selected. The galaxies are generally larger
in HI than in the optical, and with the typical beam size of the WSRT
(
declination and with blue diameters larger than 1.5'were selected. The galaxies are generally larger
in HI than in the optical, and with the typical beam size of the WSRT
(
![]() /
/
![]() )
they are well resolved.
)
they are well resolved.
In order to be sure of a sufficiently high signal-to-noise ratio, only galaxies that had a flux density larger than 100 mJy were included in the WHISP sample.
From this sample of 409 galaxies, we selected those that were highly
inclined, to be able to observe the warping of the HI layer directly
instead of having to infer it from the kinematics. For this purpose,
galaxies with optical inclination angles larger than 75![]() were
selected (we assumed an intrinsic axis ratio of 0.2 to calculate the
inclination angles). The WHISP database was not yet complete when this project
started (August 1999), thus our sample was formed from the galaxies
with data available at that time. These are listed in
Table 1. A key property of the sample is
that it was unbiased towards the existence of warps in the selected galaxies.
were
selected (we assumed an intrinsic axis ratio of 0.2 to calculate the
inclination angles). The WHISP database was not yet complete when this project
started (August 1999), thus our sample was formed from the galaxies
with data available at that time. These are listed in
Table 1. A key property of the sample is
that it was unbiased towards the existence of warps in the selected galaxies.
Note that nearby large galaxies, which have already been studied in the past have not been re-observed in the WHISP project yet, and are therefore absent from our sample. Including galaxies from the literature might bias the sample towards more "interesting'' galaxies.
For most of the galaxies in our sample there are R-band optical data obtained with the Isaac Newton Telescope at La Palma (Swaters & Balcells 2002). These data serve to study the morphology of the galaxies and to search for possible satellites which might have an influence in the bending of the HI disks. The observing procedure and data processing (bias, flat field, calibration) are described in Swaters (1999). There are three galaxies for which data from the INT could not be obtained: for UGC 2459 and UGC 8396 we used data from the Digital Sky Survey, and data for UGC 6964 were kindly provided by Verheijen (1997).
The apparent B magnitudes for the galaxies in the sample have been obtained from the LEDA catalogue (http://leda.univ-lyon1.fr), after correction for inclination and Galactic extinction.
We have used two quantities to measure the extent of the optical disk. The first one is R25, the radius where the R band surface brightness falls to 25 mag/arcsec2, which we have taken from the LEDA database.
Photometric radii, and especially the not very deep ones like R25,
are not always good indicators for the size of a disk. To
circumvent this problem, we have estimated the size of the galaxy
(
![]() )
by visually inspecting the images of each galaxy in the
sample and determining where the disk ends. These radii are listed in
Table 1. They are larger than R25, in some cases by more
than 50%. They are somewhat subjective but do provide a useful lower
limit to the optical size of the galaxy.
)
by visually inspecting the images of each galaxy in the
sample and determining where the disk ends. These radii are listed in
Table 1. They are larger than R25, in some cases by more
than 50%. They are somewhat subjective but do provide a useful lower
limit to the optical size of the galaxy.
The HI observations were obtained with the WSRT between 1995 and
1998. Most galaxies were observed for 12 hours. The typical beam size
is
![]() ,
the
channel separation 4.14 km s-1 for most of the galaxies, and 16.7 km s-1 for
the most distant ones. The observational parameters, exposure time,
resulting beam size and other relevant data are given in
Table 2. The primary beam is about 37'.
,
the
channel separation 4.14 km s-1 for most of the galaxies, and 16.7 km s-1 for
the most distant ones. The observational parameters, exposure time,
resulting beam size and other relevant data are given in
Table 2. The primary beam is about 37'.
The reduction was done using the WHISP reduction pipeline. The
detailed information about the reduction steps can be found in the
WHISP web pages, http://www.astro.rug.nl/~whisp. This results in
3 sets of channel maps for each galaxy: at full resolution,
at 30'' and at 60''.
| Galaxy |
|
Date | RA | Dec |
|
|
S. beam | Bw |
|
|
rms |
|
| UGC | hours | (1950) | (1950) | MHz | km s-1 |
|
MHz | km s-1 | mJy/beam | K/mJy | ||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) |
| 1281 | 12 | 08 Nov. 95 | 01 46 39 | 32 20 39 | 1419.79 | 157 | 11.14 |
2.48 | 127 | 5.0 | 3.2 | 2.6 |
| 2459 | 12 | 04 Jun. 97 | 02 57 06 | 48 49 59 | 1408.75 | 2464 | 13.08 |
4.92 | 63 | 20.1 | 2.1 | 2.7 |
| 3137 | 12 | 24 Jan. 96 | 04 39 24 | 76 19 59 | 1415.64 | 1020 | 11.70 |
2.48 | 127 | 5.0 | 2.9 | 4.4 |
| 3909 | 12 | 11 Jun. 97 | 07 30 52 | 73 49 27 | 1415.86 | 945 | 11.38 |
2.48 | 127 | 5.0 | 3.3 | 4.5 |
| 4278 | 12 | 01 Apr. 96 | 08 10 27 | 45 53 49 | 1417.68 | 581 | 12.05 |
2.48 | 127 | 5.0 | 2.8 | 2.9 |
| 4806 | 12 | 16 Jun. 97 | 09 06 29 | 33 19 37 | 1411.09 | 1951 | 12.57 |
4.92 | 63 | 20.0 | 1.8 | 2.0 |
| 5452 | 24 | 23 Jun. 97 | 10 04 17 | 33 16 27 | 1413.95 | 1342 | 12.06 |
2.48 | 127 | 5.0 | 2.5 | 2.3 |
| 5459 | 12 | 24 Nov. 97 | 10 04 54 | 53 19 36 | 1415.15 | 1111 | 14.39 |
2.48 | 127 | 5.0 | 4.1 | 2.4 |
| 5986 | 12 | 09 Feb. 96 | 10 49 42 | 36 53 04 | 1417.46 | 616 | 11.34 |
2.48 | 127 | 5.0 | 3.3 | 2.8 |
| 6126 | 36 | 17 Nov. 97 | 11 01 01 | 29 09 19 | 1416.99 | 705 | 12.47 |
2.48 | 127 | 5.0 | 2.6 | 1.8 |
| 6283 | 12 | 19 Sep. 97 | 11 13 06 | 41 51 48 | 1416.90 | 719 | 12.50 |
2.48 | 127 | 5.0 | 3.0 | 2.6 |
| 6964 | 12 | 12 Mar. 98 | 11 56 03 | 47 32 20 | 1416.11 | 907 | 10.24 |
2.48 | 127 | 5.0 | 1.8 | 4.5 |
| 7089 | 12 | 27 Oct. 97 | 12 03 26 | 43 25 37 | 1416.67 | 776 | 12.87 |
2.48 | 127 | 5.0 | 3.3 | 2.5 |
| 7090 | 12 | 03 Nov. 97 | 12 03 28 | 47 45 12 | 1417.64 | 566 | 12.48 |
4.92 | 63 | 19.9 | 1.7 | 2.8 |
| 7125 | 12 | 29 Nov. 96 | 12 06 10 | 37 04 51 | 1415.32 | 1071 | 12.32 |
2.48 | 127 | 5.0 | 3.3 | 2.4 |
| 7151 | 12 | 02 May 97 | 12 07 28 | 46 44 07 | 1419.13 | 267 | 12.24 |
2.48 | 127 | 5.0 | 3.2 | 2.9 |
| 7321 | 13 | 10 Nov. 97 | 12 15 02 | 22 49 00 | 1418.39 | 409 | 12.14 |
2.48 | 127 | 5.0 | 3.5 | 1.5 |
| 7483 | 12 | 12 Nov. 97 | 12 21 42 | 31 47 57 | 1414.39 | 1253 | 11.88 |
2.48 | 127 | 5.0 | 3.4 | 2.1 |
| 7774 | 24 | 10 Dec. 97 | 12 33 57 | 40 16 49 | 1417.83 | 526 | 10.67 |
2.48 | 127 | 5.0 | 2.4 | 3.4 |
| 8246 | 12 | 22 Dec. 97 | 13 07 44 | 34 26 48 | 1416.49 | 813 | 12.05 |
2.48 | 127 | 5.0 | 3.1 | 2.2 |
| 8286 | 24 | 20 Dec. 96 | 13 09 58 | 44 18 13 | 1418.40 | 407 | 12.30 |
2.48 | 127 | 5.0 | 2.3 | 2.7 |
| 8396 | 12 | 05 Jan. 98 | 13 19 09 | 38 47 58 | 1415.86 | 946 | 12.15 |
2.48 | 127 | 5.0 | 3.5 | 2.5 |
| 8550 | 11 | 12 Dec. 96 | 13 31 58 | 48 10 16 | 1418.61 | 364 | 12.88 |
2.48 | 127 | 5.0 | 3.6 | 2.8 |
| 8709 | 12 | 09 Jan. 98 | 13 44 19 | 44 07 23 | 1409.03 | 2407 | 12.56 |
4.92 | 63 | 20.1 | 1.7 | 2.6 |
| 8711 | 12 | 12 Jan. 98 | 13 44 21 | 46 21 28 | 1413.26 | 1503 | 10.87 |
4.92 | 63 | 20.0 | 1.7 | 3.7 |
| 9242 | 12 | 26 Nov. 98 | 14 23 59 | 39 45 00 | 1413.40 | 1470 | 9.83 |
2.48 | 127 | 5.0 | 3.1 | 4.1 |
The HI data presented in this article in Fig. 7 (rotation curves, HI radial surface density profiles and warp curves) and in Fig. 13 (6 panel figures for each galaxy) is also available in electronic form in the WHISP pages (http://www.astro.rug.nl/whisp), together with some other diagrams that supply extra velocity information.
The global HI line profiles were determined by adding the intensities of the CLEAN components from the 60'' Hanning smoothed datacube, corrected for primary beam attenuation.
The total HI masses were derived according to the formula
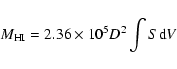 |
(1) |
To construct the total (integrated over velocity) HI maps, we used the same masks already used in the CLEANing to define the areas of emission. Outside these areas the maps were set to zero to avoid adding unnecessary noise to the total HI map. Then all the masked channels were added, creating the column density map.
This is a standard procedure which allows a higher S/N ratio to be
obtained, but it has the disadvantage
that the noise level is not the same everywhere across the map. This
is caused by the fact that at each position of the map a different
number of channels are added. We can calculate the noise at
each position as
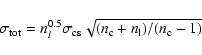 |
(2) |
Finally, we corrected the map for primary beam attenuation.
The global HI profiles, total HI maps, and position-velocity (XV) diagrams along the major axis of each galaxy are shown in Fig. 13.
Figure 1 shows the Tully-Fisher (TF) relation for our
sample obtained using the derived distances. We took the corrected apparent
magnitudes from the LEDA catalogue, and determined the absolute
magnitudes with the "virgocentric'' distances. The widths of the
profiles were corrected for instrumental
broadening (following Bottinelli et al. 1990) as well as for
inclination. The dotted line in Fig. 1 is the TF relation
derived by
Verheijen (1997) for the B band. Some points do clearly
follow the relation, but there are many outliers. Some of the
deviations are greater than 1.5 mag (a factor of two in
distance). There are various indications that the
Virgocentric inflow model may not give the correct distances: the
first is that when one looks at the distribution of galaxies in
supergalactic coordinates,
the galaxies with large discrepancies are not randomly distributed on
the sky, but grouped together. Another indication that there could be
problems with such simple, spherical virgocentric inflow model is the fact that the
Virgo Cluster may be far from spherical
(West & Blakeslee 1997). This will probably affect quite strongly the distance
determination for nearby galaxies.
| |
Figure 1: B band Tully-Fisher relation for the galaxies in the sample. We have taken apparent B magnitudes from the LEDA database, and converted them to absolute magnitudes with the distance determined as explained in Sect. 4.2. The dotted line is the TF from Verheijen (1997), the solid line indicates the fit to the data. |
| Open with DEXTER | |
We have, therefore, decided to calculate the distances using the TF relation. The estimated distance uncertainty introduced by this is expected to be 30% (0.6 mag). Of course, galaxies for which the apparent magnitude already has a large error will have a more uncertain distance.
It is necessary to know the position of the center of a galaxy to be able to determine its rotation curve, its lopsidedness and the warp asymmetry. In an axisymmetric galaxy with gas in circular orbits this location is at the same time the center of the potential, the center of the gas orbits, and the point of maximum optical emission (if dust absorption is not very important). In the case of an asymmetric galaxy, the center can be determined in several ways:
If the galaxy has a nuclear radio continuum source, this marks the position of the center with great accuracy. But this is rare.
The center may also be derived from ellipse fitting to the optical isophotes. This method has the problem that it is very sensitive to dust, and can lead to large errors. Similarly, ellipses can be fitted to the total HI maps, but since the HI often has a lot of substructure such fits are unreliable. In both HI and optical ellipse fitting, one gets a set of ellipses (thus, a set of centers) and has to extract a single center from it. Sometimes this is easy and the weighted mean of all those centers is a good measure of the "true'' center, but when the galaxy is lopsided this is no longer the case and a linear fit to the centers derived from the fits is necessary to find the center of the galaxy.
Another method is based on the position-velocity (XV) diagram along the major axis of the galaxy and consists in finding the center that minimizes the asymmetries of the XV diagram. In this way one can be sure that the derived asymmetries are a lower limit to the true asymmetries of the galaxy. Density and kinematic information are thus combined in this method, which uses the whole XV diagram and not only the rotation curve or only the density profile. The center is determined in the following way:
With a position angle and a center, we extracted the XV diagram along the major axis defined by these quantities. At this point we applied the "XV-method'' to improve the determination of the position of the center. Table 3 lists the positions of the centers obtained with this method as well as those listed in LEDA. The distances between both centers are usually not larger than 4'' and there is only one case exceeding 10'' found for UGC 5986, a very distorted galaxy both kinematically and morphologically.
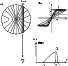 |
Figure 2:
Schematic representation of the HI detected
at each position along the major axis in an edge-on galaxy. a) At a
certain distance x0
from the center of the galaxy, all the emission from gas in the dashed
area is detected by the telescope. Isovelocity lines (with respect
to the observer) have been drawn in the figure. The XV diagram along
the major axis with the rotation curve (filled dots) is shown
in b), and a velocity profile at a certain major axis distance (x0)
in c). The rotation velocity at x0 is indicated by
|
| Open with DEXTER | |
| UGC | RA2000 LEDA | Dec2000 LEDA | RA2000 XV | Dec2000 XV | dist ('') |
| 1281 | 01 49 32.0 | 32 35 21.5 | 01 49 31.7 | 32 35 16.2 | 6.2 |
| 2459 | 03 00 37.1 | 49 02 41.3 | 03 00 36.5 | 49 02 34.2 | 9.0 |
| 3137 | 04 46 16.0 | 76 25 07.2 | 04 46 15.5 | 76 25 06.4 | 2.1 |
| 3909 | 07 36 59.1 | 73 42 50.1 | 07 36 58.8 | 73 42 48.9 | 1.7 |
| 4278 | 08 13 58.8 | 45 44 35.2 | 08 13 59.0 | 45 44 38.0 | 3.7 |
| 4806 | 09 09 33.5 | 33 07 29.4 | 09 09 33.8 | 33 07 25.1 | 5.8 |
| 5452 | 10 07 11.5 | 33 01 38.4 | 10 07 11.6 | 33 01 39.3 | 2.0 |
| 5459 | 10 08 10.1 | 53 04 58.4 | 10 08 10.3 | 53 04 58.9 | 2.2 |
| 5986 | 10 52 30.9 | 36 37 03.4 | 10 52 31.7 | 36 37 16.3 | 17. |
| 6126 | 11 03 43.6 | 28 53 05.6 | 11 03 43.6 | 28 53 07.3 | 1.7 |
| 6283 | 11 15 52.1 | 41 35 32.2 | 11 15 52.1 | 41 35 27.6 | 4.7 |
| 6964 | 11 58 37.1 | 47 15 37.1 | 11 58 37.1 | 47 15 35.1 | 2.1 |
| 7089 | 12 05 57.7 | 43 08 35.3 | 12 05 58.0 | 43 08 37.2 | 3.6 |
| 7090 | 12 06 01.5 | 47 28 47.6 | 12 06 01.2 | 47 28 40.4 | 7.9 |
| 7125 | 12 08 42.2 | 36 48 07.8 | 12 08 42.3 | 36 48 08.5 | 1.1 |
| 7151 | 12 09 58.7 | 46 27 26.5 | 12 09 58.1 | 46 27 27.8 | 6.6 |
| 7321 | 12 17 33.9 | 22 32 25.0 | 12 17 34.0 | 22 32 25.1 | 1.5 |
| 7483 | 12 24 11.4 | 31 31 17.5 | 12 24 11.8 | 31 31 14.9 | 5.1 |
| 7774 | 12 36 23.1 | 40 00 17.8 | 12 36 23.0 | 40 00 18.4 | 0.8 |
| 8246 | 13 10 04.2 | 34 10 52.5 | 13 10 04.4 | 34 10 49.8 | 3.3 |
| 8286 | 13 12 11.8 | 44 02 14.8 | 13 12 11.7 | 44 02 13.2 | 1.8 |
| 8396 | 13 21 24.7 | 38 32 15.7 | 13 21 24.9 | 38 32 16.9 | 2.6 |
| 8550 | 13 34 03.1 | 47 54 45.2 | 13 34 03.0 | 47 54 47.3 | 2.6 |
| 8709 | 13 46 23.8 | 43 52 20.3 | 13 46 23.8 | 43 52 18.9 | 1.4 |
| 8711 | 13 46 24.7 | 46 06 28.2 | 13 46 24.6 | 46 06 24.6 | 3.8 |
| 9242 | 14 25 20.8 | 39 32 21.1 | 14 25 20.6 | 39 32 19.4 | 2.8 |
In highly inclined systems, each line of sight to the galaxy contains information about different portions of that galaxy. At each position (see Fig. 2) we get the integrated signal coming from different radii, and we have to disentangle that information to get the radial density profile.
This has been done following the procedure developed by Warmels (1988). First, all the emission from the galaxy is integrated in the direction perpendicular to the major axis, resulting in an HI strip integral. This is then deconvolved using the Lucy (1974) deconvolution scheme, assuming that the HI distribution is axisymmetric, and taking into account the size of the beam. This algorithm has been applied separately to the two sides of the galaxy. This allows us to estimate the density lopsidedness in the HI gas by comparing one side with the other.
The HI radius (
![]() )
has been calculated using the average of the
two deconvolved profiles, and is defined as the radius where the HI surface density
drops to
)
has been calculated using the average of the
two deconvolved profiles, and is defined as the radius where the HI surface density
drops to
![]() .
.
For these reasons, we have focused on the derivation of the rotation curve from the position-velocity (XV) diagram along the major axis of the galaxy. In galaxies with low inclinations, the beam samples the HI emission from a small portion of the disk, and the profiles in the XV diagram are basically Gaussian, unless beam-smearing plays an important role. In a completely edge-on galaxy, however, the beam intercepts a large portion of the disk, as illustrated in Fig. 2. In this case, the derivation of the rotation curve can be done as outlined in Sancisi & Allen (1979). At each position along the major axis the maximum rotation velocity (relative to the systemic) is chosen, corrected for the instrumental broadening and random motions of the gas. This method assumes that there is gas everywhere along the line of sight, and may give the wrong rotation velocity if this is not the case.
We have determined the velocity at each position along the major
axis by fitting half a Gaussian to the edge of the profile at
that position. The width of the Gaussian is held fixed with a value
of
![]() ,
where
,
where
![]() is the instrumental broadening and
is the instrumental broadening and
![]() is the velocity
dispersion of the gas due to the random motions in the
disk. Measurements of velocity dispersion of galaxies in HI give
typical values that range from
is the velocity
dispersion of the gas due to the random motions in the
disk. Measurements of velocity dispersion of galaxies in HI give
typical values that range from ![]() 10-12 km s-1 in the
inner parts to
10-12 km s-1 in the
inner parts to ![]() 6 km s-1 in the outer parts
(Kamphuis 1993; Dickey et al. 1990).
Here we have adopted
a constant value of 8 km s-1 through the whole HI disk, which
seems a reasonable assumption.
6 km s-1 in the outer parts
(Kamphuis 1993; Dickey et al. 1990).
Here we have adopted
a constant value of 8 km s-1 through the whole HI disk, which
seems a reasonable assumption.
Figure 3 illustrates how the rotational velocity at
each radius is determined. We extract a velocity profile (see
Fig. 2) at a position along the major axis, and determine
where the emission from the galaxy begins in velocity. This is done by
looking where in the profile ![]() points lie above
3
points lie above
3![]() .
After some experimentation we have adopted
.
After some experimentation we have adopted
![]() 3. At this
moment we make a series of Gaussian fits to the edge
of the profile, varying the amount of signal points included in the fit (see
Fig. 3). The rotation velocity will be the center
of the Gaussian with a smaller reduced
3. At this
moment we make a series of Gaussian fits to the edge
of the profile, varying the amount of signal points included in the fit (see
Fig. 3). The rotation velocity will be the center
of the Gaussian with a smaller reduced ![]() of all
the fits.
of all
the fits.
 |
Figure 3:
Edge-fitting method. A profile of UGC 8286 is
plotted, along with 4 different fits. The data are displayed as
diamonds, and the fit as filled circles and dotted line. The
dotted line shows the part of the Gaussian that is not used in the fit.
From top to bottom, the fits
make use of 2, 3, 4 and 5 "signal'' points (points left of the vertical
dashed line). Each panel also shows the reduced |
| Open with DEXTER | |
The error in the determined rotation velocity is calculated from
the amplitude of the fitted Gaussian. This error also depends on the
velocity resolution compared to the dispersion of the Gaussian, and on
the dispersion of the Gaussian itself. After extensive Monte-Carlo
simulations we derived the following formula to calculate the errors
for our edge-fitting method:
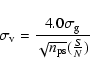 |
(3) |
A rotation curve derived by making edge-fits in the velocity direction as described above still suffers from the effects of beam smearing. The influence of this is to overestimate the velocities in the inner rising parts of the rotation curve and in some galaxies the effect is quite severe. To correct for this we have performed edge-fits in the horizontal direction as well. In these fits the width of the Gaussian depends on the slope of the rotation curve, velocity resolution and the beam width. We determined this width by fitting a full Gaussian around the center of the galaxy.
At this stage we have two determinations of the rotation curve, one from the edge-fits in the velocity direction and the other from those in the spatial direction. The final rotation curve is the minimum of the two determinations.
To assess that the errors are realistic in the rotation curve for each radius and correct artificial "bumps'' created by noise in the edge-fits, we determined the mean velocity of the data within a beam size and its dispersion. The mean value is the finally adopted rotation velocity and the error is the sum in quadrature of the formal error and the dispersion.
The rotation velocities were derived separately for the approaching and receding sides, to be able to compare them and to look for kinematic asymmetries.
We would also like to note that a number of galaxies (UGC 5986, 8246, 9242, see XV diagrams in Fig. 13) have non-circular motions in the central regions. This suggests either that orbits in these systems are elliptical, or that there are radial motions of the gas, and caution against the use of our rotation curves as tracers of the inner potential wells of these galaxies.
We have derived the curve of the warp from the total intensity maps, by fitting Gaussians to the density profiles parallel to the minor axis of the galaxy. We thereby determine the position of the HI ridge at each radius. This underestimates warps that have a line of nodes significantly different from our line of sight. For example, the ridge of the HI could warp very little, but there may be a low level envelope that bends with greater amplitude, but that would not show up in a Gaussian fit. Thus, the numbers we get from this procedure will have to be treated as lower limits for the warp amplitude.
To characterize this curve by a number, we have, first of all,
determined the warp starting radius (
![]() ). This is the radius
where the warp curve leaves significantly the plane defined
by the inner parts of the disk. Many factors (as small corrugations and
noise in the warp curve) can hamper the determination of the warp
radius. To overcome these we have devised a complex procedure which
smoothes the data at different resolutions and takes the scatter in
the inner disk into account (see Appendix A for
full details). The warp radius for one side of a galaxy (UGC 6126) was
strongly affected by the presence of spiral arms. We manually set the
warp radius of that side to that of the other side of the galaxy.
Once the warp radius has been determined, a straight
line is fitted to the points with
). This is the radius
where the warp curve leaves significantly the plane defined
by the inner parts of the disk. Many factors (as small corrugations and
noise in the warp curve) can hamper the determination of the warp
radius. To overcome these we have devised a complex procedure which
smoothes the data at different resolutions and takes the scatter in
the inner disk into account (see Appendix A for
full details). The warp radius for one side of a galaxy (UGC 6126) was
strongly affected by the presence of spiral arms. We manually set the
warp radius of that side to that of the other side of the galaxy.
Once the warp radius has been determined, a straight
line is fitted to the points with
![]() .
With this we
calculate the warp angle according to the following definition (see
Fig. 4):
.
With this we
calculate the warp angle according to the following definition (see
Fig. 4):
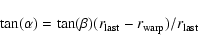 |
(4) |
| |
Figure 4:
Determination of the warp angles |
| Open with DEXTER | |
Even though for most galaxies the warps are well represented by this
angle, there are
some that are not well fitted by a straight line from
![]() to
to
![]() ,
either because they rise faster or because the gas layer
bends back towards the plane defined by the inner disk, as is the case
of the Galaxy (Burton 1988).
,
either because they rise faster or because the gas layer
bends back towards the plane defined by the inner disk, as is the case
of the Galaxy (Burton 1988).
The warping angle is calculated separately for both sides of the galaxy, and in
this way we can estimate the asymmetry of the warp using the
difference between one side and the other. Most of the warps (all
except 2 systems that are strongly interacting) have S-shape, i.e.
the gas layer bends in opposite directions on either
side of the galaxy. Taking into account that the warp angles are
measured anticlockwise and that a symmetric S-shape warp would have
![]() we have defined the warp asymmetry as:
we have defined the warp asymmetry as:
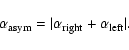 |
(5) |
There is ample evidence that a large fraction of galaxies depart from axisymmetry. This can be inferred from the asymmetric shape of the global HI profile. Such asymmetry can be caused by either a density asymmetry or a kinematic one. Richter & Sancisi (1994) estimated that at least 50% of the galaxies have asymmetric global profiles. Later work by Haynes et al. (1998) confirmed this result. Swaters et al. (1999) discussed the lopsidedness in the kinematics and concluded that probably at least half of all galaxies are kinematically lopsided.
We therefore want to find out how lopsided our galaxies are and whether there is any relationship between lopsidedness and warping. This will be investigated both in the kinematics (using the rotation curves from the approaching and receding sides) and in the density.
To quantify the lopsidedness in the HI distribution we have calculated
the HI mass for each side of the galaxy (M1, M2) and defined the
lopsidedness index as
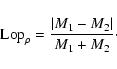 |
(6) |
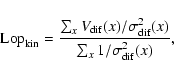 |
(7) |
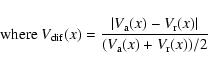 |
(8) |
One of the issues that we want to address is the role of the
environment in warp phenomena. Reshetnikov & Combes (1998) found that
the percentage of optically warped galaxies is higher in
rich environments. We want
to find out if this also holds for the HI warps or not. For that
purpose, for each galaxy we have searched in the NASA/IPAC
Extragalactic Database (NED) looking for companions which are within
100 arcmin and have a radial
velocity difference less than 150 km s-1 with respect
to our galaxies. We have also looked for companions in our HI datacubes, at full
resolution, 30'' resolution, and 60'' resolution. The
primary beam at Westerbork has a FWHM of about 37' at 21 cm, which
determines how far away from the galaxy
we are able to detect other objects. We have listed the companions
from NED and those detected in HI in Table 7. We have found two
new systems (companions to UGC 4806), and determined velocities for 4
systems that had no previous velocity determination.
| UGC | Lop
|
Lop |
|
|
|
W20 | W50 | PA | Warp1 | Warp2 | Env | ||
| % | % | ' |
|
km s-1 | km s-1 | km s-1 | degree | degree | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | ||
1281 |
3.1 | 0.0 | 3.40 | 1.2 | 157 | 132.4 | 123.3 | 39 | 5.3
|
0.7 | -0.7
|
0.7 | 0 |
| 2459 | 2.2 | 7.4 | 3.87 | 134.1 | 2465 | 335.5 | 324.7 | 64 |
|
0.6 | 1.4
|
1.1 | 2 |
| 3137 | 6.0 | 4.0 | 3.53 | 32.2 | 992 | 243.3 | 232.2 | 74 |
|
0.5 | 3.3
|
0.7 | 0 |
| 3909 | 1.7 | 0.4 | 2.29 | 10.4 | 943 | 183.6 | 167.6 | 80 |
|
2.6 | 8.8
|
1.7 | 0 |
| 4278 | 7.2 | 1.8 | 3.13 | 10.2 | 558 | 192.8 | 173.5 | 173 | - |
|
0.6 | 2 | |
| 4806 | 1.2 | 0.3 | 2.33 | 72.1 | 1950 | 351.6 | 328.1 | 148 | 3.2
|
1.4 | - | 2 | |
| 5452 | 3.1 | 9.3 | 1.94 | 23.3 | 1340 | 220.8 | 203.0 | 38 |
|
2.1 | 17.4
|
2.3 | 2 |
| 5459 | 9.2 | 3.0 | 3.58 | 37.3 | 1108 | 287.6 | 269.0 | 131 |
|
3.1 | 3.1
|
0.9 | 1 |
| 5986 | 5.4 | 6.9 | 5.29 | 27.1 | 624 | 265.6 | 243.1 | 38 | 4.6
|
0.7 | 22.4
|
3.0 | 2 |
| 6126 | 3.7 | 11.6 | 3.07 | 10.3 | 701 | 198.7 | 184.8 | 166 |
|
1.1 | 26.5
|
1.1 | 2 |
| 6283 | 2.9 | 0.4 | 3.48 | 15.1 | 715 | 214.9 | 201.8 | 8 | 6.1
|
1.8 |
|
1.3 | 0 |
| 6964 | 5.4 | 3.2 | 2.83 | 19.0 | 906 | 274.4 | 262.7 | 65 | 20.2
|
1.3 |
|
0.8 | 1 |
| 7089 | 13.4 | 15.1 | 2.13 | 5.8 | 782 | 158.3 | 141.7 | 36 | - | - | 2 | ||
| 7090 | 9.8 | 10.2 | 3.82 | 12.9 | 575 | 341.3 | 312.8 | 20 | - | - | 2 | ||
| 7125 | 5.6 | 9.5 | 3.70 | 34.2 | 1079 | 161.9 | 147.6 | 83 | - | 5.9
|
0.6 | 2 | |
| 7151 | 8.6 | 0.4 | 3.26 | 1.9 | 265 | 167.6 | 157.0 | 102 | - | - | 1 | ||
| 7321 | 2.4 | 1.5 | 3.23 | 2.4 | 407 | 230.2 | 220.9 | 82 | - |
|
0.8 | 0 | |
| 7483 | 2.5 | 2.7 | 2.47 | 21.1 | 1247 | 227.1 | 198.8 | 108 | - | - | 2 | ||
| 7774 | 5.2 | 1.9 | 2.72 | 3.4 | 522 | 203.3 | 190.3 | 102 | 15.2
|
2.5 |
|
2.7 | 1 |
| 8246 | 3.9 | 1.8 | 2.19 | 4.8 | 809 | 145.4 | 134.6 | 83 | - |
|
2.5 | 2 | |
| 8286 | 2.1 | 0.6 | 4.25 | 5.4 | 406 | 188.9 | 179.0 | 28 |
|
0.5 | 4.6
|
1.0 | 0 |
| 8396 | 7.4 | 4.9 | 1.78 | 9.8 | 951 | 173.3 | 142.2 | 128 | - | 23.9
|
6.7 | 2 | |
| 8550 | 1.9 | 3.6 | 2.85 | 2.0 | 359 | 135.4 | 124.4 | 167 | 2.5
|
1.0 | - | 1 | |
| 8709 | 4.4 | 9.5 | 3.46 | 174.2 | 2410 | 416.5 | 399.1 | 148 | - | - | 2 | ||
| 8711 | 3.9 | 0.7 | 3.10 | 53.8 | 1506 | 330.5 | 311.2 | 151 |
|
2.7 | 8.7
|
1.7 | 0 |
| 9242 | 6.8 | 2.9 | 3.13 | 31.0 | 1439 | 208.5 | 195.1 | 72 | - | - | 1 | ||
| Total | Poor | Intermediate | Rich | |
| Total | 26 | 7 | 6 | 13 |
| No warp | 6 (9) | 0 (1) | 2 (3) | 4 (5) |
| 1-warps | 7 (7) | 1 (2) | 1 (0) | 5 (5) |
| 2-warps | 13 (10) | 6 (4) | 3 (3) | 4 (3) |
| All warps | 20 (17) | 7 (6) | 4 (3) | 9 (8) |
With all this information, we have assigned a number to each galaxy depending on how close the companions are: 2 (companion within 50 arcmin), 1 (companion at distance between 50 and 100 arcmin), or 0 (no companions in 100 arcmin).
Here we present (Table 4) the determined warp angles, the density and kinematical lopsidedness and the classification according to the environment. We also present the rotation curves, the radial density profiles, and the warp curves in the combined plots of Fig. 7.
Finally, we study the influence of the environment on warping and lopsidedness, and we compare the optical and HI warps of a number of galaxies.
The first question to address
is how common warps are. Table 4 already shows
that the outer parts of
the majority of galaxies exhibit some departure from flat disks. We
detect warps in 20 of our galaxies, of which
7 show a warp only on one
side (see Table 5). If we consider only warps larger
than 2![]() ,
the number of warps decreases to 17, of which 7 are
only on one side. Taking into account that we will probably miss
most of the warps with a line of nodes close to the direction
perpendicular to the line of sight from us to the galaxy, it means
that the vast majority of galactic disks are warped.
,
the number of warps decreases to 17, of which 7 are
only on one side. Taking into account that we will probably miss
most of the warps with a line of nodes close to the direction
perpendicular to the line of sight from us to the galaxy, it means
that the vast majority of galactic disks are warped.
Warps normally start at the edge of the optical disk or further
away. This means that for the warp to be visible there must be gas
outside the optical disk. We looked at the galaxies in our sample with
no warp to see if any of them had extended HI disks, i.e. if there
was any galaxy with an extended HI disk (with respect to the optical emission)
and no warp. As a measure of the optical extent of the galaxy we used
![]() (see Sect. 3), which is more representative than
R25, particularly in edge-on galaxies. We found that all the galaxies in our
sample that have HI disks more extended than the optical are
warped. If we consider each side of the galaxy independently, there is
only one exception to this rule: one side of UGC 7125 is warped, while the
other remains flat, and both sides have HI more extended than the
optical.
(see Sect. 3), which is more representative than
R25, particularly in edge-on galaxies. We found that all the galaxies in our
sample that have HI disks more extended than the optical are
warped. If we consider each side of the galaxy independently, there is
only one exception to this rule: one side of UGC 7125 is warped, while the
other remains flat, and both sides have HI more extended than the
optical.
One of the most striking characteristics of the warps observed here is their
asymmetry. To begin with, a considerable percentage of the warped
galaxies show a warp only on one side. This is not due to an absence
of HI on the opposite side: in all cases the gas disk on the unwarped
side does extend to beyond
![]() .
Sometimes (as in UGC 7321,
8246, 8396) there are hints of the beginning of a warp in that
side but the data do not allow a firm detection of it.
.
Sometimes (as in UGC 7321,
8246, 8396) there are hints of the beginning of a warp in that
side but the data do not allow a firm detection of it.
However, the clearest sign of asymmetry in warps comes from
galaxies with both sides
warped. Figure 5 shows the warp asymmetry
(
![]() )
with
respect to the mean warp angle. Only galaxies with warps
detected on both sides of the disk are plotted. We inspected the total
HI maps of all
our galaxies looking for tidal features that would clearly indicate
strong tidal interaction with a nearby companion. Such interaction
might produce a highly asymmetric warp. These galaxies are plotted as
filled circles in Fig. 5, and indeed they appear to
possess more asymmetric warps than the rest of the galaxies. But the
remaining warped galaxies also have
large asymmetries. There are only 2 systems with large warps
and high symmetry: UGC 6964 and UGC 6126. The other galaxies
lie more or less on a straight line where the ratio of the asymmetry
to the mean warp is of about 0.7. A galaxy with this asymmetry and a
mean warp of 10
)
with
respect to the mean warp angle. Only galaxies with warps
detected on both sides of the disk are plotted. We inspected the total
HI maps of all
our galaxies looking for tidal features that would clearly indicate
strong tidal interaction with a nearby companion. Such interaction
might produce a highly asymmetric warp. These galaxies are plotted as
filled circles in Fig. 5, and indeed they appear to
possess more asymmetric warps than the rest of the galaxies. But the
remaining warped galaxies also have
large asymmetries. There are only 2 systems with large warps
and high symmetry: UGC 6964 and UGC 6126. The other galaxies
lie more or less on a straight line where the ratio of the asymmetry
to the mean warp is of about 0.7. A galaxy with this asymmetry and a
mean warp of 10![]() would have warps in each side of 6.5
would have warps in each side of 6.5![]() and
13.5
and
13.5![]() ,
which is quite asymmetric.
,
which is quite asymmetric.
Most of the galaxies with both sides warped are antisymmetric (S shape warps). We only have two cases of U-type warps, and both these galaxies are strongly interacting with nearby companions and are very disturbed.
The warp curves, together with the rotation curves and the radial
density profiles have been plotted in Fig. 7. These plots
show the shapes and amplitudes of the warps, and allow a
comparison between features in the
radial density profiles, rotation curves and warp curves. It is quite
clear from Fig. 7 that there are several distinct
warp shapes: some galaxies have monotonically increasing warps
(rising linearly or even faster), while others
have warps that at some point rise slowly, and in some cases head back
to the plane defined by the inner regions, like the southern warp in
the Milky Way. Note that the rotation curves in
Fig. 7 have been calculated along the major axis and
not along the warp line. This is the reason why the rotation curves
often stop before the HI density drops to zero, as in UGC 6964.
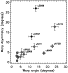 |
Figure 5: Warp asymmetry vs. mean warp angle. Filled circles represent galaxies with obvious tidal features with nearby companions, thus indicating strong interaction. The most strongly warped galaxies are identified by their UGC number. |
| Open with DEXTER | |
Lopsidedness may have some connection with warping. If, for instance, the lopsidedness of a galaxy is caused by merging, and such merging process is also causing the warping, we would expect more pronounced warps in lopsided galaxies, and small or no warps in axisymmetric galaxies.
The first indication that
lopsidedness may be the result of accretion or
interactions with nearby companions comes from the fact that the lopsidedness
we measure seems to depend quite strongly on the
environment. In Fig. 6 we have plotted histograms
for the galaxies according to their density lopsidedness index for
each type of environment: poor, intermediate and rich (see
Sect. 4.8). Clearly, galaxies with no nearby companions
are quite symmetric in mass, galaxies with companions not closer
than 50'' are somewhat more lopsided, and finally, all galaxies with
a lopsidedness greater than 5% have a companion closer than 50''. The
dependence of lopsidedness on environment found here is
remarkable if one takes into account the uncertainty of the
classification of the environment. The kinematical lopsidedness seems also
to depend somewhat on the environment, as
isolated galaxies have lower kinematical lopsidedness than the rest of
the galaxies. The way both
lopsidedness indices are measured actually makes
them lower limits due to the fact that the galaxy is edge-on: to
measure our lopsidedness indices we are comparing the approaching and receding
sides of the galaxy (integrated along the line of sight), thus if the
galaxy is asymmetric in the direction along the line of sight we would
not be able to detect it. We did not find a clear correlation between
kinematic and density lopsidedness in our galaxies.
![\begin{figure}
\par\includegraphics[width=12.6cm,clip]{h3389f6.ps}\end{figure}](/articles/aa/full/2002/42/aah3389/Timg140.gif) |
Figure 6: Histograms showing the distribution of galaxies according to the density (upper panels) and kinematical (lower panels) lopsidedness index for different environments. Galaxies in poor environments are plotted in the left panels, galaxies in intermediate environments in the middle panels, and galaxies in rich environments in the right panels. For a detailed description of the environment classification, see Sect. 4.8. |
| Open with DEXTER | |
| Galaxy | Optical | HI | |
| (NGC) | (UGC) | ||
| 3432 | 5986 | - | U |
| 3510 | 6126 | N | N |
| 3600 | 6283 | N | S |
| 4010 | 6964 | N | S |
| 4144 | 7151 | - | - |
| 5023 | 8286 | - | N |
| 5229 | 8550 | S | S? |
| 5297 | 8709 | - | - |
| 5301 | 8711 | N | N |
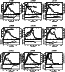 |
Figure 7:
Density - RC - warp plots. For each galaxy, the rotation
curve along the major axis, the radial HI density profile and the
curve of warp are plotted. We have measured these quantities
independently for both sides of the galaxies, and here we present them
together in the same plot. The top panel shows the rotation velocities
and radial density profiles for both sides of the galaxy. The left
axis shows the units for the rotation velocities, while the right axis
applies to the density profiles. The bottom panel shows the warp
curves for both sides. Because most of the warps have an S-shape, the
warp curve derived for the left side has been inverted, to highlight
symmetries or asymmetries between the two sides of the galaxy. With
this process, both warp curves of a galaxy with a perfect S-shape
symmetry (thus, antisymmetry) would fall on top of each other. One
side is plotted with crosses (rotation curve and warp curve) and
dotted line (density), and the other side is plotted with circles
(rotation curve and warp curve) and solid line (density). The rotation
curve and warp curves in the figure are shown at 2 different
resolutions. We derived these curves using the full resolution data
(small symbols), and then complemented it in the outer parts with the
curves obtained at 30
|
| Open with DEXTER | |
 |
Figure 7: continued. |
| Open with DEXTER | |
 |
Figure 7: continued. |
| Open with DEXTER | |
We checked our sample to see if these relations hold for the larger HI warps as well. Table 5 shows that, if anything, the trend in frequency for the occurrence of HI warps in our sample seems to go in the opposite sense: galaxies in poor environments are more frequently warped than galaxies in dense environments. However, all galaxies with an extended HI disk with respect to the optical disk are warped, therefore the frequency of warps depends on the extension of the HI disks. Thus, in our sample there are more galaxies with no extended HI in rich environments than in poor environments. The warp parameters (amplitude and asymmetry) are illustrated as a function of environment in Fig. 8.
There seems to be a tendency for galaxies in poor environments to be more prone to warping, but to have smaller warp angles than in rich environments. Warps also seem to be more symmetric in poor than in rich environments. The explanation for the asymmetry and higher amplitude of the warps in rich environments could lie in the tidal interaction with neighboring galaxies (e.g. UGC 5452, UGC 8396). The indication that galaxies in poor environments are more frequently warped may mean that tidal interactions are not the only mechanism that produces warps.
As mentioned above, warps may show a different behavior with respect to environment when observed in the optical or in HI. Unfortunately, not much work has been done about the relationship between HI and optical warps in the same galaxies, and none with high quality HI and optical data.
Sánchez-Saavedra et al. (1990) studied optical warps using POSS
plates. They looked at all NGC galaxies in the northern hemisphere
that had
![]() larger than 0.57, and determined
whether the warp was clockwise
or anti-clockwise (S or N warps). Nine of their galaxies are in our
sample, so we decided to compare with our results and find out whether
the sense of the warp
is the same or not. Table 6 shows the results. Four of the
galaxies in common do not appear to be warped in the Sánchez-Saavedra et al.
(1990) study. Two of the warped galaxies have the same sense as
found in
this work, two the opposite, and the last one has a dubious warp in
HI. In the case of UGC 6964 the
difference may be due to dust and/or spiral arms. The optical image
shows patchy emission and it indeed looks bent with an "N'' shape, while
the HI bends in the opposite direction in quite a spectacular
way. In the other case, UGC 6283, the difference is probably due
to the shape of the warp curve itself. The disk bends first slightly in one
direction, turns back and then bends in the opposite
direction. The warp seen in the optical is probably tracing that first
small "kink'' of the warp shape. So in this case the warp is correctly
detected, but the general sense of the warp is not, because the
optical disk ends
before the HI warp changes direction. This galaxy is not completely
edge-on and it is possible that this "kink'' could be due to the
presence of spiral arms.
larger than 0.57, and determined
whether the warp was clockwise
or anti-clockwise (S or N warps). Nine of their galaxies are in our
sample, so we decided to compare with our results and find out whether
the sense of the warp
is the same or not. Table 6 shows the results. Four of the
galaxies in common do not appear to be warped in the Sánchez-Saavedra et al.
(1990) study. Two of the warped galaxies have the same sense as
found in
this work, two the opposite, and the last one has a dubious warp in
HI. In the case of UGC 6964 the
difference may be due to dust and/or spiral arms. The optical image
shows patchy emission and it indeed looks bent with an "N'' shape, while
the HI bends in the opposite direction in quite a spectacular
way. In the other case, UGC 6283, the difference is probably due
to the shape of the warp curve itself. The disk bends first slightly in one
direction, turns back and then bends in the opposite
direction. The warp seen in the optical is probably tracing that first
small "kink'' of the warp shape. So in this case the warp is correctly
detected, but the general sense of the warp is not, because the
optical disk ends
before the HI warp changes direction. This galaxy is not completely
edge-on and it is possible that this "kink'' could be due to the
presence of spiral arms.
Our conclusion from this comparison is that the stellar warps studied thus far are not directly comparable to the HI warps. The latter occur at larger galactocentric radius, and generally have a considerably higher amplitude. At this point it is unclear whether (faint) stellar disks extend to these radii or not.
In our search for a common property among warped galaxies (with respect to the non warped ones), we have compared the radial HI profiles of both types of galaxies. We have excluded galaxies that are interacting with nearby neighbors, because a tidal interaction probably affects the radial profile of a galaxy. We also removed galaxies with very small warps. Thus we have constructed two groups of galaxies: the bona fide warped galaxies, UGC 1281, 2459, 3137, 3909, 5459, 6964, 7125, 7321, 7774, 8286 and 8711; and the non-warped galaxies UGC 7089, 7090, 7151, 7483, 9242.
We have scaled the radial profiles using
![]() as unit radius and
the radial densities with
as unit radius and
the radial densities with
![]() ,
where D is the distance to
the galaxy. We have
tried other scaling factors (such as the radius where the density drops
to 0.5 the peak density; and the area below the profile) with no
effect on the conclusions presented here.
,
where D is the distance to
the galaxy. We have
tried other scaling factors (such as the radius where the density drops
to 0.5 the peak density; and the area below the profile) with no
effect on the conclusions presented here.
![\begin{figure}
\par\includegraphics[width=17.1cm,clip]{h3389f8.ps}\end{figure}](/articles/aa/full/2002/42/aah3389/Timg145.gif) |
Figure 8: Warp angles for each environment class (see definition in Sect. 4.8). The left panel shows the warps of galaxies in poor environments, the middle panel the galaxies in intermediate environments, and the right panel those in rich environments. For each galaxy, the larger of both side's warp angles has been plotted on the x axis, versus the smaller one on the y axis (so the upper left part of the plots is empty). The galaxies with a detected warp on only one side lie in the y=0 line, and the non warped galaxies are in the origin. The dotted line indicates equal warp angles on both sides of the galaxy. |
| Open with DEXTER | |
Figure 9 shows the individual profiles as well as the
mean profile for each group of galaxies. A histogram showing the radius at which
warps begin is also plotted. These plots show that warped galaxies
are more extended in HI than non warped galaxies: at around 1.1
![]() the HI density of
a galaxy with no warp falls much faster than that of a warped galaxy, which
still has some more gas extending up to 1.5 and even 2
the HI density of
a galaxy with no warp falls much faster than that of a warped galaxy, which
still has some more gas extending up to 1.5 and even 2
![]() .
This
extra gas we see in the warped galaxies is the same feature as the
"shoulder'' mentioned in Sancisi (1983).
.
This
extra gas we see in the warped galaxies is the same feature as the
"shoulder'' mentioned in Sancisi (1983).
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{h3389f9.ps}\end{figure}](/articles/aa/full/2002/42/aah3389/Timg146.gif) |
Figure 9: Radial HI density profiles. The plot on the left shows the HI profiles for bona fide warped (upper panel) and non-warped (lower panel) galaxies (see Sect. 5.3 for definition of both groups). The profiles of individual warped and non warped galaxies are plotted in dotted line, and the thick line is the average profile for each group. In the upper panel a histogram of the radius where the warp begins is overplotted. We have treated both sides of the galaxy independently, to take into account that two of our bona fine warped galaxies have only one-sided warps. The plot on the right shows the mean profiles for both bona fide warped (solid line) and non warped galaxies (dotted line). |
| Open with DEXTER | |
Thus, the typical radial HI profile of a warped galaxy has the
following shape: in the inner parts it is roughly constant or slowly decreases,
around 0.5
![]() it drops faster, and further out it extends at
low levels ending at 1.5-2
it drops faster, and further out it extends at
low levels ending at 1.5-2
![]() .
It is in the second part of
the profile (the steepest part, around the optical edge) where a warp
develops in most of the galaxies.
.
It is in the second part of
the profile (the steepest part, around the optical edge) where a warp
develops in most of the galaxies.
We have also measured the extent of the HI with respect to the optical
in both non warped and warped galaxies. Figure 10 shows
the histograms for both groups, and indicates that warped
galaxies have HI layers more extended with respect to the optical than
galaxies with no warps. There is no galaxy in our sample with an
extended HI disk with respect to the optical disk and no warp.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{h3389f10.ps}\end{figure}](/articles/aa/full/2002/42/aah3389/Timg147.gif) |
Figure 10:
Histograms of the ratio
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11cm,clip]{h3389f11.ps}\end{figure}](/articles/aa/full/2002/42/aah3389/Timg148.gif) |
Figure 11:
Warp amplitude vs. the width of the global HI profile at
20% level (left) and vs.
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11cm,clip]{h3389f12.ps}\end{figure}](/articles/aa/full/2002/42/aah3389/Timg149.gif) |
Figure 12:
HI mass vs. HI radius for all the galaxies in the sample. The
left panel shows the relation among measured quantities (
|
| Open with DEXTER | |
We have plotted the warp amplitude (warp angle) vs. the width of the global HI profile at 20% level and vs. the extent of the HI with respect to the optical in Fig. 11. The objects with obvious interaction with nearby companions are shown with large filled symbols. For this class of objects there seems to be a relation between the width of the profile and the warp amplitude in the sense that galaxies with broader profiles have smaller warps.
For the rest of the galaxies we have not found any relation with either the visible mass of the galaxy or the width of the global HI profile. If warps are caused by some force realigning the disk of the galaxy (as opposed to inflow of HI gas at a different angle than that of the inner disk), this means that the force should scale (on average) with the mass of the system. The amplitude of warps does not seem to be related to either the density lopsidedness or the kinematical lopsidedness. The same is true for the asymmetry of warps.
Figure 11 also shows the amplitude of the warps vs. the
HI extent with respect to the optical. We can see that non warped
galaxies are at low
![]() ,
and that large warps only
occur in galaxies with large
,
and that large warps only
occur in galaxies with large
![]() .
.
It has been shown that there is a tight relation between
HI mass and HI radius (Broeils & Rhee 1997; Verheijen 1997), with a slope close to 2 in a
log-log scale. Figure 12 shows both
![]() vs.
vs.
![]() relation (measured quantities) and
relation (measured quantities) and
![]() vs.
vs.
![]() (after
multiplication by the distance to each galaxy). The slope of the relation changes
from 1.85 to 1.99 in these plots, which illustrates how uncertainty in
the distances to the galaxies can artificially "enhance'' relations and
alter the slopes.
But even a slope of 1.85 implies that the average HI surface
density (
(after
multiplication by the distance to each galaxy). The slope of the relation changes
from 1.85 to 1.99 in these plots, which illustrates how uncertainty in
the distances to the galaxies can artificially "enhance'' relations and
alter the slopes.
But even a slope of 1.85 implies that the average HI surface
density (
![]() )
is more or less constant
from galaxy to galaxy. The average value is
)
is more or less constant
from galaxy to galaxy. The average value is
![]() ,
consistent with the measurements by Broeils & Rhee (1997).
,
consistent with the measurements by Broeils & Rhee (1997).
| Galaxy | Companion | RA | Dec | dist |
|
|
| 1281 | 01 46 38.1 | 32 20 15 | 157 | 157 | ||
| 2459 | 02 57 08.4 | 48 50 43 | 2464 | 2469 | ||
| HFLLZOA G144.00-08.53 | 02 58 57.7 | 48 43 03 | 19.6 | 2456 | ||
| 3137 | 04 39 22.4 | 76 19 37 | 992 | 993 | ||
| 3909 | 07 30 54.0 | 73 49 28 | 945 | 943 | ||
| 4278 | 08 10 27.4 | 45 53 43 | 563 | 555 | ||
| NGC 2537A | 08 10 09.0 | 46 08 46 | 15.4 | 443 | ||
| NGC 2537 | 08 09 42.6 | 46 08 32 | 16.7 | 447 | 445 | |
| 4806 | 09 06 30.2 | 33 19 38 | 1947 | 1948 | ||
| KUG 0906+333A | 09 06 16.0 | 33 19 31 | 3.0 | |||
| ---- | 09 06 43.2 | 33 20 52 | 3.0 | |||
| ---- | 09 06 58.3 | 33 09 14 | 11.9 | |||
| IC 2445 | 09 10 10.9 | 32 00 53 | 91.4 | 1968 | ||
| CG 0010 | 09 09 50.3 | 32 53 15 | 96.1 | 1860 | ||
| UGC 04777 | 09 03 34.8 | 32 49 14 | 96.7 | 2052 | ||
| 5452 | 10 04 17.1 | 33 16 20 | 1342 | 1340 | ||
| UGC 5446 | 10 03 36.3 | 33 11 27 | 9.8 | 1383 | 1362 | |
| UGC 5482 | 10 07 22.9 | 33 31 23 | 59.5 | 1466 | ||
| KUG 1006+322 | 10 06 04.2 | 33 15 22 | 65.0 | 1390 | ||
| UGC 5393 | 09 58 46.3 | 33 22 41 | 69.4 | 1448 | ||
| 5459 | 10 04 54.7 | 53 19 39 | 1112 | 1109 | ||
| UGC 5460 | 10 04 55.0 | 52 05 20 | 74.3 | 1093 | ||
| UGC 5479 | 10 06 51.9 | 54 44 53 | 87.0 | 1105 | ||
| 5986 | 10 49 42.9 | 36 53 09 | 616 | 615 | ||
| UGC 5983 | 10 49 27.4 | 36 51 36 | 3.5 | (1) | ||
| SBS 1054+365 | 10 54 59.8 | 36 31 30 | 67.1 | 603 | ||
| VV 747 | 10 55 00.2 | 36 31 43 | 67.1 | 634 | ||
| CGCG 184-040 NED02 | 10 55 00.0 | 36 31 00 | 67.3 | 665 | ||
| 6126 | 11 01 00.6 | 29 09 17 | 705 | 704 | ||
| [M98k] 110110.0+285730 | 11 01 10.0 | 28 57 30 | 12.1 | |||
| UGCA 225 | 11 02 15.6 | 29 24 34 | 22.4 | 646 | ||
| UGC 6102 | 10 59 05.2 | 28 57 30 | 27.8 | 702 | ||
| NGC 3486 | 10 57 40.4 | 29 14 37 | 44.0 | 681 | ||
| BTS 026 | 10 57 57.0 | 29 58 18 | 63.2 | 675 | ||
| 6283 | 11 13 06.5 | 41 51 50 | 719 | 713 | ||
| 6964 | 11 56 02.9 | 47 32 20 | 907 | 902 | ||
| NGC 3949 | 11 51 05.2 | 48 08 13 | 61.5 | 807 | ||
| NGC 3985 | 11 54 06.8 | 48 36 44 | 67.3 | 950 | ||
| UGCA 259 | 11 56 18.8 | 46 00 46 | 91.6 | 1154 | ||
| MRK 1460 | 11 48 12.8 | 48 31 46 | 98.5 | 768 | ||
| 7089 | 12 03 25.6 | 43 25 25 | 776 | 774 | ||
| UGC 7094 | 12 03 38.5 | 43 14 05 | 11.6 | 780 | 786 | |
| NGC 4111 | 12 04 31.0 | 43 20 37 | 12.8 | 807 | ||
| MAPS-NGP O_217_0067378 | 12 03 26.8 | 43 10 52 | 14.5 | 756 | ||
| NGC 4117 | 12 05 14.1 | 43 24 17 | 19.7 | 943 | ||
| NGC 4118 | 12 05 20.8 | 43 23 22 | 21.0 | 661 | ||
| NGC 4138 | 12 06 58.6 | 43 57 46 | 50.3 | 888 | ||
| NGC 4143 | 12 07 04.8 | 42 48 43 | 54.3 | 985 | ||
| IC 0750 | 11 56 17.6 | 43 00 92 | 82.0 | 701 | ||
| IC 0749 | 11 55 59.5 | 43 00 44 | 84.9 | 784 | ||
| NGC 4183 | 12 10 46.6 | 43 58 33 | 86.3 | 930 | ||
| NGC 4051 | 12 00 36.4 | 44 48 35 | 88.5 | 725 | ||
| UGC 7129 | 12 06 23.4 | 42 01 10 | 90.3 | 926 | ||
| NGC 4013 | 11 55 56.6 | 44 13 32 | 94.2 | 834 | ||
| (1) No velocity available, but the optical image shows interaction with UGC 5986. | ||||||
| Galaxy | Companion | RA | Dec | dist |
|
|
| 7090 | 12 03 28.5 | 47 45 20 | 566 | 581 | ||
| PC 1200+4755 | 12 00 26.7 | 47 55 57 | 32.3 | 600 | ||
| NGC 4144 | 12 07 27.5 | 46 44 09 | 73.4 | 265 | ||
| 7125 | 12 06 10.2 | 37 04 51 | 1071 | 1072 | ||
| UGC 7207 | 12 09 47.8 | 37 17 30 | 45.2 | 1051 | ||
| UGC 7257 | 12 12 32.1 | 36 14 13 | 91.8 | 942 | ||
| 7151 | 12 07 27.5 | 46 44 09 | 265 | 263 | ||
| NGC 4096 | 12 03 28.5 | 47 45 20 | 73.4 | 566 | ||
| NGC 4242 | 12 15 01.2 | 45 53 47 | 93.1 | 517 | ||
| MRK 1471 | 12 15 21.9 | 47 41 10 | 98.7 | 484 | ||
| 7321 | 12 15 02.0 | 22 49 05 | 408 | 407 | ||
| 7483 | 12 21 41.8 | 31 47 56 | 1253 | 1247 | ||
| UGC 7428 | 12 19 32.6 | 32 22 21 | 44.0 | 1137 | ||
| KUG 1218+310 | 12 18 05.6 | 31 04 36 | 63.3 | 1010 | ||
| NGC 4314 | 12 20 01.8 | 30 10 21 | 99.9 | 963 | ||
| 7774 | 12 33 57.4 | 40 16 49 | 526 | 527 | ||
| UGC 07678 | 12 29 34.4 | 40 06 32 | 51.3 | 685 | ||
| UGC 7751 | 12 32 46.6 | 41 20 10 | 64.8 | 605 | ||
| UGC 7719 | 12 31 34.6 | 39 17 42 | 65.2 | 681 | ||
| UGCA 290 | 12 34 56.5 | 39 01 08 | 76.5 | 445 | ||
| NGC 4618 | 12 39 09.0 | 41 25 29 | 90.5 | 544 | ||
| NGC 4625 | 12 39 29.0 | 41 32 50 | 98.5 | 609 | ||
| 8246 | 13 07 44.3 | 34 26 47 | 813 | 807 | ||
| NGP9 F269-1340356 | 13 08 09.0 | 34 30 09 | 6.1 | |||
| UGC 8323 | 13 12 29.3 | 35 08 42 | 72.0 | 856 | ||
| UGC 8261 | 13 08 41.9 | 35 46 00 | 80.1 | 852 | ||
| IC 4213 | 13 09 52.1 | 35 56 11 | 93.1 | 815 | ||
| UGC 8181 | 13 03 02.9 | 33 10 02 | 96.5 | 886 | ||
| 8286 | 13 09 58.1 | 44 18 14 | 407 | 406 | ||
| 8396 | 13 19 09.3 | 38 47 57 | 946 | 947 | ||
| NGC 5112 | 13 19 41.4 | 38 59 44 | 13.3 | 965 | 971 | |
| UGC 8315 | 13 11 53.6 | 39 24 41 | 92.2 | 1164 | ||
| 8550 | 13 31 58.4 | 48 10 16 | 364 | 359 | ||
| MESSIER 051b | 13 27 52.4 | 47 31 32 | 56.6 | 465 | ||
| MESSIER 051a | 13 27 46.0 | 47 27 22 | 60.3 | 463 | ||
| SBS 1331+493 | 13 31 19.5 | 49 21 28 | 71.5 | 599 | ||
| 8709 | 13 44 18.4 | 44 07 18 | 2407 | 2402 | ||
| NGC 5296 | 13 44 13.5 | 44 06 02 | 1.5 | 2224 | ||
| UGC 08733 | 13 46 33.8 | 43 39 37 | 36.9 | 2338 | ||
| UGC 08798 | 13 50 44.5 | 44 04 25 | 69.4 | 2275 | ||
| NGC 5336 | 13 50 05.4 | 43 29 21 | 73.2 | 2338 | ||
| 8711 | 13 44 21.4 | 46 21 25 | 1503 | 1506 | ||
| 9242 | 14 23 19.7 | 39 45 50 | 1440 | 1438 | ||
| NGC 5582 | 14 18 41.3 | 39 55 18 | 54.3 | 1435 | ||
| MRK 0676 | 14 17 23.7 | 40 05 11 | 70.9 | 1734 |
![\begin{figure}
\par\includegraphics[width=11cm,clip]{u1281-plotart30.ps}\end{figure}](/articles/aa/full/2002/42/aah3389/Timg155.gif) |
Figure 13:
The HI and optical data for UGC 1281; the corresponding figures for the other
galaxies in the sample are only available in the online version. For each galaxy we have created a six
panel figure, we present an overview of the HI and optical data for all the galaxies in the sample.
For
each galaxy we have created a six panel figure, in which we have displayed the relevant
information. We have used the 30'' resolution data for the HI
except for the XV diagram where we used the full resolution data.
These panels are available in electronic form in the WHISP pages
( http://www.astro.rug.nl/~whisp). For each galaxy we have
tabulated the rotation curve, the HI radial surface density profile
and the warp curve. There is extra material as well that supplies
extra velocity information. Top left:
R-band optical image, rotated so that the major axis of the galaxy is
on the horizontal axis. Vertical dashed lines have been plotted at
R25.
Top right:
Warp curve derived from the total intensity HI map using the method
described in Sect. 4.6. Note that the scale is
not the same in the horizontal and vertical axes, and that this ratio
differs from galaxy to galaxy. This allows the reader to follow the
warp curve more precisely. A plot with the same scale on both axes is
shown in Fig. 7. The vertical dot-dashed lines mark
the warp radius.
Middle left:
total HI map. The thick contour is the locus of the points that have
three sigma rms noise as defined in Sect. 4.1. Note that this
does not mean that the line profiles have emission at three sigma level, as
low-level emission may add-up to more than three sigma. The other
contours levels are at 1, 2, 3, 4, 8, 16,... times the lowest contour,
whose level is indicated in the caption of each galaxy. The beam size
is indicated by the symbol at the lower right,
|
| Open with DEXTER | |
There seems to be a trend of the mean surface density with respect to the asymmetry of warps, in the sense that galaxies with larger mean surface densities seem to possess more symmetric warps.
We have studied the warps in the outer HI layers of a sample of 26 edge-on galaxies with particular attention to warp amplitudes, asymmetry, occurrence rates and their relationship with the environment. We have also studied the density and kinematic lopsidedness of the HI disks.
There are indications that environment may play a role in warping. It is claimed that in rich environments optical warps seem to be larger and more frequent (Reshetnikov & Combes 1998), and HI warps are larger and more asymmetric. However, the ubiquity of warps, even in low density regions and the symmetry of some warps suggest that their origin is not simply the result of interactions with the environment. The fact that all galaxies with an HI layer more extended than the optical show warps of very different amplitudes could indicate that warping is similar in a way to spiral structure. Most perturbations of a disk galaxy, arising e.g. from companions or secondary infall, will provoke a warped response.
The universality of this response makes it hard to pinpoint the perturbation that preceded it. While the trend with environment suggests that tidal effects play an important role, it seems likely that there are other, perhaps more intrinsic, effects at work that cause even quite isolated galaxies to warp. In this sense, the situation may be similar to that for spiral structure, another universal response whose origin is not clear in all details.
Late infall of HI gas might
be responsible for the warps we detect. This would explain the "extra''
HI gas that warped galaxies have outside
![]() while the inner
profiles of warped and non warped galaxies are similar. This late
infall might cause star formation at the outskirts of the
optical disk that could be detected in H
while the inner
profiles of warped and non warped galaxies are similar. This late
infall might cause star formation at the outskirts of the
optical disk that could be detected in H![]() imaging or by looking
at its color.
imaging or by looking
at its color.
To summarize, we list the main conclusions:
We detect warps in 20 out of our 26 sample galaxies confirming that warping of the HI disks is a very common phenomenon in disk galaxies. In fact all galaxies that have an HI disk more extended than the optical are warped.
The amplitude of warps varies considerably from galaxy to galaxy. Also for a given galaxy there can be a large asymmetry in amplitude and shape between the two sides. A large number of warps in our sample are asymmetric. Most of the galaxies with both sides warped are antisymmetric (S shape warps). We only have two cases of U-type warps, and both galaxies are strongly interacting with nearby companions and are very disturbed.
The warping of the disks usually starts near the edge of the optical disk where the HI density drops down.
The connection between HI and optical warps is not clear. HI warps are found in general at larger radii than the optical ones, and as a consequence they probe a different region of the potential of the galaxy. A joint optical+HI study of warps could give important insights on the formation mechanism(s) of warps.
There seems to be a dependence of warps on environment in the sense that galaxies in rich environments tend to have larger and more asymmetric warps than galaxies in poor environments.
The presence of density lopsidedness (and in a weaker way that of kinematical lopsidedness) seems to be related to the presence of nearby companions.
Acknowledgements
IGR wishes to thank Jorge Jiménez-Vicente for many stimulating discussions and useful suggestions. We are grateful to Martin Vogelaar and Hans Terlow for help and assistance in the GIPSY software package. The Westerbork Synthesis Radio Telescope is operated by the Netherlands Foundation for Research in Astronomy with financial support from the Netherlands Organization for Scientific Research (NWO). This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
In this appendix we explain how we have determined the warp radius for our
galaxies using Gaussian fits perpendicular to the
major axis of the galaxy. We take both the centroids of the Gaussian
fits (we refer to them as datapoints) and their uncertainties (![]() ).
The basic idea is to determine the radius at which the
galactic disk begins to bend away from the plane defined by the inner
disk in a systematic way.
).
The basic idea is to determine the radius at which the
galactic disk begins to bend away from the plane defined by the inner
disk in a systematic way.
We take the innermost R25/2 part of the disk as the inner disk,
which we assume is flat. We fit a straight line to it and determine
the vertical offset and the dispersion (
![]() ). The
offset will correct (to first order) possible errors in the
determination of the center of the galaxy, and we can use the
dispersion as an estimate of how noisy our disk is (influence of not
completely edge-on spiral arms and other irregularities). We then
define the warp radius as the location where a significantly large
portion of the disk (at least R25/4) departs coherently more than
). The
offset will correct (to first order) possible errors in the
determination of the center of the galaxy, and we can use the
dispersion as an estimate of how noisy our disk is (influence of not
completely edge-on spiral arms and other irregularities). We then
define the warp radius as the location where a significantly large
portion of the disk (at least R25/4) departs coherently more than
![]() from the plane defined by the inner
disk.
from the plane defined by the inner
disk. ![]() are the uncertainties of the individual datapoints in
the warped portion of the disk.
are the uncertainties of the individual datapoints in
the warped portion of the disk.
If the uncertainties in the datapoints are large we could miss some warps with this procedure. Even with large errors, a coherent smooth warp could be detected if we smooth the warp curve and apply the procedure again. Thus we smooth the warp curve to different resolutions and determine a preliminary warp radius at each resolution. The final warp radius is the minimum value of all the preliminary values. The outcome of this method is shown in the Atlas in Fig. 13, where warp curves and warp radii are shown on the same panel.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{u1281-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg160.gif) |
Figure 13:
continued.
UGC 1281: The warp is visible in the extreme velocity
channels on both sides of the disk.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u2459-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg161.gif) |
Figure 13:
continued.
UGC 2459: This galaxy is located at very low galactic
latitude (-8.6 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u3137-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg162.gif) |
Figure 13:
continued.
UGC 3137: This galaxy has a low level, very
symmetric warp that bends suddenly and then stays at a fixed height,
resembling a step.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u3909-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg163.gif) |
Figure 13:
continued.
UGC 3909: The optical disk seems to warp in the same
sense as the HI.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u4278-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg164.gif) |
Figure 13:
continued.
UGC 4278: The main disk of this galaxy is surrounded
by some faint clouds on the left side. The galaxy is also
kinematically lopsided.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u4806-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg165.gif) |
Figure 13:
continued.
UGC 4806: We detected three galaxies in HI within a
radius of 12' around this galaxy. The HI disk is only slightly
larger than the optical and shows no warp.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u5452-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg166.gif) |
Figure 13:
continued.
UGC 5452: The emission in the region of the warp (right side,
see total HI map) is very faint and barely detected.
The one-sided warp of this galaxy pointing
towards the galaxy UGC 5446 suggests a tidal origin for it. The
optical image seems to bend in the opposite direction to that of the HI warp
in the right side.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u5459-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg167.gif) |
Figure 13:
continued.
UGC 5459: This is a prototype of a kinematically
lopsided galaxy. The rotation curve rises fast and remains
approximately flat on
the receding side, whereas it keeps smoothly rising on the approaching side.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=14cm,clip]{u5986-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg168.gif) |
Figure 13:
continued.
UGC 5986: This galaxy shows major distortions both
morphologically and kinematically. The galaxy UGC 5983 (only 3.5'away) is likely to be responsible for some of these distortions. The
central part of the galaxy shows non-circular motions of the gas.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=13cm,clip]{u6126-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg169.gif) |
Figure 13:
continued.
UGC 6126: This galaxy has one of the largest warps of
the sample. It is surrounded by companion galaxies, three of which are
detect in HI. Taylor et al. (1994) observed this
galaxy with a higher resolution with the VLA and detected low level HI
emission above the end of the disk on the right side. Careful inspection of our
datacube smoothed to a 60'' beam and velocity resolution of 25 km s-1resulted in a marginal detection of that HI cloud. The warp has more
structure in density than usual at full resolution and it has
a velocity slightly higher than the maximum of the rotation curve
(which in general is not true for the warps in other galaxies).
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u6283-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg170.gif) |
Figure 13:
continued.
UGC 6283: This galaxy is the earliest type galaxy
(Sab) of our sample and has a very prominent bulge. This inner bulge is inclined
with respect to the plane defined by the HI disk by |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u6964-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg171.gif) |
Figure 13:
continued.
UGC 6964: This galaxy shows quite a large and
symmetric warp. Note the lopsided optical image. The XV diagram
shows a "bump'' very close to the center and a closer inspection of the
datacube suggests that this could be the signature of infalling (or
outflowing) gas onto the disk. That feature is kinematically connected
to the extra HI gas at the top-right part of the disk.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u7089-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg172.gif) |
Figure 13:
continued.
UGC 7089: This galaxy is very lopsided both in
the optical and the HI distribution. The HI does not extend
further than the optical.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u7090-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg173bis.gif) |
Figure 13:
continued.
UGC 7090: This galaxy has very strong kinematical and
density lopsidedness indices and a very asymmetric global profile.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u7125-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg174.gif) |
Figure 13:
continued.
UGC 7125: The warp of this galaxy on the right part of
the disk resembles that of the Milky Way: it rises and then turns
back towards the plane, crossing it.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u7151-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg175.gif) |
Figure 13:
continued.
UGC 7151: The HI is confined to the extent
of the optical disk in this galaxy. The rotation curve
reaches a flat part on the receding side but rises continuously
until the last measured point on the approaching side.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u7321-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg176.gif) |
Figure 13:
continued.
UGC 7321: This galaxy ultrathin (Goad & Roberts 1981). There is
a mild warp visible on the
receding side. This places some constrains on the
possible formation scenarios for the warp of this galaxy because some
of the processes that generate warps do also heat up the disk.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u7483-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg177.gif) |
Figure 13:
continued.
UGC 7483: We found this galaxy to be classified as
SBc. The optical picture shows a very prominent bulge and a small disk
(even in the HI) so it is likely that it is an earlier type. As with
other galaxies with bulges, we find that the optical disk is
misaligned with the HI disk by few degrees.
For this galaxy the lowest contour in the total HI map is 2 1020 HI atoms/cm2, and in the XV diagram
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{u7774-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg178.gif) |
Figure 13:
continued.
UGC 7774: This is the most remarkable galaxy in our
sample. The right side of the disk is warped at a very high angle and the
line of nodes (LON) is very close to the line of sight. However, the LON of
the SE warp is not close to the line of sight, creating a very
asymmetric warp.
Standard tilted-ring models would be unable to fit the
warp of this galaxy due to the difference in the LON for the receding
and approaching sides. The closest known galaxy is at
300 kpc (projected separation), so tidal interaction is unlikely to be
the cause of this extremely asymmetric warp.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u8246-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg179.gif) |
Figure 13:
continued.
UGC 8246: This galaxy is very close (6 arcmin) to NGP9
F269-1340356, detected at similar velocities in our 21 cm data. The
central parts of the galaxy show evidence of large non-circular motions, and
it is possible that the warped appearance is due to either spiral arms or
tidal features.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u8286-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg180.gif) |
Figure 13:
continued.
UGC 8286: This galaxy has a mild warp on
both sides of the galaxy, starting around the edge of
the optical disk.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u8396-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg181.gif) |
Figure 13:
continued.
UGC 8396: This galaxy is very close to NGC 5112 (13
arcmin) and seems to be perturbed by it. The U shaped warp seems to
'point' towards NGC 5112. We also detected some "loose'' HI
gas between UGC 8396 and NGC 5112.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u8550-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg182.gif) |
Figure 13:
continued.
UGC 8550: The disk of this galaxy looks somewhat peculiar both
in the optical and the HI. The optical image shows a faint extension
of the disk misaligned with the inner isophotes, probably due to non
edge-on spiral arms.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u8709-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg183.gif) |
Figure 13:
continued.
UGC 8709: This galaxy is not completely edge-on and two
spiral arms are clearly visible on the optical picture. Even though it has
a very close companion galaxy (NGC 5296), it has no warp.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=14cm,clip]{u8711-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg184.gif) |
Figure 13:
continued.
UGC 8711: This galaxy is isolated and exhibits
quite a large warp. The warp can not be mistaken for inclined spiral
arms because these run in the opposite directions.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{u9242-plotart30.ps}
\end{figure}](/articles/aa/full/2002/42/aah3389/Timg185.gif) |
Figure 13:
continued.
UGC 9242: This is another ultrathin galaxy. It is the flattest of
the galaxies in our sample, with deviations smaller than 2.5'' over
the 400'' diameter of the galaxy. There is evidence of non-circular motions
in the central regions.
For this galaxy the lowest contour in the total HI map is
|
| Open with DEXTER | |