A&A 394, L47-L50 (2002)
DOI: 10.1051/0004-6361:20021409

Microlensing of strongly interacting binary systems

V. Bozza1,3 - L. Mancini1,2,3


1 - Dipartimento di Fisica "E.R. Caianiello'', Università di Salerno, 84081 Baronissi (SA), Italy
2 - Institut für Theoretische Physik der Universität Zürich, 8057 Zürich, Switzerland
3 - Istituto Nazionale di Fisica Nucleare, sez. Napoli, Italy

Received 5 September 2002 / Accepted 24 September 2002

Abstract
Many binary systems are in a state of strong interaction, where mass exchanges, accretion disks, common envelopes provide circumstellar matter which can have significant effects in microlensing light curves of background sources. Such chromatic absorption effects provide very interesting information on the nature of this diffuse matter and the physics of the interaction between the two stars.

Key words: gravitational lensing - binaries: close - circumstellar matter


1 Introduction

It is well known that about one half of the stars populating our Galaxy are part of gravitationally bound multiple systems. On the other hand, binary systems acting as microlenses produce drastic modifications into microlensing light curves (Mao & Paczynski 1991). At least $10\%$ of all microlensing events clearly show the typical signatures of binary lenses, including the presence of sharp caustic crossing peaks.

A conspicuous fraction of binary systems is in a state of tight interaction, where several physical phenomena show up and accompany the basic gravitational rotation. Tidal interactions, mass exchanges, the appearance of accretion disks and circumstellar matter around compact objects in their various shapes widely enrich the phenomenology of these systems. For a detailed review on strongly interacting binary systems (hereafter SIBS), we refer the reader to Carroll & Ostlie (1996), where a full chapter is devoted to the subject.

In the present paper, we want to point out at all the possible signatures of SIBS in microlensing observations, with particular reference to chromatic absorption by circumstellar matter in microlensing light curves. These effects can be appreciated in careful observations and could provide an alternative tool to detect SIBS and determine their characteristics in a qualitative and quantitative way.

In the binary lens equation, two scales are present: the total Einstein radius $R_{\rm E}$, proportional to the square root of the total mass, and the separation between the binaries. In practice, the system will best show up its binary nature through microlensing when these two scales are of the same order. Of course, not all close binary systems will reveal their nature in a microlensing event. The separation between the two stars cannot be lower than  $0.1~R_{\rm E}$ (Gaudi & Gould 1997). If the two stars are too close, they will effectively behave as a single lens and their binary nature would be hidden to microlensing. Typical Einstein radii in galactic observations are of the order of AU, which are compatible with most classes of interacting binary systems, characterized by separations of the order of tenths of AU. However, if we also take into account astrometric observations of the center of light deformations during microlensing, the efficiency in the detection of close binaries may be decisively increased, so that even binaries with separations of the order  $0.01 R_{\rm E}$ can be detected (Chang & Han 1999).

The rotation periods of interacting binaries may range from few hours to several months. As regards those binaries which can yield distinctive features of binary microlensing (namely those which have separations larger than 0.1, 0.2 AU), for solar mass stars, the typical periods are of the order of some tens of days. This means that the rotation of the lens should be often included in a detailed study of the microlensing event. A comprehensive study of this problem has been already performed by Dominik (1998) and will not be discussed here.

2 Diffuse matter in binary systems and microlensing

If the size of one of the stars in the binary system exceeds its Roche lobe, a mass transfer process towards the other star initiates. If this happens, the star losing mass through its Roche lobe will be referred to as secondary star, while the star accreting mass will be the primary star. The matter leaving the secondary star spirals around the primary forming an accretion disk, whose size depends on the geometrical and dynamical properties of the system. The comprehension of the accretion disk around a compact object is important to obtain precious information about the nature of the collapsed object and its physical properties.

The matter in the accretion disk is hydrogen supplied by the external layers of the secondary star's atmosphere. In typical situations, the temperature of the accretion disk allows the presence of neutral hydrogen. In degenerate primaries (neutron stars or black holes), however, the temperature of the inner regions of the accretion disk may rise to 106 K, favouring a full ionization of matter.

The secondary star may also spontaneously expel mass as a natural stage in its evolutionary life or as a consequence of pulsations induced by tidal interactions. The mass lost by the the secondary star may set between the two stars, forming a circumstellar envelope of neutral hydrogen and dust (Dumm et al. 1999). If the ejection velocity is high enough, then a common envelope surrounds both stars for long periods of the life of the system.

From this discussion, we learn that the presence of gas and dust in binary systems is a typical product of strong gravitational interactions. Generically, in microlensing observations, the presence of diffuse matter shows up through chromatic absorption effects.

2.1 Chromatic absorption

The light passing through the gas and the dust within the binary system is attenuated by scattering and absorption phenomena. The Lambert's law

 \begin{displaymath} I_{\lambda}=I_{\lambda,0} {\rm e}^{-\tau_{\lambda}}, \end{displaymath} (1)

describes the suppression experienced by light travelling through gas. $I_{\lambda,0}$ is the original intensity of light, $I_{\lambda}$ is the transmitted light and  $\tau_{\lambda}$ is the optical depth of the cloud, given by

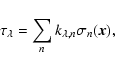\begin{displaymath}\tau_\lambda=\sum\limits_n k_{\lambda,n}\sigma_n ({\vec x}), \end{displaymath} (2)

where $k_{\lambda,n}$ is the absorption coefficient and $\sigma_n ({\vec x})$ is the column density of the gas component labeled by n at projected position ${\vec x}$.

Summing up, each image will have a total amplification given by the geometrical magnification due to gravitational light bending, weighted by the transmission coefficient  ${\rm e}^{-\tau_\lambda}$.

The absorption coefficient can be expressed as the cross section over the mass of the elementary gas/dust particle. For instance, H2 Rayleigh scattering cross section is $2.24\times 10^{-27}$ cm2 at $\lambda=4400$ Å. To appreciate a $50\%$ absorption, the column density should be about 104 kg/m2, which is the column density of one thousandth solar masses distributed on a uniform disk with radius equal to 2.7 AU. However, slight changes of the column density or the chemical nature of the gas may drive the absorption towards complete occultation or complete transparency. What is interesting for us is that the typical densities of circumstellar matter in interacting binary systems are compatible with partial or total absorption of background light and thus produce observable effects.

In binary microlensing, three images are normally present, while two more are created when the source is inside a caustic. Only the images which are formed inside the diffuse matter envelope are affected by absorption, while the others remain undisturbed. Of course, a complete classification of all possible light curve is beyond the purpose of this letter, since accretion disks and gaseous envelopes may appear in an extraordinary variety of shapes and can be oriented in whatever way with respect to the observer. However, in Fig. 1, we analyze some simple situations to give an idea of the anomalies that could appear in binary microlensing light curves, due to the presence of diffuse matter.

  \begin{figure} \par\includegraphics[width=17.5cm,clip]{LigCurves.eps} \end{figure} Figure 1: Three examples of microlensing light curves for the lens described in the text. Each column describes a different case. In the top row there are the source trajectories and the caustic. In the second row there are the images, the critical curve and the border of the disk of diffuse matter (dashed). All distances are measured in Einstein radii. In the third row there are the three amplification curves in blue band ( $\lambda=0.44~{\rm \mu m}$), along with the light curves without absorption (dashed). On the vertical axis there is the amplification; on the horizontal there is time in Einstein units. In the bottom row there are the amplification curves in red band ( $\lambda=0.7~{\rm \mu m}$).
Open with DEXTER

We consider a binary system composed by two half-solar mass stars, separated by 4.3 AU, at a distance of 8 kpc from the observer. With these values, rotational effects are negligible and will not be considered, so that we are allowed to concentrate just on chromatic absorption effects. The lensed source is 10 kpc distant and has a radius of 15.5 $R_\odot$. One of the lenses (the right one in the figures) is surrounded by a gaseous disk with projected density profile

 \begin{displaymath}\sigma(r)=1.27 M_{\rm d} \frac{\left(r_{\rm d}^2-r^2 \right)^3}{r_{\rm d}^8} \end{displaymath} (3)

where $r_{\rm d}=2.87$ AU is the radius of the disk, r is the distance from the center of the right star, $M_{\rm d}=0.01~{M}_\odot$ is the total mass of the disk. The choice of this density profile has been done just for computational reasons. In fact, the density profiles of circumstellar matter within interacting binaries are known only in some specific cases. This prevents us from operating more physical choices. However, since we are only interested in a qualitative description of the effects on microlensing light curves, we are allowed to pioneer the problem by Eq. (3), also neglecting tidal distortions, in a first extent. The gas in the disk will be taken to be a homogeneous mixture of H2-He with $24\%$ He by mass, so that the absorption coefficient is $k_{\lambda}=5.16\times 10^{-5}$ m2/kg at $\lambda=4400$ Å.

The distinctive characteristic of absorption by diffuse matter is given by its dependence on the wavelength of the light. Rayleigh scattering decreases as  $\lambda^{-4}$, so that all the anomalies would be harder in blue and softer in red. This is very important for an unambiguous identification of the effect and we shall plot light curves both in blue ( $\lambda=0.44~{\rm \mu m}$) and in red band ( $\lambda=0.7~{\rm \mu m}$).

Gravitational and refractive bending induced by gaseous matter are generally negligible with respect to absorption for our parameters (Bozza et al. 2002) and will not be considered. We have chosen three examples of light curves showing the main anomalies that can be induced by the presence of diffuse matter in the system.

$\bullet$
Figure 1 Col. a shows a microlensing light curve where the source crosses a caustic near a cusp. The right secondary image is destroyed and regenerated in two points which are completely inside the absorbing disk. This causes the two caustic crossing peaks to be highly suppressed in blue band, while very slight modifications appear in red. The secondary non-caustic peaks stay almost unmodified in both colors.

$\bullet$
In Fig. 1 Col. b the left secondary image is regenerated outside the disk and destroyed inside. As a result, only the second caustic crossing peak is depressed. Moreover, the right secondary peak, caused by the close approach between the source and the right top cusp, is suppressed as well. This is because the right secondary image, which is highly magnified by gravitational lensing during this peak, is heavily absorbed by the disk. These depressions almost disappear in red band. It is also possible to draw curves where no caustic-crossing peaks are suppressed but one secondary peak is.

$\bullet$
The scenario changes if also the principal image enters the disk. To show this case, in Fig. 1 Col. c we have enlarged the disk of diffuse matter up to 7 AU, recentering it on the center of mass (again we are neglecting any ellipsoidal distortion). The curve is gradually suppressed in every region from the outer to the inner portions, as the principal image reaches the denser inner regions. The red band light curve still resembles an ordinary binary microlensing curve, but the blue band one is heavily suppressed.
By these three examples we do not mean to give an exhaustive picture, but at least we can learn that if the diffuse matter remains in the gravitational influence of one mass only, then we can expect slight distortions on the original microlensing light curve, which can be restricted to a limited number of peaks. If the diffuse matter involves the whole system, then a general suppression of the microlensing event in all its parts should be expected.

If the deviations from standard binary microlensing light curves are small, it should not be difficult to identify these events as binary microlensing and then examine a posteriori all possible anomalies comparing the light curves in different bands. If the modifications are too strong and, in particular, depress the event towards the background noise, then it may become very difficult to identify the event as microlensing. However, (as in Fig. 1 Col. c) it may happen that events strongly absorbed in blue are still recognizable as binary microlensing in red, so that they can be recovered anyway. Of course, to perform this kind of searches, it is necessary to relax the selection procedures based on microlensing achromaticity.

The chromaticity effects of SIBS are the key to identify them. Chromatic effects in caustic crossing peaks also arise when limb-darkening of finite size sources is taken into account (Han & Park 2001). However, in this case, the color shifts towards blue, while diffuse matter in binary systems provokes a reddening of the source light. The two effects are thus clearly distinguishable.

In exceptional cases, when one of the stars in the binary system is a low density red giant, occultations of one secondary image may occur (Bromley 1996; Agol 2002). The effects on the light curve are similar to those shown in Fig. 1 Cols. a, b for diffuse matter. The only difference is in the densityprofile that should be very close to a step function.

3 Discussion

The presence of diffuse matter within SIBS shows up through absorption of one or more microlensing images. If the diffuse matter is localized around one star, we expect a partial depression of caustic-crossing or secondary peaks, depending on the geometry of the event. If the matter englobes the whole system, then all microlensing images are simultaneously affected and a general suppression of the curve occurs, which may significantly alter the original microlensing curve. Since the modifications are more evident in blue than in red, a careful analysis in different color bands is mandatory to unambiguously detect and study these events in a serious way. Moreover, if it is possible to take a spectrum during the microlensing event, the appearance of characteristic absorption lines will be the clear signature of the presence of the diffuse medium. In this case, we would also have a way to analyze the chemical nature of this diffuse matter.

Microlensing may provide a very powerful tool for a deep physical investigation of SIBS. It may help to estimate the distribution of diffuse matter in these systems, also retrieving information on their density profiles. Eventual turbulent density fluctuations would be apparent as random noise on the light curve if their length scales are comparable to the extension of the absorbed images. In this case, a statistical study of this noise would provide information on these fluctuations. Moreover, microlensing comes with its standard information on the mass ratio and the separation of the stars along with other parameters which can be useful to give a complete characterization of the system.

An important observation is that interacting binaries are detected by traditional optical observations only when their orbital plane is edge-on with respect to the observer (unless they are in the solar neighbourhood, so that the rotation can be detected by astrometric measurements, or the two components are separated interferometrically). The binary nature of the object is then revealed by the mutual eclipses produced by rotation, or by spectroscopical measurements of radial velocities. If the orbital plane is disposed face-on with respect to the observer, it is necessary to resort to indirect proofs (e.g. X-ray emission from accretion disk, cataclysmic variables). In microlensing surveys, instead, both situations are practically detectable with the same chances. It is thus possible to enlarge the sample of known binary systems and study them from a different perspective.

Acknowledgements

We wish to thank Philippe Jetzer and Gaetano Scarpetta for helpful comments.

References

 
Copyright ESO 2002