A&A 394, L39-L42 (2002)
DOI: 10.1051/0004-6361:20021378

Coronal loop oscillations

An interpretation in terms of resonant absorption of quasi-mode kink oscillations

M. Goossens1 - J. Andries1 - M. J. Aschwanden2


1 - Centre for Plasma Astrophysics, K. U. Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
2 - Lockheed Martin Advanced Technology Center, Solar and Astrophysics Lab., Hanover Street, Palo Alto, CA 94304, USA

Received 21 August 2002 / Accepted 19 September 2002

Abstract
Damped quasi-mode kink oscillations in cylindrical flux tubes are capable of explaining the observed rapid damping of the coronal loop oscillations when the ratio of the inhomogeneity length scale to the radius of the loop is allowed to vary from loop to loop, without the need to invoke anomalously low Reynolds numbers. The theoretical expressions for the decay time by Hollweg & Yang (1988) and Ruderman & Roberts (2002) are used to estimate the ratio of the length scale of inhomogeneity compared to the loop radius for a collection of loop oscillations.

Key words: Sun: corona - magnetic fields - oscillations


1 Motivation

Decaying oscillating displacements of hot coronal loops were first registered by the EUV telescope on board of the Transition Region and Coronal Explorer (TRACE) spacecraft on 14th July 1998 (Aschwanden et al. 1999; Nakariakov et al. 1999). New examples of coronal loop oscillations have been discovered in the TRACE data since then (Aschwanden et al. 2002; Schrijver et al. 2002). The observed values of the periods and decay times make it possible to obtain indirect information on the conditions of the plasma and magnetic field in coronal loops. Seismology of coronal loops requires the definition of an equilibrium model of the loop and a theoretical analysis of the oscillations in the adopted equilibrium model.

Ofman & Aschwanden (2002) use the recent data base by Aschwanden et al. (2002) to investigate coronal loop oscillations in a sample of 11 loops. They argue that the observed TRACE loops consist of multiple unresolved thin loop threads which produce inhomogeneous internal structure of the observed loop. They adopt 1-dimensional Cartesian slabs of plasma with the magnetic field lines in the z-direction and the direction of the inhomogeneity along the x-axis normal to the magnetic surfaces, as a simple model for the oscillating loops. The observed oscillations are assumed to be torsional Alfvén waves which involve displacements of the magnetic field lines about their equilibrium position along the y-axis with the displacement being independent of y. The oscillations are damped by phase mixing (Heyvaerts & Priest 1983) because the magnetic field lines at different x-positions have different oscillation frequencies due to the inhomogeneity in the x-direction. Ofman & Aschwanden (2002) find that the dependence of the decay time  $\tau_{\rm decay}$on the length L of the loop and of  $\tau_{\rm decay}$on the width w of the loop is in excellent agreement with the power law predicted by phase mixing provided that $l \sim L$ and $l \sim w$. Here l is the length scale of the inhomogeneity of the loop. In a fully nonuniform plasma it can be defined as $l=\omega_{\rm A}^2/\vert\nabla\omega_{\rm A}^2\vert$. For a constant magnetic field it reduces to $\rho/\vert\nabla\rho\vert$. In a loop which is uniform except for a thin transitional layer in which the equilibrium quantities vary from their constant internal value to their constant external value, l is the thickness of the transitional layer. The similarity of these two scalings of  $\tau_{\rm decay}$ (with L and w) is seen as support for the assumption that both L and w are proportional to l. Application of the theoretical expression for the decay time, as it is derived by Roberts (2000) from the Heyvaerts & Priest (1983) analysis, to the observed values leads to values of the Reynolds numbers for the oscillating coronal loops which are at least more than five orders of magnitude lower than the classic coronal value of 1014 if the loop radius is taken as an upper limit of the spatial scale of inhomogeneity.

The present paper adopts the classic straight cylindrical 1-dimensional flux tube as a model for the coronal loops. The only oscillations that displace the central axis of a 1-dimensional vibrating tube and produce transversal displacements of the tube have their azimuthal wave number m equal to 1. These oscillations are called kink modes. Hence, in a scenario that uses a classic straight cylindrical 1-dimensional flux tube as a model for the coronal loops, the coronal loop oscillations are kink mode oscillations. The frequencies of the fundamental kink oscillations are always in between the external and internal value of the Alfvén frequency and in a non-uniform equilibrium with a continuous variation of the Alfvén frequency, they are always in the Alfvén continuum. The kink mode oscillations are then quasi-modes that are damped in the absence of equilibrium flows. The damping rate of quasi-modes is independent of dissipation. In a different context, Hollweg & Yang (1988) were the first to note that the damping of these kink quasi-modes in coronal loops is very rapid with an e-folding time of two or three wave periods. Ofman & Aschwanden (2002) included quasi-mode damping of kink oscillations in their comparison with observational data. They assumed in absence of any known scaling between l and L that l/L and l/w are constant for all loops under investigation. Under this assumption, they found that the quasi-mode damping of kink oscillations did not give an as good representation of the data as the phase-mixing torsional Alfvén waves in 1-dimensional Cartesian slabs of plasma. Here we take a different view and allow the ratio l/w to vary from loop to loop. As a matter of fact, we use the resuls of quasi-mode damping of kink oscillations to infer the value of l/w for each loop. The aim of this letter is not to show that quasi-mode damping of kink oscillations is to be preferred over phase-mixing torsional Alfvén waves in 1-dimensional Cartesian slabs of plasma. The aim is to show that there is a mechanism that is capable of explaining the observed rapid damping of the coronal loop oscillations without having to invoke anomalously low Reynolds numbers. Very likely, nature allows for both mechanisms. In case nature is selective, observations do not yet give us clear indications which mechanism is preferred. Ofman & Aschwanden (2002) ruled out quasi-mode damping of kink oscillations by keeping the length scale of the inhomogeneity (relative to the loop radius) constant for all loops.

2 Model, equations and discussion

The present paper adopts the classic straight cylindrical 1-dimensional flux tube as a model for the coronal loops. In a system of cylindrical coordinates $(r, \varphi, z)$ with the z-axis coinciding with the axis of the cylinder (loop), the equilibrium quantities, magnetic field $\vec{B} = (0, B_{\varphi}(r), B_z(r))$, pressure p(r) and density $\rho(r)$are functions of the radial distance only. They satisfy the radial force balance equation

 \begin{displaymath}\frac{{\rm d}}{{\rm d}r}\left(p+\frac{B^{2}}{2\mu}\right) =-\frac{B_{\varphi}^{2}}{\mu r}\cdot \end{displaymath} (1)

This is one equation for four scalar functions which does not involve density. Consequently the density profile can be chosen freely. Since the plasma pressure is much smaller than the magnetic pressure in the corona, it is a good approximation to neglect plasma pressure. This classic $\beta=0$ approximation removes the slow waves from the analysis. When the magnetic field is straight, $\vec {B}= B(r)\vec{1}_z$, Eq. (1) also implies that the magnetic field is constant. The coronal loop is then a density enhancement in an almost homogeneous field. Thus this object is very different from photospheric and solar interior flux tubes which are concentrations of magnetic field surrounded by field free plasma of higher density.

Since the equilibrium quantities depend on r only, the perturbed quantities can be Fourier-analyzed with respect to the ignorable coordinates $\varphi, z$ and put proportional to $\exp [i (m\varphi + k_{z}z) ].$Here m (an integer) and kz are the azimuthal and axial wave numbers. The observed coronal loop oscillations show no nodes in the z direction so that $k_z=\pi/L$, where L is the length of the loop. For m=1 the waves are called kink modes. Since the axis of the loop is displaced, the oscillations have to be kink mode oscillations with m=1. The reason why the loops are seen to oscillate transversely to their equilibrium axis is due to the radial component of velocity. The azimuthal component of velocity is associated with internal motions on cylindrical shells and does not cause the loop to oscillate as a whole. In order to explain the observed fast damping of transverse oscillations in coronal loops we need a mechanism to explain the damping of the radial component of velocity. Quasi-mode damping provides such a mechanism.

Part of the basic physics of quasi-mode damping can be understood in ideal MHD. The relevant equations for the linear motions of a pressureless plasma superimposed on a static 1-dimensional cylindrical equilibrium model with a straight magnetic field are:

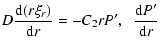$\displaystyle D\frac{\displaystyle {\rm d}(r \xi_r)}{\displaystyle {\rm d}r} = - C_2 r P', \;\; \frac{\displaystyle {\rm d} P'}{\displaystyle {\rm d}r}$ = $\displaystyle \rho (\omega^2 - \omega_{\rm A}^2) \xi_{r},$  
$\displaystyle \rho (\omega^2 - \omega_{\rm A}^2) \xi_{\varphi} = \frac{i m}{r} P', \;\; \xi_{z}$ = 0. (2)

$\vec{\xi}$ is the Lagrangian displacement and P' is the Eulerian perturbation of total pressure. The coefficient functions D and C2 are:

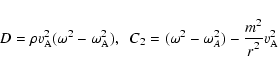\begin{displaymath}D = \rho v_{\rm A}^2 (\omega^2 - \omega_{\rm A}^2), \;\; C_{2... ...^2) - \frac{\displaystyle m^2}{\displaystyle r^2} v_{\rm A}^2 \end{displaymath} (3)

where $v_{\rm A}=B/\sqrt{\mu\rho}$ is the Alfvén speed and $\omega_{\rm A}=k_zv_{\rm A}$is the Alfvén frequency. For a 1-dimensional cylindrical equilibrium model with a straight magnetic field, $\xi_{\varphi}$ is the relevant component for Alfvén waves and $\xi_{r}$ is the relevant component for the fast waves.

Consider the equations as normal mode equations and note that the differential equations have a regular singular point at the position where D = 0 or consequently at the resonant position $r_{\rm A}$ where $\omega = \omega_{\rm A}(r_{\rm A})$. This singularity and the fact that  $\omega_{\rm A}(r)$is a function of position, give rise to a continuous range in the spectrum which is associated with resonant Alfvén waves with singular spatial solutions in ideal MHD. This continuous range of frequencies is known as the Alfvén continuum. The Alfvén continuum waves imply that in ideal MHD each magnetic surface can oscillate at its own Alfvén continuum frequency. This is the physical mechanism behind phase mixing and resonant absorption. In dissipative MHD the singular solutions are replaced with large but finite solutions (see Goossens et al. 1995; Tirry & Goossens 1996).

For m = 0 the eigenmodes are decoupled into torsional Alfvén continuum eigenmodes with $ \xi_{r} = 0 ,\; P' = 0, \; \xi_{\varphi} \neq 0$and discrete fast eigenmodes: $ \xi_{r} \neq 0 , \; P' \neq 0 , \; \xi_{\varphi}= 0.$There is no interaction between the Alfvén waves and magnetosonic waves. However, for m =1 (as a matter of fact  $\forall m \neq 0$) pure magnetosonic waves do not exist, since waves with $ \xi_{r} \neq 0 , \; P' \neq 0$necessarily have $\; \xi_{\varphi} \neq 0.$Consequently, fast discrete eigenmodes with an eigenfrequency in the Alfvén continuum couple to a local Alfvén continuum eigenmode and produce quasi-modes. These quasi-modes are the natural oscillation modes of the system (Balet et al. 1982; Steinolfson & Davila 1993). They combine the properties of a localized resonant Alfvén wave and of a global fast eigenoscillation. In dissipative MHD the singularities are removed (Goossens et al. 1995; Tirry & Goossens 1996). The small length scales that are created in the vicinity of the resonant position cause dissipation with a conversion of wave energy into heat. The damping of the global oscillation is not directly related to heating. Quasi-modes are damped because of a transfer of energy of the global fast wave to local continuum Alfvén modes. The damping rate is independent of the values of the coefficients of resistivity and viscosity in the limit of vanishing resistivity or viscosity (Poedts & Kerner 1991; Tirry & Goossens 1996). In fact, the damping rate can be obtained in ideal MHD, by analytical continuation of the Green's function (see e.g. Ionson 1978). The solutions obtained by this method are called quasi-modes as they are not eigenfunctions of the Hermitian ideal differential operator.

Quasi-modes provide an efficient mechanism for converting kinetic energy of radial motions of a global fast mode in kinetic energy of azimuthal motions of local continuum Alfvén modes which is what we need to explain the observed fast damping of coronal loop oscillations. Hence, the central question for our hypothesis is whether the kink mode oscillations have their frequencies in the Alfvén continuum and are quasi-modes or not.

When the density is uniform in the internal and external region and changes discontinuously at the loop radius r=R, the dispersion relation for these modes can be written down analytically. In the "long tube'' approximation ($R\ll L$) the frequency can be calculated explicitly:

 \begin{displaymath}\omega^2 \approx \left(\frac{\rho_{\rm i} \omega_{\rm Ai}^2+\... ...o_{\rm i}}{\rho_{\rm i}+\rho_{\rm e}}\right)\omega_{\rm Ai}^2. \end{displaymath} (4)

The indices "${\rm i}$'' and "${\rm e}$'' refer to internal and external respectively. The "long tube'' assumption is well satisfied since it can be seen from Table 1 that $\frac{R}{L}<0.06$ for all loops, and $\frac{R}{L}<0.025$for most loops.

The important point to note from Eq. (4) is that the eigenfrequency of the fundamental kink eigenmode is in between the external and internal Alfvén frequency. Hence, when the discontinuous transition from  $\rho_{\rm i}$ to  $\rho_{\rm e}$ is replaced with a continuous variation, the fundamental kink mode has its frequency in the Alfvén continuum. The obvious conclusion is that the classic kink mode oscillation is always a resonantly damped quasi-mode. This result is independent of the "long tube'' assumption that was used to obtain Eq. (4). Edwin & Roberts (1983) determined the non-leaky discrete eigenmodes of uniform cylindrical flux tubes. In their Fig. 4 for uniform coronal flux tubes, it can be seen that all fast body kink eigenmodes have frequencies in between the external and internal Alfvén frequency. Consequently, all these kink modes are resonantly damped quasi-modes when the discontinuous transition from  $\rho_{\rm i}$ to  $\rho_{\rm e}$is replaced with a continuous variation.

Ruderman & Roberts (2002) solved the initial value problem for a loop driven by a kink perturbation. The loop is a uniform plasma with density  $\rho_{\rm i}$ and radius Rand a "thin'' transitional layer of thickness l in which the density varies continuously from  $\rho_{\rm i}$ to its external value  $\rho_{\rm e}$. This "thin'' transitional layer transforms the kink modes into quasi-modes. Ruderman & Roberts (2002) show that there are two processes and two corresponding time scales involved. First, there is the damping of the global fast eigenmode by conversion of kinetic energy of its radial component into kinetic energy of the azimuthal component of the local Alfvén continuum eigenmode in the resonant layer. This is basically resonant absorption and the resonant damping of the global oscillations is independent of the Reynolds number. Second, the short scale Alfvén continuum oscillations are converted into heat by dissipative processes on time scales similar to those of phase mixing that do depend on the Reynolds number. Ruderman & Roberts (2002) point out that the observed damping rate of the coronal oscillations is due to the resonant damping of the quasi-mode. During their analysis Ruderman and Roberts calculate the frequency of the fundamental kink mode (Eq. (4)) and the damping rate of the fundamental kink mode (their Eq. (56)). They rewrite their expression for the damping rate of the quasi-mode in terms of observable quantities as

 \begin{displaymath}\tau_{\rm decay}= \mbox{Period} \frac{2}{\pi}\frac{R}{l}\frac{\rho_{\rm i}+\rho_{\rm e}}{\rho_{\rm i}-\rho_{\rm e}} \end{displaymath} (5)

where $\tau_{\rm decay}$ is the decay time. Ruderman & Roberts (2002) use this expression to estimate the inhomogeneity length scale (thickness of the boundary layer) for the loop studied by Nakariakov et al. (1999). They assume $\rho_{\rm e}/\rho_{\rm i}=0.1$ and find  l/R = 0.23.

There are two earlier papers that deal with damping rates and decay times of quasi-modes in cylindrical flux tubes and their dependence on the length scale of the inhomogeneity and the radius of the loop. Goossens et al. (1992) derived an approximate analytical expression for the damping rate of quasi-modes for cylindrical flux tubes with "thin'' transitional layers, by using connection formulae (Sakurai et al. 1991; Goossens et al. 1995). The expression found by Ruderman & Roberts (2002) (their Eq. (56)) for the damping rate turns out to be a special case of the result by Goossens et al. (1992) (their Eq. (77)). Hollweg & Yang (1988) were the first to calculate approximate analytical expressions for the decay times of quasi-modes and to apply them in a numerical example to solar coronal loops. They did not use the term quasi-mode at that time. Hollweg & Yang (1988) studied surface waves on "thin'' nonuniform layers in a planar geometry. They considered nearly perpendicular propagation in the magnetic surfaces and found decay times (their Eqs. (67) and (69)) independent of dissipation, indicative of quasi-modes. The planar result was translated to a cylindrical tube by taking the parallel wave number $k_\parallel=\pi/L$ and the perpendicular wave number in the magnetic surfaces $k_\perp=1/R$, which exactly corresponds to m=1 kink modes. They concluded that the waves are effectively damped with an e-folding time of two periods. The fast decay of coronal oscillations was predicted more than a decade before these oscillations were actually observed. When we translate Eq. (69) of Hollweg & Yang (1988) to kink waves on a cylinder, we recover (Eq. (5)) with the factor $2/ \pi$ replaced with $4/(\pi^2)$. This difference is due to the different density profiles that were used. Hollweg & Yang (1988) used a linear profile for density.

We now use the expression for the decay time in its form given by Hollweg & Yang (1988) to compute, as Ruderman & Roberts (2002) did for a single loop, l/R for all the loops in the dataset of Ofman & Aschwanden (2002):

 \begin{displaymath}\frac{l}{R} = \frac{4}{\pi^2}\frac{\mbox{Period}}{\tau_{\rm d... ...rac{\rho_{\rm i}+\rho_{\rm e}}{\rho_{\rm i}-\rho_{\rm e}}\cdot \end{displaymath} (6)

There is no particular reason for preferring the linear density profile of Hollweg & Yang (1988) over that of Ruderman & Roberts (2002). For the density contrast we take $\rho_{\rm e}/\rho_{\rm i}=0.1$. The results are shown in the last column of Table 1. The values for l/R are between 0.15 and 0.5. The fact that the inhomogeneity length scale never exceeds the loop radius supports the prediction by Ruderman & Roberts (2002) that loops with longer inhomogeneity length scales are hardly able to oscillate.
   
Table 1:

No.		 L R R/L P $\tau_{\rm decay}$ l/R
  [m] [m]   [s] [s]  

1		 1.68e8 3.60e6 2.1e-2 261 840 0.16
2 7.20e7 3.35e6 4.7e-2 265 300 0.44
3 1.74e8 4.15e6 2.4e-2 316 500 0.31
4 2.04e8 3.95e6 1.9e-2 277 400 0.34
5 1.62e8 3.65e6 2.3e-2 272 849 0.16
6 3.90e8 8.40e6 2.2e-2 522 1200 0.22
7 2.58e8 3.50e6 1.4e-2 435 600 0.36
8 1.66e8 3.15e6 1.9e-2 143 200 0.35
9 4.06e8 4.60e6 1.1e-2 423 800 0.26
10 1.92e8 3.45e6 1.8e-2 185 200 0.46
11 1.46e8 7.90e6 5.4e-2 396 400 0.49

3 Conclusions

The overall conclusion from Table 1 is that damped quasi-modes give a perfect explanation of the fast decay of the observed coronal loops if the inhomogeneity length scale is allowed to vary from loop to loop. An additional attraction is that quasi-mode damping is fully consistent with the current estimates of very large coronal Reynolds numbers (1014). Caution is called for as the values found for l/R are not all entirely consistent with the assumption of a "thin'' boundary layer used to obtain Eq. (5) and its predecessor by Hollweg & Yang (1988). There is an obvious need to relax the assumption of a "thin'' boundary layer and to calculate eigenmodes of fully non-uniform loops. A first attempt in this direction was made by Hollweg (1990) who used the width of the resonance curves to estimate the free decay times of undriven surface quasi modes. An eigenvalue computation as in Tirry & Goossens (1996) is needed here.

Acknowledgements
It is a pleasure for us to thank L. Ofman and J. V. Hollweg for their comments on previous versions of this letter.

References

 
Copyright ESO 2002