 |
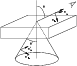
Figure 1:
Geometry of an axisymmetric radiation field
scattered in a plane-parallel slab. The incident and scattered
ray directions are given
through the polar angles |
| Open with DEXTER | |
R. Manso Sainz - E. Landi Degl'Innocenti
Università degli Studi di Firenze,
Dipartimento di Astronomia e Scienza dello Spazio, Largo Enrico Fermi 2,
50125,
Firenze, Italy
Received 13 June 2002 / Accepted 10 July 2002
Abstract
The first theoretical investigation of the formation of the
linearly polarized solar line spectrum of a complex atom, neutral titanium,
is presented.
The process of formation of line polarization is modeled by simply
considering a plane-parallel layer of Ti I atoms
illuminated from below by the photospheric radiation field,
and accounting for the differential pumping
induced in the various
magnetic sublevels by the anisotropic radiation field.
The calculated line polarization pattern
is in good qualitative agreement with reported
observations, thus showing that
the generation of population imbalances between magnetic
sublevels due to the radiation field anisotropy is the basic
physical mechanism responsible for the observed polarization pattern
in the Fraunhofer spectrum of Ti I.
The role of depolarizing collisions on the polarized spectrum of
Ti I is also investigated.
Key words: polarization - scattering - line: formation - Sun: atmosphere - stars: atmospheres
Recent advances in instrumentation and observational techniques make now possible the measurement of polarization in Fraunhofer lines with spectropolarimetric sensitivities better than 10-4and up to 10-5 (Stenflo & Keller 1996, 1997; Bianda & Stenflo 2001; Trujillo Bueno et al. 2001; Bommier & Molodij 2002). At this level of sensitivity it is possible to access the complex structure of the linearly polarized solar line spectrum observed close to the solar limb (Gandorfer 2000). The theoretical understanding of this spectrum (so-called second solar spectrum because of its aspect and nature completely different from those of the well-known intensity solar spectrum) has an enormous diagnostic potential for the thermodynamical properties of the upper layers of the solar atmosphere and, most importantly, on the weakest magnetic fields (below a few tenths of a gauss) which are believed to exist in the solar plasma. As an example of the dramatic physical results that have already been obtained from the second solar spectrum we mention here the papers by Landi Degl'Innocenti (1998), by Trujillo Bueno (2001) and by Trujillo Bueno et al. (2002). Notwithstanding these results, our understanding of the second solar spectrum is still very limited and rather fragmentary since most of the work on this subject has been devoted to the interpretation of single features, often of individual spectral lines treated with relatively simple atomic models. This article presents the first attempt to model the second solar spectrum of a complex atom. Whereas iron lines are very prominent and ubiquitous throughout the usual solar spectrum, the second solar spectrum of iron as reported by Gandorfer (2000) is notably unimpressive. On the contrary, the linearly polarized spectrum of Ti I presents some prominent features like for example, two lines at 4742.8 Å and 5644.1 Å which show a large fractional polarization signal above 0.2%, and another eight lines with fractional polarization signals of the order of 0.07% (Gandorfer 2000; see also Fig. 4). In Sect. 2 we show that these and other features of the Ti I spectrum can be qualitatively reproduced even with a very simple line formation model. It is just necessary to describe, through the density matrix formalism, how atomic polarization is generated in the titanium atoms by the anisotropic illumination of the solar atmosphere, how it is distributed throughout the various energy levels by the standard processes of absorption and emission in the many lines of the titanium spectrum, and how it finally manifests itself in the polarization spectrum. In Sect. 3 we also show how atomic polarization becomes modified in the presence of depolarizing collisions.
 |
Figure 1:
Geometry of an axisymmetric radiation field
scattered in a plane-parallel slab. The incident and scattered
ray directions are given
through the polar angles |
| Open with DEXTER | |
Consider a plane-parallel layer in the solar atmosphere formed by neutral
titanium atoms illuminated by the photospheric
radiation field (Fig. 1).
We shall assume that the radiation field is axisymmetric, the symmetry axis
being perpendicular to the slab.
Neglecting circularly polarized light, the radiation field
illuminating the layer is fully described with the two parameters
(Landi Degl'Innocenti 1983):
In stellar atmospheres the degree of polarization is usually small and the main contribution to J20 actually comes from the anisotropy of the radiation field intensity. For this reason we shall neglect in the following the second term proportional to Q in Eq. (2). Moreover, we shall assume that the radiation illuminating the slab corresponds to the observed solar continuum. The resulting values of the quantities J00 and J20 assumed in the present paper are shown in Fig. 2.
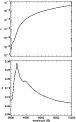 |
Figure 2:
Number of photons per mode
|
| Open with DEXTER | |
In the absence of magnetic fields, due to the axial symmetry of the radiation field, there are no coherences between magnetic sublevels when the vertical to the solar atmosphere is chosen as the quantization axis. Furthermore, neglecting hyperfine structure (which is a good approximation since 88% of titanium has zero nuclear spin), and taking into account that the separation between fine structure levels of Ti I is in general much larger than the inverse mean life time of these levels, we can also safely neglect coherences between different J-levels. Consequently, the excitation state of a level with total angular momentum J can be fully characterized by simply giving the populations NMJ of each of its 2J+1 magnetic sublevels. Actually, in the absence of circularly polarized radiation, sublevels with quantum numbers +MJ and -MJ are equally populated and only J+1 parameters (all Ti I levels have integer J-values) are needed to fully describe the excitation state of each level of the titanium atom.
Instead of the sublevel populations,
it is more convenient to introduce,
for each level, the spherical tensor components of the density matrix
(Landi Degl'Innocenti 1983) defined in terms of 3-j symbols as
 |
Figure 3: Grotrian diagram showing the 146 terms of the Ti I atomic model by Sugar & Corliss (1985). The model has 380 levels in total. |
| Open with DEXTER | |
In order to investigate the atomic polarization properties of the titanium atom we need to adopt a sophisticated atomic model. The present paper is based on the Ti I model compiled at NIST (see Fig. 3) which consists of 380 observed levels (Sugar & Corliss 1985) grouped into 146 terms and which accounts for 345 lines with measured transitions probabilities (Martin et al. 1988). To this model we have added 5 extra terms and almost 8000 extra lines contained in the compilation by Kurucz & Bell (1995) with transition probabilities obtained semiempirically (Kurucz 1988).
Titanium levels have quantum numbers
J between 0 and 7, and the total number of ![]() elements
necessary to describe its excitation state is, for our model, 1564.
However, due to the weak anisotropy
of the radiation field, the statistical tensors of rank K
larger than 2 play
only a marginal role (Landi Degl'Innocenti 1984).
In fact, we find that
neglecting the
elements
necessary to describe its excitation state is, for our model, 1564.
However, due to the weak anisotropy
of the radiation field, the statistical tensors of rank K
larger than 2 play
only a marginal role (Landi Degl'Innocenti 1984).
In fact, we find that
neglecting the ![]() elements with
K=4, 6, ..., 14 only affects the final results presented in this paper
by less than 1%.
The total number of
elements with
K=4, 6, ..., 14 only affects the final results presented in this paper
by less than 1%.
The total number of ![]() elements is thus reduced to 771.
elements is thus reduced to 771.
Neglecting, for simplicity, stimulated emission,
the statistical equilibrium equations for the ![]() element
of the ith level can be expressed as (Landi Degl'Innocenti 1983)
element
of the ith level can be expressed as (Landi Degl'Innocenti 1983)
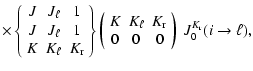 |
(5) |
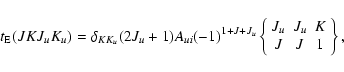 |
(6) |
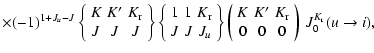 |
(7) |
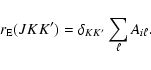 |
(8) |
To connect the values of the statistical tensors obtained through the solution of the statistical equilibrium equations to the polarization properties of the radiation, it is necessary to pass through the radiative transfer equation for polarized radiation.
Due to the symmetry of the problem, assuming the reference directions
for polarization as in Fig. 1,
the only non-vanishing
Stokes parameters are I and Q, and their corresponding transfer equations
read
 |
(14) |
| (16) | |
| (17) |
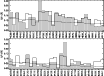 |
Figure 4:
Comparison between the observed and calculated
main polarization features in the visible line spectrum
of Ti I. Shadowed bars and dashed line represent,
respectively, the fractional
polarization in the spectral lines
and in the adjacent continuum
observed near the solar limb ( |
| Open with DEXTER | |
Figure 4 is aimed at comparing our results with the observed second solar spectrum of Ti I. Shadowed bars show the fractional polarization reported in the second solar spectrum atlas of Gandorfer (2000) for 57 lines of Ti I, while the dashed line gives the fractional polarization of the adjacent background continuum. These lines have been selected as those with a clearly identifiable polarization peak (above or below the continuum level) in Gandorfer's atlas. Thus, we have rejected lines with severe blends that do not allow us to distinguish individual polarization components. Lines lying over a structured Q/I continuum, lines with anomalous Q/I profiles, typically very weak signals that may be tentatively ascribed to interactions with the background continuum, and lines suspected of being blended with some molecular lines have been rejected as well.
The heavy line in Fig. 4 corresponds to the fractional polarization of each line obtained through Eq. (15) after solving the statistical equilibrium equations of our Ti I atomic model. Since the absolute Q/I values we obtain are larger than the observed signals, to facilitate the comparison we have multiplied all our calculated Q/I values by an arbitrary scale factor (0.022) and added the fractional polarization of the continuum close to the line. There are several reasons why the calculated Q/I values are systematically larger than the observed ones. First of all we have solved the statistical equilibrium equations for the top layer of the solar atmosphere, where the anisotropy of the radiation field has its maximum value. Clearly this is a very rough approximation which has been introduced to avoid the complications inherent to a full self-consistent solution of the polarized, non-LTE problem. It has to be expected that accounting for radiative transfer effects, the radiation field anisotropy would result in being smaller than the value adopted in the present paper. In addition, we have disregarded the existence of an unpolarized background continuum and neglected inelastic collisions, which compete with radiative processes to populate the atomic levels while do not contribute to their polarization. Finally, we have not included depolarizing collisions (see next section) and further depolarizing mechanisms that may be due to the presence of a turbulent magnetic field.
Figure 4 shows that despite its simplicity, the modeling of the formation of the second solar spectrum of Ti I considered here is in good qualitative agreement with the observed polarization pattern. In fact, the lines with the largest theoretical polarization degrees agree with the largest observed signals. Moreover, we are able to reproduce the polarization direction (i.e., the sign of Q/I) of the large majority of the observed lines. In this respect we would like to point out that, according to our modeling, lines which show a polarization degree below that of the continuum, do not imply that a true depolarization mechanism is operating (i.e., the polarized continuum photons become depolarized when diluted within the line), but rather that the algebraic sum of a negative line polarization and the positive continuum polarization signal gives a result below the continuum level. We want also to remark that the comparison between our theoretical results and the observations contained in Gandorfer's atlas have allowed us to discover two minor errors contained in the atlas itself. Indeed, the wavelength axis between 4630 and 4650 Å in Gandorfer's atlas is wrong, the 4640 Å mark being misplaced by about 0.5 Å towards the red (cf. Beckers et al. 1976). As a consequence, three important lines of titanium at 4639 Å have been misidentified. Also, the noticeable polarization peak at 4799.8 Å has been ascribed in the atlas to V I (an error carried over from Beckers et al. 1976). However, according to Moore et al. (1966), the predominant contributor to this blend is a Ti I line. This is quite consistent with our finding that the 4799.8 Å line is one of the most polarized lines of our model.
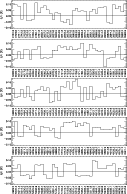 |
Figure 5: Linear polarization signals calculated for a sample of lines of the spectrum of Ti I (see text for details). Notice the decreasing number of polarized lines towards the red. |
| Open with DEXTER | |
Further results of our computations are shown in Fig. 5, where we plot the theoretical Q/I value (reduced by the same factor 0.022 and without adding the continuum) for a selected sample of lines.
The sample consists of the strongest lines of the Ti I spectrum bound in the wavelength interval 3800 Å ![]() 10000 Å among which we have made a further selection by choosing to plot only those lines which present a relatively high degree of linear polarization. To be more precise, the lines shown in Fig. 5 are those satisfying the inequalities
10000 Å among which we have made a further selection by choosing to plot only those lines which present a relatively high degree of linear polarization. To be more precise, the lines shown in Fig. 5 are those satisfying the inequalities
![]() s-1 and
s-1 and
![]() 0.022%.
Recalling that the density matrix is normalized through the trace equation, the quantity
0.022%.
Recalling that the density matrix is normalized through the trace equation, the quantity
![]() results in being roughtly proportional to the line absorption coefficient, which explains the meaning of the first inequality.
results in being roughtly proportional to the line absorption coefficient, which explains the meaning of the first inequality.
Figure 5, which covers a larger wavelength interval than the one of Gandorfer's atlas, is mainly intended to point out the titanium lines which may be the target of future observations. Indeed, our model includes many more lines yielding very high theoretical fractional polarization degrees. However, they correspond to extremely weak transitions and therefore their polarization signal can hardly be observed.
Finally, we find that intercombination lines
(i.e., transitions involving a change of atomic spin)
do not play a fundamental role
in the general distribution of atomic polarization among the
levels of Ti I.
In fact, we have solved the scattering problem for
the singlet, triplet and quintet systems, independently.
We find that, except for a few levels involved in
particularly strong intercombination transitions (having
![]() s-1),
the atomic polarization of the whole system is little affected
with respect to the general case in which all transitions are considered.
s-1),
the atomic polarization of the whole system is little affected
with respect to the general case in which all transitions are considered.
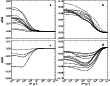 |
Figure 6:
Variation of atomic alignment with elastic depolarizing rate
for some representative levels.
Uppermost and lowermost panels correspond to levels with positive
and negative alignment, respectively.
a) Low-lying fundamental and metastable levels
|
| Open with DEXTER | |
Depolarizing collisions are due to long-range interactions
between atoms and perturbers of different species (mainly
hydrogen atoms in the solar atmosphere).
If the velocity distribution of the perturbers is isotropic they
tend to destroy coherences (if any exists) between different magnetic sublevels
of a given atomic level and to equalize their populations.
Their contribution to the rate equation for the ![]() statistical tensor of a given level is
statistical tensor of a given level is
When depolarizing collisions dominate over any other radiative (or collisional) rate, the atomic level under consideration becomes unpolarized. It is important to point out that while microturbulent magnetic fields of increasing intensity also yield a depolarization of the atomic levels, this depolarization is not complete and, beyond a saturation value, atomic polarization remains unaltered.
The role of depolarizing collisions in the solar atmosphere has not yet been fully clarified. Though it is assumed, in many cases, that the low-lying levels (ground level and metastable levels) of any atomic species are completely depolarized by collisions, there is strong observational evidence against this statement (Landi Degl'Innocenti 1998; Trujillo Bueno 1999, 2001; Manso Sainz & Trujillo Bueno 2001). We have then considered it important to study in some detail how the results presented in the former section might be affected by the introduction in the model of depolarizing collisions.
To this aim, one would need, in principle, to know the quantity D(2) (alignment depolarization rate) for any of the levels of the Ti I model described above. Unfortunately, there is no data available (at least to the authors' knowledge) on this subject, so that we have preferred to base our calculations on the simplest possible hypothesis, namely that all the levels of the Ti I atom might be characterized by a unique rate that we have considered as a free parameter.
The general behaviour of atomic alignment versus depolarizing rate is summarized in Fig. 6, which shows that the sign of the alignment of the various levels does not change with varying depolarizing collisional rates except for some very weakly polarized levels not shown in the figure. The upper and lower panels of Fig. 6 illustrate the dependence with respect to D(2) of the alignment of the levels with positive and negative alignment, respectively. The left panels refer to fundamental or metastable levels, while the right panels refer to high-lying energy levels.
Long-lived levels start to depolarize at low D(2) values and they become completely unpolarized for D(2)>107 s-1. Upper-lying levels, with shorter life-times, are unaffected by such comparatively low collisional rates but their alignment is modified due to radiative pumping and the change of atomic polarization produced in the metastable levels. It is only for much larger collisional rates that high-lying levels become depolarized, rates of the order of 1010 s-1 being necessary to completely depolarize all the atomic levels.
It is worth noting that while atomic polarization in positively aligned levels always decreases with increasing D(2) (see Figs. 6a,b), atomic polarization in negatively aligned levels, may be slightly enhanced at moderate collisional rates (see Figs. 6c, d).
 |
Figure 7:
Fractional linear polarization in the |
| Open with DEXTER | |
More interesting is to consider the dependence with the depolarizing rate
of the polarization in the spectral lines.
Since the line polarization depends on the atomic alignment in
both the upper and lower levels of the transition, this dependence
is far from being trivial.
A remarkable example is provided by the multiplet originating in the transition between
the ![]() and
and
![]() terms.
Two upper term levels (
terms.
Two upper term levels (
![]() )
are negatively aligned,
another two (
)
are negatively aligned,
another two (
![]() )
have positive alignment while
the
)
have positive alignment while
the
![]() level is unpolarized by definition.
On the other hand all the three lower (metastable) levels are
positively aligned.
level is unpolarized by definition.
On the other hand all the three lower (metastable) levels are
positively aligned.
Figure 7 shows the fractional polarization (computed according to
Eq. (15)) as a function of D(2)in the nine strongest transitions (
![]() s-1) of the
multiplet.
Solid lines correspond to the five lines, already considered
in Fig. 4, for which clear Q/I signals have been
measured near the solar limb.
It can be seen that with increasing depolarizing collisional rates
the line polarization may increase slightly (lines at 4639.4 Å and 4629.3 Å), the ratios of the
fractional polarization between different lines show large variations,
and the polarization direction can be even reversed (4639.7 Å line).
In particular we find that with
s-1) of the
multiplet.
Solid lines correspond to the five lines, already considered
in Fig. 4, for which clear Q/I signals have been
measured near the solar limb.
It can be seen that with increasing depolarizing collisional rates
the line polarization may increase slightly (lines at 4639.4 Å and 4629.3 Å), the ratios of the
fractional polarization between different lines show large variations,
and the polarization direction can be even reversed (4639.7 Å line).
In particular we find that with
![]() s-1the observed signs and relative Q/I values of four lines
are
fairly well reproduced, although the fractional polarization
in the 4639.9 Å line turns out to be overestimated by a factor of the order of 2 relative to the others.
With larger D(2) values the atomic polarization in the
metastable levels is destroyed and the 4645.2 Å line,
which has Jl=1, Ju=0 and whose polarization is entirely produced by dichroism
due to lower-level alignment, becomes completely unpolarized, contrary to what is observed.
With much smaller D(2) values, the 4639.7 Å line does not match
observations because its polarization would turn from negative to positive.
Finally, we point out that the 4629.3 Å line actually lies within
the spectral range of Gandorfer's atlas but unfortunately it is
blended with a Fe II line (both lines equally contributing
to the blend).
However, the calculated negative sign for Q/I would be
compatible with the strong depolarization observed in this blend
plus, perhaps, an additional negative contribution from the Fe II
line.
s-1the observed signs and relative Q/I values of four lines
are
fairly well reproduced, although the fractional polarization
in the 4639.9 Å line turns out to be overestimated by a factor of the order of 2 relative to the others.
With larger D(2) values the atomic polarization in the
metastable levels is destroyed and the 4645.2 Å line,
which has Jl=1, Ju=0 and whose polarization is entirely produced by dichroism
due to lower-level alignment, becomes completely unpolarized, contrary to what is observed.
With much smaller D(2) values, the 4639.7 Å line does not match
observations because its polarization would turn from negative to positive.
Finally, we point out that the 4629.3 Å line actually lies within
the spectral range of Gandorfer's atlas but unfortunately it is
blended with a Fe II line (both lines equally contributing
to the blend).
However, the calculated negative sign for Q/I would be
compatible with the strong depolarization observed in this blend
plus, perhaps, an additional negative contribution from the Fe II
line.
We point out that at this collisional regime the alignment in the lower levels of the multiplet has decreased of approximately one fifth with respect to the collisionless case (see dot-dashed lines in Fig. 6a). This could be consistent with the presence of a microturbulent magnetic field in the saturation regime for the lower level.
Due to the anisotropy of the radiation field, atoms in the outer layers of the solar atmosphere are polarized (i.e., their Zeeman sublevels are unevenly populated). As a consequence of atomic polarization the Fraunhofer spectrum is linearly polarized when observed near the solar limb.
Here we have shown that the observed polarization features of the Ti I spectrum can be qualitatively reproduced by finding the atomic polarization in each level of a realistic model of the Ti I atom involving 395 levels and nearly 8000 transitions, and by comparing the expected line polarization in a sample of selected lines with the observations contained in the atlas of the second solar spectrum by Gandorfer (2000). This result is general and independent of the transfer model, which has been reduced here to its barest essentials.
We have also investigated the role played by depolarizing collisional rates and shown how it is possible to get some hints of their actual value by comparing theoretical expectations with observations.
Acknowledgements
One of the authors (rms) gratefully acknowledges partial support from the Spanish Ministerio de Ciencia y Tecnología through project AYA 2001-1649.