

Up: Solar activity cycle and
Subsections
We studied solar cycles 19, 20, 21 and 22 separately, focusing on the ten most
active years (Fig. 4). For each cycle, a frame is given which is
composed of
17 partially overlapping bins of power spectra of 480 d, disposed in
ordinate according to the dates of the observations. The x-axis shows the
synodic rotation period. The contours represent the prominent maxima of the
power spectra. For reference, we superimposed the radio flux
variation in arbitrary units on each frame. "M" and "m" indicate respectively
the Annual Mean Sunspot Numbers' (AMSN) maxima and minima (SGD 1997).
The mark "CR" on the x-axis gives the position of the Carrington Rotation
period.
Some points relating to the Fig. 4 can be emphasized:
- Solar rotation varies according to the solar cycle. For
instance the
most active cycle, number 19, clearly shows that the synodic rotation
periods
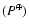 are shorter at maximum activity than before and
after:
are shorter at maximum activity than before and
after:
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{ms2771f5.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg20.gif) |
Figure 5:
Superimposition of power spectra peaks of frequencies of cycles
19 to 22. Ordinate divisions are half-years. To
distnguish the different cycles. (This figure is available in color in electronic form). |
-
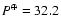 d in Jan. 1955 (2.5 y before cycle maximum),
d in Jan. 1955 (2.5 y before cycle maximum),
-
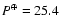 d in Jun. 1957 (cycle maximum),
d in Jun. 1957 (cycle maximum),
-
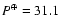 d in Feb. 1963 (5.6 y after maximum).
d in Feb. 1963 (5.6 y after maximum).
The time variation of the set of shortest rotation periods of each ordinates
(bin) traces a C-shaped inferior limit of synodic rotation period, indicated
by dotted lines. Frequencies with longer periods appear on the right hand
side of this limit,untill periods of 33 d. The other cycles (20, 21 and 22)
show the same general behavior. The right hand side end of the C-shaped limit
(the highest rotation period) will be considered as the "minimum"
of activity of the cycle. We consider periods higher than 31 d as "quiet sun".
- Table 1 displays the rotation characteristics
resulting from the
examination of the four cycles. The table gives the synodic rotation period
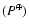 in days and the sidereal rotation rate
in days and the sidereal rotation rate
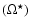 in degrees per day. For each cycle figures concerning rotation maxima are
provided in Cols. 3 and 4, those for "minima" in Cols. 5 and 6,
and those for quiet sun in Cols. 7 and 8.
in degrees per day. For each cycle figures concerning rotation maxima are
provided in Cols. 3 and 4, those for "minima" in Cols. 5 and 6,
and those for quiet sun in Cols. 7 and 8.
- No correlation can be established between the Monthly Mean
Sunspot Number (MMSN) maximum of the cycle and its minimum of rotation period.
However the four cycles have a wide variety of activity levels
(Table 2, Col. 2). The maximum of cycle 20 is only 54% of the maximum of
cycle 19, whereas the rotation rate variation is only 0.2%. We also
note that coronal rotation period maximum and sunspot number maximum do not
necessarily coincide in time (Tables 1 and 2).
Column 3 of Table 2 gives the
time difference in months between these maxima, if any.
- During the period of maximum of activity, there are broader
frequency ranges, whereas in "minimum" this range becomes narrower.
- For long periods around activity minima, no outstanding
frequencies are sufficiently revealed, because at minimum
the active regions are generally few, small and short-lived. Under these
conditions, the absence of information does not mean lack of preferential
longitudes; moreover Fig. 3 shows a outstanding frequency at
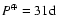 .
.
- The quiet sun is always present during the active period
(frequencies 1/31 to 1/33) and does not show significant variation.
- Time variations of rotation periods (Table 3)
are steeper
in the increasing phase (average
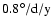 )
than in the
decreasing phase
)
than in the
decreasing phase
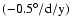 of the activity cycle.
of the activity cycle.
- The accuracy of the choice of 480 d is subsequently
justified by the extension of the y-axis of frequency peaks. It is evident
that lower time resolution analysis hides important results.
- Not all the frames of Fig. 4 show frequency
concentration around the Carringtion Rate. Keeping only the most prominent
frequencies in the four frames of Fig. 4, we superimpose them
and build Fig. 5. This shows
frequencies around the Carrington Rotation period, in agreement with
Fig. 3. We see around the activity maximum period (approximately 4 to
5 years) a richness of frequencies with values higher than the
Carrington Rate.
- Figure 5 shows a fish-bone structure,
composed of a set of three or four C-shaped layers of frequencies, making
rotation rate variation obvious throughout the cycle. All cycles
participate in each C-shaped structure, showing that this is a general
characteristic of magnetic flux related to rotation rate. All fish-bone
components show the same curvature, i.e. the same variation during the cycle.
In Fig. 4, we again find this
fish-bone structure in each frame. Do these fish-bones correspond to
the rotation rate of different components of the solar atmosphere, or are they
due to magnetic tubes rooted at different depths in the convective zone?
Table 2:
Sunspot activity maxima.
| date |
AMSN |
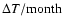 |
| 1 |
2 |
3 |
| 1957 Oct. |
190.2 |
- |
| 1969 Mar. |
105.9 |
- |
| 1979 Sep. |
155.4 |
-9 |
| 1989 Jun. |
157.2 |
-12 |
Table 3:
Acceleration of rotation period in
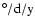 .
.
| cycle |
increasing phase |
decreasing phase |
| 19 |
0.9 |
-0.8 |
| 20 |
1.1 |
-0.6 |
| 21 |
0.8 |
-0.3 |
| 22 |
0.6 |
-0.3 |
For frequencies in Fig. 4 we compute an activity index R15,
a 15 month
mean of MMSN. The 15 month period is the closest odd number to 480 d.
Note that R15 is very close to AMSN. In Fig. 6 we plot
the sidereal rotation rate
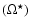 and the activity index
(R15). Solid signs mark the frequencies of the C-shaped limits of
the cycles, frequencies jointed by dotted lines in Fig. 4.
The set of solid points (cycles 19, 21 and 22) can be approximated by an
empirical equation:
and the activity index
(R15). Solid signs mark the frequencies of the C-shaped limits of
the cycles, frequencies jointed by dotted lines in Fig. 4.
The set of solid points (cycles 19, 21 and 22) can be approximated by an
empirical equation:
![\begin{displaymath}R_{15}= 32 \times (\Omega^{\star} - 13)^{2}+25 \makebox [1cm]
{for}\Omega^{\star} \rm\geq 13^{\circ}/d.
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img29.gif) |
(1) |
The open signs show the frequency of the right hand side of the C-shape
limits in Fig. 4. In the plane
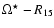 the frequency
distribution also shows a lower limit of rotation rate, following the
relation:
the frequency
distribution also shows a lower limit of rotation rate, following the
relation:
![\begin{displaymath}R_{15} = 75 \times (\Omega^{\star} - 13)^{4}+25 \makebox [1cm]
{for}\Omega^{\star} \rm\leq 13^{\circ}/d.
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img31.gif) |
(2) |
Curves (1) and (2) are shown in Fig. 6.
As far as cycle 20 (the weakest of our sample) is concerned, the
two limiting curves (1) and (2) are valid with a translation of
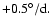 This shift indicates the necessity of a faster rotation to ensure
magnetic field
emergence. Using Eqs. (1) and (2) we can find a dependence of
sunspot number on the rotation rate:
This shift indicates the necessity of a faster rotation to ensure
magnetic field
emergence. Using Eqs. (1) and (2) we can find a dependence of
sunspot number on the rotation rate:
![\begin{displaymath}200 \geq R_{15} \geq 32 \times (\Omega^{\star} - \Omega^{\sta...
...25
\makebox [1cm] {for}\Omega^{\star} \geq \Omega^{\star}_{0}
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img33.gif) |
(3) |
![\begin{displaymath}200 \geq R_{15} \geq 75 \times (\Omega^{\star} - \Omega^{\sta...
...25
\makebox [1cm] {for}\Omega^{\star} \leq \Omega^{\star}_{0}
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img34.gif) |
(4) |
![\begin{figure}
\includegraphics[width=8.8cm,clip]{ms2771f6.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg35.gif) |
Figure 6:
Relationship between the sidereal rotation rate
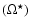 and solar activity (R15).
Cycle 19 - circles, cycle 20 - squares,
cycle 21 - triangles, cycle 22 - ellipse. Solid points are
limit of rotation period, linked by dotted lines in Fig. 4. The
curves draw the upper and lower rotation rates limits at a given
activity index, accordingly to Eqs. (1) and (2).
and solar activity (R15).
Cycle 19 - circles, cycle 20 - squares,
cycle 21 - triangles, cycle 22 - ellipse. Solid points are
limit of rotation period, linked by dotted lines in Fig. 4. The
curves draw the upper and lower rotation rates limits at a given
activity index, accordingly to Eqs. (1) and (2). |
here
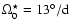 for cycles 19, 21 and 22, and
for cycles 19, 21 and 22, and
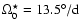 for cycle 20.
for cycle 20.
In order to express the activity index (R15) in units of total magnetic
flux
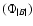 ,
we determine the following empirical relation,
based on cycle 21:
,
we determine the following empirical relation,
based on cycle 21:
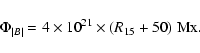 |
(5) |
Figure 6 indicates that, for a given rotation rate
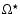 ,
only activity fluxes equal to or greater than that given
by Eqs. (1) and (2) can emerge.
Thus, the most likely rotation
rate for the emergence of the magnetic field is
,
only activity fluxes equal to or greater than that given
by Eqs. (1) and (2) can emerge.
Thus, the most likely rotation
rate for the emergence of the magnetic field is
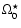 .
At high or low rates, only stronger magnetic flux emerges, the weak flux
being scattered before it reaches the top of the convective zone.
.
At high or low rates, only stronger magnetic flux emerges, the weak flux
being scattered before it reaches the top of the convective zone.
Following the time evolution of sidereal rotation of the C-shape limits
for each cycle (solid points of Fig. 6), we may see that during
the starting phase of the activity cycle, the rotation rate first grows
rapidly, whereas later the magnetic flux grows rapidly untill maximum. This
fact shows the important role of the Coriolis force in magnetic field
emergence.
We note that cycles 20, 21 and 22 display hysteresis loops
during their time evolution. No hysteresis was detected for cycle 19,
the strongest one.
Especially for cycles 21 and 22, the hysteresis shows that in
the decreasing phase higher rotation is needed
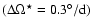 for the emergence of the same magnetic flux than during the increasing phase.
for the emergence of the same magnetic flux than during the increasing phase.


Up: Solar activity cycle and
Copyright ESO 2002
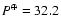 d in Jan. 1955 (2.5 y before cycle maximum),
d in Jan. 1955 (2.5 y before cycle maximum),
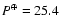 d in Jun. 1957 (cycle maximum),
d in Jun. 1957 (cycle maximum),
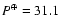 d in Feb. 1963 (5.6 y after maximum).
d in Feb. 1963 (5.6 y after maximum).
![]() and the activity index
(R15). Solid signs mark the frequencies of the C-shaped limits of
the cycles, frequencies jointed by dotted lines in Fig. 4.
The set of solid points (cycles 19, 21 and 22) can be approximated by an
empirical equation:
and the activity index
(R15). Solid signs mark the frequencies of the C-shaped limits of
the cycles, frequencies jointed by dotted lines in Fig. 4.
The set of solid points (cycles 19, 21 and 22) can be approximated by an
empirical equation:
![\begin{displaymath}R_{15}= 32 \times (\Omega^{\star} - 13)^{2}+25 \makebox [1cm]
{for}\Omega^{\star} \rm\geq 13^{\circ}/d.
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img29.gif)
![\begin{displaymath}R_{15} = 75 \times (\Omega^{\star} - 13)^{4}+25 \makebox [1cm]
{for}\Omega^{\star} \rm\leq 13^{\circ}/d.
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img31.gif)
![]() This shift indicates the necessity of a faster rotation to ensure
magnetic field
emergence. Using Eqs. (1) and (2) we can find a dependence of
sunspot number on the rotation rate:
This shift indicates the necessity of a faster rotation to ensure
magnetic field
emergence. Using Eqs. (1) and (2) we can find a dependence of
sunspot number on the rotation rate:
![\begin{displaymath}200 \geq R_{15} \geq 32 \times (\Omega^{\star} - \Omega^{\sta...
...25
\makebox [1cm] {for}\Omega^{\star} \geq \Omega^{\star}_{0}
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img33.gif)
![\begin{displaymath}200 \geq R_{15} \geq 75 \times (\Omega^{\star} - \Omega^{\sta...
...25
\makebox [1cm] {for}\Omega^{\star} \leq \Omega^{\star}_{0}
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img34.gif)
![\begin{figure}
\includegraphics[width=8.8cm,clip]{ms2771f6.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg35.gif)
![]() ,
we determine the following empirical relation,
based on cycle 21:
,
we determine the following empirical relation,
based on cycle 21:
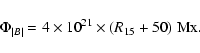
![]() for the emergence of the same magnetic flux than during the increasing phase.
for the emergence of the same magnetic flux than during the increasing phase.