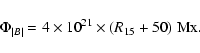A&A 394, 1103-1109 (2002)
DOI: 10.1051/0004-6361:20021244
Solar activity cycle and rotation of the corona
Z. Mouradian 1 -
R. Bocchia 2 -
C. Botton 2
1 - Observatoire de Paris, LESIA, 92195 Meudon Cedex, France
2 -
Observatoire de Bordeaux, Avenue Pierre Semirot, 33270 Floirac, France
Received 5 June 2002 / Accepted 13 August 2002
Abstract
In this paper we consider the dependence of the coronal rotation period
on solar activity. We analyzed the 10.7 cm radio emission flux covering
cycles 19 to 22. We have established a new method
for studying the rotation rate: by identifying the flux pulses
with the recurrence of active longitudes. We first determined the
frequency domain of the rotation and then analyzed each cycle separately.
The entire domain of 51.7 years was divided into 480-day sections,
which were analyzed independently and then grouped into frames
for each cycle in order to study the time variation of prominent
frequencies (Fig. 4). Power spectra were obtained with the
Maximum Entropy Method.
The 10.7 cm emission rotation varies accordingly to the activity level,
i.e. at the activity maxima the synodic period of rotation is about
25.4 days and at the minima it is around 30 days;
it is 32 days for the quiet Sun (Table 1). Empirical relations
give the ratio of maximum and minimum
sidereal rotation rate with respect to sunspot number
(Fig. 6). During the cycle increase phase, the average acceleration of
the rotation period is
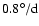 per year,
in decreasing phase that average is only -0.5.
per year,
in decreasing phase that average is only -0.5.
Key words: Sun: activity - Sun: rotation
The rotation of solar atmospheric structures is mainly affected by
magnetic tubes rooted in the convective zone. There are two causes of
the variation of rotation rates for the
various structures: the dynamics of the solar interior (differential
rotation, North/South hemisphere asymmetry, depth of anchorage of
magnetic ropes and variation of rotation according to solar activity)
and local conditions in the atmosphere (magnetic field structure, strength,
and height). The review papers of Howard (1984),
Schröter (1985), Howard et al. (1991),
Libbrecht & Morrow (1991) and
Beck (1999) summarized and analyzed the general aspects
of rotation of the solar atmosphere and quoted articles on the target.
The highest precision in rotation measurement is obtained with sunspots.
These measurements benefit from more than 100 years of high quality
photographic observation. They are generally considered as a reference for
the rotation of the solar atmosphere. Numerous authors reported sunspot
rotation rates which are in good agreement (Lustig 1983; Gilman & Howard 1984; Howard et al.
1984; Balthasar et al. 1986;
Hathaway & Wilson 1990; Howard et al. 1999).
Some papers
approach the problem of sunspot rotation in relation to the solar cycle
(Livinston & Duvall 1979; Lustig
1983; Gilman & Howard 1984; Balthasar et al. 1986;
Pulkkinen & Tuominen 1998; Gupta et al. 1999)
and they conclude that the sun rotates faster during minimum activity. More
general results of Woodard & Libbrecht (1993) from helioseismology,
or Mordvinov & Plyusinia (2000)
from MDI data, confirm the time variation of solar rotation during the cycle
of activity. We remind the reader that the Carrington Rotation period
was defined by sunspot rotation and it is the reference of solar rotation.
Studies of coronal rotation in relation to the solar cycle and
observed at the limb or on the disk, were performed
by Hansen et al. (1969),
Henze & Dupree (1973), Antonucci & Dodero (1977), Fisher &
Sime (1984), Parker (1986), Hoeksema & Scherrer (1987)
and Weber et al. (1999). According to these authors, coronal
rotation is characterized by a less pronounced differential rotation than
photospheric rotation and a near rigid rotation during minimum activity.
We found that the B coefficient (from the differential rotation rule
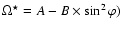 ,
which characterizes only the
differential rotation, is about 1 for the corona and about
,
which characterizes only the
differential rotation, is about 1 for the corona and about
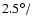 d
for sunspots. From Fig. 1 of Hoeksema & Scherrer, we obtain that the
synodic rotation period variation of sunspots and of the corona,
between the equator
and
d
for sunspots. From Fig. 1 of Hoeksema & Scherrer, we obtain that the
synodic rotation period variation of sunspots and of the corona,
between the equator
and
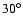 latitude, is respectively 1.32 and 0.41 d.
This last property made coronal rotation less latitude-dependent throughout the
cycle. Sky-Lab observations long ago showed that coronal holes rotate rigidly
as well as differentially. From green line data (
latitude, is respectively 1.32 and 0.41 d.
This last property made coronal rotation less latitude-dependent throughout the
cycle. Sky-Lab observations long ago showed that coronal holes rotate rigidly
as well as differentially. From green line data (
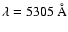 ),
Badalian & Livshits (1997) assert that coronal rotation
changes during the cycle, whereas Rybak (1994) do not find a clear
signature. On the other hand Vats et al. (1999) derive the
variation of synodic periods of coronal rotation ranging from 22 to 30 d.
),
Badalian & Livshits (1997) assert that coronal rotation
changes during the cycle, whereas Rybak (1994) do not find a clear
signature. On the other hand Vats et al. (1999) derive the
variation of synodic periods of coronal rotation ranging from 22 to 30 d.
In the present article we analyse corona rotation from 10.7 cm radio
flux. Our aim is to find the dependence of the active coronal rotation rate
on the 11-y solar cycle. We use the day (d) as the unit of synodic
rotation period and the degree per day (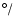 d) as the sideral rotation
rate. Note that, for the latter, case the conversion to other units is
d) as the sideral rotation
rate. Note that, for the latter, case the conversion to other units is
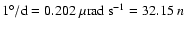 Hz.
In Sect. 2, we display the data we used in this study. In
Sect. 3 we briefly give the technique used to measure the rotation rate. In
Sect. 4 we show the results and the dependency of the rotation
rate on activity cycle. The paper ends with conclusions.
Hz.
In Sect. 2, we display the data we used in this study. In
Sect. 3 we briefly give the technique used to measure the rotation rate. In
Sect. 4 we show the results and the dependency of the rotation
rate on activity cycle. The paper ends with conclusions.
![\begin{figure}
\par\includegraphics[width=8.8cm]{ms2771f1.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg11.gif) |
Figure 1:
A thousand-day record of the slowly-varying component of
10.7 cm radio flux (February 25, 1977 to November 21, 1979). The y-axis
is the flux, in sfu and the abscissa is in days. |
| Open with DEXTER |
Our analysis of inner corona rotation related to the solar cycle is based
on the radio flux at 10.7 cm (2800 MHz) monitored by the Dominion
Astrophysical Observatory of the National Research Council of Canada
(Covington 1969). These observations started in late 1946 and are still
continuing. The daily recorded flux is the integrated emission over the solar
disk. The quoted flux values are measured around local noon (17:00 UT) and
have a relative error of 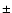 2%. Covington mentions that the 10.7 cm flux
is correlated with the active region (sunspots and plages), so that this
emission becomes a good index of solar activity. The origin of 2800 MHz
radiation is the thermal emission of plasma trapped in magnetic loops of the
active region and is consequently related to the photospheric magnetic
field flux of active regions.
The 10.7 cm emission is mainly due to
free-free radiation, as mentioned by Tapping & DeTracey (1990). The
10.7 cm rotation rate concerns
the global activity component of the solar corona. The review of
Rabin et al. (1991) shows the good correlation of 10.7 cm flux to
solar activity.
2%. Covington mentions that the 10.7 cm flux
is correlated with the active region (sunspots and plages), so that this
emission becomes a good index of solar activity. The origin of 2800 MHz
radiation is the thermal emission of plasma trapped in magnetic loops of the
active region and is consequently related to the photospheric magnetic
field flux of active regions.
The 10.7 cm emission is mainly due to
free-free radiation, as mentioned by Tapping & DeTracey (1990). The
10.7 cm rotation rate concerns
the global activity component of the solar corona. The review of
Rabin et al. (1991) shows the good correlation of 10.7 cm flux to
solar activity.
The 10.7 cm emission is located in the low corona. From high-resolution
observation of 8 sources Swarup et al. (1963) found that
the average altitude of radio emission is 15 000 km above the photosphere.
But Kundu (1965) mentioned emission altitudes two or three
times higher for some active regions observed by
Swarup. Covington (1969) determined even a height of 0.2 solar radius,
but Vats et al. (2001) gives the altitude as 60 000 km. These discrepancies in 10.7 cm emission height are due to different
magnetic complexity and strength of the active regions. Because we use the
recurrence method in the present search, the results are independent of the
altitude.
The radio flux we use is the Slowly Varying component (S component) consisting
of pulses superimposed on a background. Figure 1 shows a thousand days'
recording (February 25, 1977 to November 21, 1979) that cover the growing
to maximum phases of cycle 21. It can be seen that the background intensity
is changing during the cycle and is related to the global solar magnetic
flux. This is clearly due to the active regions distributed outside of active
longitudes, whose number varies with the phase of the activity cycle. For
our search we used the "Series D" data, which is adjusted for
solar-terrestrial distance variation and corrected to absolute units. The S component is free of bursts of transient events (flares, surges or other).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2771f2.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg13.gif) |
Figure 2:
Radio flux record showing cycles 19 to 22.
The low frequency (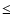 1/365 d) effect is removed. 1/365 d) effect is removed. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{ms2771f3.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg14.gif) |
Figure 3:
The power spectrum of the same period as in Fig. 2, in
abscissa frequencis 1/d. |
| Open with DEXTER |
The modulation of the S component is due to the presence of complex of
activity (Gaizauskas et al. 1983) on the solar disk.
Van Driel-Gesztelyi et al. (1992) mentioned that more than
a third of the active regions are clustered around "active longitudes".
SOHO/EIT data analyzed by Benevolenskaya et al. (2000) confirm
the reality of active
longitudes in the corona. As the life time of the active longitudes is
several times longer than the solar rotation period, their successive
passages on the solar disk modulate the 10.7 cm flux and determine the S component. Becker (1955) gives 10 to 12 solar rotations as an
average life time for sunspots "hearth" and Brouwer & Zwaan (1990)
give 4 to 6 rotations. The the solar flux is thus modulated by
the recurrence of active longitudes, thereby allowing measurement of
the rotation rate. Consequently, we introduce a new method for measuring
solar rotation rate, based on solar activity rotation with respect to Earth.
This way, our method provides solar rotation parametres in absolute units.
The emergence of any new big active region or an active longitude
on the solar disk introduces a "perturbation" in the flux modulation,
such as those visible in Fig. 1 at day 450, or a
longer period around day 700. The computed power spectra integrate the
480 d domain, including all disturbances.
In our data, the signal was neither less than 65 nor greater than 370 sfu.
We use the Butterworth numerical filter (Stearns 1975) to cut
off frequencies below 1/365 d and give in Fig. 2 the whole
period analyzed
(February 3, 1947 to November 9, 1998, or JD 2 432 258 to 2 451 127),
covering four solar cycles, 19 to 22.
A preliminary study of rotation rate versus cycle, based on the material
mentioned above, was already given by Mouradian et al. (2000).
In order to determine
the period of rotation we used a method of counting emission summits in a
given lapse of time, around the maximum, intermediary and minimum epochs of
solar activity. We found longer periods of rotation during the minima and
shorter ones during the activity maxima. In the present paper, we
perform the same task using the spectral analysis method.
Figure 3 shows the power spectrum of the 10.7 cm flux over the whole
data for period intervals from 16.5 to 50 d.
We see an large group of
frequencies spread around the Carrington Rotation period of 27.27 d. It shows
that coronal rotation is composed of multiple frequencies and
therefore has to be studied in detail. We can distinguish two groups of
frequencies, one between 0.034 and 0.040 and the second between 0.030 and
0.034 1/d. The first group is composed of well-defined frequencies, but the
second one is more confused. Later on we shall see that they correspond
respectively to active and quiet sun.
Various solar activity analyses have revealed a period of 150 to 160 d
(Ichimoto et al. 1985; Oliver et al. 1998;
the present data and others). To sample the
10.7 cm data we first chose a time lapse of 160 d and in order to
reduce the noise, we considered three times this period, i.e. 480 d
(approximately 18 solar rotations or 1.3 y). Consequently, the length of
51.7 y was covered by 77 overlapping periods of 480 d, shifted by 240 d steps. For each time interval of 480 d, we computed the power spectrum
using the Maximum Entropy Method (Press et al. 1990), which
determines the frequency variation more accurately than other methods
(Radoski et al. 1975). Each spectrum was normalized to its
maximum, so that the frequencies occurring in low-activity periods
were brought out too, thereby showing the rotation frequencies at any
point in the cycle.
![\begin{figure}
\includegraphics[width=12cm,clip]{fig4prim.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg17.gif) |
Figure 4:
Contour maps of power spectra for four cycles studied in the
rotation period range from 25 to 33.5 days. M and m on the y-axis indicate
the dates
of cycle maximum and of minimum. CR on x-axis indicates the
Carrington Rotation period in 1/d. The dotted lines join the lower limit of
rotation periods. |
| Open with DEXTER |
We studied solar cycles 19, 20, 21 and 22 separately, focusing on the ten most
active years (Fig. 4). For each cycle, a frame is given which is
composed of
17 partially overlapping bins of power spectra of 480 d, disposed in
ordinate according to the dates of the observations. The x-axis shows the
synodic rotation period. The contours represent the prominent maxima of the
power spectra. For reference, we superimposed the radio flux
variation in arbitrary units on each frame. "M" and "m" indicate respectively
the Annual Mean Sunspot Numbers' (AMSN) maxima and minima (SGD 1997).
The mark "CR" on the x-axis gives the position of the Carrington Rotation
period.
Some points relating to the Fig. 4 can be emphasized:
- Solar rotation varies according to the solar cycle. For
instance the
most active cycle, number 19, clearly shows that the synodic rotation
periods
 are shorter at maximum activity than before and
after:
are shorter at maximum activity than before and
after:
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{ms2771f5.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg20.gif) |
Figure 5:
Superimposition of power spectra peaks of frequencies of cycles
19 to 22. Ordinate divisions are half-years. To
distnguish the different cycles. (This figure is available in color in electronic form). |
| Open with DEXTER |
-
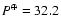 d in Jan. 1955 (2.5 y before cycle maximum),
d in Jan. 1955 (2.5 y before cycle maximum),
-
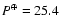 d in Jun. 1957 (cycle maximum),
d in Jun. 1957 (cycle maximum),
-
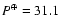 d in Feb. 1963 (5.6 y after maximum).
d in Feb. 1963 (5.6 y after maximum).
The time variation of the set of shortest rotation periods of each ordinates
(bin) traces a C-shaped inferior limit of synodic rotation period, indicated
by dotted lines. Frequencies with longer periods appear on the right hand
side of this limit,untill periods of 33 d. The other cycles (20, 21 and 22)
show the same general behavior. The right hand side end of the C-shaped limit
(the highest rotation period) will be considered as the "minimum"
of activity of the cycle. We consider periods higher than 31 d as "quiet sun".
- Table 1 displays the rotation characteristics
resulting from the
examination of the four cycles. The table gives the synodic rotation period
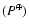 in days and the sidereal rotation rate
in days and the sidereal rotation rate
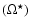 in degrees per day. For each cycle figures concerning rotation maxima are
provided in Cols. 3 and 4, those for "minima" in Cols. 5 and 6,
and those for quiet sun in Cols. 7 and 8.
in degrees per day. For each cycle figures concerning rotation maxima are
provided in Cols. 3 and 4, those for "minima" in Cols. 5 and 6,
and those for quiet sun in Cols. 7 and 8.
- No correlation can be established between the Monthly Mean
Sunspot Number (MMSN) maximum of the cycle and its minimum of rotation period.
However the four cycles have a wide variety of activity levels
(Table 2, Col. 2). The maximum of cycle 20 is only 54% of the maximum of
cycle 19, whereas the rotation rate variation is only 0.2%. We also
note that coronal rotation period maximum and sunspot number maximum do not
necessarily coincide in time (Tables 1 and 2).
Column 3 of Table 2 gives the
time difference in months between these maxima, if any.
- During the period of maximum of activity, there are broader
frequency ranges, whereas in "minimum" this range becomes narrower.
- For long periods around activity minima, no outstanding
frequencies are sufficiently revealed, because at minimum
the active regions are generally few, small and short-lived. Under these
conditions, the absence of information does not mean lack of preferential
longitudes; moreover Fig. 3 shows a outstanding frequency at
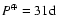 .
.
- The quiet sun is always present during the active period
(frequencies 1/31 to 1/33) and does not show significant variation.
- Time variations of rotation periods (Table 3)
are steeper
in the increasing phase (average
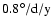 )
than in the
decreasing phase
)
than in the
decreasing phase
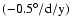 of the activity cycle.
of the activity cycle.
- The accuracy of the choice of 480 d is subsequently
justified by the extension of the y-axis of frequency peaks. It is evident
that lower time resolution analysis hides important results.
- Not all the frames of Fig. 4 show frequency
concentration around the Carringtion Rate. Keeping only the most prominent
frequencies in the four frames of Fig. 4, we superimpose them
and build Fig. 5. This shows
frequencies around the Carrington Rotation period, in agreement with
Fig. 3. We see around the activity maximum period (approximately 4 to
5 years) a richness of frequencies with values higher than the
Carrington Rate.
- Figure 5 shows a fish-bone structure,
composed of a set of three or four C-shaped layers of frequencies, making
rotation rate variation obvious throughout the cycle. All cycles
participate in each C-shaped structure, showing that this is a general
characteristic of magnetic flux related to rotation rate. All fish-bone
components show the same curvature, i.e. the same variation during the cycle.
In Fig. 4, we again find this
fish-bone structure in each frame. Do these fish-bones correspond to
the rotation rate of different components of the solar atmosphere, or are they
due to magnetic tubes rooted at different depths in the convective zone?
Table 2:
Sunspot activity maxima.
| date |
AMSN |
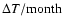 |
| 1 |
2 |
3 |
| 1957 Oct. |
190.2 |
- |
| 1969 Mar. |
105.9 |
- |
| 1979 Sep. |
155.4 |
-9 |
| 1989 Jun. |
157.2 |
-12 |
Table 3:
Acceleration of rotation period in
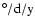 .
.
| cycle |
increasing phase |
decreasing phase |
| 19 |
0.9 |
-0.8 |
| 20 |
1.1 |
-0.6 |
| 21 |
0.8 |
-0.3 |
| 22 |
0.6 |
-0.3 |
For frequencies in Fig. 4 we compute an activity index R15,
a 15 month
mean of MMSN. The 15 month period is the closest odd number to 480 d.
Note that R15 is very close to AMSN. In Fig. 6 we plot
the sidereal rotation rate
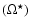 and the activity index
(R15). Solid signs mark the frequencies of the C-shaped limits of
the cycles, frequencies jointed by dotted lines in Fig. 4.
The set of solid points (cycles 19, 21 and 22) can be approximated by an
empirical equation:
and the activity index
(R15). Solid signs mark the frequencies of the C-shaped limits of
the cycles, frequencies jointed by dotted lines in Fig. 4.
The set of solid points (cycles 19, 21 and 22) can be approximated by an
empirical equation:
![\begin{displaymath}R_{15}= 32 \times (\Omega^{\star} - 13)^{2}+25 \makebox [1cm]
{for}\Omega^{\star} \rm\geq 13^{\circ}/d.
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img29.gif) |
(1) |
The open signs show the frequency of the right hand side of the C-shape
limits in Fig. 4. In the plane
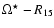 the frequency
distribution also shows a lower limit of rotation rate, following the
relation:
the frequency
distribution also shows a lower limit of rotation rate, following the
relation:
![\begin{displaymath}R_{15} = 75 \times (\Omega^{\star} - 13)^{4}+25 \makebox [1cm]
{for}\Omega^{\star} \rm\leq 13^{\circ}/d.
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img31.gif) |
(2) |
Curves (1) and (2) are shown in Fig. 6.
As far as cycle 20 (the weakest of our sample) is concerned, the
two limiting curves (1) and (2) are valid with a translation of
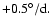 This shift indicates the necessity of a faster rotation to ensure
magnetic field
emergence. Using Eqs. (1) and (2) we can find a dependence of
sunspot number on the rotation rate:
This shift indicates the necessity of a faster rotation to ensure
magnetic field
emergence. Using Eqs. (1) and (2) we can find a dependence of
sunspot number on the rotation rate:
![\begin{displaymath}200 \geq R_{15} \geq 32 \times (\Omega^{\star} - \Omega^{\sta...
...25
\makebox [1cm] {for}\Omega^{\star} \geq \Omega^{\star}_{0}
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img33.gif) |
(3) |
![\begin{displaymath}200 \geq R_{15} \geq 75 \times (\Omega^{\star} - \Omega^{\sta...
...25
\makebox [1cm] {for}\Omega^{\star} \leq \Omega^{\star}_{0}
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img34.gif) |
(4) |
![\begin{figure}
\includegraphics[width=8.8cm,clip]{ms2771f6.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg35.gif) |
Figure 6:
Relationship between the sidereal rotation rate
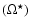 and solar activity (R15).
Cycle 19 - circles, cycle 20 - squares,
cycle 21 - triangles, cycle 22 - ellipse. Solid points are
limit of rotation period, linked by dotted lines in Fig. 4. The
curves draw the upper and lower rotation rates limits at a given
activity index, accordingly to Eqs. (1) and (2).
and solar activity (R15).
Cycle 19 - circles, cycle 20 - squares,
cycle 21 - triangles, cycle 22 - ellipse. Solid points are
limit of rotation period, linked by dotted lines in Fig. 4. The
curves draw the upper and lower rotation rates limits at a given
activity index, accordingly to Eqs. (1) and (2). |
| Open with DEXTER |
here
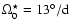 for cycles 19, 21 and 22, and
for cycles 19, 21 and 22, and
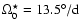 for cycle 20.
for cycle 20.
In order to express the activity index (R15) in units of total magnetic
flux
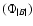 ,
we determine the following empirical relation,
based on cycle 21:
,
we determine the following empirical relation,
based on cycle 21:
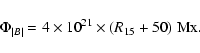 |
(5) |
Figure 6 indicates that, for a given rotation rate
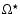 ,
only activity fluxes equal to or greater than that given
by Eqs. (1) and (2) can emerge.
Thus, the most likely rotation
rate for the emergence of the magnetic field is
,
only activity fluxes equal to or greater than that given
by Eqs. (1) and (2) can emerge.
Thus, the most likely rotation
rate for the emergence of the magnetic field is
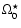 .
At high or low rates, only stronger magnetic flux emerges, the weak flux
being scattered before it reaches the top of the convective zone.
.
At high or low rates, only stronger magnetic flux emerges, the weak flux
being scattered before it reaches the top of the convective zone.
Following the time evolution of sidereal rotation of the C-shape limits
for each cycle (solid points of Fig. 6), we may see that during
the starting phase of the activity cycle, the rotation rate first grows
rapidly, whereas later the magnetic flux grows rapidly untill maximum. This
fact shows the important role of the Coriolis force in magnetic field
emergence.
We note that cycles 20, 21 and 22 display hysteresis loops
during their time evolution. No hysteresis was detected for cycle 19,
the strongest one.
Especially for cycles 21 and 22, the hysteresis shows that in
the decreasing phase higher rotation is needed
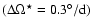 for the emergence of the same magnetic flux than during the increasing phase.
for the emergence of the same magnetic flux than during the increasing phase.
In this paper we propose a new method for measuring rotation rate and
clearly establish that: a) the active corona rotation rate
varies with respect to the 11-y sunspot cycle, b) there is a relationship
between rotation rate and magnetic flux, c) rotation grows first and then
the magnetic field emerges, d) activity increases the
rotation rate. The sidereal rotation rate of the active corona varies
between
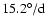 and
and
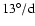 respectively,
for activity maxima
and "minima". Nevertheless 10.7 cm rates of maxima and of "minima" include
the sunspot radiation rates. Lastly, active regions in the photosphere and in
the corona averaged over the whole cycle reproduce the
Carrington Rotation Rate. On the other hand, the frequencies over the whole
observation time, given in Fig. 3, show different frequencies
grouped round the Carrington Rate.
respectively,
for activity maxima
and "minima". Nevertheless 10.7 cm rates of maxima and of "minima" include
the sunspot radiation rates. Lastly, active regions in the photosphere and in
the corona averaged over the whole cycle reproduce the
Carrington Rotation Rate. On the other hand, the frequencies over the whole
observation time, given in Fig. 3, show different frequencies
grouped round the Carrington Rate.
The rotation figures given in this paper have larger amplitudes than those
of other authors. This is due to the high temporal resolution of the data
and to the narrow windows used for computation of power spectra. Even if
sunspots and 10.7 cm coronal flux data are disk observations, a direct
comparison
cannot be done. In case of sunspots, the measurements give differential
rotation rates over long periods including cycles of activity. Data from
analyses of 10.7 cm flux are frequencies distributed with respect to time,
which cannot be averaged. According to Gilman & Howard (1984) and
to Gupta et al. (1999), at the minimum of activity,
sunspot rotation is faster than during the rest of the cycle,
whereas coronal rotation is slower at that time, as was pointed
out for all coronal observations. This remains unexplained.
Antonucci & Dodero (1977) showed the simultaneous presence
of coronal structures with
differential rotation and with rigid rotation in the same period. It is also
well known that coronal holes show either rigid or differential rotation.
This assertion is supported by the detection of Pivot Points
(Mouradian et al. 1987),
which designate regions of the solar photosphere in rigid rotation, alongside
regions in differential rotation. Stenflo's (1977) sentence, "There
is a coexistence on the sun of regions with rigid and differential-rotation
properties" is here proved for the corona too. Observations revealed
the simultaneous presence of a large number of rates, so that the
smoothed differential rotation cannot be considert as a local rule.
Acknowledgements
The 10.7 cm Solar Flux data were provided by the National Research Council of
Canada and the authors are in dept to Dr. K. Tapping. We are grateful for
clarifying discussions to Dr. D. Heristchi. The authors thank the
referee, Dr. H. Wöhl, for his valuable remarks and comments.
- Antonucci, E., & Dodero, A. 1977, Sol. Phys., 53, 179
In the text
NASA ADS
- Badalyan, O. G., & Livshits, M. A. 1997, Ap&SS, 252, 317
In the text
NASA ADS
- Balthasar, H., Vázquez, M.,
& Wöhl, H. 1986, A&A, 155, 87
In the text
NASA ADS
- Beck, G. 1999, Sol. Phys., 191, 47
In the text
- Becker, U. 1955, Z. Astrohys., 37, 47
In the text
NASA ADS
- Benevolenskaya, E. E., Kosovichev, A. G., &
Scherrer, P. H. 2000, BAAS, 32, 815
In the text
- Brouwer, M. P., & Zwaan, C. 1990, Sol. Phys., 129, 221
In the text
NASA ADS
- Covington, A. E. 1969, JRASC, 63, 125
In the text
NASA ADS
- Fisher, R. R., & Sime, D. G. 1984, ApJ, 287, 959
In the text
NASA ADS
- Gaizauskas, V., Harvey, K. L., Harvey, J. W.,
& Zwaan, C. 1983, ApJ, 265, 1056
In the text
NASA ADS
- Gilman, P. A., & Howard, R. 1984, ApJ, 283, 385
In the text
NASA ADS
- Gupta, S. S., Siviraman, K. R., & Howard, R. F.
1999, Sol. Phys., 188, 225
In the text
NASA ADS
- Hansen, R. T., Hansen, S. F., & Loomis, H. G. 1969,
Sol. Phys., 10, 135
In the text
NASA ADS
- Hathaway, D. H., & Wilson, R. M. 1990, ApJ, 357, 271
In the text
NASA ADS
- Henze, W. Jr., & Dupree, A. K. 1973, Sol. Phys., 33, 425
In the text
NASA ADS
- Hoeksema, J. T., & Scherrer, P. H. 1987, ApJ, 318, 428
In the text
NASA ADS
- Howard, R. 1984, ARA&A, 22, 131
In the text
NASA ADS
- Howard, R. F., Gilman, P. A., & Gilman, P. I. 1984,
ApJ., 283, 373
In the text
NASA ADS
- Howard, R. F., Gupta, S. S., & Siviramann, K. R. 1999,
Sol. Phys., 186, 25
In the text
- Howard, R. F., Kichatinov, L. L., Bogart, R. S.
& Ribes, E. 1991, in Solar Interior and Atmosphere, ed. A. N. Cox, W. C. Livingston, & M. S. Matthews (The University of Arizona Press,
Tucson), 748
In the text
- Ichimoto, O., Kubota, J., Suzuki, M., Tohmura, I.,
& Kurokawa, H. 1985, Nature, 316, 422
In the text
NASA ADS
- Kundu, M. R. 1965, Solar Radio Astronomy
(Interscience Publ.), 152
In the text
- Libbrecht, K. G., & Morrow, C. A. 1991, in Solar Interior and Atmosphere, ed. A. N. Cox, W. C.
Livingston, & M. S. Matthews (The
University of Arizona Press, Tucson), 479
In the text
- Livingston, W. C., & Duvall, T. L. 1979, Sol. Phys., 61, 219
In the text
NASA ADS
- Lustig, G. 1983, A&A, 125, 355
In the text
NASA ADS
- Mordvinov, A. V., & Plyusnina, L. A. 2000, Sol. Phys.,
197, 1
In the text
- Mouradian, Z., Bocchia, R., & Botton, C.
2000, C. R. Acad. Sci. Paris, 1, Ser. IV, 353
In the text
- Mouradian, Z., Martres, M. J., Soru-Escaut, I.,
& Gesztelyi, L. 1987, A&A, 183, 129
In the text
NASA ADS
- Oliver, R., Ballester, J. L., & Baudin, F. 1998,
Nature, 394, 552
In the text
NASA ADS
- Parker, G. D. 1986, Sol. Phys., 104, 333
In the text
NASA ADS
- Press, W. H., Flannery, B. P., Teukolsky, S. A.,
& Vetterling, W. T. 1990, Numerical Recipes (Cambridge Univ. Press), 447
In the text
- Pulkkinen, P., & Touminen, I. 1998, A&A, 332, 748
In the text
NASA ADS
- Rabin, D. M., DeVore, C. R., Sheeley, N. R. Jr., &
Harvey, K. L. 1991, in Solar Interior and Atmosphere, ed. A. N. Cox, W. C. Livingston, & M. S. Matthews (The University of Arizona Press, Tucson), 781
In the text
- Radoski, H. R., Fougere, P. F., & Zawalick, E. 1975,
J. Geophys. Res., 80, 619
In the text
- Rybak, J. 1994, Sol. Phys., 152, 161
In the text
NASA ADS
- Schröter, E. H. 1985, Sol. Phys., 100, 141
In the text
NASA ADS
- SGD 1997, Solar-Geophys. Data, Nr. 640, Part 1
In the text
- Stearns, S. D. 1975, Digital Signal Analysis, Hayden
Book Company, Inc., 183
In the text
- Stenflo, J. O. 1977, A&A, 61, 797
In the text
NASA ADS
- Swarup, G., Kakinuma, T., Covington, A. E., et al. 1963, ApJ, 137, 1251
In the text
NASA ADS
- Tapping, K. F., & DeTracey, B. 1990, Sol. Phys., 127, 321
In the text
NASA ADS
- Van Driel-Gesztelyi, L., van der Zalm, E. B. J., &
Zwaan, C. 1992, in The Solar Cycle, ASP Conf. Ser., 27, 89
In the text
- Vats, H. O., Deshpande, M. R., Meyta, M., et al. 1999, Adv. Space Res., 24(2), 241
In the text
NASA ADS
- Vats, H. O., Cecatto, J. R., Meyta, M., Sawant,
H. S., & Neri, A. C. F. 2001, ApJ, 548, L87
In the text
NASA ADS
- Weber, M. A., Action, L. W., Alexander, D., Kubo, S.,
& Hara, H. 1999, Sol. Phys., 189, 271
In the text
NASA ADS
- Woodard, M. F., & Libbrecht, K. G. 1993, Science, 260, 1778
In the text
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=8.8cm]{ms2771f1.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg11.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms2771f2.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg13.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{ms2771f3.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg14.gif)
![\begin{figure}
\includegraphics[width=12cm,clip]{fig4prim.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg17.gif)
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{ms2771f5.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg20.gif)
![\begin{displaymath}R_{15}= 32 \times (\Omega^{\star} - 13)^{2}+25 \makebox [1cm]
{for}\Omega^{\star} \rm\geq 13^{\circ}/d.
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img29.gif)
![\begin{displaymath}R_{15} = 75 \times (\Omega^{\star} - 13)^{4}+25 \makebox [1cm]
{for}\Omega^{\star} \rm\leq 13^{\circ}/d.
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img31.gif)
![\begin{displaymath}200 \geq R_{15} \geq 32 \times (\Omega^{\star} - \Omega^{\sta...
...25
\makebox [1cm] {for}\Omega^{\star} \geq \Omega^{\star}_{0}
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img33.gif)
![\begin{displaymath}200 \geq R_{15} \geq 75 \times (\Omega^{\star} - \Omega^{\sta...
...25
\makebox [1cm] {for}\Omega^{\star} \leq \Omega^{\star}_{0}
\end{displaymath}](/articles/aa/full/2002/42/aa2771/img34.gif)
![\begin{figure}
\includegraphics[width=8.8cm,clip]{ms2771f6.eps}\end{figure}](/articles/aa/full/2002/42/aa2771/Timg35.gif)