A&A 394, 965-969 (2002)
DOI: 10.1051/0004-6361:20021233
A more powerful evolution model for rotating stars
Y. R. Zeng
Yunnan Astronomical Observatory and National
Astronomical Observatories, PO Box 110, 650011 Kunming, PR China
Received 30 May 2002 / Accepted 1 August 2002
Abstract
A new one-dimensional rotating stellar evolution model was
developed which, distinct from its previous counterparts based on
a conservative rotation case or a "shellular rotation'' case,
made no special assumptions on the distribution of angular
velocity inside a rotating star. The results of the evolutionary
calculations are presented and compared with the results of
previous studies.
Key words: stars: evolution - stars: rotation -
stars: Hertzsprung-Russell (HR) and C-M diagrams
The study of rotating stars has attracted much attention during
the last decades as a consequence of the observational findings
such as the He- enrichments
in the fast rotators among O-stars (Herrero et al. 1992), the N/C and 13C/12C enrichments on the Red Giant Branch (see e.g. Charbonnel
1994, 1995), the He- and N-enrichments in OBA supergiants and in SN 1987A
(Walborn 1976; Fransson et al. 1989; Venn 1995A,b; Venn et al. 1996) and the
problem of the blue to red supergiants ratio in galaxies (Langer & Maeder
1995) etc.
In a rotating star, the centrifugal forces reduce the effective
gravity according to the latitude and introduce deviations from
sphericity. Thus, the structure equations of a rotating star should
be two dimensional.The original method devised by Kippenhahn,
Meyer-Hofmeister & Thomas (1970) (subsequently referred to as KMT)
and applied in most subsequent works (Meyer-Hofmeister 1972; Endal
& Sofia 1976 (hereafter ES), 1978; Pinsonneault et al. 1989, 1990;
Chaboyer et al. 1995a,b; Sills et al. 2000; Heger et al. 2000) to keep
the problem one dimensional is based on a so-called conservative
rotation case, i.e., the angular velocity is constant on
cylinders. In such a rotation case, the total potential is
conservative and the structural variables P, T, 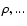 are
constant on a equipotential surface. Meynet & Maeder
(1997) (subsequently referred to as MM) argue that not a
conservative rotation case but a "shellular rotation'' case,
i.e., the angular velocity is constant on an isobar (an isobar is a
constant pressure surface) is the real rotation case in an evolved
star. In a "shellular rotation'' case, they find a
are
constant on a equipotential surface. Meynet & Maeder
(1997) (subsequently referred to as MM) argue that not a
conservative rotation case but a "shellular rotation'' case,
i.e., the angular velocity is constant on an isobar (an isobar is a
constant pressure surface) is the real rotation case in an evolved
star. In a "shellular rotation'' case, they find a
 |
(1) |
where
 ,
instead of
,
instead of  ,
is
constant on an isobar and it can denote the property of
,
is
constant on an isobar and it can denote the property of 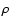 on the whole isobar. Furthermore, the temperature T and the
chemical composition
on the whole isobar. Furthermore, the temperature T and the
chemical composition 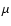 are supposed to be constant on an
isobar. Thus, if the structural equations are written on isobars,
the problem can be kept one dimensional.
are supposed to be constant on an
isobar. Thus, if the structural equations are written on isobars,
the problem can be kept one dimensional.
The distribution of angular velocity inside a real star is still a
mystery, therefore, it is important to develop an one dimensional
method which is not based on any special assumptions on the
distribution of angular velocity. I propose a method based on
Meynet & Maeder (1997) to deal with this problem.
The new structural model is introduced in Sect. 2, and the results of
evolution calculations are presented in Sect. 3.
In a Roche model, a constant total potential surface is given by
the equation:
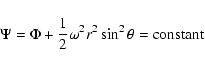 |
(2) |
where 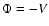 ,
and V is the gravitational potential, r is the radius,
,
and V is the gravitational potential, r is the radius, 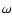 the angular velocity and
the angular velocity and 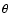 the colatitude.
the colatitude.
The constant
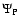 surfaces, the constant
surfaces, the constant 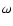 surfaces, the constant
surfaces, the constant 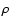 surfaces, the constant Tsurfaces, and the isobars do not correspond to each other if no
special assumption about the distribution of angular velocity is
made. However, some parameters
surfaces, the constant Tsurfaces, and the isobars do not correspond to each other if no
special assumption about the distribution of angular velocity is
made. However, some parameters 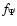 ,
,
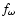 ,
,
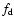 and
and
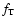 can always be found to make
can always be found to make
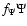 ,
,
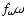 ,
,
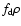 and
and
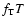 constant on an isobar, furthermore, if
constant on an isobar, furthermore, if
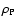 and
and 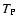 denote the value of density and temperature
of a point P (
denote the value of density and temperature
of a point P (
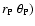 on an isobar,
on an isobar,
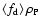 and
and
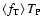 denote the properties of density and temperature on the
whole isobar, different values of
denote the properties of density and temperature on the
whole isobar, different values of
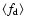 and
and
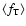 will be given for
different points P. Thus, the problem can be kept one
dimensional, if the structural equations are written on isobars.
will be given for
different points P. Thus, the problem can be kept one
dimensional, if the structural equations are written on isobars.
The four parameters 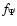 ,
,
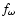 ,
,
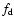 and
and 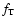 ,
indicating the relationship between the constant
,
indicating the relationship between the constant
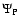 ,
,
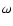 ,
,
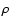 ,
T surfaces and the isobars, accordingly, are
not independent of one another. Once
,
T surfaces and the isobars, accordingly, are
not independent of one another. Once 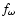 ,
the distribution
of angular velocity, is decided, the other three parameters are
decided, too. Consequently, there is only one independent
parameter need to be determined by advanced theories or by
comparing the results of evolution model with the observational
data. The relationships of
,
the distribution
of angular velocity, is decided, the other three parameters are
decided, too. Consequently, there is only one independent
parameter need to be determined by advanced theories or by
comparing the results of evolution model with the observational
data. The relationships of 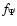 and
and 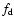 with
with 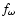 will be shown in the Appendix and how these parameters are decided
in the "shellular rotation'' case will be shown in Sect. 3.
will be shown in the Appendix and how these parameters are decided
in the "shellular rotation'' case will be shown in Sect. 3.
An isobar in a rotating star is assumed to be an ellipsoid of
resolution with the major axis a and the minor axis b, and the
volume inside an isobar is given by
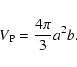 |
(3) |
For every isobar, an assumed equivalent sphere with the radius 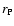 can be defined by:
can be defined by:
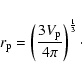 |
(4) |
The structural equations are written at the point P (
 where an isobar intersects its equivalent sphere (see Fig. 1).
where an isobar intersects its equivalent sphere (see Fig. 1).
(1) Conservation of mass
As from Eq. (4), the mass between the two isobaric surfaces is given by
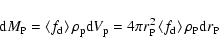 |
(5) |
which gives the equation of conservation of mass as
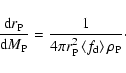 |
(6) |
(2) The hydrostatic equilibrium
The hydrostatic equilibrium implies that
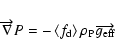 |
(7) |
where
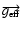 is the effective gravitational
acceleration. In the spherical coordinates, its components are given by
is the effective gravitational
acceleration. In the spherical coordinates, its components are given by
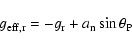 |
(8) |
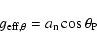 |
(9) |
where
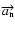 is the centrifugal acceleration,
is the centrifugal acceleration,
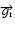 the gravitational acceleration. The values of
the gravitational acceleration. The values of
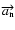 and
and
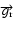 are given by
are given by
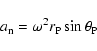 |
(10) |
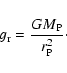 |
(11) |
The radial component of the vectorial Eq. (7) is
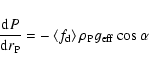 |
(12) |
where
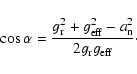 |
(13) |
From Eqs. (11), (12) and (6), the equation of hydrostatic equilibrium
is obtained as
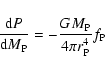 |
(14) |
where
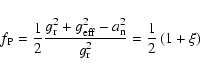 |
(15) |
and
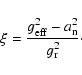 |
(16) |
(3) Conservation of the energy
The net energy outflow from a shell between the two isobaric surfaces Pand
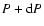 is equal to
is equal to
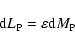 |
(17) |
where
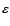 is the rate of energy production in the shell. Writing
is the rate of energy production in the shell. Writing
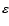 in its nuclear, internal and neutrino components,
one obtains the equation for conservation of the energy as
in its nuclear, internal and neutrino components,
one obtains the equation for conservation of the energy as
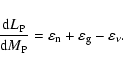 |
(18) |
(4) Energy transport in the region of radiative equilibrium
The temperature gradient in the region of radiative equilibrium is defined as
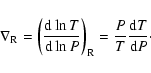 |
(19) |
Using (12) and (19), one obtains
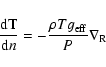 |
(20) |
where n is the unit normal of the isobar at point P.
The radiative
energy flux at the point P on the isobaric surface is given by
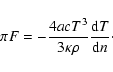 |
(21) |
Hence, one obtains the luminosity as
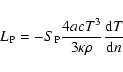 |
(22) |
where 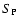 is the area of the isobaric surface. Comparing (22)
with (20), one obtains
is the area of the isobaric surface. Comparing (22)
with (20), one obtains
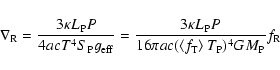 |
(23) |
where
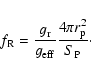 |
(24) |
Using (14) and (19), one obtains the equation of energy transport in the
region of radiative equilibrium as
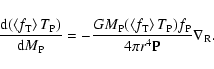 |
(25) |
(5) Energy transport in the convective region
The equation of energy transported in the convective region of stellar
interior can be written as
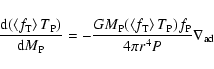 |
(26) |
where
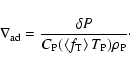 |
(27) |
In the practical calculations, the non-spherical stratification of
rotating stars can be replaced by the spherical stratification of
equivalent sphere. Thus, the calculations of the structure Eqs. (6), (14), (18), (25) and (26) are based on the equivalent sphere. However, the two factors 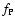 and
and 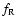 ,
defined by (15) and (24), which are related to the characteristic of rotation, should be calculated on the isobar.
,
defined by (15) and (24), which are related to the characteristic of rotation, should be calculated on the isobar.
When the radius of the equivalent sphere 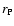 and the angular velocity
and the angular velocity 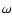 are given,the volume
are given,the volume 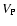 inside the isobaric surface can be
written from (4) as
inside the isobaric surface can be
written from (4) as
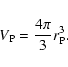 |
(28) |
From Eq. (2), one obtains
![\begin{displaymath}f_{\Psi a}\left[\frac{GM_{\rm p}}a+\frac 12(f_{\omega a}\omega )^2a^2\right]=f_{\Psi b}\left(\frac{GM_{\rm p}}b\right)
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img72.gif) |
(29) |
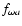 can be supposed to be 1.
can be supposed to be 1.
Then, the major and minor axis of the isobar can be obtained as
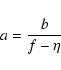 |
(30) |
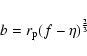 |
(31) |
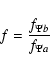 |
(32) |
where
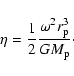 |
(33) |
Using the value b and the relation
![\begin{displaymath}f_{\Psi}\left[\frac{GM_{\rm p}}{r_{\rm p}}+\frac 12(f_\omega ...
...heta
_{\rm p}\right]=f_{\Psi b}\left(\frac{GM_{\rm p}}b\right)
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img78.gif) |
(34) |
the value of the colatitude
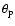 can be obtained.
can be obtained.
The factor 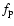 can be calculated by using (15) when the values of
can be calculated by using (15) when the values of 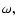
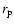 and
and
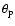 are known.
are known.
The factor 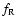 can be calculated by using (24) when the surface
area
can be calculated by using (24) when the surface
area 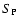 of the isobar is given by
of the isobar is given by
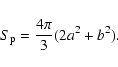 |
(35) |
The calculation of the case without rotation is performed by using
a modified version of the stellar structure and evolution program
developed by Kippenhahn et al. (1967). This version has included the
recent opacities (cf. Iglesias & Rogers 1996, complemented at
lower temperature with the low-temperature rosseland opacities by
Alexander & Ferguson 1994) and energy generating rates
(cf.
Maeder 1983; Maeder & Meynet 1987, 1989). The case with rotation
is calculated using the rotating evolution code which is modified
from the previous non-rotating program, and have included the
equations represented in Sect. 2.
To compare the new results with previous ones, the "shellular
rotation'' case (compared with MM) has been calculated.
MM assumed that the angular velocity 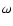 ,
the pressure P and
the temperature T and a
,
the pressure P and
the temperature T and a
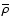 are constant on
isobars. Therefore, in the new method,
are constant on
isobars. Therefore, in the new method,
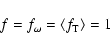 |
(36) |
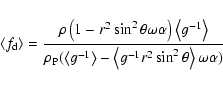 |
(37) |
where
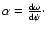
![\begin{figure}
\par\includegraphics[angle=270,width=11.2cm,clip]{27462.ps}\end{figure}](/articles/aa/full/2002/42/aa2746/Timg88.gif) |
Figure 2:
Upper ZAMS in the theoretical HR diagram for different
rotation rates. |
| Open with DEXTER |
The comparison can only be made on the ZAMS because in the new
method, the mixing of chemical species and angular momentum by
circulation currents and turbulence has not been included while it
has been considered in MM's method, and solid body rotation is
assumed on the ZAMS, therefore:
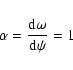 |
(38) |
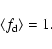 |
(39) |
Some characteristics of the models being calculated (X=0.7,
Z=0.02.) are given in Table 1 as a function of the initial mass
and angular velocity, and Fig. 2 presents the ZAMS obtained in the
theoretical HR diagram. These results do not differ from MM's very
much.
A new one-dimensional rotating stellar evolution model was
developed. Distinct from its previous counterparts based on a
conservative rotation case or a "shellular rotation'' case, it
made no special assumptions on the distribution of angular
velocity inside a rotating star.
One independent parameter 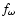 has been introduced in the
new method; to determine its value is another complicated task.
This and other improvements, such as including the mixing of
chemical species and angular momentum by circulation currents and
turbulent, will be presented in the future.
has been introduced in the
new method; to determine its value is another complicated task.
This and other improvements, such as including the mixing of
chemical species and angular momentum by circulation currents and
turbulent, will be presented in the future.
Acknowledgements
I wish to express thanks to R.Q. Huang for his most fruitful advice.
Following MM,
and under the condition of no special assumption about 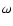 ,
one can get:
,
one can get:
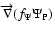 is parallel to
is parallel to
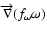 ,
thus, the effective
gravity can be expressed as
,
thus, the effective
gravity can be expressed as
![\begin{displaymath}g=\left[ \frac 1{\left\langle f_\Psi \right\rangle }-r^2\sin
...
...rangle
}\right] \frac{{\rm d}(f_\Psi \Psi _{\rm P})}{{\rm d}n}
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img111.gif) |
(A.3) |
where:
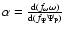 ,
or
,
or
![\begin{displaymath}g=\left[\frac \beta {\left\langle f_\Psi \right\rangle }-r^2\...
...ight\rangle
}\right]\frac{{\rm d}(f_\omega \omega )}{{\rm d}n}
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img113.gif) |
(A.4) |
where
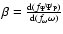 ,
hence:
,
hence:
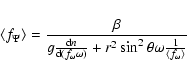 |
(A.5) |
and:
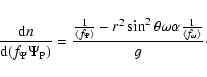 |
(A.6) |
The hydrostatic equation then becomes
![\begin{displaymath}\frac{{\rm d}P}{{\rm d}n}=-\rho \left[ \frac 1{\left\langle f...
...rangle }\right] \frac{{\rm d}(f_\Psi \Psi
_{\rm P})}{{\rm d}n}
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img117.gif) |
(A.7) |
or
![\begin{displaymath}\frac{{\rm d}P}{{\rm d}(f_\Psi \Psi _{\rm P})}=-\rho \left[ \...
...lpha \frac
1{\left\langle f_\omega \right\rangle }\right]\cdot
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img118.gif) |
(A.8) |
From this equation, one can deduce that
![$-\rho \left[ \frac
1{\left\langle f_\Psi \right\rangle }-r^2\sin ^2\theta \omega
\alpha \frac 1{\left\langle f_\omega \right\rangle }\right]$](/articles/aa/full/2002/42/aa2746/img119.gif) is
constant on an isobar.
is
constant on an isobar.
Using (A.6), one can get
and
Thus
![\begin{displaymath}\frac{{\rm d}(f_\Psi \Psi _{\rm P})}{{\rm d}M_{\rm P}}=\frac ...
...ht\rangle }\right]
\left\langle g^{-1}\right\rangle S_{\rm P}}
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img128.gif) |
(A.11) |
and
![\begin{displaymath}\frac{{\rm d}V_{\rm P}}{{\rm d}(f_\Psi \Psi _{\rm P})}=\left[...
...\alpha{\left\langle f_\omega \right\rangle }\right] S_{\rm P}.
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img129.gif) |
(A.12) |
Hence
![\begin{displaymath}\overline{\rho }=\frac{\rho \left[ \frac 1{\left\langle f_\Ps...
...le \frac
\alpha{\left\langle f_\omega \right\rangle }\right] }
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img130.gif) |
(A.13) |
![\begin{displaymath}\left\langle f_{\rm d}\right\rangle =\frac{\rho \left[ \frac
...
...rac
\alpha{\left\langle f_\omega \right\rangle }\right] }\cdot
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img131.gif) |
(A.14) |
Furthermore, once 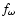 is given,
is given, 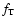 can be decided from
other ways and (A5) and (A14), which decide
can be decided from
other ways and (A5) and (A14), which decide 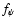 and
and 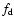 respectively, can be more applicable.
respectively, can be more applicable.
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879
In the text
NASA ADS
- Chaboyer, B., Demarque, P., & Pinsonneault, M. H.
1995a, ApJ, 441, 865
In the text
NASA ADS
- Chaboyer, B., Demarque, P., & Pinsonneault, M. H.
1995b, ApJ, 441, 876
NASA ADS
- Charbonnel, C. 1994, A&A, 282, 811
In the text
NASA ADS
- Charbonnel, C. 1995, ApJ, 453, L41
In the text
NASA ADS
- Endal, A. S., & Sofia, S. 1976, ApJ, 210,
184 (ES)
In the text
NASA ADS
- Endal, A. S., & Sofia, S. 1978, ApJ, 220, 279
NASA ADS
- Fransson, C., Cassatella, A., Gilmozzi, R., et al. 1989, ApJ, 336, 429
In the text
NASA ADS
- Heger, A., Langer, & N., Woosley, S. E. 2000, ApJ, 528, 368
In the text
NASA ADS
- Herrero, A., Kudritzki, R. P., Vilchez, J. M., et al. 1992, A&A, 261, 209
In the text
NASA ADS
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943
In the text
NASA ADS
- Kippenhahn, R., Weigert, A., & Hofmeister, E. 1967,
Meth. Comp. Phys., 7, 129
In the text
- Kippenhahn, R., Meyer-Hofmeister, E., & Thomas, H. C.
1970, A&A, 5, 155 (KMT)
NASA ADS
- Langer, N., & Maeder, A. 1995, A&A, 295, 685
In the text
NASA ADS
- Maeder, A. 1983, A&A, 120, 113
In the text
NASA ADS
- Maeder, A., & Meynet, G. 1987, A&A, 182, 243
In the text
NASA ADS
- Maeder, A., & Meynet, G. 1989, A&A, 210, 155
In the text
NASA ADS
- Meyer-Hofmeister, E. 1972, A&A, 16, 282
In the text
NASA ADS
- Meynet, G., & Maeder, A. 1997, A&A, 321, 465 (MM)
In the text
NASA ADS
- Pinsonneault, M. H., Kawaler, S. D., Sofia, S.,
& Demarque, P. 1989, ApJ, 338, 424
In the text
NASA ADS
- Pinsonneault, M. H., Kawaler, S. D., Sofia, S.,
& Demarque, P. 1990, ApJS, 74, 501
In the text
NASA ADS
- Sills, A., Pinsonneault, M. H., & Terndrup, D. M. 2000, ApJ,
534, 335
In the text
NASA ADS
- Venn, K. A. 1995a, ApJ, 449, 839
In the text
NASA ADS
- Venn, K. A. 1995b, ApJS, 99, 659
NASA ADS
- Venn, K. A., Lambert, D. L., & Lemke, M. 1996, A&A, 307, 849
In the text
NASA ADS
- Walborn, N. R. 1976, ApJ, 205, 419
In the text
NASA ADS
Copyright ESO 2002
![]() are
constant on a equipotential surface. Meynet & Maeder
(1997) (subsequently referred to as MM) argue that not a
conservative rotation case but a "shellular rotation'' case,
i.e., the angular velocity is constant on an isobar (an isobar is a
constant pressure surface) is the real rotation case in an evolved
star. In a "shellular rotation'' case, they find a
are
constant on a equipotential surface. Meynet & Maeder
(1997) (subsequently referred to as MM) argue that not a
conservative rotation case but a "shellular rotation'' case,
i.e., the angular velocity is constant on an isobar (an isobar is a
constant pressure surface) is the real rotation case in an evolved
star. In a "shellular rotation'' case, they find a
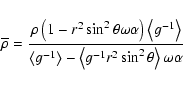
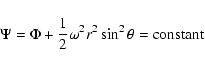
![]() surfaces, the constant
surfaces, the constant ![]() surfaces, the constant
surfaces, the constant ![]() surfaces, the constant Tsurfaces, and the isobars do not correspond to each other if no
special assumption about the distribution of angular velocity is
made. However, some parameters
surfaces, the constant Tsurfaces, and the isobars do not correspond to each other if no
special assumption about the distribution of angular velocity is
made. However, some parameters ![]() ,
,
![]() ,
,
![]() and
and
![]() can always be found to make
can always be found to make
![]() ,
,
![]() ,
,
![]() and
and
![]() constant on an isobar, furthermore, if
constant on an isobar, furthermore, if
![]() and
and ![]() denote the value of density and temperature
of a point P (
denote the value of density and temperature
of a point P (
![]() on an isobar,
on an isobar,
![]() and
and
![]() denote the properties of density and temperature on the
whole isobar, different values of
denote the properties of density and temperature on the
whole isobar, different values of
![]() and
and
![]() will be given for
different points P. Thus, the problem can be kept one
dimensional, if the structural equations are written on isobars.
will be given for
different points P. Thus, the problem can be kept one
dimensional, if the structural equations are written on isobars.
![]() ,
,
![]() ,
,
![]() and
and ![]() ,
indicating the relationship between the constant
,
indicating the relationship between the constant
![]() ,
,
![]() ,
,
![]() ,
T surfaces and the isobars, accordingly, are
not independent of one another. Once
,
T surfaces and the isobars, accordingly, are
not independent of one another. Once ![]() ,
the distribution
of angular velocity, is decided, the other three parameters are
decided, too. Consequently, there is only one independent
parameter need to be determined by advanced theories or by
comparing the results of evolution model with the observational
data. The relationships of
,
the distribution
of angular velocity, is decided, the other three parameters are
decided, too. Consequently, there is only one independent
parameter need to be determined by advanced theories or by
comparing the results of evolution model with the observational
data. The relationships of ![]() and
and ![]() with
with ![]() will be shown in the Appendix and how these parameters are decided
in the "shellular rotation'' case will be shown in Sect. 3.
will be shown in the Appendix and how these parameters are decided
in the "shellular rotation'' case will be shown in Sect. 3.
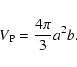
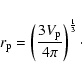
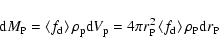
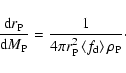
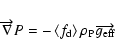
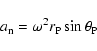
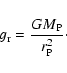
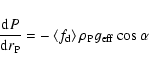
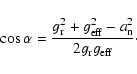
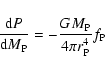
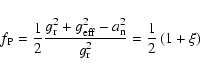
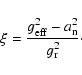
![]() is equal to
is equal to
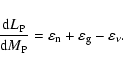
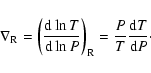
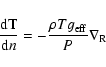
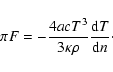
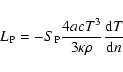
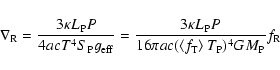
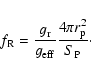
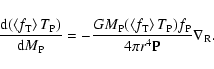
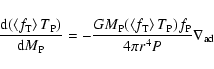
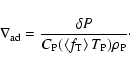
![]() and
and ![]() ,
defined by (15) and (24), which are related to the characteristic of rotation, should be calculated on the isobar.
,
defined by (15) and (24), which are related to the characteristic of rotation, should be calculated on the isobar.
![]() and the angular velocity
and the angular velocity ![]() are given,the volume
are given,the volume ![]() inside the isobaric surface can be
written from (4) as
inside the isobaric surface can be
written from (4) as
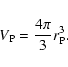
![\begin{displaymath}f_{\Psi a}\left[\frac{GM_{\rm p}}a+\frac 12(f_{\omega a}\omega )^2a^2\right]=f_{\Psi b}\left(\frac{GM_{\rm p}}b\right)
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img72.gif)
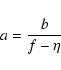
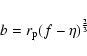
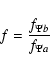
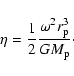
![\begin{displaymath}f_{\Psi}\left[\frac{GM_{\rm p}}{r_{\rm p}}+\frac 12(f_\omega ...
...heta
_{\rm p}\right]=f_{\Psi b}\left(\frac{GM_{\rm p}}b\right)
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img78.gif)
![]() can be calculated by using (15) when the values of
can be calculated by using (15) when the values of ![]()
![]() and
and
![]() are known.
are known.
![]() can be calculated by using (24) when the surface
area
can be calculated by using (24) when the surface
area ![]() of the isobar is given by
of the isobar is given by
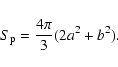
![]() ,
the pressure P and
the temperature T and a
,
the pressure P and
the temperature T and a
![]() are constant on
isobars. Therefore, in the new method,
are constant on
isobars. Therefore, in the new method,
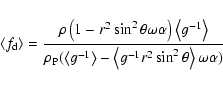
![\begin{figure}
\par\includegraphics[angle=270,width=11.2cm,clip]{27462.ps}\end{figure}](/articles/aa/full/2002/42/aa2746/Timg88.gif)
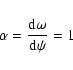
![]() has been introduced in the
new method; to determine its value is another complicated task.
This and other improvements, such as including the mixing of
chemical species and angular momentum by circulation currents and
turbulent, will be presented in the future.
has been introduced in the
new method; to determine its value is another complicated task.
This and other improvements, such as including the mixing of
chemical species and angular momentum by circulation currents and
turbulent, will be presented in the future.
![$\displaystyle -\rho \left[\frac{\overrightarrow{\nabla }\Psi
_{\rm P}}{\overrig...
...w{\nabla }
(f_\omega \omega )}\overrightarrow{\nabla }(f_\omega \omega )\right]$](/articles/aa/full/2002/42/aa2746/img107.gif)
![\begin{displaymath}g=\left[ \frac 1{\left\langle f_\Psi \right\rangle }-r^2\sin
...
...rangle
}\right] \frac{{\rm d}(f_\Psi \Psi _{\rm P})}{{\rm d}n}
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img111.gif)
![\begin{displaymath}g=\left[\frac \beta {\left\langle f_\Psi \right\rangle }-r^2\...
...ight\rangle
}\right]\frac{{\rm d}(f_\omega \omega )}{{\rm d}n}
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img113.gif)
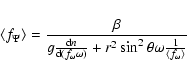
![\begin{displaymath}\frac{{\rm d}P}{{\rm d}n}=-\rho \left[ \frac 1{\left\langle f...
...rangle }\right] \frac{{\rm d}(f_\Psi \Psi
_{\rm P})}{{\rm d}n}
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img117.gif)
![\begin{displaymath}\frac{{\rm d}P}{{\rm d}(f_\Psi \Psi _{\rm P})}=-\rho \left[ \...
...lpha \frac
1{\left\langle f_\omega \right\rangle }\right]\cdot
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img118.gif)
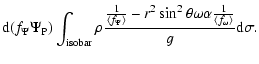
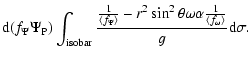
![\begin{displaymath}\frac{{\rm d}(f_\Psi \Psi _{\rm P})}{{\rm d}M_{\rm P}}=\frac ...
...ht\rangle }\right]
\left\langle g^{-1}\right\rangle S_{\rm P}}
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img128.gif)
![\begin{displaymath}\frac{{\rm d}V_{\rm P}}{{\rm d}(f_\Psi \Psi _{\rm P})}=\left[...
...\alpha{\left\langle f_\omega \right\rangle }\right] S_{\rm P}.
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img129.gif)
![\begin{displaymath}\overline{\rho }=\frac{\rho \left[ \frac 1{\left\langle f_\Ps...
...le \frac
\alpha{\left\langle f_\omega \right\rangle }\right] }
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img130.gif)
![\begin{displaymath}\left\langle f_{\rm d}\right\rangle =\frac{\rho \left[ \frac
...
...rac
\alpha{\left\langle f_\omega \right\rangle }\right] }\cdot
\end{displaymath}](/articles/aa/full/2002/42/aa2746/img131.gif)