A&A 394, 1023-1037 (2002)
DOI: 10.1051/0004-6361:20021221
A statistical analysis of the magnetic structure of CP stars
S. Bagnulo 1 -
M. Landi Degl'Innocenti 2 -
M. Landolfi 3 -
G. Mathys 1
1 - European Southern Observatory,
Alonso de Cordova 3107, Vitacura,
Santiago, Chile
2 -
C.N.R., Istituto di Radioastronomia,
Sezione di Firenze,
Largo E. Fermi 5,
50125 Firenze, Italy
3 -
Istituto Nazionale di Astrofisica,
Osservatorio Astrofisico di Arcetri,
Largo E. Fermi 5,
50125 Firenze, Italy
Received 16 May 2002 / Accepted 6 August 2002
Abstract
We present the results of a statistical study of the magnetic structure of
upper main sequence chemically peculiar stars. We have modelled a sample
of 34 stars, assuming that the magnetic morphology is described by the
superposition of a dipole and a quadrupole field, arbitrarily oriented.
In order to interpret the modelling results, we have introduced a novel set
of angles that provides one with a convenient way to represent the mutual
orientation of the quadrupolar component, the dipolar component, and the
rotation axis. Some of our results are similar to what has already been
found in previous studies, e.g., that the inclination
of the dipole axis to the rotation axis is usually large for short-period stars
and small for long-period ones - see Landstreet & Mathys (2000). We also found
that for short-period stars (approximately
 )
the plane
containing the two unit vectors that characterise the quadrupole is almost
coincident with the plane containing the stellar rotation axis and the dipole
axis. Long-period stars seem to be preferentially characterised by a
quadrupole orientation such that the planes just mentioned are perpendicular.
There is also some loose indication of a continuous transition between the two
classes of stars with increasing rotational period.
)
the plane
containing the two unit vectors that characterise the quadrupole is almost
coincident with the plane containing the stellar rotation axis and the dipole
axis. Long-period stars seem to be preferentially characterised by a
quadrupole orientation such that the planes just mentioned are perpendicular.
There is also some loose indication of a continuous transition between the two
classes of stars with increasing rotational period.
Key words: stars: magnetic fields - polarization - stars: chemically peculiar
1 Introduction
Magnetic chemically peculiar (CP) stars of the upper main sequence represent
an astrophysical laboratory for the study of the interplay between magnetic
field and the stellar photospheric plasma.
The magnetic field of CP stars is relatively strong (up to a few tens of kG)
and is characterised by a smooth geometry, thus it can be easily detected via
spectropolarimetric techniques. At the same time, magnetic CP stars are not rare
objects (they represent about 10% of all A and B stars), which makes it
possible to observe how magnetic fields affect the stellar photospheres
in many different situations (i.e., in stars of different age, mass,
temperature, etc.). It appears for instance that magnetic fields tend to be
stronger in hotter than in cooler stars (Landstreet 1992; Mathys et al. 1997; Hubrig et al. 2000).
The presence of a magnetic field is generally associated with a non-homogeneous
distribution of the chemical elements (both horizontally and vertically),
and long rotational periods (up to several decades). Studying these phenomena,
in particular the way various stellar features correlate with the magnetic field,
may permit us to improve our knowledge of stellar astrophysics in general,
as it is reasonable to hypothesise that those phenomena that are so pronounced
(thus so well observed) in magnetic CP stars play also some role in "normal''
upper main sequence stars.
As a matter of fact, most of the physics that we could learn from the
study of CP stars is not yet understood. One of the fundamental issues that
still needs to be clarified is the origin of the magnetic field.
Hints to the solution of this problem could come from more statistical information
on the magnetic field geometries. In particular it would be important to know if
there exist "typical'' magnetic structures, and if there are relationships
between magnetic fields and rotational velocity. There is an obvious need for
constraints from observations and constraints obtained from secure modelling
results.
Some important steps have been accomplished in the last few years, and
information about the magnetic strength of CP stars has been derived from simple
attempts to correlate magnetic field measurements with various stellar features.
For sharp-lined stars, Mathys et al. (1997) found that the mean field
modulus, averaged through the rotational cycle, is typically in the
interval between 3 and 9 kG, and that the 3 kG lower end represents in fact a
sharp cutoff of the distribution. (However, it should be noted that, for
mean field modulus values less than 1.5-2 kG, Zeeman splitting is typically smaller
than the intrinsic line width, so that the mean field modulus cannot be measured.
Therefore, it is more appropriate to say that the evidence found by Mathys et al. 1997 is for a shortage of sharp-lined stars with mean field modulus between
about 1.5 and 3 kG.)
Mathys et al. (1997) also discovered that the mean field modulus of stars
with rotation period longer than 150 d is never stronger than 7.5 kG, which
suggests a sort of anti-correlation between star's rotation period and mean field
modulus. Finally, one of the most important findings about the magnetic structure
of chemically peculiar stars was recently obtained from a simple modelling of the
mean longitudinal field and the mean field modulus. Assuming an axisymmetric model
described by the superposition of a dipole plus colinear quadrupole and octupole,
Landstreet & Mathys (2000) found that slow rotating CP stars (i.e., stars with
rotational period longer than one month) have a magnetic axis tilted at a small
angle (
 )
with respect to the rotation axis. It is clear that these
kinds of information are extremely valuable in order to explain the
formation of the magnetic field (see Moss 2001), and also to understand all
those phenomena that are most likely connected to the presence of a magnetic
field, such as, e.g., the loss of angular momentum (Stepien &
Landstreet 2002).
)
with respect to the rotation axis. It is clear that these
kinds of information are extremely valuable in order to explain the
formation of the magnetic field (see Moss 2001), and also to understand all
those phenomena that are most likely connected to the presence of a magnetic
field, such as, e.g., the loss of angular momentum (Stepien &
Landstreet 2002).
In the past, it has been commonly assumed that magnetic fields of CP stars
have a quasi-dipolar morphology that can be described in terms of a
low-order and axisymmetric multipolar expansion. This assumption was based
on the fact that in several cases an axisymmetric morphology was indeed found
sufficient to interpret the available observations - mainly represented
by determinations of mean longitudinal field. Recent developments of the observing
techniques (including spectropolarimetry of all Stokes profiles, see
Wade et al. 2000a), followed by attempts to interpret
the newly obtained data, point to
evidence for ubiquitous departures of the magnetic structures from axisymmetric
geometries (e.g., Mathys
et al. 1997; Bagnulo et al. 1999, hereafter Paper II; Bagnulo et al. 2001).
From the theoretical point of view we note that - should the field be
either a fossil relic or dynamo generated - there is no reason why
stellar magnetic fields should have cylindrical symmetries. In fact, there is no
reason why a fossil field should have an axisymmetric geometry, and it is
theoretically predicted that dynamo generated
fields do develop a non-axisymmetric geometry (Moss 2001).
These considerations prompt for further searches for statistical properties of
the magnetic structures of CP stars by making use of a modelling technique not
limited by simplifying approximations on the magnetic geometry. A fully adequate
modelling technique based on the inversion of Stokes profiles may exist: the Zeeman
Doppler Imaging (ZDI; see Piskunov & Kochukhov 2002). However, only few stars
have been modelled in detail through the inversion of Stokes profiles (e.g.,
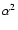 CVn, see Kochukhov et al. 2002). We are lacking sufficient
high quality data (in terms of spectral and phase coverage, spectral resolution
and signal to noise ratio) to be able to perform a
statistically meaningful analysis based on ZDI.
On the other hand, we have at our disposal a large number of magnetic field
observations obtained through measurements of Zeeman splitting and of the
low-order moments of Stokes profiles I and V, such as the aforementioned
mean field modulus and longitudinal field, but also the crossover and the mean
quadratic field. These kinds of data (referred to as "magnetic
observables'' - see, e.g., Bagnulo et al. 2000, hereafter Paper III) can be
obtained from comparatively low-resolution, low signal-to-noise ratio spectra,
even, in certain cases, from spectra recorded with photographic plates, making
it possible to extract information on the stellar magnetic geometry from
observational data that are not suitable for application of straight
inversion techniques.
CVn, see Kochukhov et al. 2002). We are lacking sufficient
high quality data (in terms of spectral and phase coverage, spectral resolution
and signal to noise ratio) to be able to perform a
statistically meaningful analysis based on ZDI.
On the other hand, we have at our disposal a large number of magnetic field
observations obtained through measurements of Zeeman splitting and of the
low-order moments of Stokes profiles I and V, such as the aforementioned
mean field modulus and longitudinal field, but also the crossover and the mean
quadratic field. These kinds of data (referred to as "magnetic
observables'' - see, e.g., Bagnulo et al. 2000, hereafter Paper III) can be
obtained from comparatively low-resolution, low signal-to-noise ratio spectra,
even, in certain cases, from spectra recorded with photographic plates, making
it possible to extract information on the stellar magnetic geometry from
observational data that are not suitable for application of straight
inversion techniques.
In this paper we present a statistical investigation of the magnetic structure
of CP stars based on the interpretation of the magnetic observables, under the
assumption that the stellar magnetic field is described by the superposition of
a dipole and a quadrupole field, arbitrarily oriented. Although it seems unlikely
that such a low-order multipolar expansion can accurately describe the real
magnetic configurations of CP stars (see, e.g., Bagnulo et al. 2001), it is
reasonable to hope that the analysis of a large sample of stars can still provide
us with some insight into the problem of whether there exist statistical
properties of the magnetic structures of CP stars other than those that have been
already found.
A formalism for the description of the magnetic field in terms of dipole plus
quadrupole (arbitrarily oriented) was presented by Bagnulo et al. (1996) and
Landolfi et al. (1998) - hereafter Paper I - and modelling results for
individual stars were
presented, e.g., in Paper II and Bagnulo & Landolfi (1999).
Preliminary statistical results were presented by Bagnulo (2001), who found for
instance that in faster rotating stars, one of the unit vectors
that define the quadrupolar component is generally aligned to the rotation axis.
Then it was realised that a set of new angles could be adopted in
order to obtain
a clearer description of the statistical results, in particular by explicitly
referring to the orientation of the plane defined by the quadrupolar
component with respect to the dipole axis and the rotation axis. Such angles
are introduced
in Sect. 2, which also presents the guidelines for the statistical analysis
performed in Sects. 3 and 4. In Sect. 5 we summarise and briefly
discuss our results.
2 Analysis of observations: Generalities
We tried to interpret the observations of mean longitudinal field,
crossover, mean quadratic field - as defined by Mathys (1995a, 1995b) - and mean
field modulus for a sample of 34 magnetic CP stars in terms of the oblique
rotator model with a dipole plus (non linear) quadrupole field.
For such model, the magnetic field vector at the point 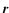 of the
stellar surface is given by (see Paper I)
of the
stellar surface is given by (see Paper I)
where
Here R* is the star's radius;
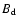 and
and
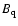 are the dipole and quadrupole amplitude, respectively; the unit vector
are the dipole and quadrupole amplitude, respectively; the unit vector
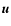 specifies the direction of the dipole axis; the unit vectors
specifies the direction of the dipole axis; the unit vectors
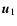 ,
,
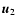 specify the orientation of the quadrupole.
specify the orientation of the quadrupole.
The four magnetic observables are denoted in this paper by the notations
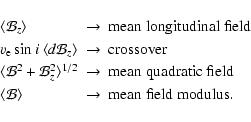 |
(1) |
The expressions relating these quantities to the model parameters were
derived, under certain assumptions on the stellar atmosphere, by Bagnulo
et al. (1996), and rewritten in a more compact form in
Papers I and III, respectively. An inversion procedure for recovering
the model parameters from observations of
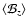 ,
,
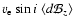 ,
and
,
and
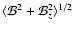 was described extensively in Papers I and II, and subsequently
generalized in Paper III to
include observations of
was described extensively in Papers I and II, and subsequently
generalized in Paper III to
include observations of
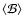 ,
measurements of projected equatorial velocity,
and estimates of the stellar radius. For this work we used the numerical code
described in Paper III, with the only difference that linear polarization
observations, not available for most of the stars in our sample, were disregarded.
,
measurements of projected equatorial velocity,
and estimates of the stellar radius. For this work we used the numerical code
described in Paper III, with the only difference that linear polarization
observations, not available for most of the stars in our sample, were disregarded.
The magnetic geometry of the dipole plus quadrupole model is illustrated
in detail in Paper I. We simply recall that such model depends on the
following 10 parameters:
- -
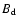 and
and 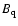 ;
;
- -
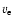 ,
the stellar equatorial velocity;
,
the stellar equatorial velocity;
- -
- i, the inclination of the stellar rotation axis to the line
of sight;
- -
 ,
the angle between the direction
,
the angle between the direction 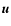 and
the rotation axis;
and
the rotation axis;
- -
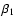 and
and  ,
the analogues of
,
the analogues of  for the
directions
for the
directions 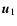 ,
,
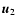 ;
;
- -
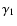 and
and 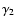 ,
the azimuthal angles of
,
the azimuthal angles of 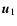 ,
,
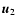 about the rotation axis;
about the rotation axis;
- -
- f0, the "reference'' rotational phase of the model (see
Fig. 1 of Paper I).
The angles i,  ,
,
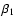 ,
,
 range from
range from
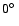 to
to
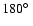 ,
while
,
while 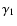 ,
,
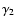 ,
f0 range from
,
f0 range from
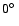 to
to
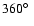 .
The rotational period P and the limb-darkening
constant u, which also affect the expressions of the magnetic quantities,
are taken as fixed. In this work we adopted u=0.5 for all stars, but the
results of the inversion procedure are only slightly influenced by the uvalue, as discussed in Papers I-III.
.
The rotational period P and the limb-darkening
constant u, which also affect the expressions of the magnetic quantities,
are taken as fixed. In this work we adopted u=0.5 for all stars, but the
results of the inversion procedure are only slightly influenced by the uvalue, as discussed in Papers I-III.
As explained in Paper III, observations of
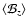 ,
,
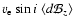 ,
,
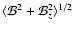 ,
and
,
and
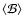 ,
do not allow one to distinguish between two magnetic
configurations symmetrical about the plane containing the rotation axis and
the dipole axis. Such configurations are characterised by the same values of
,
do not allow one to distinguish between two magnetic
configurations symmetrical about the plane containing the rotation axis and
the dipole axis. Such configurations are characterised by the same values of
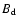 ,
,
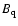 ,
,
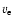 ,
,
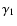 ,
,
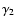 ,
f0, while the remaining angles are related by
,
f0, while the remaining angles are related by
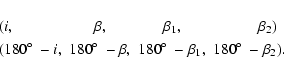 |
(2) |
On the other hand, as shown in Paper I, exchange of directions 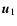 and
and 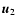 ,
as well as inversion of both
(
,
as well as inversion of both
(
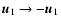 ,
,
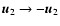 ),
leaves the magnetic configuration unchanged. This means that the sets
),
leaves the magnetic configuration unchanged. This means that the sets
![\begin{displaymath}\begin{array}{lcccr}
&(\beta_1,&\beta_2,&\gamma_1,&\gamma_2) \\ [0.1cm]
&(\beta_2,&\beta_1,&\gamma_2,&\gamma_1)
\end{array}\end{displaymath}](/articles/aa/full/2002/42/aa2699/img63.gif) |
(3) |
and
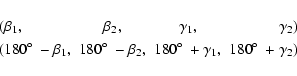 |
(4) |
describe the same magnetic configuration.
Table 1:
The star' sample analysed in this work. A dash in columns
 (an abbreviation for
(an abbreviation for
 ),
),
 (an abbreviation for
(an abbreviation for
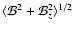 ),
),
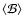 ,
and
,
and
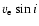 ,
means that no observation was available.
The last three columns show the value of the reduced
,
means that no observation was available.
The last three columns show the value of the reduced  corresponding to the best-fit model, as derived from 3 different
types of data analysis, i.e.,
considering all observed quantities (Col. g),
considering all observed quantities but
corresponding to the best-fit model, as derived from 3 different
types of data analysis, i.e.,
considering all observed quantities (Col. g),
considering all observed quantities but
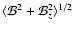 (Col. p1), and
considering all observed quantities but
(Col. p1), and
considering all observed quantities but
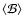 (Col. p2). A blank
in columns p1 and p2 means that the star does not pertain to the
sub-sample (see Sect. 4).
(Col. p2). A blank
in columns p1 and p2 means that the star does not pertain to the
sub-sample (see Sect. 4).
| No. |
HD |
Other Identifier |
P |
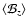 |
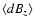 |
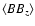 |
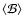 |
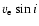 |
R* |
 |
g |
p1 |
p2 |
|
1 |
2453 |
GR And |
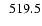 |
33 |
 6 6 |
 6 6 |
14 |
- |
2.97 |
|
2.08 |
2.25 |
1.57 |
| 2 |
12288 |
V540 Cas |
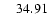 |
20 |
- |
- |
28 |
- |
3.28 |
|
1.75 |
1.75 |
|
| 3 |
14437 |
AG+42 247 |
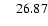 |
36 |
- |
- |
31 |
- |
3.08 |
|
1.96 |
1.96 |
|
| 4 |
24712 |
DO Eri |
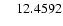 |
82 |
 7 7 |
 5 5 |
- |
 5.6 5.6 |
1.83 |
|
3.56 |
|
3.56 |
| 5 |
51684 |
CD-40 2796 |
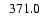 |
 7 7 |
 4 4 |
 7 7 |
10 |
- |
3.58 |
|
0.93 |
0.59 |
0.68 |
| 6 |
61468 |
CD-27 4341 |
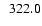 |
 5 5 |
 5 5 |
 5 5 |
15 |
- |
4.16 |
|
>8 |
6.29 |
1.57 |
| 7 |
65339 |
53 Cam |
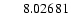 |
66 |
 6 6 |
- |
36 |
13.0 |
2.56 |
|
4.21 |
4.21 |
|
| 8 |
70331 |
CD-47 3803 |
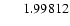 |
16 |
16 |
16 |
38 |
- |
- |
|
1.46 |
1.58 |
1.34 |
| 9 |
75445 |
CD-38 4907 |
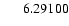 |
 3 3 |
 3 3 |
 3 3 |
11 |
- |
2.34 |
|
1.54 |
0.87 |
|
| 10 |
81009 |
KU Hya |
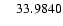 |
13 |
13 |
13 |
42 |
- |
2.61 |
|
1.95 |
1.32 |
1.38 |
| 11 |
83368 |
HR 3831 |
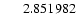 |
12 |
12 |
11 |
- |
32.6 |
2.23 |
|
2.08 |
|
2.08 |
| 12 |
93507 |
CD-67 955 |
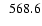 |
12 |
12 |
12 |
30 |
- |
3.73 |
|
3.70 |
1.59 |
2.03 |
| 13 |
94660 |
KQ Vel |
2764.0 |
12 |
12 |
12 |
25 |
- |
3.15 |
|
>8 |
1.60 |
1.39 |
| 14 |
96446 |
CD-59 3544 |
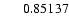 |
 9 9 |
 9 9 |
 9 9 |
- |
10.0 |
6.43 |
|
2.98 |
|
2.98 |
| 15 |
116114 |
BD-17 3829 |
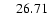 |
 7 7 |
 7 7 |
 7 7 |
24 |
- |
3.06 |
|
1.72 |
1.46 |
2.24 |
| 16 |
116458 |
HR 5049 |
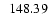 |
20 |
20 |
20 |
21 |
- |
3.54 |
|
2.42 |
1.89 |
2.01 |
| 17 |
119419 |
HR 5158 |
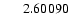 |
22 |
22 |
22 |
- |
34.8 |
2.23 |
|
1.71 |
|
1.71 |
| 18 |
125248 |
CS Vir |
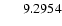 |
31 |
21 |
21 |
- |
 8.0 8.0 |
1.97 |
|
1.85 |
|
1.85 |
| 19 |
126515 |
Preston's star |
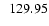 |
25 |
19 |
19 |
22 |
- |
2.35 |
|
4.56 |
2.99 |
4.35 |
| 20 |
137509 |
NN Aps |
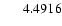 |
14 |
14 |
14 |
- |
28.1 |
3.59 |
|
1.20 |
|
1.20 |
| 21 |
137909 |
 CrB
CrB |
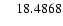 |
51 |
21 |
21 |
46 |
 3.5 3.5 |
3.25 |
|
2.09 |
2.15 |
2.45 |
| 22 |
142070 |
AG-00 2049 |
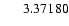 |
13 |
13 |
13 |
24 |
13.5 |
5.42 |
|
>8 |
3.19 |
2.72 |
| 23 |
144897 |
CD-40 10236 |
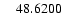 |
13 |
13 |
13 |
28 |
- |
3.97 |
|
2.53 |
1.70 |
1.93 |
| 24 |
147010 |
V933 Sco |
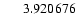 |
19 |
19 |
19 |
- |
22.1 |
2.85 |
|
1.68 |
|
1.68 |
| 25 |
153882 |
HR 6326 |
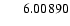 |
17 |
17 |
17 |
- |
21.0 |
3.81 |
|
2.17 |
|
2.17 |
| 26 |
175362 |
V686 CrA |
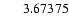 |
30 |
30 |
29 |
- |
15.0 |
2.68 |
|
3.97 |
|
3.97 |
| 27 |
187474 |
V3961 Sgr |
2364.0 |
20 |
20 |
20 |
40 |
- |
2.93 |
|
3.82 |
3.59 |
3.36 |
| 28 |
188041 |
V1291 Aql |
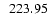 |
77 |
 8 8 |
- |
18 |
- |
3.14 |
|
1.41 |
1.41 |
|
| 29 |
192678 |
V1372 Cyg |
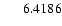 |
14 |
- |
- |
34 |
- |
3.05 |
|
2.17 |
2.17 |
|
| 30 |
200311 |
V2200 Cyg |
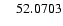 |
24 |
- |
- |
35 |
 9.0 9.0 |
2.18 |
|
2.37 |
2.37 |
|
| 31 |
208217 |
BD Ind |
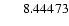 |
 8 8 |
 8 8 |
 8 8 |
38 |
15.3 |
2.60 |
|
1.58 |
1.73 |
1.64 |
| 32 |
215441 |
Babcock's star |
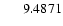 |
14 |
- |
- |
11 |
 5.0 5.0 |
2.45 |
|
2.51 |
2.51 |
|
| 33 |
318107 |
V970 Sco |
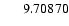 |
 6 6 |
 6 6 |
 6 6 |
36 |
- |
2.46 |
|
3.37 |
2.15 |
3.55 |
| 34 |
335238 |
AG+29 2421 |
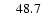 |
 3 3 |
 3 3 |
 3 3 |
18 |
- |
3.69 |
|
1.52 |
1.15 |
|
A convenient way to visualise the quadrupole orientation is to introduce
the plane containing the unit vectors 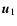 ,
,
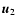 and its pole Q,
defined by
and its pole Q,
defined by
if
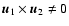 ,
undefined otherwise (see Fig. 1).
The point Q is characterised by the angles
,
undefined otherwise (see Fig. 1).
The point Q is characterised by the angles
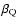 and
and
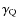 ,
while the orientation of
,
while the orientation of 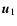 ,
,
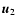 in their
plane is characterised by the angles
in their
plane is characterised by the angles 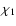 and
and 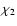 reckoned from the
"reference'' semi-meridian (through R and D), or, equivalently, by their
linear combinations
reckoned from the
"reference'' semi-meridian (through R and D), or, equivalently, by their
linear combinations 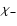 and
and 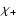 defined by
defined by
which represent the "width'' and "barycentre'' of the unit vectors
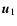 ,
,
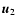 ,
respectively. In the following we will refer to
the angles
,
respectively. In the following we will refer to
the angles
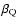 ,
,
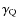 ,
,
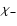 ,
,
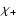 rather than to
rather than to 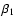 ,
,
 ,
,
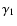 ,
,
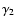 .
.
 |
Figure 1:
Geometry of the dipole plus quadrupole model. The rotation axis
intersects the stellar surface at R, and makes an angle i (not
shown in the figure) with the line of sight. D is the positive pole
of the dipole. Q is the pole of the quadrupole plane defined by the
unit vectors 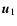 and
and 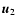 . . |
| Open with DEXTER |
The stars of our sample are listed in Table 1. The columns contain
the following data (from left to right): a reference number used in this paper;
the HD number of the object; a second identifier for the star;
the stellar rotational period in days; the
number of observations used in this work for each of the four magnetic
observables; the observational value of the projected equatorial velocity;
the estimated value of the stellar radius. The meaning of the last three
columns (labelled with g, p1, and p2) will be explained later.
Most magnetic field measurements were taken from
Mathys (1994) (mean longitudinal field),
Mathys (1995a) (crossover),
Mathys (1995b) (mean quadratic field, but the determinations were revised
as explained in Mathys et al., in preparation),
Mathys & Hubrig (1997) (longitudinal field, crossover, quadratic field),
Mathys et al. (1997) (mean field modulus).
We also considered additional measurements, to be published by Mathys et al. (in preparation), most of which were already used
by Landstreet & Mathys (2000).
Additional mean longitudinal field data were taken from
Bagnulo et al. (2001),
Borra & Landstreet (1977, 1978),
Hildebrandt et al. (1997),
Hill et al. (1998), Leone et al. (2000),
Leone & Catanzaro (2001),
Preston & Stepien (1968),
Wade et al. (1996, 1997, 2000a, 2000b, 2000c).
Further mean field modulus data were taken from Huchra (1972), and Preston (1969).
The adopted value of the rotational period and estimates of the projected equatorial
velocity come mainly from the same references as for the magnetic data.
However, in many cases, the rotational period was re-computed through a least-square
technique based on a second-order Fourier expansion to the longitudinal field and
mean field modulus measurements.
Estimates for the stellar radius R* were taken from North (1998) and Hubrig et al. (2000). Additional R* estimates were kindly provided to us by North (2001,
private communication).
The aim of this study is not so much to find the "best'' magnetic model for
each individual star as to characterise the sample as a whole in order to
see whether there are any "preferred'' magnetic geometries (in the framework
of the assumed dipole plus quadrupole model) and/or correlations between
magnetic model and the rotational period.
The main difficulty underlying an analysis of this kind is due to the fact that
the inversion algorithm usually produces, for a given star, several
different models, i.e., several sets of parameters, corresponding to local
minima of the  hypersurface. As discussed in Papers I, II, and III,
this is primarily due to the relatively large observational errors. For some
stars the
hypersurface. As discussed in Papers I, II, and III,
this is primarily due to the relatively large observational errors. For some
stars the  values at the various minima are very different from each
other, but in other cases these values are not so different. Therefore, it looks
rather unsafe to restrict the statistical analysis to best-fit models (i.e.,
those corresponding to the absolute
values at the various minima are very different from each
other, but in other cases these values are not so different. Therefore, it looks
rather unsafe to restrict the statistical analysis to best-fit models (i.e.,
those corresponding to the absolute  minimum). Furthermore, even if
this restriction were applied, the magnetic models of the individual stars
could not be considered equally reliable, being characterised by different
minimum). Furthermore, even if
this restriction were applied, the magnetic models of the individual stars
could not be considered equally reliable, being characterised by different
 values.
values.
The most natural way to deal with these problems is to "weight'' the
parameter sets associated with the  minima. In this work we
introduced a weight
minima. In this work we
introduced a weight 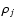 for each star, defined by
for each star, defined by
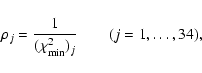 |
(5) |
where
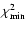 is the value of the reduced
is the value of the reduced  corresponding to the absolute minimum, and a weight
corresponding to the absolute minimum, and a weight 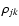 for the
kth parameter set, defined by
for the
kth parameter set, defined by
![\begin{displaymath}\rho_{jk}=\frac{c_j}{[(\chi^2_{jk})]^p}\qquad(k=1,\ldots,m(j)),
\end{displaymath}](/articles/aa/full/2002/42/aa2699/img111.gif) |
(6) |
where m(j) is the "multiplicity'' of the jth star, i.e., the number of
minima in the  hypersurface. The quantity cj is determined by
requiring that
hypersurface. The quantity cj is determined by
requiring that
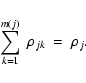 |
(7) |
The figures presented in the following were obtained for p=2, but the
value p=1 leads to quite similar results.
An additional difficulty concerns the type of observations to be used for
the modelling. In particular, as noticed already in previous works (e.g.,
Paper III; Landstreet & Mathys 2000), for many stars,
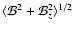 and
and
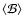 measurements are not consistent among themselves. For this reason we performed
separate investigations, by using all observations together (Sect. 3),
and by disregarding either
measurements are not consistent among themselves. For this reason we performed
separate investigations, by using all observations together (Sect. 3),
and by disregarding either
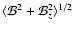 or
or
 observations (Sect. 4).
The former kind of analysis, i.e., based on all observations together,
has the obvious advantage that all the information available for a given star
is used in the modelling; moreover, all the 34 stars listed in Table 1
can be considered. The latter kind of analysis may help to reveal if some results
are likely biased by systematic measurement errors.
observations (Sect. 4).
The former kind of analysis, i.e., based on all observations together,
has the obvious advantage that all the information available for a given star
is used in the modelling; moreover, all the 34 stars listed in Table 1
can be considered. The latter kind of analysis may help to reveal if some results
are likely biased by systematic measurement errors.
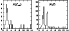 |
Figure 2:
Left: distribution of the minimum  values for the magnetic
models of the 34 stars of the sample (see Col. g of
Table 1). Right: same for the models corresponding to
all (absolute and relative)
values for the magnetic
models of the 34 stars of the sample (see Col. g of
Table 1). Right: same for the models corresponding to
all (absolute and relative)  minima. Further
absolute and relative minima with larger minima. Further
absolute and relative minima with larger  values are not
shown in the figure. See text for details.
values are not
shown in the figure. See text for details. |
| Open with DEXTER |
3 Analysis based on 4 magnetic observables
In this section we present the results of the "global'' analysis, i.e.,
based on all the observations![[*]](/icons/foot_motif.gif) . Column gof Table 1 shows the value of the reduced
. Column gof Table 1 shows the value of the reduced  corresponding
to the best fit - absolute minimum of the
corresponding
to the best fit - absolute minimum of the  hypersurface.
The same data is plotted, in the form of a histogram, in Fig. 2
(left). One can see that most of the best fits are characterised by
hypersurface.
The same data is plotted, in the form of a histogram, in Fig. 2
(left). One can see that most of the best fits are characterised by
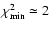 ,
with a secondary group at
,
with a secondary group at
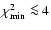 .
However, for three stars - HD 61468, HD 94660, and
HD 142070 - no reasonable fit was found. This may be ascribed to
inconsistencies between
.
However, for three stars - HD 61468, HD 94660, and
HD 142070 - no reasonable fit was found. This may be ascribed to
inconsistencies between
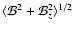 and
and
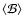 observations: in fact, if either
of them is neglected, the
observations: in fact, if either
of them is neglected, the  value decreases considerably
(see Cols. p1 and p2 of Table 1). However, we suspect that the magnetic
morphology may be rather more complex than a dipole plus quadrupole field, especially
in the case of HD 142070, which exhibits a strongly anharmonic mean field modulus
curve. Those three stars were excluded from the analysis described in this section.
value decreases considerably
(see Cols. p1 and p2 of Table 1). However, we suspect that the magnetic
morphology may be rather more complex than a dipole plus quadrupole field, especially
in the case of HD 142070, which exhibits a strongly anharmonic mean field modulus
curve. Those three stars were excluded from the analysis described in this section.
Figure 2 (right) shows the distribution of the reduced  values for all the fits (corresponding either to the absolute minimum
or to relative minima of the
values for all the fits (corresponding either to the absolute minimum
or to relative minima of the  hypersurface). Altogether there are
168 minima, 12 of which with
hypersurface). Altogether there are
168 minima, 12 of which with 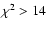 .
The relevant distribution is quite
similar to that of the left panel, with a main group around
.
The relevant distribution is quite
similar to that of the left panel, with a main group around 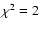 and
a secondary group at
and
a secondary group at
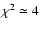 ;
for larger values, the number of
minima decreases rapidly. We decided to confine our study to models with
;
for larger values, the number of
minima decreases rapidly. We decided to confine our study to models with
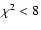 :
this leads to 147 models, associated with the 31 stars of the
sample.
:
this leads to 147 models, associated with the 31 stars of the
sample.
Consider first the magnetic field strength. Figure 3 (left) shows
the distribution of the dipole amplitude, 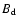 .
It is a rather
regular, bell-shaped distribution peaking at something less than 10 kG; most
models are characterised by
.
It is a rather
regular, bell-shaped distribution peaking at something less than 10 kG; most
models are characterised by 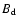 values ranging from 3 kG to 20 kG.
We recall that the histogram represents the
values ranging from 3 kG to 20 kG.
We recall that the histogram represents the 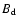 distribution
weighted according to Eqs. (5)-(7): explicitly, the height of
the histogram in the ith interval is
distribution
weighted according to Eqs. (5)-(7): explicitly, the height of
the histogram in the ith interval is
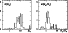 |
Figure 3:
Left: distribution of the dipole field amplitude. 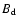 is expressed in kG. The isolated tooth on the far right is
associated with Babcock's star (HD 215441,
is expressed in kG. The isolated tooth on the far right is
associated with Babcock's star (HD 215441,
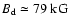 ). Right: distribution of the
ratio of quadrupole to dipole field amplitude. ). Right: distribution of the
ratio of quadrupole to dipole field amplitude. |
| Open with DEXTER |
where
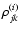 is given by Eq. (6) if the
is given by Eq. (6) if the  value
of the kth model of the jth star falls in the ith interval, and is
zero otherwise. The right panel of Fig. 3 shows the distribution of
the ratio between quadrupole and dipole amplitude. It appears that the
quadrupolar contribution is generally important, with
value
of the kth model of the jth star falls in the ith interval, and is
zero otherwise. The right panel of Fig. 3 shows the distribution of
the ratio between quadrupole and dipole amplitude. It appears that the
quadrupolar contribution is generally important, with  values varying approximately between 1/3 and 10 times the
values varying approximately between 1/3 and 10 times the  value.
Finally, Fig. 4 shows the distribution of the phase-averaged mean
field modulus,
value.
Finally, Fig. 4 shows the distribution of the phase-averaged mean
field modulus,
![\begin{figure}
\par\includegraphics[width=4cm,clip]{fig4.ps} \end{figure}](/articles/aa/full/2002/42/aa2699/Timg126.gif) |
Figure 4:
Distribution of the phase-averaged mean field modulus
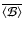 (expressed in kG). The tooth on the
right is Babcock's star. (expressed in kG). The tooth on the
right is Babcock's star. |
| Open with DEXTER |
which quantifies the typical field strength for the stars in the sample.
Contrary to 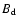 and
and 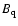 ,
the value of
,
the value of
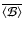 is - as expected - practically the same for
all models of a given star: this explains why the histogram of Fig. 4
is less "scattered'' than those of Fig. 3. Obviously, the quantity
is - as expected - practically the same for
all models of a given star: this explains why the histogram of Fig. 4
is less "scattered'' than those of Fig. 3. Obviously, the quantity
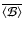 is not (contrary to
is not (contrary to 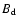 and
and
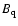 )
intrinsic to the individual star, because it depends on the
inclination of the rotation axis with respect to the line of sight (the angle
i). We will comment further on this figure in Sect. 4.
)
intrinsic to the individual star, because it depends on the
inclination of the rotation axis with respect to the line of sight (the angle
i). We will comment further on this figure in Sect. 4.
Next we consider the distributions of the different angles. These are plotted
in Fig. 5, together with the curves describing the relevant random
distributions (sinusoidal variation for i,  ,
,
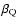 ,
,
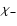 ;
flat distribution for
;
flat distribution for
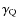 and
and 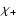 ). It should
be noticed that the apparent symmetry characteristics of several histograms
is just a consequence of the properties in Eqs. (2)-(4). The
distributions of i and
). It should
be noticed that the apparent symmetry characteristics of several histograms
is just a consequence of the properties in Eqs. (2)-(4). The
distributions of i and  are symmetrical about
are symmetrical about
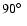 because of
the degeneracy of Eq. (2), the distribution of
because of
the degeneracy of Eq. (2), the distribution of
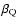 because of Eq. (3); similarly, the distributions of
because of Eq. (3); similarly, the distributions of
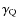 and
and 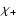 are invariant under a
are invariant under a
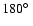 shift owing to Eqs. (2)
and (4), respectively. By contrast, the distribution of
shift owing to Eqs. (2)
and (4), respectively. By contrast, the distribution of 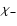 is
unaffected by those properties (no symmetry characteristics).
is
unaffected by those properties (no symmetry characteristics).
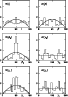 |
Figure 5:
Distributions of the angles specifying the magnetic geometry,
compared with the relevant random distributions. Angles are
expressed in degrees. |
| Open with DEXTER |
It is obvious from Fig. 5 that most distributions, and especially
that of
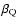 ,
are very different from the relevant random
distributions. In order to quantify such difference, we decided to apply the
Kolmogorov-Smirnov test (see, e.g., Press et al. 1986) to
each distribution. As is well known, the test is based on the measurement of the
maximum distance, D, between the cumulative distribution of the
observational data and the corresponding theoretical distribution. Such
distributions are shown in Fig. 6.
,
are very different from the relevant random
distributions. In order to quantify such difference, we decided to apply the
Kolmogorov-Smirnov test (see, e.g., Press et al. 1986) to
each distribution. As is well known, the test is based on the measurement of the
maximum distance, D, between the cumulative distribution of the
observational data and the corresponding theoretical distribution. Such
distributions are shown in Fig. 6.
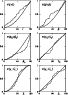 |
Figure 6:
Cumulative distributions of the angles in Fig. 5, and the
corresponding random distributions. |
| Open with DEXTER |
Strictly speaking, the Kolmogorov-Smirnov test in not applicable in our case,
because it presupposes a set of "unweighted'' measurements of the
observational quantity, whereas our determinations are weighted as described in
Sect. 2. For a set of N unweighted (different) measurements, all
the "steps'' of the cumulative distribution are the same (=1/N). The
probability that the distribution of the measurements is consistent with an
assigned theoretical distribution obviously depends both on Dand on N, and, for a given D value, decreases strongly with
increasing N.
In our case, we are forced to introduce an "effective number'' of
measurements,
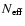 .
The choice
.
The choice
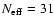 (the number
of stars in the sample) would be correct if we had just one model (with the
same
(the number
of stars in the sample) would be correct if we had just one model (with the
same  value) for each star: as this is not the case, the value
value) for each star: as this is not the case, the value
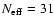 is certainly an underestimate. The choice
is certainly an underestimate. The choice
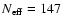 (the overall number of models) would be correct if all
the determinations had the same weight: as many models are characterised by
rather large
(the overall number of models) would be correct if all
the determinations had the same weight: as many models are characterised by
rather large  values (hence, rather small weights),
values (hence, rather small weights),
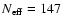 is certainly an overestimate. The most reasonable choice
is something intermediate: for instance, one could take the quadratic mean
of the steps' heights
is certainly an overestimate. The most reasonable choice
is something intermediate: for instance, one could take the quadratic mean
of the steps' heights 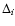 ,
,
![\begin{displaymath}\langle\Delta\rangle=
\biggl[\frac{1}{n}\;\sum_{i=1}^n~\Delta_i^2\biggr]^{1/2},
\end{displaymath}](/articles/aa/full/2002/42/aa2699/img131.gif) |
(8) |
where n is the number of models considered, and set
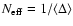 .
.
Table 2 shows the test results for the distributions of the six
angles, according to different choices of
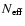 .
It is clear that
all the distributions are non-random, and that the largest discrepancies
concern
.
It is clear that
all the distributions are non-random, and that the largest discrepancies
concern
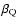 ,
,
 ,
and i.
,
and i.
Table 2:
Results of the Kolmogorov-Smirnov test for each angle and for
different estimates of the number of measurements,
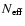 .
The p's are the probabilities (ranging from 0 to 1) that the
observed and random distributions are consistent. p1 corresponds
to
.
The p's are the probabilities (ranging from 0 to 1) that the
observed and random distributions are consistent. p1 corresponds
to
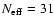 ,
the number of stars in the sample. p2 corresponds to
,
the number of stars in the sample. p2 corresponds to
 for i,
for i,  ,
,
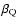 ,
,
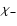 ;
90 for
;
90 for
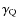 ;
91 for
;
91 for 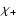 :
these are the nearest-integer approximations to
:
these are the nearest-integer approximations to
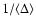 ,
where
,
where
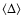 is given by
Eq. (8).
p3 corresponds to
is given by
Eq. (8).
p3 corresponds to
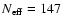 for i,
for i,  ,
,
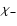 ;
146 for
;
146 for
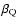 ;
134 for
;
134 for
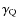 ;
137 for
;
137 for 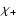 :
these are the numbers
of models considered. The reason why this number is less than 147 for
:
these are the numbers
of models considered. The reason why this number is less than 147 for
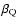 ,
,
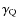 and
and 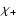 is that
we ruled out those models where either the "reference'' semi-meridian
or the point Q were poorly defined (cf. Fig. 1: very small
is that
we ruled out those models where either the "reference'' semi-meridian
or the point Q were poorly defined (cf. Fig. 1: very small
 ,
,
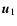 and
and 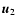 lying almost in the geographic
equator, or nearly parallel to each other).
lying almost in the geographic
equator, or nearly parallel to each other).
| angle |
D |
 |
p1 |
p2 |
p3 |
| i |
0.24 |
|
0.05 |
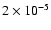 |
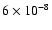 |
 |
0.29 |
|
0.01 |
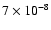 |
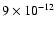 |
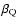 |
0.33 |
|
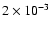 |
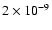 |
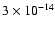 |
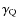 |
0.16 |
|
0.35 |
0.01 |
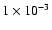 |
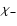 |
0.12 |
|
0.69 |
0.09 |
0.02 |
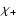 |
0.12 |
|
0.72 |
0.13 |
0.03 |
One might suspect that deviations from the random distribution like those of
Figs. 5 and 6 could be an artifact due to the inversion
algorithm. Because of the large number of parameters and the ensuing
complexity of the  hypersurface, noisy observational data might
generate some unexpected systematic effect. To check this point we performed
extensive numerical simulations, by presenting to the fitting code synthetic
and noisy data for a variety of dipole plus quadrupole, randomly oriented
models. Such calculations showed that non-random distributions like those of
Figs. 5 and 6 can by no means be ascribed to systematic effects
of the inversion code.
hypersurface, noisy observational data might
generate some unexpected systematic effect. To check this point we performed
extensive numerical simulations, by presenting to the fitting code synthetic
and noisy data for a variety of dipole plus quadrupole, randomly oriented
models. Such calculations showed that non-random distributions like those of
Figs. 5 and 6 can by no means be ascribed to systematic effects
of the inversion code.
Let us consider the inclination angle i - the only "non-magnetic'' angle.
Its distribution clearly shows an excess of small values. It should be noticed,
however, that for most of the stars (22 out of 31) the mean field modulus
was actually detected: this means that the sample is certainly
affected by a selection effect which tends to favour small i values, since
positive detections of that quantity require small equatorial velocity,
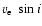 .
In fact, the distribution of i for the 9
remaining stars (Fig. 7 left) is very different from that
in Fig. 5, and much closer to the random distribution: for
.
In fact, the distribution of i for the 9
remaining stars (Fig. 7 left) is very different from that
in Fig. 5, and much closer to the random distribution: for
 ,
14, and 16 (corresponding to the criteria adopted in
Table 2 for p1, p2, and p3, respectively) the probability
p resulting from the Kolmogorov-Smirnov test is 0.91, 0.73, and 0.65,
respectively.
,
14, and 16 (corresponding to the criteria adopted in
Table 2 for p1, p2, and p3, respectively) the probability
p resulting from the Kolmogorov-Smirnov test is 0.91, 0.73, and 0.65,
respectively.
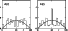 |
Figure 7:
Distribution of the inclination angle i for the 9 stars with no
 observations (left), and for the 10 stars with
rotational period larger than 40 days (right).
observations (left), and for the 10 stars with
rotational period larger than 40 days (right). |
| Open with DEXTER |
Following another approach, we might consider the distribution of i for all
stars with sufficiently small rotational velocity (period P>P0): such sample
should likely be unaffected by selection effects. Setting
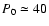 days
- actually, any number of days between 35 and 48 - we get a sub-sample of 10
stars (none of which pertaining to the former 9-star sample) leading to the
distribution of Fig. 7, right. For
days
- actually, any number of days between 35 and 48 - we get a sub-sample of 10
stars (none of which pertaining to the former 9-star sample) leading to the
distribution of Fig. 7, right. For
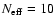 ,
30, and 37,
corresponding to the same criteria as above, we have p=0.82, 0.21, and
0.12, respectively. This probability decreases strongly with decreasing
P0.
,
30, and 37,
corresponding to the same criteria as above, we have p=0.82, 0.21, and
0.12, respectively. This probability decreases strongly with decreasing
P0.
On the whole, the difference from the random distribution looks rather reduced,
though some excess of small i values remains. This is not fully understood.
It could be due either to inadequacy of the dipole plus quadrupole model,
or to a weak, but real intrinsic non-randomness of the star sample, although
it should be noted that this latter phenomenon does not have an obvious physical
justification. We recall that - contrary to axisymmetric models - our magnetic
model involves no degeneracy between the angles i and  ,
the only
"physical'' degeneracy being that of Eq. (2). Thus a randomization - so
to say - of the i distribution at expense of the
,
the only
"physical'' degeneracy being that of Eq. (2). Thus a randomization - so
to say - of the i distribution at expense of the  distribution is not
allowed in our case (see Landstreet & Mathys 2000).
distribution is not
allowed in our case (see Landstreet & Mathys 2000).
Let us now turn our attention to the "magnetic'' parameters of the model.
Since the magnetic structure may plausibly be connected with the star's rotation,
we looked for possible correlations between the magnetic parameters and
the rotational period P.
Figure 8 shows the dipole amplitude 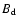 (upper panel)
and the ratio of quadrupole to dipole amplitude
(upper panel)
and the ratio of quadrupole to dipole amplitude
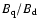 (lower panel) as
functions of P. The figure refers to all the 147 models associated with the
31 stars of our sample. Both quantities, and particularly the latter, decrease
on average with increasing P: faster rotators seem to be characterised by
stronger and predominantly quadrupolar fields.
(lower panel) as
functions of P. The figure refers to all the 147 models associated with the
31 stars of our sample. Both quantities, and particularly the latter, decrease
on average with increasing P: faster rotators seem to be characterised by
stronger and predominantly quadrupolar fields.
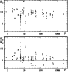 |
Figure 8:
Dipole amplitude (upper panel) and ratio of quadrupole to
dipole amplitude (lower panel) versus rotational period. P is
expressed in days, 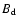 in kG. The dots' area is proportional to
the weight
in kG. The dots' area is proportional to
the weight 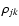 of Eq. (6).
of Eq. (6). |
| Open with DEXTER |
Similarly, Fig. 9 shows the phase-averaged mean field modulus as a
function of P. The number of dots is much smaller than in Fig. 8
because - as already noted - the different models of a given star yield
almost the same
 value. Consistently with the
data in Fig. 8,
value. Consistently with the
data in Fig. 8,
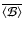 tends to decrease with
increasing P.
tends to decrease with
increasing P.
As far as the magnetic geometry is concerned, consider first the
quadrupolar component. The first step is to find the location of the
point Q on the stellar surface (cf. Fig. 1). The plot in
Fig. 10 shows the location of Q in the
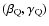 plane for all models
plane for all models![[*]](/icons/foot_motif.gif) . It turns out that the
dots tend to cluster round
. It turns out that the
dots tend to cluster round
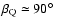 ,
and, to a smaller
extent, round
,
and, to a smaller
extent, round
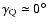 and
and
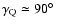 :
such characteristics were already apparent
from the histograms of Fig. 5. But the most interesting aspect arises
when connecting the dots corresponding to all the models of a given star: one
finds that, for a number of stars, the location of the point Q lies within a
small region around the point
:
such characteristics were already apparent
from the histograms of Fig. 5. But the most interesting aspect arises
when connecting the dots corresponding to all the models of a given star: one
finds that, for a number of stars, the location of the point Q lies within a
small region around the point
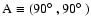 .
There are
seven stars of this kind, shown in the lower panel of Fig. 10. For
three of them - HD 96446, HD 119419, and HD 147010, labelled in the figure as
No. 14, 17, and 24, respectively - the location of the point Q is univocal
(one minimum in the
.
There are
seven stars of this kind, shown in the lower panel of Fig. 10. For
three of them - HD 96446, HD 119419, and HD 147010, labelled in the figure as
No. 14, 17, and 24, respectively - the location of the point Q is univocal
(one minimum in the  hypersurface), while for the others - HD 70331,
HD 137509, HD 208217 and HD 318107 (labelled in the figure with 8, 20, 31, and
33, respectively) - there are several possible locations. In any case, for all
of them the point Q lies within a small spherical cap, centred at the point A
and having a width
hypersurface), while for the others - HD 70331,
HD 137509, HD 208217 and HD 318107 (labelled in the figure with 8, 20, 31, and
33, respectively) - there are several possible locations. In any case, for all
of them the point Q lies within a small spherical cap, centred at the point A
and having a width
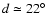 (which amounts to about 7% of the spherical
surface) - see Fig. 11. These stars will be referred to in the
following as "class I''.
(which amounts to about 7% of the spherical
surface) - see Fig. 11. These stars will be referred to in the
following as "class I''.
 |
Figure 9:
The phase-averaged mean field modulus (in kG) against the rotational
period (in days). |
| Open with DEXTER |
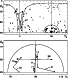 |
Figure 10:
Upper panel: the position of the point Q in the
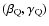 plane for each of the fitting models. Angles
are expressed in degrees. The
plane for each of the fitting models. Angles
are expressed in degrees. The
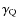 axis spans a
axis spans a
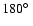 interval centred at
interval centred at
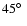 in order to show clearly
the regions of interest (cf. Fig. 11): two spherical caps
with widths
in order to show clearly
the regions of interest (cf. Fig. 11): two spherical caps
with widths
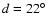 and
and
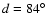 centred at the point
centred at the point
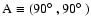 .
The dots' area is proportional
to .
The dots' area is proportional
to 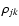 defined in Eq. (6). Full dots indicate
"class I'' and "class II'' stars, labelled according to their
reference number in Table 1. Class II stars HD 2453, HD 12288,
and HD 187474 (labelled as 1, 2, and 27) have five, one, and two
models, respectively. Lower panel: an
enlargement of the class I region, showing the connections between
models of the same star. Class I stars are HD 70331, HD 96446,
HD 119419, HD 137509, HD 147010, HD 208217, and HD 318107
(indicated in the figure as No. 8, 14, 17, 20, 24, 31, and 33).
defined in Eq. (6). Full dots indicate
"class I'' and "class II'' stars, labelled according to their
reference number in Table 1. Class II stars HD 2453, HD 12288,
and HD 187474 (labelled as 1, 2, and 27) have five, one, and two
models, respectively. Lower panel: an
enlargement of the class I region, showing the connections between
models of the same star. Class I stars are HD 70331, HD 96446,
HD 119419, HD 137509, HD 147010, HD 208217, and HD 318107
(indicated in the figure as No. 8, 14, 17, 20, 24, 31, and 33). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{fig11.ps} \end{figure}](/articles/aa/full/2002/42/aa2699/Timg157.gif) |
Figure 11:
Location of the quadrupole pole Q on the stellar surface for
"class I'' and "class II'' stars. |
| Open with DEXTER |
Similarly, we found that for 3 other stars - HD 2453, HD 12288, and
HD 187474 (No. 1, 2, and 27, respectively) - the point Q lies within a
small "ring'' between
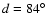 and
and
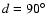 ,
i.e., a
,
i.e., a
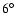 ring around the meridian containing the stellar rotation axis and
the dipole axis (about 10% of the spherical surface). These stars, denoted
as "class II'' in the following, are shown in the upper panel of
Fig. 10.
ring around the meridian containing the stellar rotation axis and
the dipole axis (about 10% of the spherical surface). These stars, denoted
as "class II'' in the following, are shown in the upper panel of
Fig. 10.
For the remaining stars, the location of the point Q is usually scattered
throughout the
 plane according to the
different models, so that no precise characterisation is possible.
plane according to the
different models, so that no precise characterisation is possible.
It should be noticed that, in terms of the angles 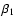 ,
,
 ,
,
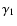 ,
,
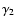 ,
class I stars are characterised by the property
,
class I stars are characterised by the property
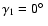 or
or
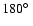 and
and
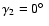 or
or
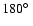 (the unit
vectors
(the unit
vectors 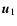 and
and 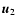 lie in the plane of the rotation axis and
dipole axis). It follows that the degeneracy of Eq. (2) does not apply
to such stars: this can be formally seen by combining Eqs. (2) and
(4).
lie in the plane of the rotation axis and
dipole axis). It follows that the degeneracy of Eq. (2) does not apply
to such stars: this can be formally seen by combining Eqs. (2) and
(4).
Let us now examine whether any correlation exists between the location of the
point Q on the stellar surface and the rotational period. If we restrict
attention to class I and class II stars (for which such location is more
precise), we obtain the remarkable result shown in Fig. 12: there
is striking evidence that class I stars are short-period, and
class II stars are long-period. A similar result was anticipated by
Bagnulo (2001).
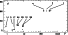 |
Figure 12:
The angular distance d (in degrees) of the point Q from the
point
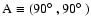 as a function of the
rotational period (in days), for class I (lower left) and class II
(upper right) stars. Dots' area is proportional to
as a function of the
rotational period (in days), for class I (lower left) and class II
(upper right) stars. Dots' area is proportional to 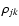 of
Eq. (6).
of
Eq. (6). |
| Open with DEXTER |
The idea of a general "law'', valid for all the stars in our sample,
according to which the angular distance d of the point Q from the point
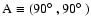 is an increasing function of the
rotational period, looks really tempting. However, we just observed that for
a star other than class I or II, the locations of the point Q associated with
the various models are generally far apart in the
is an increasing function of the
rotational period, looks really tempting. However, we just observed that for
a star other than class I or II, the locations of the point Q associated with
the various models are generally far apart in the
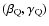 plane - which entails scattered values (i.e., both large
and small) for d. In fact, when d is plotted against P for all models
of all the stars in the sample, we obtain the results of Fig. 13,
which look rather ambiguous. In particular, some long-period stars (especially
HD 116458, HD 188041, HD 51684, and HD 93507 - No. 16, 28, 5, and 12,
respectively) have both large-d and small-d models. (Note that in the case
of HD 93507, the determination of the magnetic observables - hence the
modelling - is hampered by the fact that the distribution of Fe over the
stellar surface is rather strongly inhomogeneous.)
plane - which entails scattered values (i.e., both large
and small) for d. In fact, when d is plotted against P for all models
of all the stars in the sample, we obtain the results of Fig. 13,
which look rather ambiguous. In particular, some long-period stars (especially
HD 116458, HD 188041, HD 51684, and HD 93507 - No. 16, 28, 5, and 12,
respectively) have both large-d and small-d models. (Note that in the case
of HD 93507, the determination of the magnetic observables - hence the
modelling - is hampered by the fact that the distribution of Fe over the
stellar surface is rather strongly inhomogeneous.)
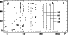 |
Figure 13:
Same as Fig. 12 for all models of all the stars in the
sample. The vertical lines connect the dots corresponding to the
different models of stars HD 116458, HD 188041, HD 51684, and
HD 93507, that are labelled in the figure as 16, 28, 5, and 12,
respectively. |
| Open with DEXTER |
However, if we restrict attention to the best model (associated
with the absolute  minimum) of each of the 31 stars, we obtain the
plot in Fig. 14. It really seems that the data of the whole sample
support (approximately) the "law'' mentioned above.
minimum) of each of the 31 stars, we obtain the
plot in Fig. 14. It really seems that the data of the whole sample
support (approximately) the "law'' mentioned above.
Finally, one could suspect that a relationship exists between d and
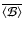 ,
since both quantities are somewhat related to the rotation
period. However, inspection to the plot of d vs.
,
since both quantities are somewhat related to the rotation
period. However, inspection to the plot of d vs.
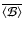 did not
reveal any obvious correlation.
did not
reveal any obvious correlation.
 |
Figure 14:
Same as Fig. 13 for the best models of all the
stars in the sample. Full dots are class I and class II stars.
Dots' area is proportional to the weight 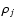 of Eq. (5),
which is more appropriate in this context.
of Eq. (5),
which is more appropriate in this context. |
| Open with DEXTER |
In order to characterise the quadrupole orientation, one needs to know
- beside the location of the point Q - the directions of the unit vectors
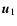 and
and 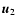 in their plane, i.e., the angles
in their plane, i.e., the angles 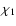 and
and
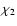 or, equivalently,
or, equivalently, 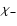 and
and 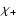 .
Contrary to Q, those
directions proved to be basically uncorrelated with the rotational period: this
is obvious even if we restrict the analysis to the best models, as shown in
Fig. 15. The only "anomalies'' of
.
Contrary to Q, those
directions proved to be basically uncorrelated with the rotational period: this
is obvious even if we restrict the analysis to the best models, as shown in
Fig. 15. The only "anomalies'' of 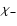 and
and 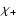 are those
appearing in Fig. 5: some excess of
are those
appearing in Fig. 5: some excess of 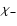 values around
values around
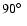 ,
and of
,
and of 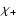 values around
values around
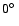 and
and
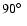 .
Though the discrepancies
from the relevant random distributions are less marked than for the other
angles (cf. Table 2), it is interesting to observe that the
.
Though the discrepancies
from the relevant random distributions are less marked than for the other
angles (cf. Table 2), it is interesting to observe that the 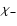 distribution tends to rule out linear quadrupole models
(
distribution tends to rule out linear quadrupole models
(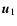 parallel or antiparallel to
parallel or antiparallel to 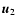 ,
which entails
,
which entails
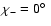 or
or
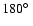 ).
).
 |
Figure 15:
The angles 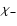 (upper panel) and
(upper panel) and 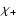 (lower
panel) - expressed in degrees - against the rotational period in days.
Only the best-fit values are shown. Full/open dots and dots' area have the
same meaning as in Fig. 14.
(lower
panel) - expressed in degrees - against the rotational period in days.
Only the best-fit values are shown. Full/open dots and dots' area have the
same meaning as in Fig. 14. |
| Open with DEXTER |
Next we consider the dipole orientation. Figure 16 shows the
angle  as a function of the rotational period. The upper panel refers
to all models of all the 31 stars, and shows a deficiency of large
as a function of the rotational period. The upper panel refers
to all models of all the 31 stars, and shows a deficiency of large  values for long period stars. If we confine attention to the best-fit models
(lower panel), we better see that
values for long period stars. If we confine attention to the best-fit models
(lower panel), we better see that  tends to decrease with increasing
rotational period. This is in agreement with the main result of Landstreet
& Mathys (2000):
tends to decrease with increasing
rotational period. This is in agreement with the main result of Landstreet
& Mathys (2000):  is usually small for slow rotators and large for fast rotators. Such agreement
is especially significant for long-period stars, where the quadrupolar
component is less important (see Fig. 8, lower panel), so that the
orientation of the magnetic structure is dominated by the dipole orientation.
A notable exception to this general trend is represented by HD 187474. This
star has a rotation period of 2364 d (the longest in the g sample), and the
best-model predicts a tilt angle between dipole axis and rotation axis of
80
is usually small for slow rotators and large for fast rotators. Such agreement
is especially significant for long-period stars, where the quadrupolar
component is less important (see Fig. 8, lower panel), so that the
orientation of the magnetic structure is dominated by the dipole orientation.
A notable exception to this general trend is represented by HD 187474. This
star has a rotation period of 2364 d (the longest in the g sample), and the
best-model predicts a tilt angle between dipole axis and rotation axis of
80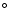 .
A detailed study of its chemical peculiarity has been recently presented
by Strasser et al. (2001).
.
A detailed study of its chemical peculiarity has been recently presented
by Strasser et al. (2001).
 |
Figure 16:
The angle  (in degrees) versus the rotational period (in
days), for all models (upper panel) and for best-fit models
(lower panel). Dot's area is proportional to
(in degrees) versus the rotational period (in
days), for all models (upper panel) and for best-fit models
(lower panel). Dot's area is proportional to 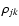 and to
and to
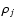 in the upper and lower panel, respectively. Full dots are class I
and class II stars.
in the upper and lower panel, respectively. Full dots are class I
and class II stars. |
| Open with DEXTER |
On the whole, the results above show the existence of some correlation between
the magnetic structure of the stars of our sample and the rotational period.
4 Analysis based on 3 magnetic observables
As recalled at the end of Sect. 2, the consistency of
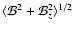 and
and
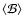 observations is not completely
ascertained. For this reason we repeated the analysis of Sect. 3 by
neglecting either kind of measurements. However, such "partial'' analyses
imply that some stars "go out'' of the sample, so that the "global'' sample
of Sect. 3 and the two partial samples are not directly comparable.
observations is not completely
ascertained. For this reason we repeated the analysis of Sect. 3 by
neglecting either kind of measurements. However, such "partial'' analyses
imply that some stars "go out'' of the sample, so that the "global'' sample
of Sect. 3 and the two partial samples are not directly comparable.
In fact, in Paper III we determined the minimum combinations of magnetic
observables which allow a dipole plus (non linear) quadrupole
configuration to be recovered. In particular, Table 1 of that paper shows that
the configuration can be recovered from (a sufficient number of)
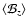 and
and
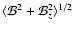 observations, as well as from
observations, as well as from
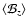 and
and
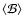 observations; whereas it
cannot be recovered either from
observations; whereas it
cannot be recovered either from
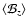 alone, or from
alone, or from
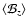 and
and
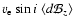 .
Bearing
in mind these results, we see that the sub-samples for our partial analyses
contain 25 stars each.
.
Bearing
in mind these results, we see that the sub-samples for our partial analyses
contain 25 stars each.
These are shown in the last two columns of Table 1, where the label
"p1'' means that the fit is based on all available observations
except
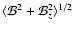 ,
while the label "p2'' means that it
is based on all available observations except
,
while the label "p2'' means that it
is based on all available observations except
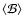 .
It should be noticed that stars HD 75445 and HD 335238, which in principle
pertain to sub-sample p2 as for both of them there are measurements of
.
It should be noticed that stars HD 75445 and HD 335238, which in principle
pertain to sub-sample p2 as for both of them there are measurements of
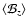 ,
,
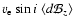 ,
and
,
and
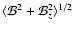 ,
are actually excluded from p2 because of the small
number of observations (9 in all), which renders the fit impossible.
On the other hand, stars HD 61468, HD 94660, and HD 142070, which in the "global''
investigation give rise to low-quality fits (
,
are actually excluded from p2 because of the small
number of observations (9 in all), which renders the fit impossible.
On the other hand, stars HD 61468, HD 94660, and HD 142070, which in the "global''
investigation give rise to low-quality fits (
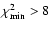 )
so that
they were excluded from the statistical analysis, in the "partial''
investigations give rise to much better fits, thus they have been included in
the analysis.
)
so that
they were excluded from the statistical analysis, in the "partial''
investigations give rise to much better fits, thus they have been included in
the analysis.
If we restricted the study to the stars common to all three samples g, p1,
and p2, we would be left with only 13 objects - too small a number for a
statistical analysis. On the other hand, a direct comparison of samples gand p1, or g and p2, is not very meaningful because the fit of several of the
common stars is identical by definition: for instance, this is the case for
the g-fit and the p1-fit of star HD 12288, because for that star there are no
observations of
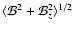 ,
hence either fit is in fact the same
fit (based on
,
hence either fit is in fact the same
fit (based on
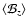 and
and
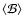 observations).
observations).
For these reasons, the correct attitude is to forget comparisons and to look
at the "global'' and "partial'' analyses as separate investigations. The
final goal is to see whether the overall picture of magnetic CP stars arising
from analyses of different kind (in the sense specified above) is the same or
not; where by "overall picture'' we intend the presence of recurrent features
and/or correlations among the parameters of the magnetic model.
Columns p1 and p2 of Table 1 show the value of the reduced  for the best-fit model of the 25 stars pertaining to either sample. Such data
is also shown in the left panels of Fig. 17. The two distributions
are similar to that of the g-case (cf. Fig. 2 left), though somewhat
displaced towards smaller values - which reflects the difficulties encountered
in fitting together
for the best-fit model of the 25 stars pertaining to either sample. Such data
is also shown in the left panels of Fig. 17. The two distributions
are similar to that of the g-case (cf. Fig. 2 left), though somewhat
displaced towards smaller values - which reflects the difficulties encountered
in fitting together
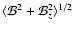 and
and
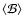 observations.
In the right panels of Fig. 17 we show the distributions of the
reduced
observations.
In the right panels of Fig. 17 we show the distributions of the
reduced  for all models (absolute and relative
for all models (absolute and relative  minima): on the whole, there are 140 models for the p1-case (7 of which with
minima): on the whole, there are 140 models for the p1-case (7 of which with
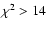 )
and 60 models for the p2-case (20 of which with
)
and 60 models for the p2-case (20 of which with 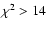 ).
These figures show that the average number of models per star - i.e., the
number of minima in the
).
These figures show that the average number of models per star - i.e., the
number of minima in the  hypersurface - increases strongly when
hypersurface - increases strongly when
 observations are included: from 2.4 for the p2-case to 4.9
for the g-case and 5.6 for the p1-case. Thus inclusion of
observations are included: from 2.4 for the p2-case to 4.9
for the g-case and 5.6 for the p1-case. Thus inclusion of
 observations renders the
observations renders the  hypersurface much more complex: this is
possibly due to a stronger degeneracy of
hypersurface much more complex: this is
possibly due to a stronger degeneracy of
 compared to the
other magnetic observables (different dipole plus quadrupole
configurations leading to similar
compared to the
other magnetic observables (different dipole plus quadrupole
configurations leading to similar
 curves). As in
Sect. 3, we restricted the statistical analysis to the models with
curves). As in
Sect. 3, we restricted the statistical analysis to the models with
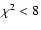 .
.
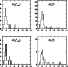 |
Figure 17:
Same as Fig. 2 for the stars of samples p1 (upper
panels) and p2 (lower panels). Either sample contains 25 stars. |
| Open with DEXTER |
Figure 18 shows the distributions of the dipole amplitude, and of the
ratio between quadrupole and dipole amplitude, for the two "partial''
samples, while Fig. 19 refers to the phase-averaged mean field
modulus. Such distributions are in fact quite similar to those of
Sect. 3 (cf. Figs. 3 and 4). Note that Babcock's
star does not belong to the p2-sample (see Table 1).
It is interesting to compare our Figs. 4 and 19 with the histogram showing the
observed phase-averaged magnetic field modulus presented in Fig. 47 of
Mathys et al. (1997). We recall that Fig. 4 is based on the modelling results
of all available magnetic observables; the left panel of Fig. 19 is obtained
from
the results of the analysis of all quantities except the mean quadratic field;
the right panel of Fig. 19 from results of the analysis of all quantities except
the mean field modulus; Fig. 47 of Mathys et al. (1997) is purely based on
the observations, and includes stars that have not been monitored throughout
the rotation cycle. A similar overall picture emerges from all these figures.
A certain degree of consistency is to be expected for the
following reason: the mean field modulus is generally a quantity that does
not change much over the rotation phase, and even few observed points, or a
very rough model are sufficient to characterise the
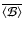 curve
with good approximation. We note in particular that all figures show
a definite lower limit in the
curve
with good approximation. We note in particular that all figures show
a definite lower limit in the
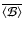 distribution at about 3 kG
- this characteristic has been already discussed in Mathys et al. (1997),
and in Hubrig et al. (2000). It is interesting to note that the same result
is here recovered also for stars with no magnetically split lines,
though still with relatively low
distribution at about 3 kG
- this characteristic has been already discussed in Mathys et al. (1997),
and in Hubrig et al. (2000). It is interesting to note that the same result
is here recovered also for stars with no magnetically split lines,
though still with relatively low
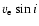 values. Notably the same sharp
cut-off is found from the modelling of
values. Notably the same sharp
cut-off is found from the modelling of
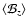 ,
,
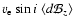 ,
and
,
and
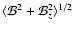 (see right panel
of Fig. 19).
(see right panel
of Fig. 19).
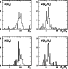 |
Figure 18:
Same as Fig. 3 for samples p1 (upper panels) and p2 (lower panels). |
| Open with DEXTER |
The distributions of the angles i,  ,
,
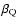 ,
,
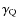 ,
,
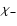 ,
,
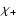 for the p1 and p2 cases are shown in
Figs. 20 and 21, respectively. It appears that the
deviations from the relevant random distributions are basically the same as
in the g-case (cf. Fig. 5). These include an excess of small
for the p1 and p2 cases are shown in
Figs. 20 and 21, respectively. It appears that the
deviations from the relevant random distributions are basically the same as
in the g-case (cf. Fig. 5). These include an excess of small  values and large
values and large
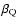 values, and, to a smaller extent, of
values, and, to a smaller extent, of
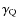 and
and 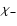 values around
values around
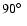 .
The peaks of the
"barycentric angle''
.
The peaks of the
"barycentric angle'' 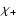 around
around
 and
and
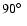 are still visible,
though the latter is somewhat shifted in the p2-case.
are still visible,
though the latter is somewhat shifted in the p2-case.
As far as the inclination angle i is concerned, it should be borne in mind
that - contrary to the g-case -
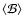 was detected for
all stars of the p1-sample. The selection effect is therefore larger
than in the g-case, so that the excess of small i values is even more
prominent (see Fig. 20). On the other hand, the p2-sample contains
a larger percentage of long-period stars (say, with
was detected for
all stars of the p1-sample. The selection effect is therefore larger
than in the g-case, so that the excess of small i values is even more
prominent (see Fig. 20). On the other hand, the p2-sample contains
a larger percentage of long-period stars (say, with
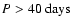 )
with respect to the g-sample, which explains why the excess of small ivalues is less prominent (see Fig. 21).
)
with respect to the g-sample, which explains why the excess of small ivalues is less prominent (see Fig. 21).
Consider next the correlations with the rotational period. Concerning the
field strength, the behaviour of the dipole and quadrupole amplitudes
is quite similar to the g-case; we show only the phase-averaged mean field
modulus (Fig. 22), which tends to decrease with increasing P as in
Fig. 9.
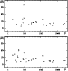 |
Figure 22:
Same as Fig. 9 for cases p1 (upper panel) and p2 (lower panel). The larger dots' area in the lower panel is just
a consequence of the smaller average number of models per star in the
p2-case. |
| Open with DEXTER |
As to the quadrupole orientation, we repeated for the p1 and p2 cases the
same analysis on the location of the point Q on the spherical surface described
in Sect. 3 (see Fig. 10). For both cases, we found a number
of "class I'' and "class II'' stars (cf. Fig. 11), and we plotted
the angular distance d between points Q and A against the rotational period
(cf. Figs. 12 to 14). The final results (based on the
best fit of each star) are shown in Fig. 23.
 |
Figure 23:
Same as Fig. 14 for cases p1 (upper panel) and p2 (lower panel). Full dots represent class I and class II stars,
defined as in Sect. 3. Some stars are labelled by their
reference number of Table 1. |
| Open with DEXTER |
Altogether, the p1-case yields a picture similar to the g-case (see
Fig. 14), with the exception of star HD 94660 (absent in the g-sample)
- which is the longest-period star of all the 34 objects and which is
characterised by a small d value - and possibly of HD 116458.
By contrast, the p2-case yields a very different picture, which tends to deny
the existence of a correlation between d and P. In particular, it is worth
noticing the behaviour of stars HD 116458, HD 93507, and HD 51684. As shown in
Fig. 13, in the g-case they have both large-d and small-d models,
but the best-fit ones are the former (see Fig. 14). In the p2-case,
on the contrary, the best-fit models of all three stars correspond to
small d values. On the other side, it should also be noticed that
the short-period star HD 142070 (absent in the g-case) proves to be a class I
object both in the p1 and the p2 case, and that the long-period star HD 61468
(also absent in the g-case) proves to be of class II in the p1-case and nearly
of class II in the p2-case, in accordance with the tentative "law'' of
Sect. 3.
On the whole, the existence of some correlation between d and P (small-dmodels for short-period stars, large-d models for long-period ones) seems
somewhat related to the reliability of
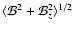 observations,
being more likely if they were not fully reliable, and vice versa.
In any case, there is a considerable excess of models with
observations,
being more likely if they were not fully reliable, and vice versa.
In any case, there is a considerable excess of models with
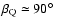 and/or
and/or
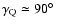 :
this comes out clearly from all three samples (see Figs. 5, 20, and 21).
:
this comes out clearly from all three samples (see Figs. 5, 20, and 21).
As for the angles 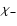 and
and 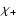 ,
they seem to be uncorrelated - as in
the g-case - with the rotational period. For the angle
,
they seem to be uncorrelated - as in
the g-case - with the rotational period. For the angle  ,
characterising
the dipole orientation, we found the results presented in Fig. 24.
They roughly confirm, though with a larger scattering, the behaviour deduced
from the g-case (cf. Fig. 16): large
,
characterising
the dipole orientation, we found the results presented in Fig. 24.
They roughly confirm, though with a larger scattering, the behaviour deduced
from the g-case (cf. Fig. 16): large  values for short-period
stars, small
values for short-period
stars, small  values for long-period ones.
values for long-period ones.
 |
Figure 24:
Same as the lower panel of Fig. 16 for cases p1 (upper
panel) and p2 (lower panel). |
| Open with DEXTER |
5 Discussion and conclusions
We have carried out a study of the magnetic morphologies of some thirty CP stars,
by interpreting the observations of mean longitudinal field, crossover, mean
quadratic field, and mean field modulus in terms of a magnetic dipole plus
non-linear quadrupole model.
In most of the cases we could not obtain a unique model, even for those stars
whose magnetic geometry seems strongly constrained by the observations.
This is related to the relatively large observational errors, and possibly
to the fact that the actual magnetic geometry of CP stars is too complex
to be described in terms of a second-order multipolar expansion. We thus decided
to follow an approach that gives a limited importance to the best-model of the
individual stars, searching instead for characteristics that emerge from the
whole set of models (corresponding to the absolute and relative minima
of the  hypersurface), and weighting the model parameters with the
hypersurface), and weighting the model parameters with the
 value.
value.
Furthermore, we had to face the problem of the inconsistency of mean field
modulus and mean quadratic field measurements: in fact, evidence exists
that for many stars, either the former are systematically slightly overestimated,
or the latter are systematically slightly underestimated. To deal with this
problem, we repeated our analysis considering different observational datasets.
We first performed a modelling considering all the kinds of measurement
that were available for each individual star. Then we repeated the same analysis
neglecting the observations of mean quadratic field; finally, we performed
the analysis considering all available data but the observations of mean
field modulus. Numerical simulations performed by Bagnulo, Mathys, & Stift
(in preparation) suggest that the technique used to determine the mean quadratic
field tends to underestimate the measurement. In addition to these numerical
simulations, another argument supports the view that measurements of the mean
field modulus are likely more reliable than determinations of the mean quadratic
field. Field modulus measurements rely directly on the basic physics of the
Zeeman effect and, for simple lines such as the Fe II
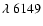 magnetic
doublet, are for all practical purposes independent of radiative transfer
effects (Mathys 1989, Sect. 4.2.1), in contrast to quadratic field determinations,
which involve fairly gross approximations of the effects of the radiative transfer
in the stellar atmosphere. Accordingly, one could be tempted
to give more weight to the results obtained neglecting quadratic field
measurements. We nevertheless decided to accept as reliable only those results
that were recovered in all three kinds of analysis. These are as follows.
magnetic
doublet, are for all practical purposes independent of radiative transfer
effects (Mathys 1989, Sect. 4.2.1), in contrast to quadratic field determinations,
which involve fairly gross approximations of the effects of the radiative transfer
in the stellar atmosphere. Accordingly, one could be tempted
to give more weight to the results obtained neglecting quadratic field
measurements. We nevertheless decided to accept as reliable only those results
that were recovered in all three kinds of analysis. These are as follows.
i)
The dipolar strength is usually comprised in the interval 3-20 kG, with a
peak at something less than 10 kG. The strength of the quadrupolar component
is the same as, or larger than the dipole strength.
ii)
The dipole and quadrupole amplitude, as well as the ratio of quadrupole
to dipole amplitude, tends to decrease with increasing rotational period.
Consistently, the phase-averaged mean field modulus, an indicator of the
typical field strength, also tends to decrease with increasing P.
iii)
The inclination of the dipole axis to the rotation axis is usually large
for short-period stars, and small for long-period ones. This is in accordance
with a recent result obtained by Landstreet & Mathys (2000), who found
a similar result for the magnetic axis of the axisymmetric model that they
adopted in their best-fit technique.
iv)
For several stars, the plane containing the two unit vectors that characterise
the quadrupole is almost coincident with the plane containing the stellar
rotation axis and the dipole axis. These are basically short-period stars
(approximately,
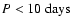 ). Long-period stars seem to be
preferentially characterised by a quadrupole orientation such that the
planes just mentioned are perpendicular. There is also some indication of a
continuous transition between the two classes of stars with increasing
rotational period, but the existence of such a "law'' is partly related to
the question of the reliability of mean quadratic field observations. This
result is not recovered by the analysis performed neglecting the observations
of mean field modulus (thus when quadratic field measurements have a larger
weight).
). Long-period stars seem to be
preferentially characterised by a quadrupole orientation such that the
planes just mentioned are perpendicular. There is also some indication of a
continuous transition between the two classes of stars with increasing
rotational period, but the existence of such a "law'' is partly related to
the question of the reliability of mean quadratic field observations. This
result is not recovered by the analysis performed neglecting the observations
of mean field modulus (thus when quadratic field measurements have a larger
weight).
It should be noted that the results of this analysis pertain to a
sample of relatively slow rotating stars; many of them are in fact very
long-period stars.
It is an unanswered question whether the magnetic field of CP stars is the
relic of an interstellar field that became stronger and stronger as the
primordial nebula collapsed into a star ("freezing'' the field flux in a
smaller and smaller plasma surface), or whether the field is at least in
part dynamo generated. The results of our and previous studies show that
there is some correlation between magnetic structure and rotational period,
which encourages one to think in terms of the dynamo theory. In reality, it is
not obvious to determine what is the consequence of what. For instance,
Stepien & Landstreet (2002) have argued that the interaction of the
magnetic field and a circumstellar disk before the star reaches the
Zero-Age-Main-Sequence tends to slow-down preferentially those stars
that have magnetic field
vectors tilted at a small angle with respect to the rotation axis (thus presumably
with the field lines perpendicular to the disk). Therefore, the long rotational
period would be a consequence of the magnetic structure, and the magnetic field
itself could well be a fossil relic. On the other hand, finding within the
framework of a fossil field an explanation for the statistical properties of
the quadrupolar component that were found in this work may be less easy. In any
case we still need firmer conclusions about the geometrical structures of
magnetic CP stars, that could come for instance from extensive applications of
Zeeman Doppler Imaging. At the same time, there is a strong need for a theory
explaining the origin of the magnetic fields in A and B type stars capable of
leading to predictions about the geometrical structures to be compared
with the modelling results.
Acknowledgements
Many thanks to Pierre North for providing us with (unpublished) estimates of
the radius for some of the stars of Table 1.
- Bagnulo, S. 2001, in Magnetic fields across the
Hertzsprung-Russel Diagram, ed. G. Mathys, S. K. Solanki, & D. T. Wickramasinghe,
ASP Conf. Ser., 248, 287
- Bagnulo, S., & Landolfi, M. 1999, A&A, 346, 158
NASA ADS
- Bagnulo, S., Landi Degl'Innocenti, M., & Landi Degl'Innocenti, E. 1996, A&A, 308, 115
In the text
NASA ADS
- Bagnulo, S., Landolfi, M., & Landi Degl'Innocenti, M. 1999, A&A, 343, 865 (Paper II)
In the text
NASA ADS
- Bagnulo, S., Landolfi, M., Mathys, G., & Landi Degl'Innocenti, M. 2000, A&A, 358, 929 (Paper III)
In the text
NASA ADS
- Bagnulo, S., Wade, G. A., Donati, J. F., et al.
2001, A&A, 369, 889
In the text
NASA ADS
- Borra, E. F., & Landstreet, J. D. 1977, ApJ, 212, 141
In the text
NASA ADS
- Borra, E. F., & Landstreet, J. D. 1978, ApJ, 222, 226
In the text
NASA ADS
- Hildebrandt, G., Scholz, G., & Woche, M. 1997, Astron. Nachr., 318, 291
In the text
NASA ADS
- Hill, G. M., Bohlender, D. A., & Landstreet, J. D., et al. 1998, MNRAS, 297, 236
In the text
NASA ADS
- Hubrig, S., North, P., & Mathys, G. 2000, ApJ, 539, 352
In the text
NASA ADS
- Huchra, J. 1972, ApJ, 174, 435
In the text
NASA ADS
- Kochukhov, O., Piskunov, N., Ilyin, I., Ilyina, S.,
& Tuominen, I. 2002, A&A, 389, 420
In the text
NASA ADS
- Landolfi, M., Bagnulo, S., & Landi Degl'Innocenti, M.
1998, A&A, 338, 111 (Paper I)
In the text
NASA ADS
- Landstreet, J. D. 1992, A&A Rev., 4, 35
In the text
- Landstreet, J. D., & Mathys, G. 2000, A&A, 359, 213
In the text
NASA ADS
- Leone, F., Catanzaro, G., & Catalano, S. 2000, A&A, 355, 315
In the text
NASA ADS
- Leone, F., & Catanzaro, G. 2001, A&A, 365, 118
In the text
NASA ADS
- Mathys, G. 1989, Fundam. Cosmic Phys., 13, 143
In the text
- Mathys, G. 1994, A&AS, 108, 547
In the text
NASA ADS
- Mathys, G. 1995a, A&A, 293, 733
In the text
NASA ADS
- Mathys, G. 1995b, A&A, 293, 746
In the text
NASA ADS
- Mathys, G., & Hubrig, S. 1997, A&AS, 124, 475
NASA ADS
- Mathys, G., Hubrig, S., Landstreet, J. D., Lanz, T., & Manfroid, J. 1997, A&AS, 123, 353
In the text
NASA ADS
- Moss, D. 2001, in Magnetic fields across the
Hertzsprung-Russel Diagram, ed. G. Mathys, S. K. Solanki, & D. T. Wickramasinghe, ASP Conf. Ser., 248, 305
In the text
- North, P. 1998, A&A, 334, 181
NASA ADS
- Press, W. H., Teukolsky, S. A., Vetterling, W. T.,
& Flannery, B. P. 1986, Numerical Recipes (Cambridge University Press,
Cambridge)
In the text
- Piskunov, N., & Kochuckov, O. 2002, A&A, 381, 736
In the text
NASA ADS
- Preston, G. W. 1969, ApJ, 157, 247
In the text
NASA ADS
- Preston, G. W., & Stepien, K. 1968, ApJ, 151, 583
In the text
NASA ADS
- Stepien, K., & Landstreet, J. D. 2002, A&A, 384, 554
In the text
NASA ADS
- Strasser, S., Landstreet, J. D., & Mathys, G. 2001, A&A, 378, 153
In the text
NASA ADS
- Wade, G. A., Elkin, V. G., Landstreet, J. D., et al. 1996, A&A, 313, 209
In the text
NASA ADS
- Wade, G. A., Elkin, V. G., Landstreet, J. D., & Romanyuk, I. I. 1997, MNRAS, 292, 748
In the text
NASA ADS
- Wade, G., Donati, J.-F., Landstreet, J. D.,
& Shorlin, S. L. S. 2000a, MNRAS, 313, 851
In the text
NASA ADS
- Wade, G. A., Kudryavtsev, D., Romanyuk, I. I.,
Landstreet, J. D., & Mathys, G. 2000b, A&A, 355, 1080
In the text
NASA ADS
- Wade, G. A., Debernardi, Y., Mathys, G., et al.
2000c, A&A, 361, 991
In the text
NASA ADS
Copyright ESO 2002
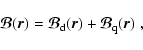
![$\displaystyle -\frac{B_{{\rm d}}}{2}
\left[~\vec{u}-3~\frac{\vec{u}\cdot\vec{r}}{R_*^2}\;\vec{r}~\right]$](/articles/aa/full/2002/42/aa2699/img39.gif)
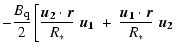
![$\displaystyle \left.+\left(\frac{\vec{u_1}\cdot\vec{u_2}}{R_*}-
5~\frac{(\vec{u_1}\cdot\vec{r})(\vec{u_2}\cdot\vec{r})}
{R_*^3}
\right)\vec{r}~\right]\!.$](/articles/aa/full/2002/42/aa2699/img42.gif)
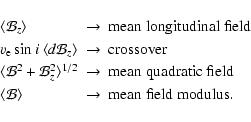
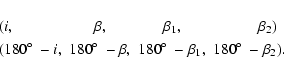
![\begin{displaymath}\begin{array}{lcccr}
&(\beta_1,&\beta_2,&\gamma_1,&\gamma_2) \\ [0.1cm]
&(\beta_2,&\beta_1,&\gamma_2,&\gamma_1)
\end{array}\end{displaymath}](/articles/aa/full/2002/42/aa2699/img63.gif)
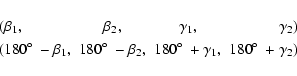
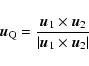
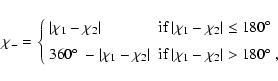
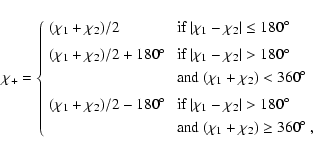

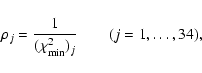
![\begin{displaymath}\rho_{jk}=\frac{c_j}{[(\chi^2_{jk})]^p}\qquad(k=1,\ldots,m(j)),
\end{displaymath}](/articles/aa/full/2002/42/aa2699/img111.gif)
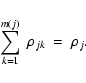
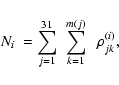
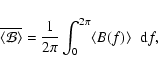


![\begin{displaymath}\langle\Delta\rangle=
\biggl[\frac{1}{n}\;\sum_{i=1}^n~\Delta_i^2\biggr]^{1/2},
\end{displaymath}](/articles/aa/full/2002/42/aa2699/img131.gif)


![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{fig11.ps} \end{figure}](/articles/aa/full/2002/42/aa2699/Timg157.gif)