A&A 394, 863-872 (2002)
DOI: 10.1051/0004-6361:20021246
F. Courbin 1, 2 - G. Letawe 1 - P. Magain 1 - L. Wisotzki 3 - P. Jablonka 4 - K. Jahnke 5 - B. Kuhlbrodt 5 -
D. Alloin 6 - G. Meylan 7 - D. Minniti 2 - I. Burud 7
1 - Institut d'Astrophysique et de Géophysique, Université de
Liège, Allée du 6 Août, 17 Sart Tilman (Bat. B5C), Liège 1, Belgium
2 - Universidad Católica de Chile, Departamento de
Astronomia y Astrofisica,
Casilla 306, Santiago 22, Chile
3 -
Institut für Physik, Universität Potsdam, Am Neuen Palais 10,
14469 Potsdam, Germany
4 -
GEPI, Observatoire de Paris, Place Jules Janssen, 92915 Meudon Cedex, France
5 -
Hamburger Sternwarte, Universität
Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
6 -
European Southern Observatory, Casilla 19, Santiago, Chile
7 - Space Telescope Science institute, 3700 San Martin Drive,
Baltimore, MD 21218, USA
Received 14 May 2002 / Accepted 23 August 2002
Abstract
We present the first result of a comprehensive spectroscopic
study of quasar host galaxies. On-axis, spatially resolved spectra of
low redshift quasars have been obtained with FORS1, mounted on the
8.2 m ESO Very Large Telescope, Antu. The spectra are spatially
deconvolved using a spectroscopic version of the "MCS deconvolution
algorithm''. The algorithm decomposes two dimensional spectra into the
individual spectra of the central point-like nucleus and of its host
galaxy. Applied to HE 1503+0228 at z=0.135 (MB=-23.0),
it provides us with the
spectrum of the host galaxy between 3600 Å and 8500 Å
(rest-frame), at a mean resolving power of 700. The data allow us to
measure several of the important Lick indices. The stellar populations
and gas ionization state of the host galaxy of HE 1503+0228 are very similar
to the ones measured for normal non-AGN galaxies. Dynamical
information is also available for the gas and stellar components of
the galaxy. Using deconvolution and a deprojection algorithm,
velocity curves are derived for emission lines, from the center up to
4
![]() away from the nucleus of the galaxy.
Fitting a simple
three-components mass model (point mass, spherical halo of
dark matter, disk) to the
position-velocity diagram, we infer a mass of
away from the nucleus of the galaxy.
Fitting a simple
three-components mass model (point mass, spherical halo of
dark matter, disk) to the
position-velocity diagram, we infer a mass of
![]() within the central kiloparsec of the galaxy, and a
mass integrated over 10 kpc of
within the central kiloparsec of the galaxy, and a
mass integrated over 10 kpc of
![]() ,
with an additional 10% error due to the uncertainty on the
inclination of the galaxy. This, in combination with the analysis of
the stellar
populations indicates that the host galaxy of HE 1503+0228 is a normal
spiral galaxy.
,
with an additional 10% error due to the uncertainty on the
inclination of the galaxy. This, in combination with the analysis of
the stellar
populations indicates that the host galaxy of HE 1503+0228 is a normal
spiral galaxy.
Key words: galaxies: kinematics and dynamics - galaxies: stellar content -
quasars: individual: HE 1503+0228 -
techniques: image processing
![\begin{figure}
\par\includegraphics[height=7.8cm]{SOFIfield.eps}\includegraphics[height=7.8cm]{fentes.eps}\end{figure}](/articles/aa/full/2002/42/aa2687/Timg20.gif) |
Figure 1:
Left: field of view of
|
| Open with DEXTER | |
Luminous quasars are now known to be generally located at the cores of large galaxies. With the recent discovery that supermassive black holes appear to reside in most if not all galaxies with substantial bulges (e.g., Magorrian et al. 1998), it is now quite likely that quasar-like activity is an extremely common but transient phenomenon, linking the growth of now extinct black holes to the violent processes during phases of active accretion (cf. McLeod et al. 1999). However, very little of the physical processes operating during such episodes of nuclear activity is actually understood: neither do we know the actual conditions for fueling (or refueling) massive black holes, nor the time-scales involved. A particularly interesting problem is the importance of the feedback from a high-luminosity Active Galactic Nucleus (AGN) onto its host galaxy, in the form of huge quantities of ionizing radiation as well as possible mechanical outflows (jets).
Quasar host galaxies have been studied almost exclusively by imaging (e.g., Bahcall et al. 1997; Stockton et al. 1998; Márquez et al. 2001). Recent Hubble Space Telescope optical studies have established that high-luminosity quasars generally reside in big ellipticals, irrespective of radio properties (McLeod & Rieke 1995; Disney et al. 1995; Hughes et al. 2000). There also seems to be a trend that more luminous quasars are hosted by more massive galaxies (McLure et al. 1999; McLeod & Rieke 1995).
A more detailed understanding of the physical conditions in host
galaxies can only be obtained from spectroscopic
observations. Available evidence in this field is extremely scarce,
and although extensive quasar host spectroscopy was conducted already
in the early 1980s (e.g., Boroson et al. 1985), they have
never really been followed up with improved instrumentation and
analysis techniques, except for a few isolated objects (among them
3C 48 being the probably best-studied case in this field - e.g.,
Chatzichristou et al. 1999; Canalizo & Stockton
2000). Particularly important is the fact that nearly all
these observations up to now were designed as "off-nuclear''
spectroscopy, avoiding the strong contamination from the AGN itself,
but yielding only information on the host for distances of ![]() 5-10 kpc from the nucleus.
5-10 kpc from the nucleus.
| |
Figure 2: Left and middle: deconvolved NTT and VLT images, where the quasar has been removed from the data. Right: zoom on the host galaxy and position of the slitlet used to obtain the spectroscopic data. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8.1cm]{HE1503_B.ps}\hspace*{4mm}
\includ...
...r\mbox{\hspace*{4.5cm}
\includegraphics[width=8.1cm]{HE1503_I.ps} }
\end{figure}](/articles/aa/full/2002/42/aa2687/Timg23.gif) |
Figure 3: One dimensional deconvolved spectrum of HE 1503+0228 and its host galaxy. Each panel corresponds to one FORS1 grism and displays the individual flux calibrated spectrum of the quasar and its host alone. Note that the host spectrum shows no trace of the AGN broad emission lines, that are seen narrow in the host galaxy. Note also the very good agreement in the deconvolution of the 3 grisms in the overlapping regions. |
| Open with DEXTER | |
With the aim of studying the stellar and gas content of quasar host
galaxies, as well as their dynamics, we have initiated a spectroscopic
campaign with the ESO-VLT to observe a sample of luminous radio-quiet
quasars at low redshift. The sample is based on the Hamburg/ESO
Survey (HES; Wisotzki et al. 2000), a wide-angle (![]() 7500 deg2) search for optically bright (
7500 deg2) search for optically bright (
![]() )
quasars in
the southern sky. This survey is particularly suited to provide
samples for host galaxy studies, mainly because of two reasons: (1)
because of its bright limiting magnitude, the survey yields
low-redshift quasars in large numbers, (2) the selection does not
encompass morphological criteria, i.e., there is no limitation to
point sources as in most other optical quasar surveys. This fact and
the wide range of selection criteria employed in the HES (cf. Wisotzki
et al. 2000) ensure that quasars are selected irrespective of
morphological properties of their host galaxies (see also Köhler et
al. 1997). Our objects all have MB < -23 and z<0.33.
)
quasars in
the southern sky. This survey is particularly suited to provide
samples for host galaxy studies, mainly because of two reasons: (1)
because of its bright limiting magnitude, the survey yields
low-redshift quasars in large numbers, (2) the selection does not
encompass morphological criteria, i.e., there is no limitation to
point sources as in most other optical quasar surveys. This fact and
the wide range of selection criteria employed in the HES (cf. Wisotzki
et al. 2000) ensure that quasars are selected irrespective of
morphological properties of their host galaxies (see also Köhler et
al. 1997). Our objects all have MB < -23 and z<0.33.
The present paper is aimed at exposing the techniques used to obtain high quality spectra of quasar hosts, decontaminated from the contamination by the quasar, and to show their application to one object, taken as a test case: HE 1503+0228, at z=0.135.
We have obtained H-band images of HE 1503+0228, at La Silla observatory
(ESO, Chile) on the night of 1999 February 24th. SOFI was used,
the near-IR imager of the 3.5 m ESO New Technology Telescope (NTT).
The pixel size was 0.29
![]() and numerous dithered images of the
field were taken in order to produce a combined sky subtracted frame
with a total exposure time of 480 s and a final mean seeing of
0.8
and numerous dithered images of the
field were taken in order to produce a combined sky subtracted frame
with a total exposure time of 480 s and a final mean seeing of
0.8
![]() .
The image is displayed on the left panel of Fig. 1.
It shows the environment of the quasar on a
.
The image is displayed on the left panel of Fig. 1.
It shows the environment of the quasar on a
![]() field, with no obvious companion.
field, with no obvious companion.
Additional data were obtained with the first of the four 8.2 m
telescopes (UT1) at Paranal observatory. A shallow 30 s R-band image
was taken, in order to design the spectroscopic mask. The seeing was
0.62
![]() ,
sampled with a pixel scale of 0.2
,
sampled with a pixel scale of 0.2
![]() .
.
Both the near-IR and optical images were deconvolved using the MCS deconvolution algorithm (Magain et al. 1998). While one single optical image of HE 1503+0228 was obtained, many dithered IR images were available in the H-band. Eight stacks of images were produced with the data and simultaneously deconvolved as explained in Courbin et al. (1998). This procedure allows for better decomposition of the data into a sum of point source and "background'' channels, hence a better extraction of the image of the host, uncontaminated by the AGN's light. The deconvolved data are shown in Fig. 2, where the quasar has been subtracted.
The photometry of the host of HE 1503+0228 has been performed on the
deconvolved images, in a 10
![]() diameter aperture. The magnitudes
we infer in that way are
diameter aperture. The magnitudes
we infer in that way are
![]() and
and
![]() .
.
Determining the shape of the galaxy is of importance as the inclination of the disk component in the mass model (see next sections) depends on the observed galaxy shape, hence affecting the mass determination of the galaxy. We make the assumption that the galaxy has an intrinsic circular geometry, to turn the fitted ellipticities into an inclination angle. Given the relatively low signal-to-noise of our images we chose to determine the shape of the host by fitting analytical profiles to the data (Kuhlbrodt et al. in preparation). Our model is composed of a nucleus, a disk, and a spheroid, convolved with the observed PSF before any fitting is performed. In the case of HE 1503+0228 the spheroid is used to model a bar-like feature in the center of the galaxy, that may affect the fit of the disk component if it were not taken properly into account.
The analysis yields the Position Angle (
![]() )
of
the host, its inclination (
)
of
the host, its inclination (
![]() ), and the angle
(
), and the angle
(
![]() )
between the slit and the major axis of the
galaxy. These values are in fact very close to the values found just
by measuring the outmost isophotes in the VLT images.
)
between the slit and the major axis of the
galaxy. These values are in fact very close to the values found just
by measuring the outmost isophotes in the VLT images.
The spectroscopic data were taken on the night of 2000, April
11th with FORS1 mounted on Antu, the first of the four 8.2 m VLT
Unit Telescopes at Paranal observatory (ESO, Chile). Three grisms were
used (G600B, G600R, G600I) to cover the whole optical spectral range
4000-9500 Å with a mean spectral resolution of about 700. The
seeing during the observations was good, about 0.6
![]() .
Each grism
was exposed 1200 s, under photometric conditions and dark time,
which yields a mean S/N of about 150-200 per pixel (quasar+host). The
large pixel size of the detector was used, 0.2
.
Each grism
was exposed 1200 s, under photometric conditions and dark time,
which yields a mean S/N of about 150-200 per pixel (quasar+host). The
large pixel size of the detector was used, 0.2
![]() .
.
We show in the right panel of Fig. 1 and in Fig.
2 the orientation of the slitlets relative to the quasar
host and to the PSF star. In Fig. 2, the images have
been deconvolved and the quasar
has been removed from the data. The FORS mask consists of 19 slitlets
with fixed length and width (
![]() ). One slit was
centered on HE 1503+0228, one slit was centered on a bright PSF star and the
rest of the slits were used either to observe fainter PSF or
galaxies. Galaxy G1 is indicated in Fig. 1. It is at
). One slit was
centered on HE 1503+0228, one slit was centered on a bright PSF star and the
rest of the slits were used either to observe fainter PSF or
galaxies. Galaxy G1 is indicated in Fig. 1. It is at
![]() and is unrelated to the quasar.
and is unrelated to the quasar.
At the adopted spectral resolution, the area accessible on the CCD
without loosing spectral information at the edges of the array is
restricted to a strip of sky about 40
![]() wide. As we have to
observe simultaneously the quasar and at least one PSF star, the PA of
the mask is therefore imposed to us by the instrumental design, i.e.,
the 40
wide. As we have to
observe simultaneously the quasar and at least one PSF star, the PA of
the mask is therefore imposed to us by the instrumental design, i.e.,
the 40
![]() strip of sky has to include both the quasar and the
PSF star(s). This means that the slitlet centered on the quasar is
not necessarily oriented along one of the axes of symmetry of our
targets. It also means that we do not observe at parallactic
angle. This is however not a major problem as FORS1 has an efficient
atmospheric refraction corrector and the data remain unaffected by
slit losses.
strip of sky has to include both the quasar and the
PSF star(s). This means that the slitlet centered on the quasar is
not necessarily oriented along one of the axes of symmetry of our
targets. It also means that we do not observe at parallactic
angle. This is however not a major problem as FORS1 has an efficient
atmospheric refraction corrector and the data remain unaffected by
slit losses.
A two-dimensional wavelength calibration was applied in order to correct for slit curvature, followed by a two-dimensional sky subtraction. The spectrum of HE 1503+0228 and of the PSF star were reduced exactly in the same way, and they were rebinned to a common pixel size of 1 Å in the spectral direction. They were also rebinned to a common starting wavelength, which ensures that to each spectral resolution element of the quasar, corresponds the same spectral resolution element in the PSF.
Most current spectroscopic studies of quasar host galaxies are designed as off-axis observations, with the slit of the spectrograph placed one to several times the size of the seeing disk away from the center of the AGN (e.g., Hughes et al. 2000).
While such an observational strategy is minimizing contamination by the quasar, it has severe drawbacks. First, one can only study the outer parts of the galaxy. This is limiting the study to particular regions of the hosts. It also requires very long exposure times on large telescopes to detect the extremely faint wings of the hosts. Second, all velocity information is lost, as is the spatial information in general, along the galaxy's axes of symmetry. Finally, the method is still restricted to the most extended objects and does not allow a full decontamination of the quasar's light.
Instead, our observations are taken on-axis, placing the slit of the spectrograph on the quasar's center of light. This avoids all drawbacks of the off-axis observations, but requires clean post-processing techniques in order to remove accurately the spectrum of the AGN. For this purpose we use the spectroscopic version of the MCS deconvolution algorithm (Magain et al. 1998; Courbin et al. 2000). Using the spatial information contained in the spectrum of PSF stars located close to the object of interest, the algorithm sharpens the data in the spatial direction, sub-samples them in order to achieve smaller pixel size, and decomposes them into two channels containing (i) the spectrum of the AGN and (ii) the two-dimensional spectrum of the host galaxy.
In the deconvolved spectrum, the new sub-sampled pixel size is
0.1
![]() and 1 Å in the spectral direction. In Fig. 3
are displayed the one dimensional flux calibrated
spectra, integrated along the spatial direction on the deconvolved
data. Interestingly, the three FORS1 grisms have significant regions
of overlap that are in perfect agreement with one another. In
addition, at the redshift of HE 1503+0228, most emission lines are present in
two grisms. This allowed us to construct a combined 2-D flux
calibrated spectrum. All measurements presented in this paper, except
for velocity curves, are done on the final combined spectrum.
and 1 Å in the spectral direction. In Fig. 3
are displayed the one dimensional flux calibrated
spectra, integrated along the spatial direction on the deconvolved
data. Interestingly, the three FORS1 grisms have significant regions
of overlap that are in perfect agreement with one another. In
addition, at the redshift of HE 1503+0228, most emission lines are present in
two grisms. This allowed us to construct a combined 2-D flux
calibrated spectrum. All measurements presented in this paper, except
for velocity curves, are done on the final combined spectrum.
From the different emission lines of the quasar and of the galaxy, we can extract a sharp value for the redshift of HE 1503+0228, by simple Gaussian fitting. The lines of the host galaxy in the deconvolved spectrum have to be measured with particular care: in the center of the host, the lines are double, due to the velocity field of the galaxy and to the deconvolution method. This is mainly due to the extreme contrast between the narrow emission lines of the host, and the broad lines of the quasar: some of the flux in the sharpest parts of the host's emission lines is taken in the point-source component (the quasar) of the deconvolved spectrum, i.e., the central parts of the lines are dimmed. We have therefore taken the mean wavelength between the two sides of emission lines, when measuring the host's redshift. The results for each line are given in Table 1. The details of the individual emission lines is accessible via a method described in Sect. 4.2, which does not alter the center of the lines.
| Line | Redshift | Redshift |
| (host only) | (quasar only) | |
| OII (3727 Å) | 0.1353 | 0.1352 |
| H |
0.1357 | 0.1352 |
| OIII (4959 Å) | 0.1362 | 0.1349 |
| OIII (5007 Å) | 0.1356 | 0.1348 |
| OI (6300 Å) | 0.1355 | 0.1352 |
| NII (6548 Å) | 0.1352 | - |
| H |
0.1353 | 0.1352 |
| NII (6583 Å) | 0.1354 | - |
| SII (6716 Å) | 0.1356 | 0.1343 |
| Mean | <0.1355> | <0.1350> |
| Mean error | ( |
( |
In the spectroscopic version of the MCS algorithm (Courbin et al. 2000), the difference in spatial properties between the AGN (point source) and the host galaxy (extended component) is used to separate the spectra of these two sources. A smoothing in the spatial direction is applied for this purpose to the extended component. While such a decomposition method is well suited to most spectral regions of the host, it is not optimal for deriving velocity curves: spatial smoothing (which is not precisely known as it varies with the local S/N) may modify the spectral position of the lines at a given spatial position, by averaging spatial components of different radial velocities.
We have devised another method which is better suited for extracting radial velocity curves of the host galaxy. Instead of using the difference in spatial properties to extract the spectra, we take advantage of the different spectral properties of the AGN and host to determine the radial velocity as a function of distance.
The fact that the spectral lines of the host are much narrower than any feature in the AGN spectrum is used to determine the spectral position and intensities of the host spectral lines as a function of spatial position. More specifically, at each spatial coordinate we fit the sum of a Gaussian profile of variable width representing the host emission line, plus a smooth numerical curve accounting for the AGN spectrum plus the continuum of the host.
In doing this fit, we also take advantage of the constant shift in
wavelength between two given emission lines: several emission
lines are fitted simultaneously under the constraint that they are
separated by a fixed gap in wavelength. Thus, when we refer to the
H![]() velocity curve, we in fact use the H
velocity curve, we in fact use the H![]() and
[NII ] emission lines simultaneously. Similarly, the H
and
[NII ] emission lines simultaneously. Similarly, the H![]() curve is obtained from the H
curve is obtained from the H![]() and the [OIII ]
(5007 Å) lines, simultaneously. An example of such an extraction
is displayed in Fig. 4.
and the [OIII ]
(5007 Å) lines, simultaneously. An example of such an extraction
is displayed in Fig. 4.
| |
Figure 4:
Example of emission lines extraction. Here are the
H |
| Open with DEXTER | |
In converting the wavelength shifts into velocity curves, we take several effects into account:
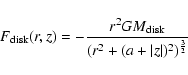 |
(2) |
| |
Figure 5: Schematic illustration of geometrical effects considered for deriving the velocity curves. Top: the original face-on galaxy is assumed to be circular (dotted line). Seen with an inclination i, it appears elliptical (dashed line). In addition, the slit is not aligned with the major axis of the inclined galaxy. Bottom: the mean velocity at one position along the slit, which would be integrated along a line perpendicular to the slit (dashed-dotted line) if the galaxy was seen face-on, has now to be integrated along a line which is inclined (and lengthened) with respect to the slit (dotted line; see text). |
| Open with DEXTER | |
Dark matter is assumed to be spherically symmetrical about the
galaxy's center. The force it creates at the distance r away from
the center, given a radially dependent density distribution is:
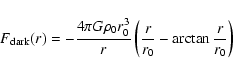 |
(3) |
The force from the central mass
![]() is simply
is simply
All the calculations in Eq. (5) assume that the galaxy is
seen face-on, the inclination being taken into account by the
![]() term. Due to the non-zero angle
term. Due to the non-zero angle ![]() between the slit and
the major axis of the galaxy, the velocity in Eq. (5) is a
weighted mean
between the slit and
the major axis of the galaxy, the velocity in Eq. (5) is a
weighted mean
![]() of several velocity components
across the slit.
of several velocity components
across the slit.
For each pixel j along the slit, lets say at point P (see Fig. 6), one can compute a mean velocity as follows:
| |
Figure 6:
Description of the integration domain for the computation of
|
| Open with DEXTER | |
![]() is the average of all the velocity components
located along the dash-dotted line in Fig. 5. If the
galaxy was seen face-on (as we would like it to be in
Eq. (5)), this line would be rotated and lengthened, and
mapped onto the dotted line of Fig. 5. The integral in
Eq. (6) runs along this dotted line. Its equation
(Eq. (7)) is easily obtained from geometrical
considerations, given the inclination i of the galaxy with respect
to the plane of the sky and given the orientation
is the average of all the velocity components
located along the dash-dotted line in Fig. 5. If the
galaxy was seen face-on (as we would like it to be in
Eq. (5)), this line would be rotated and lengthened, and
mapped onto the dotted line of Fig. 5. The integral in
Eq. (6) runs along this dotted line. Its equation
(Eq. (7)) is easily obtained from geometrical
considerations, given the inclination i of the galaxy with respect
to the plane of the sky and given the orientation ![]() of the slit
relative to the major axis of the galaxy:
of the slit
relative to the major axis of the galaxy:
The integration in Eq. (6) is then performed as follow: for
each position x along the major axis of the galaxy, we calculate the
distance r(x) from the galaxy's center O to the point of the
integration line that is considered. This distance is used to weight
each velocity component
![]() of the velocity
model, according to the light distribution of the galaxy in the
emission line. We have estimated the light distribution I(r) of the
galaxy, assuming it is intrinsically symmetrical about the center of the
galaxy. We model it by fitting a Moffat profile to the 1-dimensional
intensity profile along the emission line, and applying deprojection
(note that the fit of the emission line is one-dimensional, but since
I(r) is known analytically, one can compute weights in 2 dimensions
when calculating the integral in Eq. (6)). When
doing the fit, the Moffat profile is convolved with the PSF.
Correct normalisation is
assured by
of the velocity
model, according to the light distribution of the galaxy in the
emission line. We have estimated the light distribution I(r) of the
galaxy, assuming it is intrinsically symmetrical about the center of the
galaxy. We model it by fitting a Moffat profile to the 1-dimensional
intensity profile along the emission line, and applying deprojection
(note that the fit of the emission line is one-dimensional, but since
I(r) is known analytically, one can compute weights in 2 dimensions
when calculating the integral in Eq. (6)). When
doing the fit, the Moffat profile is convolved with the PSF.
Correct normalisation is
assured by
![]() :
the total flux of the regions
contributing to the measured emission at position P along the slit.
:
the total flux of the regions
contributing to the measured emission at position P along the slit.
The term
![]() in Eq. (6) is the projection of the
rotation velocity on the minor axis of the galaxy, which will give
rise to a radial velocity once inclination is taken into account. The
component of the velocity along the X-axis does not contribute to the
mean velocity calculation, once inclination has been taken into
account.
The intersections between the integration line and the slit edges, fiand
in Eq. (6) is the projection of the
rotation velocity on the minor axis of the galaxy, which will give
rise to a radial velocity once inclination is taken into account. The
component of the velocity along the X-axis does not contribute to the
mean velocity calculation, once inclination has been taken into
account.
The intersections between the integration line and the slit edges, fiand ![]() ,
give us the limits of the integration, as shown in
Figs. 5 and 6.
,
give us the limits of the integration, as shown in
Figs. 5 and 6.
An example of a inclination/seeing-corrected velocity curve is given
in Fig. 7 for the H![]() /N[II ] lines. In our
calculations of the linear scales and distances we have used H0=65 km s-1 Mpc-1,
/N[II ] lines. In our
calculations of the linear scales and distances we have used H0=65 km s-1 Mpc-1, ![]() ,
and
,
and
![]() ,
leading to a
scale of
,
leading to a
scale of
![]() kpc.
kpc.
![\begin{figure}
\par\includegraphics[width=8.8cm]{halpha.ps}\end{figure}](/articles/aa/full/2002/42/aa2687/Timg57.gif) |
Figure 7:
Inclination/seeing corrected velocity curves for the
H |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8.8cm,clip]{moy}\end{figure}](/articles/aa/full/2002/42/aa2687/Timg58.gif) |
Figure 8:
Mean velocity curve
between four models fitted on the H |
| Open with DEXTER | |
We give in Table 2 the best fit for the 5 parameters
of our mass model. The mean velocity curve, as extracted from
the H![]() and H
and H![]() lines is displayed in
Fig. 8. This mean corresponds to four independent curves
obtained for the H
lines is displayed in
Fig. 8. This mean corresponds to four independent curves
obtained for the H![]() and the H
and the H![]() lines, both seen
in two different grisms.
lines, both seen
in two different grisms.
Table 3 gives our mass estimates which are weighted means of the four fits presented in Table 2, the weights being a function of the residuals after modeling of the data obtained in each individual grism. These weights are the same as the ones applied to compute the mean velocity curve of Fig. 8.
We investigate in Table 4 the effect of the error on the inclination of the galaxy and on its PA. Uncertainties on inclination and orientation of the major axis lead to error bars on masses, which are summarized in Table 4.
| Line | Grism | a |
|
r0 |
|
|
| H |
R | 1088 |
|
0.30 | 2033 | 6.1 107 |
| H |
I | 1163 |
|
0.31 | 2074 | 4.8 107 |
| H |
B | 908 |
|
0.56 | 1753 | 3.5 106 |
| H |
R | 1428 |
|
0.23 | 2196 | 2.5 105 |
| Masses | r< 1 kpc | r< 3 kpc | r< 10 kpc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Masses ( |
r< 1 kpc | r< 3 kpc | r< 10 kpc |
| Inclination | |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Major axis | |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
These results should be interpreted with care, as there is a strong correlation between the model parameters and since the adopted model is simpler than reality. However, while the details of the mass distribution within the galaxy remain inaccurate, we can still determine the total mass of dark matter and as well the disk mass enclosed in a given radius.
Given the results in Tables 2-4, we infer a mass estimate of
![]() .
The corresponding mass,
integrated over 10 kpc is
.
The corresponding mass,
integrated over 10 kpc is
![]() .
Table 4 shows that an additional error
of 10% should be added, due in part to the uncertainty on the PA of the
major axis of the host, but mainly to the uncertainty on its inclination.
.
Table 4 shows that an additional error
of 10% should be added, due in part to the uncertainty on the PA of the
major axis of the host, but mainly to the uncertainty on its inclination.
One of the primary goals of our study is to infer the characteristics of the stellar population of quasar host galaxies: does the stellar population of HE 1503+0228 match that of a normal galaxy? Where does it lie in the Hubble sequence?
Let us first note that H = 14.57 mag corresponds, with the same
cosmological parameters used earlier, to an absolute magnitude of
![]() mag. This, in addition to the profile fitting described
in the previous sections, indicates a normal early type local spiral galaxy
(Bothun et al. 1985; Arimoto & Jablonka 1991). While the
photometric data alone already allow to point out a plausible
morphological type for the host of HE 1503+0228, spectroscopy is the key to
the determination of its stellar content. A few considerations have to
be made before looking at the spectral features in any detail.
mag. This, in addition to the profile fitting described
in the previous sections, indicates a normal early type local spiral galaxy
(Bothun et al. 1985; Arimoto & Jablonka 1991). While the
photometric data alone already allow to point out a plausible
morphological type for the host of HE 1503+0228, spectroscopy is the key to
the determination of its stellar content. A few considerations have to
be made before looking at the spectral features in any detail.
First, galactic extinction has to be taken into account. The extinction towards HE 1503+0228 is AB = 0.217 corresponding to E(B-V)=0.05 (Schlegel et al. 1998). Our spectrum of HE 1503+0228 has been corrected accordingly.
![\begin{figure}
\par\includegraphics[width=8.8cm]{HalphaOII.ps}\end{figure}](/articles/aa/full/2002/42/aa2687/Timg92.gif) |
Figure 9:
The relation between the equivalent widths of
H |
| Open with DEXTER | |
Second, although no velocity standard stars were taken during the
observations, the resolution in the R-grism (4.9 Å; 3.6 Å at
rest-frame) is good enough to make use of the stellar library of Jacoby
et al. (1984) (FWHM =3.5 Å). This gives a velocity dispersion of ![]() 170 km s-1, which we only take as an indicative upper limit value.
170 km s-1, which we only take as an indicative upper limit value.
Third, we observed HE 1503+0228 with three different grisms, each having a
different dispersion. The three spectra were combined in order to
cover the wide wavelength range 3670 Å to 9165 Å (3150 Å to
8073 Å once corrected from the redshift z=0.1355, or v=37837.4 km s-1). In doing this, we have degraded the observations to the
resolution of the less resolving grism, i.e., 5.7 Å (or ![]() 5 Å at rest-frame).
5 Å at rest-frame).
Finally, due to the low signal-to-noise ratio of the spectrum in its bluer part, we consider only features from 4000 Å on (3523 Å at rest-frame).
We have only considered the integrated spectrum of HE 1503+0228. In fact, the signal-to-noise of the measurements on each individual spatial resolution element of the 2D data varies between 3 and 6, and therefore does not give much hope in tracing any radial variation in the stellar population, unless deeper data are obtained.
In the following, we measure well known indicators for the underlying stellar populations, for the host of HE 1503+0228, and we compare them with the values obtained for two control samples: the one of Trager et al. (1998) for the elliptical galaxies, and the one of Kennicutt (1992a,b) for the spiral galaxies.
![\begin{figure}
\par\includegraphics[width=8.8cm]{D4000Hbeta.ps}\end{figure}](/articles/aa/full/2002/42/aa2687/Timg93.gif) |
Figure 10:
The relation between the 4000 Å break and the equivalent
width of H |
| Open with DEXTER | |
One of our concern was to verify that the deconvolution procedure had indeed left out any non thermal excitation process.
We have measured the equivalent widths (EW) of the most prominent
emission lines seen in the spectrum of HE 1503+0228, i.e., [OII ],
[OIII ](4959 Å), [OIII ](5007 Å) and H![]() +[NII ]
(see Table 5).
+[NII ]
(see Table 5).
Kennicutt (1992a) provided measurement of the Oxygen lines [OII ]
(3727 Å), [OIII ] (5007 Å) and H![]() +[NII ]. He noted
that among galaxies with normal star formation rates
(EW(H
+[NII ]. He noted
that among galaxies with normal star formation rates
(EW(H![]() +[NII ])
+[NII ]) ![]() 40 Å), the [OIII ] lines are
rarely detected at all (
40 Å), the [OIII ] lines are
rarely detected at all (
![]() Å). For HE 1503+0228, while
EW(H
Å). For HE 1503+0228, while
EW(H![]() +[NII ])
+[NII ]) ![]() 30 Å, we detect [OIII ], with
an equivalent width of
30 Å, we detect [OIII ], with
an equivalent width of ![]() 4 Å. This is the only and discreet
sign of an excitation process in or surrounding HE 1503+0228 which is not
directly related to star formation and, hence, which might be
triggered by the central AGN radiation field. Kennicutt (1992a) also
reported that galaxies dominated by stellar photoionization follow a
mean relation EW([OII ])
4 Å. This is the only and discreet
sign of an excitation process in or surrounding HE 1503+0228 which is not
directly related to star formation and, hence, which might be
triggered by the central AGN radiation field. Kennicutt (1992a) also
reported that galaxies dominated by stellar photoionization follow a
mean relation EW([OII ]) ![]() 0.4
EW(H
0.4
EW(H![]() +[NII ]) (with an rms of 50%). HE 1503+0228 falls nearly
exactly on this relation, as shown in Fig. 9. Kennicutt's
galaxies are represented by plain dots, the mean relationship between
H
+[NII ]) (with an rms of 50%). HE 1503+0228 falls nearly
exactly on this relation, as shown in Fig. 9. Kennicutt's
galaxies are represented by plain dots, the mean relationship between
H![]() +[NII ] and [OII ] is the solid line. The position
of HE 1503+0228 in this plane is indicated by a cross.
+[NII ] and [OII ] is the solid line. The position
of HE 1503+0228 in this plane is indicated by a cross.
HE 1503+0228 exhibits a weak [OIII ] (5007 Å) line. We have left out from the Kennicutt sample the objects which displays strong [OIII ] (5007 Å) lines, when analysing in the next section the absorption line features. This ensures that we compare HE 1503+0228 with objects of similar properties.
| Name | D4000 | G4300 | Ca4455 | Mg2 | Fe5270 | Fe5335 | [OIII ] | H |
| Value | 1.48 | 3.41 | 2.03 | 0.157 | 1.89 | 1.12 | 4.2 | 30. |
| Error | 0.04 | 0.16 | 0.12 | 0.002 | 0.08 | 0.11 | 0.3 | 2. |
To further investigate this matter, we have measured the line
intensity ratios, [OIII ]/H![]() (0.05), [OIII ]/H
(0.05), [OIII ]/H![]() (0.54), [NII ]/H
(0.54), [NII ]/H![]() (-0.20).
Due to the deconvolution procedure, the ratios between Oxygen and
Balmer lines are upper limits. Indeed, the Balmer lines are probably
underestimated. When placed in the diagnostic diagrams of Sodré &
Stasinska (1999), the host galaxy of HE 1503+0228 falls perfectly on
the sequence drawn by the normal spiral galaxies.
(-0.20).
Due to the deconvolution procedure, the ratios between Oxygen and
Balmer lines are upper limits. Indeed, the Balmer lines are probably
underestimated. When placed in the diagnostic diagrams of Sodré &
Stasinska (1999), the host galaxy of HE 1503+0228 falls perfectly on
the sequence drawn by the normal spiral galaxies.
To summarize, our analysis of the emission lines suggests that HE 1503+0228 is a perfectly normal spiral galaxy, where the gas emission is dominated by ionization by stars rather than by the central AGN.
![\begin{figure}
\par\includegraphics[width=8.8cm]{Fe5270Mg2.ps}\end{figure}](/articles/aa/full/2002/42/aa2687/Timg96.gif) |
Figure 11: The relation between the Fe5270 and Mg2 index for the normal spirals of Kennicutt et al. (1992) (dots) and the ellipticals of Trager et al. (1998) (open triangles). As in Figs. 9 and 10, the cross indicates the position of HE 1503+0228. |
| Open with DEXTER | |
Our spectra have sufficient signal-to-noise to measure the Lick
indices for several stellar absorption features. As the spectral
resolution of the Lick system is lower than the resolution of our
data, we have convolved the spectrum of HE 1503+0228 with the appropriate
Gaussian kernel, in order to match a 200
![]() rest-frame resolution.
rest-frame resolution.
For a full compatibility between the measurements done for HE 1503+0228 and for the galaxy control sample (see previous section), we have re-measured the Lick indices on Kennicutt's galaxies in exactly the same way as for HE 1503+0228.
A difficulty when looking at the stellar population in HE 1503+0228 is to
avoid contamination due to the gas emission. This emission can either
"fill-in'' absorption lines - the Balmer lines is a well known
example, but Mgb can be affected as well (Goudfrooij & Emsellem
1996) - or contaminate the continuum side bands used for the
measurements of the equivalent widths. We have identified four
absorption lines that are strong enough and free of this contamination
by emission lines. They correspond to the Lick indices G4300, Ca4455,
Ca4668, Fe5270 and Fe5335. With only a tiny change in the definition
of the continuum window used for the Mg2 index, we could avoid
contamination by the [OIII ] (4959 Å) emission line for this
index. The small change we impose on the continuum side bands produces
a change of at most ![]() 0.04 mag (or 20%) in the measurement of the
Mg2 index. In addition to the indices for the absorption lines, we
also measure the important calcium break at 4000 Å, which gives the
D4000 index (Bruzual 1983).
0.04 mag (or 20%) in the measurement of the
Mg2 index. In addition to the indices for the absorption lines, we
also measure the important calcium break at 4000 Å, which gives the
D4000 index (Bruzual 1983).
Table 5 summarizes the results of our measurements. The
available signal-to-noise ratio (per Å) for performing the
measurements varies between ![]() 10 (blue part) and
10 (blue part) and ![]() 25 (red
part).
25 (red
part).
The continuum shape of HE 1503+0228 is rather flat, indicative of on-going
star formation. Similarly to the result of Fig. 9,
Fig. 10 puts
HE 1503+0228 among normal spiral galaxies. The latter figure compares the
index D4000, which measures the 4000 Å break, with the equivalent
width of H![]() which is indicative of the presence of star
formation. HE 1503+0228 nicely falls on the sharp relation traced by normal
spirals.
which is indicative of the presence of star
formation. HE 1503+0228 nicely falls on the sharp relation traced by normal
spirals.
As for the chemical abundances, we chose to present in Fig.
11 the Mg2 and Fe5270 indices. They trace the
![]() and iron peak-elements, respectively. Here again, HE 1503+0228 is
located exactly on the Hubble sequence, at the location of spiral
galaxies, rather than ellipticals. Furthermore, the values of the
absorption line equivalent widths strongly suggests the stellar
population of an early type spiral galaxy.
and iron peak-elements, respectively. Here again, HE 1503+0228 is
located exactly on the Hubble sequence, at the location of spiral
galaxies, rather than ellipticals. Furthermore, the values of the
absorption line equivalent widths strongly suggests the stellar
population of an early type spiral galaxy.
We have undertaken a VLT program aimed at unveiling the spectroscopic properties of quasar host galaxies for a sample of radio quiet, bright quasars at low redshift. Our long term scientific goal is double: (1) to compare the stellar populations of quasar hosts with those of other ("normal'') galaxies, and (2) to study their dynamics, as close as possible to the central AGN.
The present paper considers HE 1503+0228 as a test case. An important part of our work is dedicated to the correction of geometrical effects and removal of the atmospheric blurring. This is crucial in the central parts of the galaxy, with sizes comparable to the seeing disk.
We find that the stellar population of the host galaxy of HE 1503+0228
compares well with that of the normal non-AGN spiral galaxies of
Kennicutt (1992a,b) and Trager et al. (1998). They show no
trace of enhanced star formation. The interstellar medium does not
show significant ionization by the central AGN. Its mass
![]() also compares
very well with that of other spiral galaxies. To summarize, the host
galaxy of HE 1503+0228 is a normal spiral galaxy.
also compares
very well with that of other spiral galaxies. To summarize, the host
galaxy of HE 1503+0228 is a normal spiral galaxy.
Acknowledgements
The authors would like to thank Sandrine Sohy for help with some of the intensive programing involved in this work. Géraldine Letawe is a teaching assistant supported by the University of Liège, (Belgium) and is partially funded by the Pôle d'Attraction Interuniversitaire, P4/05 (SSTC, Belgium). Frédéric Courbin acknowledges financial support through Marie Curie grant MCFI-2001-0242. Chilean grant FONDECYT/3990024 and additional support from the European Southern Observatory are also gratefully acknowledged. Dante Minniti is supported in part by Fondap Center for Astrophysics.