In our sample, the core is the brightest VLBI component in 152 of the 165 VLBA images. It usually contains 50-90% of the total flux density of the source. Typically it is the core region that becomes brighter and fainter during the TFD flares. Similar behaviour has been noted previously in, for example, 3C 279 (Wehrle et al. 2001). This pattern is completely different from that observed in 3C 345, in which the fluxes of the components peak well downstream of the core (Valtaoja et al. 1999). In our sample there is one source, PKS 0202+149, with a component (B) whose flux clearly peaks downstream. However, this component is not very strong (0.3 Jy at maximum) and it still peaks quite close to the core - at a separation of only 0.36 mas. There are also a few other sources in our sample with a component that might peak downstream, but we do not have sufficiently well-sampled observations to confirm these. In any case, these features are considerably weaker than the flux level involved in most of the core flares.
These apparent VLBI core flares are therefore largely responsible for the TFD variability in our sources. The question is: Are these core flares due to true changes in the radio core (changes in bulk Lorentz factor, electron energy spectrum, etc.) or are they associated with the birth of new moving VLBI components that blend with the core at the resolution of the images?
We define a core flare to be an increase in the VLBI core-region flux that is (1) >30%
within one year and (2) greater than the noise level of the TFD curve. There were altogether
24 core flux variations satisfying our conditions. When analysing these VLBI core flares and
coincident TFD variations, we noticed that, in 11 cases, after the core flare and an associated
TFD outburst had peaked and were already fading, a new VLBI component appeared in the jet (see
Table 5). Moreover, the flux of this new component was decreasing as well.
Of 13 cases not showing a new component after the core flare, 6 simply did not have enough data
because the core flare occurred during the last observing epoch. Thus, in 11 of the 18 cases
(61%) the observed increase in VLBI core flux is consistent with being caused by the
appearance of a new moving component, which brightens and then starts to decay within
![]() 0.15 mas (the typical VLBA beamsize at 43 GHz) of the actual radio core. This
represents a high percentage if we consider the sparsity of the VLBI time coverage, systematic
uncertainties in VLBI model fitting, and the problems related to component identification
across epochs.
0.15 mas (the typical VLBA beamsize at 43 GHz) of the actual radio core. This
represents a high percentage if we consider the sparsity of the VLBI time coverage, systematic
uncertainties in VLBI model fitting, and the problems related to component identification
across epochs.
We explore the above interpretation further by reconstructing the core flares under the assumption that only new components contribute to the variations in flux while the brightness of the actual core remains constant. We then decompose the total flux into a constant baseline flux from the core plus a new shock component with variable flux. We choose the value of the baseline flux density to be the lowest observed level (either the minimum core-region flux or the weakest TFD flux, whichever is lower). Two examples of our reconstructions are presented in Figs. 5 and 6 (PKS 0420-014 and PKS 0528+134).
![\begin{figure}
\par\includegraphics[angle=90,width=16.9cm,clip]{MS2682f5.eps}\end{figure}](/articles/aa/full/2002/42/aa2682/Timg70.gif) |
Figure 5: Reconstruction of the "core flare'' in quasar PKS 0420-014. The upper panel shows the 37 GHz light curve, three exponential flare models, and the summed model fit to the TFD. The lower panel presents the light curves of the individual VLBI components. The VLBI core flare in 1995 is decomposed into a core component with a constant flux (horizontal dashed line) and a new component with decreasing flux (dotted curve). The figure also displays the estimated fluxes and separations from the core for component B of Jorstad et al. (2001a). The arrow gives the estimated epoch of zero separation from the core, obtained by extrapolation of the VLBI data. |
![\begin{figure}
\par\includegraphics[angle=90,width=16.9cm,clip]{MS2682f6.eps}\end{figure}](/articles/aa/full/2002/42/aa2682/Timg71.gif) |
Figure 6: A reconstruction of the "core flares'' in quasar PKS 0528+134. That corresponding to the TFD flare in 1995.5 and component B3 of Jorstad et al. (2001a) can be reconstructed easily (dotted line), but for the flare in 1995.9 (corresponding to component B4 of Jorstad et al. 2001a) we do not have enough VLBI observations to determine whether its behaviour is similar. |
| Source |
|
|
|
|
R [mas] | |
| 0219+428 | 43 | 1995.47-1996.60 | 0.45 | 1996.60 | 0.22 | 0.51 |
| 0420-014 | 43 | 1995.31-1995.59 | 1.04 | 1996.34 | 0.09 | 0.21 |
| 0458-020 | 43 | 1995.31-1995.47 | 0.40 | 1995.47 | 0.60 | 0.20 |
| 0528+134 | 22 | 1994.65-1995.01 | 2.30 | 1995.01 | 1.69 | 0.19 |
| 0528+134 | 43 | 1995.01-1995.47 | 2.24 | 1995.47 | 3.47 | 0.14 |
| 0851+202 | 43 | 1995.47-1996.34 | 1.91 | 1996.34 | 0.28 | 0.36 |
| 1156+295 | 22 | 1996.34-1996.60 | 0.31 | 1996.60 | 0.34 | 0.20 |
| 1222+216 | 22 | 1996.90-1997.58 | 0.40 | 1997.58 | 0.09 | 0.45 |
| 1633+382 | 22 | 1994.76-1995.79 | 1.04 | 1995.79 | 0.60 | 0.13 |
| 2230+114* | 43 | 1996.60-1998.48 | 5.00 | 1998.48 | 2.14 | 0.11 |
| 2251+158 | 43 | 1995.01-1995.31 | 4.92 | 1995.31 | 4.43 | 0.06 |
* Includes 1998 VLBA data from Rantakyr
![]() et al. (2002).
et al. (2002).
In order to test the above scenario, we estimate the separation between the true core and the new VLBI component during core flares by assuming that the proper motions remain constant from the birth of a knot to its last appearance on the images of Jorstad et al. (2001a). We find five cases (PKS 0420-014: 1995 Apr. 22, 1995 Jun. 21, 1995 Aug. 04; PKS 0528+134: 1995 Apr. 22, and 1156+295: 1996 May 04) in which the expected separation during a VLBA observation was larger than about one-third of the beam size. If the source is not very complicated, i.e., if it can be described using a small number of circular-Gaussian components, partially resolved compact structure is revealed by non-zero closure phases on the longest baselines. Closure phases are constructed to cancel out antenna-based calibration errors, hence they indicate the presence of non-point components in a model-independent fashion.
Partially resolved structure in the core region can take on two basic forms: (1) a slightly extended core with no other components or (2) one or more non-core components within one beamwidth of the brightness centroid of the core. To compare these two hypotheses we plot closure phases from triangles consisting of both long and short baselines (Figs. 7 and 8). We superimpose two best-fit models corresponding to the above hypotheses. It is evident - and also expected - that these models differ significantly only on long baselines. It can be clearly seen that the two-component core models provide much better fits to the data than do the single-component models. Also, in Fig. 7 the progressively increasing absolute value of the closure phase over the three successive epochs can be explained by a moving component close to the core.
![\begin{figure}
\par\includegraphics[width=16.9cm,clip]{MS2682f7.eps}\end{figure}](/articles/aa/full/2002/42/aa2682/Timg73.gif) |
Figure 7: Closure phases from triangles consisting of long (left panels) and short (right panels) baselines from a series of observations of PKS 0420-014. Two core-region models are superimposed: dashed curve: a single, perhaps extended component; solid curve: a point-like core plus a second point-like component. The fourth epoch (1997 July 31) is for comparison only: no component close to the core is expected from the TFD light curves nor indicated by the VLBA data. |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{MS2682f8.eps}\end{figure}](/articles/aa/full/2002/42/aa2682/Timg74.gif) |
Figure 8: Closure phases from observations of 0528+134 and 1156+295. Continued from Fig. 7. |
We therefore find evidence for new components in the vicinity of the VLBI core during major TFD
flares, but the brightness of these moving knots has usually decayed considerably
by the time the features become distinct from the core on VLBI maps. This implies that a
majority - perhaps all - of the strongest TFD flares are associated with bright knots that
fade within ![]() 0.1-0.3 mas of the core. (The only source in our data set that has
substantial variations in flux outside the core region is 3C 454.3, where stationary
feature C has brightness and variability comparable to the core.) If the moving components are
shock waves, the shocks must therefore develop much more quickly, and closer to the core, than
previously thought. The bright features found in jets of classical superluminal radio sources
well downstream of the core are mainly lower-frequency phenomena, although in some objects (e.g.,
3C 279; see Wehrle et al. 2001) an occasional prominent component remains bright long
after it detaches from the core on the images. The implication is that the critical synchrotron
frequency of the highest energy electrons in the knot decays rapidly beyond the core region. This
is probably the combination of (1) radiative energy losses near the core, (2) decay of the
magnetic field and electron energies from downstream expansion of the jet, and (3) weak
in situ particle acceleration outside the core region. These conditions have important
implications for models of shocks and other structures in relativistic jets.
0.1-0.3 mas of the core. (The only source in our data set that has
substantial variations in flux outside the core region is 3C 454.3, where stationary
feature C has brightness and variability comparable to the core.) If the moving components are
shock waves, the shocks must therefore develop much more quickly, and closer to the core, than
previously thought. The bright features found in jets of classical superluminal radio sources
well downstream of the core are mainly lower-frequency phenomena, although in some objects (e.g.,
3C 279; see Wehrle et al. 2001) an occasional prominent component remains bright long
after it detaches from the core on the images. The implication is that the critical synchrotron
frequency of the highest energy electrons in the knot decays rapidly beyond the core region. This
is probably the combination of (1) radiative energy losses near the core, (2) decay of the
magnetic field and electron energies from downstream expansion of the jet, and (3) weak
in situ particle acceleration outside the core region. These conditions have important
implications for models of shocks and other structures in relativistic jets.
It is possible that all of the variations in flux in the VLBI core region during these flares actually occur in new moving knots. However, our observations are also consistent with the possibility that a disturbance both creates a new shock wave and brightens the core itself as it passes through the core region. There may be some evidence supporting this scenario, since in two sources, 3C 279 and 1510-089, the new VLBI component is observed during (rather than only after) a major core flare. Based on the present data, we cannot determine which scenario is correct. The model in which the TFD variability is completely due to shocks is the simpler and requires fewer assumptions. On the other hand, it would be surprising (and revealing in terms of models for the core; see Daly & Marscher 1988) if the disturbance in velocity and/or energy density that creates the shock did not also affect the core (see, e.g., the hydrodynamical simulations of Gómez et al. 1997).
We calculate the distance from the core where a new component reaches its maximum luminosity:
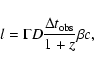 |
(2) |
Copyright ESO 2002