The first-order Fermi acceleration process at an ultra-relativistic shock wave is expected to create a particle spectrum with the unique asymptotic spectral index
A&A 394, 1141-1144 (2002)
DOI: 10.1051/0004-6361:20021173
M. Ostrowski1,2 - J. Bednarz1
1 - Obserwatorium Astronomiczne, Uniwersytet Jagiellonski,
ul. Orla 171, 30-244 Kraków, Poland
2 -
Institut für Theoretische Physik, Lehrstuhl IV: Weltraum und
Astrophysik, Ruhr-Universität Bochum, Germany
Received 17 April 2002 / Accepted 23 July 2002
Abstract
The first-order Fermi acceleration process at an ultra-relativistic
shock wave is expected to create a particle spectrum with the unique
asymptotic spectral index
![]() .
Below,
we discuss this result and differences in its various derivations, which
- explicitly or implicitly - always require highly turbulent
conditions downstream of the shock. In the presence of medium amplitude
turbulence the generated particle spectrum can be much steeper than the
above asymptotic one. We also note problems with application of the
pitch angle diffusion model for particle transport near the
ultra-relativistic shocks.
.
Below,
we discuss this result and differences in its various derivations, which
- explicitly or implicitly - always require highly turbulent
conditions downstream of the shock. In the presence of medium amplitude
turbulence the generated particle spectrum can be much steeper than the
above asymptotic one. We also note problems with application of the
pitch angle diffusion model for particle transport near the
ultra-relativistic shocks.
Key words: acceleration of particles - shock waves - X-rays: bursts - gamma-rays: bursts - ISM: cosmic rays
In the discussion below we neglect the strictly parallel shocks, where some of our objections can be invalid. However, such shocks are not expected to frequently occur in the universe.
The work of Bednarz & Ostrowski (1997, 1998) was based on Monte Carlo
simulations of particle transport governed by small amplitude pitch
angle scattering. Thus, depending on the scattering parameter ![]() (a mean time between successive scattering acts) and
(a mean time between successive scattering acts) and
![]() (the maximum angular scattering amplitude), we were able
to model situations with different mean field configurations and
different amounts of turbulence. One should note that the mean field
configuration downstream of the shock was derived here from the mean
upstream field using the appropriate jump conditions and trajectories of
particles interacting with the shock discontinuity were derived exactly
for such fields. A particle trajectory was derived in the respective
local plasma rest frame, with the Lorentz transformation applied at each
particle shock crossing. The approach takes into account correlations in
the process due to the regular part of the magnetic field, but
irregularities responsible for pitch angle scattering are introduced at
random. In order to model particle pitch angle diffusion upstream of the
shock, with nearly a delta-like angular distribution
(the maximum angular scattering amplitude), we were able
to model situations with different mean field configurations and
different amounts of turbulence. One should note that the mean field
configuration downstream of the shock was derived here from the mean
upstream field using the appropriate jump conditions and trajectories of
particles interacting with the shock discontinuity were derived exactly
for such fields. A particle trajectory was derived in the respective
local plasma rest frame, with the Lorentz transformation applied at each
particle shock crossing. The approach takes into account correlations in
the process due to the regular part of the magnetic field, but
irregularities responsible for pitch angle scattering are introduced at
random. In order to model particle pitch angle diffusion upstream of the
shock, with nearly a delta-like angular distribution
![]() (
(![]() - a momentum vector inclination to the shock
normal), an extremely small scattering amplitude should be used
- a momentum vector inclination to the shock
normal), an extremely small scattering amplitude should be used![]() ,
,
![]() .
Increasing the
shock Lorentz factor results in decreasing the momentum perturbation
required for its transmission downstream and leaves a shorter time for
this perturbation, t1. In the applied pitch angle diffusion approach,
the momentum variation due to the regular component of the magnetic
field scales like t1, whence the diffusive change scales like
t11/2. Thus growing
.
Increasing the
shock Lorentz factor results in decreasing the momentum perturbation
required for its transmission downstream and leaves a shorter time for
this perturbation, t1. In the applied pitch angle diffusion approach,
the momentum variation due to the regular component of the magnetic
field scales like t1, whence the diffusive change scales like
t11/2. Thus growing ![]() leads to decreasing t1 and the
diffusive term has to dominate at sufficiently large
leads to decreasing t1 and the
diffusive term has to dominate at sufficiently large ![]() .
It is
the reason why in our simulations the orientation of the regular
magnetic field ceases to play a role in the limit
.
It is
the reason why in our simulations the orientation of the regular
magnetic field ceases to play a role in the limit
![]() ,
resulting in the spectral index convergence to its asymptotic value.
,
resulting in the spectral index convergence to its asymptotic value.
However, one should note that with decreasing ![]() and
and
![]() ,
when the interaction proceeds at the sub-resonance
(
,
when the interaction proceeds at the sub-resonance
(![]()
![]() )
spatial scale, a serious physical problem with the applied
approach appears. In order to scatter particle momentum uniformly
within a narrow cone centred on the initial momentum, it requires the
short wave turbulence to be non-linear at the shortest scales. In our
discussion of the "effective'' magnetic field,
)
spatial scale, a serious physical problem with the applied
approach appears. In order to scatter particle momentum uniformly
within a narrow cone centred on the initial momentum, it requires the
short wave turbulence to be non-linear at the shortest scales. In our
discussion of the "effective'' magnetic field, ![]() ,
in the pitch angle
diffusion simulations (Bednarz & Ostrowski 1996; cf. Appendix below) we
evaluate the lower limit of such an effective field from the curvature of
simulated particle trajectories as
,
in the pitch angle
diffusion simulations (Bednarz & Ostrowski 1996; cf. Appendix below) we
evaluate the lower limit of such an effective field from the curvature of
simulated particle trajectories as
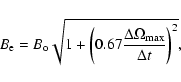 |
(1) |
An analogous pitch angle diffusion modelling appended the considerations of
Gallant et al. (1999; for a more detailed description see Achterberg et al. 2001). They considered the highly turbulent conditions near the shock
leading to the particle pitch angle diffusion with respect to the
shock normal, i.e. the regular part of the magnetic field was
neglected. These computations gave essentially the same spectral indices
as the asymptotic one derived by Bednarz & Ostrowski (1998). Also, in a
variant of this model with uniform magnetic field upstream of the shock
and fully chaotic turbulent field downstream, the resulting spectral
index did not vary substantially. The physical content of the
discussed model is substantially different from the Bednarz &
Ostrowski one because it neglects the influence of the uniform field (or
long wavelength perturbations with
![]() )
resulting in
magnetic field correlations at both sides of the shock. Thus, it
provides spectra with the asymptotic spectral index at quite moderate
)
resulting in
magnetic field correlations at both sides of the shock. Thus, it
provides spectra with the asymptotic spectral index at quite moderate
![]() ,
a feature also present in the Bednarz & Ostrowski
simulations for parallel shocks. However, if the amplitude of the
magnetic field turbulence is limited, these simulations cannot
reproduce spectrum steepening (or flattening at intermediate Lorentz
factors) in the presence of oblique magnetic fields (cf. Ostrowski 1993;
Bednarz & Ostrowski 1998; Begelman & Kirk 1990). Both the above models
describe essentially the same physical situation for shocks
propagating in the highly turbulent medium and, of course, in rarely -
if ever - occurring parallel relativistic shocks.
,
a feature also present in the Bednarz & Ostrowski
simulations for parallel shocks. However, if the amplitude of the
magnetic field turbulence is limited, these simulations cannot
reproduce spectrum steepening (or flattening at intermediate Lorentz
factors) in the presence of oblique magnetic fields (cf. Ostrowski 1993;
Bednarz & Ostrowski 1998; Begelman & Kirk 1990). Both the above models
describe essentially the same physical situation for shocks
propagating in the highly turbulent medium and, of course, in rarely -
if ever - occurring parallel relativistic shocks.
An alternative discussion of the acceleration process presented by Gallant & Achterberg (1999) was based on a simple turbulence model. In their approach a highly turbulent magnetic field configuration was assumed upstream and downstream of the shock, idealized as cells filled with randomly oriented, uniform (within a cell) magnetic fields. With such an approach, particles crossing the shock enter a new cell with a randomly selected magnetic field configuration. Thus, there always occur configurations allowing some particles crossing downstream to reach the shock again and again. As a result of successive energy increases of the same finite fraction of accelerated particles, the power law spectrum is formed. In this model there is no need for upstream magnetic field perturbations if the considered oblique magnetic field configuration can turn all upstream particles back to the shock.
Two quasi-analytic approaches to the considered acceleration process
were presented by Kirk et al. (2000) and Vietri (2002). Both provide
methods to solve the Fokker-Planck equation describing particle
advection with the general plasma flow and the small amplitude
scattering of particle pitch angle as measured with respect to the
shock normal. The important work of Kirk et al. modified the Kirk &
Schneider (1987) series expansion approach to treat the delta-like
angular distribution upstream of the shock. An analytically more simple
Vietri approach applies convenient ansatz'es for the anisotropic
upstream and downstream particle distributions, resembling the Peacock
(1981) approach to acceleration at "ordinary'' relativistic shocks. Both
methods confirm the results of the earlier numerical modelling. A
deficiency of the above semi-analytic approaches is its inability to
treat situations with mildly perturbed magnetic fields, on average
oblique to the shock normal. If considered valid for different
configurations of the mean magnetic field, these models require the large
amplitude short wave turbulence to remove signatures in particle
trajectories of the uniform background field or of the long wave
perturbations. Thus it provides an alternative description of the same
physical situation discussed earlier with numerical methods by Bednarz
& Ostrowski (1998) in the
![]() limit or their parallel
shock results and all other authors applying small amplitude pitch angle
scattering simulations at parallel shock waves.
limit or their parallel
shock results and all other authors applying small amplitude pitch angle
scattering simulations at parallel shock waves.
The discussed approaches to the
cosmic ray first-order Fermi acceleration at relativistic shocks yield
consistent estimates of the asymptotic spectral index ![]() (2.2,
2.3). However, the result is not as universal as one could infer from
the convergent conclusions of different authors, because all presented
derivations require (explicitly or implicitly) large amplitude MHD
turbulence near the shock. Only the Bednarz & Ostrowski (1998) modelling
allows one to treat - in a simplified way - conditions with medium
amplitude perturbations of the magnetic field. In such conditions
particle spectra are expected to be very steep at high shock Lorentz
factors. The spectra considered by Bednarz & Ostrowski flatten at large
(2.2,
2.3). However, the result is not as universal as one could infer from
the convergent conclusions of different authors, because all presented
derivations require (explicitly or implicitly) large amplitude MHD
turbulence near the shock. Only the Bednarz & Ostrowski (1998) modelling
allows one to treat - in a simplified way - conditions with medium
amplitude perturbations of the magnetic field. In such conditions
particle spectra are expected to be very steep at high shock Lorentz
factors. The spectra considered by Bednarz & Ostrowski flatten at large
![]() due to an implicit increase of the short wave turbulence in
their model, approaching closer and closer the parallel shock
configuration considered by the other authors. Until now the situation
with the medium amplitude turbulence,
due to an implicit increase of the short wave turbulence in
their model, approaching closer and closer the parallel shock
configuration considered by the other authors. Until now the situation
with the medium amplitude turbulence,
![]() ,
has not been
studied
in the limit of large
,
has not been
studied
in the limit of large ![]() ,
however, from comparison with the
results of Begelman & Kirk (1990), Ostrowski (1993) and of Bednarz &
Ostrowski (1998) for intermediate shock Lorentz factors, we expect
very steep spectra to be formed in such conditions. Thus, if the
conditions with limited turbulence are met at a large
,
however, from comparison with the
results of Begelman & Kirk (1990), Ostrowski (1993) and of Bednarz &
Ostrowski (1998) for intermediate shock Lorentz factors, we expect
very steep spectra to be formed in such conditions. Thus, if the
conditions with limited turbulence are met at a large ![]() shock, it
can be unable to accelerate particles to very high energies in the
first-order Fermi mechanism. On the other hand the "low'' energy
electrons radiating from ultra-relativistic shocks could be accelerated
by the non-first-order processes, analogous to the ones discussed by
Hoshino et al. (1992) or Pohl et al. (2001).
shock, it
can be unable to accelerate particles to very high energies in the
first-order Fermi mechanism. On the other hand the "low'' energy
electrons radiating from ultra-relativistic shocks could be accelerated
by the non-first-order processes, analogous to the ones discussed by
Hoshino et al. (1992) or Pohl et al. (2001).
The main deficiency of the approaches applying the pitch angle diffusion equation, in particular of our own attempt to discuss cases with oblique background magnetic fields, is their limitation to particular, highly turbulent conditions near the shock. This limitation may be significant or non-significant, depending on whether such conditions exist downstream of the ultra-relativistic shock. In the process discussed by Medvedev & Loeb (1999) such short-wave non-linear turbulence is created downstream of the shock, in the non-resonant wave-vector range for the shock accelerated particles.
Acknowledgements
MO is grateful to Reinhard Schlickeiser for the invitation to the Institute for Theoretical Physics of the Ruhr University, where this work was partly done, and to Yves Gallant and Bohdan Hnatyk for valuable discussions. The work was supported by the Komitet Badan Naukowych through the grant PB 258/P03/99/17.
Let us evaluate the magnetic field components responsible for regular,
![]() ,
and turbulent,
,
and turbulent,
![]() ,
angular deviations
of the particle momentum during a single particle propagation time-step
,
angular deviations
of the particle momentum during a single particle propagation time-step
![]() .
For the regular deviation due to the mean magnetic field
.
For the regular deviation due to the mean magnetic field
![]()
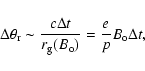 |
(A.1) |
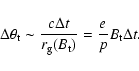 |
(A.2) |
![\begin{displaymath}B_{\rm e} = B_{\rm o} \sqrt{ 1 + \left[ {2 \over 3} {\Delta \...
... max}} \over
{e B_{\rm o} \over p} \Delta t } \right]^2 }\cdot
\end{displaymath}](/articles/aa/full/2002/42/aa2588/img42.gif) |
(A.3) |