A&A 394, 1009-1021 (2002)
DOI: 10.1051/0004-6361:20021223

Measuring starspot temperature from line depth ratios

I. The method

S. Catalano ¹ - K. Biazzo ² - A. Frasca ¹ - E. Marilli ¹

1 - Catania Astrophysical Observatory, via S. Sofia 78, 95123 Catania, Italy
2 - Dep. of Physics and Astronomy, University of Catania, via S. Sofia 78, 95123 Catania, Italy

Received 8 April 2002 / Accepted 29 July 2002

Abstract
Gray and collaborators have recently demonstrated that line-depth ratios are a powerful tool for temperature discrimination, able to resolve differences $\leq$10 K.
The method has been applied to detect temperature variations in the 5-15 K range due to activity cycles (e.g. Gray et al. 1996a, 1996b) or to rotation modulation produced by large surface features, called "star-patches", like that detected in $\xi$ Boo A by Toner & Gray (1988).
Cool starspots of a few tenths of the stellar surface produce bumps in a line profile, which migrate through the line profile allowing Doppler-imaging in fast rotating stars. In the hypothesis that in slowly-rotating stars the passage of dark spots produces modulation of the center line depth of different amount in lines of different sensitivity to temperature, we have made test observations on three active binaries of the RS CVn type.
Based on observations made at the Catania Astrophysical Observatory at a resolution R = 14 000, we show that line-depth ratios can be effectively used to determine spot temperatures of active binary systems.
Using, on average, ten line pairs, selected in the 6100-6300 Å wavelength range, with the help of observations of 30 main sequence and giant stars, we have derived a calibration relation of line-depth ratios (LDR) in an absolute temperature scale, taking into account the gravity effect in the calibration relation.
Single LDRs converted to temperature through the calibration relations have led to clear rotational modulation of the average surface temperature with amplitudes of 177 K, 119 K, and 127 K for VY Ari, IM Peg and HK Lac, with average estimated errors of about 10 K.
We show that the observed temperature variation amplitude allows us to define a minimum fractional spotted area coverage as a function of spot-photosphere temperature ratio.
Adopting the maximum value of average temperature, determined from the LDRs, as that of the unspotted photosphere, we computed the average spot temperature corresponding to the minimum spot coverage. Although not univocally constrained, the temperature difference ( $\Delta T = T_{\rm ph}-T_{\rm sp}$) obtained for the three systems, $\Delta T$ = 890 K for VY Ari, $\Delta T$ = 750 K for IM Peg, and $\Delta T$ = 810 K for HK Lac, are in good agreement with values derived with other methods.

Key words: stars: late-type - stars: activity - stars: starspots - stars: individual: VY Ari, HK Lac, IM Peg

1 Introduction

Photometric variations attributed to starspots clearly depend on a number of physical parameters, i.e. size, location, effective temperature of the spots or spot groups. The numerous attempts made to extract this information by modelling the photometric light curve unavoidably meet with the non-uniqueness of the solutions. While a certain spot configuration can reasonably reproduce the photometric variations, it is not possible to invert models to derive unique values for spot sizes, shapes and temperatures. There is a fundamental trade-off between spot area and spot temperature. Very precise data at least in two colors are required to resolve this ambiguity. Unfortunately the most used color index, the B-V, is not of great help because, as the spot becomes darker its contribution to the color of the visible stellar hemisphere decreases and the observed color variation associated with the rotational modulation is always small. The use of the V-R color is more effective for the contemporaneous determination of starspot temperature and area, as earlier shown by Vogt (1981). The method determines the V-R color difference between the star and spot, while the spot temperature is derived through the (V-R)- $T_{\rm eff}$ calibration.

The Doppler-imaging technique (e.g. Vogt et al. 1987; Piskunov 1991) based on a series of high resolution spectral line profiles allows us to produce an image of the stellar surface with high degree of sophistication and accuracy (for recent developments see Rice & Strassmeier 2000). However, the temperature scale remains model dependent, in the sense that with a given set of stellar atmosphere models, the stellar image can be considered as the distribution of effective temperature across the stellar surface. The temperature scale of the image can be fixed by simultaneous photometric observations.

Following the earlier suggestions that TiO bands at 8860 Å  could be used to measure starspot temperatures (e.g. Vogt 1979; Ramsey & Nations 1980), Huenemoerder & Ramsey (1987) attempted a quantitative study of the effect of spots on the TiO bands to derive spot temperatures and surface coverage. Recently Neff et al. (1995) and O'Neal et al. (1996) obtained an evaluation of spot temperature with an estimated error of $\pm$100-200 K and of the surface filling factor for a number of active stars using both bands of TiO at 7055 and 8860 Å. Although the method looks very effective for stars with spot temperatures lower than 3500 K, it fails for stars with effective temperature higher than 5000 K if the average temperature difference is $T_{\rm eff}-$ $T_{\rm sp} \leq$ 1500 K, as generally observed. Moreover, the method requires an independent determination of $T_{\rm eff}$.

In a series of recent works Gray and collaborators have demonstrated that line-depth ratios are a powerful temperature discriminant, capable of resolving differences $\leq$10 K, and have determined $T_{\rm eff}$ of several main sequence (Gray & Johanson 1991) and giant stars (Gray & Brown 2001). Although the effective temperature scale calibration can be set to few tens of a degree, temperature differences can be measured with a precision less than one degree. Temperature variation in the 5-15 K range over the rotational period and the activity cycle has been reported for $\epsilon$ Eri (Gray & Baliunas 1995), $\sigma$ Dra (Gray et al. 1992), as well as for the Sun along the 11-year cycle (Gray & Livingston 1997).

Application of this method to the study of temperature variations associated with stellar surface features, as discussed by Gray (1996), is particularly challenging because several physical variables interact simultaneously, each impressing their signature on the spectral lines. In particular, cool surface features (spots) cause bumps in a line profile, which migrate through the line profile allowing Doppler-imaging in fast rotating stars. Since the size of the bump, to the first order, is determined by the loss of continuum light at the Doppler position of the bump, in a slowly rotating star we cannot see a clear Doppler shift but can expect a slight rotational modulation of the central line depth. For example, following Gray (1996), if the passage of a dark spot at the central meridian produces a decrease of 10% in the stellar disk light, then the bump would have a height of 10% of the depth of the line. The line depth will be reduced by about this quantity.

Let us now consider the line-depth ratios in a slowly rotating star and select two lines, one insensitive and one very sensitive to temperature. Due to the presence of a dark spot that produces a decrease of 10% in the continuum, the depth of both lines would be equally affected, and reduced by 10% and their depth ratio would remain unchanged. But due to the lower temperature in the spot, the line sensitive to the temperature will change its intrinsic depth and consequently also the depth ratio of the two lines will change. The amount of depth ratio variation should depend on the sensitivity to the temperature variation of the specific lines considered, and the fraction of surface covered by the spot.

On the basis of these considerations we have made some test observations on rather active, slowly rotating RS CVn binaries, namely VY Ari, IM Peg and HK Lac to investigate the applicability of the method and its ability to determine the spot temperature. The paper develops as follows: in Sect. 2 we present the observations and data reduction; in Sect. 3 the temperature calibration of the line-depth ratios; in Sect. 4 the results of temperature modulation of the active stars will be discussed, and in Sect. 5 a method to determine the spot temperature and the filling factor will be discussed.

2 Data analysis

2.1 Observations and reduction

Spectroscopic observations have been performed with the REOSC échelle spectrograph at the 91-cm telescope of Catania Astrophysical Observatory - M. G. Fracastoro station (Serra La Nave, Mt. Etna). The spectrograph is fed by the telescope through an optical fibre (UV - NIR, 200$~\mu$m core diameter) and is placed in a stable position in the room below the dome level. Spectra were recorded on a CCD camera equipped with a thinned back-illuminated SITe CCD of 1024 $\times$ 1024 pixels (size 24 $\times$ 24 $\mu$m). The échelle crossed configuration yields a resolution of about 14 000, as deduced from the FWHM of the lines of the Th-Ar calibration lamp. The observations have been made in the red region. The detector allows us to record five orders in each frame, spanning from about 5860 to 6700 Å. In this spectral region there are several line pairs of low and high excitation potential, whose depth ratios are suitable for effective temperature determination.

The data reduction was performed by using the ECHELLE task of IRAF package following the standard steps: background subtraction, division by a flat field spectrum given by a halogen lamp, wavelength calibration using the emission lines of a Th-Ar lamp, and normalization to the continuum through a polynomial fit. Particular care was paid to the continuum level definition. The IRAF task CONTINUUM was used for such a purpose and we chose a low-order (3rd-4th) Legendre polynomial to follow the continuum behaviour in each spectral order that is the result of the true spectral shape and of residual instrumental effects, like the blazing curvature, spectrograph sensitivity, etc., that are not fully removed by the reduction process.

The choice of a low-order polynomial guarantees a good definition of the continuum level at least on a spatial scale of a few tens of Å, much more than the typical wavelength separation of line pairs.

   

Table 1: Main parameters of observed active stars.

HD	Name	Sp. Type	V	$v\sin i$	$P_{\rm rot}$
			(mag)	(km s-1)	(days)
209813	HK Lac	K0III	6.52	15	24.4284
216489	IM Peg	K2III-II	5.60	26	24.494
17433	VY Ari	K3-4V-IV	6.9	6	16.1996

Observations were carried out from August 2000 to January 2001, on three selected targets, i.e. VY Ari, HK Lac, IM Peg, whose main parameters are reported in Table 1. The main requirement for the selection was the known strong spottedness and low $v\sin i$. The $v\sin i$ of the targets is in the 6-24 km s^-1 range, so if the spots or the spotted area is large enough to feel the rotation broadening effect the width of the bumps caused by the spot visibility would be of the same order as the width of a spectral resolution element. The slow rotation combined with the relatively low spectral resolution will ensure the non-detection of the Doppler shift of the bump along the spectral lines due to the spot rotation.

In addition to the active stars, a number of giant and main sequence stars of spectral type in the range G2III-M0III and F8V-K7V, respectively, have been observed to establish the temperature scale of the line-depth ratios.

The average signal-to-noise ratio (S/N) at continuum in the spectral region of interest was 200-500 for the calibration stars and about 100-150 for the active stars.

2.2 Calibration stars and temperature scale

   

Table 2: Standard stars observed for the depth- $T_{\rm eff}$ calibrations.

HD	Name	Sp. T.	V	$\pi$	B-V	$T_{\rm eff}$
			(mag)	(mas)		(K)
GIANTS
161239	84 Her	G2IIIb	5.714	26.13	0.654	5732
196755	$\kappa$ Del	G2IV	5.069	33.27	0.705	5583
161797	$\mu$ Her	G5IV	3.417	119.05	0.752	5451
188512	$\beta$ Aql	G8IV	3.715	72.95	0.855	5183
23249	$\delta$ Eri	K0IV	3.527	110.58	0.922	5024
62345	$\kappa$ Gem	G8IIIa	3.568	22.73	0.932	5001
216131	$\mu$ Peg	G8III	3.488	27.95	0.934	4996
22796	12 Tau	G6III	5.565	8.14	0.934	4996
28100	$\pi$ Tau	G7IIIa	4.692	7.17	0.982	4891
197989	$\epsilon$ Cyg	K0III	2.467	45.26	1.034	4783
74442	$\delta$ Cnc	K0IIIb	3.937	23.97	1.082	4687
12929	$\alpha$ Ari	K2III	2.009	49.48	1.153	4552
54719	$\tau$ Gem	K2III	4.407	10.81	1.261	4350
43232	$\gamma$ Mon	K1.5III	3.972	5.06	1.320	4239
49161	17 Mon	K4III	4.758	6.73	1.394	4096
69267	$\beta$ Cnc	K4III	3.532	11.23	1.481	3923
29139	$\alpha$ Tau	K5III	0.868	50.09	1.537	3813
60522	$\upsilon$ Gem	M0IIIb	4.058	13.57	1.539	3809
DWARFS
187691	54 Aql	F8V	5.116	51.57	0.552	6045
22484	10 Tau	F9IV-V	4.290	72.89	0.574	5976
157214	72 Her	G0V	5.394	69.48	0.619	5837
186408	16 CygA	G1.5Vb	5.960	46.25	0.645	5758
217014	51 Peg	G2.5IV	5.463	65.10	0.665	5699
20630	$\kappa$1 Cet	G5V	4.836	109.18	0.679	5658
10700	$\tau$ Cet	G8V	3.496	274.17	0.727	5520
3651	54 Psc	K0V	5.879	90.03	0.849	5197
22049	$\epsilon$ Eri	K2V	3.726	310.75	0.882	5117
16160	HR 753	K3V	5.821	138.72	0.972	4912
201091	61 CygA	K5V	5.224	287.13	1.169	4522
201092	61 CygB	K7V	6.046	285.42	1.360	4162

To convert the depth ratio variation of our active stars into temperature variation we need to define a temperature scale for the measured line-depth ratios. We have then observed a number of single stars of different spectral type in the range from F8 to M0 and luminosity class from V to III. Main criteria for the selection were: (i) a low rotation velocity, (ii) a reasonably good parallax value, (iii) accurate B-V color index. Since the line-depth ratio is dependent on gravity also for some temperature-sensitive lines, we have observed main sequence and giant stars to correct the gravity effect and eventually set separate temperature scales to be used for active main sequence and giant stars. The calibration stars are listed in Table 2 together with their spectral type, V magnitude, parallax, B-V and effective temperature. Spectral types are from the Bright Star Catalogue (Hoffleit & Warren 1991), visual magnitudes V and B-V color indices are from the Geneva Web database (Mermilliod et al. 1997) and the parallaxes are from the Hipparcos Catalogue (ESA 1997).

Since effective temperatures are available for very few of our calibration stars, we used color indices B-V to set the effective temperature of each calibration star. Although interstellar reddening is not expected to be large, since all the stars in Table 2, with few exceptions, are closer than 100 pc, we applied an isotropic extinction correction to obtain the (B-V)₀. We used $A_{\rm V}$ = 0.8 mag kpc^-1 and a ratio of total to selective extinction of 3.3 as suggested by Henry et al. (2000). Conversion of (B-V)₀ to effective temperature has been made through the empirical relation proposed by Gray (1992):

 

$$\log T_{\rm eff}$$ - 3.614(B-V)₀³ + 3.2637(B-V)₀⁴

- 1.4727(B-V)₀⁵ + 0.2600(B-V)₀⁶. (1)

This relation is quite accurate for $(B-V)_0~\leq~$1.5, i.e. within the color range of our calibration stars.

The metallicity effects can alter the B-V indices. Gray (1994) has investigated the influence of metallicity on color indices, finding an empirical relation between B-V and $\rm [Fe/H]$. The B-V color index is only very slightly dependent on $\rm [Fe/H]$, its maximum variation being of about $0\hbox{$.\!\!^{\rm m}$ }015$. According to the calibration relation given in Eq. (1), the corresponding temperature change is about 20-30 K. Given the uncertainties in the B-V values and in the setting of the temperature scale, such effects appears to be statistically not significant in our LDR-temperature calibrations.

2.3 Line identification in the 6100-6300 Å  range

Within the spectral range covered by our échelle frames, 5870-6700 Å, there are several pairs of lines suitable for temperature determination, the more frequently used being in the spectral region around 6200 Å (Gray & Johanson 1991; Gray & Brown 2001; Hatzes et al. 1998) and 6400 Å(Strassmeier & Fekel 1990; Strassmeier & Schordan 2000). We preferred to use lines in the 6100-6200 Å range because we were able to select a larger number of unblended pairs with separation smaller than 5 Å thus avoiding problems of different setting of the continuum, and less contamination from telluric lines that at our resolution is difficult to remove properly.

	Figure 1: Sample of standard star spectra in the region around 6250 Å.
Open with DEXTER

Figure 1 displays a portion of the 6200 Å region for a series of spectra of giant stars representative of spectral type from K0III to K4III. From this figure the strengthening of Fe I and V I lines with decreasing temperature is evident, while the $\lambda$6247 Fe II shows the opposite behaviour. Furthermore, the growth of low-excitation lines (like those of V I) is faster than that of iron lines. Altogether we identify 15 spectral lines forming 10 pairs suitable for line-depth ratios. These lines were identified through the solar spectral atlas (Moore et al. 1966), choosing the unblended lines. The only exception is the $\lambda$6243 V I line that is indeed composed of two very close V I lines of comparable intensities and with the same temperature dependence that appear as a single line at our resolution. Line identification and excitation potential, $\chi$, taken from Moore et al. (1966) and Bashkin & Stoner (1975) are listed in Table 3.

   

Table 3: Spectral lines used for LDR.

$\lambda$	Element	$\chi$
(Å)		(eV)
6199.19	VI	0.29
6200.32	FeI	2.61
6210.67	ScI	0.00
6215.15	FeI	4.19
6215.22	TiI	2.69
6216.36	VI	0.28
6243.11	VI	0.30
6246.33	FeI	3.60
6247.56	FeII	3.89
6251.83	VI	0.29
6252.57	FeI	2.40
6265.14	FeI	2.18
6266.33	VI	0.28
6268.87	VI	0.30
6270.23	FeI	2.86
6274.66	VI	0.27

2.4 Measurement of line depth

The lines for each ratio are chosen to be close together in order to minimize errors in choosing the continuum. The lowest five points in the core of each measured line were fitted with a cubic spline and the minimum of this cubic polynomial was taken as the line depth. Writing the line depth d as

 

$$d = \frac{S_{\rm c} - S_{\rm b}}{S_{\rm c}} = 1 - \frac{S_{\rm b}}{S_{\rm c}},$$ (2)

where $S_{\rm c}$ and $S_{\rm b}$ are the signals in ADU (Analog to Digital Units) or in photons of continuum and bottom of the line, respectively, the fractional error on d can be expressed as

 

$$\frac{\sigma_{d}}{d} = \frac{\sigma_{\frac{S_{\rm b}}{S_{\rm c}}}}{d} = \frac{1 - d}{d}~\sqrt{\frac{1}{S_{\rm b}} + \frac{1}{S_{\rm c}}}\cdot$$ (3)

This relation has been used to evaluate observational errors on line-depth ratios.

	Figure 2: An example of LDR as a function of effective temperature. Different symbols refer to different luminosity classes. The solid line is the polynomial fit to evolved star LDR; the dashed line represents the fit to main sequence LDR.
Open with DEXTER

3 The temperature line-depth ratio calibration

Using the measured depths we are now able to construct temperature line-depth ratio (LDR) calibration for the different line pairs. We select the $\lambda$6269 V I-$\lambda$6270 Fe I to illustrate the analysis. The other nine pairs are treated in a similar way. The plot of the observed LDR (Fig. 2) versus effective temperature displays two separate dependences: the main-sequence star dependence (squares) and the evolved star dependence, sub-giants (circles) and giants (triangles). For this line pair a significant gravity effect on the LDR is apparent.

In principle we need to determine the temperature variation of active giants as well as main-sequence active stars, so we need to set appropriate temperature scales. To use all the observations we have in hand, we proceeded in the following way: (i) first we defined separated temperature scales by doing low-order polynomial fits through main sequence and giant stars, (ii) then we determined the difference of the observed LDR with respect to the fits. Defining as gravity index the absolute magnitude difference $\Delta M_{\rm V}$ with respect to the ZAMS magnitude for the star's temperature we plot in Fig. 3 the LDR difference with respect to the giant fit, $\Delta {\rm Ratio}_{\rm GIA}$, and in Fig. 4 the LDR difference for the MS fit, $\Delta {\rm Ratio}_{\rm MS}$, as a function of $\Delta M_{\rm V}$. In both cases a clear correlation is apparent. We have fitted this dependence with a linear regression function (continuous line in Figs. 3 and 4). The absolute-magnitude corrected line-depth ratio for main sequence and giant are then

$${\rm LDR}_{\rm MS,G} = {\rm LDR} - (a_{\rm MS,G} + b_{\rm MS,G} \Delta M_{\rm V})$$ (4)

with b and a the slope and the intercept of regression line of $\Delta {\rm Ratio}$ on $\Delta M_{\rm V}$-magnitude correlation lines. With few exceptions, the scatter of the points around the correlation line is consistent with the error of line-depth ratio determination, thus giving confidence in the correction procedure and in the adoption of $\Delta M_{\rm V}$ as the gravity index.

	Figure 3: Residuals of LDRs with respect to the polynomial fit to MS data of Fig. 2 plotted as a function of the gravity indicator  $\Delta M_{\rm V}$ (dots). The continuous line represents a linear fit to the data.
Open with DEXTER

	Figure 4: Residuals of LDRs with respect to the polynomial fit to Giant-stars data of Fig. 2 plotted as a function of the gravity indicator  $\Delta M_{\rm V}$ (dots). The continuous line represents a linear fit to the data.
Open with DEXTER

Plots of the temperature calibration as a function of corrected LDRs are displayed in Figs. 5 and 6. Data points for stars of different luminosity class mix very well, leading to well-defined unique correlations, alternatively applicable to MS and Giant stars. The spread around the polynomial fits (continuous lines in the figures) is greatly reduced and is consistent with the uncertainties and errors in the temperature and LDR determination. The rms of the fits in this case are of 89 K and 73 K for MS and Giant-stars calibrations, respectively. This values are comparable with the uncertainty on the setting of the temperature scale (see e.g. Gray 1992). Similar values are found for most of the LDRs.

	Figure 5: Effective temperature as a function of corrected LDR for MS stars. The solid line represents a polynomial fit to all data. The dotted line is the polynomial fit to LDR data corrected for Giant-star calibration (solid line in Fig. 6).
Open with DEXTER

	Figure 6: Effective temperature as a function of corrected LDR for Giant stars. The solid line represents a polynomial fit to all data. The dotted line is the polynomial fit to LDR data corrected for MS-star calibration (solid line in Fig. 5).
Open with DEXTER

New low-order polynomial fits were placed through the plots of temperature versus LDRs to obtain separate temperature calibrations for MS and giant stars. Final fits of temperature versus LDR for the other line pairs are illustrated in Fig. 7. Some of the line pair ratios display a clear gravity effect like the $\lambda$6211 Sc I-$\lambda$6215 Fe I+Ti I or the $\lambda$6275 V I-$\lambda$6270 Fe I, that becomes very strong for the two ratios $\lambda$6243 V I-$\lambda$6247 Fe II and $\lambda$6246 Fe I-$\lambda$6247 Fe II. Other ratios, like the $\lambda$6252 V I-$\lambda$6253 Fe I or $\lambda$6266 V I-$\lambda$6265 Fe I, do show a very marginal gravity effect. In all cases we have made separate temperature calibrations.

For the two LDRs involving the $\lambda$6247 Fe II line, the gravity dependence is so high that the correction method described above could not be applied to derive average relations for the MS stars and for Giant stars, using all standard stars.

In order to measure the temperature sensitivity of each line-depth ratio we have calculated the slopes of the polynomial fits $\frac{{\rm d}T}{{\rm d}r}$ at temperatures of 4500 K, 5000 K and 5500 K (typical of most of active RS CVn binaries), for a 0.01 variation in LDR, which represents the typical uncertainty for the LDR determination in well exposed spectra. From single LDR-dependence we derived typical sensitivities of 10-20 K, and in some case even smaller, for a 0.01 variation in r (see Table 4).

	Figure 7: $T_{\rm eff}$-LDR calibrations for Giant stars. The meaning of symbols and curves is as in Figs. 5 and 6.
Open with DEXTER

   

Table 4: Temperature sensitivity of LDRs.

Lines pair	$\Delta T$ for $\Delta r$ = 0.01			$\Delta T$ for $\Delta r$ = 0.01
	4500 K			4500 K
		DWARFS			GIANTS
6199/6200	10.4	11.4	14.1	11.7	13.0	15.3
6211/6215	10.5	12.4	-	10.4	12.3	-
6216/6215	18.4	15.3	20.2	18.8	15.6	20.5
6243/6246	9.1	11.1	14.3	9.9	12.1	15.7
6243/6247	-	1.2	91.8	2.0	5.4	6.0
6246/6247	-	1.3	87.7	7.2	20.1	11.8
6252/6253	22.1	23.5	25.0	21.9	23.2	24.7
6266/6265	17.1	18.1	19.1	16.2	16.5	16.8
6269/6270	5.8	7.6	11.0	6.0	8.2	12.8
6275/6270	8.5	9.7	11.4	8.6	9.9	11.8

4 Line depth ratio and temperature variation of the active stars

Line-depth ratios variations are analysed separately for each active star considered. Since we have 10 different pairs of lines we have first analysed each ratio as a function of the rotational phase for the three stars and then we have transformed the LDRs in temperature. Some line pairs could not be used for our active star due to the non-negligible $v\sin i$ of the targets that causes blending of the lines that are too close in wavelength. Temperature values from all pairs for each spectrum were finally combined to yield an average temperature value, thus reducing the temperature errors. We have excluded from the means those LDR values that are outside the 3$\sigma$ box around the mean value.

Temperature variation curves have been obtained for each active star by folding in phase individual $<T_{\rm eff}>$ data, analogously to what is performed with photometric measurements.

As can be seen from Tables 5-7, our $<T_{\rm eff}>$ measurements span a time range of 4-5 stellar rotations, but it has been shown that the big spots observed in very active stars have typical lifetimes of several rotations. For a set of four spotted RS CVn stars, Henry et al. (1995) observed individual spot lifetimes between 0.5 years and over 6 years. Spot lifetimes in the same range were also found for other RS CVn stars, including VY Ari, IM Peg and HK Lac (Strassmeier & Bopp 1992; Strassmeier et al. 1994; Oláh et al. 1997; Strassmeier et al. 1997; Frasca et al. 1998).

4.1 VY Ari

Due to blends induced by the rotational broadening and by the crowding related to the spectral type of the visible component of VY Ari (K3-4 V-IV) only seven combinations of LDRs could be used for the temperature variation study. The useful measured line-depth ratios of VY Ari are plotted in Fig. 8 as a function of the rotational phase, computed from the following ephemeris

$${\rm HJD}_{\phi=0} = 24~~ 51856.0+16\hbox{$.\!\!^{\rm d}$ }1996~\times~E,$$ (5)

where the rotational period is taken from Strassmeier et al. (1997) and the epoch of zero phase corresponds to the first observing date (November 7th, 2000) at noon.

   

Table 5: Average surface temperature of VY Ari.

HJD	$\phi$	$~~<T_{\rm eff}>$
(+2 451 000)		(K)
856.4761	0.029	4799$~\pm~$16
857.4544	0.090	4767$~\pm~$9
859.4971	0.216	4760$~\pm~$13
860.4516	0.275	4798$~\pm~$5
861.4502	0.336	4822$~\pm~$6
862.4862	0.400	4821$~\pm~$13
863.5280	0.465	4850$~\pm~$4
864.5596	0.528	4895$~\pm~$4
865.4910	0.586	4916$~\pm~$21
866.5074	0.649	4899$~\pm~$7
867.5400	0.712	4850$~\pm~$12
913.3357	0.539	4855$~\pm~$8
915.3436	0.663	4909$~\pm~$2
916.3325	0.724	4888$~\pm~$9
917.4153	0.791	4881$~\pm~$4

	Figure 8: LDRs of VY Ari versus rotational phase as computed according to Eq. (5). The temperature scale for each ratio is displayed on the right side of the boxes.
Open with DEXTER

All LDRs show a clear modulation with the rotational phase with a maximum around $0~\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }2$ and a minimum around $0~\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }6$. The latter value, for all the LDRs, corresponds to the maximum temperature value as displayed on the right side scale. The amplitude variation of the LDRs ranges from 16% for the $\lambda$6252 V I-$\lambda$6253 Fe I ratio to 46% for the $\lambda$6266 V I-$\lambda$6265 Fe I ratio which appears to be the more sensitive to the temperature. These variations are well above (3-5 times) the average errors, which are determined according to error propagation rule as:

 

$$\frac{\sigma_r}{r} = \sqrt{\left( \frac{\sigma_{d_1}}{d_1} \right)^2 + \left( \frac{\sigma_{d_2}}{d_2} \right)^2},$$ (6)

where d₁ and d₂ are the line depths and $\sigma_{d_1}$ and $\sigma_{d_2}$ are the corresponding absolute errors as fixed by the S/Nratio for the measured continuum and central line flux.

	Figure 9: Temperature curves of VY Ari obtained from the LDRs in Fig. 8 (upper panel). Different symbols have been used for the different ratios. The average effective temperature $<T_{\rm eff}>$ as a function of rotational phase is displayed in the lower panel.
Open with DEXTER

Temperature values derived from the LDR- $T_{\rm eff}$ calibration from each pair are plotted in Fig. 9 using different symbols.

The temperature variation derived from all the LDRs displays a common behaviour, with a spread consistent with error estimate. Apart from the very similar shape, the temperature curves derived from different LDRs display a small offset one with respect to the other. Since we are mainly interested in the temperature variation, not in its absolute value, we have evaluated the average $T_{\rm eff}$ from all curves and have shifted each $T_{\rm eff}$ curve of the offset needed to make its average level equal to the average from all curves. These temperature offsets are in the range 20-50 K and may be due to some residual gravity dependence that has not been completely accounted for by the correction procedure or to the influence of some other physical parameter that has a minor effect on the LDR. This scaling procedure, applied to several LDRs, can statistically compensate for such effects and, also in the present case with only 6 or 7 useful LDRs, will give also a good evaluation of the absolute temperature scale that, however, has its intrinsic setting uncertainty of a few tens of Kelvin degrees (see e.g. Gray 1992).

We have then derived an average temperature variation by making a weighted mean of the values obtained from each spectrum. The weighted mean has been given by:

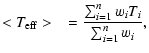$$<T_{\rm eff}>~~= \frac{\sum_{i=1}^{n} w_{i}T_{i}}{\sum_{i=1}^{n} w_i},$$ (7)

and the corresponding error has been computed as:

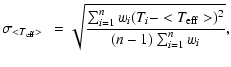$$\sigma_{<T_{\rm eff}>}~~ = \sqrt{\frac{\sum_{i=1}^{n} w_i(T_i - <T_{\rm eff}>)^2}{(n - 1)\sum_{i=1}^{n} w_i}},$$ (8)

where T_i = T(r_i) is the effective temperature obtained from the ith line-depth ratio, and $w_i = 1/\sigma_{T_i}^2$ is the corresponding statistical weight.

The final temperature variation ranges from 4739 K to 4916 K, i.e. with a $\Delta <T_{\rm eff}>$ = 177 K. As can be seen in Table 5, $\sigma_{<T_{\rm eff}>}$ errors are typically of a few Kelvin degree.

4.2 IM Peg

	Figure 10: LDRs of IM Peg versus rotational phase as computed according to Eq. (9). The temperature scale for each ratio is displayed on the right side of the boxes.
Open with DEXTER

For IM Peg we were also able to use seven LDRs, but with some differences, as displayed in Fig. 10, where single LDR values are plotted as function of the rotational phase. Phases are reckoned from the ephemeris given by Strassmeier et al. (1997)

$${\rm HJD}_{\phi=0} = 24~~ 43734.0+24\hbox{$.\!\!^{\rm d}$ }494~\times~E.$$ (9)

In this case the amplitude of the LDR variation is smaller and the average behaviour is more noisy and not well defined.

IM Peg actually represents a proper test case for the application and reliability of the method. Its rotational broadening (26.5 km s^-1) is a bit larger than our spectral resolution so that the Doppler shifts of the bumps produced by the spots could be partially resolved in our spectra, and for sure are responsible for the larger noise. As a matter of fact, Berdyugina et al. (2000) from high resolution spectra (R = 30 000-80 000) were able to obtain surface images with the Doppler-imaging technique.

Notwithstanding this limitation a maximum LDR variation of 37% is obtained for the $\lambda$6275 V I-$\lambda$6270 Fe I ratio.

   

Table 6: Average surface temperature of IM Peg.

HJD	$\phi$	$~~<T_{\rm eff}>$
(+2 451 000)		(K)
798.4555	0.242	4615$~\pm~$8
800.4203	0.322	4608$~\pm~$4
801.4724	0.365	4666$~\pm~$7
829.4298	0.507	4654$~\pm~$18
830.3874	0.546	4645$~\pm~$19
831.3436	0.585	4622$~\pm~$13
833.3725	0.668	4589$~\pm~$6
835.3963	0.750	4569$~\pm~$9
856.3316	0.605	4621$~\pm~$11
859.3944	0.730	4585$~\pm~$10
860.2836	0.766	4606$~\pm~$9
861.2989	0.808	4593$~\pm~$5
862.3525	0.851	4578$~\pm~$25
863.3614	0.892	4547$~\pm~$6
865.3533	0.973	4613$~\pm~$14
913.2565	0.929	4582$~\pm~$14
915.2733	0.011	4574$~\pm~$7
917.3364	0.096	4585$~\pm~$12

However, all the LDRs converted to temperature and combined in a single temperature curve, as displayed in Fig. 11, lead to a fairly well-defined temperature variation as a function of the rotational phase. The average curve obtained from the weighted mean (lower panel in Fig. 11) appears still well defined. The temperature maximum, with a value of 4666 K, occurs around phase $0~\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }5$. The full amplitude variation is $\Delta <T_{\rm eff}>$ = 119 K, corresponding to a 3% of the determined average temperature value.

	Figure 11: Temperature curves of IM Peg obtained from the LDRs in Fig. 10 (upper panel). Different symbols have been used for the different ratios. The average effective temperature $<T_{\rm eff}>$ as a function of rotational phase is displayed in the lower panel.
Open with DEXTER

4.3 HK Lac

	Figure 12: LDRs of HK Lac versus rotational phase as computed according to Eq. (10). The temperature scale for each ratio is displayed on the right side of the boxes.
Open with DEXTER

For HK Lac we were able to use six LDRs, as displayed in Fig. 12 where single values are plotted as a function of the rotational phase computed from the ephemeris

$${\rm HJD}_{\phi=0} = 24~~ 40017.17+24\hbox{$.\!\!^{\rm d}$ }4284~\times~E,$$ (10)

which is the orbital ephemeris already given by Gorza & Heard (1971) with the initial epoch given by Strassmeier et al. (1993) corresponding to inferior conjunction (more massive star closer to the observer).

All the ratios exhibit a well-defined parallel behaviour; even single values have slightly larger errors due to the average lower S/N ratio of the observations.

   

Table 7: Average surface temperature of HK Lac.

HJD	$\phi$	$~~<T_{\rm eff}>$
(+2 451 000)		(K)
798.4325	0.277	4686$~\pm~$3
800.4422	0.360	4716$~\pm~$15
801.4907	0.402	4698$~\pm~$52
830.3564	0.584	4765$~\pm~$8
831.3613	0.625	4720$~\pm~$12
833.3913	0.708	4734$~\pm~$12
835.4153	0.791	4709$~\pm~$3
836.4205	0.832	4689$~\pm~$12
856.3085	0.646	4741$~\pm~$33
858.2968	0.728	4708$~\pm~$15
860.2632	0.808	4724$~\pm~$19
861.2775	0.850	4702$~\pm~$17
862.3297	0.893	4660$~\pm~$6
863.3362	0.934	4682$~\pm~$8
865.3329	0.016	4640$~\pm~$14
913.2360	0.977	4651$~\pm~$11
915.2508	0.059	4656$~\pm~$2
916.2584	0.101	4641$~\pm~$7
917.3159	0.144	4638$~\pm~$31

The largest amplitude variation is displayed by the V I-Fe II at 6243 Å and 6247 Å, with a full variation of 40%. The corresponding temperature range is very similar for all the LDRs, as displayed in Fig. 13 (upper panel) where the temperature values deduced according to the above calibrations are plotted. The spread of the points is consistent with the estimated errors, and the mean curve resulting from weighted average has a well defined variation. The temperature maximum of 4765 K seems to occur around phase $0~\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }6$. The temperature variation we get is 127 K, corresponding to $\simeq$3% of the average value.

	Figure 13: Temperature curves of HK Lac obtained from the LDRs in Fig. 12 (upper panel). Different symbols have been used for the different ratios. The average effective temperature $<T_{\rm eff}>$ as a function of rotational phase is displayed in the lower panel.
Open with DEXTER

5 Discussion

Only a few active stars investigated until now have shown clear rotational modulation of line-depth ratios (e.g. $\sigma~$Dra, Gray et al. 1992; $\xi~$Boo A, Toner & Gray 1988). However all these studies have been devoted to young main-sequence stars with an activity degree detectably lower than RS CVn and BY Dra binaries and, consequently, with a temperature variation of only a few degrees or a bit more. Conversely, many more cases of long-term variation of average temperature have been found and have been attributed to stellar activity cycles similar to the 11-year solar one (e.g. Gray et al. 1996a, 1996b). These detections have been possible thanks to the large number of spectra collected in each season and averaged together with a great improvement of the S/N ratio.

Since the temperature curves we obtained are $T_{\rm eff}$ averaged over the visible hemisphere, it is not possible to deduce directly the value of the spot temperature because the effect of the filling factor influences also this diagnostic. The dependence of average temperature on the spot relative area is different that of light curves. We can express the hemisphere-averaged temperature as

 

$$T_{\rm m} = \frac{\int\displaylimits_{{\rm disk}} F T {\rm d}A}{\... ... F_{\rm ph} T_{\rm ph}}{A_{\rm rel} F_{\rm sp} + (1 - A_{\rm rel}) F_{\rm ph}},$$ (11)

where $A_{\rm rel}$ is the projected area of the spot (or spots) relative to the stellar disk, $T_{\rm sp}$ and $T_{\rm ph}$ are the temperatures of spot and quiet photosphere, respectively, and $F_{\rm sp}$ and $F_{\rm ph}$ are the fluxes emitted per unit area by the spot and the photosphere at the continuum of observation wavelength, respectively.

Equation (11) can be also written as

 

$$T_{\rm m} = \frac{\gamma T_{\rm sp} + T_{\rm ph}}{\gamma + 1},$$ (12)

where $\gamma = \frac{A_{\rm rel}}{1 - A_{\rm rel}} \frac{F_{\rm sp}}{F_{\rm ph}}$.

If the spot is very cool, its contribution to the mean temperature is negligible because the flux ratio $\frac{F_{\rm sp}}{F_{\rm ph}}$ goes very rapidly to zero (much faster than $\frac{T_{\rm sp}}{T_{\rm ph}}$) with the decrease of $T_{\rm sp}$. Then $\gamma$ tends to zero and the average temperature tends to equal the photospheric one, so that a very large spot area would be required to account for the observed temperature variation.

In the opposite case, when $\frac{T_{\rm sp}}{T_{\rm ph}}$ approaches unity, the average temperature $T_{\rm m}$ is not appreciably changed by the passage of spots over the visible hemisphere. Again, very large spots are needed to reproduce the observed $T_{\rm m}$ variation. Then, there is a limited range for physically reliable solutions. In particular, given an observed variation amplitude $\Delta T_{\rm eff}$, there is a minimum spot area that can reproduce the observations.

As a first approximation we can estimate this minimum spotted area assuming that it is concentrated in only one hemisphere, and its passage causes the observed temperature decrease $\Delta T_{\rm eff}$. The maximum temperature value is assumed as the effective unspotted temperature ( $T_{\rm ph}$) of the star.

Starting from relation 12, we have numerically searched in the $\frac{T_{\rm sp}}{T_{\rm ph}}$- $A_{\rm rel}$ plane the solution for the minimum $A_{\rm rel}$ value compatible with the observed $\Delta T_{\rm eff}$ for each program star. The flux ratio $\frac{F_{\rm sp}}{F_{\rm ph}}$ has been evaluated as the ratio of the Planck functions at the average wavelength of observations, $\frac{B(\lambda,T_{\rm sp})}{B(\lambda,T_{\rm ph})}$.

We have no information on the maximum magnitude at the time of observation with respect to the unspotted magnitude of our program stars, however, we would like to remark that the maximum values of temperature we determined for all the three active stars are in very good agreement with the effective temperature reported in the literature. This proves the power of LDRs as temperature indicators as already pointed out by previous works (Gray 1989; Gray & Johanson 1991). The largest uncertainty in this task, as stressed by Gray (1989), is given by the setting of the absolute scale of temperature for a set of standard stars, while it is differentially possible to put in a growing temperature order each observed star with a precision of about 10 K, which amounts to about one hundredth of spectral subclass or 0.004 mag on B-V color index (Gray 1989; Gray & Johanson 1991).

Figure 14 displays the solutions in the plane $\frac{T_{\rm sp}}{T_{\rm ph}}$- $A_{\rm rel}$ for VY Ari with $T_{\rm ph}$ = 4916 K and $\Delta T_{\rm eff}=$ 177 K. The plot shows the parabolic shape of the family of solutions, which has a minimum fractional area 41% of the projected disk (corresponding to a radius of 40$^{\circ}$ for a single circular spot passing at the disk center) for a temperature ratio of 0.82. This constitutes a lower limit for the spot filling factor, and an average temperature for the spotted area $T_{\rm sp}$ = 4030 K.

	Figure 14: Solutions of VY Ari $T_{\rm eff}$ curve for different spots temperature $\frac{T_{\rm sp}}{T_{\rm ph}}$. A lower limit for the fractional area $A_{\rm rel}$ of about 41% for $\frac{T_{\rm sp}}{T_{\rm ph}}~\simeq~0.82$ is apparent.
Open with DEXTER

The solutions in the plane $\frac{T_{\rm sp}}{T_{\rm ph}}$- $A_{\rm rel}$ for IM Peg are shown in Fig. 15. A lower limit for the projected fractional area $A_{\rm rel}$ of $\simeq$32% (corresponding to a radius of 34$^{\circ}$ for a single circular spot passing at the disk center) is found for a temperature ratio of about 0.84. Given a maximum temperature $T_{\rm ph}$ = 4666 K, we obtain a spot temperature $T_{\rm sp}$ = 3920 K.

	Figure 15: Solutions of IM Peg $T_{\rm eff}$ curve for different spots temperature $\frac{T_{\rm sp}}{T_{\rm ph}}$. A lower limit for the fractional area $A_{\rm rel}$ of about 32% for $\frac{T_{\rm sp}}{T_{\rm ph}}~\simeq~0.84$ is apparent.
Open with DEXTER

The solutions in the plane $\frac{T_{\rm sp}}{T_{\rm ph}}$- $A_{\rm rel}$ for HK Lac are shown in Fig. 16. The minimum projected fractional area 34% (corresponding to a radius of 35$^{\circ}$ for a single circular spot passing at the disk center) is obtained for a temperature ratio of about 0.83. The assumed temperature maximum is $T_{\rm ph}$ = 4765 K, and the corresponding spot temperature is $T_{\rm sp}$ = 3955 K.

	Figure 16: Solutions of HK Lac $T_{\rm eff}$ curve for different spots temperature $\frac{T_{\rm sp}}{T_{\rm ph}}$. A lower limit for the fractional area $A_{\rm rel}$ of about 34% for $\frac{T_{\rm sp}}{T_{\rm ph}}~\simeq~0.83$ is apparent.
Open with DEXTER

If the maximum temperature does not really represent the unspotted photospheric temperature, we would be underestimating the spots area at each fixed $\frac{T_{\rm sp}}{T_{\rm ph}}$. In any case, we are considering the area of unevenly distributed spots, i.e. those giving rise to the observed modulation. We cannot argue, on the basis of only one temperature maximum value, the presence of a contribution from additional evenly distributed spot groups, like for example an equatorial spot belt or a large polar spot, because we would have information about the "unspotted temperature"; likewise the unspotted magnitude is needed for photometric analysis. The effect of such structures on average temperature is only to lower the presumed unspotted temperature by a few tens of degrees, but its influence over the solutions is very limited, because the observed relative variations $\frac{\Delta T_{\rm eff}}{T_{\rm eff}}$ are only of a few percent.

6 Conclusion

The line-depth ratio method has proved to be very effective in detecting low variations of the disk-averaged temperature in active stars. The simultaneous use of many line pairs remarkably enhances the precision of the temperature measurements. Though the precision of the absolute value of temperature is limited by the accuracy with which the temperature scale itself can be established, i.e. $\sim$100 K (e.g. Gray 1992), the resolution in temperature is much higher, with errors in the 5-15 K range.

A well-defined rotational modulation of the average temperature, with amplitudes ranging from 119 K to 177 K, has been detected in all three systems studied in the present work.

Though an accurate modelling of the temperature curves could give information on spot distribution, in the present work we have performed a simple analysis of these curves, based essentially on their variation amplitude interpreted in terms of a dark spot crossing the star disk during its rotation. We have derived the possible solutions for such a spot in the parameters space $\frac{T_{\rm sp}}{T_{\rm ph}}- A_{\rm rel}$ (fractional temperature, fractional area). The possible solutions define a parabolic-shaped locus in the plane $\frac{T_{\rm sp}}{T_{\rm ph}}- A_{\rm rel}$, providing a lower limit for the fractional area of the starspot (or starspots). The lower limits we found indicate large spot coverage in all stars, with relative areas of 41%, 32% and 34% of star disk for VY Ari, IM Peg, and HK Lac, respectively. The filling factors, in units of star surface, are of 11.7%, 8.5%, and 9.0%, respectively. The temperature difference between spot and photosphere corresponding to these filling factors is $\Delta T \simeq 890$ K for VY Ari, $\Delta T \simeq 750$ K for IM Peg, and $\Delta T \simeq 810$ K for HK Lac.

Values of $\Delta T$, obtained by means of light and color curve analysis, comparable with ours have been found by previous investigations into these systems.

For instance, Eaton & Poe (1986) found $\Delta T \simeq 760$ K for VY Ari from a spot modelling applied to their BVRI, while Strassmeier & Bopp (1992) found $\Delta T \simeq 1200$ K from their UBVRI photometry.

For IM Peg, values of $\Delta T \simeq 920$ K (Poe & Eaton 1985) and  $\Delta T \simeq 1130$ K (Padmakar & Pandey 1999) are reported.

For HK Lac, values of $\Delta T \simeq 950$ K (Vogt 1981), $\Delta T \simeq 1080$ K (Poe & Eaton 1985), and $\Delta T \simeq 1200$ K (Olàh et al. 1997) are reported.

We remark that, although the spot parameters we find are only indicative, because they are based only on a lower limit of the spot filling factor, they are well within the values found with other methods.

The simultaneous use of LDR and photometry, combined with a detailed spot-model, can lead to univocal solutions, since we expect a different behaviour of the locus of light-curve solutions in the $\frac{T_{\rm sp}}{T_{\rm ph}}- A_{\rm rel}$ plane that can solve the ambiguity.

This matter will be the subject of a forthcoming paper.

Acknowledgements

This work has been supported by the Italian Ministero dell'Istruzione, Università e Ricerca (MIUR) and by the Regione Sicilia which are gratefully acknowledged. We are grateful to prof. D. Gray for several useful suggestions. We would like to thank the referee, Dr. Artie Hatzes, for his helpful comments and suggestions.

References

 
• Bashkin, S., & Stoner, J. O. Jr. 1975, Atomic Energy Levels & Grotrian Diagrams (North-Holland Publ. Comp. - Amsterdam, Oxford Am. Elsevier Publ. Comp. Inc. - New York) In the text  
• Berdyugina, S. V., Berdyugin, A. V., Ilyin, I., & Tuominen, I. 2000, A&A, 360, 272 In the text NASA ADS  
• Eaton, J. A., & Poe, C. H. 1986, IBVS, No. 2846 In the text  
• ESA 1997, The Hipparcos and Tycho Catalogue, ESA SP-1200 In the text  
• Frasca, A., Marilli, E., & Catalano, S. 1998, A&A, 333, 205 In the text NASA ADS  
• Gorza, W. L., & Heard, J. F. 1971, Publ. David Dunlap Obs., 3, 107 In the text  
• Gray, D. F. 1989, ApJ, 347, 1021 In the text NASA ADS  
• Gray, D. F. 1992, The Observation and Analysis of Stellar Photospheres, 2nd ed. (Cambridge University Press), 344 In the text  
• Gray, D. F. 1994, PASP, 106, 1248 In the text NASA ADS  
• Gray, D. F. 1996, in Stellar Surface Structure, ed. K. G. Strassmeier, & J. L. Linsky (Dordrecht: Kluwer), IAU Symp., 176, 227 In the text  
• Gray, D. F., & Baliunas, S. L. 1995, ApJ, 441, 436 In the text NASA ADS  
• Gray, D. F., Baliunas, S. L., Lockwood, G. W., & Skiff, B. A. 1992, ApJ, 400, 681 In the text NASA ADS  
• Gray, D. F., Baliunas, S. L., Lockwood, G. W., & Skiff, B. A. 1996a, ApJ, 456, 365 In the text NASA ADS  
• Gray, D. F., Baliunas, S. L., Lockwood, G. W., & Skiff, B. A. 1996b, ApJ, 465, 945 In the text NASA ADS  
• Gray, D. F., & Brown, K. 2001, PASP, 113, 723 In the text NASA ADS  
• Gray, D. F., & Johanson, H. L. 1991, PASP, 103, 439 In the text NASA ADS  
• Gray, D. F., & Livingston, W. C. 1997, ApJ, 474, 802 In the text NASA ADS  
• Hatzes, A. P., Cochran, W. D., & Bakker, E. J. 1998, ApJ, 508, 380 In the text NASA ADS  
• Henry, G. W., Eaton, J. A., Hamer, J., & Hall, D. S. 1995, ApJS, 97, 513 In the text NASA ADS  
• Henry, G. W., Fekel, F. C., Henry, S. M., & Hall, D. S. 2000, ApJS, 130, 201 In the text NASA ADS  
• Hoffleit, D., & Warren, W. H. Jr. 1991, Bright Star Catalogue, 5th revised ed. (preliminary version), In the text http://cdsweb.u-strasbg.fr/cats/Cats.htx  
• Huenemoerder, D. P., & Ramsey, L. W. 1987, ApJ, 319, 392 In the text NASA ADS  
• Mermilliod, J. C., Mermilliod, M., & Hauck, B. 1997, A&AS, 124, 349 In the text NASA ADS  
• Moore, C. E., Minnaert, M. G. J., & Houtgast, J. 1966, The Solar Spectrum 2935 Åto 8770 Å(National Bureau of Standards: Washington), Monograph 61 In the text  
• Neff, J. E., O'Neal, D., & Saar, S. H. 1995, ApJ, 452, 879 In the text NASA ADS  
• Oláh, K., Kövári, Zs., Bartus, J., et al. 1997, A&A, 321, 811 In the text NASA ADS  
• O'Neal, D., Saar, S. H., & Neff, J. E. 1996, ApJ, 463, 766 In the text NASA ADS  
• Padmakar, & Pandey, S. K. 1999, A&AS, 138, 203 In the text NASA ADS  
• Piskunov, N. E. 1991, in The Sun and Cool Stars, Activity, Magnetism, Dynamos., ed. I. Tuominen, D. Moss, & G. Rüdiger (Springer-Verlag, Berlin), IAU Coll., 130, 309 In the text  
• Poe, C. H., & Eaton, J. A. 1985, ApJ, 289, 644 In the text NASA ADS  
• Ramsey, L. W., & Nations, H. L. 1980, ApJ, 239, 121 In the text NASA ADS  
• Rice, J. B., & Strassmeier, K. G. 2000, A&AS, 147, 151 In the text NASA ADS  
• Strassmeier, K. G., Bartus, J., Cutispoto, G., & Rodonò, M. 1997, A&AS, 125, 11 In the text NASA ADS  
• Strassmeier, K. G., & Bopp, B. W. 1992, A&A, 259, 183 In the text NASA ADS  
• Strassmeier, K. G., & Fekel, F. C. 1990, A&A, 230, 389 In the text NASA ADS  
• Strassmeier, K. G., Hall, D. S., Fekel, F. C., & Scheck, M. 1993, A&AS, 100, 173 In the text NASA ADS  
• Strassmeier, K. G., Hall, D. S., & Henry, G. W. 1994, A&A, 282, 535 In the text NASA ADS  
• Strassmeier, K. G., & Schordan, P. 2000, Astronomische Nachrichten, 321, 277 In the text NASA ADS  
• Toner, C. G., & Gray, D. F. 1988, ApJ, 334, 1008 In the text NASA ADS  
• Vogt, S. S. 1979, PASP, 91, 616 In the text NASA ADS  
• Vogt, S. S. 1981, ApJ, 150, 327 In the text  
• Vogt, S. S., Penrod, G. D., & Hatzes, A. P. 1987, ApJ, 321, 496 In the text NASA ADS