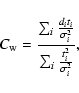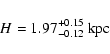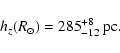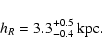A&A 394, 883-899 (2002)
DOI: 10.1051/0004-6361:20021175
Old stellar Galactic disc in near-plane regions according
to 2MASS:
Scales, cut-off, flare and warp
M. López-Corredoira1,2 - A. Cabrera-Lavers2 -
F. Garzón2,3 - P. L. Hammersley2
1 - Astronomisches Institut der Universität Basel,
Venusstrasse 7, 4102 Binningen, Switzerland
2 -
Instituto de Astrofísica de Canarias, 38200 La Laguna,
Tenerife, Spain
3 -
Departamento de Astrofísica, Universidad de La Laguna, Tenerife, Spain
Received 21 December 2001 / Accepted 7 August 2002
Abstract
We have pursued two different methods to analyze the old stellar
population near the Galactic plane, using data from the 2MASS survey.
The first method is based on the isolation of the red clump giant
population in the color-magnitude diagrams and
the inversion of its star counts to obtain directly
the density distribution along the line of sight. The second method
fits the parameters of a disc model to the star counts
in 820 regions.
Results from both independent methods are consistent with each other.
The qualitative conclusions are that the disc is well fitted by
an exponential distribution in both the galactocentric distance and height.
There is not an abrupt cut-off in the stellar disc (at least within
R<15 kpc). There is a strong flare (i.e.
an increase of scale-height towards the outer Galaxy) which
begins well inside the solar circle, and hence there
is a decrease of the scale-height towards the inner Galaxy.
Another notable feature is the existence of a warp in the old stellar
population whose amplitude is coincident with the amplitude of the gas warp.
It is shown for low latitude stars
(mean height:
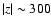 pc) in the outer disc (galactocentric radius
R> 6 kpc) that: the scale-height in the solar
circle is
pc) in the outer disc (galactocentric radius
R> 6 kpc) that: the scale-height in the solar
circle is
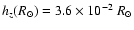 ,
the scale-length of the
surface density is
,
the scale-length of the
surface density is
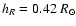 and the scale-length
of the space density in the plane (i.e. including the effect of the
flare) is
and the scale-length
of the space density in the plane (i.e. including the effect of the
flare) is
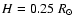 .
The variation of the scale-height
due to the flare follows roughly a law
.
The variation of the scale-height
due to the flare follows roughly a law
![$h_z(R)\approx h_z(R_\odot)
\exp \left(\frac{R-R_\odot}{[12-0.6R({\rm kpc})]\ {\rm kpc}}\right)$](/articles/aa/full/2002/42/aa2213/img30.gif) (for
(for 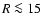 kpc;
kpc;
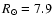 kpc).
The warp moves the mean position of the disc to a height
kpc).
The warp moves the mean position of the disc to a height
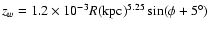 pc
(for
pc
(for 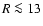 kpc;
kpc;
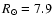 kpc).
kpc).
Key words: Galaxy: general - Galaxy: stellar content -
Galaxy: structure - infrared: stars
Star counts have been widely used for the study of Galactic structure (see Paul
1993), and are becoming increasingly important with the appearance of
wide area surveys in the
last decades (see for example Bahcall 1986; Majewski 1993; Reid 1993; Garzón et al. 1993;
Price 1988). The use of progressively larger and more sensitive
samples combined with detailed models of stellar galactic distribution (for example Bahcall &
Soneira 1980; Wainscoat et al. 1992) has overcome most of the original
uncertainties and difficulties in the analysis and interpretation of star count
data. The advent of NIR detector arrays has permitted
the detailed exploration of the stellar structure in hitherto hidden areas of the Milky
Way, such as the Galactic Plane and Bulge (Eaton et al. 1984; Habing 1988;
Garzón et al. 1993; Hammersley et al. 1994; Ruphy et al. 1996;
López-Corredoira et al. 2000; Epchtein 1997;
Skrutskie et al. 1997). This is because at these wavelengths
interstellar extinction is significantly less when compared
to the visible, while keeping the individual stellar contribution to the
observed flux.
There are, however, still controversial or totally unknown parameters
in the description of the detailed stellar structure. Some of these
are concerned with the radial and vertical distribution of the Galactic
disc, and its specific morphology. Several radial scale-lengths have
been determined by different groups, even when using the same data
sets. As a general trend, the shorter scale-lengths are found for the
surveys using longer wavelengths (Kent et al. 1991), although it
could equally be that different source type or regions of the Galaxy
are being examined. There is far less debate on the vertical
scale-height, with the canonical value for the old population in the
Solar vicinity being about 300 pc. Still more work is needed, however,
to differentiate between the distribution being an exponential or the
sech2 (van der Kruit 1988). Finally, features in the stellar disc
like internal (Freudenreich 1998; López-Corredoira et al. 2001) or
external (Habing 1988; Ruphy et al. 1996) cut-offs radii,
flares (Kent et al. 1991; Alard 2000), warps
(Djorgovski & Sosin 1989; Freudenreich 1998;
Porcel & Battaner 1995; Alard 2000; Drimmel & Spergel 2001)
and/or local corrugations of the
galactic plane (Hammersley et al. 1995) are less well studied,
and are more controversial.
In this paper we will address some of the above topics by analyzing the
shape of the stellar Galactic disc in two ways. We will first extract a
single stellar type by using the deep NIR color-magnitudes diagrams
(CMD) from the 2MASS survey (Skrutskie et al. 1997). The analysis will
be based on the red clump giants, whose relatively high density and bright
absolute magnitude give rise to an identifiable feature in the CMDs.
Hence, the distance and extinction to each star can be directly
determined only assuming the absolute magnitude and color of the
sources. As a second approach, we will use the star counts, also taken
from 2MASS, and the results will then be compared with those
obtained from the red clump method. Both methods will be used to examine the
scale-length, scale-height, flare, outer disc cut-off and warp.
The data for this work has been taken from the 2nd release of the 2MASS project
(Skrutskie et al. 1997,
http://www.ipac.caltech.edu/2mass/releases/docs.html).
We have made use of the available data in that
second release for near plane regions in
the outer Galaxy (
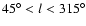 ).
).
In order to help to
interpret the 2MASS star counts a simple model of the density distribution in the disc was built.
The Galactic disc is assumed to be an exponential distribution whose
star density is:
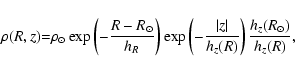 |
(1) |
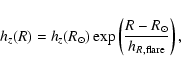 |
(2) |
where
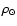 is the space density on the plane in the
neighborhood of the Sun.
is the space density on the plane in the
neighborhood of the Sun.
Hence the density falls exponentially with the galactocentric
radius R (scale-length hR), and with the height z. We have
preferred an exponential scale-height rather than a sech2, as Hammersley et al. (1999)
shows that a sech2 law did not give a good fit to the TMGS star
counts near the plane. The effect of the flare is to increase the
scale-height of the sources in the outer Galaxy,
hence the scale-height (hz(R)) is dependent on R.
We have assumed that the total number of stars at a specific
galactocentric radius remains the same as it would have been without the flare
and so all the flare is doing is to
distribute the sources further from the plane. In the model
this is included by having the scale-height increase exponentially
with galactocentric radius and then have a normalizing factor
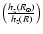 for the density.
Whilst this is not the first model to include a flare, it
is the first to use an exponential rather than a linear flare.
for the density.
Whilst this is not the first model to include a flare, it
is the first to use an exponential rather than a linear flare.
Another way of expressing the density is:
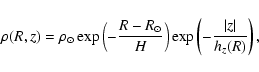 |
(3) |
where
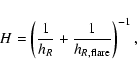 |
(4) |
i.e. H is the equivalent scale-length which is
the combination of the intrinsic scale-length
of the disc with that of the flare. Written in this form the equivalent
scale-length
takes the place of the normalizing factor.
The flare increases with R and so
removes proportionally more stars from the plane with increasing distance.
The net effect is that on the plane the star density falls far more rapidly
with increasing galactocentric distance than the intrinsic scale-length
predicts. Hence, hR is the scale-length of
surface density, and H is the scale-length of the
space density in the plane.
We have assumed a distance from the Sun to the Galactic center to be
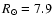 kpc
(López-Corredoira et al. 2000).
kpc
(López-Corredoira et al. 2000).
Therefore, this model contains only
three free parameters (hR,
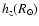 ,
,
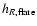 )
whose determination is carried out by minimizing the
)
whose determination is carried out by minimizing the 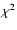 of the
fit in the following way.
of the
fit in the following way.
For a given set of
parameters, the space density on the plane in the neighborhood
of the Sun can be determined using the formula
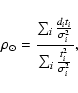 |
(5) |
where di is the measured density in each region, 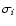 the
poissonian errors in the counts and
ti is the model prediction with
the
poissonian errors in the counts and
ti is the model prediction with
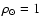 .
Hence, for each set of model parameters we calculate
.
Hence, for each set of model parameters we calculate
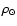 through Eq. (5), and after that we calculate
through Eq. (5), and after that we calculate 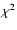 for that particular fit.
Once we have calculated all the
for that particular fit.
Once we have calculated all the 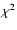 for all sets in the parameter
space, we select the one which gives a minimum
for all sets in the parameter
space, we select the one which gives a minimum 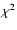 .
The errors are due to the errors in the counts (assumed to be
poissonian) and errors coming from the calculation.
.
The errors are due to the errors in the counts (assumed to be
poissonian) and errors coming from the calculation.
The density equation can be further simplified on plane (
 ), as long as
|z|/hz(R)<<1 along the whole line of sight:
), as long as
|z|/hz(R)<<1 along the whole line of sight:
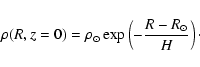 |
(6) |
If the external disc were truncated, then another parameter that
could be added is the radius of the cut-off
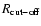 .
It will
be shown in the analysis presented here (Sect. 3.5), however, that
there is no evidence for a cut-off to at least R=15 kpc,
and so this parameter will be unnecessary in the fits. Beyond
.
It will
be shown in the analysis presented here (Sect. 3.5), however, that
there is no evidence for a cut-off to at least R=15 kpc,
and so this parameter will be unnecessary in the fits. Beyond
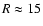 kpc, there are very few stars detected and so very little can be said.
kpc, there are very few stars detected and so very little can be said.
We have ignored the contribution of the spiral arms
since in the outer Galaxy their contribution to the star count is small
and even then it will be at the brightest magnitudes being considered
here, giving negligible contribution for mK<14.0.
Other possible additions to the standard disc model are large scale warps and the
presence of the thick disc.
The warp will be considered separately in Sect. 5.
The thick disc (Gilmore & Reid 1983; Buser et al. 1998, 1999; Ojha 2001)
will not be studied here as a separate population
since the analysis presented here is not sensitive to thick disc, as
regions in general near the plane are used where its relative contribution
is small. It will be shown in Sects. 3.5 and 4 that the thick disc
could constitute as much as a 10% of the total low latitude sources
selected in this paper, so the derived
scale-height will be somewhat larger than would be the case for the thin
disc alone. Here we will use the term "old disc'' as the average structure
traced by the old disc stars, including any thick disc component (mean height
around 300 pc). The determined mean scale-height might be larger at higher latitudes if there
is a thick disc.
3 Using CMDs to obtain the parameters of the disc
3.1 The selection of giants
We have built (J-K,mK) CMDs from the 2MASS data set for selected regions
of the sky (Fig. 1). We have taken the data "as is'', without further
processing. The data have been grouped in regions covering between 2 and 5
squared degrees on the sky (see Sect. 3.4 for details).
The position on a CMD of a star is determined from its absolute magnitude, intrinsic color, distance and
extinction. Any horizontal displacement is caused by extinction alone,
and hence if the intrinsic color of the source is known, the
total extinction can be directly determined from the measured color.
The vertical motion, however, is caused by both distance (doubling the distance
makes the source 1.5 mag fainter) and extinction. So if the absolute magnitude
of the source is already known, the extinction can be determined from the
reddening and hence the distance is directly determined (see formulae
in Sect. 3.2).
When there are a number stars of the same spectral class (i.e approximately the same absolute magnitude
and color) but at different distances from the Sun, these will be situated
along a line on the CMD. Increasing the distance shifts the star
to a fainter magnitude, while extinction by itself shifts the stars diagonally.
Hence, combining these two effects would mean that sources from a single
spectral class will form a line (or stripe) on a CMD. In areas of the Galaxy
where extinction is low this line will be almost vertical whereas for lines
of sight into the inner Galaxy, the line will have a considerable angle as
the extinction becomes the dominant effect.
On a color-absolute magnitude diagram (CAMD), the majority of the
stars lie in the main sequence or giant branch. When there is a wide
range of distances being sampled, each part of the CAMD
produces its own stripe on a CMD and so the overall effect is more
of a broad smear rather than a well defined line. By
far the most common type of giant, however, are the early K giants or red clump
giants. These produce a very well defined grouping, with a density far
higher than the surrounding areas, on a visible CAMD (e.g. Hoeg et al.
1997). On an IR CAMD (e.g. Cohen et al. 2000) the grouping
is even tighter. For V-[8.3]
CAMD the total spread of the red clump is
about 0.5 in color and 1 mag in absolute magnitude. There
are sufficient of these sources to produce a clearly recognizable
feature in a CMD, and this was used in Hammersley et al. (2000) to examine
lines of sight into the inner Galaxy. The
luminosity function derived in Hammersley et al. (2000) shows
that at the peak of the red clump there are about 10 times the numbers
of sources as there are either 0.8 mag brighter or fainter, and
the sigma in absolute magnitude is about 0.3 mag. The MKof the center of the red clump is -1.65, although there is a possible
error of about 0.1 mag. Using the tables in Wainscoat et al.
(1992) an MK=-1.65 corresponds to a K2III and hence the J-K color
is
(J-K)0=0.75.
Figure 1 shows the CMD for two of the fields used in this
study. The red clump stripe can be clearly seen. In order to isolate
the red clump sources, we have made histograms of horizontal cuts (i.e.
in color) through the CMDs, varying the mK range used. A Gaussian
was then fitted to histogram (i.e. the region containing the red
clump giants) to determine the position of the peak in each horizontal cut.
Stars lying well to the left of the maxima are almost
totally dwarfs, as there are very few giants with colors bluer than the
red clump stars. Stars lying to the right will be predominantly the M giants and AGBs, at least brighter than mK=13.
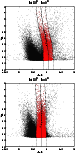 |
Figure 1:
Color-magnitude diagrams for two studied fields. The higher extinction
causes a slight broadening in the K-giants strip for in-plane regions.
Maxima obtained by a Gaussian fitting to star distribution in the
red clump strip. The solid line shows the fitted trace that we assign to red clump giants
population. The dashed lines show the limits for the red clump giants
extraction within a width of 0.4 mag. |
| Open with DEXTER |
In order to simplify the parameter fitting it will be assumed that
the red clump giants all have MK=-1.65 (i.e. luminosity function
becomes a Dirac delta function) instead of a more realistic case with
some dispersion (see in Sect. 3.3 a discussion about this approximation).
The peak of the histogram is used to trace the red clump giants
empirically. However, it can be seen in Fig. 1 that at
fainter magnitudes the effect of the K dwarf population becomes
significant and swamps the red clump sources. Hence, this limits the
method to
mK<13.0. Figure 1 show the position of the
peaks on each of the CMDs. Using the fitted trace for the red clump
giants extinction along the line of sight for each field can be
determined (see Sect. 3.2).
The red clump giants can be directly extracted using the fitted trace.
Sources with a (J-K) within 0.2 mag of the center of the fitted
red clump line were extracted, and the star counts were then obtained. The
width was determined after a number of trials and is a compromise between
the necessity to avoid other stars types but include most of the red clump
giants. If too small a width were chosen then any error in the
determination of the position peak would lead to a loss of sources at
that point and so reduce the measured density. Using this width, most
of the red clump giants for low extinction regions will be extracted.
However, where the extinction is somewhat patchy (for
instance in negative latitudes) the strip broadens and a
significant number of stars are lost. Therefore, those regions have been
excluded from the analysis.
One of the main strengths of this method is that it is empirical and
the only assumption being made is that the absolute magnitudes of all of
the sources being extracted is fixed. If, however, we had taken a
theoretical trace for the red clump giants using a model and isolated
the stars around this, then any difference between the predicted and
actual extinction would directly lead to errors in the extracted
counts. Another advantage of this method is that the spatial
information is obtained directly from the counts. The position
of the sources can be determined directly from the magnitude and extinction
without the need to resort to models.
The error analysis presented in the following sections will only
include the random errors in the fitting and not the systematic errors
outlined in this section. The error in the determination of the
absolute magnitude is taken to be 0.1 mag, which corresponds to a
distance error of 5%. The possible error in (J-K)0 only affects
the calculation of the extinction, as the peaks of the
color histograms are derived directly from the data. An error
of 0.1 mag in (J-K)0 would lead to an error of 0.07 mag in the extinction
(see Eq. (8)) and hence an error of 3% in distance.
The errors in assuming that the luminosity is a
delta function are also of the order 5%. To these should be added the
errors in the 2MASS zero points or the assumed extinction coefficients
although these are likely to be small. The photometric error in 2MASS sources
with mK<13 is  0.03 mag., however the error
is much lower when using the mean magnitude in
a bin with tens of stars. Similarly, the error in the 2MASS-color is negligible
for of the same reason. Hence, as well as the stated
error there will be a systematic error in the distances, but this
should be under 10%.
0.03 mag., however the error
is much lower when using the mean magnitude in
a bin with tens of stars. Similarly, the error in the 2MASS-color is negligible
for of the same reason. Hence, as well as the stated
error there will be a systematic error in the distances, but this
should be under 10%.
3.2 Stars density. Disk scale-length
Using the red clump star counts, we can directly obtain the star
density (stars pc-3) by means of the stellar statistics equation:
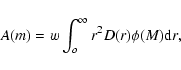 |
(7) |
where A(m) is the number of stars per unit area of solid
angle w at m in interval dm, and 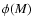 is the luminosity
function. The bins used in this paper have dm=0.1 in the range
mk=8.5 to mk=13.0.
is the luminosity
function. The bins used in this paper have dm=0.1 in the range
mk=8.5 to mk=13.0.
As has been already discussed, we have assumed MK=-1.65 and an
intrinsic color
(J-K)0=0.75 for a red clump giants. The extinction
AK(mk), to a distance
r, can be determined by tracing how (J-K) of the peak of the red
clump counts changes with mK. The extinction is calculated for
any mK using the measured (J-K) of the peak, the intrinsic mean
color of the stars in the apparent magnitude bin (J-K)0, and the color
excess definition and the interstellar extinction values for AJand AK, as given by Rieke & Lebofsky (1985):
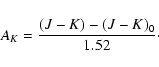 |
(8) |
Since we have assumed that red clump giants have an absolute magnitude
of
MK=-1.65, 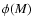 is replaced by a
delta function. Furthermore, by choosing apparent-magnitude intervals of
0.1 mag (
is replaced by a
delta function. Furthermore, by choosing apparent-magnitude intervals of
0.1 mag ( )
and the related distance intervals(
)
and the related distance intervals(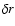 ), the star
density can be directly determined using:
), the star
density can be directly determined using:
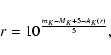 |
(9) |
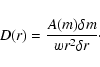 |
(10) |
The galactocentric mean distance of the stars per
bin (R) is calculated using the
measured mean distance (r) in the following equation:
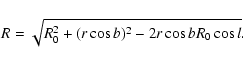 |
(11) |
With this method, we are inverting the star counts of the red clump
population to obtain the stellar density along the line of sight. This is a simple and direct method and although some assumptions and approximates are required, these can be justified.
Another method of inversion of star counts is presented in López-Corredoira
et al. (2000)
which solved for the both density and luminosity function. However, this method only works for the bulge and would not be appropriated for the disc.
3.3 Testing the method
In order to to verify that the proposed method is correct a number of
tests were made.
To further explore the form of red clump, we have calculated the distribution of
K magnitudes and (J-K)0 colors using the "SKY'' model,
but updating the density function of the
giant populations (Wainscoat et al. 1992; Cohen M., private communication).
In Fig. 2, the part of the luminosity function
pertaining to the G5 to M0 giants is shown.
The right hand plot shows the predicted form of
the (J-K) histogram at mK=+11 (but with no extinction) along a
line of sight towards the anti-center. In both plots
the predominance of the red clump giants is evident.
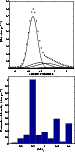 |
Figure 2:
Distribution of K absolute magnitudes and (J-K)0 colors
at mK=11 along a line of sight towards the anti-center
corresponding to the sum of all giant types in the disc according to
the updated "SKY'' model (Wainscoat et al. 1992; M. Cohen, private
communication). The maxima of these plots corresponds
the red clump, which are predominant in the giant population. |
| Open with DEXTER |
In order to determine the effect of using a Dirac delta as
the luminosity function for the red clump,
we have carried out a simple calculation. The red
clump giants are assumed to have a Gaussian dispersion in magnitude with
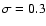 .
From Eqs. (7) and (10),
the density in the direction of the anticenter can then be written as:
.
From Eqs. (7) and (10),
the density in the direction of the anticenter can then be written as:
where 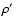 is the density derived with the method developed in this
section (see Sect. 3.2), while
is the density derived with the method developed in this
section (see Sect. 3.2), while 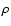 is the real
density distribution. Using Eq. (6) with
H=2.0 kpc,
is the real
density distribution. Using Eq. (6) with
H=2.0 kpc,
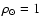 ,
gives the result plotted in Fig. 3. The difference between the two curves is the
error introduced by the approximation, hence it is negligible.
The scale-length that is determined assuming MK=-1.65 for all of the
sources is H'=1.96 pc, i.e. the error
in the calculation of the scale-length is around 2%.
Therefore, the simplification is justified and it does not produce
significative differences.
,
gives the result plotted in Fig. 3. The difference between the two curves is the
error introduced by the approximation, hence it is negligible.
The scale-length that is determined assuming MK=-1.65 for all of the
sources is H'=1.96 pc, i.e. the error
in the calculation of the scale-length is around 2%.
Therefore, the simplification is justified and it does not produce
significative differences.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{MS2213f3.eps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg65.gif) |
Figure 3:
Comparison between a real density
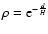 and the convolved distribution of Eq. (12)
obtained under the assumption of Dirac delta luminosity function
instead of the real Gaussian distribution with and the convolved distribution of Eq. (12)
obtained under the assumption of Dirac delta luminosity function
instead of the real Gaussian distribution with
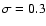 . . |
| Open with DEXTER |
One critical aspect of the method is the assumption that there are only
red clump sources being extracted (i.e. MK=-1.65). However, the CAMD
presented in Cohen et al. (2000, their Fig. 4), shows that there are
lower luminosity sources with the same color as the red clump. (The
range of (J-K) used for extracting the red clump corresponds to a
V-[8.3] of about 1.2). The magnitude limit for the CAMD is about
![$m_{\rm [8.3]}=6.5$](/articles/aa/full/2002/42/aa2213/img66.gif) and so in the 100 pc plot of Fig. 4 in
Cohen et al. (2000), the source count is
complete for all absolute magnitudes brighter than 1.5. There are
some higher luminosity sources with the same color and the red clump,
but these are relatively few and can be ignored. However, there are
significant numbers of lower luminosity giants. These
giants will have
+2>MK>-1.4 and could mask a cut off.
and so in the 100 pc plot of Fig. 4 in
Cohen et al. (2000), the source count is
complete for all absolute magnitudes brighter than 1.5. There are
some higher luminosity sources with the same color and the red clump,
but these are relatively few and can be ignored. However, there are
significant numbers of lower luminosity giants. These
giants will have
+2>MK>-1.4 and could mask a cut off.
In order to gauge the effect of these sources on the method, a simple luminosity
function was built which had half of the giants with
-1.45>MK>-1.85 and
the other half of giants with
+2>MK>-1.4.
This is probably an overestimate of the importance of the lower
luminosity sources and so should be considered a worse case scenario.
We have carried out the same type of convolution in the anticenter
of the previous subsubsection but with this luminosity function, and we
have used a truncated exponential disc. The result is shown in 4.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2213f4.eps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg67.gif) |
Figure 4:
Comparison between a real density
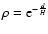 ,
truncated at R=12.9 kpc (distance from the Sun: 5 kpc) and
and the convolved distribution
obtained under the assumption of Dirac delta luminosity function
instead of the real distribution with 50% of the stars with MK=-1.65and 50% of the stars between
+2 >MK>-1.4 (lower luminosity giants). ,
truncated at R=12.9 kpc (distance from the Sun: 5 kpc) and
and the convolved distribution
obtained under the assumption of Dirac delta luminosity function
instead of the real distribution with 50% of the stars with MK=-1.65and 50% of the stars between
+2 >MK>-1.4 (lower luminosity giants). |
| Open with DEXTER |
As can be observed, the only significant change is in the amplitude because
half of the stars with MK=-1.65 have been lost. However, this is
not important as the total number of the giants is not used in the
analysis. Also the derived scale-length changes by 7%. The cut-off,
however, is not masked as there is a clear change of slope in 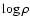 around
around
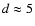 kpc. Hence, if there were a cut-off at
about 13 kpc it should still be visible even with the presence of
possible lower luminosity giants.
As will it be shown below (Figs. 7 and 9), we do not observe any change of slope in
kpc. Hence, if there were a cut-off at
about 13 kpc it should still be visible even with the presence of
possible lower luminosity giants.
As will it be shown below (Figs. 7 and 9), we do not observe any change of slope in 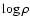 ,
so
the absence of cut-off seems clear and cannot be criticized as an
effect of the contamination of low luminosity giants.
,
so
the absence of cut-off seems clear and cannot be criticized as an
effect of the contamination of low luminosity giants.
Another critical aspect that must be considered is the dwarf contamination.
There is an important contribution to the stars counts from dwarf stars for faint
apparent magnitudes (mK>14; Fig. 1). The selection method used here cannot separate
between these two star populations at these magnitudes, as the main
sequence and the K-giant strip overlap. In order to estimate
the dwarf contamination for mK<13.0, the luminosity and
densities functions of the giants and dwarf stars from the model of
Wainscoat et al. (1992) were used to calculate the predicted ratio
between dwarf and the total of giants plus dwarfs in the counts. The result is shown in Fig. 5. It is clear that for faint apparent magnitudes (
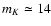 )
the dwarf contribution is important, accounting for almost 50% of the total counts.
However, the contribution decreases at brighter magnitudes such that for mK< 13 less
than
)
the dwarf contribution is important, accounting for almost 50% of the total counts.
However, the contribution decreases at brighter magnitudes such that for mK< 13 less
than 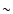 10% of the stars are dwarfs. This was calculated for off-plane regions, where the extinction is almost negligible. It is
expected that for regions close to the Galactic plane, where the extinction is
higher, the dwarf contamination will be even less,
because the reddening will shift the giants to the right whilst the dwarfs will be less affected, and so the dwarf-giant separation is improved. Hence,
here we will only use the red clump star counts for
mK<13.0, where the dwarf contamination is small.
10% of the stars are dwarfs. This was calculated for off-plane regions, where the extinction is almost negligible. It is
expected that for regions close to the Galactic plane, where the extinction is
higher, the dwarf contamination will be even less,
because the reddening will shift the giants to the right whilst the dwarfs will be less affected, and so the dwarf-giant separation is improved. Hence,
here we will only use the red clump star counts for
mK<13.0, where the dwarf contamination is small.
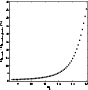 |
Figure 5:
Percentage of predicted dwarf stars in the total star counts extracted from the
color-magnitude diagram for
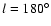 , ,
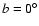 . . |
| Open with DEXTER |
When the metallicity decreases the stars become bluer, and hence the
reddening could be underestimated.
We have assumed that the stellar populations throughout the disc is homogeneous
and therefore, there are no large gradients in the metallicity.
However, even in the case of small metallicity variations
(Cameron 1985, has measured a radial metallicity gradient of
-0.11 dex kpc-1), the change to the result is small as
the red clump color is practically independent
of age and metallicity (Sarajedini et al. 1995).
The variations are limited within
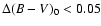 (Sarajedini
et al. 1995), which means
(Sarajedini
et al. 1995), which means
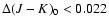 ,
i.e. an error
in the extinction less than 0.015, which is negligible.
,
i.e. an error
in the extinction less than 0.015, which is negligible.
Table 1:
Selected regions used with the red clump extraction.
| l (deg) |
b (deg) |
area (deg2) |
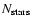 (
mk<14.5)
(
mk<14.5) |
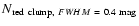 (mK<13)
(mK<13) |
|---|
| 180 |
0 |
3.84 |
68 492 |
2588 |
| 180 |
3 |
5 |
98 473 |
4881 |
| 180 |
6 |
5 |
64 366 |
3777 |
| 180 |
9 |
5 |
49 614 |
7161 |
| 180 |
12 |
5 |
39 017 |
5191 |
| 220 |
0 |
5 |
111 788 |
5100 |
| 220 |
3 |
3.88 |
69 659 |
3756 |
| 220 |
6 |
5 |
75 411 |
4024 |
| 220 |
9 |
4.99 |
54 672 |
6555 |
| 220 |
12 |
3.55 |
30 867 |
3992 |
| 155 |
0 |
2.07 |
24 189 |
1225 |
| 165 |
0 |
4.22 |
71 731 |
3765 |
3.4 Selected regions
Twelve fields were chosen from the available 2MASS data,
which are summarized in Table 1.
In each field a large area of sky was covered (between 2 and 5 square
degrees) as a large number of stars are needed to determined the
color of the peak of the red clump distribution. The high number of
red clump giants also minimizes the poissonian noise in the star
counts and so improves the subsequent fitting of the density
distributions. The fields were 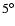 in longitude by
in longitude by 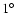 in
latitude, although the actual area covered depends on the available
2MASS data within each region. The star density is changing far
more rapidly in latitude than longitude so it is important not to
include a wide spread of latitudes in each region. Positive
latitude regions were selected because these are less affected by
patchy extinction, which causes a significant dispersion of the red
clump strips.
We have only used regions
in
latitude, although the actual area covered depends on the available
2MASS data within each region. The star density is changing far
more rapidly in latitude than longitude so it is important not to
include a wide spread of latitudes in each region. Positive
latitude regions were selected because these are less affected by
patchy extinction, which causes a significant dispersion of the red
clump strips.
We have only used regions
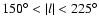 so as to avoid the northern and southern warps, which produce
large asymmetries between positive and negative latitudes (see Sect. 5).
Furthermore, the lines of sight in
so as to avoid the northern and southern warps, which produce
large asymmetries between positive and negative latitudes (see Sect. 5).
Furthermore, the lines of sight in
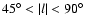 travel
for large distances at approximately
the same galactocentric distance before reaching the outer disc,
which would increase the error in obtaining the scale-length.
travel
for large distances at approximately
the same galactocentric distance before reaching the outer disc,
which would increase the error in obtaining the scale-length.
The main characteristics of the chosen fields are summarized in Table 1. Columns (1) and (2) give
the Galactic coordinates of the center of the field.
Column (3) is the total area in the field which has 2MASS
data. The total number of stars with
mk<14.5 is given in Col. (4), and finally Col. (5)
gives the total number of red clump giant stars extracted from the
color-magnitude diagram, with mk<13.
3.5 Results
A sequential fitting procedure has been used to obtain the model parameters
for Eqs. (1) and (2) (or Eqs. (3) and (4)).
First, to restrict the number of free parameters we have used only the
data at b=0 to obtain the radial scale-length H (i.e., Eq. (6)), so that there would
be no dependence on height. This scale-length is then used in the
off-plane regions to derive the values of the scale-height (hz(R)) and flare (
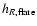 ).
).
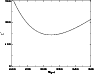 |
Figure 6:
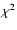 vs. H of the fit of red clump star density in the plane of
the model (6).
vs. H of the fit of red clump star density in the plane of
the model (6). |
| Open with DEXTER |
An exponential disc (Eq. (6)) was fitted
to the data with
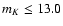 in the plane
for longitudes of
in the plane
for longitudes of 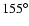 ,
,
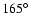 ,
,
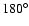 and
and 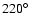 .
The value of H which gives the
minimum
.
The value of H which gives the
minimum 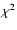 (
(
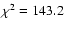 for a number of data points
N=184, see Fig. 6) and
assuming that the errors for each data point are poissonian
was for:
for a number of data points
N=184, see Fig. 6) and
assuming that the errors for each data point are poissonian
was for:
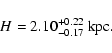 |
(13) |
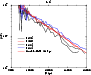 |
Figure 7:
Fit of red clump star density in the plane of
the model (6). |
| Open with DEXTER |
As described in Sect. 3.1, the red clump sources are extracted from
the general star counts by means of the (J-K) CMD. Inserting these number
counts in Eq. (5), with the help of Eq. (6) with the
calculated value for H, we derive a density for these sources in the solar
neighborhood
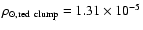 stars
pc-3. The disc model with the optimum value of H is shown in Fig. 7 together with the density distribution of the red clump
stars derived as explained in Sect. 3.2. The small differences in the
density for the different lines of sight stem presumably from the differences
in the patchiness of the extinction, which spreads out the red clump giants,
or contamination. Even so, it is noticeable how well the analytical function
matches the data.
stars
pc-3. The disc model with the optimum value of H is shown in Fig. 7 together with the density distribution of the red clump
stars derived as explained in Sect. 3.2. The small differences in the
density for the different lines of sight stem presumably from the differences
in the patchiness of the extinction, which spreads out the red clump giants,
or contamination. Even so, it is noticeable how well the analytical function
matches the data.
Using the value of H determined above with off-plane regions at
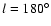 and
and
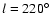 ,
allows the disc scale-height
and the flare scale-length
to be examined. As before, the disc model of Eqs. (3) and (4)
are matched to the number counts by minimising the
,
allows the disc scale-height
and the flare scale-length
to be examined. As before, the disc model of Eqs. (3) and (4)
are matched to the number counts by minimising the 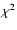 of the fit, being
now the free parameters
of the fit, being
now the free parameters
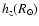 and
and
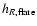 .
The best fit
(
.
The best fit
(
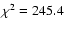 for N=460) is for:
for N=460) is for:
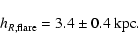 |
(14) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS2213f8.eps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg93.gif) |
Figure 8:
The red clump star density obtained from the data and the lines showing a model (3) with H=2.1 kpc,
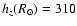 pc, pc,
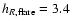 kpc. Note that the data show a slower decrease of density
for larger R, and this fact can be modeled with the flare
hz=580 pc, 1055 pc, 1905 pc respectively for
R=10,12,14 kpc (the data belong
to a range of 0.5 kpc centered in these galactocentric radii). kpc. Note that the data show a slower decrease of density
for larger R, and this fact can be modeled with the flare
hz=580 pc, 1055 pc, 1905 pc respectively for
R=10,12,14 kpc (the data belong
to a range of 0.5 kpc centered in these galactocentric radii). |
| Open with DEXTER |
The errors are calculated for H=2.10 kpc and other
values of H could slightly change the error ranges.
The stated errors are determined to be changing the
parameters such that 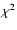 becomes a factor f larger than the minimum
(which corresponds to a 68% confidence level and is specified in
statistics manuals).
The correlations between the different parameters do not significatively
change the errors.
Figures 8 and 9 show the comparison of this
model with the observational data at different heights above the plane.
Since the heliocentric distance to the
extracted stars can be measured (see Sect. 3.2), their distance
from the Galactic plane is also known.
Both figures show that there is an increase in scale-height with increasing R.
Furthermore, in Fig. 8, the data show a slower decrease of
stellar density with zat larger R (hz=580 pc, 1055 pc, 1905 pc for
R=10, 12, 14 kpc respectively).
Both of these effects can only be produced by a flare.
becomes a factor f larger than the minimum
(which corresponds to a 68% confidence level and is specified in
statistics manuals).
The correlations between the different parameters do not significatively
change the errors.
Figures 8 and 9 show the comparison of this
model with the observational data at different heights above the plane.
Since the heliocentric distance to the
extracted stars can be measured (see Sect. 3.2), their distance
from the Galactic plane is also known.
Both figures show that there is an increase in scale-height with increasing R.
Furthermore, in Fig. 8, the data show a slower decrease of
stellar density with zat larger R (hz=580 pc, 1055 pc, 1905 pc for
R=10, 12, 14 kpc respectively).
Both of these effects can only be produced by a flare.
This result cannot be produced by a combination of a thick disc and a thin
disc with constant scale-heights and the scale-lengths because, then
the global scale-height would be independent of R.
If there is a thick disc with, for example, hz=910 pc,
a density on the plane of 5.9% of the thin disc (Buser et al. 1999)
and assuming that there is not significative difference in the abundances
in the red clump population, then the
thick disc would become dominant for z>1300 pc whereas
for z<500 pc the thin disc would be by far the more important.
Figure 8 shows very
different slopes for different R at z<500 pc,
and even the combination of thin and thick disc
with different scale-lengths cannot reproduce this effect
because the thin disc is highly dominant for z<500 pc.
Furthermore, the thick disc cannot
produce significant errors in the calculated scale-length,
since this was derived in the plane where the thin disc always dominates.
The scale-height, however, would be representative of an average
of thin and thick discs. The average source height in the data set used is
 300 pc, where the thin disc is
300 pc, where the thin disc is  10 times denser
than the Buser thick disc.
10 times denser
than the Buser thick disc.
Another noticeable feature of Figs. 7 and 9 is that the density follows the exponential to at least
15 kpc. As has already been discussed, if the disc had a sharp cut-off then this would cause an abrupt
drop in the density. Hence the absence of such a sharp
drop implies that there is no abrupt cut-off to the disc until at least
 15 kpc. By 15 kpc the star density has become too low to determine
if there is a cut-off beyond that point.
15 kpc. By 15 kpc the star density has become too low to determine
if there is a cut-off beyond that point.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS2213f9.eps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg94.gif) |
Figure 9:
The red clump star density obtained from the data and the lines
showing a model (3) with H=2.1 kpc,
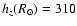 pc, pc,
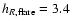 kpc at kpc at
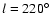 and the latitudes stated on the
plot.
and the latitudes stated on the
plot. |
| Open with DEXTER |
3.6 Flare in the inner Galaxy?
 |
Figure 10:
The red clump star density obtained from the data and the lines showing a model (3) with H=2.1 kpc,
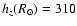 pc
and different flare scale-lengths ( pc
and different flare scale-lengths (
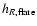 )
at )
at
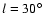 , ,
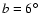 .
As can be seen, a flare is necessary in the inner Galaxy, and
its best scale-length is around 9 kpc. .
As can be seen, a flare is necessary in the inner Galaxy, and
its best scale-length is around 9 kpc. |
| Open with DEXTER |
The regions used in the previous subsection all had
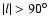 ,
and hence the lines of sight run external to the solar circle
(
,
and hence the lines of sight run external to the solar circle
(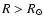 ). Therefore, the results are valid only
for the outer disc. Moreover, the flare
scale-length of around 3.4 kpc is really only a
description of the flare for R> 10 kpc, as between 8 and 10 kpc
there is little data which is also very noisy (Fig. 7). Hence,
whether this law is applicable to R<10 kpc is something that cannot
be deduced from the previous analysis, and data with a
range of lower galactocentric distances is required.
). Therefore, the results are valid only
for the outer disc. Moreover, the flare
scale-length of around 3.4 kpc is really only a
description of the flare for R> 10 kpc, as between 8 and 10 kpc
there is little data which is also very noisy (Fig. 7). Hence,
whether this law is applicable to R<10 kpc is something that cannot
be deduced from the previous analysis, and data with a
range of lower galactocentric distances is required.
In order to examine the effect of the flare in the inner Galaxy this
method should not be applied to lines of sight which cover only small a
range of Galactocentric distances inside the solar circle,
as these provide only a small range of values with which to attempt
fitting R. For instance, on plane regions with
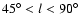 would only give values of R between 6 and 8 kpc.
Therefore, in order to explore the inner
disc using this method, we must use regions with
would only give values of R between 6 and 8 kpc.
Therefore, in order to explore the inner
disc using this method, we must use regions with
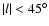 .
Furthermore, the near plane regions with
.
Furthermore, the near plane regions with
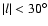 should also
be avoided, as the inner Galaxy components become important, e.g. the
in-plane bar (Hammersley et al. 1994; López-Corredoira et al. 2001).
At present the available 2MASS data in the regions of interest is very
restricted and so we will concentrate in only one region:
should also
be avoided, as the inner Galaxy components become important, e.g. the
in-plane bar (Hammersley et al. 1994; López-Corredoira et al. 2001).
At present the available 2MASS data in the regions of interest is very
restricted and so we will concentrate in only one region:
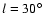 ,
,
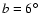 .
.
Figure 10 shows the density of the red clump giants along
this line of sight determined using the same method as in Sect. 3.2.
As well as the measured density, various model predictions are plotted.
It shows that a flare is necessary to describe
the data with a disc of H=2.1 kpc and
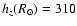 pc. However, the
scale-length of the flare cannot be as low as 3.4 kpc, but rather around 9 kpc.
The scale-height in the inner Galaxy is smaller than the scale-height
in the solar neighborhood, however the difference is only
pc. However, the
scale-length of the flare cannot be as low as 3.4 kpc, but rather around 9 kpc.
The scale-height in the inner Galaxy is smaller than the scale-height
in the solar neighborhood, however the difference is only
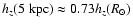 .
A flare scale-length of 3.4 kpc would imply
.
A flare scale-length of 3.4 kpc would imply
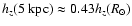 .
Hence, although the flare
begins well inside the solar circle, the increase of the scale-height with R is significantly slower in the inner Galaxy.
.
Hence, although the flare
begins well inside the solar circle, the increase of the scale-height with R is significantly slower in the inner Galaxy.
This result is consistent with previous work. For instance, Kent et al. (1991)
has measured
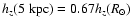 by fitting the parameters
of the disc in a 2.4
by fitting the parameters
of the disc in a 2.4 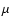 m map of the northern Galactic plane.
m map of the northern Galactic plane.
4 Using the star counts to obtain the parameters of the disc
The second method used for determining the parameters for the stellar density
is by the fitting of star counts in different regions.
For each of the line of sight centered on Galactic coordinates (l,b)i,
(i is the field number)
the cumulative star counts (NK) observed in K,
up to a magnitude mK in a given solid angle 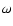 is
the sum of the stars within the beam brighter than the given apparent magnitude
(Bahcall 1986).
Assuming that the luminosity function does not vary with the
spatial position, this is
is
the sum of the stars within the beam brighter than the given apparent magnitude
(Bahcall 1986).
Assuming that the luminosity function does not vary with the
spatial position, this is
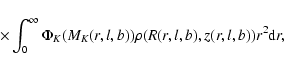 |
(15) |
where
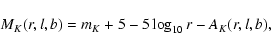 |
(16) |
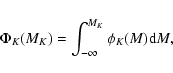 |
(17) |
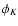 is the normalized luminosity function for the K band in the disc and
AK(r,l,b) is the K extinction along the line of sight (l,b)
up to distance r.
We have used a standard
disc luminosity function given in Eaton et al. (1984, see Fig. 11) and
the extinction model given by Wainscoat et al. (1992)
(except with
is the normalized luminosity function for the K band in the disc and
AK(r,l,b) is the K extinction along the line of sight (l,b)
up to distance r.
We have used a standard
disc luminosity function given in Eaton et al. (1984, see Fig. 11) and
the extinction model given by Wainscoat et al. (1992)
(except with
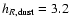 kpc to scale the distance to the center of
the Galaxy to 7.9 kpc). Fitting could also be used to constrain
the extinction, however it is preferable to have as few free parameters
as possible. The extinction model of Wainscoat et al. (1992) is axisymmetric and does not include
a flare or a warp in the dust distribution. However,
K-band counts are not very sensitive to small variations of the
extinction and were extinction the goal of the paper shorter wavelengths
would be more appropriate. Therefore, as the lines of sight are in general
looking towards the outer Galaxy and the extinction is low, a
simple extinction model will suffice.
kpc to scale the distance to the center of
the Galaxy to 7.9 kpc). Fitting could also be used to constrain
the extinction, however it is preferable to have as few free parameters
as possible. The extinction model of Wainscoat et al. (1992) is axisymmetric and does not include
a flare or a warp in the dust distribution. However,
K-band counts are not very sensitive to small variations of the
extinction and were extinction the goal of the paper shorter wavelengths
would be more appropriate. Therefore, as the lines of sight are in general
looking towards the outer Galaxy and the extinction is low, a
simple extinction model will suffice.
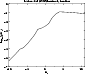 |
Figure 11:
K-band normalized
luminosity function used in the second method of this paper,
from Eaton et al. (1984). |
| Open with DEXTER |
The stellar density (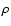 )
parameters (Eq. (3)) were determined using the
available 2MASS data at
)
parameters (Eq. (3)) were determined using the
available 2MASS data at
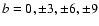 degrees;
degrees;
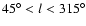 .
On or near-plane regions were preferred because these
are more sensitive to the variations in the parameters, and there are
significantly more stars. Again the central regions of the Galaxy were
avoided so that other components other than the disc would not be
included. It should be noted that even when the local stars dominate the counts there are still sufficient giants to constrain the large scale structure.
Each region used an area of 1 square degree (
.
On or near-plane regions were preferred because these
are more sensitive to the variations in the parameters, and there are
significantly more stars. Again the central regions of the Galaxy were
avoided so that other components other than the disc would not be
included. It should be noted that even when the local stars dominate the counts there are still sufficient giants to constrain the large scale structure.
Each region used an area of 1 square degree (
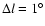 ,
,
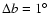 ). However, some areas are only partially
covered and in these cases the counts were divided by the actual area
available to obtain the counts per unit area. In total 820 lines of
sight with areas between 0.5 and 1.0 deg2 are used. This gives a
very large area coverage along the Galactic plane, and so can
constrain the parameters of the disc. Other authors have used 2MASS
star counts to study the disc however the number of regions used is much
lower. Ojha (2001) used seven independent regions quite far from the plane
but does not study the warp, flare and cut-off whilst
Alard (2000) only looked at three strips in latitude across the plane.
). However, some areas are only partially
covered and in these cases the counts were divided by the actual area
available to obtain the counts per unit area. In total 820 lines of
sight with areas between 0.5 and 1.0 deg2 are used. This gives a
very large area coverage along the Galactic plane, and so can
constrain the parameters of the disc. Other authors have used 2MASS
star counts to study the disc however the number of regions used is much
lower. Ojha (2001) used seven independent regions quite far from the plane
but does not study the warp, flare and cut-off whilst
Alard (2000) only looked at three strips in latitude across the plane.
As noted, this method assumes that all sources have the same spatial
distribution, i.e. the scale-height and scale-lengths in a given
galactocentric radius are the same. For
the scale-height, in particular, this is known not to be true with the
younger components having a scale-height far less than the older
components. However, the young components only make a significant
contribution to the counts at the brightest magnitudes (mK<8) and
even then only on the plane towards the inner Galaxy (Hammersley et al. 1999). For this study we have used
2MASS counts up to
mK = 14.0. This magnitude limit, coupled
with using lines of sight away from the inner Galaxy, means that the
counts will be completely dominated by the old population of
the disc rather than the young disc and spiral arms. Hence the
assumption that all of the sources will have, at least,
very similar scale-heights is justified.
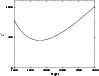 |
Figure 12:
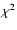 of the fit of star counts in the plane for
the model (6).
of the fit of star counts in the plane for
the model (6). |
| Open with DEXTER |
We have limited the maximum apparent magnitude in K band to 14.0.
This is well below the limiting magnitude of 2MASS and ensures that
there are complete statistics in all regions. Moreover, with
this limiting magnitude, stars brighter than MK=0 can be detected
to over 6 kpc which means the results are sensitive to the shape of the
very outer disc. However, one of the curious features of stars counts
is that the fainter the magnitude the closer on average are the sources
being detected. This is caused by the steeply rising luminosity
function and means that the dwarfs will dominate the fainter counts.
The result is that the red clump giant method, which isolates a
specific group of stars, will provide a better contrast for the more
external part of the disc.
As discussed previously, the "old disc'' analyzed here includes
all the old stars of the disc within the selected regions (average latitude
4-5 degrees). If there is a thick disc like the one proposed
by Buser et al. (1999), the mean contribution to the star counts in
the selected regions would be around 10%, assuming a
thick disc luminosity function similar to that of the halo
in Wainscoat et al. (1992).
Hence, the scale-height determined here would be
representative of an average of the thin and thick discs but with 90% of the
sources coming from thin disc.
Star counts cannot easily distinguish between the cut-off and the loss
of stars in the plane due to the flare. However, it was shown in the previous section that
it there is no cut-off to at least 15 kpc, and so we will continue
to assume there is not a cut-off.
4.1 Results
As in Sect. 3, the fitting of the parameters will be in
two steps. The first step is to fit H using the on plane regions (b=0) and then fit
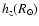 and
and
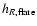 using all of the regions.
using all of the regions.
Using the available regions in the plane the minimum 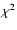 (
(
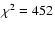 ,
N=114) was obtained for (see Fig. 12):
,
N=114) was obtained for (see Fig. 12):
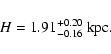 |
(18) |
The stellar density in the solar neighborhood is
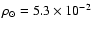 star pc-3. This is somewhat lower than the value measured in
other surveys (e.g., 0.13 star/pc3, Bahcall 1986). This discrepancy
is most probably due to using different luminosity functions, here we
used the normalized luminosity function by Eaton et al. (1984).
In any case the normalization does not affect the other disc parameters. The
best fit is shown in the Fig. 13 (dashed line).
star pc-3. This is somewhat lower than the value measured in
other surveys (e.g., 0.13 star/pc3, Bahcall 1986). This discrepancy
is most probably due to using different luminosity functions, here we
used the normalized luminosity function by Eaton et al. (1984).
In any case the normalization does not affect the other disc parameters. The
best fit is shown in the Fig. 13 (dashed line).
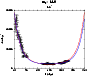 |
Figure 13:
Fit of star counts in the plane. The dashed line is
the best non-warped model (H=1.91 kpc).
Solid line is the best warped model (H=1.97 kpc;
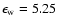 , ,
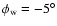 , ,
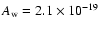 pc). pc). |
| Open with DEXTER |
The other two parameters were then fitted using all the available data
at
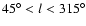 and
and
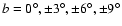 .
The minimum
.
The minimum 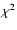 is found for
is found for
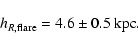 |
(19) |
These errors are for H=1.91 kpc and other
values of H could slightly change the error ranges.
In this case, the best fit was for
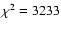 with N=820. The fits are shown in Figs. 13 and 14 (dashed line).
with N=820. The fits are shown in Figs. 13 and 14 (dashed line).
![\begin{figure}
\includegraphics[width=13.5cm,clip]{MS2213f14.ps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg125.gif) |
Figure 14:
Data and fit of star counts.
The dashed line is
the best non-warped model (H=1.91 kpc,
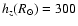 pc, pc,
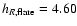 kpc).
The solid line is the best warped model (H=1.97 kpc, kpc).
The solid line is the best warped model (H=1.97 kpc,
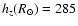 pc, pc,
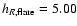 kpc; kpc;
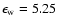 , ,
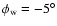 , ,
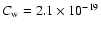 pc). pc). |
| Open with DEXTER |
In general there is a good fit, although there are some asymmetries
between
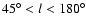 and
and
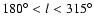 and also
between b>0 and b<0. These can be attributed principally to the
warp (see Sect. 5), but there are also some
other minor fluctuations, possibly due to the patchiness of the extinction
or contamination from other Galactic components.
and also
between b>0 and b<0. These can be attributed principally to the
warp (see Sect. 5), but there are also some
other minor fluctuations, possibly due to the patchiness of the extinction
or contamination from other Galactic components.
![\begin{figure}
\includegraphics[width=6cm,clip]{MS2213f15.eps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg129.gif) |
Figure 15:
Positive counts divided by the negative counts. The solid line
stands for a warped model with H=1.91 kpc,
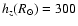 pc, pc,
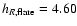 kpc; kpc;
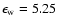 , ,
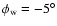 , ,
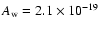 pc. The dashed line stands for the best "tilted disc''
model with H=1.91 kpc, pc. The dashed line stands for the best "tilted disc''
model with H=1.91 kpc,
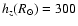 pc, pc,
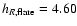 kpc; kpc;
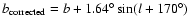 . . |
| Open with DEXTER |
5 In search of the stellar warp
If there were neither a warp nor other asymmetries,
the ratio of counts above and below the plane (Fig. 15) should be
nearly the same for all Galactic longitudes, with only a
small offset due to the height of the Sun above the plane.
However, the plot clearly show a sinusoidal behavior.
There is an excess of counts at positive latitudes with respect the negatives
for
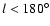 and the opposite for
and the opposite for
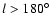 .
A warp, together with a small offset due the height of the Sun above the
plane, can explain what is seen.
.
A warp, together with a small offset due the height of the Sun above the
plane, can explain what is seen.
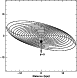 |
Figure 16:
A schematic of the warp showing the relative location of the Sun.
The rings are each kpc, and the line of the maximum warp is shown. |
| Open with DEXTER |
A model similar to Eq. (3) will be used,
but with
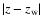 instead of
|z|, where
instead of
|z|, where 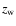 is the average elevation of the disc above a
plane which is parallel with b=0 but runs though the local center of
mass (i.e. 15 pc below the Sun).
is the average elevation of the disc above a
plane which is parallel with b=0 but runs though the local center of
mass (i.e. 15 pc below the Sun).
![\begin{displaymath}z_{\rm w}=\left[C_{\rm w}R({\rm pc})^{\epsilon _{\rm w}}\sin (\phi -\phi _{\rm w})+15\right] \ {\rm pc}.
\end{displaymath}](/articles/aa/full/2002/42/aa2213/img135.gif) |
(20) |
Hence, the model describes the warp as a series of tilted
rings, where the amount of tilt is the galactocentric distance raised
to a power
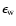 .
The 15 pc term is due to the height of the Sun above the plane
(Hammersley et al. 1995). Since the value of about 15 pc
is well constrained by other studies we will not carry out an analysis
of this parameter. The two warp parameters,
.
The 15 pc term is due to the height of the Sun above the plane
(Hammersley et al. 1995). Since the value of about 15 pc
is well constrained by other studies we will not carry out an analysis
of this parameter. The two warp parameters,
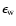 ,
and the
galactocentric angle
,
and the
galactocentric angle
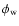 (
(
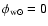 ), are determined
from the division of star counts data in Fig. 15.
Once the parameters are fixed then
), are determined
from the division of star counts data in Fig. 15.
Once the parameters are fixed then 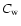 is obtained from:
is obtained from:
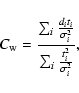 |
(21) |
where
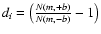 with N(m,b) the observational
cumulative counts,
with N(m,b) the observational
cumulative counts, 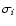 the errors of di, and ti is the model
prediction for di with
the errors of di, and ti is the model
prediction for di with
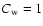 .
.
In this way, there are only two free parameters in the model and so it is simpler to constrain the warp. The model assumes that the northern and southern warp
are symmetric, apart from the effect of the height of the
Sun above the plane. This is an approximation and it is known that the gas warp is not symmetric (Burton 1988). However, the asymmetries of the warp
are produced over galactocentric distances
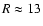 kpc
(distance from the Sun: r>8 kpc for
kpc
(distance from the Sun: r>8 kpc for
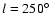 ),
where there are few stars from the total sample of
stars with mK<14.0.
),
where there are few stars from the total sample of
stars with mK<14.0.
The best fit is found for:
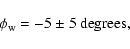 |
(22) |
which gives
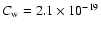 pc with
pc with
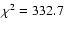 ,
N=217.
The best fit is shown in Fig. 15 (solid line).
Although there are few points which do not fit very well
(perhaps due to irregularities in the extinction
or in the distribution, contamination of the spiral arms, etc.)
again the general fit is good. Hence, a warp does accurately
describe the deviations from the best symmetric disc.
In Fig. 16, a representation of the warp is plotted.
,
N=217.
The best fit is shown in Fig. 15 (solid line).
Although there are few points which do not fit very well
(perhaps due to irregularities in the extinction
or in the distribution, contamination of the spiral arms, etc.)
again the general fit is good. Hence, a warp does accurately
describe the deviations from the best symmetric disc.
In Fig. 16, a representation of the warp is plotted.
An alternative hypothesis that could explain the asymmetries is that
the disc is locally tilted with respect to the global galactic plane.
Hammersley et al. (1995) showed that a similar asymmetry COBE-DIRBE
surface brightness-maps could be caused by a local tilt to the
disc. However, Hammersley et al. (1995) deliberately chose regions well
away from the plane, so that the results would be dominated by
local sources and there would be little contribution from regions where
the warp becomes significant (R>11 kpc).
Star count data provide direct information on the distance
to the sources, something not available with surface brightness-maps and
so can better distinguish between a tilt and warp.
In Fig. 15, it is shown the best fit for a tilted disc
model, i.e. assuming that the asymmetries are only due to
the height of the Sun above the plane and the local tilt of the disc
plane, which corrects the Galactic latitude as (Hammersley et al. 1995):
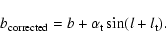 |
(23) |
The best fit for the tilt corresponds to
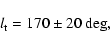 |
(24) |
which gives a value of
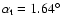 and
and
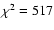 (N=217).
The orientation found is in good agreement with Hammersley et al. (1995),
but the tilt is some 4 times greater indicating sources at a significantly
larger distance are being detected.
(N=217).
The orientation found is in good agreement with Hammersley et al. (1995),
but the tilt is some 4 times greater indicating sources at a significantly
larger distance are being detected.
The predictions for the tilt are significantly poorer than for the model
of the warp, as can be seen in Fig. 15 (dashed line).
Hence, whilst a small tilt is sufficient to describe the geometry of local disc,
beyond a few kpc this simplification is no longer valid.
Interestingly the average tilt predicted by the warp model over the
distance range used in Hammersley et al. (1995) (i.e. about 2 kpc) is
still about twice as large as that measured from the surface
brightness map. This suggests that the warp actually starts just
outside the solar circle, although it should be noted that the predicted
effect in the solar vicinity is small in any case and the star counts
are not sensitive for very short distances from the Sun.
5.3 Confirmation of the warp with the red clump giants
A warp should also leave a clear imprint in the distribution of the
red clump giants (Sect. 3).
Since the warp will affect the distant sources most, the asymmetries
should be greater at larger galactocentric distances.
This can be seen in Fig. 17, where the ratio of densities at
positive and negative latitude is shown for the region
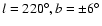 .
The data show a strong asymmetry with most points having a ratio <0.8
whilst for those beyond 13 kpc it drops to under 0.6.
This again shows that the asymmetries in the counts are larger for
distant sources.
To confirm that asymmetries cannot be due to the height of the Sun above
the plane, the dashed line in Fig. 17 shows the predicted
level of this effect. The predicted warp, however, is shown as the solid line
and this does provide a reasonable fit.
.
The data show a strong asymmetry with most points having a ratio <0.8
whilst for those beyond 13 kpc it drops to under 0.6.
This again shows that the asymmetries in the counts are larger for
distant sources.
To confirm that asymmetries cannot be due to the height of the Sun above
the plane, the dashed line in Fig. 17 shows the predicted
level of this effect. The predicted warp, however, is shown as the solid line
and this does provide a reasonable fit.
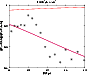 |
Figure 17:
Ratio of densities between
positive and negative latitude for (
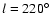 , ,
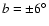 ).
The solid line shows the predicted ratio for the warp model with H=1.91 kpc, ).
The solid line shows the predicted ratio for the warp model with H=1.91 kpc,
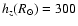 pc, pc,
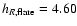 kpc; kpc;
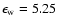 , ,
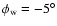 , ,
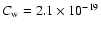 pc. The dashed line
shows the effect of the height of the Sun above the plane (+15 pc). pc. The dashed line
shows the effect of the height of the Sun above the plane (+15 pc). |
| Open with DEXTER |
Another aspect which needs to be commented upon is that the measured flare
scale-length may be affected by the warp, even in regions where the warp
is not very conspicuous (
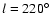 ). Figure 17 shows
that the ratio may be as low as 0.6, i.e. an error of around 20% for each
of the densities at positive and negative latitude. This is
one reason why the results from (14) should be taken with some care.
However, in the second method, the relative contribution from the very distant
stars (
). Figure 17 shows
that the ratio may be as low as 0.6, i.e. an error of around 20% for each
of the densities at positive and negative latitude. This is
one reason why the results from (14) should be taken with some care.
However, in the second method, the relative contribution from the very distant
stars (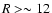 kpc) is much lower and the effect of the warp is
smaller (compare the results between Sects. 4.1 and 5.5).
Hence, the parameters derived from the star counts are probably
more trustworthy than those derived from the red clump giants in Sect. 3.
kpc) is much lower and the effect of the warp is
smaller (compare the results between Sects. 4.1 and 5.5).
Hence, the parameters derived from the star counts are probably
more trustworthy than those derived from the red clump giants in Sect. 3.
The measurements of stellar warp presented here are totally
independent of those used to determine gas warp (Burton 1988;
Diplas & Savage 1991). It is noticeable however,
that the stellar warp is nearly identical to that of the gas. Not
only is the angle of orientation of the maximum amplitude (
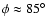 )
coincident, but the amplitude as well (see Fig. 18). The
northern warp in both the gas and stars are very similar to R>
13 kpc, as shown in Fig. 18. The southern gas warp differs
from the northern gas warp, becoming constant or decreasing with height
for R> 13 kpc. However, since a large majority of the stars along the
line of sight of southern warp (
)
coincident, but the amplitude as well (see Fig. 18). The
northern warp in both the gas and stars are very similar to R>
13 kpc, as shown in Fig. 18. The southern gas warp differs
from the northern gas warp, becoming constant or decreasing with height
for R> 13 kpc. However, since a large majority of the stars along the
line of sight of southern warp (
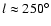 )
have R<13 kpc
(r<8 kpc), the data are not sensitive enough to detect the differences
between the northern and southern warp.
)
have R<13 kpc
(r<8 kpc), the data are not sensitive enough to detect the differences
between the northern and southern warp.
Other authors have also looked for the stellar warp. Djorgovski & Sosin (1989)
obtained a similar result with IRAS sources.
Alard (2000) also measured the stellar warp using 2MASS data, and
also concluded that the amplitude is roughly coincident with the gas
warp. Although the present results are more accurate, Alard (2000) showed that the amplitude of the stellar warp is consistent with the HI
to within about 30%.
Drimmel & Spergel (2001) found from COBE-DIRBE data that the
stellar warp is more or less coincident with the stellar warp found here (and
Burton 1988 gas warp):
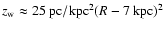 and Freudenreich (1998) obtained similar results in his independent
determination of warp parameters.
and Freudenreich (1998) obtained similar results in his independent
determination of warp parameters.
 |
Figure 18:
Maximum amplitude of the stellar warp (solid line:
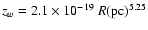 pc, which is the best power-law
fit to the data)
in comparison with the one measured by Burton (1988) for the northern and
southern warp gas scaled to pc, which is the best power-law
fit to the data)
in comparison with the one measured by Burton (1988) for the northern and
southern warp gas scaled to
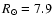 kpc (dashed and dot-dashed lines). kpc (dashed and dot-dashed lines). |
| Open with DEXTER |
From the presented results,
it is clear that the form of the stellar warp is identical to that of
the gas warp. Hence, whatever is causing of the warp affects both to
the stars (including the old population) and gas in approximately
the same way.
Whilst the stellar and gas warps are coincident for the Milky way,
this may not necessarily be the case in other galaxies.
5.5 A new fit of the disc including the warp
After obtaining the parameters of the warp, which is a second order effect on
the total counts, it is possible update the disc model to include the
warp and then redetermine the parameters using the cumulative
star counts. As expected, there are no major
changes with respect to the previous values (18), (19):
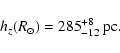 |
(25) |
The errors in
 and
and
 are
for the fixed value of H=1.97 kpc. Other
values of H could change very slightly the error ranges.
This best fit gives
are
for the fixed value of H=1.97 kpc. Other
values of H could change very slightly the error ranges.
This best fit gives
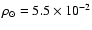 and corresponds to
and corresponds to
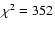 for the data in the plane (N=114), and
for the data in the plane (N=114), and
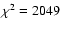 for the whole sample (N=820).
The fits are plotted in Figs. 13 and 14 (solid line).
Using Eq. (4), this provides a constraint on the intrinsic
scale-length of the disc:
for the whole sample (N=820).
The fits are plotted in Figs. 13 and 14 (solid line).
Using Eq. (4), this provides a constraint on the intrinsic
scale-length of the disc:
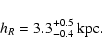 |
(26) |
It should be remembered that these parameters have between determined
between about R=6 and R=15 kpc (between 0.75 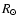 and 1.9
and 1.9 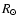 ).
No data comes from R<6 kpc as the limit in longitude is
).
No data comes from R<6 kpc as the limit in longitude is 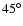 and
beyond 15 kpc the data becomes uncertain.
and
beyond 15 kpc the data becomes uncertain.
In Sect. 3, red clump giants gives values
compatible with those from the star counts except for the
 ,
which is 2.8
,
which is 2.8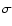 lower (3.4 kpc instead of 5.0 kpc).
It is unlikely that this is a separate population with different flare,
because the scale-height at the solar circle is coincident. We suspect
the difference stems from a selection effect. Apart from the
fact the measurement of red clump giants is affected by the warp and hence
the value of 3.4 is somewhat less trustworthy (Sect. 5.3), it must be remembered that most
of the giants are at R>12 kpc, i.e.
are dominated by distant stars. However, the
flare scale-length is not constant, it is higher for smaller R (Sect. 3.6 shows that
lower (3.4 kpc instead of 5.0 kpc).
It is unlikely that this is a separate population with different flare,
because the scale-height at the solar circle is coincident. We suspect
the difference stems from a selection effect. Apart from the
fact the measurement of red clump giants is affected by the warp and hence
the value of 3.4 is somewhat less trustworthy (Sect. 5.3), it must be remembered that most
of the giants are at R>12 kpc, i.e.
are dominated by distant stars. However, the
flare scale-length is not constant, it is higher for smaller R (Sect. 3.6 shows that
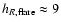 kpc between R=4 kpc and
R=7 kpc). Hence, a systematic difference between the two values should
be expected.
kpc between R=4 kpc and
R=7 kpc). Hence, a systematic difference between the two values should
be expected.
The flare scale-length can be expressed as:
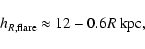 |
(27) |
where R is in kpc.
This gives the values of 9.0 kpc for R=5 kpc (close to the average
galactocentric distance of the sources along
 ,
,
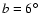 );
5.0 kpc for R=11.7 kpc (representative of the range between 6 and 15 kpc);
and 3.4 kpc for R=14.3 kpc (representative of the range occupied
by the distant giants). In the solar
neighborhood, the value of
);
5.0 kpc for R=11.7 kpc (representative of the range between 6 and 15 kpc);
and 3.4 kpc for R=14.3 kpc (representative of the range occupied
by the distant giants). In the solar
neighborhood, the value of
 would be 7.3 kpc.
would be 7.3 kpc.
In comparison, Alard (2000) has described the flare in 2MASS data by
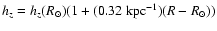 .
This is similar
to our results in the range 8<R<12 kpc.
Hence these results are in agreement with Alard (2000) and
the thickening of the disc explains the rapid drop of the density in
the outer Galaxy without the need to invoke a cut-off for R<15 kpc.
Indeed, as we have seen in
Sect. 3, the cut-off at R<15 kpc is not only unnecessary but
inconsistent with the data.
.
This is similar
to our results in the range 8<R<12 kpc.
Hence these results are in agreement with Alard (2000) and
the thickening of the disc explains the rapid drop of the density in
the outer Galaxy without the need to invoke a cut-off for R<15 kpc.
Indeed, as we have seen in
Sect. 3, the cut-off at R<15 kpc is not only unnecessary but
inconsistent with the data.
The flare, like the warp, is another characteristic of the gas in the outer
Galaxy. Again the parameters determined for the stars are very similar
to that of the gas (Wouterloot et al. 1990), although the gas scale-height
is always far lower.
 |
Figure 19:
Variation of the amplitude
 as a function of
the maximum K-band magnitude when we use the disc model of
this paper together with Eaton et al. (1984) luminosity function.
Solid line is Eq. (28).
as a function of
the maximum K-band magnitude when we use the disc model of
this paper together with Eaton et al. (1984) luminosity function.
Solid line is Eq. (28). |
| Open with DEXTER |
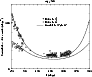 |
Figure 20:
Data and fit of star counts for mK<9.0.
The dashed line is the best warped model (H=1.97 kpc,
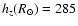 pc, pc,
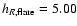 kpc; kpc;
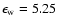 , ,
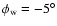 , ,
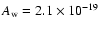 pc). pc). |
| Open with DEXTER |
An aspect which must be examined is the possible variation of
the measured local stellar density
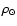 when using a range
of magnitudes other than mK<14.0. In principle, the given density
distribution should be independent of the magnitude range used,
however, there may be errors in Eaton's normalized luminosity function that
has been used here. Alternatively there could be source confusion at
the faintest 2MASS magnitudes, although such an effect would at most
only affect the sources within a magnitude of the survey limit in the regions measured.
Both errors would affect the measured
density,
when using a range
of magnitudes other than mK<14.0. In principle, the given density
distribution should be independent of the magnitude range used,
however, there may be errors in Eaton's normalized luminosity function that
has been used here. Alternatively there could be source confusion at
the faintest 2MASS magnitudes, although such an effect would at most
only affect the sources within a magnitude of the survey limit in the regions measured.
Both errors would affect the measured
density,
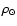 .
Figure 19 shows
the variation of
.
Figure 19 shows
the variation of
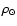 with limiting magnitude
with limiting magnitude
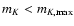 .
This can be described as
.
This can be described as
The data were obtained by normalizing the star counts with a circular
region centered in
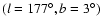 with
with
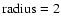 degrees.
The form of variation is not consistent with there being confusion and so
it has to be due to errors in the form of Eaton's luminosity function.
degrees.
The form of variation is not consistent with there being confusion and so
it has to be due to errors in the form of Eaton's luminosity function.
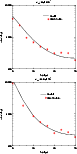 |
Figure 21:
Star counts in high latitude regions. Note how the model derived
in the present paper (fitting low latitude regions) also fit
approximately these high latitude regions. Data come from the available
covered regions in the different coordinates within a radius of 2 degrees. |
| Open with DEXTER |
An alternative possibility for this variation could have been the density
parameters are not correct and for this reason
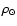 is not
constant with mK. This
can be checked by fitting
of the star counts with the model described in Sect. 5.5 but changing the
limiting magnitude and hence
is not
constant with mK. This
can be checked by fitting
of the star counts with the model described in Sect. 5.5 but changing the
limiting magnitude and hence
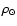 using Eq. (28).
It is found that the model still predicts the measured star
counts (some excess in the anticenter could be due to
some contaminant of bright sources). As an example Fig. 20 shows the fit for the whole plane for mK<9.0.
using Eq. (28).
It is found that the model still predicts the measured star
counts (some excess in the anticenter could be due to
some contaminant of bright sources). As an example Fig. 20 shows the fit for the whole plane for mK<9.0.
Figure 21 shows how well the model fits the counts
at high latitude regions.
Even near polar regions (
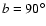 )
the model predictions do not
systematically deviate from the counts. It should be noted that the model does not include a bimodal
distribution, containing both a thin and thick disc with different populations and
scale-heights. None the less using the thin disc alone the model gives an accurate prediction of the counts, for the magnitude range being used.
It is beyond the scope of this paper to discuss whether this result should be interpreted as an absence of thick disc or whether it is simply that the analysis presented here is not sensitive to the thick disc.
A more detailed
examination of high galactic latitudes, including an analysis of the
colors and luminosity function, would be required.
)
the model predictions do not
systematically deviate from the counts. It should be noted that the model does not include a bimodal
distribution, containing both a thin and thick disc with different populations and
scale-heights. None the less using the thin disc alone the model gives an accurate prediction of the counts, for the magnitude range being used.
It is beyond the scope of this paper to discuss whether this result should be interpreted as an absence of thick disc or whether it is simply that the analysis presented here is not sensitive to the thick disc.
A more detailed
examination of high galactic latitudes, including an analysis of the
colors and luminosity function, would be required.
In this paper we examine both quantitatively and qualitatively the
large-scale structures in the Galactic disc. Two independent methods
are applied to the 2MASS data. The first isolates red clump
giants in a number of regions near the plane, the counts are
then inverted to directly obtain the disc density. The second fits the parameters of a disc model in 820 independent near-plane regions.
Results from both methods are consistent with each other implying
that both methods are valid.
For instance, magnitude and color of the red clump giants must be close to
the correct values otherwise there would be significant difference between the
two methods for H and
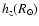 .
.
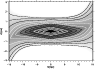 |
Figure 22:
Cut in the plane YZ of the Galaxy as described by the final disc model. |
| Open with DEXTER |
The distribution of sources within the disc is well described by
an exponential distribution in both the galactocentric distance and height
above the plane. There is a strong flare, i.e.
an increase of scale-height towards the outer Galaxy. This flare
starts well inside the solar circle, hence
there is a decrease of the scale-height towards the inner Galaxy.
This is consistent with the observation that the large majority
of galaxies have flares (de Grijs & Peletier 1997) and
theoretically consistent with some scenarios of self-graviting stellar
discs (Narayan & Jog 2002).
The flare removes the need to invoke a cut-off in the outer Galaxy,
and certainly there is no evidence for an abrupt cut-off
in the stellar disc, to at least
R<15 kpc (=4.5hR). For the analysis it was asssumed that the
red clump luminosity function could be described as a delta function
and whilst it is shown that this could have some minor effect on the result,
it could not mask a cut off.
In other spiral galaxies, the question of the cut-off
is still not very clear. Pohlen et al. (2002) find that typical radial profiles are better
described by a two-slope exponential profile, characterized by an inner and
outer scale-length separated at a break radius, rather than a
sharply-truncated exponential model. Florido et al. (2001), however, argue
that there are some cases of abrupt truncation in the near infrared emission
of the stellar profile. Kregel et al. (2002) finds that 60% of
the spiral galaxies are truncated, although he also finds that the
truncation is beyond 4.4 hR for galaxies with hR<4 kpc;
so probably, if there existed a cutoff in our Galaxy, it would not
be detected in R<4.5 hR.
Another noticeable feature is the warp in the old stellar
population whose amplitude is coincident with the amplitude of the gas warp.
Figures 22 and 23 show the form of
the disc. Sánchez-Saavedra et al. (1990,
2002) or Reshetnikov & Combes (1998) claim that most spiral galaxies are
warped at optical wavelengths, but it is not easy to disentangle
the stellar and gaseous warp.
![\begin{figure}
\includegraphics[width=8cm,clip]{MS2213f23.ps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg186.gif) |
Figure 23:
Isodensity surface with
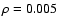 star/pc3 as described by the final disc model. Vertical scale multiplied by
a factor 5.
star/pc3 as described by the final disc model. Vertical scale multiplied by
a factor 5. |
| Open with DEXTER |
Various parameters of the old stellar disc have been measured
based on an analysis over galactocentric distances between 6 kpc and 15 kpc.
The study of the inner disc would be somewhat more complicate,
especially in the plane, because the disc component is no longer
isolated and it is mixed with other possible components: bulge, bar, ring, etc.
As is shown in López-Corredoira et al. (2001), the disc might be
a Freeman type II disc and inside about 3.5 kpc the disc would be truncated;
this deserves another detailed study which is beyond the scope of this paper.
At present we can talk about the distribution at R>5-6 kpc and
representative of the mean old disc at low latitudes
(with mean |z| around 300 pc).
If there exists a thick disc, the results for higher latitudes
would be substantially different.
In the following are presented the
results from the star counts, since they are potentially more accurate.
- The scale-height in the solar circle is
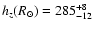 pc;
pc;
- the scale-length of the space density in the plane is
H=1.97+0.15-0.12 kpc;
- the scale-length of the surface density is
hR=3.3+0.5-0.4 kpc.
The errors do not include systematic uncertainties, which we know
to be lower than a 10%. For the flare and the warp:
- the variation of the scale-height due to the flare follows
roughly a law
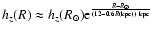 (for
(for 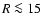 kpc);
kpc);
- the warp moves the mid plane of the disc to the height
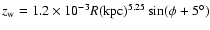 pc
(for
pc
(for 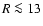 kpc), where
kpc), where 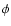 is the galactocentric
angle (
is the galactocentric
angle (
 ).
).
The results presented here constitute an important step in
constraining of the disc structure, especially for the stellar
populations in outer disc, which were previously not very well known.
Theoretical implications are not discussed here but it is expected that
these results will constitute a valuable test for many
theories about the formation and evolution of the galactic discs, as well
as studies about the formation of warps, flares.
Acknowledgements
This publication makes use of data products from 2MASS, which is
a joint project of the Univ. of Massachusetts and the Infrared Processing
and Analysis Center, funded by the NASA and the NSF.
We gratefully acknowledge the anonymous referee whose detail report has
helped improve the paper. Thanks are also given to O. E. Gerhard,
N. Bissantz and C. Alard for helpful comments.
- Alard, C. 2000, preprint [astro-ph/0007013]
In the text
- Bahcall, J. N. 1986, ARA&A, 24, 577
In the text
NASA ADS
- Bahcall, J. N., & Soneira, R. M.
1980, ApJS, 44, 73
In the text
NASA ADS
- Burton, W. B. 1988, in
Galactic and Extragalactic Radio Astronomy, ed. K. I. Kellerman,
& G. L. Verschuur (Springer-Verlag, Berlin), 295
In the text
- Buser, R., Rong, J., & Karaali, S. 1998, A&A, 331, 934
In the text
NASA ADS
- Buser, R., Rong, J., & Karaali, S. 1999, A&A, 348, 98
In the text
NASA ADS
- Cameron, L. M. 1985, A&A, 147, 47
In the text
NASA ADS
- Cohen, M.,
Hammersley, P. L., & Egan, M. P. 2000, AJ, 120, 3362
In the text
NASA ADS
- de Grijs, R., & Peletier, R. F. 1997, A&A, 320, L21
In the text
NASA ADS
- Diplas, A., & Savage, B. D. 1991, ApJ, 377, 126
In the text
NASA ADS
- Djorgovski, S., & Sosin, C. 1989, ApJ, 342, L13
In the text
- Drimmel, R., & Spergel, D. N. 2001,
ApJ, 556, 181
In the text
NASA ADS
- Eaton, N., Adams, D. J, &
Gilels, A. B. 1984, MNRAS, 208, 241
In the text
NASA ADS
- Epchtein, N. 1997, in The Impact of
Large Scale Near-IR Sky Surveys, ed. F. Garzón, N. Epchtein, A. Omont,
B. Burton, & P. Persi (Kluwer, Dordrecht), 15
In the text
- Florido, E., Battaner, E., Guijarro, A., Garzón, F.,
& Jiménez-Vicente, J. 2001, A&A, 378, 82
In the text
NASA ADS
- Freudenreich, H. T. 1998, ApJ, 492, 495
In the text
NASA ADS
- Garzón, F., Hammersley, P. L.,
Mahoney, T., et al. 1993,
MNRAS, 264, 773
In the text
NASA ADS
- Gilmore, G., & Reid, N. 1983, MNRAS, 202, 1025
In the text
NASA ADS
- Gyuk, G., Flynn, C., & Evans, N. W.
1999, ApJ, 521, 190
NASA ADS
- Habing, H. J. 1988, A&A, 200, 40
In the text
NASA ADS
- Hammersley, P. L., Garzón, F.,
Mahoney, T., & Calbet, X. 1994, MNRAS, 269, 753
In the text
NASA ADS
- Hammersley, P. L., Garzón, F.,
Mahoney, T., & Calbet, X. 1995, MNRAS, 273, 206
In the text
NASA ADS
- Hammersley, P. L., Cohen, M.,
Garzón, F., Mahoney, T., & López-Corredoira, M. 1999, MNRAS, 308, 333
In the text
NASA ADS
- Hammersley, P. L.,
Garzón, F., Mahoney, T. J., López-Corredoira, M., & Torres, M.
A. P. 2000, MNRAS, 317, L45
In the text
NASA ADS
- Hoeg, E., Bässgen, G., Bastian, U., et al. 1997, A&A, 323, L57
In the text
NASA ADS
- Kent, S. M., Dame, T. M.,
& Fazio, G. 1991, ApJ, 378, 131
In the text
NASA ADS
- Kregel, M., van der Kruit, P. C., & de Grijs, R. 2002,
MNRAS, 334, 646
In the text
NASA ADS
- López-Corredoira, M.,
Hammersley, P. L., Garzón, F., Simonneau, E., & Mahoney, T. J. 2000, MNRAS,
313, 392
In the text
NASA ADS
- López-Corredoira, M.,
Hammersley, P. L., Garzón, F., et al. 2001, A&A, 373, 139
In the text
NASA ADS
- Majewski, S. R. 1993, ARA&A,
31, 375
In the text
- Narayan, C. A., & Jog, C. J. 2002, A&A, 390, L35
In the text
NASA ADS
- Ojha, D. K. 2001, MNRAS, 322, 426
In the text
NASA ADS
- Paul, E. R. 1993, in The Milky
Way Galaxy and Statistical Cosmology, 1890-1924 (Cambridge University Press,
Cambridge)
In the text
- Pohlen, M., Dettmar, R. J., Luetticke, R., & Aronica, G. 2002,
in Disks of Galaxies: Kinematics, Dynamics and Perturbations,
ed. E. Athanassoula, & A. Bosma (ASP Conf. Ser., S. Francisco),
in press, preprint [astro-ph/0201010]
In the text
- Porcel, C., & Battaner, E. 1995,
MNRAS, 274, 1153
In the text
NASA ADS
- Price, S. D. 1988, PASP, 100, 171
In the text
NASA ADS
- Reid, M. J. 1993, ARA&A, 31, 345
In the text
NASA ADS
- Reshetnikov, V., & Combes, F. 1998, A&A, 337, 9
In the text
NASA ADS
- Rieke, G. H., & Lebofsky, M. J. 1985,
ApJ, 288, 618
In the text
NASA ADS
- Ruphy, S., Robin, A. C., Epchtein, N., et al. 1996, A&A, 313, L21
In the text
NASA ADS
- Sánchez-Saavedra, M. L., Battaner, E., & Florido, E. 1990,
MNRAS, 246, 458
In the text
NASA ADS
- Sánchez-Saavedra, M. L., Battaner, E., Guijarro, A.,
López-Corredoira, M., & Castro-Rodríguez, N. 2002, A&A,
submitted
In the text
- Sarajedini, A., Lee, Y. W., & Lee, D. H. 1995, ApJ, 450, 712
In the text
NASA ADS
- Skrutskie, M. F., Schneider, S. E.,
Stiening, R., et al. 1997, in The Impact of
Large Scale Near-IR Sky Surveys, ed. F. Garzón, N. Epchtein, A. Omont,
B. Burton, & P. Persi (Kluwer, Dordrecht), 25
In the text
- van der Kruit, P. C. 1988,
A&A, 192, 117
In the text
NASA ADS
- Wainscoat, R. J., Cohen, M., Volk, K.,
Walker, H. J., & Schwartz, D. E. 1992, ApJS, 83, 111
In the text
NASA ADS
- Wouterloot, J. G. A., Brand, J.,
Burton, W. B., & Kwee, K. K. 1990, A&A, 230, 21
In the text
NASA ADS
Copyright ESO 2002
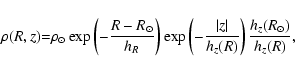
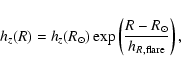
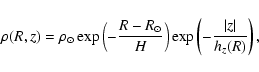
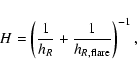
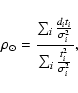
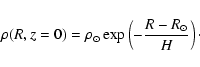

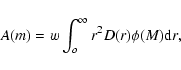
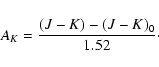
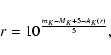
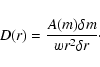
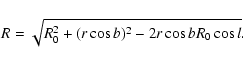

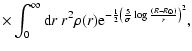
![\begin{figure}
\includegraphics[width=8.8cm,clip]{MS2213f3.eps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg65.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2213f4.eps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg67.gif)


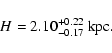

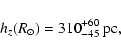
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS2213f8.eps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg93.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS2213f9.eps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg94.gif)

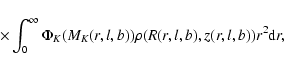
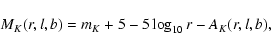
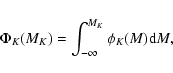


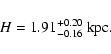

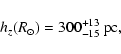
![\begin{figure}
\includegraphics[width=13.5cm,clip]{MS2213f14.ps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg125.gif)
![\begin{figure}
\includegraphics[width=6cm,clip]{MS2213f15.eps}\end{figure}](/articles/aa/full/2002/42/aa2213/Timg129.gif)

![\begin{displaymath}z_{\rm w}=\left[C_{\rm w}R({\rm pc})^{\epsilon _{\rm w}}\sin (\phi -\phi _{\rm w})+15\right] \ {\rm pc}.
\end{displaymath}](/articles/aa/full/2002/42/aa2213/img135.gif)