A&A 394, 807-822 (2002)
DOI: 10.1051/0004-6361:20021234

An inverse method to recover the SFR and reddening properties from spectra of galaxies

J.-L. Vergely1 - A. Lançon1 - Mouhcine1

Observatoire Astronomique de Strasbourg (UMR 7550), 11 rue de l'Université, 67000 Strasbourg, France

Received 17 July 2001 / Accepted 26 August 2002

Abstract
We develop a non-parametric inverse method to investigate the star formation rate, the metallicity evolution and the reddening properties of galaxies based on their spectral energy distributions (SEDs). This approach allows us to clarify the level of information present in the data, depending on its signal-to-noise ratio. When low resolution SEDs are available in the ultraviolet, optical and near-IR wavelength ranges together, we conclude that it is possible to constrain the star formation rate and the effective dust optical depth simultaneously with a signal-to-noise ratio of 25. With excellent signal-to-noise ratios, the age-metallicity relation can also be constrained.
We apply this method to the well-known nuclear starburst in the interacting galaxy NGC 7714. We focus on deriving the star formation history and the reddening law. We confirm that classical extinction models cannot provide an acceptable simultaneous fit of the SED and the lines. We also confirm that, with the adopted population synthesis models and in addition to the current starburst, an episode of enhanced star formation that started more than 200 Myr ago is required. As the time elapsed since the last interaction with NGC 7715, based on dynamical studies, is about 100 Myr, our result reinforces the suggestion that this interaction might not have been the most important event in the life of NGC 7714.

Key words: methods: statistical - stars: formation - ISM: dust, extinction - galaxies: individual: NGC 7714 -
galaxies: stellar content


1 Introduction

The integrated spectra of galaxies contain information about the ages of their stellar populations, the metallicity of the stars and the effects of dust extinction.

In order to infer the history of the star formation rate (SFR), one usually tries to match the spectral energy distribution (SED) as closely as possible with model populations computed with various scenarios for the SFR. The quality of the SED fit is assessed either qualitatively by visual inspection or quantitatively, e.g. by the $\chi^2$-test or a more general expression of the likelihood. Often, the SFR is represented by a number of discrete values or by a predefined analytic form. This approach, which could be called the direct or synthetic method, has been largely used in the field of population synthesis (see Heavens et al. 2000; Reichardt et al. 2001 for efficient recent implementations). Since one usually keeps the number of free parameters as small as possible, the adopted functional forms for the SFR and age-metallicity relation (AMR) impose certain limitations on what type of model populations can be considered. Typically, these will be combinations of instantaneous bursts and episodes of constant star formation. Some inverse methods (Craig & Brown 1986; Tarantola & Valette 1982a,b) deal with such a problem in an opposite way: one tries to determine the functional form of e.g. the SFR with as much freedom as possible, with a resolution in time that is dictated by the information contained in the data. Because of the latter property, these methods are called non-parametric.

This work presents a non-parametric inverse method to estimate characteristics of galaxy evolution such as the SFR, the AMR and the intrinsic dust extinction. As for all such approaches, the method is based on a probabilistic formulation of inverse problems (in our case the formalism of Tarantola & Valette 1982a,b). We apply the method in the framework of evolutionary population synthesis. In other words, possible solutions are only sought among those compatible with our current understanding of star formation and evolution: the relative fraction of stars of various masses is not arbitrary but follows an initial mass function, and theoretical evolutionary tracks combined with stellar spectral libraries determine the possible emission spectra of isochrone stellar populations. A probabilistic formulation for the alternative empirical population synthesis has been developed recently in the parametric case by Cid Fernandes et al. (2001). As noted by these authors, the exploration of solutions to an inversion problem can be tackled as a minimization problem or with an adequate sampling algorithm for the space of parameters. The second type of approach provides a complete description of the uncertainties on the estimated parameters, but may become difficult to implement in practice when some of the unknowns are non-parametric functions of time, which can take an immense variety of shapes. Here a minimization procedure is adopted. In addition, specific tools are used in order to estimate the validity of the inverse procedure, like the a posteriori covariance and resolution, and the mean index.

The nature of the available data determines many of the capabilities and limitations of inversion procedures. Sets of equivalent widths in the optical spectrum have been used because these measurements are relatively easy to acquire (Pelat 1997; Boisson et al. 2000). Cid Fernandes et al. (2001) combined equivalent widths and colours in order also to constrain dust extinction. However, they used a classical one parameter description of extinction and reddening. The effects of dust are rarely that simple (Witt & Gordon 2000). The work we present here was partly motivated by previous studies of starburst galaxy spectra, which not only made it clear that average obscuration laws depend on the type of galaxy observed (Calzetti et al. 1994), but also showed that complex distributions of the stars and the dust in space can lead to significant local deviations from this average. Lançon et al. (2001) studied the $\sim$330 central parsecs of the nuclear starburst galaxy NGC 7714, and emphasized the effects of the different optical depths of dust along various lines of sight within their small aperture. They demonstrated that in dusty objects it is necessary to combine SEDs and emission lines from the optical, the ultraviolet and the near-IR spectral ranges if one aims at recovering the SFR over a wide range of ages and useful information on the wavelength dependent attenuation by dust. With those results in mind, we chose to apply the inversion method to data sets such as those of Lançon et al. (2001): in this paper, the empirical constraints are combined low resolution SEDs in the three spectral ranges together with emission lines of H II. Computation times were not prohibitive in the present case.

The paper is organised as follows. Section 2 presents our model assumptions for the SEDs and reddening. Section 3 introduces the inverse method. After applying this technique to simulated SEDs in Sect. 4, we give new constraints on the SFR and the reddening law for the nuclear starburst of NGC 7714 in Sect. 5.

   
2 Modeling galaxy spectra

2.1 The basis B $_{{\sf\lambda }}$(t)

The intrinsic SED of a synthetic stellar population depends on the following model ingredients:

Without extinction, the simulated flux distribution $F_{\lambda}$ is written as follows:

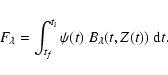\begin{displaymath}F_{\lambda}=\int_{t_f}^{t_i} \psi(t)~ B_{\lambda}(t,Z(t))~ {\rm d}t. \end{displaymath} (1)

As $\psi(t)$ is always positive, it will be convenient to write

 \begin{displaymath}\psi(t) = \psi_{\rm o}~\exp(\alpha(t)) \end{displaymath} (2)

where $\psi_{\rm o}$ is a constant (arbitrary, but fixed). $B_{\lambda}(t,Z(t))$ is the spectrum of a coeval stellar population of current age t. We considered ages between tf=1 Myr and ti=16 Gyr. This model basis implicitly assumes a certain initial mass function and rests on a particular set of stellar evolution and stellar atmosphere models. In the following, we will test the IMFs of Scalo (1998) and of Salpeter (1955), with a lower stellar mass limit of 0.1 $M_{\odot}$and an upper mass limit of 120 $M_{\odot}$. We construct basis spectra for a grid of ages and metallicities with the population synthesis code P´EGASE (Fioc & Rocca-Volmerange 1997). They are based on the stellar evolutionary tracks of the Stellar Astrophysics group of the Astronomical Observatory of Padua (and extensions thereof), and on the semi-empirical spectral library of Lejeune et al. (1997, 1998). We refer to Fioc & Rocca-Volmerange (1997) for details. Time is sampled with logarithmic timesteps of $\sim$0.1; the applications in the following sections will show this is fine enough to not limit the resolution of the estimated evolutionary properties. The adopted grid in metallicity is Z=0.02, 0.016, 0.012, 0.008.

With extinction:

 \begin{displaymath} F_{\lambda}=\int_{t_f}^{t_i} \psi(t)~ B_{\lambda}(t,Z(t))~ f_{\rm ext}(\lambda,t)~ {\rm d}t. \end{displaymath} (3)

The wavelength dependence of $f_{\rm ext}$ results from the assumed extinction model, as recalled below.

2.2 Adopted extinction models

The extinction in galaxies depends on two factors: the spatial distribution of the dust and the properties of the dust grains, which we describe with an opacity coefficient $k_{\lambda}$. In Sects. 2.2.1 and 2.2.2, we adopt simple models which assume the knowledge of the dust distribution and of $k_{\lambda}$. Opacity curves are known to vary from one galaxy to the other, or even from one line of sight to the other within the Milky Way. For the foreground extinction due to our own Galaxy, we use the opacity curve of Seaton (1979) at optical wavelengths, and of Howarth (1983) in the UV and IR. This curve is an average over many lines of sight towards Milky Way stars. Due to the presence of graphite grains, it shows a characteristic feature around 2200 Å. Because the dust in many galaxies has an extinction curve that lacks a 2200 Å bump, it has been argued that the Small Magellanic Cloud (SMC) opacity is more convenient for the modeling of galaxies' intrinsic extinction (Gordon et al. 1997). For the intrinsic extinction of our synthetic galaxies, we adopt the SMC opacity curve of Prévot et al. (1984) as listed by Gordon et al. (1997), except where we explicitly allow it to vary.

In reality, the interstellar medium of a galaxy is not homogeneous, and is probably a mixture of different types of clouds (diffuse and compact) and different types of grains. Moreover, the light is scattered by the interstellar matter, so it is not possible to model the effective dust opacity in a simple way (e.g. Witt & Gordon 2000). This led Calzetti et al. (1994, 2000) to derive an obscuration curve empirically from the integrated spectra of a sample of diverse starburst galaxies (Sect. 2.2.3). In Sect. 2.2.4 we generalize this idea: it is suggested to use the inversion technique to recover both the wavelength dependence of the effective optical depth, and the time dependance of the SFR.

   
2.2.1 Foreground dust screen

In this simplest model, one has:

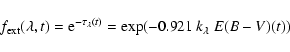\begin{displaymath}f_{\rm ext}(\lambda,t)={\rm e}^{-\tau_{\lambda}(t)}= \exp(-0.921~ k_{\lambda}~ E(B-V)(t)) \end{displaymath} (4)

where E(B-V)(t) is proportional to the column density of dust. Stellar populations with different ages can be affected with different amounts of extinction, but all stars of a given age are affected identically. As already mentioned, the values of $k_{\lambda}$ are those of Prévot et al. (1984). In this case, $\tau_{\lambda}$ is directly representative of the optical properties of dust grains on the line of sight towards stars. Representative plots of $k_{\lambda}$ can be found, for instance, in the review of Calzetti (2001).

   
2.2.2 Dust clouds in front of the stellar population

In real galaxies, it is unlikely that all stars even of a given age see the same distribution of dust. Various mixed gas+stars models and clumpy gas distribution models have been considered in the literature, to allow for this natural complexity. The model considered here consists of dust clouds (or clumps) distributed between the stars and the observer. The number of clumps on the line of sight to a star of age t obeys Poisson statistics: $\overline{n}(t)$ describes the average number of clumps along the line of sight. With this model, a fraction $\exp(-\overline{n}(t))$ of all stars of age t are seen without any obscuration.

As demonstrated in Appendix A, $f_{\rm ext}$ has the following analytical expression for the clumpy model:

 \begin{displaymath}f_{\rm ext}(\lambda,t)=\exp\left\{-\overline{n}(t) \left(1-{\... ...rm c}}} \right)\right\} ={\rm e}^{-\tilde{\tau}_{\lambda}(t)}. \end{displaymath} (5)

In this equation, $\tau_{\lambda ,{\rm c}}$ is the optical depth for a single cloud:

 \begin{displaymath}\tau_{\lambda ,{\rm c}}= 0.921~ k_{\lambda}~ E(B-V)_{\rm c} \end{displaymath} (6)

$E(B-V)_{\rm c}$ is the colour excess for one cloud. The resulting extinction is described equivalently with an effective optical depth  $\tilde{\tau}_{\lambda}(t)$.

Note that when $\tau_{\lambda ,{\rm c}}\ll 1$, $f_{\rm ext}$ becomes indistinguishable from a dust screen with total optical depth $\overline{n}(t)~\tau_{\lambda ,{\rm c}}$, and when $\tau_{\lambda ,{\rm c}}\gg 1$ the attenuation becomes independent of wavelength. In the former case, the attenuated spectra contain information on the product $\overline{n}(t)~\tau_{\lambda ,{\rm c}}$ but the two factors cannot be separated; in the latter case, no signature of extinction will appear in the spectrum (the dust would only be revealed by infrared emission).

   
2.2.3 Empirical extinction model of Calzetti et al.

In the starburst extinction models of Calzetti et al. (1994, 2000), $f_{\rm ext}(\lambda,t)$ is an unknown which can be determined directly from observations assuming that all galaxies in the samples have similar star formation histories.
Again, $f_{\rm ext}$ is written:

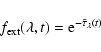\begin{displaymath}f_{\rm ext}(\lambda,t)={\rm e}^{-\tilde{\tau}_{\lambda}(t)} \end{displaymath} (7)

where:

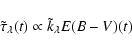\begin{displaymath}\tilde{\tau}_{\lambda}(t) \propto \tilde{k}_{\lambda} E(B-V)(t) \end{displaymath} (8)

E(B-V) is the colour excess to the stellar continuum. The empirical obscuration coefficient $\tilde{k}_{\lambda}$results from the wavelength dependence of the grain properties, as well as from the space distribution of the dust, averaged over a typical starburst galaxy. The proportionality constant in the above relation is determined by Calzetti et al. (2000) from the energy budget of the galaxies, which requires far-IR observations.

   
2.2.4 Effective optical depth

Inversion methods make it possible to explore whether the available spectrophotometric data contain enough information to recover both the time dependence of the SFR and the effective optical depth $\tilde{\tau}_{\lambda}$. Thus, we may consider the effective optical depth, $\tilde{\tau}_{\lambda}$, as an unknown. In this paper, we then restrict ourselves to the assumption of a constant $\tilde{\tau}_{\lambda}$in time.

In fact, the opacity information lies principally in the emission lines. The differential optical depth between wavelengths $\lambda_1$and $\lambda_2$ is given by:

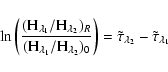\begin{displaymath}\ln\left(\frac{({\rm H}_{\lambda_1}/{\rm H}_{\lambda_2})_R} {... ..._0} \right)= \tilde{\tau}_{\lambda_2}-\tilde{\tau}_{\lambda_1} \end{displaymath} (9)

where ${\rm H}_{\lambda}$ is the emission in the line at wavelength $\lambda$. The subscripts R and 0 correspond, respectively, to the reddened and the intrinsic emission line ratios. In a similar fashion, the slope of the spectrum yields complementary information on the opacity distribution. However, this approach does not provide the ratio of absolute to differential extinction. If $\tilde{\tau}_{\lambda}$ is a solution, another possible solution is given by:

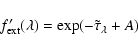\begin{displaymath}f'_{\rm ext}(\lambda) = \exp(-\tilde{\tau}_{\lambda}+A) \end{displaymath} (10)

where A is an arbitrary constant. The solution for the SFR then becomes:

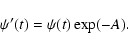\begin{displaymath}\psi' (t)=\psi(t) \exp(-A). \end{displaymath} (11)

So, in the framework described in this subsection, one only obtains information about relative fluctuations in the SFR. In practice, one could force the curve $\tilde{\tau}_{\lambda}$ to vanish when $\lambda$ tends towards infinity or use the far-infrared thermal emission to determine the absolute extinction.

   
3 The inverse method

The determination of scalar functions (such as the SFR and the extinction law) from observational data is an underdetermined problem, because the amount of observational data is only finite and thus cannot provide the information for every detail of these functions. Application of a straight inversion technique to Eq. (3) could be very sensitive to the noise in the data, and could well give mathematically correct but unphysical results (Craig & Brown 1986). The problem must be regularized, which corresponds to a smoothing operation (Twomey 1977; Tikhonov & Arsénine 1976).

3.1 A generalized least-squares approach

The inverse method we use comes from statistical techniques that have been applied in geophysical analyses (Tarantola & Valette 1982a,b; Tarantola & Nercessian 1984; Nercessian et al. 1984). The method resembles Bayesian approaches in that a priori ideas about the unknowns are used to regularize the inversion.

The conditional probability density $f_{\rm post}(M\vert D)$ for the vector M of the unknown parameters, given the observed data D obeys:

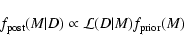\begin{displaymath}f_{\rm post}(M\vert D) \propto {\cal L}(D\vert M)f_{\rm prior}(M) \end{displaymath} (12)

where $\cal L$ is the likelihood function and $f_{\rm prior}$ stands for the a priori probability distribution for the model parameters. M will typically contain a sequence of values of the SFR at all ages, followed by the other adopted functional or discrete parameters (e.g. the metallicity at all ages, the optical depth in the case of a dust screen, the effective optical depth at all wavelengths in the framework of Sect. 2.2.4). If we assume that both the a priori probability and the errors in the data are distributed as Gaussian functions, and that there are no correlations between data and model parameters, we can write:
 
  $\textstyle f_{\rm post}(M\vert D) \propto \exp\bigg( -\displaystyle\frac{1}{2}(D-g(M))^{*} \cdot C_{\rm d}^{-1} \cdot (D-g(M))$    
  $\textstyle \qquad \qquad -\displaystyle\frac{1}{2}(M-M_0)^{*} \cdot C_0^{-1} \cdot (M-M_0)\bigg)$   (13)

M0 is the mean of the prior (i.e. the a priori guess for the model parameters), and C0 is the variance-covariance matrix of the prior (see Sect. 3.2.1). The operator g associates observable properties with model M: D=g(M) if the model parameters are correct and there is no noise in the data. In our case, Eq. (3) shows that g provides the spectral energy distribution  $F_{\lambda}$through a set of equations of the form $F_{\lambda}=g_{\lambda}(\psi,Z,...)$. $C_{\rm d}$ is the data variance-covariance matrix, which describes the observational uncertainties. The superscript * refers to the adjoint operator.

The best estimate M minimizes the quantity:

 
$\displaystyle { \mbox{$\displaystyle\frac{1}{2}$ }(D-g(M))^{*} \cdot C_{\rm d}^{-1} \cdot (D-g(M)) }$
  $\textstyle \qquad \qquad + \displaystyle\frac{1}{2}(M-M_0)^{*} \cdot C_0^{-1} \cdot (M-M_0) .$   (14)

In the linear case, the minimum would be reached in one step (Tarantola & Valette 1982a,b):
 
$\displaystyle M=M_0 + C_0 \cdot G ^{*} \cdot (C_{\rm d} + G \cdot C_0 \cdot G^{*})^{-1} \cdot (D-g(M_0))$     (15)

G is the matrix of partial derivatives of g. In our case however, g is not linear, and the minimum is reached iteratively:
 
M[k+1]=$\displaystyle M_0 + C_0 \cdot G_{[k]} ^{*} \cdot (C_{\rm d} + G_{[k]} \cdot C_0 \cdot G_{[k]}^{*})^{-1} \cdot$  
$\displaystyle (D + G_{[k]} \cdot (M_{[k]} -M_0)-g(M_{[k]}))$ (16)

k counts the number of iterations and G[k] is the matrix of partial Frechet derivatives at step k:

\begin{displaymath}G_{[k]}=\left(\frac{\partial g}{\partial M}\right)_{[k]}\cdot \end{displaymath} (17)

In subsequent equations we shall abbreviate:

\begin{displaymath}S_{[k]}:=C_{\rm d}+G_{[k]} \cdot C_0 \cdot G^{*}_{[k]}. \end{displaymath} (18)

To control the algorithm convergence at step k, we test the stabilisation of $\chi^2$, with:

 \begin{displaymath}\chi^2_{[k]}=(D-g(M_{[k]}))^{*} \cdot C_{\rm d}^{-1} \cdot (D-g(M_{[k]})). \end{displaymath} (19)

3.2 Choice of the model parameters and the prior M0

   
3.2.1 The a priori variance-covariance operator C0

The model parameters may include single value parameters as well as functions (an example is described in detail in Appendix B.2). For discrete parameters, C0 is the matrix of the a priori variances and a priori covariances between the parameters. Large values of the variances must be chosen in the absence of any initial knowledge about the parameter values. Otherwise, the second term of expression 14 prevents the algorithm from moving away from a meaningless prior. Let us define a temporal variable u ($u=\log(t)$ or u=t for instance; see Appendix B.1). For an unknown function such as $\alpha(u)$ (i.e. the star formation history of Eq. (2)), defined at each time point, C0 incorporates a functional operator $C_{\alpha}$(see Eq. (B.7)). Given the limited number of data, we must assume some regularizing properties for $\alpha$.

 \begin{displaymath} C_{\alpha}(u,u')=\sigma_{\alpha}(u) \sigma_{\alpha}(u') \mbox{Cor}(u,u'). \end{displaymath} (20)

The parameter $\sigma_{\alpha}$ is the prior standard deviation. It controls the acceptable amplitude of the deviations from the prior. Cor(u,u') is the adopted autocorrelation function between two points of age u and u'. We adopt:

 \begin{displaymath} \mbox{Cor}(u,u')=\exp\left(- \frac{(u-u')^2}{\xi_{\alpha}^2} \right)\cdot \end{displaymath} (21)

The parameter $\xi_{\alpha}$ is the prior correlation length. It defines the resolution (in age) with which one expects to recover the galaxy history functions. A large value of $\sigma_{\alpha}$ will allow for more contrast in the function $\alpha(u)$ than a small one. On the other hand, if too large a value of $\xi_{\alpha}$ is chosen, the small (short timescale) details of the function $\alpha$ will disappear and the parameter fluctuations will become too smoothed. The adequate choice of the two a priori parameters ( $\xi_{\alpha}$ and $\sigma_{\alpha}$) is conditioned by the stability of the inversion process, which itself is determined by the extent of the available data and its signal-to-noise ratio (see also Sect. 3.3.2).

3.3 Quality of the inversion

   
3.3.1 The posterior variance-covariance matrix

Approximate internal errors on the estimation of the parameters can be computed once the minimization algorithm has converged. This is done by considering the local behaviour of the posterior probability density distribution around the best solution (see also Reichardt et al. 2001; Moultaka & Pelat 2000). From a second-order expansion of the posterior density distribution in this neighbourhood, one obtains:

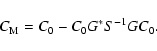\begin{displaymath}C_{\rm M} = C_0-C_0G^{*}S^{-1} G C_0. \end{displaymath} (22)

Again, $C_{\rm M}$ is a set of discrete values if the considered parameters have discrete values. In the functional case, $C_{\rm M}$ is a set of functions of two variables. For instance, if the star formation history is one of the unknowns, $C_{\rm M}$ incorporates terms of the form $C_{\rm M,\alpha}(u,u')$. The diagonal terms such as $C_{\rm M,\alpha}(u,u)$ measure how fast the exponent of Eq. (13) increases when $\alpha$ is moved away from its best estimate. Note that in general this a posteriori variance is lower than the a priori variance $\sigma_{\alpha}^2$ of Eq. (20). The smaller the a posteriori variance is, compared to the a priori variance, the more we have increased our knowledge of the value of the parameter by using the available data.

   
3.3.2 The resolving kernel and the mean index

Suppose that we knew the true model $M_{\rm true}$. Then the observed data would be (if the errors are negligible):

\begin{displaymath}D = g(M_{\rm true}). \end{displaymath} (23)

After the linearisation of g near $M_{\rm true}$, so that Gk = G = g, Eq. (15) shows how the deviation of the true model parameters from a nearby initial guess would be degraded into the derived one:

 \begin{displaymath} M-M_0 = C_0 G^{*} S^{-1} G(M_{\rm true}-M_0). \end{displaymath} (24)

The operator defined by

K := C0 G* S-1 G (25)

describes this degradation of information and is called the resolving kernel. Let's again, for illustration, focus on the part of K relevant to the star formation history $\alpha(u)$. Equation (24) writes:

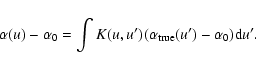\begin{displaymath}\alpha(u)-\alpha_0=\int K(u,u') (\alpha_{\rm true}(u')- \alpha_0) {\rm d} u'. \end{displaymath} (26)

If the real star formation history deviated from a constant by a delta function at age $u_{\delta }$, the shape of the star formation history obtained by the algorithm would be $K(u,u_{\delta })$. Because of the linearisation invoked, this response is only indicative. One of its major powers is to draw attention to potential degeneracies, that may appear in $K(u,u_{\delta })$ as very broad or multiple peaks.

Another important and useful concept is a measure of the information present in the data. This is closely linked to the resolving kernel. Suppose that the parameter of interest is nearly constant within the width of the kernel K. Then Eq. (24) gives

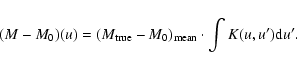\begin{displaymath}(M-M_0)(u)= (M_{\rm true}-M_0)_{\rm mean} \cdot \int K(u,u') {\rm d}u'. \end{displaymath} (27)

The integral is called the mean index I(u)

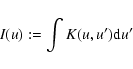\begin{displaymath}I(u) := \int K(u,u') {\rm d}u' \end{displaymath} (28)

and has the following meaning. If I(u) has a very low value ($\ll $1) the model resulting from the minimization algorithm is expected to lie close to the prior, whatever this prior is. The quality of the M estimate thus is poor. But if $I(u)\simeq 1$ the model obtained from the algorithm is close to the average true model. In other words, only $I(u)\simeq 1$ ensures that the available data contained significant information on the estimated model parameter function. In practice, a compromise has to be found. A mean index close to 1 can be obtained by an increase in the smoothing length $\xi_{\alpha}$ of the a priori variance-covariance operator. However, increasing $\xi_{\alpha}$ reduces the resolution (in age). The adequate choice for $\xi_{\alpha}$ is the smallest value that produces a mean index close to 1.

   
4 Determining SFR and reddening from mock spectra

We have generated mock spectra from a given SFR ($\alpha(t)$), AMR (Z(t)), E(B-V) and average number of clouds ( $\overline{n}(t)$) in order to test and illustrate the inverse procedure. The spectra extend through parts of the UV [1180-1680 Å], the optical [3690-6600 Å and 7000-9000 Å] and the near-IR [2.06-2.39 $\mu$m], as appropriate for the subsequent analysis of NGC 7714 data (see Sect. 5). The spectral resolution matches that of the models, which are based on the library of stellar spectra of Lejeune et al. (1998; $\lambda/\Delta \lambda \simeq 100$). The IMF of Scalo (1998) is adopted.

The noise added to the input spectra corresponds to a signal-to-noise ratio (S/N) equal respectively to 500 (Fig. 1) and 25 (Fig. 2), and is assumed to be gaussian. Iterations were stopped when $\chi^2$ was stable to one part in 104 (typically 7 to 9 iterations). The prior properties adopted for the figures are summarized in Table 1. The quality of the fits of the spectral energy distribution is evaluated by means of a reduced $\chi^2$, $\chi ^2_{\nu }$(the $\chi^2$ of Eq. (19) divided by the number of data points). The results are not affected much by the prior provided that the reduced $\chi^2$ and the mean index are close to 1. Details of the implementation of the inversion method are provided in Appendix B.2.


 

 
Table 1: Priors for the inversions in Sect. 4.
Dust clouds with individual E(B-V)=0.2 (Figs. 1 and 2)
parameter prior prior $\sigma$ prior $\xi$
$\alpha(t)$ 0 1 0.3-0.5 [log(t)]
$\overline{n}(t)$ 1 1 0.3-0.5 [log(t)]
E(B-V) 0.5 0.25 not applicable
Z(t) 0.014 0.001 0.5 [log(t)]
Unknown effective optical depth (Fig. 3).
parameter prior prior $\sigma$ prior $\xi$
$\alpha(t)$ 0 0.5 0.7 [log(t)]
$\tilde{\tau}_{\lambda}$ 1 3 ( $\lambda <1~\mu$m) 1000 Å
    0.1 ( $\lambda >1~\mu$m)  


Note: $\alpha(t)$ is the natural logarithm of the SFR expressed in $M_{\odot}$ yr-1.



  \begin{figure} \par\includegraphics[angle=-90,width=0.97\textwidth]{MS1691f1.eps} \end{figure} Figure 1: Inversion results from a spectrum with a signal-to-noise ratio of 500. The left column focuses on the the SFR, the middle column on the mean number of dust clouds on the line of sight, and the right column on the AMR. In the top panels, the solid lines describe the inputs used to construct the mock spectrum. The dashed lines are the best estimates from the noisy mock spectrum. The dot-dashed lines, and the middle and bottom panels allow us to asses the quality of the inversion. In the middle panels, the response functions $K(u,u_{\delta })$ are shown for ages $u_{\delta }$ = log(t) = 6.8 (solid), 7.7 (dashed), 8.5 (dot-dashed) and 9.4 (dotted). See text (Sect. 4) for details.
Open with DEXTER

In Fig. 1 the results obtained with S/N=500 are shown. The input parameters are drawn in full lines in the top panels. The input value of E(B-V) for individual clouds is 0.2. The dashed lines show the best estimates of these parameters resulting from the inversion. They led to a $\chi ^2_{\nu }$ of 1.028. The dot-dashed lines show the standard deviations from these best estimates, computed from the diagonal terms of the posterior variance-covariance matrix of Sect. 3.3.1. For E(B-V), the resulting estimate is 0.194, and the posterior standard deviation is 0.03.

The global features in the SFR are recovered well, whereas the smallest are not. The posterior resolution can be examined in the middle panels. They display the response of the inversion algorithm to delta-function inputs in SFR(t), $\overline{n}(t)$ and Z(t), located at ages $\log(t) = 6.8$, 7.7, 8.5 and 9.4. The computation is based on the resolving kernel K of Sect. 3.3.2. It is seen that the resolution compatible with the mock data is about 0.3-0.6 in log(age). The mean index for the SFR is uniformly close to 1 over the age range. Together with the fact that the posterior standard deviation is much smaller than the prior value, this tells us the SFR is well constrained.

The average number of clumps and the AMR are not resolved as well as the SFR. The reddening of individual clouds, E(B-V), has been recovered well. Note that its value is compatible with the recovery of $\overline{n}(t)$ (see end of Sect. 2.2.1). If E(B-V) had been found close to 0 a degeneracy with $\overline{n}(t)$ would have been suspected; if it had been very large both its own value and $\overline{n}(t)$ would have been very uncertain.

Despite the high signal to noise ratio, the mean index associated with the AMR begins to weaken. Note that the smallest values of the mean index tend to appear at ages where the star formation rate is low: it is not surprising that little information on the metallicity of the corresponding stars can be found in the data.


  \begin{figure} \par\includegraphics[angle=-90,width=0.92\textwidth]{MS1691f2.eps} \end{figure} Figure 2: Same as previous figure from a mock spectrum with a signal-to-noise ratio equal to 25.
Open with DEXTER

Figure 2 shows how much information can be recovered when the available data has S/N=25. Only the global trends are recovered for the SFR and the average number of clumps. For the AMR, the resolution and the mean index fall down after ${\rm log(age)}=7$ (10 Myr): the recovered AMR corresponds to the prior. Searching for the AMR should be avoided with this type of data.

In Fig. 3, we test how well the method is able to reconstruct the SFR and the effective optical depth $\tilde{\tau}_{\lambda}$from simulated spectra with S/N=25 (see Appendix B.3). Here, we do not consider the AMR as an unknown, because at this level of noise and spectral resolution, the information present in the data is too poor. As mentioned in Sect. 2.2.4, we assume $\tilde{\tau}_{\lambda}$is the same for populations of all ages. The three top panels show respectively the SFR, the resolution in age and the SFR mean index as in previous figures. Only a large smoothing length $\xi_{\alpha}$ gives a decent mean index: the age resolution on the SFR is poor.


  \begin{figure} \par\includegraphics[angle=0,width=8.8cm,clip]{MS1691f3.eps} \end{figure} Figure 3: Inversion results from a spectrum with a S/N = 25, when the wavelength dependence of the effective optical depth is also considered as an unknown. Metallicity is assumed to be known. The first three panels correspond to the first column of Figs. 1 and 2. The bottom panel shows the assumed optical depth (full line), the recovered one (dashed line) and the internal error (dot-dashed).
Open with DEXTER

The input and output effective optical depths are presented in the bottom panel. The mean index for $\tilde{\tau}_{\lambda}$ takes values close to 1 in the UV, then drops progressively to poor values, of order 0.5 at 1 $\mu$m and 0.1 around 2 $\mu$m. The low index values at long wavelengths are due essentially to the degeneracy between the absolute values of the effective obscuration and of the SFR (see Sect. 2.2.4): with a small prior standard deviation, the prior sets the result (with larger prior standard deviations, the algorithm doesn't converge). In Fig. 3 we have forced the near-IR match of $\tilde{\tau}_{\lambda}$, so input and output SFRs are comparable. As the UV emission can only come from young stars, the UV slope provides a strong constraint on that part of the reddening law. The emission of the young component at longer wavelengths does not by itself match the data. The optical and near-IR fluxes directly provide a minimum contribution of older stars and the main constraints on their age distribution. Freedom in the extinction law acts as a correction to improve the fit. A relatively long prior correlation length for $\tilde{\tau}_{\lambda}$(1000 Å) avoids excessive freedom, that would lead to the fitting of the noise in the data.

In view of the limited resolution, spectral coverage and signal-to-noise ratio assumed here, the results of Fig. 3 are very satisfactory and the method is promising.

   
5 An example: NGC 7714

NGC 7714 is a well studied interacting spiral galaxy which hosts a starburst in its nucleus (Arp 1966, Weedman et al. 1981; Calzetti 1997). The peaked ground based morphology of the starburst, the small inclination of the galaxy disk seen from our perspective, and the relatively low extinction suggested by the ultraviolet (UV) brightness (Markarian & Lipovetskij 1974), motivated detailed studies of this apparently simple system. As a result of high resolution imaging and spectroscopy, the simplest models for the nucleus had to be successively excluded (González-Delgado et al. 1995, 1999, and references therein). The central $\sim$330 pc of the galaxy were found to contain a variety of stellar populations, ranging from very young ($\sim$5 Myr) to old (the population of the underlying spiral). Simple dust screen extinction models, that were initially compatible with the scarce available data (Puxley & Brand 1994), were found to be inappropriate (Lançon et al. 2001, hereafter LGLG01).

The study of the central $\sim$330 pc of the galaxy by LGLG01 was based on a "manual'' exploration of a set of model star formation histories. The SFR was assumed to be a combination of a maximum of four components, each component being represented either by a standard spiral galaxy SFR, an instantaneous burst, an episode of constant star formation or an exponentially decreasing star formation episode. The exploration of this parameter space was guided by preliminary studies in individual wavelength ranges. Such an exploration method is tedious and cannot be exhaustive. A chance remains that the best fitting model may be missed. On the other hand, this exploration has provided a range of constraints that are considered robust because they are common to most of the satisfactory model adjustments to the data. Among those were the following.

(i) The nucleus of NGC 7714 has been forming stars off and on over the past several hundred millions of years at an average rate of the order of 1 $M_{\odot}$ yr-1, with a brief enhancement of a factor of a few about 5 Myr ago.

(ii) The extinction even in the central 300 pc of NGC 7714 is inhomogeneous; for instance, most of the UV luminosity of this area is due to an obscuration-free line of sight towards a young cluster which does not coincide with the maximum Brackett $\gamma$ (Br$\gamma$) emission.

(iii) Assuming a constant IMF in time, the recent star formation episodes have enhanced the stellar mass in the central area by at least 10%, and more likely by 25%.

(iv) Most of the satisfactory models implied that the level of star formation had increased already several 100 Myr ago. This timescale called for confirmation, as dynamical modeling of the interacting system indicates that only about 100 Myr have elapsed since closest approach between NGC 7714 and NGC 7715 (Smith & Wallin 1992; Smith et al. 1997; Struck & Smith 2002).

The existence of multiwavelength data and previous detailed investigations of plausible models for the central regions of NGC 7714 make this galaxy a target of choice for the application of our automatic inversion method. The available data are described in detail in LGLG01. The spectral coverage is as in Sect. 4. We have degraded the resolution of the observations to match the wavelength sampling of the models. A correction for foreground extinction due to the Milky Way was also applied ( E(B-V)=0.08). The signal-to-noise ratio varies along the spectrum with a typical value of 25. The gap in the optical part of the spectrum is due to the removal of data of poorer quality (due to telluric absorption).

   
5.1 Estimation of the SFR with simple extinction models

In this section, we apply the three extinction models presented previously in Sect. 2.2: a screen of SMC-type dust, clouds of SMC-type dust, and the empirical attenuation law of Calzetti et al. (2000). The priors are listed in Table 2 and discussed in Sect. 5.2.


 

 
Table 2: Priors for the inversions in Sect. 5.
Inversions of Sect. 5.1, 5.4 and 5.5.
parameter prior prior $\sigma$ prior $\xi$
$\alpha(t)$ -1.2 0.4 0.5 [log(t)]
   SMC or Calzetti-type dust screen:  
E(B-V)(t) 0.2 0.2 0.5 [log(t)]
   Dust clouds:    
$\overline{n}(t)$ 2 2 0.5 [log(t)]
$E(B-V)_{\rm c}$ 0.2 0.2 none
Inversions of Sect. 5.6.
parameter prior prior $\sigma$ prior $\xi$
$\alpha(t)$ -1.2 0.8 0.6 [log(t)]
ln $(\tilde{\tau}_{\lambda})$ 0 ( $\lambda <1~\mu$m) 1.5 ( $\lambda <1~\mu$m) 3000 Å
  -2 ( $\lambda >1~\mu$m) 0.1 ( $\lambda >1~\mu$m)  


Note: $\alpha(t)$ is the natural logarithm of the SFR expressed in $M_{\odot}$ yr-1.



 

 
Table 3: $\chi ^2_{\nu }$ values for different extinction models and different IMF slopes.
model Scalo IMF Salpeter IMF
dust screen 2.5 2.3
dust clouds 2.3 2.0
Calzetti 2.1 1.9



  \begin{figure} \par\includegraphics[angle=0,width=8.8cm,clip]{MS1691f4.eps}\end{figure} Figure 4: Properties obtained for the nucleus of NGC 7714, assuming a Salpeter IMF and solar metallicity (Z=0.02). The top panel shows the star formation histories. The middle panel shows the differential extinction and the bottom panel the cumulative contributions of stars of various ages to the total stellar mass. Solid: Calzetti dust (the errors given by the posterior standard deviation are indicated with dotted lines in the top panel); dot-dashed: dust screen; dashed: dust clouds.
Open with DEXTER

The main results are plotted in Fig. 4. The derived star formation histories and extinctions are in good global agreement with the previous study of LGLG01. A bimodal SFR is found, with two peaks respectively centered at log(age)=6.4 (2.5 Myr) and 8.5 (300 Myr). The average level of the SFR over the last few 108 yr is of the order of 1 $M_{\odot}$ yr-1. Stars younger than 109 yr contribute about 20% of the total stellar mass that has ever been produced. The most recent episode of activity however, despite its high star formation rate, only added a few percent to the stellar mass.

The posterior standard deviation and mean index shows that the SFR is well constrained, except around log(age)=7.5. The stars at these ages contribute little to the light, compared to the youngest burst in the UV, or to the bulk of the somewhat older intermediate age stars at optical wavelengths. The amount of obscuration is constrained tightly for the youngest stars, and reasonably well for the oldest, but the mean index is poor at intermediate ages.

In the case of the cloudy dust model, $\overline{n}(t)$ and the reddening per cloud are searched for. $E(B-V)_{\rm c}=0.17$ is found for the individual clouds (with a posterior standard deviation of 0.03). $\overline{n}(t)$ varies between 1 and 2 at young and intermediate ages, and increases to about 6 for the old populations. $\overline{n}(t)$ and $E(B-V)_{\rm c}$ are combined using Eqs. (5) and (6) to provide the final colour excess plotted in Fig. 4. Note that this value is systematically smaller than the simple product $\overline{n}(t)~E(B-V)_{\rm c}$.


  \begin{figure} \par\includegraphics[width=8cm,clip]{MS1691f5.eps}\end{figure} Figure 5: Adjustment of the NGC 7714 data obtained with the dust description of Calzetti. Thick line: data (Gaussian fits to the emission lines have been subtracted before resampling). Thin solid line: model SED (interpolated through regions with no data). Also shown are the respective contributions of stars in the following age ranges: < 107 yr (dotted), 107-109 yr (dashed), >109 yr (dot-dashed).
Open with DEXTER

The dependence of the colour excess on stellar age is consistent with the results of LGLG01. Relatively large values are found at old ages. This trend is necessary in order to reach the near-IR flux level without compromising the fit at optical wavelengths (Fig. 5; see however Sect. 5.2).

In the UV, the SMC opacity curve is the steepest of the reddening laws we have considered. With that law, the blue slope of the UV emission of NGC 7714 sets the strongest limitation on the amount of dust towards young stars. Consequently, a smaller SFR is sufficient to produce the observed level of UV flux. The shape of the opacity curves also explains the differences at old ages: the different E(B-V)of Fig. 4 produce old components of very similar shape and contributions in plots such as Fig. 5.

The reduced $\chi^2$ values in Table 3 show that the effect of the IMF on the quality of the best fits is small, the Salpeter IMF being favoured. The clumpy dust model and the attenuation law of Calzetti et al. produce a slightly better agreement with the observed SED than a simple SMC dust screen.

An important caveat for all the results of this section is that the Br$\gamma$ emission line is underestimated by a factor of two by the models, and this even though we do not apply stronger extinction to the emission lines than to the stellar continua (i.e. we deviate from the prescription of Calzetti et al. 2000 in this point). The missing Br$\gamma$ emission corresponds to a nebular emission excited by a young population that is not found by the inversion algorithm when the wavelength dependence of the extinction is one of the laws considered here. The young population is likely to be underestimated. We note that the same problem was faced by LGLG01 when they sought to adjust only the continuum, and led them to invoke additional highly obscured young stars. A similar ad hoc fix would also be successful here. As a partial answer to the lack of Br$\gamma$ photons, the age found by automated inversion for the most recent starburst is younger than the 5 Myr of LGLG01.

   
5.2 Discussion of the inversion assumptions

It is important to analyse the effects of the adopted priors. As expected, the numerical values of the priors given in Table 2 are of no consequence where the mean index is close to 1, as long as they remain in a range in gross agreement with the flux level of the data, i.e. within reach of the iteration procedure given the adopted prior standard deviations. In practice, reasonable starting points are obtained after a small number of initially random trials which show into which direction the algorithm pulls.

Increasing the prior standard deviations or reducing the correlation lengths significantly from the values in the table results either in loss of convergence, or in unacceptably small values of the mean indices, or in large posterior variances: the information in the data becomes insufficient.


  \begin{figure} \par\includegraphics[width=8cm,clip]{MS1691f6.eps}\end{figure} Figure 6: Effects of the prior assumptions on the estimated parameters, in the case of Calzetti-type dust. The thick lines are the results of Fig. 4. The thin solid line is the result of double iteration (see text). The two other lines are obtained with priors designed to pull the SFR towards low (dot-dashed) and high (dotted) values at intermediate ages (i.e. where the mean index of E(B-V) is low). The values of $\chi ^2_{\nu }$ remain between 1.85 (double iteration) and 1.94.
Open with DEXTER

As it is, the mean index of the extinction is low at intermediate ages. Nevertheless, the results are found to be quite stable against changes in the priors. In Fig. 6, extreme results are plotted in the illustrative case of Calzetti-type dust. They were obtained by modifying the initial guesses of both the SFR and the extinction in order to pull towards higher or lower resulting SFRs. The shape of the SFR appears to be robust, although the mass ratio of old to relatively young stars (which is sensitive to small changes in the actual value of the early SFR) appears to be uncertain to within a factor of two.

Also plotted in Fig. 6 is the result obtained when the outputs of Sect. 5.1 are used as priors for a new iteration. This step provides a good test of the initial convergence. The changes are satisfactorily small. After successfully performing the test in several cases, we have stopped applying it systematically.

Finally, we have neglected until now the uncertainties due to possible aperture mismatch between the UV, optical and near-IR observations. LGLG01 estimate that errors in the relative flux levels of the three spectral segments are below 15%. Although it is possible to build this uncertainty directly into the inversion algorithm, we have more conservatively run inversions on a series of modified data. Factors between 0.85 and 1.15 were applied to the UV and near-IR parts of the spectrum. The resulting fits are poor ( $\chi^2_{\nu}>2.5$) when the near-IR flux is increased above the reference value. The best fits ( $\chi^2_{\nu}=1.8$) are obtained with a reduced near-IR flux. These solutions are appealing because they don't require higher extinctions for the old populations than for the intermediate age ones. The earliest star formation rates are correspondingly smaller, and the intermediate age and young populations becomes more important in terms of total stellar mass. However, all the tests run here provide results within the global envelope of the results already discussed above or in the previous section.

None of our attempts have a provided a solution in which the increase in the SFR responsible for the large intermediate age population occured less than about 300 Myr ago.

   
5.3 Discussion of star formation history

Struck & Smith (2002) discuss possible causes for a star formation episode that would have started 300 Myr or longer ago, but favour none in particular. The strength and extent of the stellar ring of NGC 7714 and of the tidal tails of the system suggest that the galaxies are observed shortly after closest approach and well before their probable merger (Toomre & Toomre 1972; Barnes & Hernquist 1992; Gerber & Lamb 1994). What "shortly after'' precisely means remains dependent on the model. Struck & Smith (2002) caution that modest changes of orbital inclination or distance of closest approach can significantly change the structure of the disk waves, and thus the central SFR in NGC 7714. At the same time, they admit a variety of imperfections in their final choices (for instance, they attribute the lack of a strong stellar ring in their hydrodynamical simulation to a slightly overestimated impact parameter). Furthermore, the timescale of the formation and disruption of tidal features depends on impact speed (Dubinski et al. 1999). Although the choice of initially parabolic galaxy orbits made by Struck & Smith is reasonable, the previous histories of the galaxies, or galaxy halo structures different from those adopted may have led to a slower encounter with longer timescales.

Various dynamical or hydrodynamical simulations of mergers produce double star formation episodes over timescales of the order of 109 yr, but the second one usually corresponds to the final merger, which is not appropriate for our case study (Mihos & Hernquist 1994; Bekki 1998; Gerritsen & Icke 1999). However, some models predict that each of these SF episodes, especially the first one, will last for several 100 Myr (Bekki 1998). If these models incorporated feedback mechanisms associated with star formation, such as local heating of the ISM that partially prevents star formation, the predicted SFR would be much more irregular (Gerritsen & Icke 1999) and might describe what happened in NGC 7714.

From the simulations available in the literature, our conclusion is that the last interaction with NGC 7715 might explain SF timescales of up to about 200 Myr, while longer SF timescales call for a previous event. A previous passage of the companion galaxy and related (or unrelated) bar instabilities, are options worth considering (Smith & Wallin 1992; Friedli & Benz 1995).

   
5.4 The influence of the assumed metallicity

Section 5.1 considers a solar metallicity for NGC 7714. Here we investigate the effect of the assumed metallicity on the estimated SFR.

Figure 7 compares the SFRs obtained for Z=0.02 and Z=0.008. Due to the smaller opacities of metal poor stellar atmospheres, a stellar population of a given age is intrinsically bluer at Z=0.008 than at Z=0.02. To reproduce the spectrum with a given effective extinction law, a shift of the star formation episodes to somewhat larger ages is therefore required at Z=0.008. Even the oldest stars are not red enough to explain the near-IR flux, and enhanced reddening towards the old populations results. The resulting absorption is compensated with a higher early star formation rate, and the predominance of old stars in the mass budget is reinforced.

The larger width of the recent star formation episode compensates for the lower value of the maximum SFR, and the total amount of UV light produced is similar to the Z=0.02case.


  \begin{figure} \par\includegraphics[width=8cm,clip]{MS1691f7.eps}\end{figure} Figure 7: Determination of the NGC 7714 star formation rate for two different metallicities, assuming a Salpeter IMF and the attenuation law of Calzetti et al. (2000). Solid line: Z=0.02; dashed line: Z=0.008. The layout is as in Fig. 4.
Open with DEXTER

   
5.5 Using a new basis of model spectra

Spectrophotometric properties of stellar populations with complex star formation histories depend critically on the properties of the building blocks of evolutionary models, the so-called single stellar population models that define the basis  $B_{\lambda}$. In addition to the basis of the previous sections, we constructed a second set using the new grid of Mouhcine (2001) and Mouhcine & Lançon (2002). In this grid particular care was taken to model the near-infrared properties of intermediate age stellar populations. The major difference relative to the inputs of P´EGASE lies in the modeling of the Thermally Pulsing Asymptotic Giant Branch (TP-AGB). TP-AGB stars dominate the near-infrared light of intermediate-age (0.1-2 Gyr) stellar populations. As a result of the interplay between mass loss, the third dredge-up process and, most importantly, envelope burning, the new models predict that the TP-AGB stars with the longest lifetime are born from stars with main sequence lifetimes of 0.8-1 Gyr rather than 0.1-0.2 Gyr (see also Girardi & Bertelli 1998; Marigo 1998). Consequently, the new integrated spectra evolve from bluer to redder colours between 0.1 and 1 Gyr rather than the opposite, in better agreement with constraints from the clusters of the Magellanic Clouds. One motivation for using the new models was to test whether they would allow for a more recent onset of the intermediate age star formation episode.


  \begin{figure} \par\includegraphics[width=8cm,clip]{MS1691f8.eps}\end{figure} Figure 8: Same as Fig. 4, but with the stellar populations of Mouhcine & Lançon (2002). Solid: Calzetti-type dust; dot-dashed: SMC dust screen; dashed: dust clouds.
Open with DEXTER

Figure 8 is the equivalent of Fig. 4, for the new basis of single population spectra. The results are not significantly different. The intermediate age star formation episode starts early again. In the nucleus of NGC 7714, because of the large contribution of the old stars of the underlying spiral bulge, there is no need to invoke the reddest AGB-dominated populations that would differentiate between the two sets of basis spectra.

   
5.6 Deriving the optical depth from the spectrum

The $\chi ^2_{\nu }$ values of the previous models are of about 2, meaning that better models can be sought for. Moreover, the adjustment of the emission lines showed a specific problem: Br$\gamma$ is systematically underestimated by a factor of two. So, a possibility is that the extinction laws we have used do not correspond to reality. In this section, we derive a new extinction law, compatible with the data, emission lines included. More precisely, the model is written as follows:

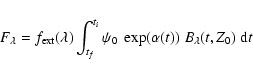\begin{displaymath}F_{\lambda}= f_{\rm ext}(\lambda) \int_{t_f}^{t_i} \psi_0 ~ \exp(\alpha(t)) ~ B_{\lambda}(t,Z_0)~ {\rm d}t \end{displaymath} (29)

with:

\begin{displaymath}f_{\rm ext}(\lambda) = \exp(-\tilde{\tau}_{\lambda}). \end{displaymath} (30)

Here, we consider the effective optical depth $\tilde{\tau}_{\lambda}$ as an unknown but assume it is independent of age, and we adopt solar metallicity for all stellar populations. We apply the same extinction to the stellar continuum and to the nebular emission. The basis spectra used are those of Sect. 5.1. Appendix B.3 provides computational details and Table 2 the priors.


  \begin{figure} \par\includegraphics[width=8cm,clip]{MS1691f9.eps}\end{figure} Figure 9: Simultaneous determination of the star formation rate (top panel) and of the optical depth (middle panel, full line) for the central 300 pc of NGC 7714. We have superimposed the Calzetti law, rescaled to E(B-V)=0.3 (dashed line). The bottom panel shows the cumulative mass contribution of the stars.
Open with DEXTER

The SFR obtained here and shown in the top panel of Fig. 9 provides a good fit to the data ( $\chi^2_{\nu}=1.4$; Fig. 10). The hydrogen lines are reproduced to within 10%. The mean index for the SFR is remarkably similar to the curves plotted in Figs. 4 or 8. The mean index for $\tilde{\tau}_{\lambda}$ behaves as described and explained in Sect. 4. The plotted attenuation law is derived to within an additive constant, which corresponds to multiplicative factor on the SFR. A minimum level of the SFR is set by the constraint of positive extinction at all wavelengths. If extinction were nil in the near-IR, the SFR would be reduced by only $\exp(-0.1)$, i.e. about 10% as compared to the plotted curve. Much larger values of $\tilde{\tau}_{\lambda}$ and the SFR can be excluded when considering the far-IR emission of the galaxy, a constraint that we have not incorporated in the inversion procedure. LGLG01 verified that, with 4 times as many hot stars as directly derived from the UV flux with standard extinction laws, the nuclear $\sim$330 pc would already produce over a third of the total far-IR light of the galaxy. This factor of 4 is already present in the SFR of Fig. 9.


  \begin{figure} \par\includegraphics[width=8cm,clip]{MS1691f10.eps}\end{figure} Figure 10: Adjustment of the spectrum of the nucleus of NGC 7714, with the SFR and attenuation obtained in Sect. 5.6. The line types are as in Fig. 5.
Open with DEXTER

Interstingly, the wavelength dependence of the derived attenuation is close to the empirical law of Calzetti et al. (2000). The differences, however, are significant: in the UV, the estimated law is flatter (otherwise the blue slope of the observed UV continuum could not be reproduced with this amount of attenuation). The present results mimic what imaging suggests is the real situation in the central 300 pc of NGC 7714 (LGLG01): a significant fraction of the UV-emitting stars are heavily attenuated in the UV, and contribute mainly to Br$\gamma$, while a smaller fraction of these hot stars is practically unobscured, explaining the small apparent reddening at UV wavelengths.

The SFR found here exceeds 1 $M_{\odot}$ yr-1 only in the last 20 Myr. This timescale is consistent with the dynamical models of Struck & Smith (2002). Nevertheless, there is an enhancement in the SFR about $7\times10^8$ yr ago (from about 0.1 to about 0.5 $M_{\odot}$ yr-1).

Despite the appeal of this solution, we express some caution. First, the fit of Fig. 10 shows the stars with ages below 107 yr as the strongest contributors around the Balmer jump. The fit in this region is good because of a bump in the obscuration law at the appropriate place. There is no physical reason to expect such a bump. At higher spectral resolution, the shape of Balmer line wings would be able to confirm the need for a stronger contribution of intermediate age stars (LGLG01). Second, we have made the strong assumption here that a single empirical attenuation law applies to stellar populations of all ages. The solutions of LGLG01, based on the integrated spectrum and direct constraints from high resolution imaging, assigned populations of different ages different apparent obscurations. In a way, we have traded freedom in the wavelength dependence of $\tilde{\tau}_{\lambda}$ against freedom in its time dependence. Unfortunately, considering the quasi-infinite possible combinations of dust properties and dust distributions in a starburst, we doubt that any spatially integrated spectroscopic data will be able to fully break the degeneracies and make multiwavelength images redundant.

6 Conclusions

In this paper we have presented an inversion method designed to estimate the SFR, the AMR and the reddening properties of galaxies from their spectra. This method allows us not only to derive best values for these functional parameters, but also to estimate the amount of information actually present in the data for each of the unknowns, as well as the posterior resolution in time, depending on the S/N of the studied spectra.

The main conclusions based on the inversion of simulated spectra are:

The inversion method applied to the spectrum of NGC 7714 confirms that the reddening properties of this galaxy cannot be modeled with simple extinction models. In order to obtain satisfactory fits to both the stellar energy distribution and the nebular emission lines, one has to allow the wavelength dependence of attenuation to deviate from "standard'' laws (this work) or to allow for variations in the attenuation between different coexisting stellar populations (LGLG01).

The main results obtained for NGC 7714 can be compared to the previous results from non-automated studies (LGLG01):

The precious information of the spatial distribution of stars and dust within the region observed spectroscopically is not always accessible. The detailed study of objects for which high resolution imaging is possible remains essential, and gives us insight into the fundamental uncertainties involved when only integrated light is available. Improvements will come naturally from a wider spectral coverage (if possible with overlaps between spectral ranges observed independently), and from the use of models with higher spectral resolution.

Acknowledgements
We thank an anonymous referee for a careful reading and for requests that significantly improved the paper.

   
Appendix A: Dust clouds and Poisson law

When clouds are distributed homogeneously in space we can describe correctly the extinction as due to a Poisson distribution of clouds. The quantity $\overline{n}(t)$ represents the mean number of clouds encountered on the line of sight.

We assume here that the clouds are of a typical size independent of age, so that the column density per cloud $E(B-V)_{\rm c}$ is constant. In other words, we assume that the variation of the extinction in time depends only on the density of clouds.

The probability to find i clouds in a given direction will follow a Poisson law:

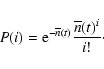\begin{displaymath}P(i)={\rm e}^{-\overline{n}(t)} \frac{\overline{n}(t)^i}{i!}\cdot \end{displaymath} (A.1)

The proportion of the stellar population that is reddened by i clouds is P(i). The absorption by i clouds is ${\rm e}^{-i k_{\lambda} E(B-V)_{\rm c}}$. Then, the resulting flux is (Natta & Panagia 1984):

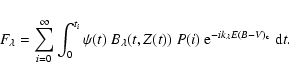\begin{displaymath}F_{\lambda}=\sum_{i=0}^{\infty} \int_0^{t_i} \psi(t)~ B_{\lam... ...))~ P(i) ~{\rm e}^{-i k_{\lambda} E(B-V)_{\rm c}} ~ {\rm d}t. \end{displaymath} (A.2)

That yields:
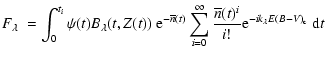$\displaystyle F_{\lambda} \ = \int_0^{t_i} \psi(t) B_{\lambda}(t,Z(t)) ~ {\rm e... ...\frac{\overline{n}(t)^i}{i!} {\rm e}^{-i k_{\lambda} E(B-V)_{\rm c}} ~ {\rm d}t$      
      (A.3)

with:

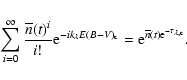\begin{displaymath}\sum_{i=0}^{\infty}\frac{\overline{n}(t)^i}{i!} {\rm e}^{-i k... ... {\rm e}^{\overline{n}(t) {\rm e}^{-\tau_{\lambda ,{\rm c}}}}. \end{displaymath} (A.4)

Appendix B: Estimation of the parameters

   
B.1 Change of variable: u = log(t)

Massive stars evolve more rapidly than small mass stars, and a given absolute difference in initial masses has more effect on stellar evolution in the high mass regime than in the low mass one. As a consequence, the time interval over which spectrophotometric properties of isochrone stellar populations vary significantly increases quasi-linearly with age. The resolution in time expected for the SFR is thus almost constant in $\log(t)$ (see references in Hubeny et al. 1999, and Lançon 2000). The following change of variable is natural:

\begin{displaymath}u=\log(t). \end{displaymath} (B.1)

The fundamental equation (Eq. (3)) should be written as follows:

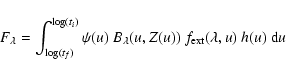\begin{displaymath}F_{\lambda}=\int_{\log(t_f)}^{\log(t_i)} \psi(u) ~ B_{\lambda}(u,Z(u)) ~ f_{\rm ext}(\lambda,u) ~ h(u) ~ {\rm d}u \end{displaymath} (B.2)

with $h(u)=10^u \ln (10)$.

So, the prior variance-covariance operators defined below ( $C_{\alpha}$, CZ,... etc.) are expressed with the new variable u. For instance, $C_{\alpha}$ is written as:

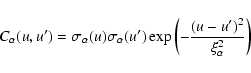\begin{displaymath}C_{\alpha}(u,u')=\sigma_{\alpha}(u) \sigma_{\alpha}(u') \exp\left(- \frac{(u-u')^2}{\xi_{\alpha}^2} \right) \end{displaymath} (B.3)

so $\xi_{\alpha}$ is expressed in units of log(t).

   
B.2 Determination of $\mathsfsl{\psi}$, Z, $\mathsfsl{\overline{n}}$ and $\mathsfsl{E(B-V)}$

In this section, we clarify the main steps of the inversion procedure, in the case one wishes to derive the time dependence of $\psi$, Z and $\overline{n}$, and the value of E(B-V) (the extinction per cloud on the line of sight).

Since the star formation rate is always positive, changing over from $\psi(u)$ to $\alpha(u)$ in Eq. (3) yields:

\begin{displaymath}\alpha(u) := \ln(\psi(u)/\psi_0) \end{displaymath} (B.4)

where $\psi_0$ is a constant. We shall assume that the uncertainties in the function $\alpha(u)$ follow a Gaussian law. This implies that the errors in $\psi(u)$ follow a log-normal distribution. Similarly, the equations can be rewritten with logarithmic variables for all unknowns that must be forced to positive values.

The flux at the wavelength $\lambda_i$ is modeled as follows:

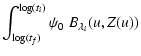$\displaystyle F_{\lambda_i}$=$\displaystyle \int_{\log(t_f)}^{\log(t_i)} \psi_0 ~ B_{\lambda_i}(u,Z(u))$
$\displaystyle \ \exp\left\{\alpha(u)+\overline{n}(u) \left({\rm e}^{-k_{\lambda_i} E(B-V)}-1\right)\right\} ~ h(u)~ {\rm d}u$
=$\displaystyle g_{\lambda_i}(\alpha(u),Z(u),\overline{n}(u),E(B-V)).$ (B.5)

This formulation requires use of the inverse method in the non-linear case (Eq. (16)). We drop the [k] index in order to simplify the notation.

The vector M of unknown parameters is:

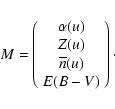\begin{displaymath}M = \left( \begin{array}{c} \alpha(u) \\ Z(u) \\ \overline{n}(u) \\ E(B-V) \\ \end{array} \right)\cdot \end{displaymath} (B.6)

The prior variance-covariance matrix shall be written:

 \begin{displaymath}C_0=\left(\begin{array}{cccc} C_{\alpha} & 0 & 0 & 0 \\ 0 ... ... 0 & 0 & 0 & \sigma^2_{E(B-V)} \\ \end{array} \right)\cdot \end{displaymath} (B.7)

Here $C_{\alpha}$ (for instance) contains diagonal terms of the form $C_{\alpha}(u,u)=\sigma_{\alpha}^2(u)$ and non-diagonal terms of the form $C_{\alpha}(u,u')$ (see Eq. (20)).

The matrix of partial derivatives is (with s the number of wavelengths sampled):

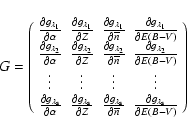\begin{displaymath}G=\left( \begin{array}{cccc} \frac{\partial g_{\lambda_1}}{\... ...g_{\lambda_{\rm s}}}{\partial E(B-V)} \\ \end{array} \right) \end{displaymath} (B.8)

E(B-V) being a discrete parameter, the corresponding partial derivative is not a functional operator. $\partial g_{\lambda}/ \partial E(B-V)$ is written:
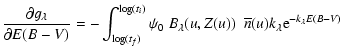$\displaystyle \frac{\partial g_{\lambda}}{\partial E(B-V)} = -\int_{\log(t_f)}^... ..._{\lambda}(u,Z(u)) ~~ \overline{n}(u) k_{\lambda} {\rm e}^{-k_{\lambda} E(B-V)}$
$\displaystyle \quad \quad \exp\left\{\alpha(u)+\overline{n}(u) \left({\rm e}^{-k_{\lambda} E(B-V)}-1\right)\right\}~ h(u) ~{\rm d}u.$ (B.9)

Conversely, $\alpha$, Z and $\overline{n}$ are functions of the time variable. The corresponding partial derivatives are functional operators. $\frac{\partial g_{\lambda}}{\partial \alpha}$, $\frac{\partial g_{\lambda}}{\partial Z}$ and $\frac{\partial g_{\lambda}}{\partial \overline{n}}$have respectively the following kernels:
$\displaystyle { K_1(u) = \psi_0 ~ B_{\lambda}(u,Z(u)) }$
  $\textstyle \qquad \exp\left\{\alpha(u)+\overline{n}(u) \left({\rm e}^{-k_{\lambda} E(B-V)}-1\right)\right\} h(u)$   (B.10)


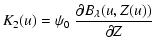$\displaystyle { K_2(u) = \psi_0 ~ \frac{\partial B_{\lambda}(u,Z(u))}{\partial Z} }$
  $\textstyle \qquad \exp\left\{\alpha(u)+\overline{n}(u) \left({\rm e}^{-k_{\lambda} E(B-V)}-1\right)\right\} h(u)$   (B.11)


$\displaystyle { K_3(u) = \left({\rm e}^{-k_{\lambda} E(B-V)}-1\right) ~ \psi_0 ~ B_{\lambda}(u,Z(u)) }$
  $\textstyle \qquad \exp\left\{\alpha(u)+\overline{n}(u) \left({\rm e}^{-k_{\lambda} E(B-V)}-1\right)\right\} h(u) .$   (B.12)

These kernels $K_{\rm i}(u)$ act on a function f(u) as follows:

 \begin{displaymath} <K_{\rm i},f>~=\int_{\log(t_f)}^{\log(t_i)} f(u) K_{\rm i}(u) {\rm d}u \end{displaymath} (B.13)

where <,> is the scalar product in L2 Hilbert space.

The ith component of the vector $V_i=D + G \cdot (M -M_0)-g(M)$ (in Eq. (16)) is: 2pt

Vi=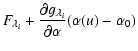$\displaystyle F_{\lambda_i} + \frac{\partial g_{\lambda_i}}{\partial \alpha} (\alpha(u)-\alpha_0)$
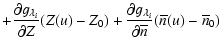$\displaystyle + \frac{\partial g_{\lambda_i}}{\partial Z} (Z(u)-Z_0) + \frac{\partial g_{\lambda_i}}{\partial \overline{n}}(\overline{n}(u)- \overline{n}_0)$
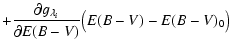$\displaystyle +\frac{\partial g_{\lambda_i}} {\partial E(B-V)} \big(E(B-V)-E(B-V)_0\big)$
$\displaystyle - ~ g_{\lambda_i}\big(\alpha(u),Z(u),\overline{n}(u),E(B-V)\big)$ (B.14)

where $\alpha_0$, Z0, $\overline{n}_0$ and E(B-V)0 are respectively the priors of $\alpha(u)$, Z(u), $\overline{n}(u)$ and E(B-V). The (i,j)th component of $(G C_0 G^{*} + C_{\rm d})$ is:

 
Si,j=$\displaystyle \frac{\partial g_{\lambda_i}}{\partial \alpha} ~C_{\alpha} \frac{... ...ine{n}}~ C_{\overline{n}}~ \frac{\partial g_{\lambda_j}}{\partial \overline{n}}$
$\displaystyle + \frac{\partial g_{\lambda_i}}{\partial E(B-V)} \sigma^2_{E(B-V)} \frac{\partial g_{\lambda_j}}{\partial E(B-V)} +\delta_{i,j}~\sigma_i~\sigma_j$
(B.15)

where $\delta_{i,j}$ is the Kronecker symbol and $\sigma_i$ the root mean square of the noise in the data $F_{\lambda_i}$ (here we assume uncorrelated noise in the data).

Defining the vector:

 
W=S-1V, (B.16)

the estimation number (k+1) for the parameters is computed from the previously estimated values by:
$\displaystyle \alpha_{[k+1]}(u)=\alpha_0+\sum_i W_i \int_{\log(t_f)}^{\log(t_i)} C_{\alpha}(u,u')K_1(u') {\rm d} u'$      
      (B.17)
$\displaystyle Z_{[k+1]}(u)=Z_0 + \sum_i W_i \int_{\log(t_f)}^{\log(t_i)} C_Z(u,u')K_2(u') {\rm d} u'$      
      (B.18)
$\displaystyle \overline{n}_{[k+1]}(u)=\overline{n}_0+ \sum_i W_i \int_{\log(t_f)}^{\log(t_i)} C_{\overline{n}}(u,u') K_3(u') {\rm d} u'$      
      (B.19)

and
$\displaystyle E(B-V)_{[k+1]} = E(B-V)_0 + \sigma_{E(B-V)}^2 \sum_i W_i \frac{\partial g_{\lambda_i}}{\partial E(B-V)} \cdot$     (B.20)

   
B.3 Determination of ${\sf\psi }$ and ${\sf\tilde{\tau}_{\lambda}}$

In this section, the model and the observations are linked by the relation:
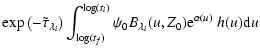$\displaystyle F_{\lambda_i}$=$\displaystyle \exp\left(-\tilde{\tau}_{\lambda_i} \right) \int_{\log(t_f)}^{\log(t_i)} \psi_0 B_{\lambda_i}(u,Z_0) {\rm e}^{\alpha(u)}~ h(u) {\rm d}u$
=$\displaystyle g_{\lambda_i}(\alpha(u),\tau_{\lambda})$ (B.21)

where the metallicity is fixed. The unknown parameters are $\alpha(u)$ and $\tilde{\tau}_{\lambda}$ with the respective variance-covariance operators  $C_{\alpha}$ and $C_{\tilde{\tau}}$.

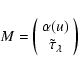\begin{displaymath}M = \left( \begin{array}{c} \alpha(u) \\ \tilde{\tau}_{\lambda} \\ \end{array} \right) \end{displaymath} (B.22)


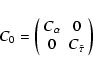\begin{displaymath}C_0=\left(\begin{array}{cc} C_{\alpha} & 0 \\ 0 & C_{\tilde{\tau}} \\ \end{array} \right) \end{displaymath} (B.23)

with:

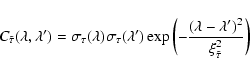\begin{displaymath}C_{\tilde{\tau}}(\lambda,\lambda')= \sigma_{\tau}(\lambda) \s... ...eft( -\frac{(\lambda-\lambda')^2}{\xi_{\tilde{\tau}}^2}\right) \end{displaymath} (B.24)

$C_{\alpha}$ is given by Eq. (20). To force positive values of $\tilde{\tau}_{\lambda}$, the equations are rewritten with ln( $\tilde{\tau}_{\lambda}$) as the unknown.

The matrix of partial derivatives of Eq. (16) is:

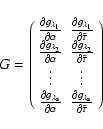\begin{displaymath}G=\left( \begin{array}{cc} \frac{\partial g_{\lambda_1}}{\pa... ...ambda_{\rm s}}}{\partial \tilde{\tau}}\\ \end{array} \right) \end{displaymath} (B.25)

$\frac{\partial g_{\lambda}}{\partial \alpha}$, $\frac{\partial g_{\lambda}}{\partial \tilde{\tau}}$ respectively have the following kernels:
K1(u)=$\displaystyle \psi_0 \exp\left(\alpha(u)-\tilde{\tau}_{\lambda}\right) B_{\lambda}(u,Z_0) h(u)$ (B.26)
$\displaystyle K_2(\lambda)$=$\displaystyle \psi_0 \exp\left(\alpha(u)-\tilde{\tau}_{\lambda}\right) B_{\lambda}(u,Z_0) \delta(\lambda-\lambda_i) h(u)$ (B.27)

where $\delta$ is the Dirac function. These kernels act on a function as shown in Eq. (B.13).

The ith component of the vector $V_i=D + G \cdot (M -M_0)-g(M)$ is:

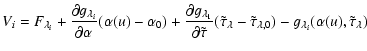$\displaystyle V_i= F_{\lambda_i} + \frac{\partial g_{\lambda_i}}{\partial \alph... ...da}-\tilde{\tau}_{\lambda,0}) - g_{\lambda_i}(\alpha(u),\tilde{\tau}_{\lambda})$     (B.28)

where $\alpha_0$ and $\tilde{\tau}_{\lambda,0}$ are respectively the priors of $\alpha(u)$ and $\tilde{\tau}_{\lambda}$.
The matrix S (Eq. (B.15)) is computed as follows:

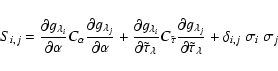\begin{displaymath}S_{i,j} = \frac{\partial g_{\lambda_i}}{\partial \alpha} C_{... ...artial \tilde{\tau}_{\lambda}} +\delta_{i,j}~\sigma_i~\sigma_j \end{displaymath} (B.29)

where W is a vector defined by Eq. (B.16). The estimation of the parameters is given by:

\begin{displaymath}\alpha_{[k+1]}(u)=\alpha_0+\sum_i W_i \int_{\log(t_f)}^{\log(t_i)} C_{\alpha}(u,u')K_1(u') {\rm d} u' \end{displaymath} (B.30)


\begin{displaymath}\tilde{\tau}_{\lambda[k+1]}=\tilde{\tau}_{\lambda,0} + \sum_i... ...\tilde{\tau}}(\lambda,\lambda')K_2(\lambda') {\rm d} \lambda'. \end{displaymath} (B.31)

References

 

Copyright ESO 2002