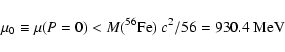A&A 394, 641-645 (2002)
DOI: 10.1051/0004-6361:20021177

On the minimum radius of strange stars with crust

J. L. Zdunik

N. Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland

Received 29 May 2002 / Accepted 9 August 2002

Abstract
The minimum value of the radius of a strange star covered by the crust of nuclear matter is determined. The results for the maximum possible thickness of the crust (up to the neutron drip) as well as the possibility of thinner crust postulated by some authors are discussed. The minimum radius of the strange star with maximal crust is 5.5 km. The useful scaling formulae with respect to the main parameters describing strange matter and the density at the bottom of the crust are presented.

Key words: dense matter - equation of state - stars: neutron


1 Introduction

The idea of compact stars build of strange matter was presented by Witten (1984) and the models of stars were calculated using various models of strange matter by Haensel et al. (1986) and Alcock et al. (1986). The main idea is that the u, d, s matter is ground state of matter at zero pressure (self-bound strange quark matter) i.e. its energy per baryon is smaller than that of iron:

 \begin{displaymath}\mu_0\equiv\mu(P=0) < {M}({\rm ^{56}Fe})~c^2/56=930.4~{\rm MeV} \end{displaymath} (1)

where ${M}({\rm ^{56}Fe})$ is the mass of the ${\rm ^{56}Fe}$ atom.

Recently the increasing interest in strange stars is connected with some estimations of the radius of the isolated neutron (or strange) stars from some limits on the temperature of such a star. Some indications that the radius is small favor strange stars as a possible explanation.

A bare strange star surface is very poor emitter of photons with energies lower than $\sim$20 MeV (Alcock et al. 1986; Chmaj et al. 1991). However strange star could be covered by a crust of nuclear matter, which changes the properties of the star allowing for the emission of photons of lower energies and the black body radiation from the stellar surface (Alcock et al. 1986). The additional mechanism of the radiation from a bare strange star due to e+e- pair creation has recently been proposed by Usov (1998, 2001), but its contribution for T<109 K is negligible.

As a result of observational data one can try to determine the apparent radius of the neutron star $R_{\infty}$. If $R_{\infty}$ would be smaller than $\sim$12 km the only solution seems to be the strange star (Haensel 2001). Recent observations of the isolated neutron star candidate RX J1856.5-3754 have been interpreted as a star with the radius $R_{\infty}\sim 3.8{-}8.2$ km (Drake et al. 2002) (but see also Walter & Lattimer 2002).

In this Paper I present some limits on the radius of strange stars if they are covered by a crust of nuclear matter.

2 Strange stars with crust

2.1 Equations of state

In this Paper I consider two types of EOSs of strange matter: MIT Bag Model and models presented by Dey et al. (1998).

In the framework of the phenomenological MIT bag model the quark matter is the mixture of the massless u and d quarks, electrons and massive s quarks. The model is described in detail in Farhi & Jaffe (1984), where the formulae for physical parameters of strange matter are also presented. There are the following physical quantities entering this model: B - the bag constant, $\alpha_{\rm c}$ - the QCD coupling constant and $m_{\rm s}$ - the mass of the strange quark. It is necessary to introduce also the parameter $\rho_N$ - the renormalization point. Following Farhi & Jaffe (1984) we choose $\rho_N=313$ MeV.

The consequence of this model of strange matter is scaling of all thermodynamic functions and parameters of the strange stars (mass, radius etc.) with some powers of B (Haensel et al. 1986; Zdunik 2000).

The main model considered in this paper corresponds to the following set of the MIT Bag Model model parameters for strange matter: bag constant $B=56~{\rm MeV/fm^3}$, mass of the strange quark $m_{\rm s}=200~{\rm MeV/c^2}$, and QCD coupling constant $\alpha_{\rm c}=0.2$. This EOS of strange quark matter (called SQM1 as in Zdunik et al. 2001) had been also used in Zdunik 2000 and Zdunik & Gourgoulhon 2001). It yields an energy per unit baryon number at zero pressure $E_0=918.8 ~{\rm MeV} <E(^{56}{\rm Fe})=930.4~$MeV. The maximum allowable mass for strange stars is $M_{\rm max}^{\rm stat}=1.8~{M_\odot}$.

I also consider two cases of strange matter based on MIT Bag Models for massless strange quarks in which the dependence $P(\rho)$ is exactly linear and scaling laws with B are exact (Zdunik 2000). These two models correspond to "standard" value of the bag constant $B=60~{\rm MeV~fm^{-3}}$ and to the maximum possible value of B consistent with the requirement of the stability of strange matter (Eq. (1)): $B_{\max}=91.5~{\rm MeV~fm^{-3}}$.

The second EOS of strange matter considered in this paper is based on the model of strange matter proposed by Dey et al. (1998) which incorporates restoration of chiral quark masses at high densities. Two sets of parameters describing this model have been used to determine properties of strange stars (see e.g. Li et al. 1999a,b) and usually referred to as SS1 and SS2.

The main property of the self bound strange matter is the large density at zero pressure and the equation of state which can be very accurately approximated by the linear dependence $P(\rho)$.

As it has been shown in Zdunik (2000); Gondek-Rosinska et al. (2000) in both cases (MIT and Dey et al. (1998) models) with accuracy of the order of 1-2% we can write:

 \begin{displaymath}P=a c^2 (\rho-\rho_0) \end{displaymath} (2)

where $a\simeq 1/3$ and $\rho_0$ is the density of self bound strange matter at zero pressure. Both a and $\rho_0$ are functions of the parameters describing the model of strange matter.

In all considered models the crust is described by the BPS model of dense matter below neutron drip Baym et al. (1971). The maximum pressure and density at the bottom of the crust which can be formed on strange star are defined by the neutron drip point (Alcock et al. 1986) and are equal to: $P_{\rm ND}=7.8\times 10^{29}~ {\rm dyn~ cm^{-2}}$, $\rho_{\rm ND}= 4.3\times 10^{11}~ {\rm g~ cm^{-3}}$.

As has been pointed out by Alcock et al. (1986) the width of the gap between the strange core and the crust could determine the density at the bottom of the crust and the crust could be significantly thinner (see e.g. Huang & Lu 1997; Phukon 2000). We can study this effect by considering different values of the pressure $P_{\rm b}$(and density $\rho _{\rm b}$) at the bottom of the crust i.e. treating $P_{\rm b}$ as a free parameter resulting from other considerations, not necessarily equal to $P_{\rm ND}$. Of course the condition $P_{\rm b}< P_{\rm ND}$ has to be fulfilled.

2.2 The role of the size of the crust

The strange star configurations are calculated by solving Oppenheimer-Volkoff equations in the case of spherical symmetry.

 \begin{displaymath}{{\rm d}P\over {\rm d}r}=-{Gm\rho\over r^2 }\left(1-{2Gm\over... ...r \rho c^2}\right)\left(1+{4 \pi r^3 P\over m c^2}\right)\cdot \end{displaymath} (3)

It has been shown by Zdunik et al. (2001) that for strange stars the thickness of the crust can be well described by the approximate formula valid for large and intermediate values of the stellar mass.

The formula presented in Zdunik et al. (2001) does not render the properties of the M(R) dependence for small stellar masses (say $ M < 0.5 ~M_{\odot}$), especially the existence of the minimum radius of the star.

This effect could be quite easily obtained by more careful approximation of Eq. (3) in the crust region. The essential point is that although for small masses (close to the minimum radius) the mass is concentrated in the strange core (more than 99.9%) the thickness of the crust is relatively large compared to the core radius. Thus in approximation we can assume that $M={\rm const.}=M_{\rm core}$ but we have to take into account the changes of r thorough the crust. This effect has not been considered in our previous paper (Zdunik et al. 2001). We can safely neglect in the crust the last two terms of Eq. (3). In the crust the maximum values of the factors $P/\rho c^2$ and ${4 \pi r^3 P/ m c^2}$ are of the orders 10-3 and 10-6 respectively. As a result we obtain:

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3728f1.eps}\end{figure} Figure 1: The function $\chi=\int_0^{P_{\rm b}} \rho^{-1} $dP for the BPS equation of state of the outer crust. The open circles denote the parameters of the bottom of the crust for which the structure of the stellar configurations has been calculated (see Fig.  2 and Table  1).
Open with DEXTER


 \begin{displaymath}{{\rm d}P\over \rho}=-GM {{\rm d}r \over r^2 \left(1-{2GM\over rc^2}\right)} \end{displaymath} (4)

which results in the following equation for the stellar radius R:

 \begin{displaymath}\chi={1\over2}~c^2~\ln\left[{1-{2GM\over Rc^2}\over 1-{2GM\over R_{\rm core}c^2}}\right] \end{displaymath} (5)

where

 \begin{displaymath}\chi=\int_0^{P_{\rm b}} {{\rm d}P\over \rho} \end{displaymath} (6)

is thermodynamic potential characteristic to the equation of state and $P_{\rm b}$ is the pressure at the bottom of the crust.

The function $\chi(\rho_{\rm b})$ is plotted in Fig. 1.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3728f2.eps}\end{figure} Figure 2: The mass vs. radius relation for strange stars with crust for different choices of the pressure at the bottom of the crust. From the right to the left $P_{\rm b}$ is equal to 100%, 50%, 20%, 10% and 5% of the pressure at the neutron drip point $P_{\rm ND}=7.8\times 10^{29}~ {\rm dyn~ cm^{-2}}$. The corresponding densities are given in Table 1. The dashed line corresponds to the bare strange star. The dotted lines presenting the results of the approximate Eq. (7) for the cases 100% and 5% are nearly undistinguishable from the exact solutions (solid lines) (the small difference could be seen for the $P_{\rm b}=P_{\rm ND}$ case in the insert showing the enlarged region of the minimum radius). The EOS of strange matter is given by the model SQM1 (see the text).
Open with DEXTER

The solution of Eq. (5) can be written in the form:

 \begin{displaymath}{1\over R}={1\over R_{\rm core}}\exp{\left(2\chi/c^2\right)}+{c^2\over 2GM} \left(1-\exp{(2\chi/c^2)}\right) \end{displaymath} (7)

which in the limit up to the first order in 1/c2results in the formula:

 \begin{displaymath}{1\over R}={1\over R_{\rm core}}-{\chi\over GM}+ 2{\chi\over c^2}\left({1\over R_{\rm core}}-{\chi\over 2GM}\right)\cdot \end{displaymath} (8)

In Fig. 2 one can see the accuracy of our approximation 7 in which we have used the values of the mass and radius of bare strange star ( $R_{\rm core}$ and $M_{\rm core}$ depicted by the dashed line) to determine the radius of strange star with crust (the mass is assumed to have the same value). In Fig. 2 the results of Eq. (7) cannot be distinguished from the exact solution (the very small difference can be seen in the insert showing the enlarged region near to the minimum radius).

The minimum radius of the star can be easily obtained by differentiating Eq. (7) with respect to Massuming that $M\sim R_{\rm core}^3$ which for self bound stars of small masses is a very good approximation. As a result we obtain:

 
$\displaystyle R={3\over2}R_{\rm core}\exp{(-2\chi/c^2)}$     (9)
$\displaystyle {GM\over Rc^2}=\exp{(2\chi/c^2)}-1.$     (10)

If we are interested in the minimum radius of the strange star with crust we can safely work in the nonrelativistic limit (the relativistic parameter GM/Rc2 is of the order of 2%). In the nonrelativistic limit we obtain:
 
$\displaystyle {GM\over R_{\rm core}}={4\over 3} \pi G \rho_0 R_{\rm core}^2=3\chi$     (11)
$\displaystyle R={3\over2}R_{\rm core}.$     (12)

It should be noted that the determination of the minimum radius in the nonrelativistic limit is consistent with the assumption of the constant density of the core build of strange matter. For the small mass strange stars with EOS 2 the density in the center is larger then $\rho_0$ by $\delta \rho$ given by the formula:

 \begin{displaymath}{\delta\rho\over \rho_0}\simeq{1\over2 a}{GM_{\rm core}\over R_{\rm core}c^2} \end{displaymath} (13)

which follows from the expansion of the equation of hydrostatic equilibrium in $\delta\rho/\rho$ in Newtonian limit. The central pressure is given by:

 \begin{displaymath}P_c\simeq{1\over2 }{GM_{\rm core}\rho_0\over R_{\rm core}}\cdot \end{displaymath} (14)

In this approximation the mass of the strange core is:
 
$\displaystyle M_{\rm core}=M_0\left(1+{1\over5 a}{GM_0\over R_{\rm core}c^2}\right)$     (15)
$\displaystyle M_0={4\over 3}\pi\rho_0R_{\rm core}^3.$     (16)

The interesting consequence of Eq. (13) is that the self-bound star with crust reaches its minimum radius at the central density $\rho_{\rm c}\simeq\rho_0~(1+1.5\chi/ac^2)$ and central pressure $P_{\rm c}\simeq 1.5\chi\rho_0$. The accuracy of this expansion at this mass is 10% for $\delta\rho/\rho_0$which corresponds to 10% error in $P_{\rm c}$ and 1% in $\rho_{\rm c}$.

In Fig. 2 we present mass versus radius relations for the SQM1 Eos of the quark matter and different choices of $P_{\rm b}$ equal to 1, 0.5, 0.2, 0.1, 0.05 of the pressure at the neutron drip point.


 

 
Table 1: The parameters of the strange star at the minimum radius for different choices of the pressure at the bottom of the crust (first column). The first three columns characterize the properties of the crust - the pressure and density at the bottom of the crust. The model of strange matter is SQM1 (see text) and the crust is described by the BPS equation of state.

$P_{\rm b}/c^2$		 $\rho _{\rm b}$ $\chi $ $\rho_{\rm c}$ R M zs $R_{\rm core}/R$ $M_{\rm core}/M$
${\rm g~cm^{-3}}$ ${\rm g~cm^{-3}}$ ${\rm cm^2~s^{-2}}$ ${\rm g~cm^{-3}}$ ${\rm km}$ $M_{\odot}$      

$8.6787\times10^{8}$		 $4.3051\times10^{11}$ $8.761\times10^{18}$ $4.751\times10^{14}$ 6.616 0.09216 0.0208 0.6856 0.999765
$4.3393\times10^{8}$ $2.3864\times10^{11}$ $7.561\times10^{18}$ $4.712\times10^{14}$ 6.177 0.07348 0.0177 0.6822 0.999860
$1.7357\times10^{8}$ $1.0856\times10^{11}$ $6.148\times10^{18}$ $4.670\times10^{14}$ 5.602 0.05363 0.0143 0.6791 0.999929
$0.8679\times10^{8}$ $0.6452\times10^{11}$ $5.233\times10^{18}$ $4.643\times10^{14}$ 5.188 0.04229 0.0121 0.6778 0.999958
$0.4339\times10^{8}$ $0.3676\times10^{11}$ $4.450\times10^{18}$ $4.621\times10^{14}$ 4.800 0.03300 0.0102 0.6759 0.999975


The parameters of stellar configurations at the point with minimum radius are presented in Table 1. The gravitational redshift of photon emitted from from the surface

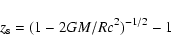
\begin{displaymath}z_{\rm s}=(1-2GM/Rc^2)^{-1/2}-1\end{displaymath}

measures the importance of relativistic effects. As we see this value is comparable to the departure of $R_{\rm core}/R$ from the Newtonian value 2/3 (Eq. (12)). The factor $(1+z_{\rm s})$ connects also the radius of the star and the "apparent radius":

 \begin{displaymath}R_{\infty}=R~(1+z_{\rm s}). \end{displaymath} (17)

At its minimum value the "apparent radius" is larger than the radius of the star by $\sim$$1{-}2\%$.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h3728f3.eps}\end{figure} Figure 3: The minimum radius of the star (top) and corresponding mass (bottom) as a function of the density at the bottom of the crust.
Open with DEXTER

The dependence of $R_{\min}$ and $M(R_{\min})$ on $P_{\rm b}$ and $\rho _{\rm b}$ is nearly power-law (see Fig. 3), due to the fact that the equation of state of the crust can be very well approximated by the polytrope. For polytropic EOS we have:

 \begin{displaymath}P\sim \rho^\gamma~~~~~~~~\chi={\gamma \over \gamma-1}{P\over \rho}\cdot \end{displaymath} (18)

From Eq. (12) we see that for polytropic EOS $R_{\min}\sim {P_{\rm b}}^{(\gamma-1)/2\gamma}\sim {\rho_{\rm b}}^{(\gamma-1)/2}$ and $M(R_{\min})\sim {P_{\rm b}}^{3(\gamma-1)/2\gamma}\sim {\rho_{\rm b}}^{ 3(\gamma-1)/2}$.

2.3 The role of the strange matter EOS


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{2728f4.eps}\end{figure} Figure 4: The mass vs. radius relation for strange stars with maximum crust for two choices of the bag constant in the MIT model of strange matter and for two models of Dey et al. (1998). The dot-dashed line corresponds to the pressure at the bottom of the crust equal to $0.1P_{\rm ND}$.
Open with DEXTER

The mass vs. radius relation for different models of strange matter is presented in Fig. 4 and the main parameters of these models ($\rho_0$, a) and stellar configurations at minimum radius are given in Table 2.


 

 
Table 2: The parameters of the strange star at the minimum radius for different choices of the parameters of strange matter. The first two columns characterize the EOS of the strange star core ( $P=a c^2 (\rho -\rho _0)$). The bottom of the crust corresponds to the neutron drip point (the maximum crust) and the parameter of the crust ($P_{\rm b}$, $\rho _{\rm b}$, $\chi $) are given in the first row of Table 1.
Model a $\rho_0$ $\rho_{\rm c}$ R M $z_{\rm s}$ $R_{\rm core}/R$ $M_{\rm core}/M$
    ${\rm g~cm^{-3}}$ ${\rm g~cm^{-3}}$ km $M_{\odot}$      

B=60.0		 1/3 $4.278\times 10^{14}$ $4.486\times 10^{14}$ 6.795 0.09235 0.02070 0.6844 0.999750
B=91.5 1/3 $6.523\times 10^{14}$ $6.839\times 10^{14}$ 5.503 0.07452 0.02062 0.6836 0.999836
SQM1 0.301 $4.500\times 10^{14}$ $4.751\times10^{14}$ 6.616 0.09041 0.02081 0.6856 0.999765
SS1 0.463 $1.154\times 10^{15}$ $1.194\times 10^{15}$ 4.148 0.05607 0.02058 0.6831 0.999906
SS2 0.455 $1.332\times 10^{15}$ $1.378\times 10^{15}$ 3.861 0.05221 0.02059 0.6832 0.999919


The radius of the strange star with crust at its minimum point is a very simple functional of the equation of state of strange matter. In the nonrelativistic limit it depends on the value of the density of the matter at zero pressure $\rho_0$ independently of the specific EOS of the self-bound matter. The parameter acorresponding to the sound velocity of the matter enters next term in Eq.  (16) via the slight increase of the density in the center of the strange core. For given $\chi $ we obtain from Eq.  (12):

 \begin{displaymath}R_{\min}={9\over4}~\sqrt{\chi\over\pi G}~\rho_0^{-1/2}=4.9~\sqrt{{\chi_{}}_{18}\over{\rho_0}_{14}}~{\rm km} \end{displaymath} (19)

where ${\chi_{}}_{18}$ and ${\rho_0}_{14}$ denotes $\chi $ and $\rho_0$ in units $10^{18}~{\rm cm^2~s^{-2}}$ and $10^{14}~{\rm g~cm^{-3}}$ respectively.

As we see from Eq. (19) the minimum radius corresponds to the maximum $\rho_0$. In the MIT bag model of strange matter $\rho_0$ is limited by the assumption of the stability of the matter at zero pressure (Eq.  (1)). The maximum $\rho_0$corresponds then to $B=91.5~{\rm MeV~fm^{-3}}$ for massless strange quarks. The numerical values of the stars at minimum radius as a function of $\rho_0$ are presented in Table  2. For other model of the self bound matter the parameters of the star with minimum radius can be easily obtained from the Table 2 using scaling relations with $\rho_0^{-1/2}$

 
$\displaystyle R_{\min}(\overline{\rho}_0)=R_{\min}(\rho_0)\sqrt{\rho_0\over\overline{\rho}_0}$     (20)
$\displaystyle M(R_{\min}(\overline{\rho}_0))=M(R_{\min}(\rho_0))\sqrt{\rho_0\over\overline{\rho}_0}\cdot$     (21)

As can be seen from Table  2 the accuracy of these scalings is better than 1%.

The surface redshift at minimum radius depends only on the value of $\chi $and for fixed density at the bottom of the crust the points with minimum radius and different B (or $\rho_0$) lie in the M(R) plane on the straight line $GM/Rc^2={\rm const.}$. The small differences in z in Table  2 reflects the accuracy of our approximations in Newtonian approach.

3 Conclusions

The radius of the strange star with crust can be very accurately calculated from the parameters of the bare strange stars. Equation (5) gives us the stellar radius for a very wide range of stellar masses from the maximum one down to the masses $\sim$ $0.02~M_{\odot}$. The only important assumption is the concentration of the mass in the core built of strange matter. This assumption is fulfilled well below the star with minimum radius, thus the minimum radius of the star can be safely calculated using the given equations. It should be however mentioned that this method fails in determination of the point with minimum mass since the mass of the crust plays a crucial role there.

Acknowledgements
This research was partially supported by the KBN grant No. 5P03D.020.20. I am very grateful to P. Haensel for careful reading of manuscript and helpful comments and suggestions.

References

 

Copyright ESO 2002