

Up: VLT observations of metal-rich
Subsections
5 Detailed comparison of WR populations with synthesis models
5.1 Procedure
To interpret quantitatively the observational data we use evolutionary synthesis models and
proceed essentially as in SGIT00.
The following main observational constraints are used:
- 1.
-
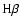 and
and
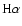 equivalent widths. The former is used as a primary
age indicator; once
equivalent widths. The former is used as a primary
age indicator; once
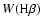 is reproduced
is reproduced
 may serve as an independent
consistency test for the predicted spectral energy distribution (SED) in the red
(cf. SGIT00).
may serve as an independent
consistency test for the predicted spectral energy distribution (SED) in the red
(cf. SGIT00).
- 2.
- Nebular line intensities.
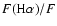 (
(
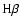 )
determines the extinction
of the gas. The use of other line intensities requires detailed photoionization
modeling which is beyond the scope of this paper.
)
determines the extinction
of the gas. The use of other line intensities requires detailed photoionization
modeling which is beyond the scope of this paper.
- 3.
- Intensities and equivalent widths of the main WR features.
The blue bump and C IV
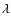 5808 (red bump)
serve as main constraints on the WR population. To avoid uncertainties
in deblending individual contributions of the blue bump we prefer to
use measurements for the entire bump.
In contrast to the spectra of metallicity objects our spectra show
no evident contamination from nebular lines (e.g. [Fe III]
5808 (red bump)
serve as main constraints on the WR population. To avoid uncertainties
in deblending individual contributions of the blue bump we prefer to
use measurements for the entire bump.
In contrast to the spectra of metallicity objects our spectra show
no evident contamination from nebular lines (e.g. [Fe III] 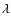 4658,
nebular He II).
4658,
nebular He II).
To potentially disentangle between various effects (underlying "non-ionizing''
population, loss of photons, differential extinction between gas and stars)
it is important to use both equivalent widths and relative
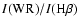 intensities
(cf. Schaerer et al. 1999a).
intensities
(cf. Schaerer et al. 1999a).
For the model comparisons we use calculations based on the evolutionary synthesis code
of SV98, which in particular includes the most recent calibration of WR line
luminosities used to synthesize the WR features, up-to-date stellar tracks,
CoStar stellar atmospheres for O stars, pure H-He models for WR stars
and Kurucz models for cooler stars
(see SV98 for a full description).
Except for the improved O star atmospheres used by SV98 the Starburst99
synthesis models (Leitherer et al. 1999) use the same basic input physics.
New generation
stellar atmosphere models for O and WR stars including a full treatment of non-LTE
line blanketing and stellar winds
have just now become available for the
use in synthesis models (Smith et al. 2002).
However, as the quantities of interest here depend only on the total number of
Lyman continuum photons which is not altered, the use of these more sophisticated
atmosphere models does not affect our results.
It is important to stress that in all cases the high-mass loss stellar tracks
of Meynet et al. (1994) are used.
It is thought that this adjustment of mass-loss, treated like a free parameter,
will become ultimately obsolete when a proper treatment of the various effects
of stellar rotation is made in the stellar evolution models.
First results tend to indicate that this may indeed be the case
(Meynet 1999).
The Meynet et al. (1994) tracks are chosen as they reproduce a large number of
properties of individual WR stars and WR populations (including especially
relative WR/O ratios for a standard Salpeter IMF) in Local Group galaxies
(Maeder & Meynet 1994).
The use of other tracks (e.g. the "normal'' mass loss tracks)
which are known to disagree with these basic constraints on WR and O star populations,
would imply a strong inconsistency with the Local Group data.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{plot_std_wrbump.eps}\hspace*{4mm}
\includegraphics[width=8.6cm,clip]{plot_lihb_wr.eps}\end{figure}](/articles/aa/full/2002/41/aa2816/Timg89.gif) |
Figure 8:
Observed and predicted equivalent width (left panel) and line intensity
with respect to
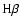 (right panel) as a function of
(right panel) as a function of
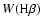 .
Our VLT sample is shown by (black) triangles, the BK02 sample with (red) squares.
Typical uncertainties are 5-10% for .
Our VLT sample is shown by (black) triangles, the BK02 sample with (red) squares.
Typical uncertainties are 5-10% for
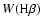 , ,
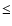 10% for W(WR bump),
and 10% for W(WR bump),
and 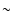 0.05 dex in 0.05 dex in 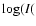 WR)/ WR)/
 ).
Model predictions are shown for instantaneous bursts with "standard'' IMFs
at Z=0.008 (dashed line), ).
Model predictions are shown for instantaneous bursts with "standard'' IMFs
at Z=0.008 (dashed line),
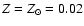 (solid line), and Z=0.04 (long dashed line).
Note the overprediction of the WR bump strength in high metallicity models compared
with the observations.
(solid line), and Z=0.04 (long dashed line).
Note the overprediction of the WR bump strength in high metallicity models compared
with the observations. |
The basic model parameters we consider are:
- a)
- Metallicity. Stellar tracks covering metallicities
Z= 0.008, 0.02 (solar), and 0.04.
- b)
- IMF slope and upper mass cut-off (
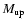 ). We adopt a Salpeter IMF
(slope
). We adopt a Salpeter IMF
(slope
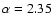 ), and
), and
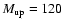
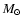 as our standard model.
as our standard model.
- c)
- Star formation history (SFH). Models for instantaneous bursts
(coeval population), extended burst durations (constant SF during period
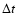 ;
in this case age = 0 is defined at the onset of SF, i.e. corresponds to that of
the oldest stars present),
and constant SF are considered.
;
in this case age = 0 is defined at the onset of SF, i.e. corresponds to that of
the oldest stars present),
and constant SF are considered.
- d)
- Fraction of ionizing Lyman continuum photons (
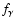 ).
).
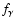 indicates the fraction of ionizing photons absorbed by the gas.
Our standard value is
indicates the fraction of ionizing photons absorbed by the gas.
Our standard value is
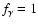 .
Values
.
Values
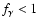 are used to simulate various effects (e.g. dust absorption, photon
leakage outside regions, etc.) leading to a reduction of photons available for
photoionization.
are used to simulate various effects (e.g. dust absorption, photon
leakage outside regions, etc.) leading to a reduction of photons available for
photoionization.
Unless stated otherwise our models are calculated assuming an IMF fully
sampled over the entire mass range (as in SV98).
For some cases we have also done model calculations
based on a Monte Carlo sampling of the IMF, in order to quantify the effects
of statistical fluctuations due to the finite number of massive stars.
We have verified our calculations by comparison with the Monte Carlo models and
analytical results of Cerviño et al. (2000, 2002).
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{plot_mup_effects.eps}\hspace*{4mm}
\includegraphics[width=8.6cm,clip]{plot_alpha_effects.eps}\end{figure}](/articles/aa/full/2002/41/aa2816/Timg94.gif) |
Figure 9:
Observed and predicted WR bump equivalent width as a function of
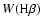 .
Standard model predictions are shown for instantaneous bursts at .
Standard model predictions are shown for instantaneous bursts at
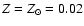 (solid line), and Z=0.04 (long dashed line).
Left panel:
Thick (green) lines with the same styles show models with a standard IMF slope
(
(solid line), and Z=0.04 (long dashed line).
Left panel:
Thick (green) lines with the same styles show models with a standard IMF slope
(
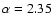 )
and upper mass cut-offs of )
and upper mass cut-offs of
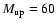 and 30
and 30 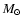 delimiting the singly and doubly shaded regions respectively.
Right panel:
Thick (green) lines with the same styles show models with a IMF slope
of
delimiting the singly and doubly shaded regions respectively.
Right panel:
Thick (green) lines with the same styles show models with a IMF slope
of
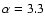 and
and
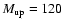 . . |
5.2 Results
A comparison of the observed equivalent widths and relative intensity of the
WR bump with standard model predictions at different metallicities is presented
in Fig. 8. The following points can be seen from this
figure:
The following possibilities (one or a combination thereof) could be invoked to
explain the discrepancy between our observations and models:
- 1.
- The metallicities of our HII regions are overestimated.
Indeed the observations could be reconciled with burst models with a
"standard'' IMF for metallicities
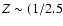 -1)
-1) 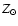 ,
as shown in the left
panel of Fig. 8 (short dashed line).
However, despite the uncertainties in the O/H determinations (cf. Sect. 3) such low average metallicities seem very implausible.
,
as shown in the left
panel of Fig. 8 (short dashed line).
However, despite the uncertainties in the O/H determinations (cf. Sect. 3) such low average metallicities seem very implausible.
- 2.
- Extended bursts. Such a scenario has been invoked by SGIT00 for the
sample of metal-rich starbursts based on the finding of red supergiant features
in their spectra and the fact that these distant objects are mostly nuclear starbursts
observed through apertures corresponding to relatively large spatial scales.
In this case all observed properties could quite well be fitted with "standard''
solar metallicity models for burst durations
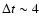 -10 Myr.
However, in view of the different nature (disk H II regions) of the present sample,
indications of relatively short formation time scales of H II regions
(e.g. Massey et al. 1995),
and the lack of direct signatures of older/red supergiant populations (cf. below)
it seems quite unjustified to appeal to extended burst to solve the observed discrepancy.
-10 Myr.
However, in view of the different nature (disk H II regions) of the present sample,
indications of relatively short formation time scales of H II regions
(e.g. Massey et al. 1995),
and the lack of direct signatures of older/red supergiant populations (cf. below)
it seems quite unjustified to appeal to extended burst to solve the observed discrepancy.
- 3.
- A modified IMF (upper mass cut-off and/or slope).
In a plot like Fig. 8, a Salpeter IMF with a lower upper mass
cut-off simply implies that the curve plotted here (for
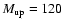
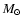 )
is joined
at lower
)
is joined
at lower
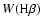 as the WR stars from the most massive stars are absent.
This is illustrated for the cases of
as the WR stars from the most massive stars are absent.
This is illustrated for the cases of
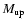 = 30 and 60
= 30 and 60 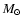 by the shaded domains
in Fig. 9.
The shape of the predicted WR equivalent width or line intensity remains, however,
unchanged. Therefore the observed discrepancy cannot be resolved with an
IMF of Salpeter slope and a lower value of
by the shaded domains
in Fig. 9.
The shape of the predicted WR equivalent width or line intensity remains, however,
unchanged. Therefore the observed discrepancy cannot be resolved with an
IMF of Salpeter slope and a lower value of
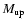 (see also Sect. 6).
(see also Sect. 6).
Models with steeper, variable IMF slopes (
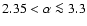 )
and
)
and
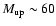 -120
-120 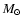 could reproduce most of the objects, with the exception
of the lowest
could reproduce most of the objects, with the exception
of the lowest
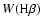 objects (see Fig. 9).
As the least metal-poor objects in our sample are probably of similar nature
as young clusters or H II regions in our Galaxy whose stellar content has
been studied in detail, we may presume that their IMF (slope and
objects (see Fig. 9).
As the least metal-poor objects in our sample are probably of similar nature
as young clusters or H II regions in our Galaxy whose stellar content has
been studied in detail, we may presume that their IMF (slope and
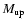 )
should
be similar.
Since none of the Galactic regions have shown convincing evidence of a
strong deviation of the IMF slope from the Salpeter value (see Massey 1998
and references therein),
we think that such a steeper slope is an unlikely explanation.
)
should
be similar.
Since none of the Galactic regions have shown convincing evidence of a
strong deviation of the IMF slope from the Salpeter value (see Massey 1998
and references therein),
we think that such a steeper slope is an unlikely explanation.
- 4.
- Incorrect stellar evolution models and/or "calibration data''
Although the adopted tracks (Meynet et al. 1994) compare fairly well with
various observations, several failures of the non-rotating stellar models are also
known (see e.g. Maeder 1999).
However, the used tracks have essentially been calibrated/adjusted to fit the
observed WR/O ratio in various regions of our Galaxy and Local Group objects
which are though to be at equilibrium, i.e. showing relative populations
corresponding to constant star formation (see compilation in Maeder & Meynet 1994).
The relative WR/O star ratio is the one most directly related to our (time resolved)
observables.
As this calibration yields a fairly good agreement over a large metallicity
range (
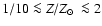 )
there seems little room for changes in the tracks which could reduce the predicted
WR bump by the required factor of
)
there seems little room for changes in the tracks which could reduce the predicted
WR bump by the required factor of 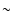 2 without violating the WR/O constraints
in the Local Group.
2 without violating the WR/O constraints
in the Local Group.
One could argue that the calibration data, the observed WR/O number ratio
at solar metallicity and above could be incorrect due to possible
incompleteness or biases in the stellar counts (see e.g. related discussions
in Massey & Johnson 1998).
However, to reconcile our WR observations in H II regions with the corresponding
counts for our Galaxy and M31 would require a downward revision of the
relative WR/O ratio by up to a factor of 2, which seems highly unlikely.
- 5.
- Uncertainties in synthesis of the WR bump.
Presently the calculation of observables related to WR stars is simply done in
the following way in evolutionary synthesis models.
The different emission line strengths are computed by multiplying the predicted
number of WR stars (grouped in different types and/or subtypes) with their
average line luminosity as derived from observations of a sample of WR stars
(see SV98).
Interestingly the intrinsic line luminosity of the strongest line of the WR bump,
He II
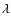 4686, shows a rather large scatter, namely
4686, shows a rather large scatter, namely
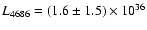 erg s-1 in the Galactic and LMC
WNL calibration sample of SV98 with a possible increase of
erg s-1 in the Galactic and LMC
WNL calibration sample of SV98 with a possible increase of
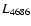 with
the stellar bolometric luminosity L (see Fig. 1 of SV98).
Such a luminosity dependence of
with
the stellar bolometric luminosity L (see Fig. 1 of SV98).
Such a luminosity dependence of
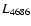 with L could in fact
(partly or fully) explain the observed discrepancy as we will now show.
with L could in fact
(partly or fully) explain the observed discrepancy as we will now show.
Splitting the WNL calibration in two domains with luminosities above/below
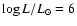 ,
SV98 found average line luminosities
,
SV98 found average line luminosities
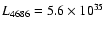 (
(
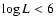 )
and
)
and
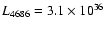 (
(
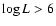 ).
Replacing in the synthesis models the overall average for WNL stars by these
quantities leads to an important reduction of
).
Replacing in the synthesis models the overall average for WNL stars by these
quantities leads to an important reduction of
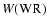 in solar metallicity bursts with
in solar metallicity bursts with
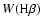
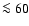 -70 Å, as shown
in Fig. 10
-70 Å, as shown
in Fig. 10![[*]](/icons/foot_motif.gif) .
At larger
.
At larger
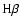 equivalent widths (corresponding to ages
equivalent widths (corresponding to ages 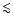 4-5 Myr for
Z=0.02) the WR bump predictions are less modified, since a)
WC stars contribute more importantly to the bump and b) only the youngest
bursts with very high
4-5 Myr for
Z=0.02) the WR bump predictions are less modified, since a)
WC stars contribute more importantly to the bump and b) only the youngest
bursts with very high
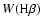 are dominated by very luminous WNL stars showing
thus larger
are dominated by very luminous WNL stars showing
thus larger
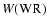 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{plot_wnl_mod.eps}\end{figure}](/articles/aa/full/2002/41/aa2816/Timg114.gif) |
Figure 10:
Observed and predicted WR bump equivalent width as a function of
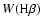 .
Standard model predictions are shown for instantaneous bursts at .
Standard model predictions are shown for instantaneous bursts at
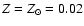 (solid line), and Z=0.04 (long dashed line).
Thick (green) lines with the same styles show the predictions with the
modified
(solid line), and Z=0.04 (long dashed line).
Thick (green) lines with the same styles show the predictions with the
modified
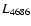 calibration for WNL stars leading to an important
reduction of the WR bump for
calibration for WNL stars leading to an important
reduction of the WR bump for
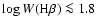 ,
due to the lower average
luminosity of WNL stars in bursts with ages ,
due to the lower average
luminosity of WNL stars in bursts with ages
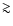 4-5 Myr (for Z= 0.02). 4-5 Myr (for Z= 0.02). |
The last option (5) seems the most likely explanation to explain the
surprisingly low WR equivalent widths and intensities in our sample of
metal-rich H II regions.
Implications on earlier studies of
WR galaxies are briefly discussed in Sect. 5.3.
In contrast, the following hypothesis or effects altering observed equivalent widths
and/or relative line intensities cannot be the cause of the discrepancy:
- Underlying (old) populations diluting the
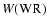 measurements.
The line intensities are unaffected by underlying populations and show the same
discrepancy as
measurements.
The line intensities are unaffected by underlying populations and show the same
discrepancy as
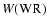 (cf. above).
Furthermore, inspection of our spectra show little or no indication of
signatures of older stellar populations.
(cf. above).
Furthermore, inspection of our spectra show little or no indication of
signatures of older stellar populations.
- Differential extinction between gas and stars as frequently observed
in H II galaxies and starbursts (cf. Fanelli et al. 1988; Calzetti 1997;
Mas-Hesse & Kunth 1999, SGIT00). If present such an effect alters
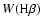 and
and
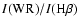 but not
but not
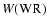 .
To bring the observations to agreement with standard models
would require that the gas suffered a lower extinction than the stars
(implying thus lower corrected
.
To bring the observations to agreement with standard models
would require that the gas suffered a lower extinction than the stars
(implying thus lower corrected
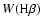 and larger
and larger
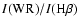 ), opposite to what is
found empirically.
), opposite to what is
found empirically.
- Leakage of ionising photons outside the observed regions, dust absorption
of ionising photons, or other mechanisms reducing the fraction
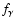 of Lyman continuum photons used for photoionisation. Correcting the observations
for such an effect would increase the observed
of Lyman continuum photons used for photoionisation. Correcting the observations
for such an effect would increase the observed
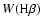 and decrease
and decrease
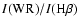 ,
which does not reconcile observations and theory (see Fig. 8).
,
which does not reconcile observations and theory (see Fig. 8).
- Effects due to varying seeing conditions and limited slit widths could
lead to a loss of nebular emission in the aperture or a fraction of the stellar
light. The former was just discussed ("leakage''). If the WR distribution were
systematically more extended than the other stars responsible of the continuum,
this effect could lead to reduced WR bump equivalent widths.
No such trend between
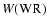 and the seeing conditions is found.
and the seeing conditions is found.
- Stochastical fluctuations of the IMF due to small number statistics
of the massive stars, as invoked by Bresolin & Kennicutt (2002).
Although indeed expected to introduce some scatter (see Cerviño et al. 2000, 2002)
this effect cannot explain the discrepancy for several reasons.
First, the sample discussed here is sufficiently large and shows clear
observational trends with relatively small scatter.
In addition, no systematic trend of
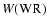 (and
(and
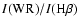 )
with absolute
scale, such as measured by the continuum luminosity or
)
with absolute
scale, such as measured by the continuum luminosity or
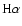 luminosity,
is observed in our sample as shown in Fig. 11.
Second, Monte Carlo simulations we have undertaken for cluster sizes
corresponding roughly to
the observed average continuum luminosity of
luminosity,
is observed in our sample as shown in Fig. 11.
Second, Monte Carlo simulations we have undertaken for cluster sizes
corresponding roughly to
the observed average continuum luminosity of
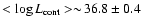
![[*]](/icons/foot_motif.gif) predict a typical relative scatter
of
predict a typical relative scatter
of
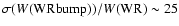 % (cf. Cerviño et al. 2002)
- too small to account for the discrepancy - and no significant bias towards
lower values as illustrated in Fig. 12.
% (cf. Cerviño et al. 2002)
- too small to account for the discrepancy - and no significant bias towards
lower values as illustrated in Fig. 12.
- The use of different stellar tracks, such as e.g. the Geneva tracks with
standard mass loss tracks adopted by Bresolin & Kennicutt (2002) for the
Monte Carlo models, which do not reproduce basic constraints of massive stars
and stellar populations in Local Group objects
cannot be a solution as they would lead to important inconsistencies (cf.
discussion in Sect. 5.1).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{plot_abs_scales.eps}\end{figure}](/articles/aa/full/2002/41/aa2816/Timg120.gif) |
Figure 11:
Equivalent widths of the WR bump as a function of the monochromatic continuum
luminosity at
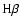 in erg s-1 Å-1 (top panel), and as a function of the
in erg s-1 Å-1 (top panel), and as a function of the
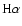 luminosity for the WR regions of our sample.
The mean and dispersion (1
luminosity for the WR regions of our sample.
The mean and dispersion (1 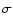 )
of )
of
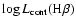 is plotted in the
top panel.
is plotted in the
top panel. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{mc_wrbump.eps}\end{figure}](/articles/aa/full/2002/41/aa2816/Timg122.gif) |
Figure 12:
Same as Figs. 8 (left) and 10
showing the comparison between model predictions using a fully sampled, analytical
IMF (dotted line, black) and the predicted mean
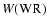 and
and 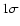 scatter
(solid line, blue) for a burst of scale/mass corresponding to the average observed
continuum luminosity. Observations are shown using the same symbols and in the previous
figures. Note, the deviation of the mean values for
scatter
(solid line, blue) for a burst of scale/mass corresponding to the average observed
continuum luminosity. Observations are shown using the same symbols and in the previous
figures. Note, the deviation of the mean values for
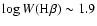 -2.2
is due to a numerical artifact.
The comparison shows that no significant bias is expected and that the
scatter is too small to resolve the discrepancy with observations. -2.2
is due to a numerical artifact.
The comparison shows that no significant bias is expected and that the
scatter is too small to resolve the discrepancy with observations. |
5.3 Discussion
In Sect. 5.2 we have argued that, compared to the normal
prescription used in our SV98 synthesis models, a different prescription
should preferrably be adopted to predict more accurately the He II 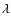 4686
emission from WN stars.
As several earlier studies including ours (e.g. Schaerer 1996, 1999;
Schaerer et al. 1999a; Guseva et al. 2000, SGIT00) are based on the
use of the simple average He II
4686
emission from WN stars.
As several earlier studies including ours (e.g. Schaerer 1996, 1999;
Schaerer et al. 1999a; Guseva et al. 2000, SGIT00) are based on the
use of the simple average He II 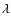 4686 line luminosity of SV98 for WNL stars,
it is important to assess if or to what extent the use of a luminosity dependent
prescription would affect the results from previous studies.
4686 line luminosity of SV98 for WNL stars,
it is important to assess if or to what extent the use of a luminosity dependent
prescription would affect the results from previous studies.
To verify this we have recomputed several sets of models for sub-solar metallicities.
The maxima of the WR bump intensity and
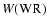 (cf. Fig. 6)
are only slightly modified (increased at
(cf. Fig. 6)
are only slightly modified (increased at
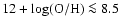 ,
and decreased above)
and lead to a somewhat smaller increase with O/H, improving the agreement
with the observations.
For metallicities
,
and decreased above)
and lead to a somewhat smaller increase with O/H, improving the agreement
with the observations.
For metallicities 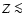 1/2
1/2 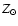 the predicted WR bump is found to be
larger at all ages (as the bulk of WN stars are of high luminosity),
whereas for higher metallicities both larger/smaller WR bump strengths
are predicted depending on the burst age (
the predicted WR bump is found to be
larger at all ages (as the bulk of WN stars are of high luminosity),
whereas for higher metallicities both larger/smaller WR bump strengths
are predicted depending on the burst age (
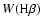 ), as for the cases shown
in Fig. 10.
These changes improve the comparison with observations at low Z (see e.g. Fig. 7 of Guseva et al. 2000). No clear statement can be made for intermediate
metallicities.
A better understanding of the dependence of the WR emission lines on the stellar
parameters appears necessary to improve the accuracy of the predictions
of WR features in evolutionary synthesis models.
The impact of newly available stellar evolution models including the effects
of rotation on interior mixing and mass loss on massive star populations
remains also to be explored.
), as for the cases shown
in Fig. 10.
These changes improve the comparison with observations at low Z (see e.g. Fig. 7 of Guseva et al. 2000). No clear statement can be made for intermediate
metallicities.
A better understanding of the dependence of the WR emission lines on the stellar
parameters appears necessary to improve the accuracy of the predictions
of WR features in evolutionary synthesis models.
The impact of newly available stellar evolution models including the effects
of rotation on interior mixing and mass loss on massive star populations
remains also to be explored.


Up: VLT observations of metal-rich
Copyright ESO 2002
![]() intensities
(cf. Schaerer et al. 1999a).
intensities
(cf. Schaerer et al. 1999a).
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{plot_std_wrbump.eps}\hspace*{4mm}
\includegraphics[width=8.6cm,clip]{plot_lihb_wr.eps}\end{figure}](/articles/aa/full/2002/41/aa2816/Timg89.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{plot_mup_effects.eps}\hspace*{4mm}
\includegraphics[width=8.6cm,clip]{plot_alpha_effects.eps}\end{figure}](/articles/aa/full/2002/41/aa2816/Timg94.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{plot_wnl_mod.eps}\end{figure}](/articles/aa/full/2002/41/aa2816/Timg114.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{plot_abs_scales.eps}\end{figure}](/articles/aa/full/2002/41/aa2816/Timg120.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{mc_wrbump.eps}\end{figure}](/articles/aa/full/2002/41/aa2816/Timg122.gif)