We show in Fig. 1 the MOS1+MOS2 image of the cluster, produced simply by adding the data from each camera without accounting for vignetting. The image is striking: the cluster displays an unmistakably elliptical shape, with a clear brightness enhancement directly to the south, and there are a large number of sources in the field of view.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{MS2734f1.eps}
\end{figure}](/articles/aa/full/2002/41/aa2734/Timg34.gif) |
Figure 1: The MOS1 + MOS2 counts image of the whole field of view of the A1413 observation. Note the large number of sources and in particular, what appears to the an extended source to the south of the cluster itself. |
Motivated by the apparent excess of counts to the south of the cluster
(see Fig. 1) we fitted the MOS1 +MOS2 image with a 2D ![]() -model in order to quantify the significance of this feature.
In fitting the image, we followed closely the procedure described in
Neumann & Böhringer (1997). Images were extracted in
the (0.3-1.4) keV band from the weighted MOS event files in pixels of
size 3
-model in order to quantify the significance of this feature.
In fitting the image, we followed closely the procedure described in
Neumann & Böhringer (1997). Images were extracted in
the (0.3-1.4) keV band from the weighted MOS event files in pixels of
size 3
![]() 4 and added to make a combined MOS image. Since in the
case of weighted events Poissonian errors do not apply, errors were
correctly calculated from the weights using
4 and added to make a combined MOS image. Since in the
case of weighted events Poissonian errors do not apply, errors were
correctly calculated from the weights using
![]() (see Arnaud et al. 2001b). An error image was
generated for each instrument, and these images were added
quadratically. The fitting procedure described below was tested and
optimised on simulated data before application to the real data.
(see Arnaud et al. 2001b). An error image was
generated for each instrument, and these images were added
quadratically. The fitting procedure described below was tested and
optimised on simulated data before application to the real data.
The ![]() test used in the fitting procedure assumes Gaussian
statistics, for which the mean is the most likely value. The
statistics are actually not Gaussian in the external regions of the
field of view, dominated by the background. In these regions the
number of photons per pixel is low and follows a Poisson distribution
for which the mean is larger than the most likely value. If the image
is not smoothed before fitting, there is thus a tendency to
underestimate the mean background level, leading to erroneous values
for the fitted cluster parameters.
The combined MOS image was thus smoothed with a
Gaussian of with
test used in the fitting procedure assumes Gaussian
statistics, for which the mean is the most likely value. The
statistics are actually not Gaussian in the external regions of the
field of view, dominated by the background. In these regions the
number of photons per pixel is low and follows a Poisson distribution
for which the mean is larger than the most likely value. If the image
is not smoothed before fitting, there is thus a tendency to
underestimate the mean background level, leading to erroneous values
for the fitted cluster parameters.
The combined MOS image was thus smoothed with a
Gaussian of with
![]() before fitting. The error image
was treated according to the error propagation function for Gaussian
filtered images described in Neumann & Böhringer
(1997). We fix all error pixels with a value of 0 to have
a value of 1 before fitting, meaning that we can use
before fitting. The error image
was treated according to the error propagation function for Gaussian
filtered images described in Neumann & Böhringer
(1997). We fix all error pixels with a value of 0 to have
a value of 1 before fitting, meaning that we can use ![]() fitting
but are unable to determine confidence parameters on the fit. The
data were then fitted with a 2D
fitting
but are unable to determine confidence parameters on the fit. The
data were then fitted with a 2D ![]() -model of the form:
-model of the form:
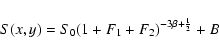 |
(1) |
![\begin{displaymath}F_1 = \frac{[ \cos{\alpha} (x - x_0) + \sin{\alpha} (y-y_0)]^2}{a_1^2}
\end{displaymath}](/articles/aa/full/2002/41/aa2734/img40.gif)
![\begin{displaymath}F_2 = \frac{[-\sin{\alpha} (x - x_0) + \cos{\alpha}
(y-y_0)]^2}{a_2^2}\cdot
\end{displaymath}](/articles/aa/full/2002/41/aa2734/img41.gif)
We fit the image between
![]() (see below) and
(see below) and
![]() from the
cluster center, excluding obvious point sources. The results of the
2D fit are shown in Table 1. Note that the fitted
parameters are slightly dependent on the outer radius and the
from the
cluster center, excluding obvious point sources. The results of the
2D fit are shown in Table 1. Note that the fitted
parameters are slightly dependent on the outer radius and the ![]() of the Gauss filter, but the results are always in good agreement with
the 1D fit, described below.
of the Gauss filter, but the results are always in good agreement with
the 1D fit, described below.
| Parameter | |
|
|
0.72 |
| 284.6 kpc | |
| 201.2 kpc | |
| PA | 2 |
| Centre |
11 |
| Centre Dec | 23 |
We extracted the spectrum from a circular region of radius ![]()
![]() centred on the excess. This spectrum unfortunately does not
contain sufficiently strong line emission for a redshift estimate, so
we fitted using a MEKAL model with the same redshift as A1413,
absorbed with the galactic column density toward the cluster
(
centred on the excess. This spectrum unfortunately does not
contain sufficiently strong line emission for a redshift estimate, so
we fitted using a MEKAL model with the same redshift as A1413,
absorbed with the galactic column density toward the cluster
(
![]() cm-2 from Dickey & Lockman
1990). We find
cm-2 from Dickey & Lockman
1990). We find
![]() .
An overlay of the significance
contours on the DSS plate of the image did not reveal any obvious
sources associated with the excess, and a hardness ratio map did not
reveal any interaction with the main cluster. Our tentative
conclusion is that the source is either a foreground or background
cluster: deeper optical observations of the region should resolve the
issue.
.
An overlay of the significance
contours on the DSS plate of the image did not reveal any obvious
sources associated with the excess, and a hardness ratio map did not
reveal any interaction with the main cluster. Our tentative
conclusion is that the source is either a foreground or background
cluster: deeper optical observations of the region should resolve the
issue.
Copyright ESO 2002