A&A 394, 617-624 (2002)
DOI: 10.1051/0004-6361:20021162
B. F. Yudin1,2,3 - J. D. Fernie4 - N. R. Ikhsanov2,5 - V. I. Shenavrin1 - G. Weigelt2
1 - Sternberg Astronomical Institute, Universitetskii
prospect 13, 119899 Moscow, Russia
2 -
Max-Planck-Institut für Radioastronomie, Auf dem
Hügel 69, 53121 Bonn, Germany
3 -
Isaac Newton Institute of Chile, Moscow Branch, Russia
4 -
David Dunlap Observatory, University of Toronto,
Box 360, Richmond Hill, Ontario L4C 4Y6, Canada
5 -
Central Astronomical Observatory RAS at Pulkovo,
Pulkovo 65/1, 196140 St. Petersburg, Russia
Received 26 April 2002 / Accepted 7 August 2002
Abstract
We present the results of UBVJHKLM photometry of R CrB
spanning the period from 1976 to 2001. Studies of the optical
light curve have shown no evidence of any stable harmonics in the
variations of the stellar emission. In the L band we found
semi-regular oscillations with the two main periods of ![]() 3.3 yr and
3.3 yr and ![]() 11.9 yr and the full amplitude of
11.9 yr and the full amplitude of ![]()
![]() and
and ![]()
![]() ,
respectively. The colors of the warm dust
shell (resolved by Ohnaka et al. 2001) are found to be
remarkably stable in contrast to its brightness. This indicates
that the inner radius is a constant, time-independent
characteristic of the dust shell. The observed behavior of the IR light curve is mainly caused by the variation of the optical
thickness of the dust shell within the interval
,
respectively. The colors of the warm dust
shell (resolved by Ohnaka et al. 2001) are found to be
remarkably stable in contrast to its brightness. This indicates
that the inner radius is a constant, time-independent
characteristic of the dust shell. The observed behavior of the IR light curve is mainly caused by the variation of the optical
thickness of the dust shell within the interval
![]() -0.4. Anticorrelated changes of the optical brightness (in particular with
-0.4. Anticorrelated changes of the optical brightness (in particular with
![]() yr) have not been found. Their
absence suggests that the stellar wind of R CrB deviates from
spherical symmetry. The light curves suggest that the stellar wind
is variable. The variability of the stellar wind and the creation
of dust clouds may be caused by some kind of activity on the
stellar surface. With some time lag, periods of increased
mass-loss cause an increase in the dust formation rate at the
inner boundary of the extended dust shell and an increase in its
IR brightness. We have derived the following parameters of the
dust shell (at mean brightness) by radiative transfer modeling:
inner dust shell radius
yr) have not been found. Their
absence suggests that the stellar wind of R CrB deviates from
spherical symmetry. The light curves suggest that the stellar wind
is variable. The variability of the stellar wind and the creation
of dust clouds may be caused by some kind of activity on the
stellar surface. With some time lag, periods of increased
mass-loss cause an increase in the dust formation rate at the
inner boundary of the extended dust shell and an increase in its
IR brightness. We have derived the following parameters of the
dust shell (at mean brightness) by radiative transfer modeling:
inner dust shell radius
![]() ,
temperature
,
temperature
![]() K, dust density
K, dust density
![]() ,
optical depth
,
optical depth
![]() at 0.55
at 0.55 ![]() m, mean dust
formation rate
m, mean dust
formation rate
![]() ,
mass-loss rate
,
mass-loss rate
![]() ,
size of
the amorphous carbon grains
,
size of
the amorphous carbon grains ![]()
![]() m, and
m, and
![]() .
.
Key words: stars: carbon - stars: circumstellar matter - stars: individual: R CrB - infrared: stars
R Coronae Borealis is the prototype of a small group of yellow supergiants (about 35 known members in our Galaxy) characterized by sudden declines in their optical brightness and extremely hydrogen-deficient, carbon-rich atmospheres. The visual light curve of R CrB contains quasi-regular low-amplitude variations without any dominating periods. These are commonly interpreted in terms of stellar pulsations and episodic deep declines, which typically last a few months and have amplitudes of up to 8 mag. Such events are thought to be the result of obscuration by dust clouds generated spasmodically and blown away from the star by radiation pressure (Clayton 1996 and references therein).
The near-infrared excess, discovered by Stein et al. (1969),
is assigned to a warm dust shell (blackbody temperature of ![]() 900 K). This extended dust shell was resolved for the first time
by speckle interferometric observations with the SAO 6 m telescope
(Ohnaka et al. 2001). The IR excess contributes about 30%
of the total flux and is permanently present, regardless of the
visual brightness of the object. The L flux of , which is
mainly due to dust emission, varies semi-regularly with a period
of 1260 days (Feast et al. 1997 and references therein).
The analysis of IRAS observations at 60
900 K). This extended dust shell was resolved for the first time
by speckle interferometric observations with the SAO 6 m telescope
(Ohnaka et al. 2001). The IR excess contributes about 30%
of the total flux and is permanently present, regardless of the
visual brightness of the object. The L flux of , which is
mainly due to dust emission, varies semi-regularly with a period
of 1260 days (Feast et al. 1997 and references therein).
The analysis of IRAS observations at 60 ![]() m and 100
m and 100 ![]() m
(Gillett et al. 1986) led to the discovery of a very extended
"fossil'' shell around , whose diameter and temperature are
m
(Gillett et al. 1986) led to the discovery of a very extended
"fossil'' shell around , whose diameter and temperature are
![]()
![]() and 30 K, respectively.
and 30 K, respectively.
In this paper we focus on the investigation of the time-dependent characteristics of the extended warm dust shell and their interpretation. In the next section we present the results of our photometric observations of R CrB (UBV in 1994-1999 and JHKLMin 1983-2001) and the complete tables of photometric observations of the star in 1976-2001. The basic characteristics of the optical and IR radiation of the star during its bright state are analyzed in Sect. 3. Radiative transfer modeling of the warm dust shell at its average brightness is described in Sect. 4. The variations of the dust shell brightness and colors, and, correspondingly, its structural parameters, are investigated in Sect. 5. Our results are discussed in Sect. 6.
Our UBV observations of R CrB were carried out in the period
1994-1999 with the 0.25 m telescope of the Fairborn observatory
(Genet et al. 1987). The results of these observations
together with those of earlier observations (1985-1993) by Fernie
& Seager (1994) are summarized in Table 1 in
http://infra.sai.msu.ru/ftp/rcrb. This table contains 1170 measurements with the accuracy of
![]() or better. The standard
star was HD 141352: V=7.476, B-V=0.439 and
U-B=-0.003.
or better. The standard
star was HD 141352: V=7.476, B-V=0.439 and
U-B=-0.003.
JHKLM observations were carried out between 1983 and 2001 with
the 1.25 m telescope of the Crimean Station of the Sternberg
Astronomical Institute (for technical details see Nadjip et al.
1986). The results our observations, together with those
obtained in 1976-1979 (Shenavrin et al. 1979), are
summarized in Table 2 in http://infra.sai.msu.ru/ftp/rcrb. This table contains 252 measurements with the accuracy of
![]() or better. The standard
star was BS 5947: J=2.09, H=1.60, K=1.30, L=1.12 and M=1.35.
or better. The standard
star was BS 5947: J=2.09, H=1.60, K=1.30, L=1.12 and M=1.35.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{2631_f1.eps} \end{figure}](/articles/aa/full/2002/41/aa2631/Timg31.gif) |
Figure 1: VJKLM light curves of . The dots represent the observations reported in this paper. The crosses in the visual light curve denote the data of VSOLJ (http://www.kusastro.kyoto-u.ac.jp/vsnet), and in the Jand L light curves, the data reported by Feast et al. (1997). The vertical bars in the L and M panels mark the times of the minima calculated from Eqs. (14) and (15), respectively. |
| Open with DEXTER | |
The VJKLM light curves of R CrB during the period 1983-2001 are presented in Fig. 1. Also plotted are a few estimates in the V band taken from the internet page of the association of amateur astronomers VSOLJ (http://www.kusastro.kyoto-u.ac.jp/vsnet) and the measurements reported by Feast et al. (1997) in the J and L bands. As one can see in this figure, a number of deep declines of the star's visual brightness were observed in 1983-1989 and 1995-2001, while during the interval 1989-1995 the V flux was almost constant. The very different behavior of the L and M light curves will be discussed in subsequent sections.
We call the state of R CrB as bright, if
![]() and
and
![]() .
In this state the contribution of the dust to the optical
radiation of R CrB is negligible. The average UBVJHKLM and RI magnitudes of R CrB in the bright state are summarized in
Table 3. These values were derived from Tables 1 and 2,
and the data presented by Fernie (1982) and Fernie et al.
(1986). The maximum magnitudes of R CrB during the whole
observing period are
.
In this state the contribution of the dust to the optical
radiation of R CrB is negligible. The average UBVJHKLM and RI magnitudes of R CrB in the bright state are summarized in
Table 3. These values were derived from Tables 1 and 2,
and the data presented by Fernie (1982) and Fernie et al.
(1986). The maximum magnitudes of R CrB during the whole
observing period are
![]() and
and
![]() .
.
| Bands | <m> |
|
|
| U | 6.55 | 6.38 | 6.82 |
| B | 6.49 | 6.35 | 6.70 |
| V | 5.91 | 5.81 | 6.08 |
| R | 5.49 | 5.40 | 5.62 |
| I | 5.31 | 5.23 | 5.40 |
| J | 5.08 | 5.01 | 5.11 |
| H | 4.91 | 4.76 | 5.08 |
| K | 4.13 | 3.74 | 4.56 |
| L | 2.38 | 1.79 | 3.12 |
| M | 1.70 | 0.97 | 2.48 |
The Fourier analysis of the visual light curve (1985-1999) during
the bright state has revealed a number of harmonics with the full
amplitude of ![]()
![]() concentrated in the interval of
30-60 days. The maximum amplitude of
concentrated in the interval of
30-60 days. The maximum amplitude of
![]() has the mode with
the period
has the mode with
the period
![]() days (see Fig. 2). The
corresponding harmonic with the full amplitude of
days (see Fig. 2). The
corresponding harmonic with the full amplitude of ![]()
![]() was also found from the analysis of the B-V curve. The
brightness maxima follow the color minima with a lag of 3 days,
and the ratio of the amplitudes of (B-V) and V harmonics is
about 0.3. No trend has been found in the optical brightness. It
should be noted that on a time-scale of several hundreds of days
R CrB can occasionally exhibit well-developed pulsations with
periods of 35, 44 and 51 days (Fernie & Seager 1994
and references therein).
was also found from the analysis of the B-V curve. The
brightness maxima follow the color minima with a lag of 3 days,
and the ratio of the amplitudes of (B-V) and V harmonics is
about 0.3. No trend has been found in the optical brightness. It
should be noted that on a time-scale of several hundreds of days
R CrB can occasionally exhibit well-developed pulsations with
periods of 35, 44 and 51 days (Fernie & Seager 1994
and references therein).
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2631_f2.eps} \end{figure}](/articles/aa/full/2002/41/aa2631/Timg40.gif) |
Figure 2: The V and L light curves of R CrB folded with the periods 39.82, 1206 and 4342 days, from bottom to top. |
| Open with DEXTER | |
The low-amplitude quasi-regular variability in the J band
resembles that in the optical region. A period search has revealed
three main harmonics with periods of 43.7, 33.2, and 28.1 days
and an amplitude of about
![]() .
At the same time Rao et al.
(1999) have found that the radial velocity curve exhibits
the only one stable pulsation period of about 42.7 days.
.
At the same time Rao et al.
(1999) have found that the radial velocity curve exhibits
the only one stable pulsation period of about 42.7 days.
The spectral energy distribution (SED) of R CrB relating to its average brightness in bright state (see Table 3) is shown in Fig. 3.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2631_f3.eps} \end{figure}](/articles/aa/full/2002/41/aa2631/Timg42.gif) |
Figure 3: SED of R CrB for average brightness in bright state (circles). Long- and short-dashed lines denote the SED of the star and the dust shell, respectively. The solid line is the fitted SED (see text). |
| Open with DEXTER | |
The stellar magnitudes were corrected for the interstellar
reddening according to the color excess
E(B-V) = 0.05 (Asplund
et al. 1997). The flux at 0.23 and 0.25 ![]() m was measured
with IUE on 31.05.1991 (see INES data from the IUE satellite),
when the star brightness in the visual and near IR was close to its average values in bright state presented in Table 3.
m was measured
with IUE on 31.05.1991 (see INES data from the IUE satellite),
when the star brightness in the visual and near IR was close to its average values in bright state presented in Table 3.
To reconstruct the SED beyond 10 ![]() m we used observation of R CrB
with IRAS on 12-13.09.1983 (Rao & Nandy 1986).
The L flux of the star on these dates was
smaller than its average value (
m we used observation of R CrB
with IRAS on 12-13.09.1983 (Rao & Nandy 1986).
The L flux of the star on these dates was
smaller than its average value (
![]() ). To account
for this difference the fluxes measured by IRAS at 12, 25, 60 and 100
). To account
for this difference the fluxes measured by IRAS at 12, 25, 60 and 100 ![]() m were increased by 8%, taking into account that
m were increased by 8%, taking into account that
![]() (Forrest et al.
1972).
(Forrest et al.
1972).
Integrating the SED presented in Fig. 3 we evaluate the
average bolometric flux of R CrB during its bright state as
![]() .
About 85% of the radiation detected from
the star is emitted within the interval
.
About 85% of the radiation detected from
the star is emitted within the interval ![]() m
m
![]() m, which is completely covered by our photometric
observations. The contributions at
m, which is completely covered by our photometric
observations. The contributions at
![]() m,
m,
![]() m and
m and
![]() m are 4%, 10% and 3%, respectively. In particular, this indicates that the possible
errors in the correction of the IRAS data cannot significantly
change the estimates of the bolometric flux.
m are 4%, 10% and 3%, respectively. In particular, this indicates that the possible
errors in the correction of the IRAS data cannot significantly
change the estimates of the bolometric flux.
The strong infrared excess (i.e. the bolometric flux of the dust shell)
can be evaluated as
![]() .
Here
.
Here
![]() is the observed bolometric flux and
is the observed bolometric flux and
![]() is the bolometric flux emitted by the central star and
passed through the dust shell.
is the bolometric flux emitted by the central star and
passed through the dust shell.
To evaluate the infrared excess we have to reconstruct the
observed SED of the star (
![]() ). The upper limit of
the contribution of the dust shell in the J band can be derived
directly from our observations in 1996. In this year a deep
decline was observed (
). The upper limit of
the contribution of the dust shell in the J band can be derived
directly from our observations in 1996. In this year a deep
decline was observed (
![]() ), while its Lbrightness was close to the average value presented in
Table 3. Attributing the observed J flux in minimum to
the dust shell we conclude that its contribution to the total flux
out of minimum is smaller than 4%. This indicates that within the
interval
), while its Lbrightness was close to the average value presented in
Table 3. Attributing the observed J flux in minimum to
the dust shell we conclude that its contribution to the total flux
out of minimum is smaller than 4%. This indicates that within the
interval
![]() m the total flux is approximately
equal to
m the total flux is approximately
equal to
![]() .
.
To evaluate
![]() in HKLM we use the intrinsic
colors of R CrB stars calculated by Asplund et al. (1997). They
depend on the effective temperature and the gravitational
acceleration on the star surface. For R CrB we take
in HKLM we use the intrinsic
colors of R CrB stars calculated by Asplund et al. (1997). They
depend on the effective temperature and the gravitational
acceleration on the star surface. For R CrB we take
![]() K,
K,
![]() ,
,
![]() ,
radius
,
radius
![]() ,
and
correspondingly the intrinsic colors
,
and
correspondingly the intrinsic colors
![]() ,
,
![]() and
and
![]() (Asplund et al.
1997; Asplund 2000). These colors were corrected
for the interstellar and circumstellar reddening although both of
these corrections have only a minor effect on the evaluation of
(Asplund et al.
1997; Asplund 2000). These colors were corrected
for the interstellar and circumstellar reddening although both of
these corrections have only a minor effect on the evaluation of
![]() .
For
.
For
![]() m we approximate
m we approximate
![]() by the blackbody spectrum with the effective
temperature 6750 K.
by the blackbody spectrum with the effective
temperature 6750 K.
The derived SED of the star is presented in Fig. 3
(long-dashed line). Integrating
![]() we find
we find
![]() and
and
![]() .
This means that about 24% of the stellar
radiation is absorbed and re-emitted by the dust shell. Assuming
the geometry of the dust shell to be spherically symmetric, one
can estimate its optical depth as
.
This means that about 24% of the stellar
radiation is absorbed and re-emitted by the dust shell. Assuming
the geometry of the dust shell to be spherically symmetric, one
can estimate its optical depth as
![]() .
For yellow stars and amorphous carbon grains the value of
the
.
For yellow stars and amorphous carbon grains the value of
the
![]() differs from the optical thickness at
0.55
differs from the optical thickness at
0.55 ![]() m (
m (![]() (V)) by a few percent.
(V)) by a few percent.
![\begin{figure}
\par\includegraphics[height=13.8cm,width=8.8cm,clip]{2631_f4.eps} \end{figure}](/articles/aa/full/2002/41/aa2631/Timg71.gif) |
Figure 4: (U-B, V), (B-V, V), (V-R, V), (V-I, V) and (V-J, V) diagrams. The solid lines denote the approximations by linear Eqs. (1)-(5). |
| Open with DEXTER | |
The derived color-brightness diagrams (U-B, V), (B-V, V),
(V-R, V), (V-I, V) and (V-J, V) are presented in
Fig. 4. These diagrams have been constructed using the
data from Tables 1 and 2 and the values reported by Fernie
(1982) and Fernie et al. (1986). For the diagram
(V-J, V) we have chosen the estimates which were obtained in all
three bands on the same date. Only the data relating to the star
brightness in the L band smaller than the average value were
used. The J flux has been reduced by 4% in order to exclude the
contribution of the dust shell. The linear approximation of the
diagrams yields
| B-V = 0.280 V - 1.08, | (2) |
| V-R = 0.301 V - 1.36, | (3) |
| V-I = 0.430 V - 1.94, | (4) |
Using the quasi-diffusion method of Leung (1976), as implemented in the CSDUST3 code (Egan et al. 1988), we have constructed radiative transfer models which match the SED of . The input parameters of the models were the same as described by Yudin et al. (2001).
As a first approximation we have assumed that the warm dust shell
is spherical and consists of amorphous carbon grains with the
radius
![]() m. The efficiencies of absorption
and scattering of the dust grains were calculated using the Mie
theory. The refractive index was taken from Jäger et al.
(1998, sample cel1000). The intrinsic SED of the star
emission,
m. The efficiencies of absorption
and scattering of the dust grains were calculated using the Mie
theory. The refractive index was taken from Jäger et al.
(1998, sample cel1000). The intrinsic SED of the star
emission,
![]() ,
was calculated as
,
was calculated as
![]() ,
where
,
where
![]() is the total optical depth at a given reference
wavelength. The reference wavelength was chosen to be
0.55
is the total optical depth at a given reference
wavelength. The reference wavelength was chosen to be
0.55 ![]() m, and the model SED is normalized to the observed one
in the V band.
m, and the model SED is normalized to the observed one
in the V band.
We have derived the following parameters of the dust shell which
refer to its mean brightness in bright state. The optical
depth at 0.55 ![]() m and 2.2
m and 2.2 ![]() m are
m are
![]() and
and
![]() ,
respectively. The inner radius of the dust
shell is
,
respectively. The inner radius of the dust
shell is
![]() .
The temperature and the
dust density at the inner radius of the dust shell are
.
The temperature and the
dust density at the inner radius of the dust shell are
![]() K and
K and
![]() ,
respectively, and the
density distribution of the dust shell is
,
respectively, and the
density distribution of the dust shell is
![]() .
.
Using these parameters we have evaluated the dust formation rate
at the inner boundary of the dust shell as
![]() .
If one
assumes that almost all carbon is bound in the dust grains and
uses the chemical composition of the atmosphere of R CrB from
Asplund et al. (2000), the gas density at the inner radius of
the dust shell is
.
If one
assumes that almost all carbon is bound in the dust grains and
uses the chemical composition of the atmosphere of R CrB from
Asplund et al. (2000), the gas density at the inner radius of
the dust shell is
![]() .
Correspondingly, with a stellar wind
velocity of
.
Correspondingly, with a stellar wind
velocity of
![]() ,
which is
typical for stars of this type, one finds a mass outflow rate in
R CrB of
,
which is
typical for stars of this type, one finds a mass outflow rate in
R CrB of
![]() .
If, however, a fraction of the carbon and
almost all of the oxygen are bound in the CO molecule, the
corresponding estimates of
.
If, however, a fraction of the carbon and
almost all of the oxygen are bound in the CO molecule, the
corresponding estimates of
![]() and
and
![]() turn out to be larger by a factor of 2.5.
turn out to be larger by a factor of 2.5.
As follows from our modeling, the visual brightness of the dust
shell is
![]() and its color indices are
and its color indices are
![]() ,
,
![]() ,
,
![]() and
and
![]() .
The SED of the dust shell is plotted in Fig. 3
(short-dashed line). The radiation of the dust shell in UBVR is
dominated by scattering. Since the radius of the grains is
significantly smaller than the wavelength, the scattering is
governed by the Rayleigh law (
.
The SED of the dust shell is plotted in Fig. 3
(short-dashed line). The radiation of the dust shell in UBVR is
dominated by scattering. Since the radius of the grains is
significantly smaller than the wavelength, the scattering is
governed by the Rayleigh law (
![]() ). This explains the blue colors of the dust shell in
this part of the spectrum. In the I band the thermal emission of
the grains begins to dominate over the scattering.
). This explains the blue colors of the dust shell in
this part of the spectrum. In the I band the thermal emission of
the grains begins to dominate over the scattering.
The visual magnitude of R CrB observed during the deepest declines
is about
![]() .
Thus, the visual magnitude of the dust shell
should be fainter than
.
Thus, the visual magnitude of the dust shell
should be fainter than
![]() .
This was the reason for choosing
a small radius of the dust grains (
.
This was the reason for choosing
a small radius of the dust grains (![]()
![]() m) in our
calculations. If one assumes that the radius of the dust grains is
larger, the visual brightness of the dust shell becomes greater
than that of the star brightness in deep minima. For instance,
increasing the radius of the dust grains by a factor of 2.5 (i.e. to 0.025
m) in our
calculations. If one assumes that the radius of the dust grains is
larger, the visual brightness of the dust shell becomes greater
than that of the star brightness in deep minima. For instance,
increasing the radius of the dust grains by a factor of 2.5 (i.e. to 0.025 ![]() m), one finds a visual magnitude of the dust shell
of
m), one finds a visual magnitude of the dust shell
of
![]() .
This reflects the fact that the albedo of
dust grains rapidly increases with their radius.
.
This reflects the fact that the albedo of
dust grains rapidly increases with their radius.
We have also found the colors of the dust shell to be sensitive to
the value of
![]() .
Variations of this parameter of only
10% lead to variations of the IR excess color indices
.
Variations of this parameter of only
10% lead to variations of the IR excess color indices
![]() and
and
![]() by
by ![]()
![]() .
At the same time
these indices are observed to be remarkably stable in contrast to
the brightness of the dust shell (see Sect. 5). In the context of
our model this means that the value of the inner radius
.
At the same time
these indices are observed to be remarkably stable in contrast to
the brightness of the dust shell (see Sect. 5). In the context of
our model this means that the value of the inner radius
![]() is a fairly constant, time-independent characteristic of the
extended warm dust shell. It should be noted, however, that the
absolute value of
is a fairly constant, time-independent characteristic of the
extended warm dust shell. It should be noted, however, that the
absolute value of
![]() depends on the optical properties
of the dust grains included in the model calculations. If we used
the extinction of amorphous carbon obtained by Colangeli et al.
(1995) (ACAR sample) instead of cel1000 (Jäger et al.
1998), the value of
depends on the optical properties
of the dust grains included in the model calculations. If we used
the extinction of amorphous carbon obtained by Colangeli et al.
(1995) (ACAR sample) instead of cel1000 (Jäger et al.
1998), the value of
![]() would be smaller by a factor of
would be smaller by a factor of ![]() 1.4.
1.4.
Finally, according to Reimers equation (Reimers 1975),
the average mass loss by a yellow supergiant can be estimated as
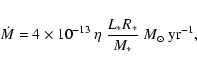 |
(6) |
The large value of
![]() ,
which does not
change significantly with time, suggests that the extended warm
dust shell of R CrB originates in a similar way as in the case of
ordinary supergiants, i.e. it is caused by the stellar wind and at
a large distance from the star. In addition to this common type of
dust shell of supergiants, the circumstellar shell of R CrB contains
dust clouds which condense somewhere in the vicinity of the star
from high density gas clumps (Feast 1997). These
additional dust clouds can explain the deep minima in the visual
light curve. If the dust clouds are considered as an additional
source of the IR emission, then the effective size of this source
is much smaller then the size of the above extended dust shell,
which condenses from the stellar wind. Until now all efforts to
pick out the emission of this consortium of the dust clouds from
the total IR excess were unsuccessful (Feast 1997).
,
which does not
change significantly with time, suggests that the extended warm
dust shell of R CrB originates in a similar way as in the case of
ordinary supergiants, i.e. it is caused by the stellar wind and at
a large distance from the star. In addition to this common type of
dust shell of supergiants, the circumstellar shell of R CrB contains
dust clouds which condense somewhere in the vicinity of the star
from high density gas clumps (Feast 1997). These
additional dust clouds can explain the deep minima in the visual
light curve. If the dust clouds are considered as an additional
source of the IR emission, then the effective size of this source
is much smaller then the size of the above extended dust shell,
which condenses from the stellar wind. Until now all efforts to
pick out the emission of this consortium of the dust clouds from
the total IR excess were unsuccessful (Feast 1997).
The UBVRIJHKLM magnitudes of R CrB during its maximum (in 1994 April-May) and minimum (in 1999 May-June) brightness in L are presented in the second and third columns of Table 3, respectively. The corresponding bolometric flux and infrared excess of , and the optical thickness of the dust shell derived using these data are presented in Table 4.
|
|
|
|
|
|
|
|
||
| Maximum |
|
|
0.39 |
| Minimum |
|
|
0.19 |
As follows from Table 4, the amplitude of variations of
the optical thickness of the dust shell in R CrB is
![]() .
At the same time, the value of the color index
.
At the same time, the value of the color index
![]() of the IR excess, estimated during maximum and
minimum brightness in the L band, proves to be the same:
of the IR excess, estimated during maximum and
minimum brightness in the L band, proves to be the same:
![]() .
This indicates that the
variations of the optical depth of the dust shell cannot be
explained by the variations of its inner radius, but reflect the
changes of the dust formation rate at a certain distance from
the star.
.
This indicates that the
variations of the optical depth of the dust shell cannot be
explained by the variations of its inner radius, but reflect the
changes of the dust formation rate at a certain distance from
the star.
Figure 5 shows the color diagrams
![]() ,
(
,
(
![]() ), and (
), and (
![]() ). The dots in these diagrams denote IR observations
of R CrB when the star was in its bright state. It was assumed that
the contribution of the dust shell to the flux in J band is
negligibly small. The stellar magnitudes in HKLM and the
infrared excess have been derived using the method described
above. The linear approximation of the diagrams gives
). The dots in these diagrams denote IR observations
of R CrB when the star was in its bright state. It was assumed that
the contribution of the dust shell to the flux in J band is
negligibly small. The stellar magnitudes in HKLM and the
infrared excess have been derived using the method described
above. The linear approximation of the diagrams gives
| (8) |
As follows from Eqs. (7)-(9), the variations of the dust
shell brightness are not accompanied by remarkable variations of its
colors. Hence, there is a proportionality between the
bolometric stellar magnitude of the dust shell,
![]() ,
and its L magnitude:
,
and its L magnitude:
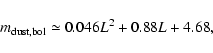 |
(11) |
![\begin{figure}
\par\includegraphics[height=13.9cm,width=8.8cm,clip]{2631_f5.eps} \end{figure}](/articles/aa/full/2002/41/aa2631/Timg124.gif) |
Figure 5:
The
|
| Open with DEXTER | |
The dust formation rate depends on the gas density at the inner
boundary of the dust shell and, therefore, on the intensity of the
mass-loss. The time lag between the increase of the stellar wind
and the increase of gas density at the inner radius of the shell
is
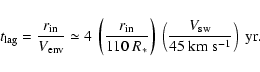 |
(13) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2631_f6.eps} \end{figure}](/articles/aa/full/2002/41/aa2631/Timg126.gif) |
Figure 6:
Optical thickness
|
| Open with DEXTER | |
In order to search for the periodicity in the variations of the
dust shell brightness, i.e. of the mass-loss rate, the L light
curve has been analyzed using the code developed by
Yu. K. Kolpakov (http://infra.sai.msu.ru/prog/kolpakov). We combined our observations with the data presented by Strecker
(1975; 35 points during 1968-1974) and Feast et al.
(1997; 24 points during 1983-1991), and removed the
points obtained during visual declines. Two harmonics of
semi-regular variations of the star brightness in the L band
were derived:
![]() days,
days,
![]() and
and
![]() days,
days,
![]() .
The
corresponding phase diagrams are presented in Fig. 2. The
dates of minima of these harmonics are given by the following
expressions:
.
The
corresponding phase diagrams are presented in Fig. 2. The
dates of minima of these harmonics are given by the following
expressions:
In the bright state of , the L variability is mainly caused by
changes of the optical depth of the shell. Hence, if the dust
shell is spherical, we would expect to find the corresponding
semi-regular variations in the visual star brightness with period
![]() days, which are anti-phased to those in the
L band. According to Eq. (14) their full amplitude would
be
days, which are anti-phased to those in the
L band. According to Eq. (14) their full amplitude would
be
![]() mag. However, a period search has not
revealed this harmonic in the V light curve. This indicates that
the density of the stellar wind (and, correspondingly, the shell
density) along the line of sight is smaller than the average one,
i.e. the dust shell is asymmetric.
mag. However, a period search has not
revealed this harmonic in the V light curve. This indicates that
the density of the stellar wind (and, correspondingly, the shell
density) along the line of sight is smaller than the average one,
i.e. the dust shell is asymmetric.
In this case the derived optical depth of the dust shell can be
considered as the sphere-averaged one. If the dust shell is
optically thin, then its bolometric flux is proportional to the
optical depth averaged over the sphere. Since the shell's SED is
primarily defined by the value of the inner radius (i.e.,
![]() )
our above results concerning the inner radius
(its size and time-independence) and mass-loss rate would be
valid.
)
our above results concerning the inner radius
(its size and time-independence) and mass-loss rate would be
valid.
We have presented optical and IR long-term monitoring and
radiative transfer modeling of . These studies have allowed the
derivation of various time-dependent properties of both (i) the
star itself at bright state and (ii) an extended dust shell
(similar to that observed around many supergiants) which condenses
from the supergiant wind at a large distance of approximately 100 stellar radii from the star. This extended dust shell is larger
than the suggested region of dust clouds (distance approx. 2-30 stellar radii, see, e.g. Clayton 1996; Fadeyev
1988), which causes the deep minima in the visual light
curve. The extended dust shell (radius ![]() mas) was first
resolved by speckle interferometric observations with the SAO 6 m
telescope (Ohnaka et al. 2001).
mas) was first
resolved by speckle interferometric observations with the SAO 6 m
telescope (Ohnaka et al. 2001).
In the V and L light curves probably a ![]() 4-year wind
travel time from the stellar surface to the extended dust shell
with a radius of approximately 110 stellar radii can be seen. The
comparison of the V and L light curves shows that the period
1994-1998 of an increased (and decreasing) L and M brightness
started approximately 4 years after the end (in 1990) of a period
with many deep minima in the visual light curve. This can be
explained if we assume that during phases of increased stellar
magnetic activity (see studies by Soker & Clayton 1999)
there is a simultaneous increase of both (i) the supergiant wind
and (ii) the rate of formation of dust clouds. If this assumption
is true, the increased stellar wind period ended in 1990. The L band brightness increased until 1994. This can be explained by the
increased stellar wind until 1990 and a wind travel time of 4 years from the stellar surface to the extended dust shell region.
In the period 1994-1999 the L band brightness was decreasing
because in this period only lower intensity stellar wind arrived,
which was produced during the low-activity period 1990-1995. We
believe that the variation of the stellar wind can be considered
as an indirect argument in favor of active phenomena on the
surface of .
4-year wind
travel time from the stellar surface to the extended dust shell
with a radius of approximately 110 stellar radii can be seen. The
comparison of the V and L light curves shows that the period
1994-1998 of an increased (and decreasing) L and M brightness
started approximately 4 years after the end (in 1990) of a period
with many deep minima in the visual light curve. This can be
explained if we assume that during phases of increased stellar
magnetic activity (see studies by Soker & Clayton 1999)
there is a simultaneous increase of both (i) the supergiant wind
and (ii) the rate of formation of dust clouds. If this assumption
is true, the increased stellar wind period ended in 1990. The L band brightness increased until 1994. This can be explained by the
increased stellar wind until 1990 and a wind travel time of 4 years from the stellar surface to the extended dust shell region.
In the period 1994-1999 the L band brightness was decreasing
because in this period only lower intensity stellar wind arrived,
which was produced during the low-activity period 1990-1995. We
believe that the variation of the stellar wind can be considered
as an indirect argument in favor of active phenomena on the
surface of .
Acknowledgements
Nazar Ikhsanov acknowledges the support of the Alexander von Humboldt Foundation within the Long-term Cooperation Program. This research was partly supported by Russian Foundation for Basic Research (project No. 02-02-16235).